Similar presentations:
Уравнение Ландау-Лифшица. Тензор магнитной проницаемости и восприимчивости
1.
2.
Уравнение Ландау-Лифшица. Тензормагнитной проницаемости и
восприимчивости.
Из каких соображений было получено уравнение
Ландау-Лифшица?
Что описывает это уравнение?
Что мы получили с помощью этого уравнения?
Зачем уравнение Ландау-Лифшица вводят
релаксационный член?
Что такое ферромагнитный резонанс?
Какова структура тензора магнитной
восприимчивости?
Как зависят от частоты действительная и мнимая
компоненты тензора магнитной восприимчивости?
Какова величина диагональной компоненты
тензора μ на оптических частотах?
3.
Продольные и поперечныемагнитооптические эффекты.
• Распространение электромагнитной волны
в среде. Уравнения Максвелла
• Показатель преломления при продольном
распространении волны
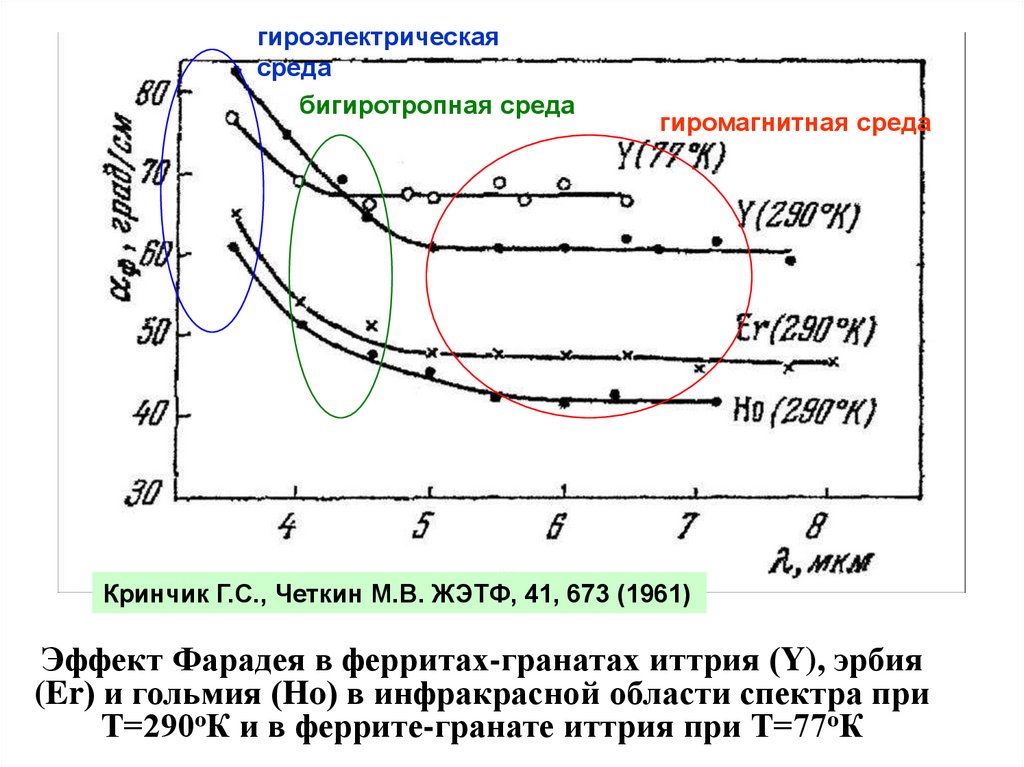
Гироэлектрическая, гиромагнитная и
бигиротропная среды
Частотно независимый эффект Фарадея
• Показатель преломления при поперечном
распространении волны
4.
Тензор магнитной проницаемостиo M o
1 4 2
2
o
i M o
4 2 2
o
0
i M o
4 2
2
o
o M o
1 4 2
2
o
0
0
0
1
o M o
4 107 1010 103
7
4 2
10
10 28
o 2
Поправка к 1 в
диагональной компоненте
M o
4 107 1014 103
3
4 2
10
10 28
o 2
Недиагональная
компонента
5.
Уравнения Максвелла1 D
rot H
c t
D E
div D 0
1 B
rot E
c t
B H
div B 0
i Q
i Q
0
0
0
0
i Q'
i Q'
o
Q и Q’ – магнитооптические параметры
0
0
0
0
o
6.
Тензор магнитной проницаемостиo M o
o 2 2
i M o
4 2 2
o
1 4
0
i M o
o 2 2
o M o
1 4 2
o 2
0
4
0
0
i Q'
i Q'
0
0
0
0
o
1
o M o
4 107 1010 103
7
4 2
10
10 28
o 2
Поправка к 1 в
диагональной компоненте
M o
4 107 1014 103
3
4 2
10
10 28
o 2
Недиагональная
компонента
7.
Электромагнитная волнаE Eo e
i ( t
x y z
c
n)
H H oe
i ( t
x y z
c
;
α, β и γ – направляющие косинусы
электромагнитной волны.
1
2
2
2
n – комплексный показатель преломления.
n)
8.
Вектор DE Eo e
i Q
D E i Q
0
0
i ( E x E y i Q )
D
i ( E x i Q E y )
t
i E z o
0
Ex
i ( t
x y z
c
E x E y i Q
0 E y E x i Q E y
o Ez
E z o
n)
9.
Вектор Bi Q '
B H i Q '
0
0
i ( H x H y i Q ' )
B
i ( H xi Q ' H y )
t
i H z o
0
Hx
H x H y i Q '
0 H y H xi Q ' H y
o H z
H z o
10.
rot Hi
rot H
x
Hx
j
y
Hy
H z H y
i
z
y
k
z
Hz
H x H z H y H x
j
k
x x
y
z
11.
Компоненты rot HH H oe
i ( t
x y z
c
n)
H z
i n
Hz
y
c
H x
i n
Hx
z
c
H y
H y
H z
i n
Hz
x
c
H x
i n
Hx
y
c
i n
Hy
z
c
i n
Hy
x
c
i n
i n
rot H i
H z
H y
c
c
i n
i n i n
i n
j
H x
H z k
H y
H x
c
c
c
c
12.
Имеем уравненияi
i
nH z nH y Ex i QE y
c
c
i
i
nH x nH z i QE x E y
c
c
i
i
nH y nH x o Ez
c
c
1 D
rot H
c t
13.
rot Ei
rot E
x
Ex
j
y
Ey
k
z
Ez
Ez E y Ex Ez E y Ex
j
i
k
z z
x x
y
y
14.
Компонентыrot E
E Eo e
i ( t
x y z
c
n)
Ez
i n
Ez
y
c
Ex
i n
Ex
z
c
E y
E y
E z
i n
Ez
x
c
Ex
i n
Ex
y
c
i n
Ey
z
c
i n
Ey
x
c
i n
i n
rot E i
Ez
E y
c
c
i n
i n i n
i n
j
Ex
Ez k
Ey
Ex
c
c
c
c
15.
Имеем уравнения1 B
rot E
c t
i
i
nEz nE y H x i Q' H y
c
c
i
i
nEx nEz i Q' H x H y
c
c
i
i
nE y nEx o H z
c
c
16.
Система уравнений для компонентвекторов E и H
nH z nH y E x i QE y
nH nH i QE E
x
z
x
y
nH y nH x o E z
nE nE H i Q ' H
z
y
x
y
nE x nE z i Q ' H x H y
nE y nE x o H z
17.
Расположим компоненты векторовE
и H по порядку
E x i QE y nH y nH z 0
i QE E nH nH 0
x
y
x
z
o E z nH x nH y 0
nE nE H i Q ' H 0
y
z
x
y
nE x nE z i Q' H x H y 0
nE x nE y o H z 0
18.
Однородная система имеетрешение, если ее определитель
равен нулю
i Q
i Q
0
0
n
n
n
0
0
0
0
n
n
n
0
n
i Q'
0
0
o
n
n
n
n
i Q'
n
0
0
0
o
0
0
19.
Пусть α,β=0, γ=1.(Продольные эффекты.)
i Q
i Q
0
0
n
0
0
0
0
n
n
n
0
n
i Q'
0
0
o
n
n
n
n
i Q'
n
0
0
0
o
n
n
0
0
20.
Пусть α,β=0, γ=1.(Продольные эффекты.)
i Q
i Q
0
0
n
0
0
n
0
0
0
0
o
0
0
0
0
n
0
i Q '
0
n
0
0
i Q'
0
0
0
0
0
0
o
По шестой строке и шестому столбцу
21.
i Qi Q
o
0
0
n
0
n
0
0
0
o
0
0
0
n
0
i Q'
n
0
0
i Q'
По третьей строке и третьему столбцу
22.
o oi Q
i Q
0
n
n
0
0
n
i Q'
n
0
i Q'
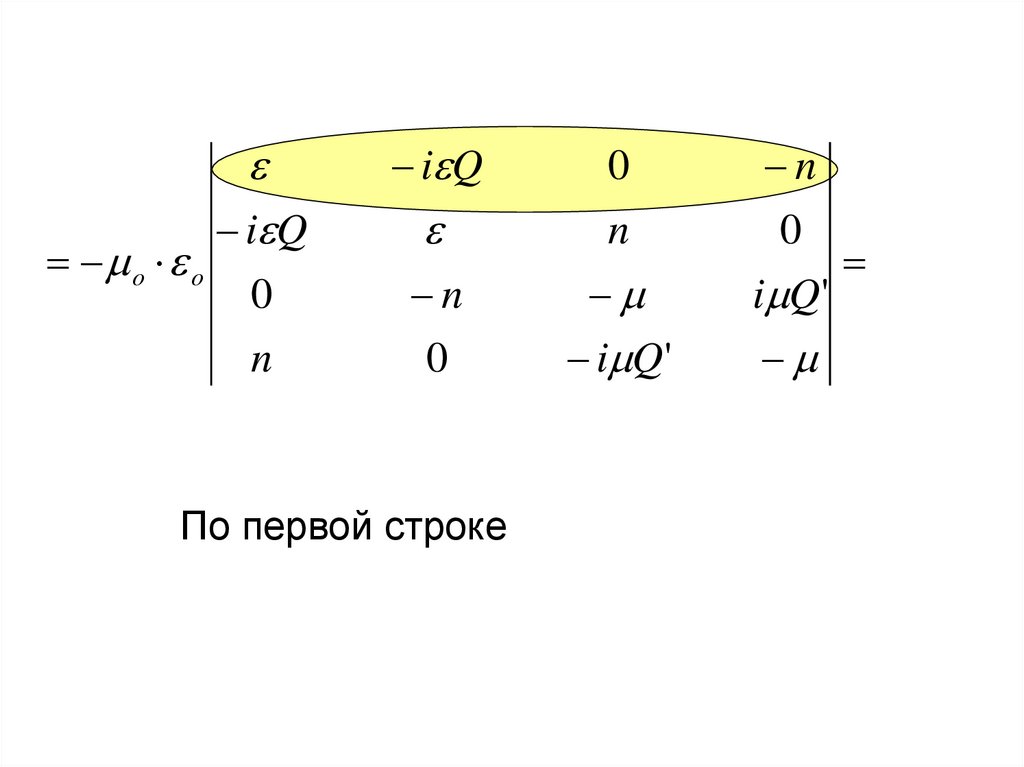
По первой строке
23.
n0
i Q
n
0
o o n
i Q' i Q 0
i Q'
0 i Q'
n i Q'
i Q
n 0
n
n o o 2 2Q'2 n 2
0 i Q'
n
i Q i 2 Q i n 2Q' i 2 QQ '2 n QQ' n n n3
o o n 4 n 2 QQ ' QQ ' 2 2 2 2Q'2
2 2Q 2 2 2Q 2Q'2 0
24.
Имеем биквадратное уравнение относительно nn 4 n 2 2 2 QQ' 2 2 1 Q'2 Q 2 Q 2Q'2 0
n 4 2n 2 1 QQ' 2 2 1 Q'2 Q 2 Q 2Q'2 0
D 4 1 QQ ' 4 2 2 1 Q'2 Q 2 Q 2Q'2
2
2
2
4 2 2 1 2QQ ' Q 2Q'2 1 Q'2 Q 2 Q 2Q'2
4 Q Q'
2
2
2
0
2 (1 QQ ' ) 2 (Q' Q) 2
n1, 2
(1 QQ ' (Q' Q))
2
2
2
n1, 2 (1 (Q' Q))
2
25.
Поворот плоскости поляризацииd d
n1 n2 d n
t d
c
c c
V1 V2
d – толщина пластинки, n – показатель преломления
n1, 2 (1 (Q' Q))
2
Учтем, что
Q' Q 1
n1, 2 (1 (Q' Q)) 1 (Q' Q)
0, 5
1 0,5(Q' Q)
1+





















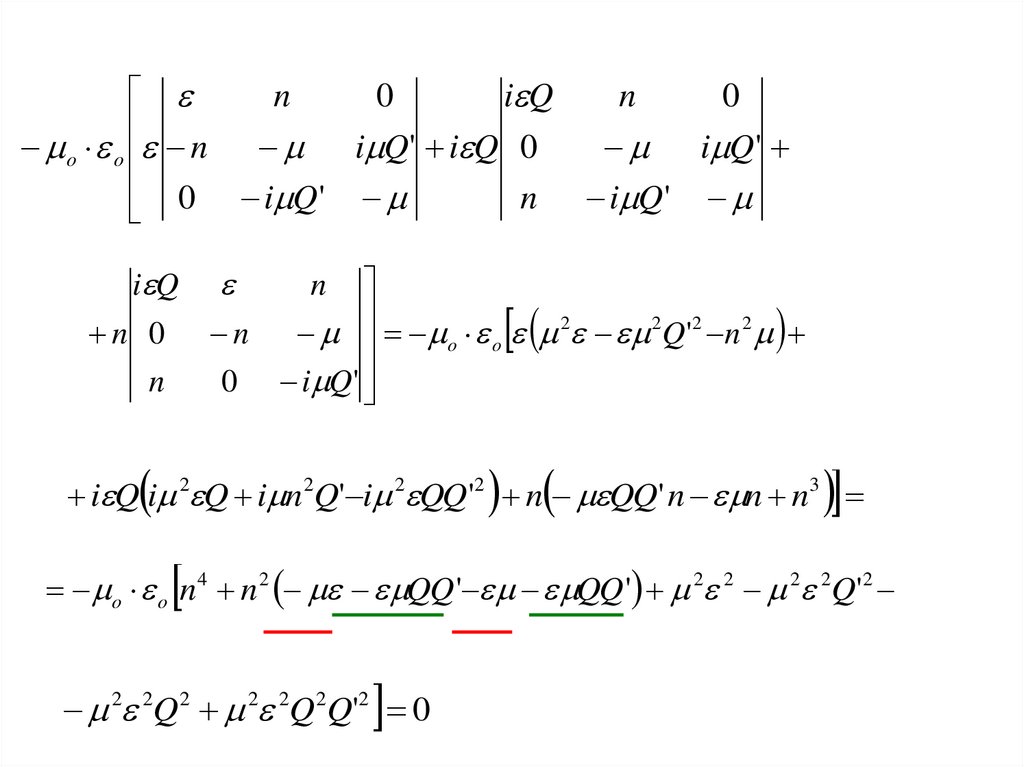













 physics
physics








