Продольные и поперечные магнитооптические эффекты

1. Продольные и поперечные магнитооптические эффекты.

• Распространение электромагнитной волны
в среде. Уравнения Максвелла
• Показатель преломления при продольном
распространении волны
Гироэлектрическая, гиромагнитная и
бигиротропная среды
Частотно независимый эффект Фарадея
• Показатель преломления при поперечном
распространении волны

2. Двулучепреломление

• Cимметрия тензоров [ε] и [μ].
• Анизотропные среды. Оптическая ось.
Одноосные и двуосные кристаллы.
Обыкновенный и необыкновенный луч.
• Двулучепреломление в одноосном
кристалле. «Положительные» и
«отрицательные» кристаллы.
• Линейно поляризованная волна в
одноосном кристалле.
• Случай изотропной среды

3. Симметрия тензора [ε].

Di ij E j – компоненты вектора индукции электрического поля
j
Плотность энергии электрического поля в среде
1
1
1
w E D Ei Di Ei ij E j
2
2 i
2 i, j
1
Поменяем местами
w E j ji Ei
2 i, j
индексы i и j, получим
Почленно вычитаем
1
0 Ei E j ij ji
2 i, j
1
0 Ei ij E j E j ji Ei
2 i, j
Поскольку Еi и Ej независимы, то
следовательно
ij ji 0
ij ji
Тензор [ε] симметричен для анизотропной среды без поглощения.

4. Аналогично доказывается симметрия тензора [μ]

5. Симметричный тензор можно привести к диагональному виду

1
1
2
2
2
w ji Ei E j xx E x yy E y zz E z
2 i, j
2
Уравнение имеет вид:
1
2
2
2
xx E x yy E y zz E z 1
2w
Сделаем замену переменных
Тогда уравнение имеет вид:
Ex
Ez
Ey
x
, y
,
,z
2w
2w
2w
x x2 y y 2 z z 2 1

6.

Уравнение эллипсоида
x x2 y y 2 z z 2 1
2
x2
y
z2
2 2 1
2
a
b
c
Это уравнение описывает эллипсоид, главные оси которого равны
1
,
εx
1
,
εy
1
εz
В общем случае
Это величины, обратные
показателям преломления по
разным направлениям.
x y z

7. Уравнение эллипсоида

2
x2
x2
y
z2
1
1
1
1
2
z2
2
1
1 1
x y
z
y z
В левой части уравнения умножим числитель и знаменатель на с2.
cx 2
c
x
2
1
x
2
y2
cy 2
c
y
2
cz 2
c
z
2
1
c
c
, Vy
,
Сделаем замены переменных: Vx
εx
εy
X cx, Y cy ,
Z cz
c
Vz
,
εz

8. Окончательно уравнение имеет вид:

X 2 Y2 Z2
2
2
2 1
Vx Vy Vz
Это уравнение – эллипсоид скоростей,
а Vx, Vy, Vz – главные лучевые скорости.
Через центр эллипсоида можно провести два круговых сечения.
Направление, перпендикулярное
плоскости кругового сечения –
оптическая ось.
Если Vx=Vy=Vz, эллипсоид
– сфера, среда изотропна.
Если Vx=Vy≠Vz, одноосный
кристалл.
Если Vx≠Vy≠Vz, двуосный
кристалл.

9.

Двулучепреломление
Erasmus Bartholinus
1625−1698
Впервые явление было
обнаружено в 1669 году
датским учёным Э.
Бартолиным (Бартолиниусом)
на кальците (исландский
шпат).
Тогда спец.комиссия
Английского королевского
общества посчитала это
курьёзом.
Через 20 лет в "Трактате о
свете" Гюйгенс объяснил это
явление с позиций волновых
представлений о свете.

10.

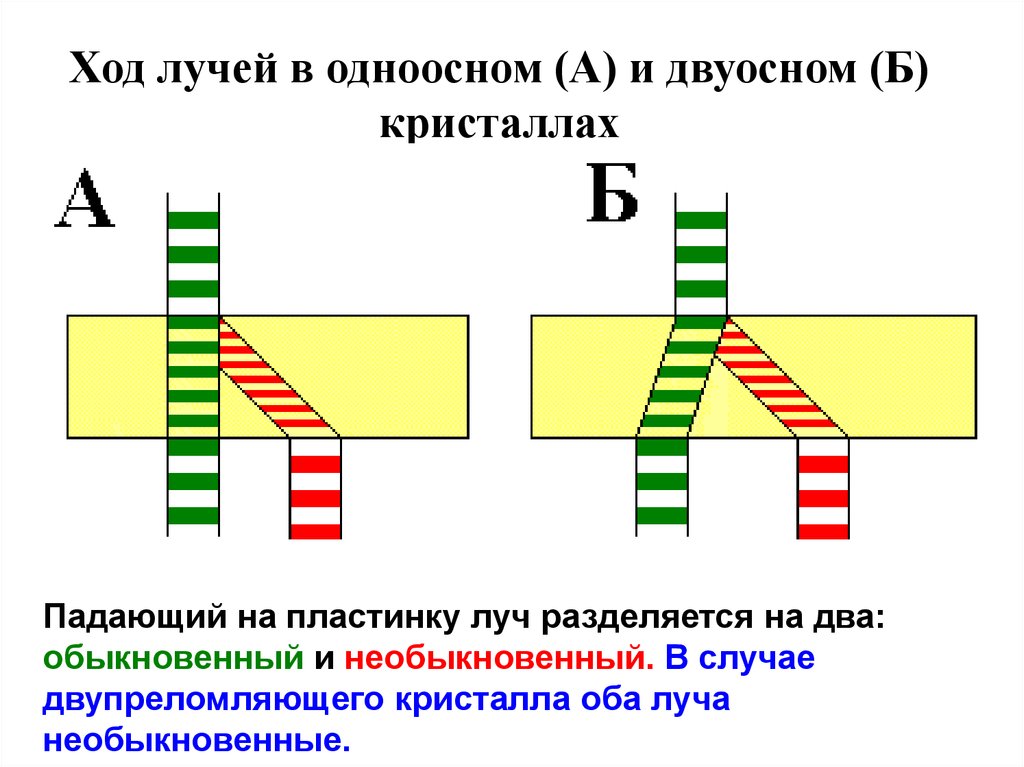
Двулучепреломление

11. Ход лучей в одноосном (А) и двуосном (Б) кристаллах

Падающий на пластинку луч разделяется на два:
обыкновенный и необыкновенный. В случае
двупреломляющего кристалла оба луча
необыкновенные.

12. Ход лучей в одноосном отрицательном (А) и положительном (Б) кристаллах

(о) – обыкновенный луч
(е) – необыкновенный луч
У «−» кристаллов Vo<Ve
У «+» кристаллов Vo>Ve

13. Уравнения Максвелла

Двулучепреломление в одноосном
кристалле
Уравнения Максвелла
1 D
rot H
c t
D E
div D 0
1 B
rot E
c t
B H
div B 0
xx
i xy
i xy
0
yy
0
0
zz
0
1

14.

Электромагнитная волна
E Eo e
i ( t
x y z
c
n)
H H oe
i ( t
x y z
c
n)
α, β и γ – направляющие косинусы
электромагнитной волны.
n – комплексный показатель преломления.
В случае продольного эффекта 0; 1
E Eo e
z
i ( t n )
c
H H oe
z
i ( t n )
c
H H
0
x y
E E
0
x y

15. Вектор D

xx
D E i xy
0
i xy
yy
0
E x xx E y i xy
D
i E xi xy E y yy
t
E z zz
0
Ex
E x xx E y i xy
0 E y E xi xy E y yy
zz E z
E z zz

16. Вектор B

B H
Вектор B
i
rot H
x
Hx
j
y
Hy
H z H y
i
z
y
H y
i
z
Hx
B
i H y
t
Hz
k
z
Hz
H x H z H y H x
j
k
x x
y
z
H x
j
z

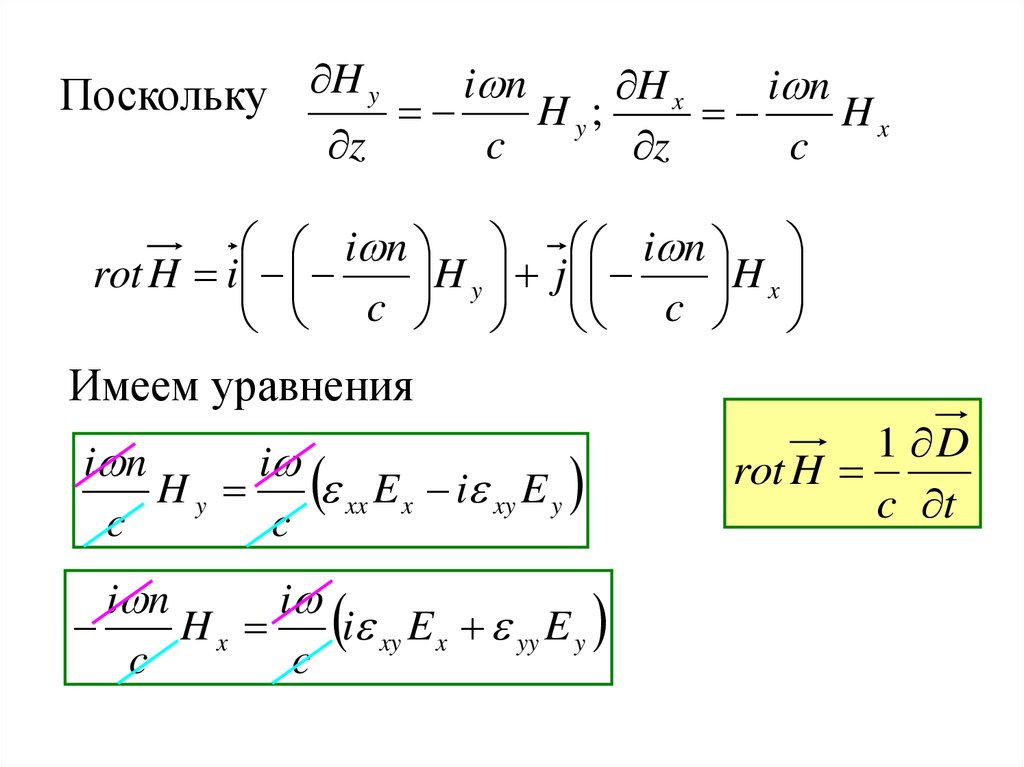
17. Поскольку

H y i n H ; H x i n H
y
x
z
z
c
i n
rot H i
H y
c
c
i n
j
H x
c
Имеем уравнения
i n
i
xx E x i xy E y
Hy
c
c
i n
i
i xy E x yy E y
Hx
c
c
1 D
rot H
c t

18. Ротор Е

i
rot E
x
Ex
j
y
Ey
E z E y
i
z
y
Учитывая, что
k
z
Ez
Ротор Е
1 B
rot E
c t
E x E z E y E x
j
k
x x
y
z
E x
i n
Ex
z
c
i n
rot E i
E y
c
Имеем уравнения
i
i n
E
Hx
y
c
c
E y Ex
j
i
z z
E y
i n
Ey ;
z
c
i n
j
Ex
c
i n
i
Ex H y
c
c

19. Система уравнений для компонент векторов и .

Система уравнений для компонент
векторов E и H .
nH y xx E x i xy E y
nH i E E
x
xy x
yy y
nE H
y
x
nE x H y
Подставим два последние уравнения системы в первые два.
n 2 E x xx E x i xy E y
2
n E y i xy E x yy E y
E x (n 2 xx ) i xy E y 0
2
i
E
E
(
n
) 0
xy x
y
yy

20. Однородная система уравнений имеет решение, если ее определитель равен 0.

n n ( xx yy ) xx yy xy 0
4
2
2
D ( xx yy ) 4 yy xx 4 xy
2
2
( xx yy ) 4 xy
2
2
xx yy ( xx yy ) 4 xy
2
n1, 2
2
2
2
Поскольку существуют два различных значения n, в
веществе могут распространяться две различные волны.

21. Из уравнения получим величину эллиптичности этих волн

Из уравнения
Ex (n2 xx ) i xy E y 0
Ey
получим величину эллиптичности этих волн
Ex
xx n 2 i (n 2 xx )
Ex
i xy
xy
Ey
Ey
Ex
Ey
Ex
1, 2
i xx
yy
xy
1, 2
i yy xx
xy
xx yy 4 xy
2
2
2
xx
yy 4 xy
i K1, 2
2
2
xx
2

22. Определим связь эллиптичностей первой и второй волн.

Ey Ey
E x 1 E x 2
i
xy
2
xx
yy
xx
yy
2
2
4
xx
yy
xy
2
2
2
4
xx
yy
xy
1
2
Эллиптичности первой и второй волн обратны.

23. Рассмотрим случай , т.е.

Рассмотрим случай
xx yy xy , т.е.
2
2
xy 2
yy
2
xx
1
При этом эллиптичность волн имеет вид:
Ey
i yy
xx
E
xy
x 1
2
2
4
xx
yy
xy
2
2
2 xy
Ey
i
yy xx xx yy 1
2
Ex 1 2 xy
xx
yy
2
2
2 xy
2 xy
i
i
yy xx xx yy
2 xy
xx yy 2 xy xx yy
i xy
xx yy
Поскольку
xy
1,
xx yy
первая волна малая

24. В силу того, что эллиптичности волн обратны, эллиптичность второй волны имеет вид:

E y xx yy i ( yy xx )
i xy
xy
Ex 2
Вторая волна является «большой».

25. Рассмотрим линейно поляризованную волну в одноосном кристалле

Линейно поляризованную волну представим в виде суммы
двух эллиптически поляризованных волн.
E=E1+E2
x a cos
x a e i
Эллипс можно задать: y b sin или y ib e i
Компоненты волн имеют вид:
zn
i t 1
E1 x a1 e c
zn
i t 1
c
E
ib
e
1 y
1
zn
i t 2
E2 x a2 e c
zn
i t 2
c
E
ib
e
2 y
2

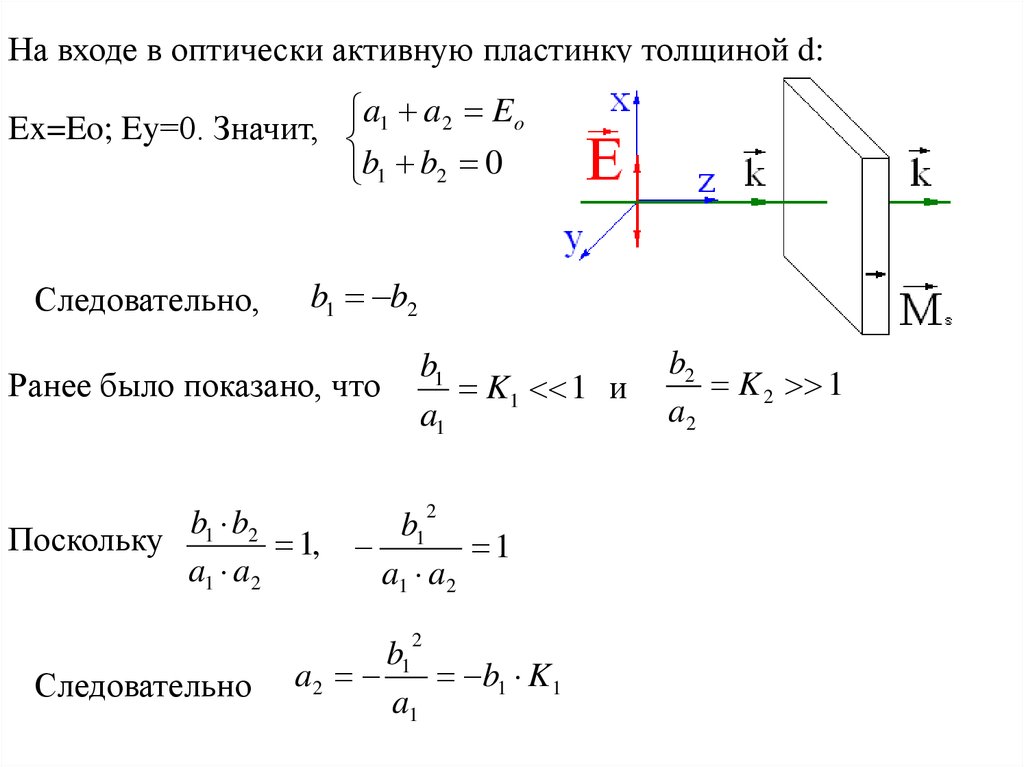
26. На входе в оптически активную пластинку толщиной d:

a1 a2 Eo
Ex=Eo; Ey=0. Значит,
b1 b2 0
Следовательно,
b1 b2
Ранее было показано, что
b1
K1 1 и
a1
2
b1 b2
b
Поскольку
1, 1 1
a1 a2
a1 a 2
2
Следовательно
b1
a2
b1 K1
a1
b2
K 2 1
a2

27. На выходе из пластинки толщиной d имеем волну с компонентами:

Ex d E1 x E2 x a1 e
E E E
y d
1 y
2 y
dn
i t 1
c
a2 e
dn
i t 2
c
dn
dn
i t 1
i t 2
i b1 e c b2 e c
dn
dn
i t 1
i t 2
i b1 e c b1 e c

28. Тогда эллиптичность волны на выходе:

dn
dn
i t 1
i t 2
i b1 e c b1 e c
Ey
dn
dn
i t 1
i t 2
E
x d
a1 e c a2 e c
d ( n1 n2 )
i
b1
c
K1
i b1 e
1 e
a1
dn
d ( n1 n2 )
i t 1
i
a
a1 e c 1 2 e c
a1
d ( n1 n2 )
i
c
i K1 1 e
a2 b1 K1
d ( n1 n2 )
i
1
2
c
1 K e
1
K1 1
dn
i t 1
c

29. Действительная часть эллиптичности «отвечает» за поворот плоскости поляризации (большой оси эллипса), а мнимая – за

d ( n1 n2 )
i
c
i K1 1 e
d (n1 n2 )
d (n1 n2 )
i K1 1 cos
i sin
c
c
d (n2 n1 )
d (n1 n2 )
K1 sin
K1 i 1 cos
c
c
d (n2 n1 )
2 d ( n1 n2 )
K1 sin
2 K1 i sin
c
2c
Действительная часть эллиптичности «отвечает» за поворот
плоскости поляризации (большой оси эллипса), а мнимая – за
эллиптичность.

30. Угол поворота плоскости поляризации на выходе:

Ey
d (n2 n1 )
tg Re K1 sin
Ex
c
d
xy
d (n2 n1 )
sin
xx yy
c
Тангенс угла поворота пропорционален недиагональной
компоненте тензора ε.

31. Определим величину угла поворота плоскости поляризации из условия . Показатели преломления:

Определим величину угла поворота плоскости поляризации
из условия
n1, 2
xy 2
yy
2
xx
1
. Показатели преломления:
( ) 2 4 2
xx
xx
yy
xy
yy
2
0
2
2
xy
( ) 1
xx
xx
yy
( xx yy ) 2
yy
2
n1 xx
n2 yy
1
2
1
2

32. Угол поворота плоскости поляризации:

xy
d (n2 n1 )
tg
sin
xx yy
c
xy
d
sin
( yy xx )
xx yy
c

33. Для изотропной среды ( ).

Для изотропной среды ( xx yy ).
d
xy sin
( yy xx )
c
tg
( xx yy ) ( xx yy )
Для малых углов
tg
xy d
c
d
xy sin
c xy d xy d
tg lim
0 (
c
c
xx yy )
где
xx yy
Ранее для гироэлектрической среды было получено:
xy
Q
, μ=1
Здесь Q
c
d
d xy d xy
Q
c
c
c
d
Формулы совпадают!

34. Разложение линейно поляризованной волны на две эллиптически поляризованные

1
8
2
2
7
3
6
4
5
1
8
7
3
4
5 6

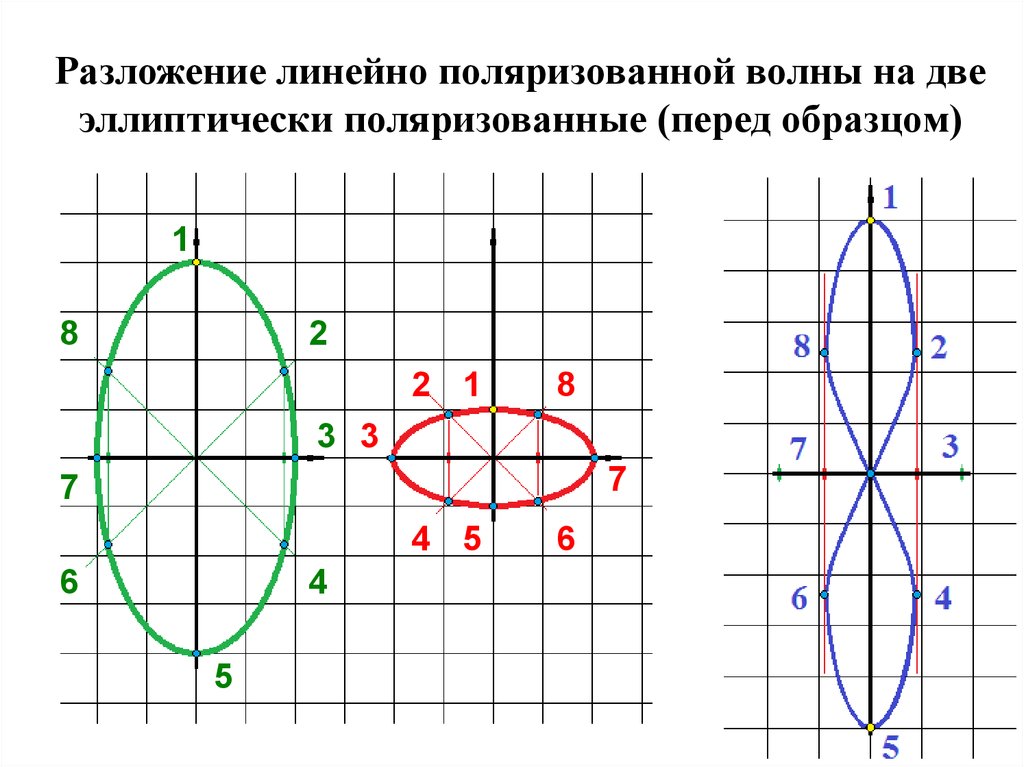
35. Разложение линейно поляризованной волны на две эллиптически поляризованные (перед образцом)

●1
1
8
8
2
2 1
8
3 3
7
7
7
4 5
6
4
5
2
3
6
6
●4
5

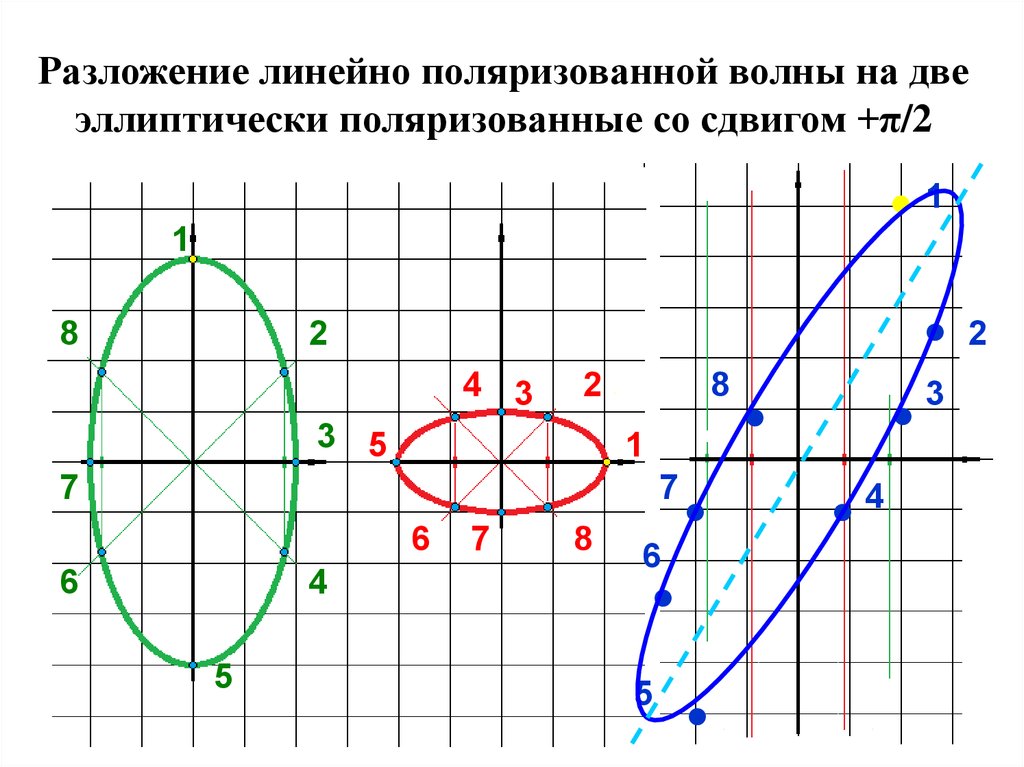
36. Разложение линейно поляризованной волны на две эллиптически поляризованные со сдвигом +π/2

●1
1
8
● 2
2
4 3
2
3 5
8
1
7
7
6
6
4
5
7
8
6
5
●4
3

37. Разложение линейно поляризованной волны на две эллиптически поляризованные со сдвигом –π/2

1
1
8
8
7
2
8
7
3
1
5
2 3
6
4
5
7 6
4
●2
6
3
● 4
●5

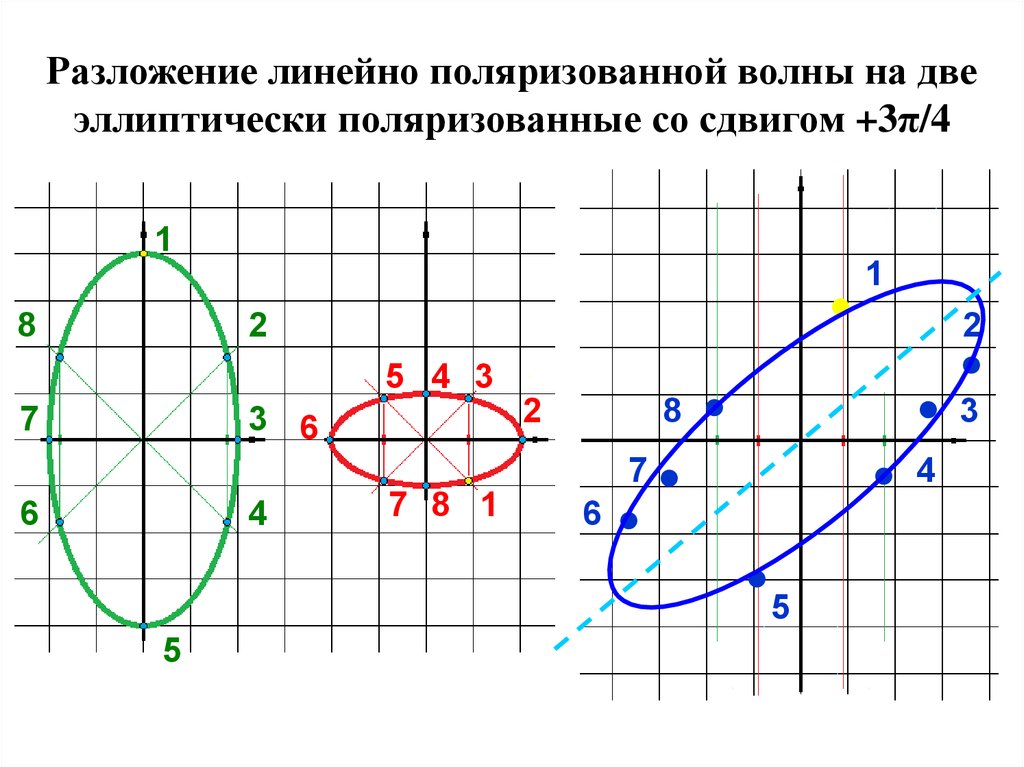
38. Разложение линейно поляризованной волны на две эллиптически поляризованные со сдвигом +3π/4

1
8
2
5 4 3
7
6
4
7 8 1
● 3
● 4
7
6
5
2
8
2
3 6
1
5

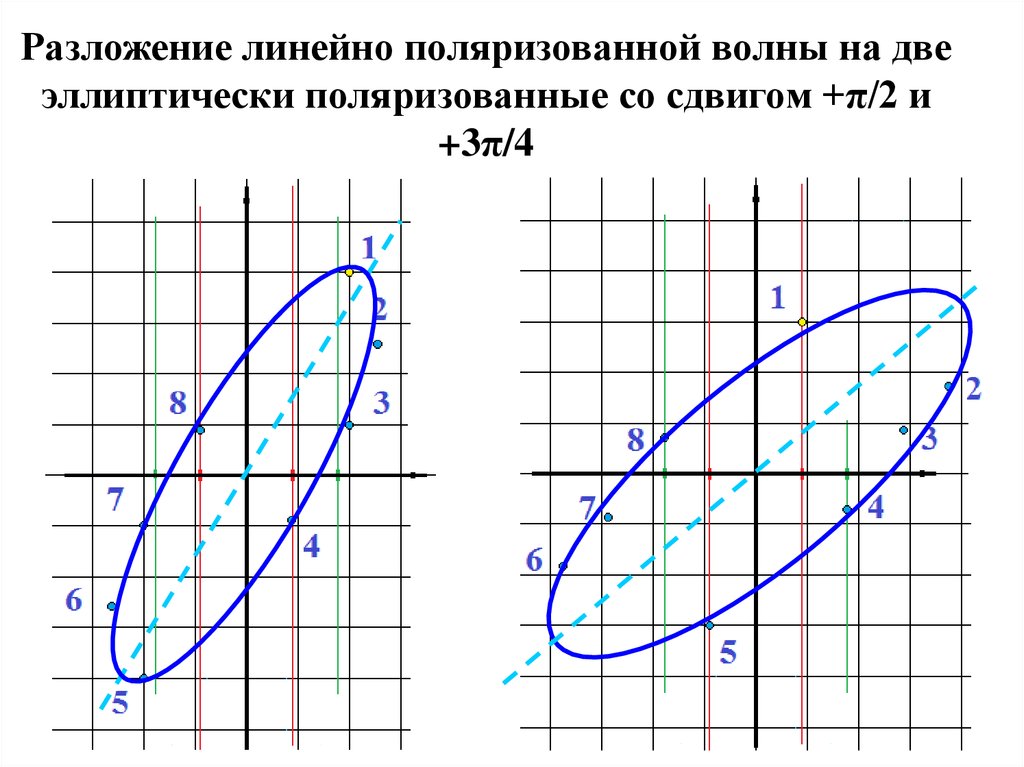
39. Разложение линейно поляризованной волны на две эллиптически поляризованные со сдвигом +π/2 и +3π/4

40. Эллиптичность волны на выходе:

dn
dn
i t 1
i t 2
i b1 e c b1 e c
Ey
dn
dn
i t 1
i t 2
E
x d
a1 e c a2 e c
d (n2 n1 )
2 d ( n1 n2 )
K1 sin
2 K1 i sin
c
2c

41.

Зависимость угла поворота
большой оси эллипса
поляризации в пластинках
ортоферрита иттрия YFeO3,
перпендикулярных оси [001],
разных толщин:
а – 750 мкм, б – 515 мкм,
в – 210 мкм.
Ey
d (n2 n1 )
Re K1 sin
Ex
c
d
Четкин М.В., Щербаков Ю.И.
ФТТ, 11, 1620 (1969)

42. Двулучепреломление

Cимметрия тензоров [ε] и [μ].
Анизотропные среды. Оптическая ось.
Двулучепреломление в одноосном кристалле
Линейно поляризованная волна в одноосном
кристалле.
Если в одноосном кристалле линейно
поляризованный свет распространяется не по
оптический оси, то на выходе из кристалла свет
становится эллиптически поляризованным
• Случай изотропной среды