Четные и нечетные функции. Периодичность функций

1.

Четные и
нечетные
функции.
Периодичность
функций

2.

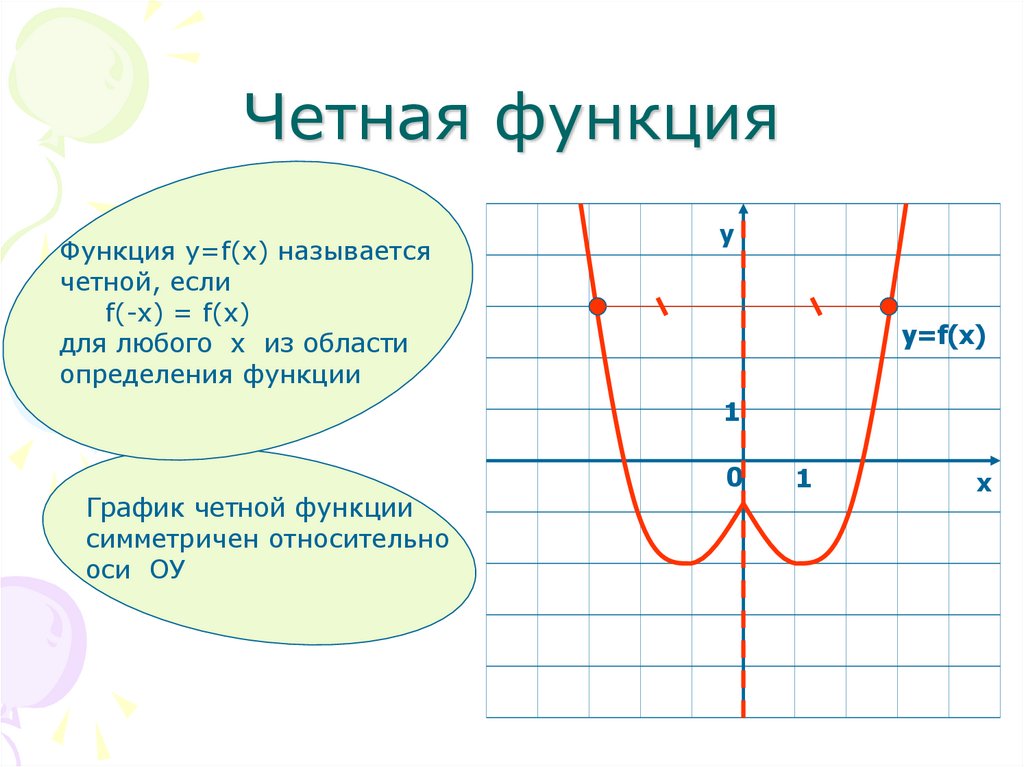
Четная функция
Функция у=f(x) называется
четной, если
f(-x) = f(x)
для любого х из области
определения функции
у
y=f(x)
1
График четной функции
симметричен относительно
оси ОУ
0
1
х

3.

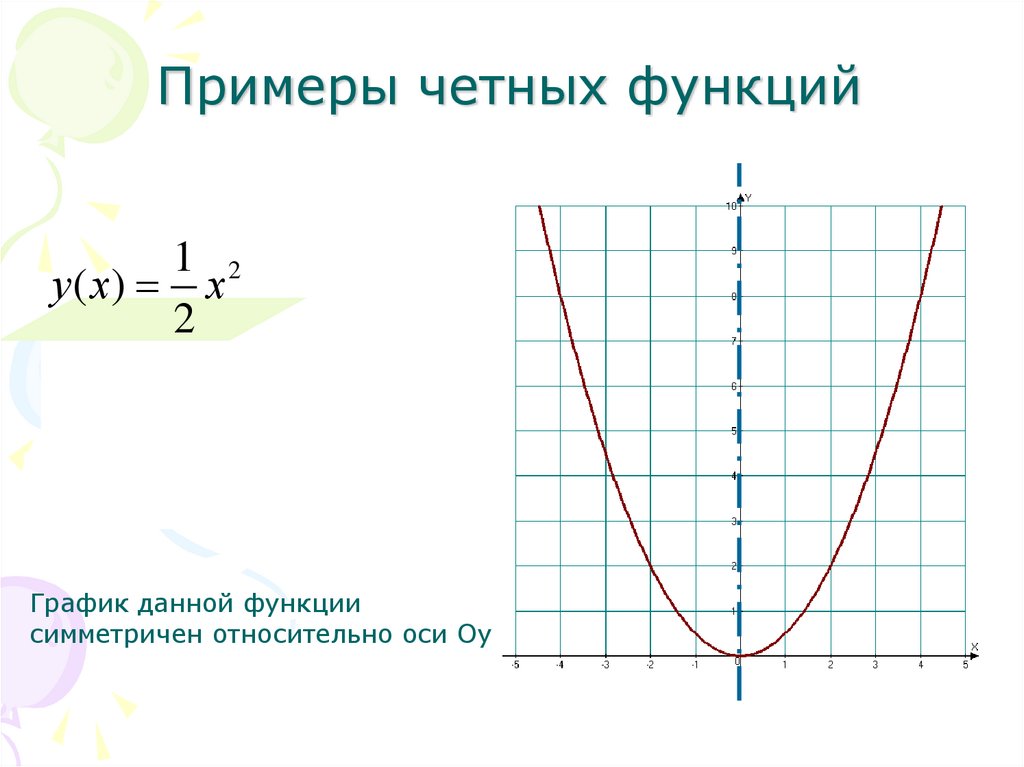
Примеры четных функций
1 2
у ( х) х
2
1
1 2
2
у ( х) ( х) х
2
2
у ( х) у ( х)
График данной функции
симметричен относительно оси Оу

4.

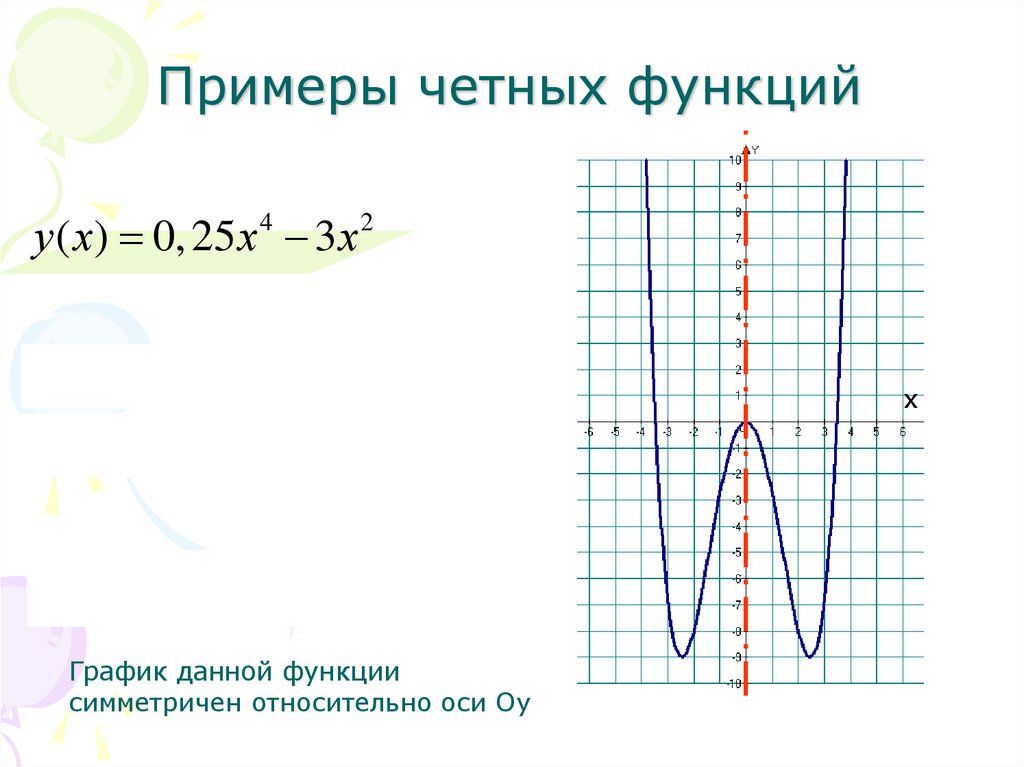
Примеры четных функций
у ( х) 0, 25 х 3 х
4
2
у ( х) 0, 25( х) 4 3( х) 2
0, 25 х 3 х
4
2
у ( х) у ( х)
График данной функции
симметричен относительно оси Оу
х

5.

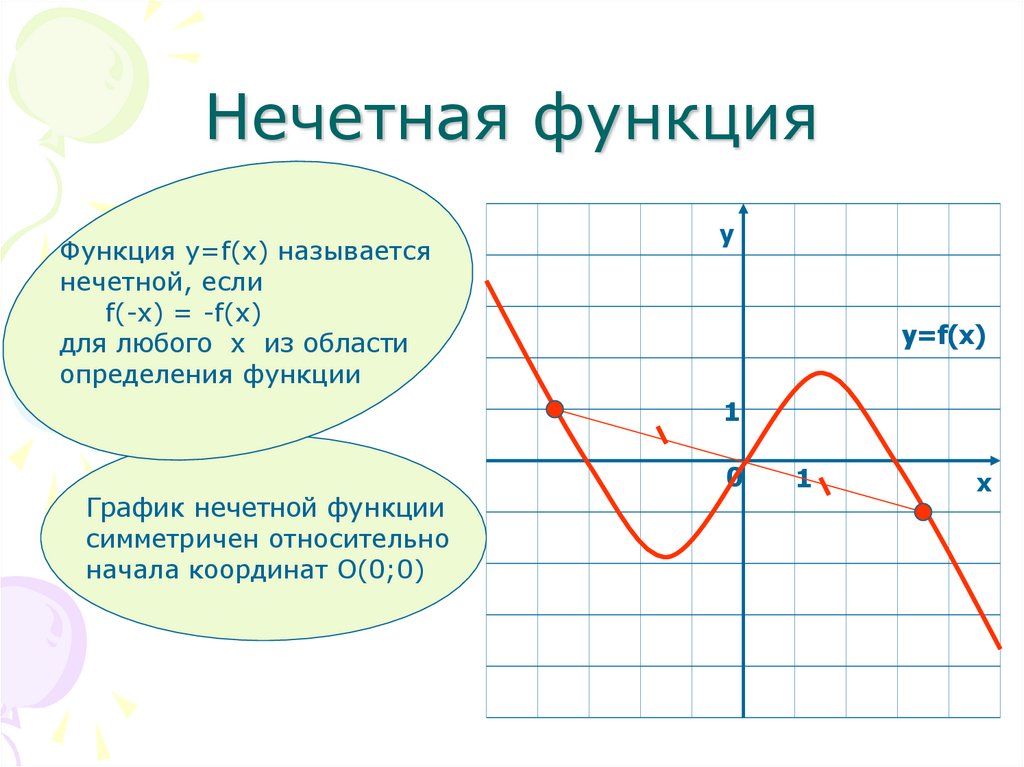
Нечетная функция
Функция у=f(x) называется
нечетной, если
f(-x) = -f(x)
для любого х из области
определения функции
у
y=f(x)
1
График нечетной функции
симметричен относительно
начала координат О(0;0)
0
1
х

6.

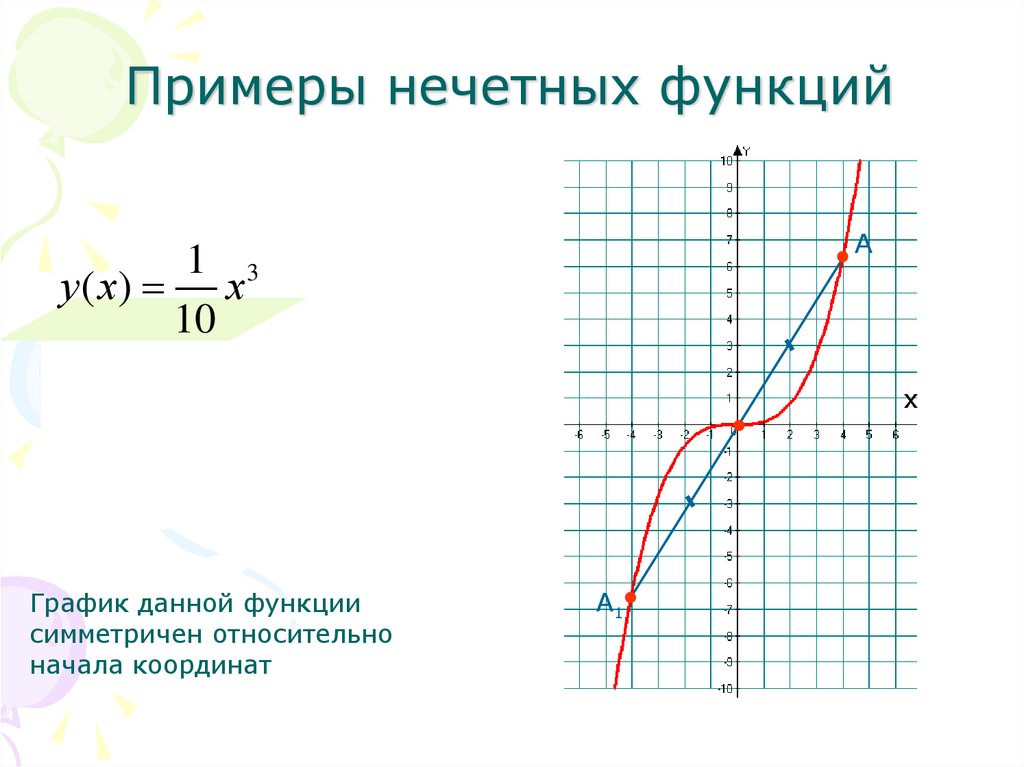
Примеры нечетных функций
А
1 3
у ( х) х
10
1
1 3
3
у ( х) ( х) х
10
10
у ( х) у ( х)
График данной функции
симметричен относительно
начала координат
х
А1

7.

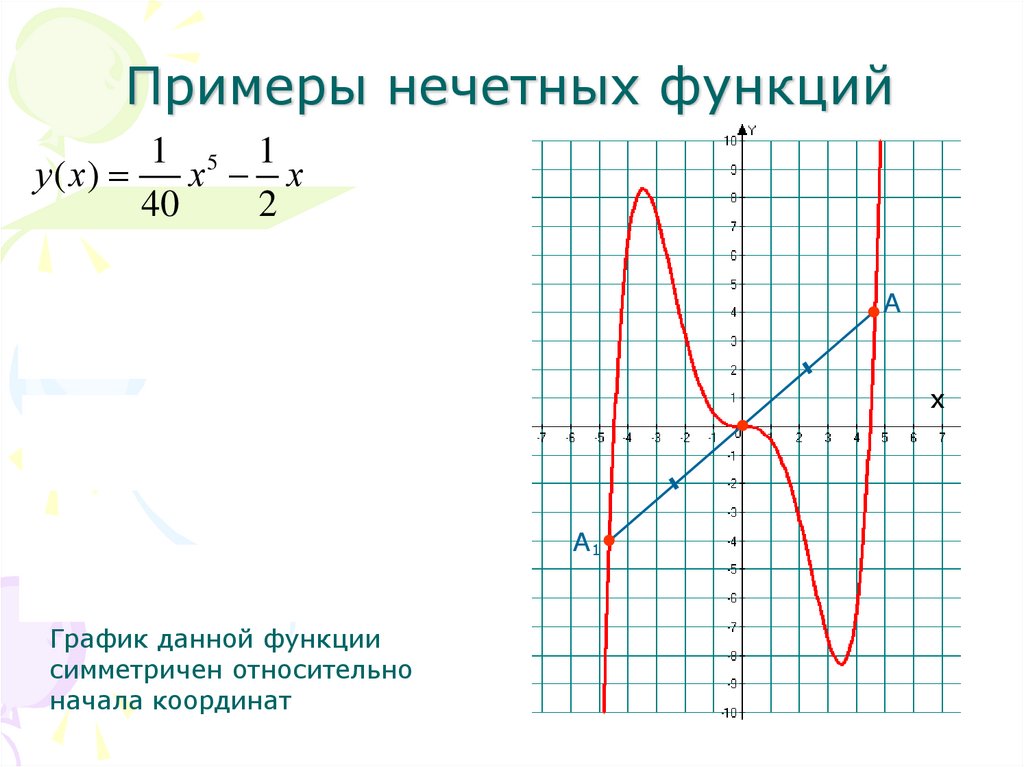
Примеры нечетных функций
1 5 1
у ( х)
х х
40
2
А
1
1
5
у ( х)
( х ) ( х)
40
2
1 5 1
1 5 1
х х х х
40
2
2
40
у ( х) у ( х)
График данной функции
симметричен относительно
начала координат
х
А1

8.

Периодические функции
• Функция называется периодической, если
существует такое число Т = 0, что для любого
х из области определения этой функции
выполняется равенство f(x-T)=f(x)=f(x+T)
Графики периодических функций:
Т
у
TT
1
0
1
y=f(x)
х