Similar presentations:
Магнитное поле. Лекция 26
1. Магнитное поле
ВоГУЛекция 26 (8)
Магнитное поле
Кузина Л.А.,
к.ф.-м.н., доцент
2017 г.
1
2. План
23.
Магнитное поле. Индукция поля BМагнитное поле создаётся токами
Взаимодействие токов происходит посредством магнитного поля
На токи, помещённые в магнитное поле, действует сила:
Магнитное поле поворачивает магнитную стрелку (компаса):
F
M pm B
M pm B sin
F
B
– силовая характеристика поля – магнитная индукция
pm
– магнитный момент стрелки (или контура с током)
3
4.
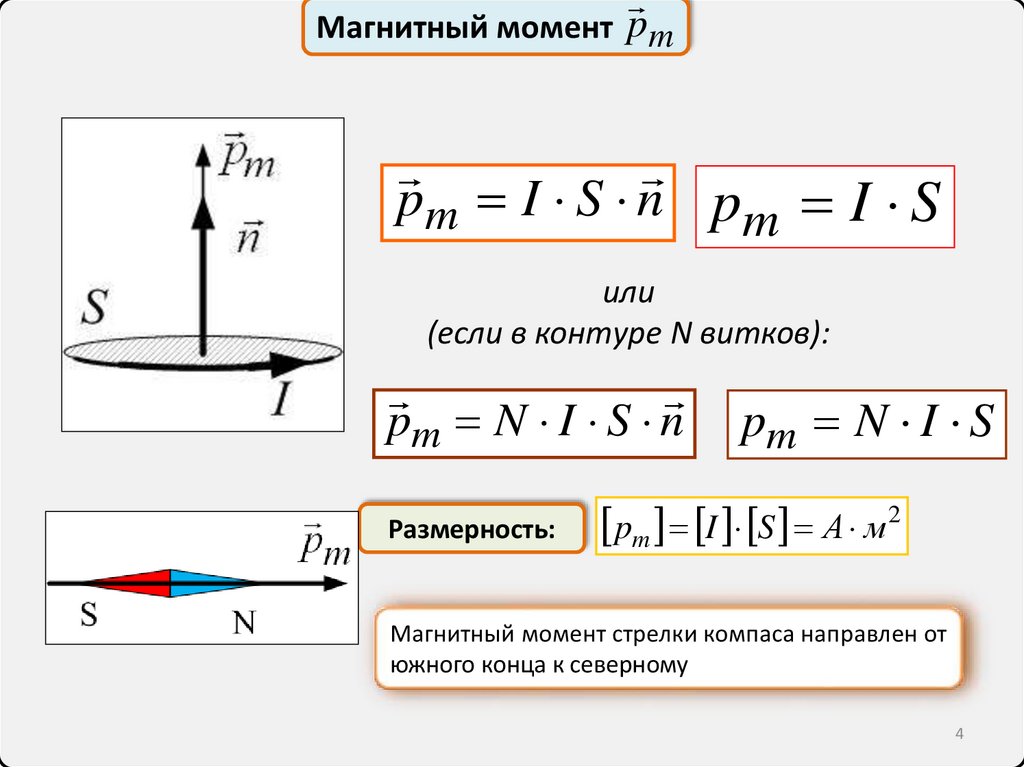
Магнитный момент pmpm I S n pm I S
или
(если в контуре N витков):
pm N I S n
Размерность:
pm N I S
pm I S А м2
Магнитный момент стрелки компаса направлен от
южного конца к северному
4
5.
Индукция магнитного поля BM max
B
pm
Величина магнитной индукции B в данной точке поля
численно равна максимальному вращающему моменту
силы, действующему на виток (или магнитную стрелку) с
единичным магнитным моментом:
M pm B sin
M pm B
В – силовая векторная характеристика поля
M F l Н м
Н
B
Тл
2
pm pm А м А м
5
6.
Магнитный момент в магнитном поле ориентируется по полю:M pm B sin
M pm B
6
7.
Напряжённость магнитного поляH
Ещё одна характеристика поля – напряжённость поля
H
Напряжённость поля H описывает только поле макротоков
(токов проводимости)
Напряжённость поля одинакова в вакууме и в веществе
7
8.
Аналогия характеристик электростатического поля и магнитного полей:Индукция магнитного
поля описывает
суммарное поле токов
проводимости и
микротоков вещества
Напряжённость
магнитного поля
описывает только
поле макротоков
(токов проводимости)
и одинакова в вакууме
и в веществе
B
H
аналогично E
аналогично
Напряжённость
электрического поля
описывает суммарное
поле свободных и
связанных зарядов
D
Вектор электрического
смещения описывает
только поле свободных
зарядов и одинаков в
вакууме и в веществе 8
9.
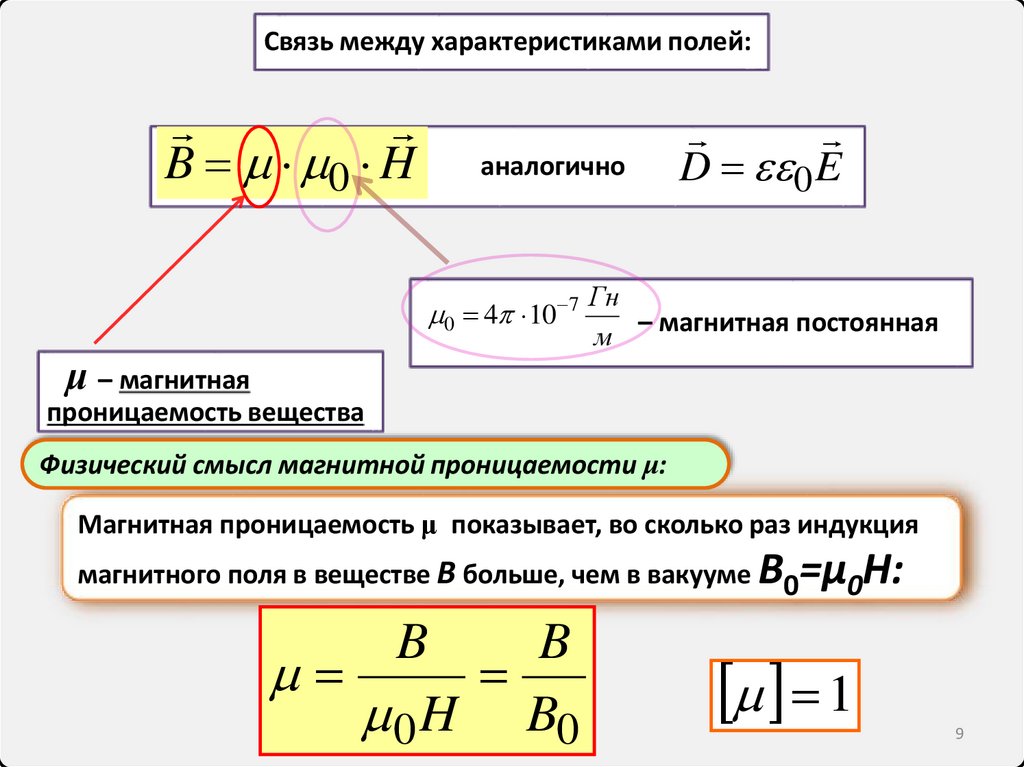
Связь между характеристиками полей:B 0 H
аналогично
0 4 10 7
D 0 E
Гн
– магнитная постоянная
м
μ – магнитная
проницаемость вещества
Физический смысл магнитной проницаемости μ:
Магнитная проницаемость μ показывает, во сколько раз индукция
магнитного поля в веществе B больше, чем в вакууме B0=μ0H:
B
B
0 H B0
1
9
10.
Задача электродинамики –вычисление полей, созданных зарядами и
токами
решается с помощью
Закона Био-Савара-Лапласа
И
принципа суперпозиции:
B Bi
i
Индукция поля, созданного в данной точке несколькими токами, равна
векторной сумме индукций полей, созданных в данной точке каждым
током в отдельности
10
11.
Принцип суперпозиции(в случае непрерывных проводников)
B dB
L
Индукция, созданная проводником с током, равна
интегралу от элементарных индукций полей,
созданных каждым элементом тока
в отдельности
проводник непрерывный;
интеграл по всему проводнику
создано элементом тока I.dl
Элемент тока :
I dl
11
12.
Закон Био-Савара-Лапласа0 I dl r
dB
3
4
r
Вектор dB направлен по правилу буравчика
dB r
dB I dl
0 I dl sin
dB
2
4
r
12
13.
Индукция поля прямого бесконечного проводника с током2
0 I dl sin
B dB
2
4
r
1
2
1
2
0 I r d 2 0 I d
B
2
r
r
4
4
1
1
d r sin
r
d
sin
2
0 I sin d
B
d
4
1
13
CD dl sin r d
14.
20 I sin d
B
d
4
1
2
0 I
B
sin d
4 d
1
0 I
2
B
cos
1
4 d
0 I
cos 1 cos 2
B
4 d
15.
0 Icos 1 cos 2
B
4 d
Если проводник бесконечен, α1=0; α2=π
0 I
0 I
0 I
cos0 cos
1 1
B
4 d
4 d
2 d
15
16.
Индукция в центре кругового тока0 I dl sin
dB
4
r2
0 I dl sin 90 0
dB
4
R2
B dB
L
0 I dl 0 I
B
dl
2
2
4
4
R
R
L
L
B
0 I
4 R
2
2 R
0 I
2R
16
17.
B dBИндукция на оси кругового тока
L
B By dBy sin dB
L
sin
R
r
L
0 I dl sin 900
dB
4
r2
r R 2 h2
0 I dl
0 I
B
2 sin
sin dl
2
r
4 r
L 4
по
окруж
ности
B
Bна
оси
0 I R 2
2
R
2
h
2 3
0 I R
4 r
2
r
2 R
Bна
оси
0 I R 2
2 r3
0 I
2 R
sin 3
17
18.
Поле соленоидаB
0 I n
2
cos 1 cos 2
N
n
l
Для длинного соленоида:
B
солен.
0 In
2
1 0
2
1 1
B
солен.
0 In
18
19.
Поле соленоидаdN n dx
- число витков на длине dx
dI I dN I n dx
dB
0 I n dx
2 R
- суммарный ток этих витков
sin 3 - индукция поля, созданного током этих витков
20.
Поле соленоида,
R
sin
r
CD dx sin r d
r d
dx
sin
21.
Поле соленоидаdB
0 I n dx
2 R
sin 3
r d
dx
sin
dB
2
B dB
1
2
0
dB
0 I n r sin 2 d
2 R
0 I n sin d
R
sin
r
2
I n sin d
2
1
B
0 I n
2
2
sin d
1
B
0 I n
2
cos
2
1
22.
Поле соленоидаB
0 I n
2
B
cos 2
1
0 I n
2
cos 1 cos 2
23.
Поле движущегося заряда0 I dl r
dB
3
4
r
Замена:
I dl
dB
0 q v r
B
3
4
r
0 q v sin
B
2
4
r
q v
B
I dl А м
q v Кл м Кл м А м
с
с
23
24.
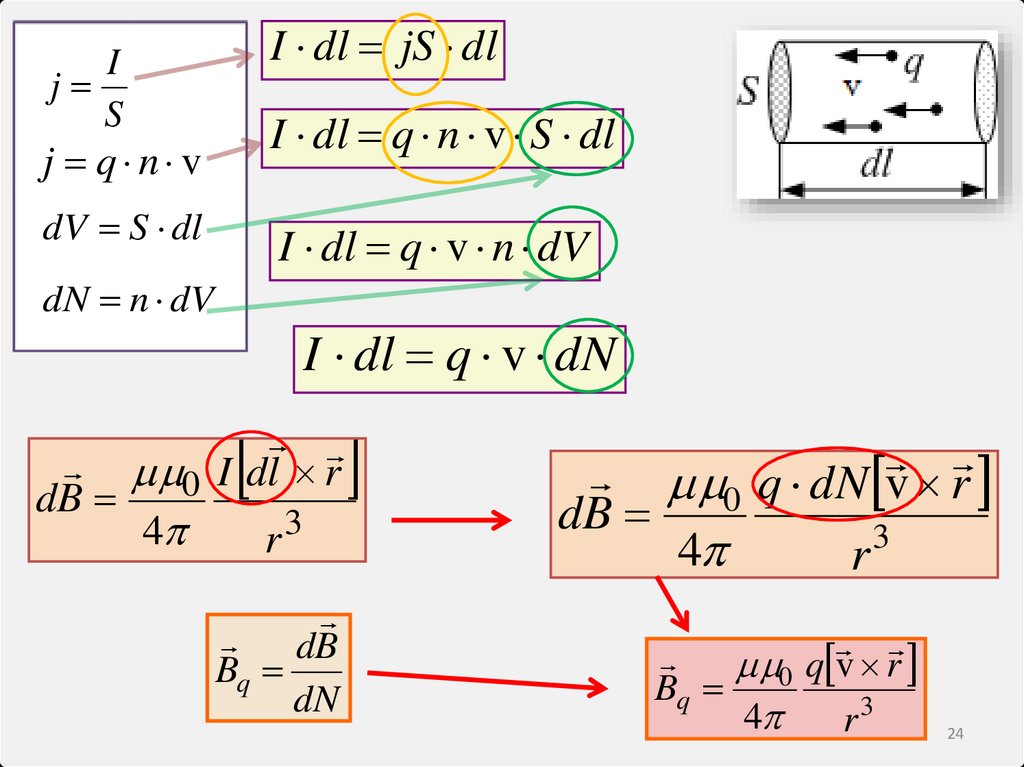
I dl jS dlI
j
S
I dl q n v S dl
j q n v
dV S dl
I dl q v n dV
dN n dV
I dl q v dN
0 I dl r
dB
3
4
r
dB
Bq
dN
0 q dN v r
dB
3
4
r
0 q v r
Bq
4
r3
24
25.
Закон полного тока (теорема о циркуляции)для магнитного поля в вакууме
Циркуляция вектора:
Bdl B cos dl Bl dl
L
Теорема о циркуляции:
L
L
Bdl 0 I i
L
i
Циркуляция вектора магнитной индукции для поля в
вакууме по произвольному замкнутому контуру равна
алгебраической сумме токов, охваченных контуром,
умноженной на магнитную постоянную
25
26.
Пример применения теоремы о циркуляции (закона полного тока)Bdl 0 I i
i
L
Bdl 0 I 2 2I3
L
Теорема о циркуляции, если заданы не
токи, а плотность тока:
Bdl 0 j dS
L
Интеграл берётся по поверхности, натянутой на контур
S
26
27.
Применение закона полного токаПоле прямого бесконечного провода
Bdl 0 I i
L
i
В любой точке контура вектор B одинаков и
направлен по касательной к нему
Bdl B dl B 2 R
L
L
B 2 R 0 I
0 I
B
2 R
27
28.
Bdl 0 I iПоле длинного (бесконечного) соленоида
i
L
Контур – узкий длинный прямоугольник
В интеграл даёт вклад только эта сторона
Bdl B dl B l
L
L
B l 0 I N
Ток I пронизывает контур N раз:
Ii I N
i
B
0 I N
l
0 I n
28
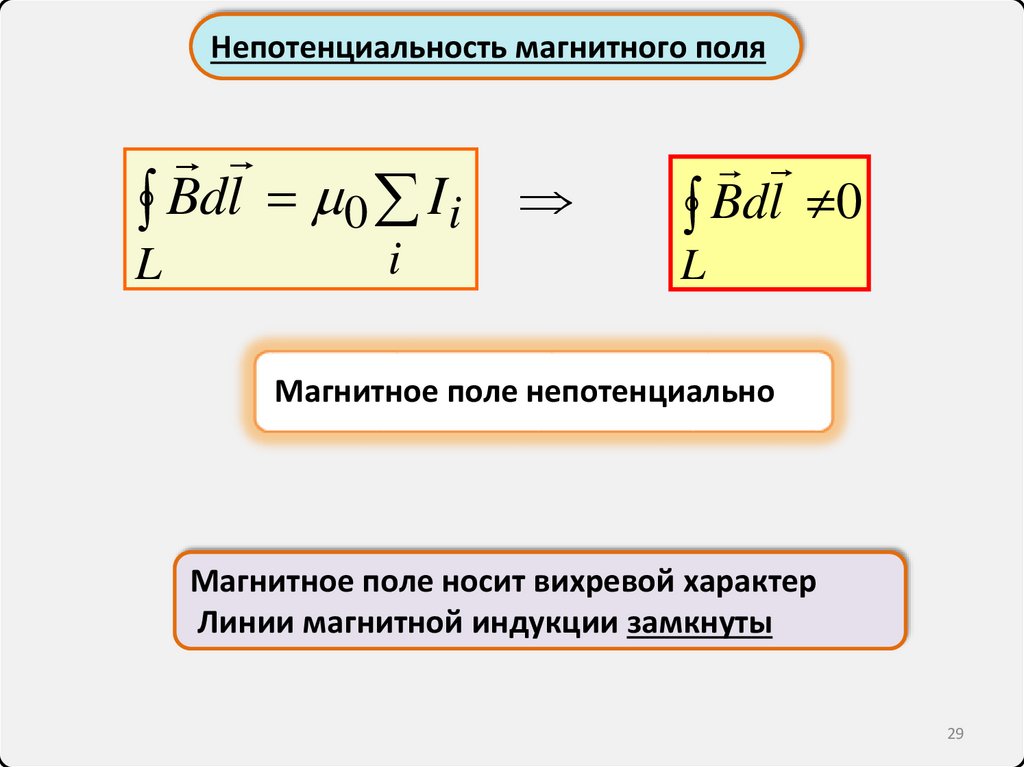
29.
Непотенциальность магнитного поляBdl 0 I i
L
i
Bdl 0
L
Магнитное поле непотенциально
Магнитное поле носит вихревой характер
Линии магнитной индукции замкнуты
29
30.
Непотенциальность магнитного поляЛинии магнитной индукции замкнуты
Поле кругового тока
Поле прямого провода
30
31.
Непотенциальность магнитного поляЛинии магнитной индукции замкнуты
Поле соленоида
Поле полосового магнита
31



























 physics
physics








