Лекция 13 Магнитное поле

1. Магнитное поле

Иллюстративный материал к
лекции №13
суббота, 21 июня 2025 г.

2.

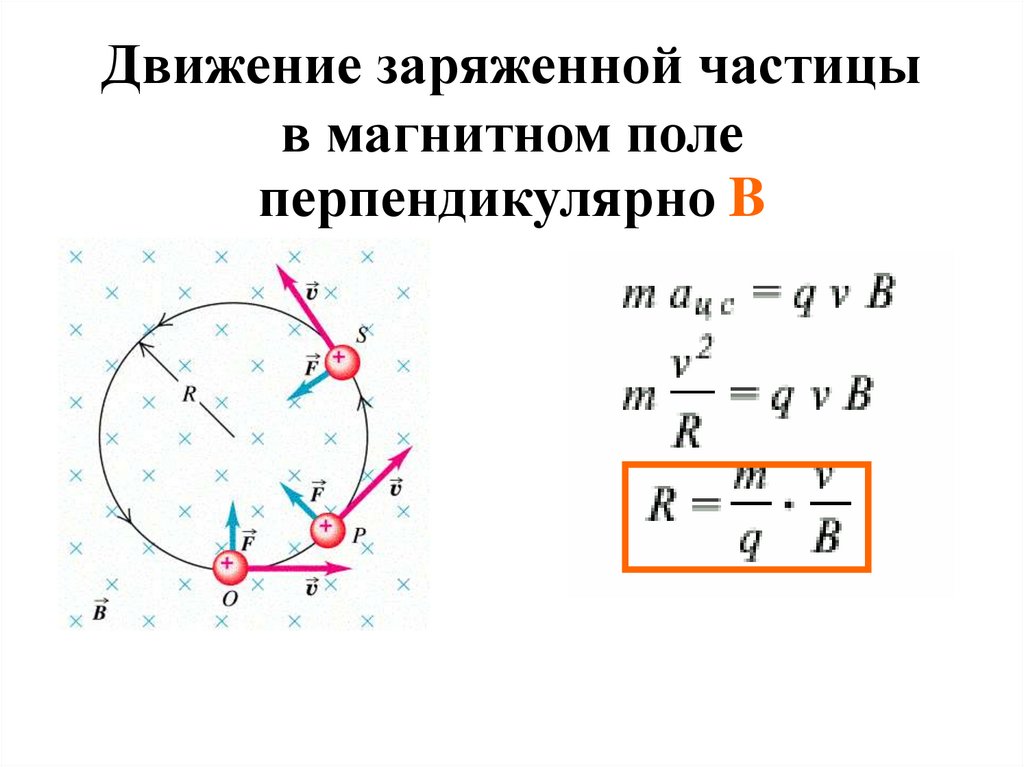
Движение заряженной частицы
в магнитном поле
перпендикулярно B

3.

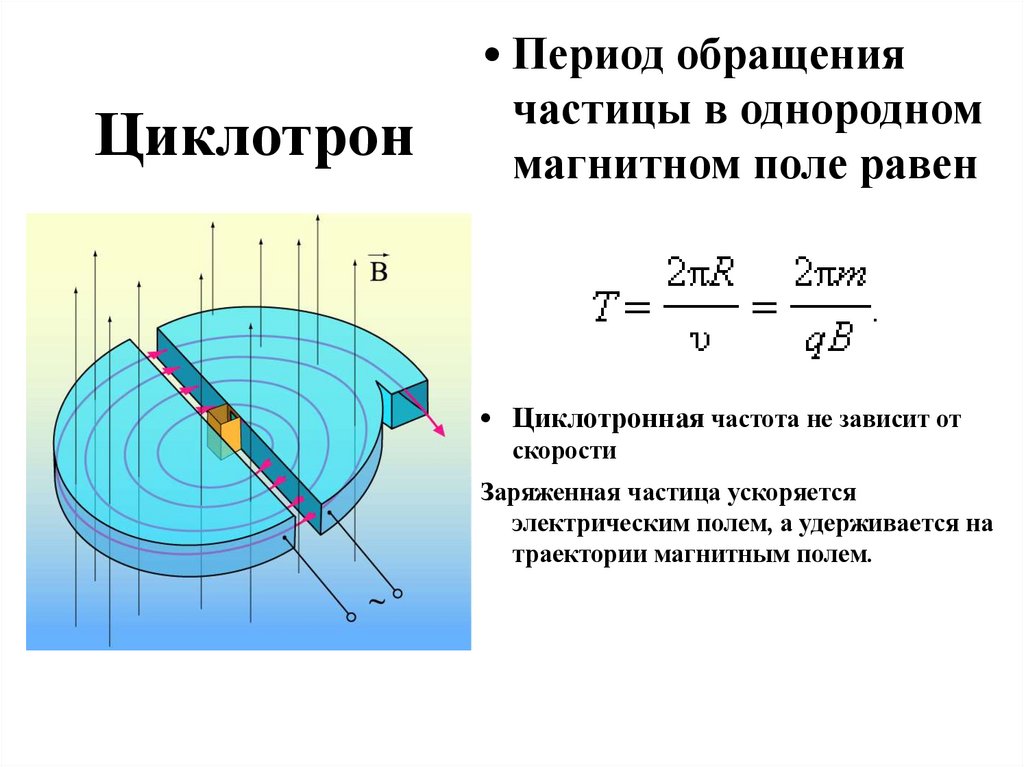
Циклотрон
• Период обращения
частицы в однородном
магнитном поле равен
• Циклотронная частота не зависит от
скорости
Заряженная частица ускоряется
электрическим полем, а удерживается на
траектории магнитным полем.

4.

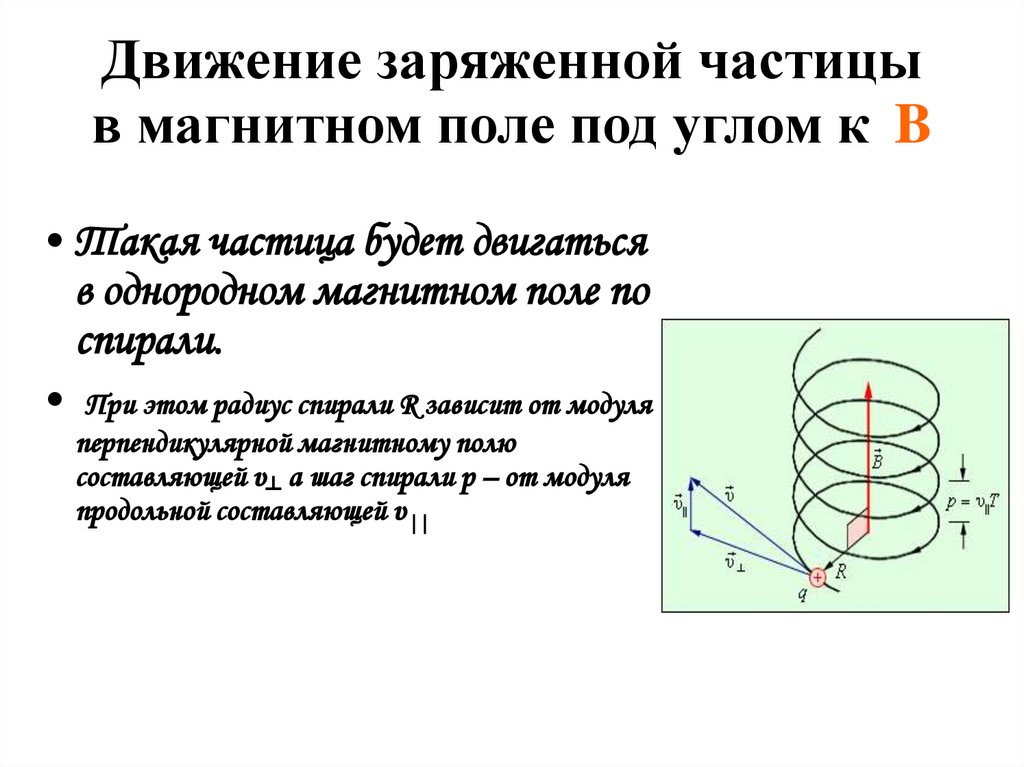
Движение заряженной частицы
в магнитном поле под углом к B
• Такая частица будет двигаться
в однородном магнитном поле по
спирали.
• При этом радиус спирали R зависит от модуля
перпендикулярной магнитному полю
составляющей υ┴ а шаг спирали p – от модуля
продольной составляющей υ||

5.

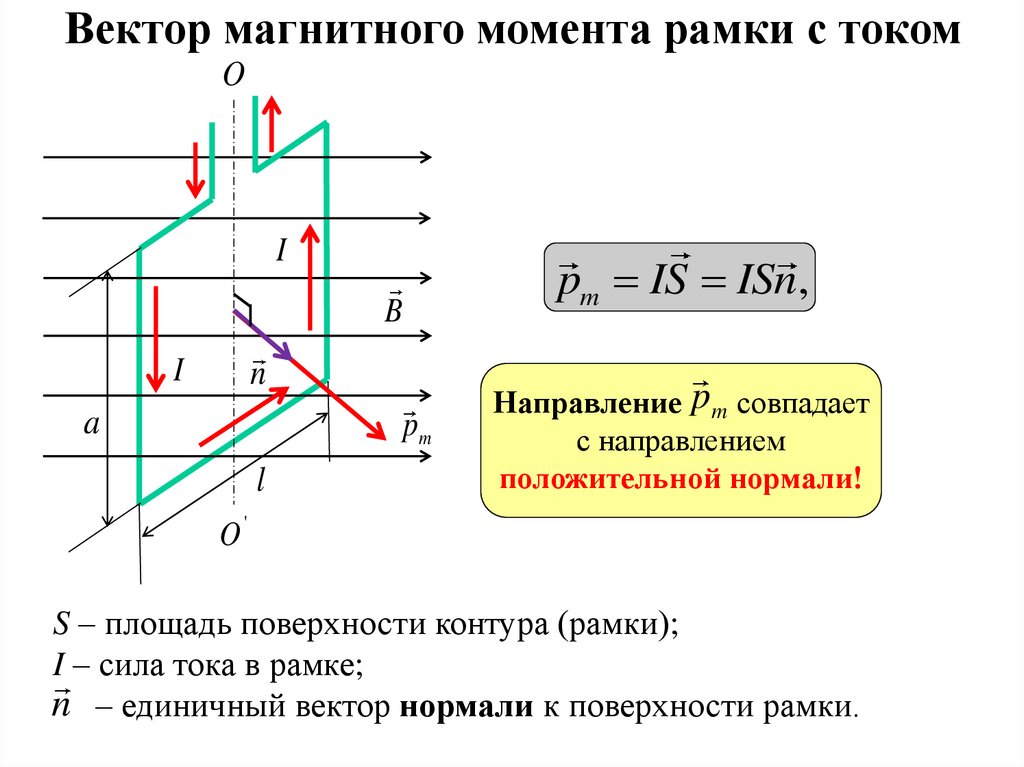
Вектор магнитного момента рамки с током
O
I
pm IS ISn,
B
I
n
a
pm
l
Направление pm совпадает
с направлением
положительной нормали!
O'
S – площадь поверхности контура (рамки);
I – сила тока в рамке;
n – единичный вектор нормали к поверхности рамки.

6.

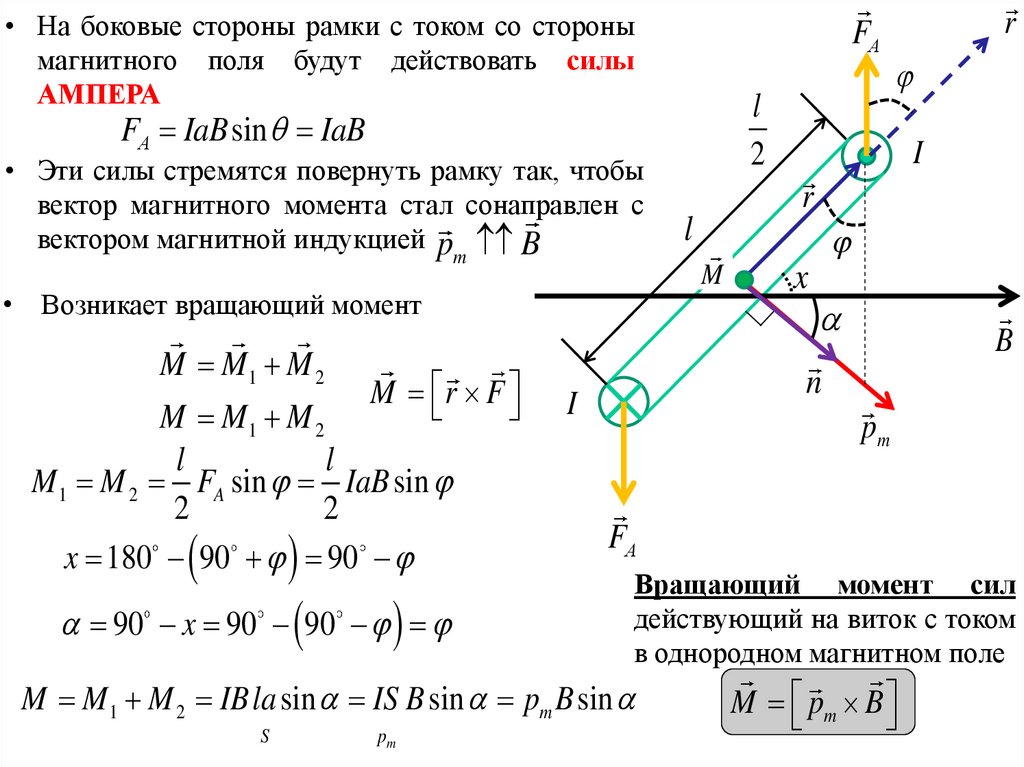
• На боковые стороны рамки с током со стороны
магнитного поля будут действовать силы
АМПЕРА
FА
l
2
FА IaB sin IaB
• Эти силы стремятся повернуть рамку так, чтобы
вектор магнитного момента стал сонаправлен с
вектором магнитной индукцией p B
m
M M1 M 2
M r F
M M1 M 2
l
l
M 1 M 2 FA sin IaB sin
2
2
x 180 90 90
90 x 90 90
pm
I
l
x
B
n
I
pm
FА
Вращающий момент сил
действующий на виток с током
в однородном магнитном поле
M M 1 M 2 IB la sin IS B sin pm B sin
S
r
M
• Возникает вращающий момент
r
M pm B

7.

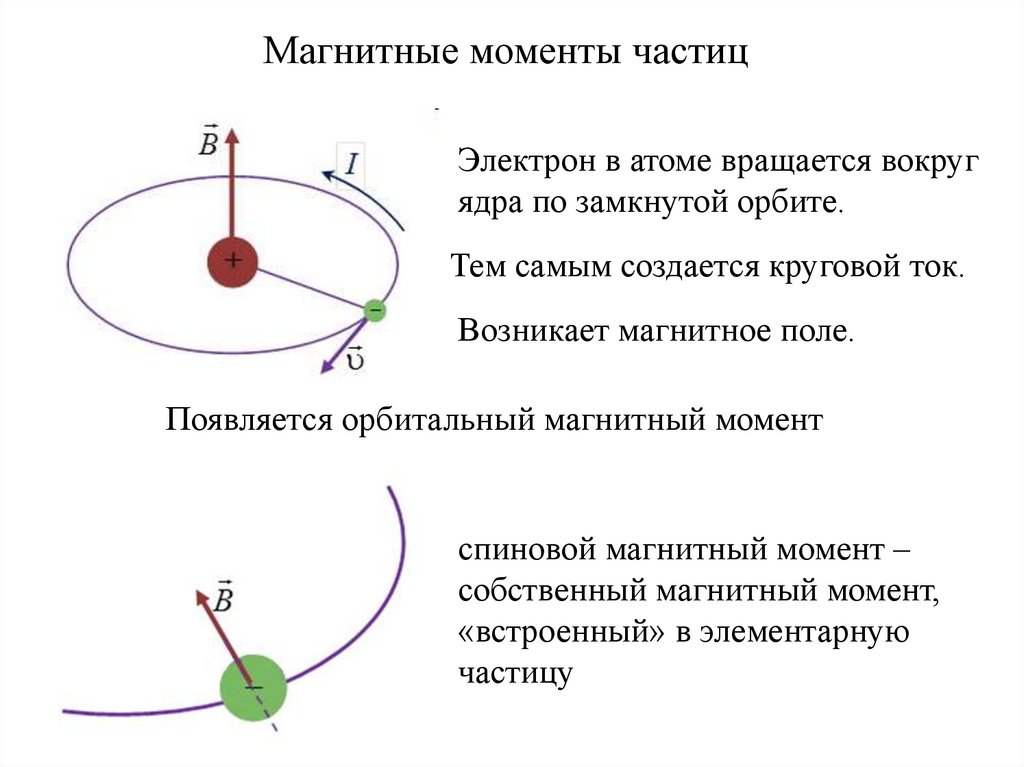
Магнитные моменты частиц
Электрон в атоме вращается вокруг
ядра по замкнутой орбите.
Тем самым создается круговой ток.
Возникает магнитное поле.
Появляется орбитальный магнитный момент
спиновой магнитный момент –
собственный магнитный момент,
«встроенный» в элементарную
частицу

8.

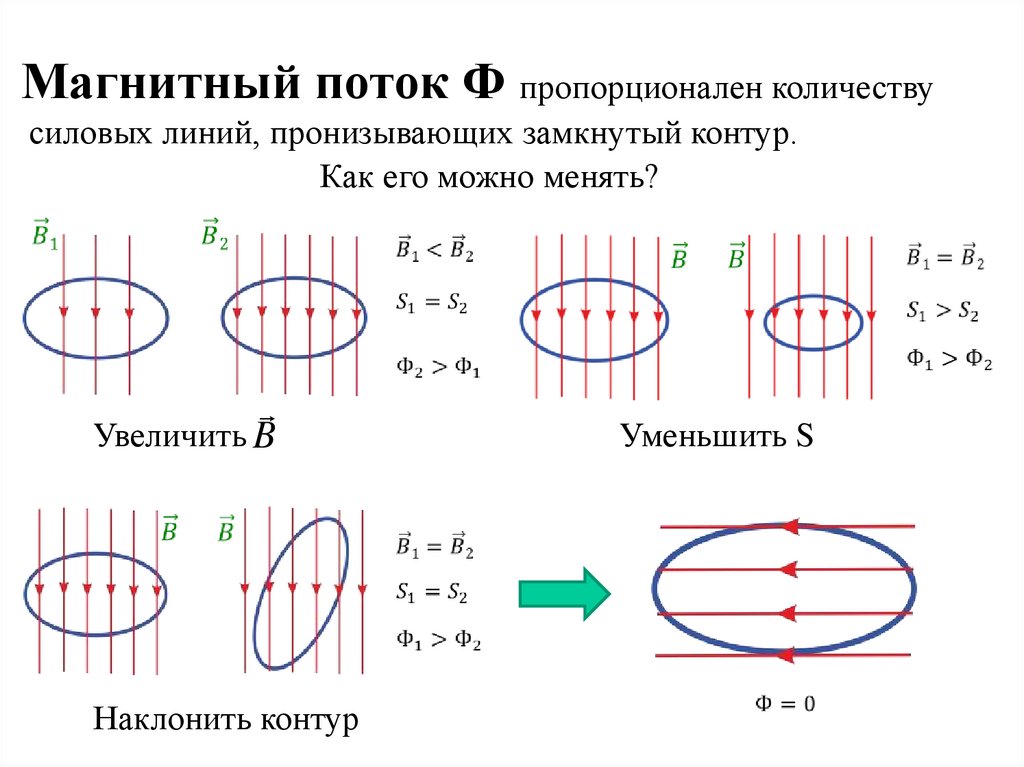
Магнитный поток Ф пропорционален количеству
силовых линий, пронизывающих замкнутый контур.
Как его можно менять?
Увеличить B
Наклонить контур
Уменьшить S

9.

Магнитный поток через плоскую поверхность — это скалярная физическая
величина, численно равная произведению модуля магнитной индукции на
площадь поверхности, ограниченной контуром, и на косинус угла между
нормалью к поверхности и магнитной индукцией.
1 вебер — это магнитный
поток однородного
магнитного поля с индукцией
1 Тл через перпендикулярную
ему поверхность площадью 1
м2.
Ф B, dS B dS cos
S
S
B cos dS B S cos
S

10.

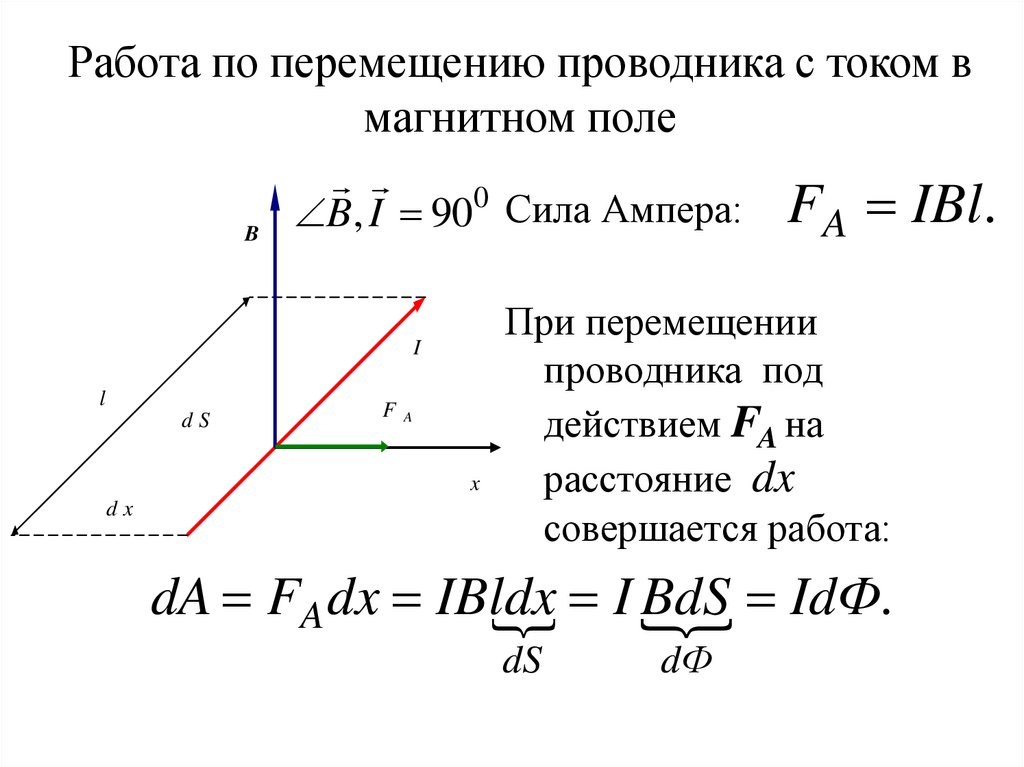
Работа по перемещению проводника с током в
магнитном поле
B
B, I 900 Сила Ампера:
I
l
dS
dx
FA
FA IBl.
При перемещении
проводника под
действием FA на
x
расстояние dx
совершается работа:
dA FA dx IBldx
I BdS
IdФ.
dS
dФ

11.

Работа по перемещению проводника с
током в магнитном поле равна
произведению
силы
тока
на
магнитный
поток,
пересеченный
движущимся проводником.
dA IdФ
Формула остаётся справедливой, если проводник
любой формы движется под любым углом к
линиям вектора магнитной индукции.

12.

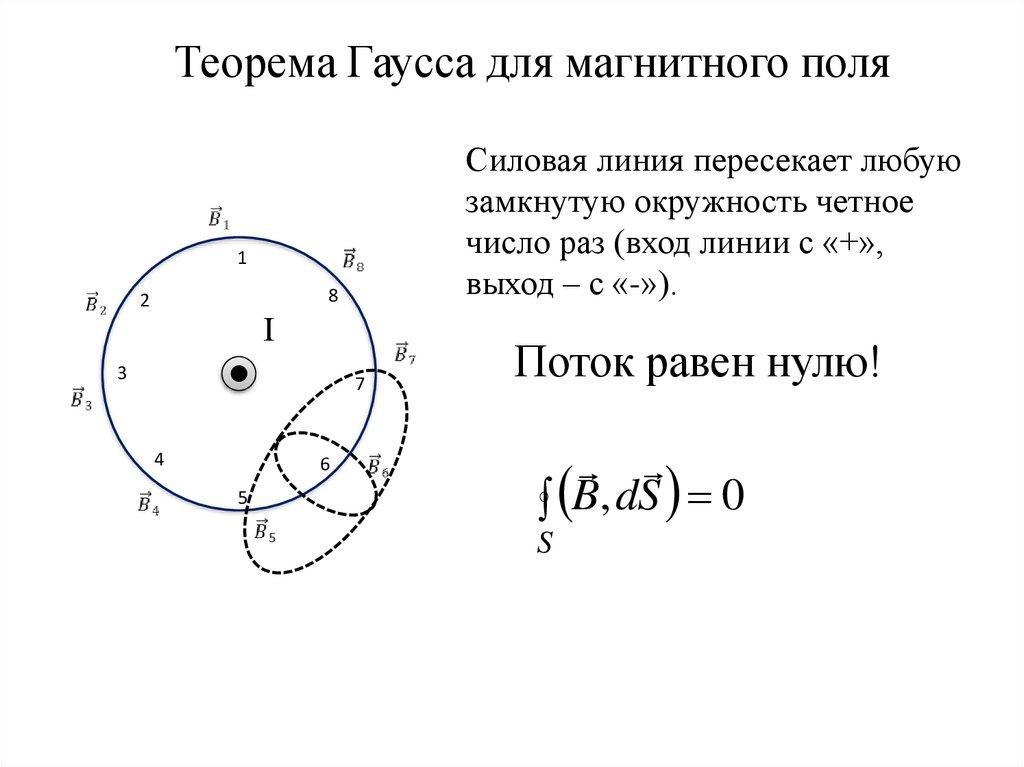
Теорема Гаусса для магнитного поля
Силовая линия пересекает любую
замкнутую окружность четное
число раз (вход линии с «+»,
выход – с «-»).
1
8
2
I
3
7
4
6
5
Поток равен нулю!
B, dS 0
S

13.

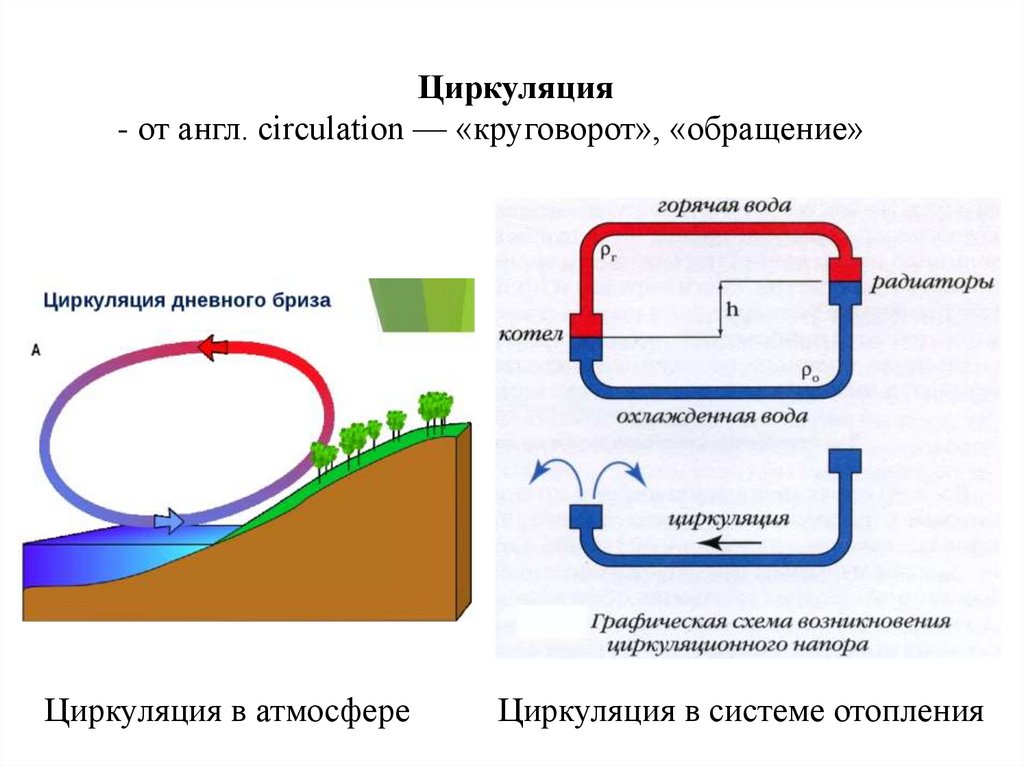
Циркуляция
- от англ. circulation — «круговорот», «обращение»
Циркуляция в атмосфере
Циркуляция в системе отопления

14.

Циркуляция вектора магнитной индукции
Циркуляцией вектора B по замкнутому контуру L
называется следующий интеграл по этому контуру:
Ц B B, dL B cos dl
L
L
• dl –
элемент
длины
контура,
направленный вдоль обхода контура;
• α – угол между векторами B и dl.
dl
L
B

15.

Теорема о циркуляции вектора магнитной
индукции:
Циркуляция вектора магнитной индукции
по произвольному замкнутому
контуру равна алгебраической сумме
токов, охватываемых этим контуром,
умноженной на магнитную постоянную
Bdl 0 I i
l
где
i
0 4 10 7 Гн м

16.

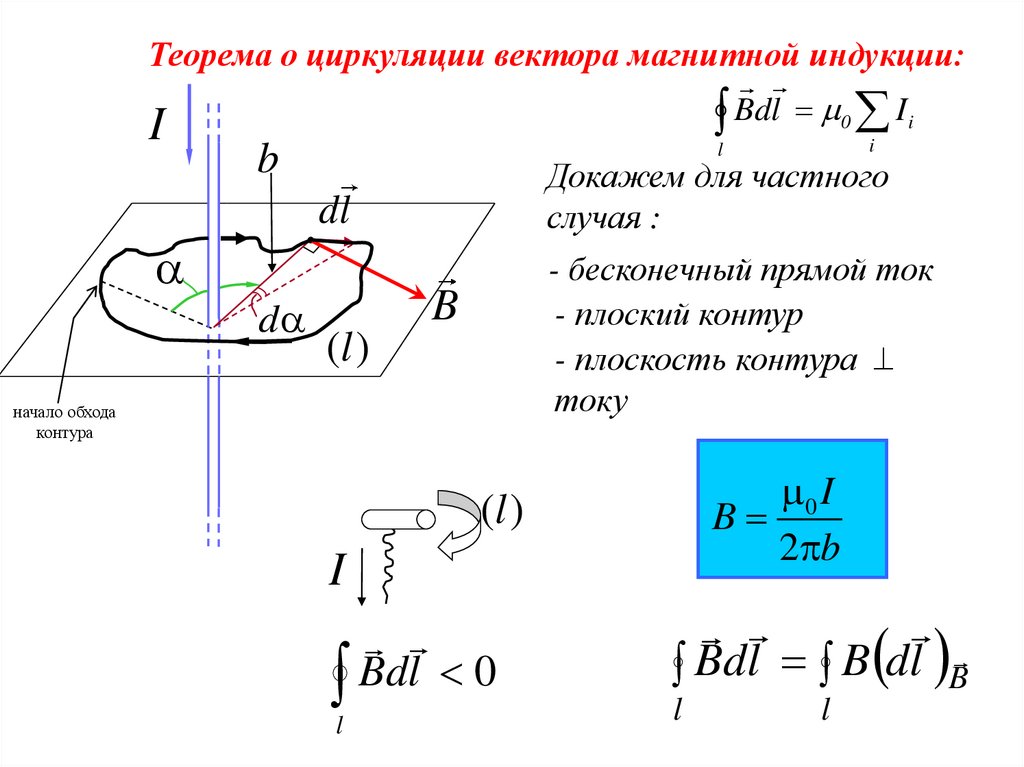
Теорема о циркуляции вектора магнитной индукции:
Bdl 0 I i
I
b
Докажем для частного
случая :
dl
d
i
l
- бесконечный прямой ток
- плоский контур
- плоскость контура
току
B
(l )
начало обхода
контура
0 I
B
2 b
(l )
I
B dl 0
l
Bdl B dl B
l
l

17.

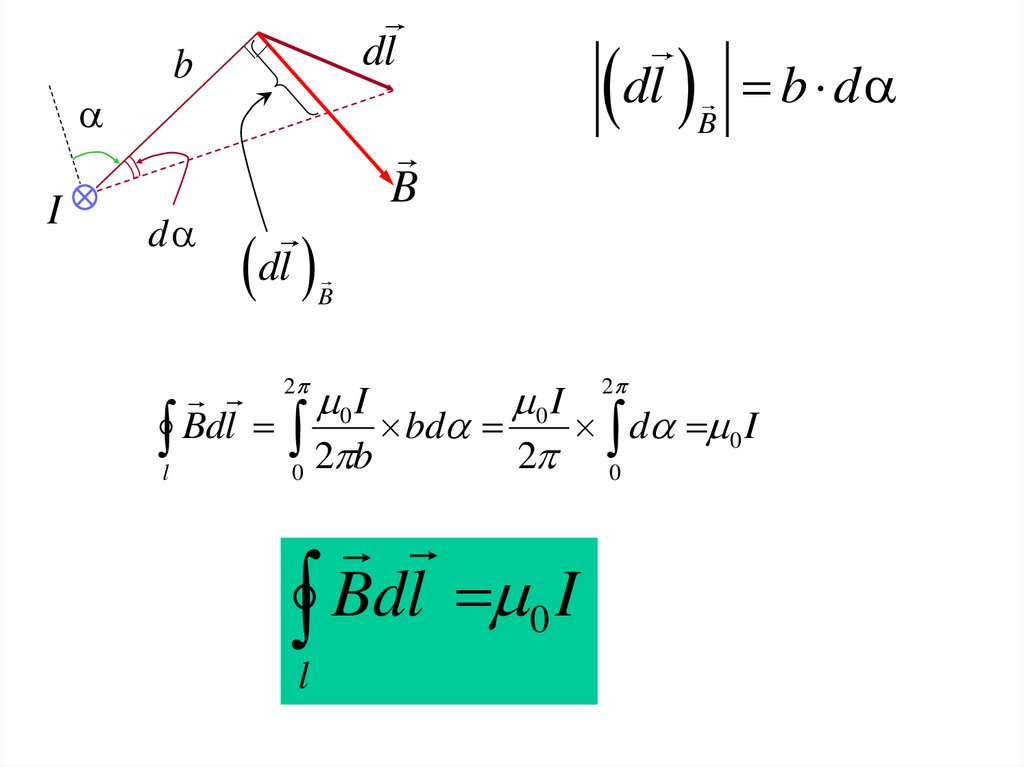
dl
b
I
dl b d
B
B
d
dl
B
2 0 I
0 I 2
l Bdl 0 2 b bd 2 0 d 0 I
B
d
l
I
0
l

18.

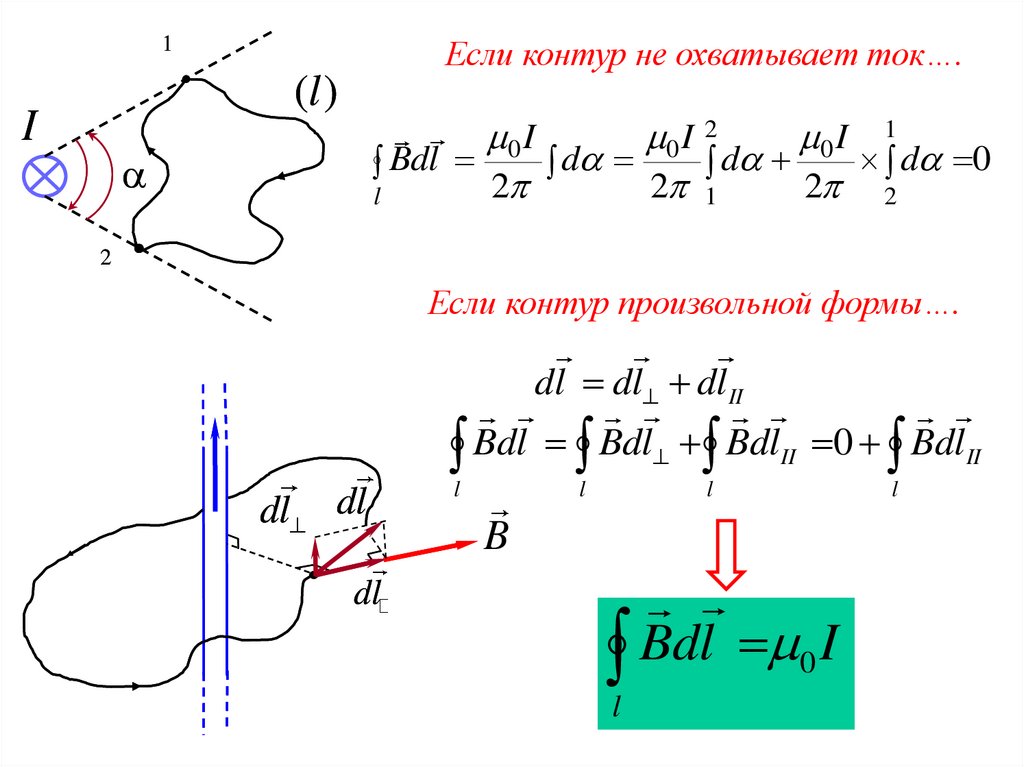
Если контур не охватывает ток….
1
(l )
I
0 I
0 I 2
0 I 1
d 0
Bdl
d
d
2
2 1
2 2
l
2
Если контур произвольной формы….
dl dl dlII
Bdl Bdl BdlII 0 BdlII
dl
dl
dl
l
l
l
B
B
d
l
I
0
l
l

19.

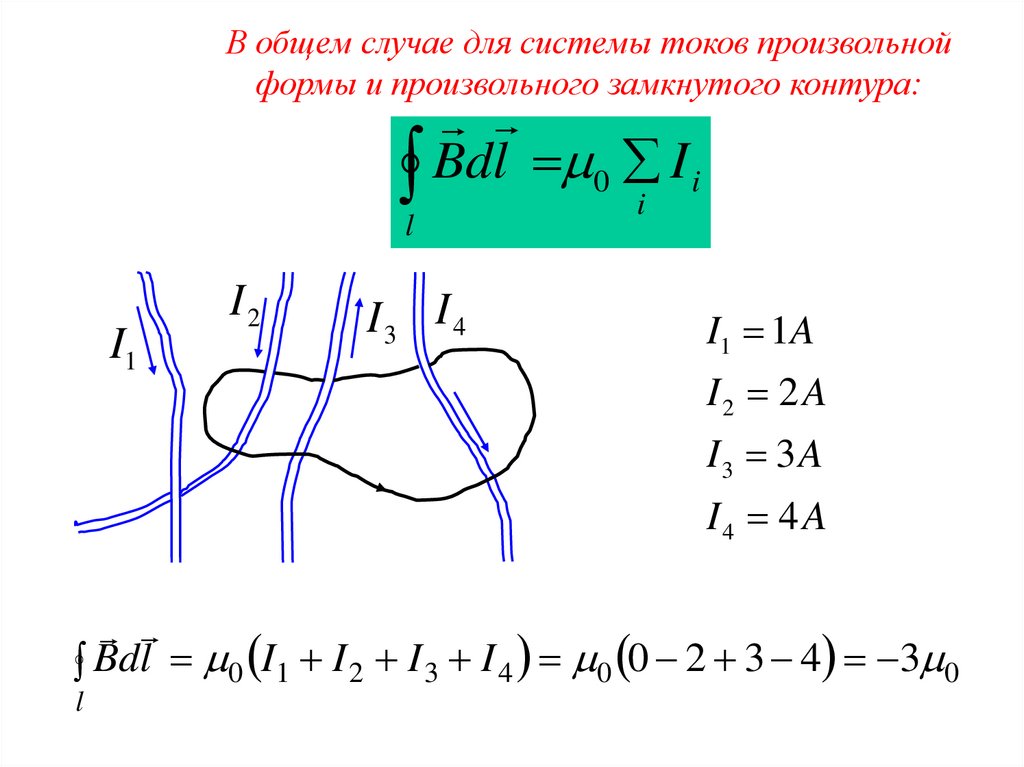
В общем случае для системы токов произвольной
формы и произвольного замкнутого контура:
Bdl 0 I i
l
I1
I2
I3 I 4
i
I1 1A
I2 2 A
I3 3 A
I4 4 A
Bdl 0 I1 I 2 I 3 I 4 0 0 2 3 4 3 0
l

20.

Примеры применения
теоремы о циркуляции вектора B
Магнитное поле прямого тока
• Замкнутый контур представлен
окружности радиуса b.
B
в
dl
виде
• В каждой точке этой окружности вектор
магнитной индукции B одинаков по модулю
и направлен по касательной к окружности:
r
I
L
Bdl B cos dl B dl B 2 b 0 I
l
l
l
0 I
B
2 b

21.

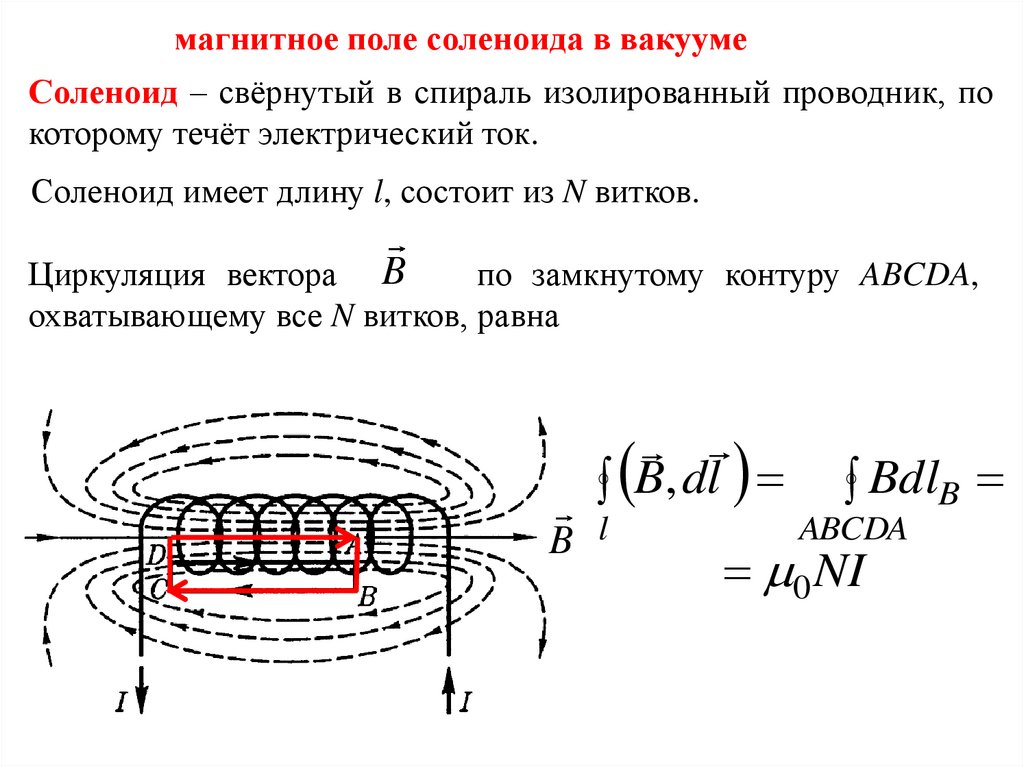
магнитное поле соленоида в вакууме
Соленоид – свёрнутый в спираль изолированный проводник, по
которому течёт электрический ток.
Соленоид имеет длину l, состоит из N витков.
Циркуляция вектора B
по замкнутому контуру ABCDA,
охватывающему все N витков, равна
B, dl
B l
BdlB
ABCDA
0 NI

22.

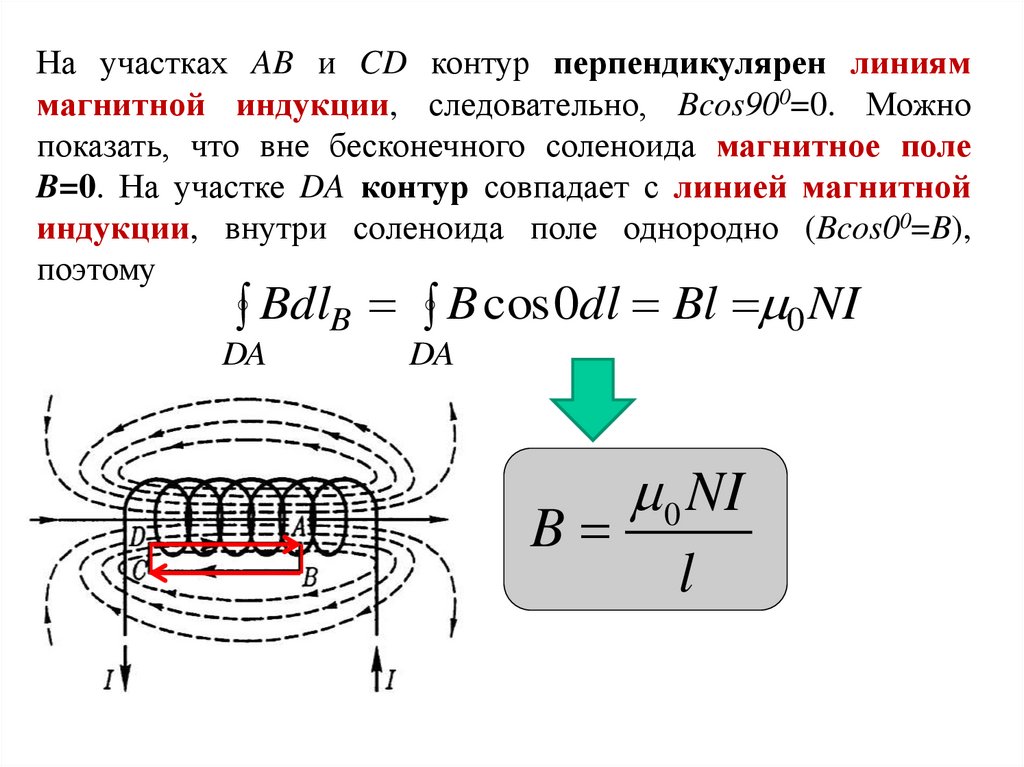
На участках AB и CD контур перпендикулярен линиям
магнитной индукции, следовательно, Bcos900=0. Можно
показать, что вне бесконечного соленоида магнитное поле
B=0. На участке DA контур совпадает с линией магнитной
индукции, внутри соленоида поле однородно (Bcos00=B),
поэтому
BdlB B cos 0dl Bl 0 NI
DA
DA
B
0 NI
l

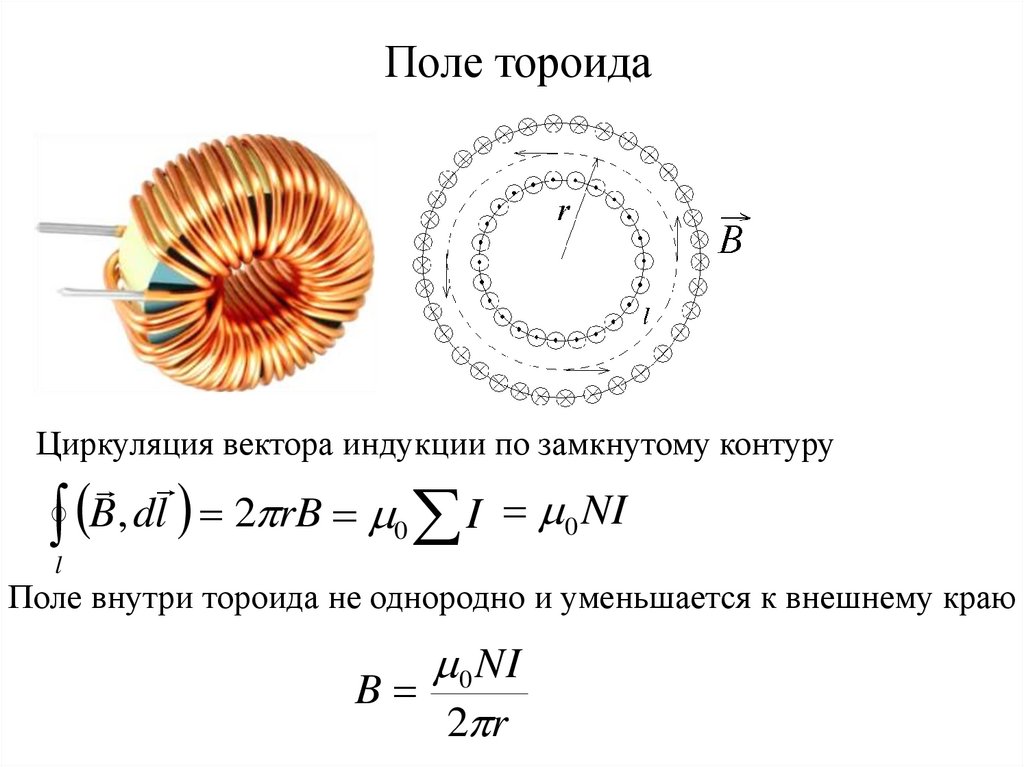
23.

Поле тороида
Циркуляция вектора индукции по замкнутому контуру
B, dl 2 rB 0 I 0 NI
l
Поле внутри тороида не однородно и уменьшается к внешнему краю
0 NI
B
2 r