Вычисление площади поверхности

1. Задача для самостоятельного решения.

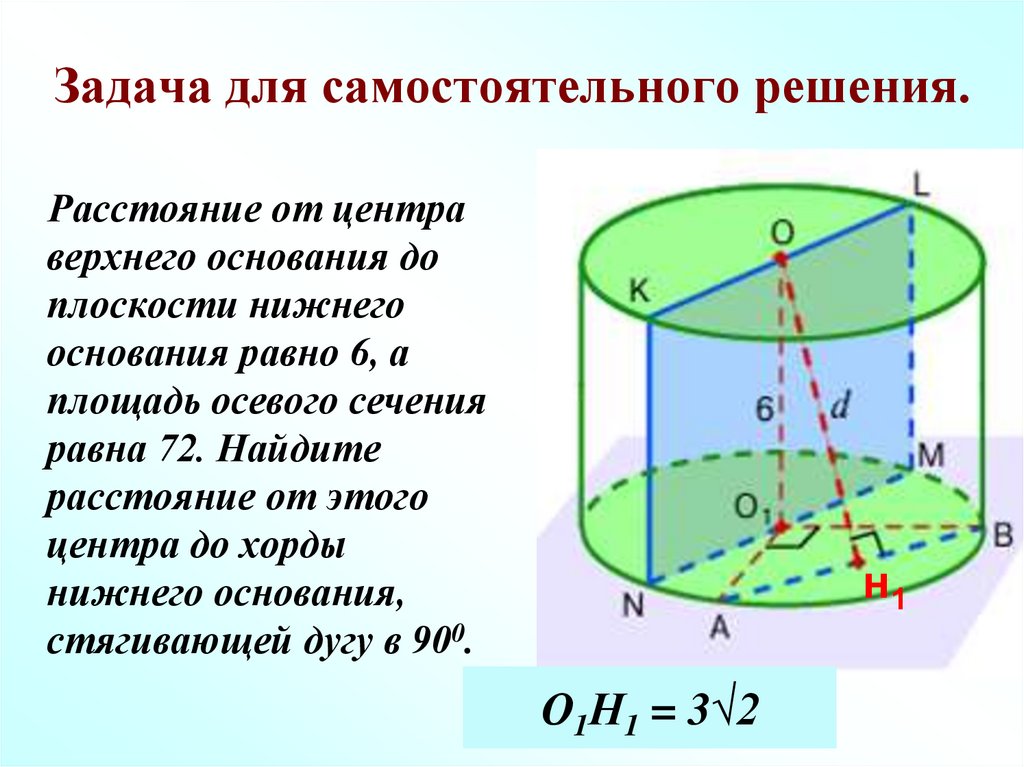
Расстояние от центра
верхнего основания до
плоскости нижнего
основания равно 6, а
площадь осевого сечения
равна 72. Найдите
расстояние от этого
центра до хорды
нижнего основания,
стягивающей дугу в 900.
н1
О1Н1 = 3√2

2.

3.

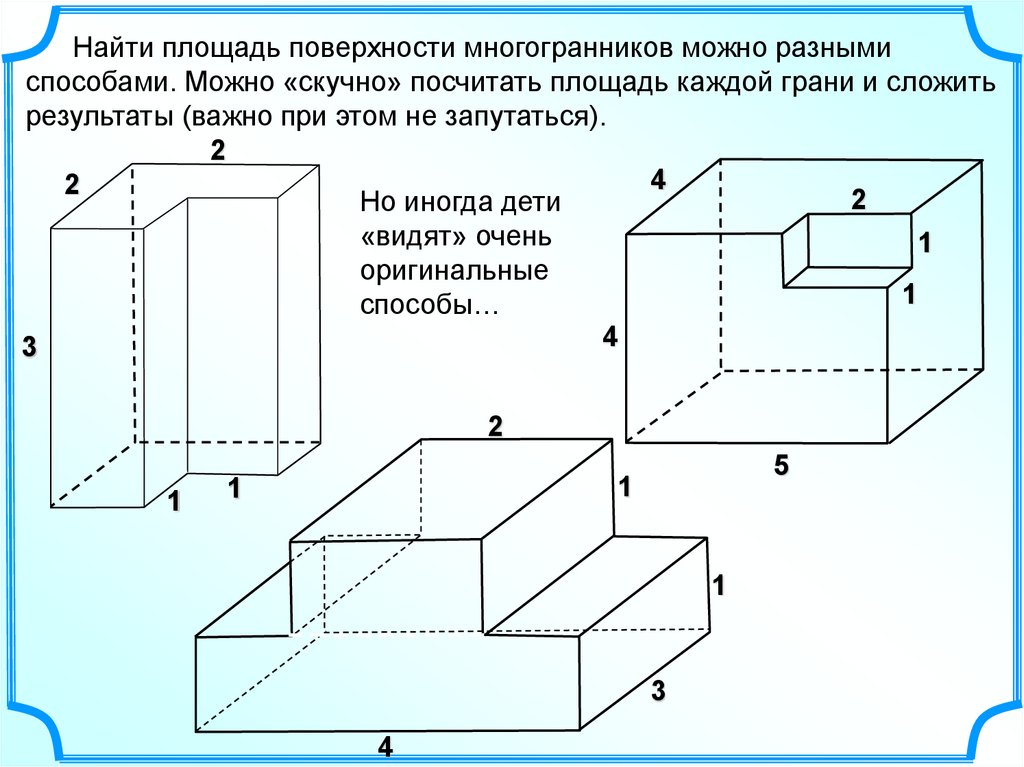
Найти площадь поверхности многогранников можно разными
способами. Можно «скучно» посчитать площадь каждой грани и сложить
результаты (важно при этом не запутаться).
2
4
2
2
Но иногда дети
«видят» очень
1
оригинальные
1
способы…
4
3
2
1
5
1
1
1
3
4

4.

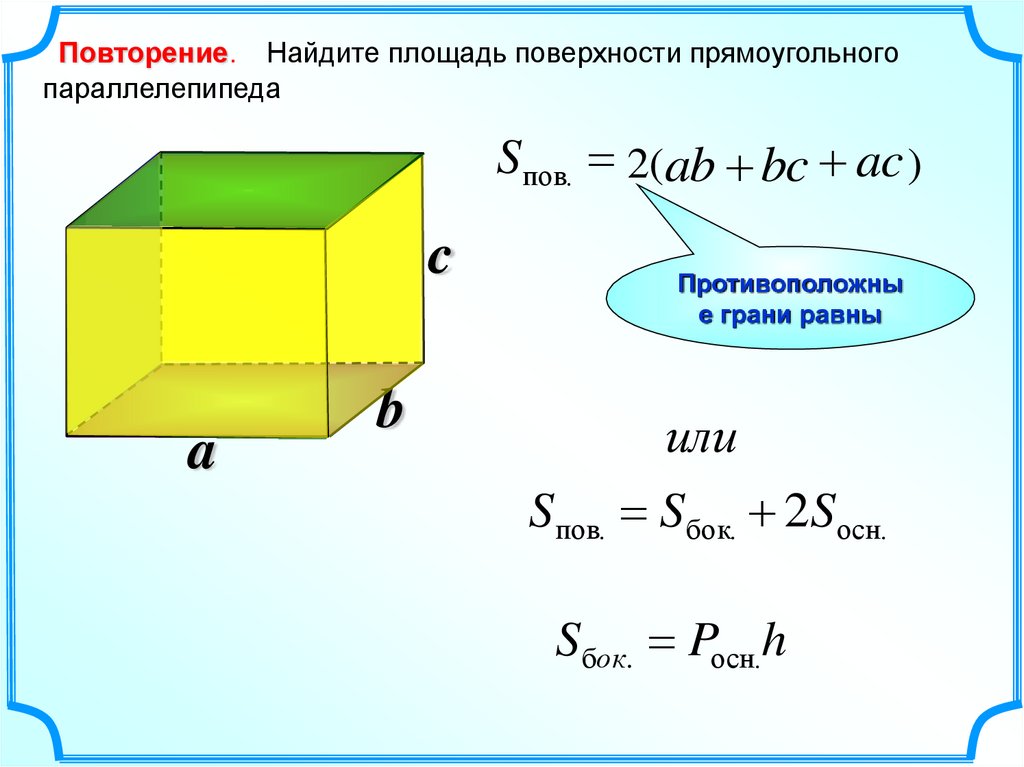
Повторение. Найдите площадь поверхности прямоугольного
параллелепипеда
Sпов. 2(ab bc ac )
c
a
b
Противоположны
е грани равны
или
Sпов. Sбок. 2Sосн.
Sбок. Pосн.h

5.

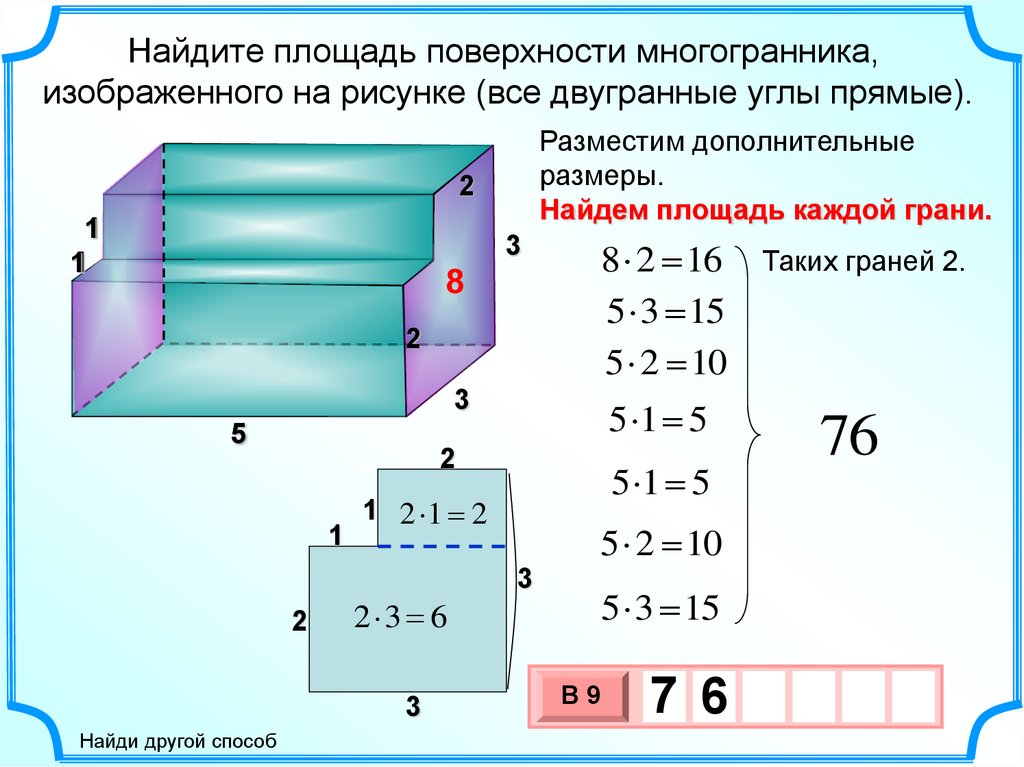
Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
Разместим дополнительные
размеры.
Найдем площадь каждой грани.
2
1
1
3
8 2 16
5 3 15
5 2 10
8
2
3
5
5 1 5
2
1
1 2 1 2
5 2 10
Найди другой способ
5 3 15
2 3 6
3
76
5 1 5
3
2
Таких граней 2.
В9
7 6
3
10 х
х

6.

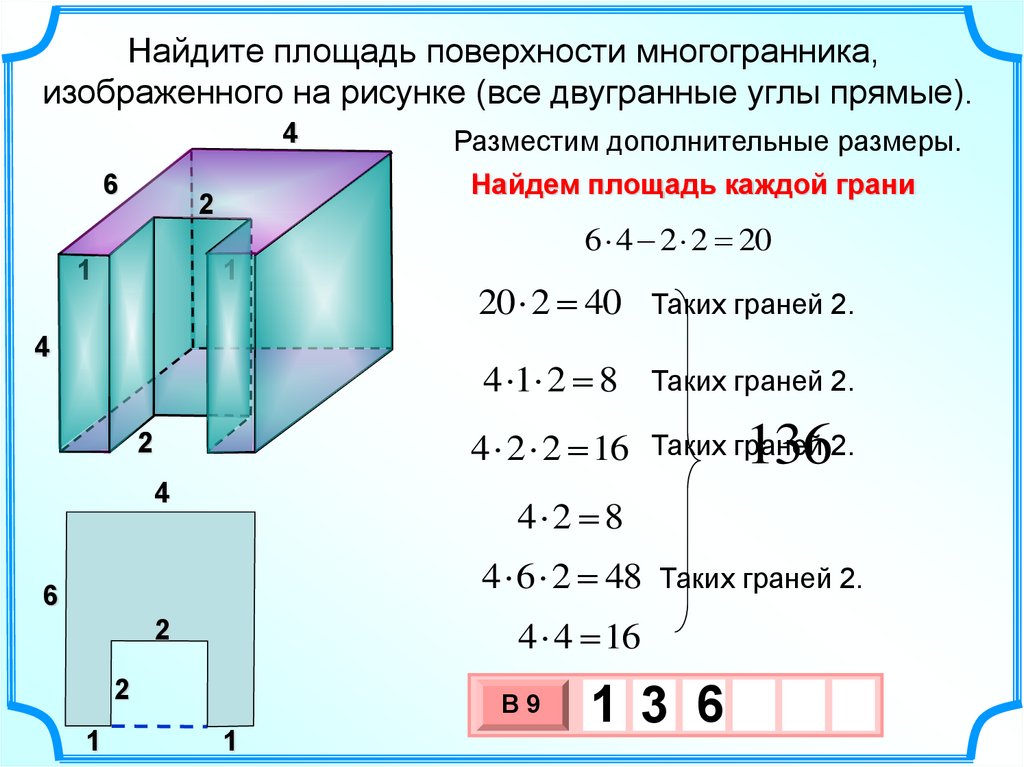
Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
4
6
2
1
Разместим дополнительные размеры.
Найдем площадь каждой грани
6 4 2 2 20
1
4
2
4
20 2 40
Таких граней 2.
4 1 2 8
Таких граней 2.
4 2 2 16
Таких граней 2.
4 2 8
4 6 2 48
6
Таких граней 2.
4 4 16
2
2
1
136
В9
1
1 3 6
3
10 х
х

7.

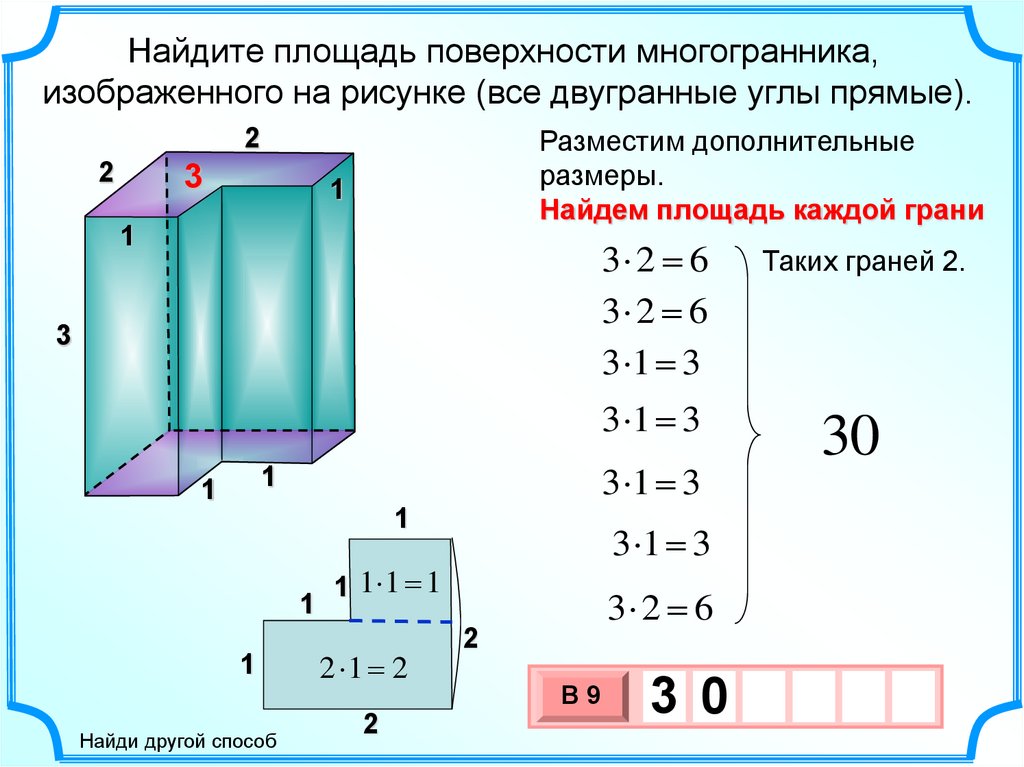
Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
Разместим дополнительные
размеры.
Найдем площадь каждой грани
2
2
3
1
1
3 2 6
3 2 6
3 1 3
3
Таких граней 2.
3 1 3
3 1 3
1
1
1
1
1
Найди другой способ
30
3 1 3
1 1 1 1
2 1 2
2
3 2 6
2
В9
3 0
3
10 х
х

8.

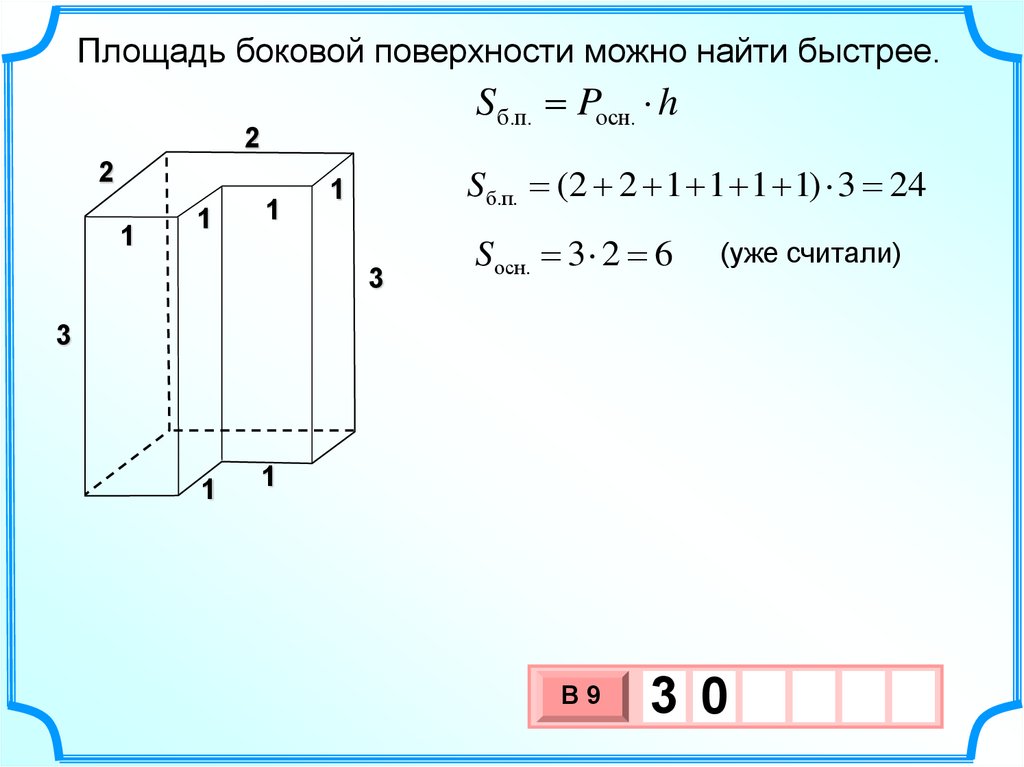
Площадь боковой поверхности можно найти быстрее.
Sб.п. Pосн. h
2
2
1
1
1
Sб.п. (2 2 1 1 1 1) 3 24
1
3
Sосн. 3 2 6
(уже считали)
3
1
1
В9
3 0
3
10 х
х

9.

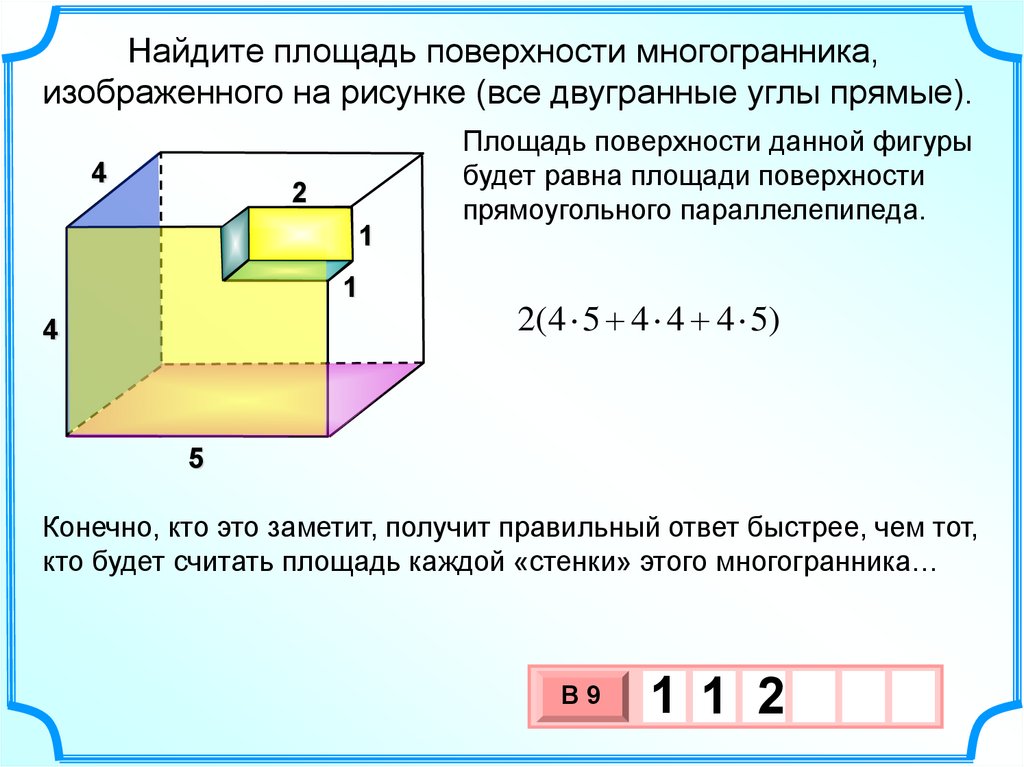
Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
4
2
1
1
4
Площадь поверхности данной фигуры
будет равна площади поверхности
прямоугольного параллелепипеда.
2(4 5 4 4 4 5)
5
Конечно, кто это заметит, получит правильный ответ быстрее, чем тот,
кто будет считать площадь каждой «стенки» этого многогранника…
В9
1 1 2
3
10 х
х

10.

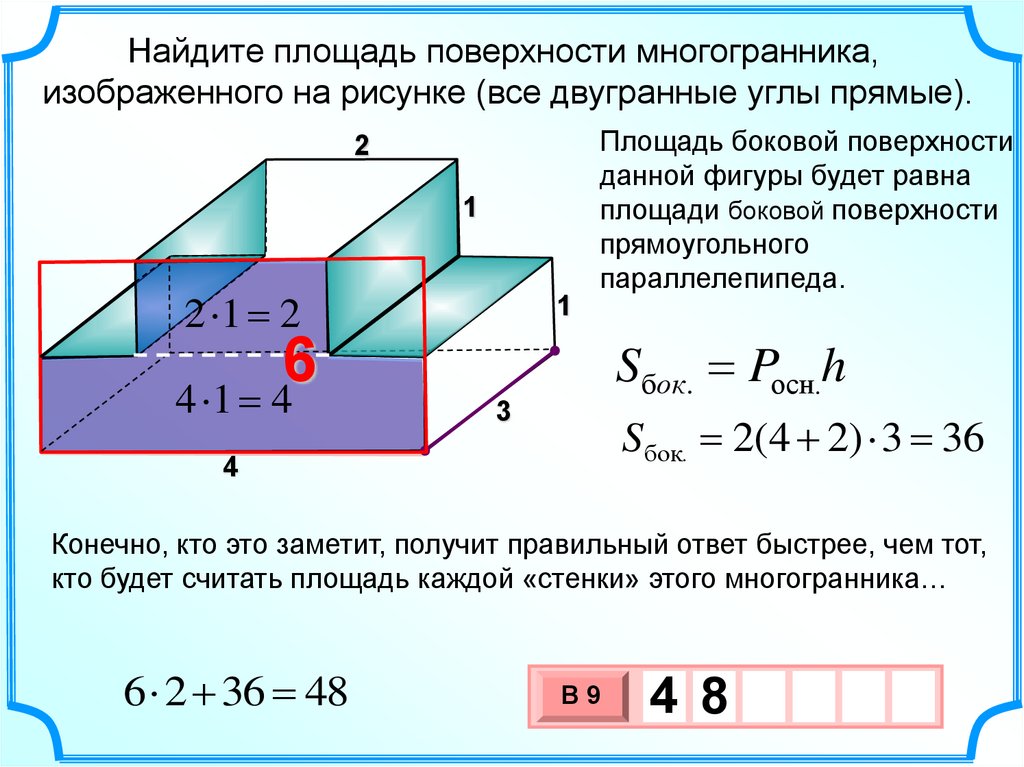
Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
Площадь боковой поверхности
данной фигуры будет равна
площади боковой поверхности
прямоугольного
параллелепипеда.
2
1
2 1 2
6
4 1 4
1
Sбок. Pосн.h
3
Sбок. 2(4 2) 3 36
4
Конечно, кто это заметит, получит правильный ответ быстрее, чем тот,
кто будет считать площадь каждой «стенки» этого многогранника…
6 2 36 48
В9
4 8
3
10 х
х

11.

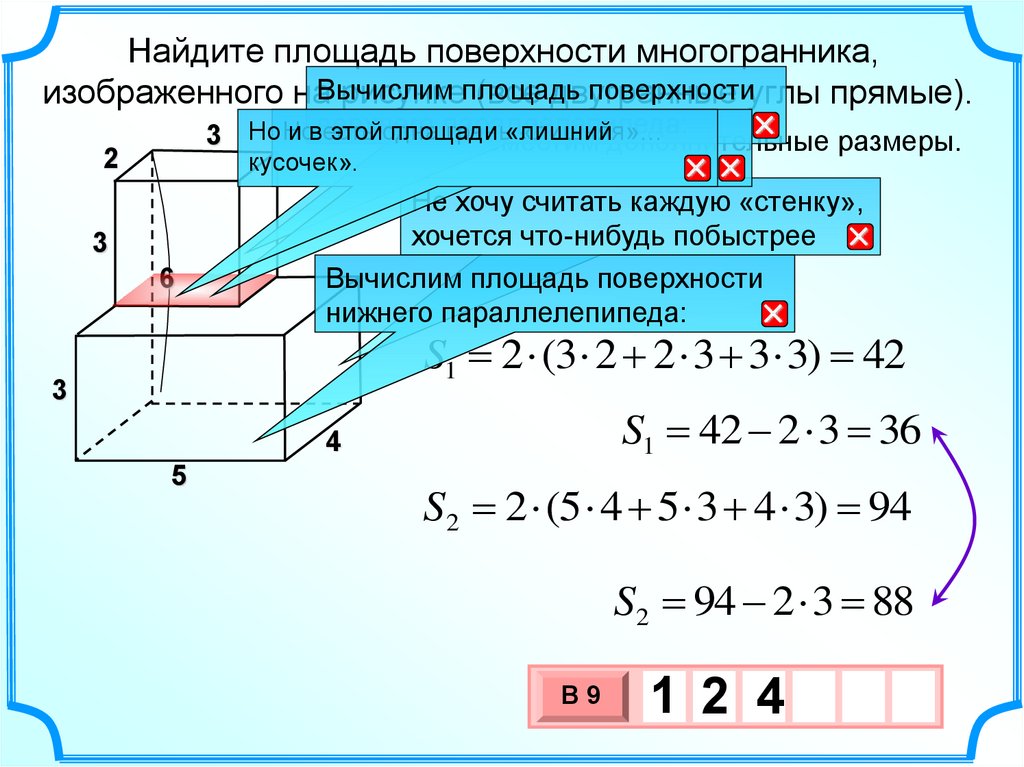
Найдите площадь поверхности многогранника,
поверхностиуглы прямые).
изображенного наВычислим
рисункеплощадь
(все двугранные
параллелепипеда:
и вверхнего
есть
этойодна
площади
грань
«лишний
«лишняя»…
3 Но Но
Разместим
дополнительные размеры.
кусочек».
2
3
6
Не хочу считать каждую «стенку»,
хочется что-нибудь побыстрее
Вычислим площадь поверхности
нижнего параллелепипеда:
S1 2 (3 2 2 3 3 3) 42
3
S1 42 2 3 36
4
5
S2 2 (5 4 5 3 4 3) 94
S2 94 2 3 88
В9
1 2 4
3
10 х
х

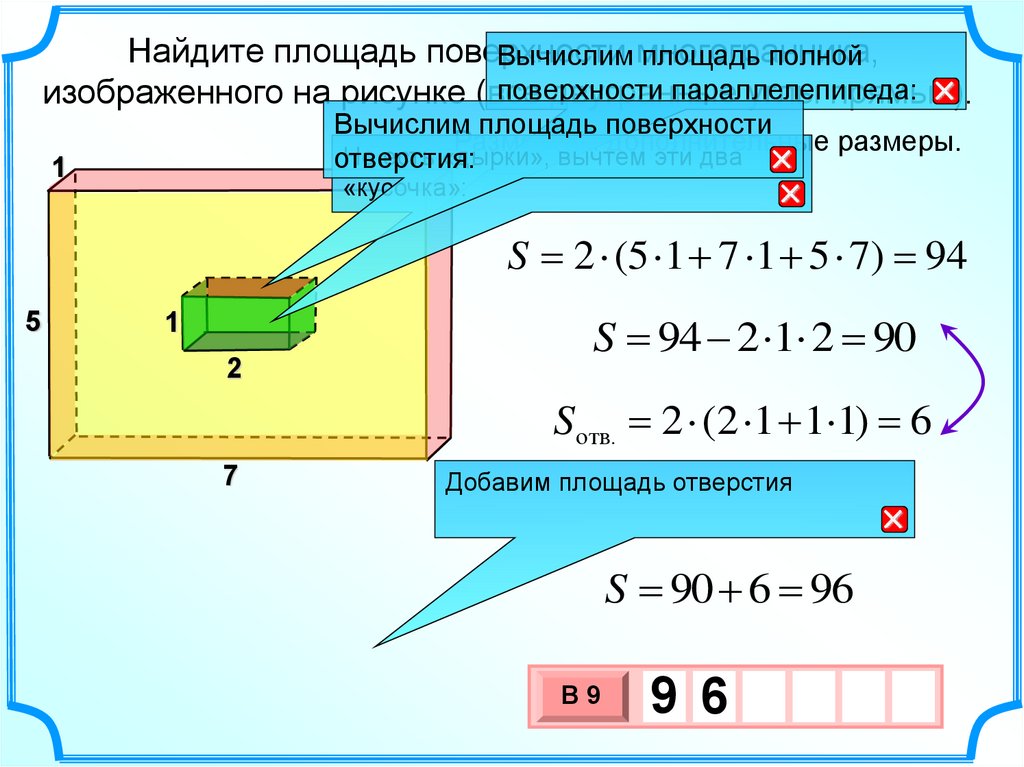
12.

Найдите площадь поверхности
Вычислим многогранника,
площадь полной
поверхности
параллелепипеда:
изображенного на рисунке (все
двугранные
углы прямые).
Вычислим площадь поверхности
Разместим дополнительные размеры.
Но есть «дырки», вычтем эти два
отверстия:
1
«кусочка»:
S 2 (5 1 7 1 5 7) 94
5
1
2
S 94 2 1 2 90
Sотв. 2 (2 1 1 1) 6
7
Добавим площадь отверстия
S 90 6 96
В9
9 6
3
10 х
х

13.

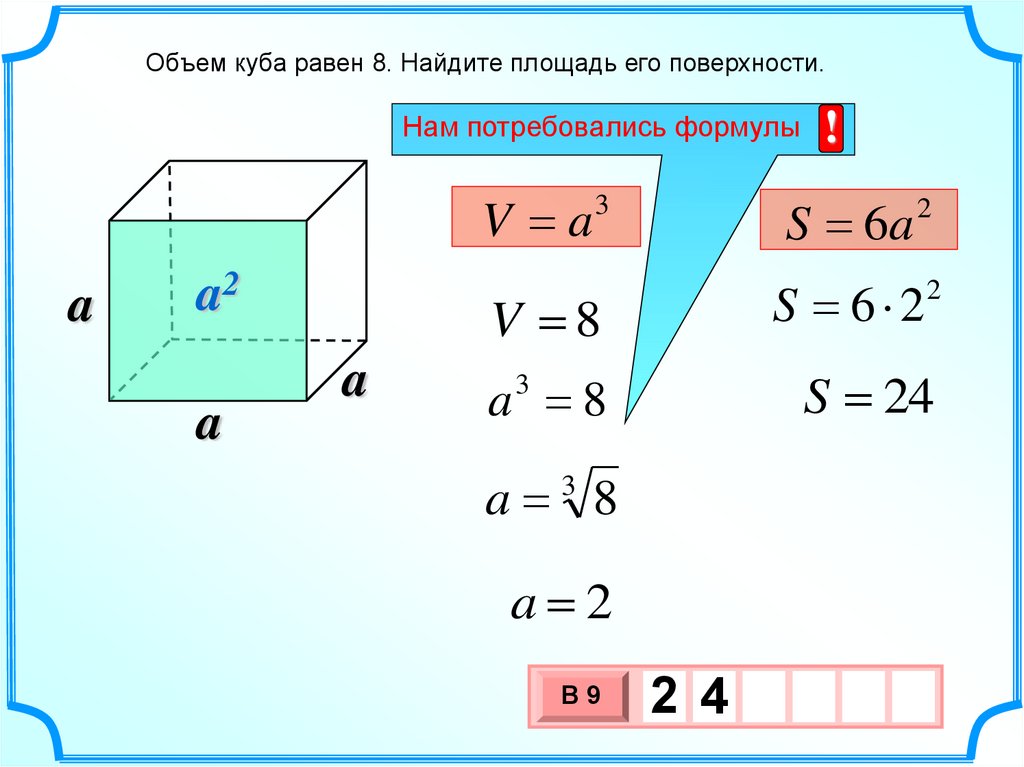
Объем куба равен 8. Найдите площадь его поверхности.
!
Нам потребовались формулы
V a
a
a2
a
a
S 6a
3
2
V 8
S 6 2
a 8
S 24
3
a 8
3
a 2
В9
2 4
3
10 х
х
2

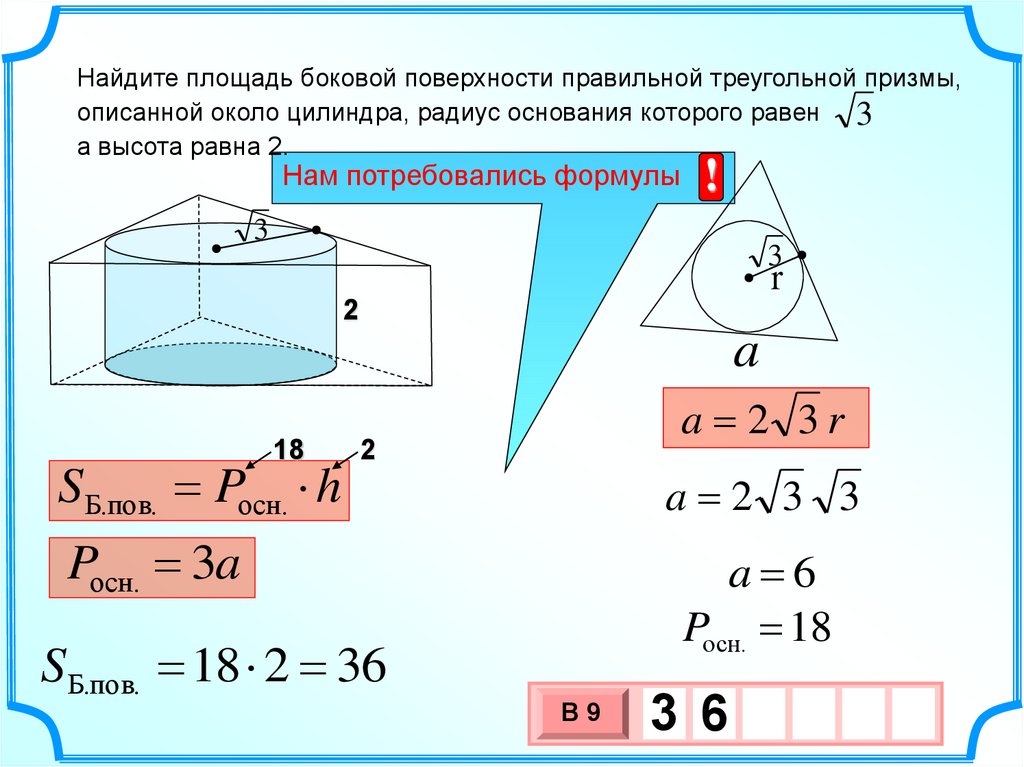
14.

Найдите площадь боковой поверхности правильной треугольной призмы,
описанной около цилиндра, радиус основания которого равен 3
а высота равна 2.
Нам потребовались формулы
!
3
3
r
2
a
18
S Б.пов. Pосн. h
a 2 3r
2
a 2 3 3
Pосн. 3a
S Б.пов. 18 2 36
a 6
Pосн. 18
В9
3 6
3
10 х
х

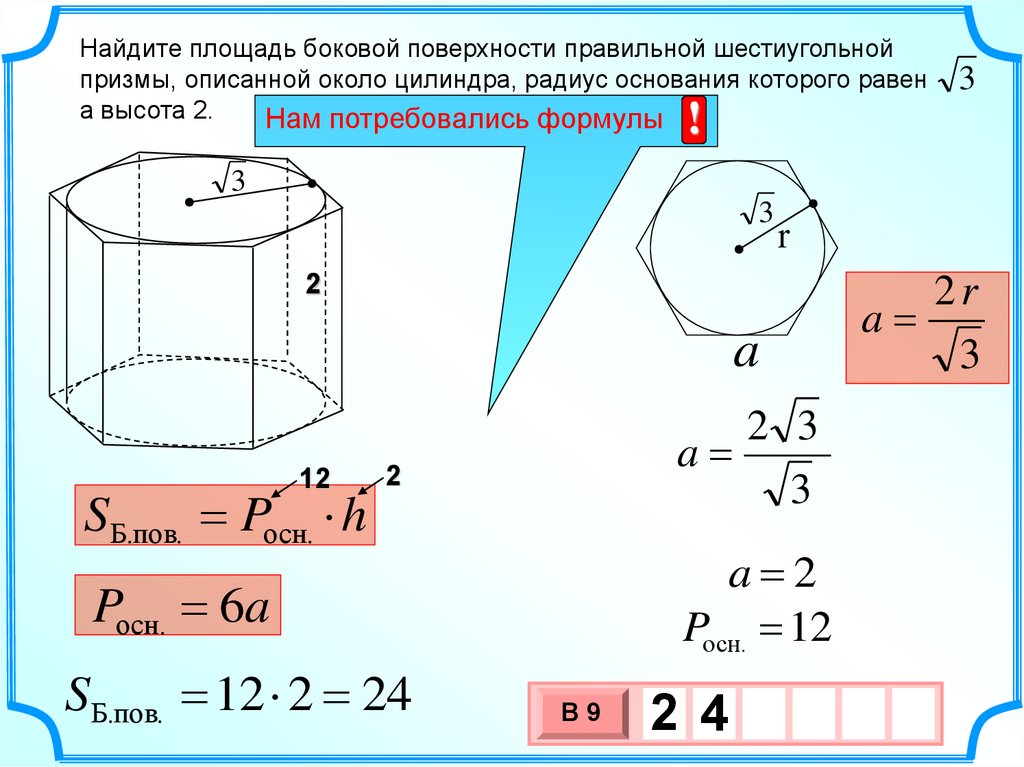
15.

Найдите площадь боковой поверхности правильной шестиугольной
призмы, описанной около цилиндра, радиус основания которого равен
а высота 2.
Нам потребовались формулы
3
!
3
3
r
2
2r
a
3
a
12
S Б.пов. Pосн. h
2 3
a
3
2
a 2
Pосн. 12
Pосн. 6a
SБ.пов. 12 2 24
В9
2 4
3
10 х
х

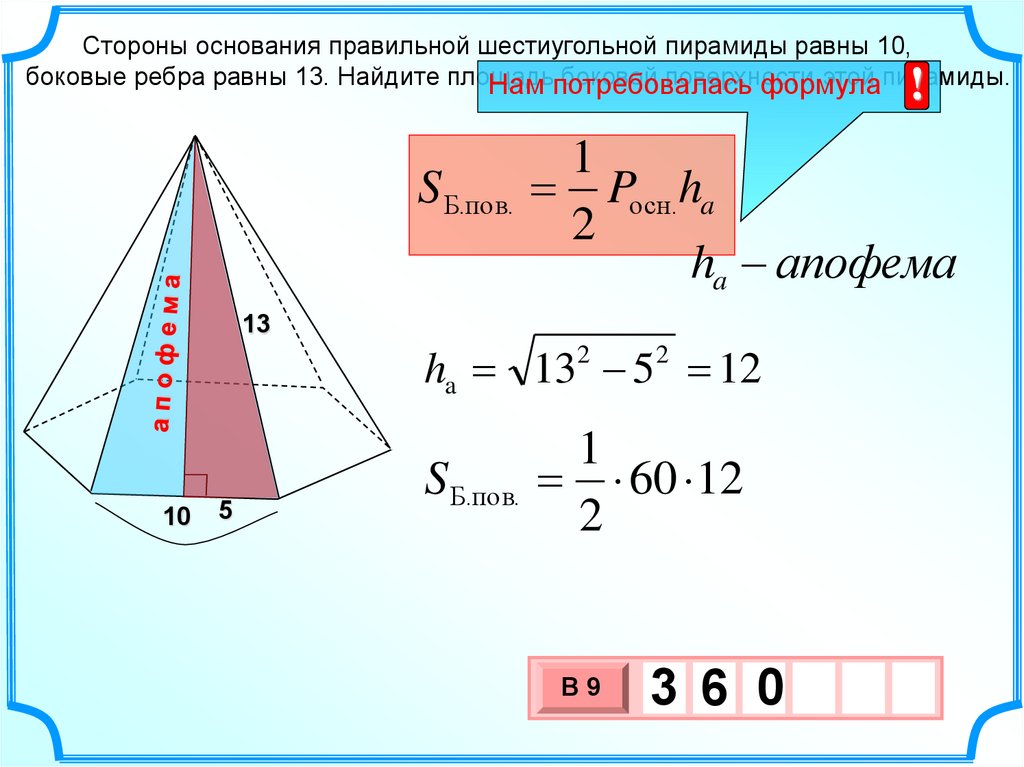
16.

Стороны основания правильной шестиугольной пирамиды равны 10,
боковые ребра равны 13. Найдите площадь
боковой поверхности
этой пирамиды.
Нам потребовалась
формула
!
S Б.пов.
13
1
Pосн.ha
2
ha апофема
ha 13 5 12
2
10
5
S Б.пов.
2
1
60 12
2
В9
3 6 0
3
10 х
х

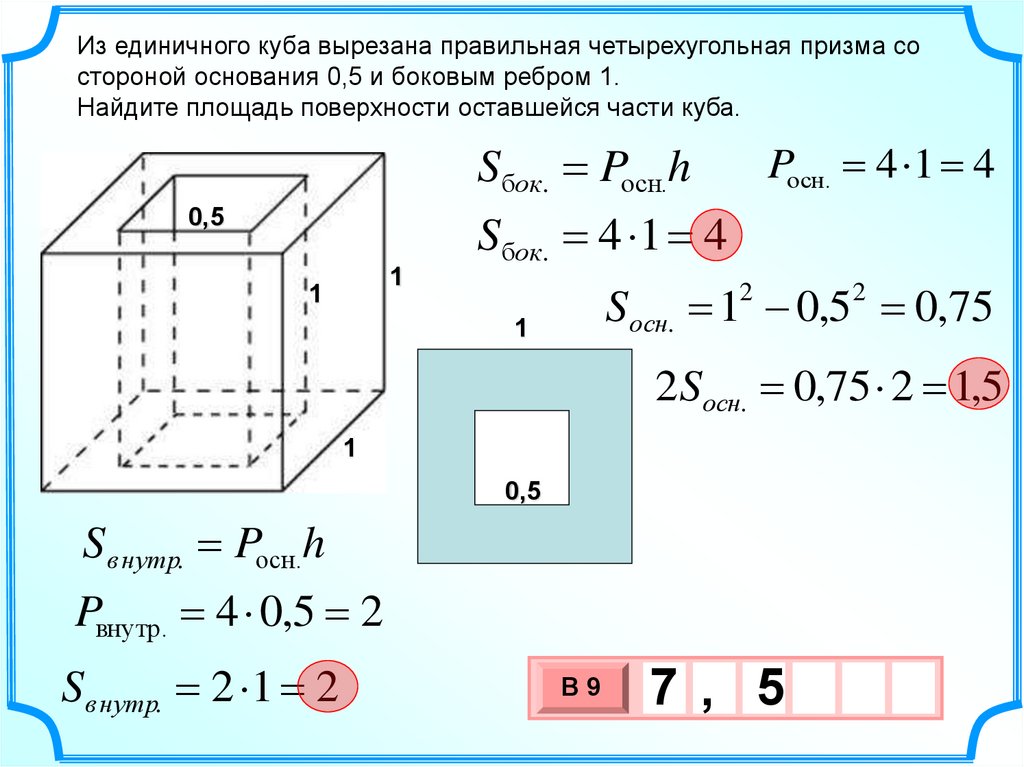
17.

Из единичного куба вырезана правильная четырехугольная призма со
стороной основания 0,5 и боковым ребром 1.
Найдите площадь поверхности оставшейся части куба.
Sбок. Pосн.h
Pосн. 4 1 4
Sбок. 4 1 4
0,5
1
1
S осн. 1 0,5 0,75
2
1
2
2Sосн. 0,75 2 1,5
1
0,5
S внутр. Pосн.h
Pвнутр. 4 0,5 2
S внутр. 2 1 2
В9
7 , 5
3
10 х
х

18.

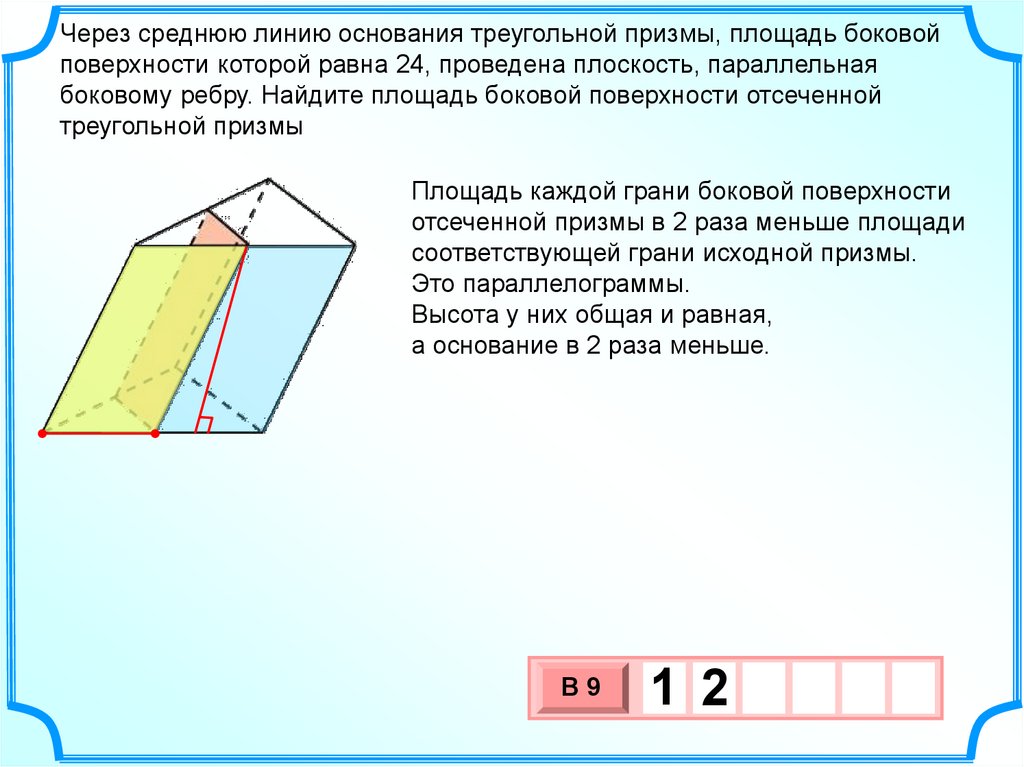
Через среднюю линию основания треугольной призмы, площадь боковой
поверхности которой равна 24, проведена плоскость, параллельная
боковому ребру. Найдите площадь боковой поверхности отсеченной
треугольной призмы
Площадь каждой грани боковой поверхности
отсеченной призмы в 2 раза меньше площади
соответствующей грани исходной призмы.
Это параллелограммы.
Высота у них общая и равная,
а основание в 2 раза меньше.
В9
1 2
3
10 х
х