Similar presentations:
Законы сохранения
1.
Законы сохраненияПлан лекции
1. Импульс тела.
2. Энергия.
2.
импульс телаИмпульс тела – векторная физическая величина равная произведению
массы тела на его скорость.
p mv
Единица измерения - кг*м/с.
P
3.
и н а я ф о р м ул и р о в ка 2 з а ко н а Н ь юто н аma F
d md d (m ) dp
ma m
dt
dt
dt
dt
dp
F
dt
Производная импульса тела по времени равна действующей на
него силе (сумме сил).
4.
З а ко н с ох р а н е н и я и м п ул ь с аСумма импульсов тел системы называют импульсом системы:
pñèñò m1v1 m2v2 .... mnvn
Система называется замкнутой, если на неё не действуют
внешние силы, либо действуют, но их равнодействующие равны
нулю.
F
âí åø í
0
В замкнутой системе действуют только внутренние силы
5.
Закон сохранения импульса.в замкнутой системе векторная сумма импульсов тел, входящих
в данную систему, остается постоянной во времени:
m1v1 m2v2 .... mnvn const
Главным моментом является то, что в замкнутой системе тел векторная
сумма импульсов всех тел остается постоянной. И совершенно не важно,
что происходит в системе - сумма импульсов всегда одна и та же.
6.
Импульс замкнутой системы сохраняется:pñèñò const
7.
це н т р м а с сЦентром масс системы материальных точек называется точка С,
положение которой в пространстве задается радиус-вектором ,
определяемым следующим образом:
m1r1 m2 r2 ... mn rn
Rc
M
где r – радиус-вектор тела, m – масса
тела, M – масса системы.
M m1 m2 ... mn
mi ri
Rc
M
8.
Если система замкнута, то центр масс движется прямолинейно иравномерно, либо остается неподвижным
Vc const
Центр масс
9.
Реактивное движениеРеактивное движение - движение, возникающее при отделении от тела
с некоторой скоростью какой-либо его части.
В случае реактивного движения масса тела не остается постоянной, она
уменьшается, т.к. часть массы отбрасывается.
10.
ЭнергияЭнергия является универсальной мерой движения и взаимодействия любых
объектов в природе. Имеются различные формы энергии: механическая,
тепловая, электромагнитная, ядерная. . .
Опыт показывает, что энергия не появляется ниоткуда и не исчезает бесследно,
она лишь переходит из одной формы в другую. Это фундаментальное свойство
энергии. Каждый вид энергии представляет собой некоторое математическое
выражение.
Виды механической энергии.
1. Кинетическая энергия
Кинетическая энергия – энергия движения тела.
m 2
Åê
2
m – масса тела, v - его скорость
11.
2. Потенциальная энергияПотенциальная энергия – энергия взаимодействия тела.
2.1 Потенциальная энергия упруго деформированного тела
k – жесткость пружины
2.2 Потенциальная энергия тела вблизи поверхности Земли
Åï mgh
m – масса тела, h – высота
12.
Механическая энергия E тела равна сумме его кинетической ипотенциальной энергий:
Å Åê Åï
Механическая энергия системы тел равна сумме их кинетических энергий и
потенциальной энергии их взаимодействия друг с другом.
Eпол Eк E п
Закон сохранения механической энергии:
Если в замкнутой системе действуют только консервативные силы,
то механическая энергия системы сохраняется.
13.
Механическая работаМеханическая работа некоторой силы F есть скалярная величина равная
произведению этой силы на перемещение и на угол между направлениями силы
и перемещением.
A F s Cos
F
s
Или, используя векторную алгебру, можем записать так:
A (F s )
Единица измерения работы – 1 Джоуль.
14.
Работа переменной силы на криволинейной траектории:Â
A FdsCos
À
15.
О ко н с е р в а т и в н ы х с и л а хЕсть особые силы, работа которых не зависит от формы траектории, а
определяется только начальным и конечным положением тел.
Такие силы называют консервативными.
Например, к консервативным силам относятся сила тяжести, сила
упругости.
Неконсервативной силой является сила трения.
16.
мощностьЧасто имеет значение быстрота, с которой совершается работа.
Мощность N есть отношение работы A ко времени t, за которое эта
работа совершена:
A
N
t
Мощность численно равна работе совершённой в единицу времени. Единица
измерения мощности – 1 Ватт.
Математически мощность можно определить через
производную работы по времени:
dA
N
dt
Мощность, развиваемая силой F при движении тела со скоростью V:
N F
17.
С вя з ь р а б от ы и э н е р г и иТеорема о кинетической энергии.
Изменение кинетической энергии тела равно работе, совершённой
приложенными к телу внешними силами за рассматриваемый промежуток
времени.
Åê 2 Åê1 À
Работа консервативной силы равна убыли потенциальной энергии:
Åï 1 Åï 2 À
18.
Це н т р а л ь н ы й уд а р ш а р о вУдар – кратковременное взаимодействие тел, при котором возникают
деформации и ударные силы значительной величины.
Различают два предельных случаев удара:
1. Абсолютно упругий удар.
После такого удара тела полностью восстанавливают свои формы,
полная механическая энергия не переходит в другие формы, то есть
сохраняется.
2. Неупругий удар.
После такого удара тела деформируются, слипаются и движутся с
одной скоростью. Механическая энергия частично переходит в
тепловую , то есть не сохраняется.
19.
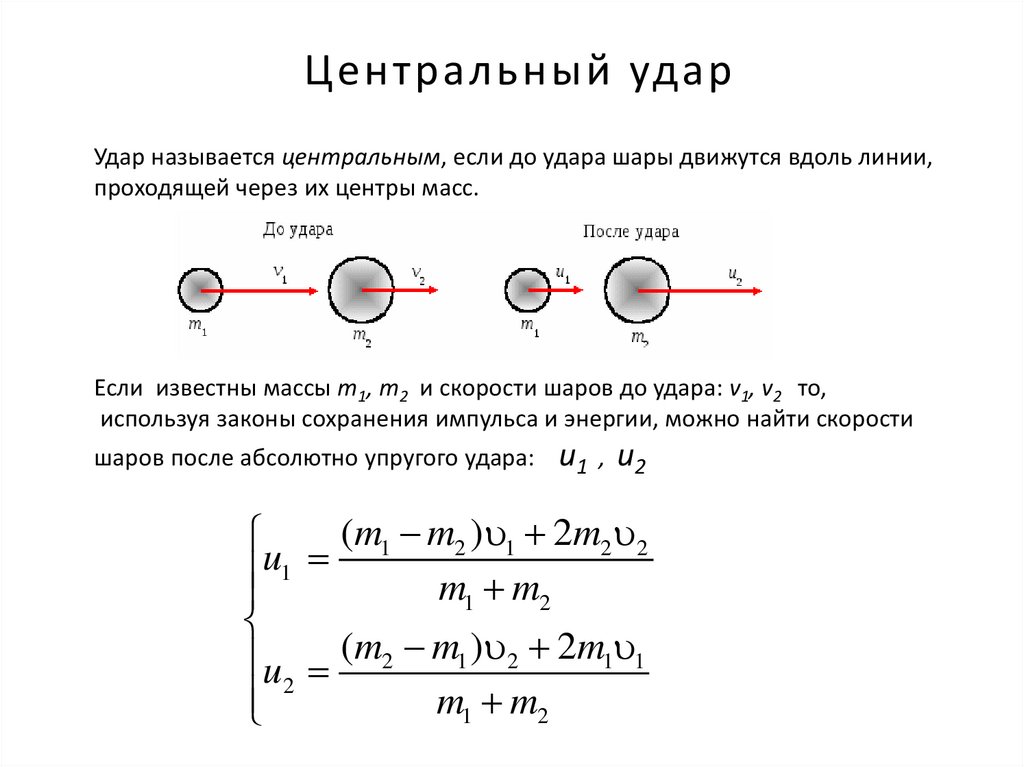
Центральный ударУдар называется центральным, если до удара шары движутся вдоль линии,
проходящей через их центры масс.
Если известны массы m1, m2 и скорости шаров до удара: v1, v2 то,
используя законы сохранения импульса и энергии, можно найти скорости
шаров после абсолютно упругого удара:
u1 , u2
(m1 m2 ) 1 2m2 2
u1
m1 m2
u (m2 m1 ) 2 2m1 1
2
m1 m2


















 physics
physics








