Особые приёмы решения логарифмических неравенств с переменной в основании

1.

Особые приёмы решения
логарифмических
неравенств с переменной
в основании
Занятие №2
Методическая разработка
учителя Поляковой Е. А.

2.

Решение простейших
логарифмических неравенств:
log a x1 log a x2
log a x1 log a x2
a>1
x1 > x 2 > 0
0<a<1
x2 > x 1 > 0
a>1
x2 > x 1 > 0
0<a<1
x1 > x 2 > 0

3.

В предыдущем занятии
было доказано:
выражения
log a b и (b – 1)(a – 1)
имеют один знак

4.

Решение логарифмических
неравенств с применением
доказанного свойства:
неравенство log h(x) f(x) > log h(x) g(x) равносильно
неравенству (f – g)(h – 1) > 0 на ОДЗ
неравенство log h(x) f(x) < log h(x) g(x) равносильно
неравенству (f – g)(h – 1) < 0 на ОДЗ

5.

Алгоритм решения неравенства log h(x) f(x) > log h(x) g(x)
1) Находим область допустимых значений переменной (ОДЗ):
f ( x ) 0,
g ( x ) 0,
h( x ) 0,
h( x ) 1.
(Условимся далее две последние строки
системы писать одной так: 0 < h(x) ≠ 1)
2) Решаем неравенство (f(х) – g(х))(h(х) – 1) > 0.
3) Для найденного решения учитываем ОДЗ.
4) Записываем ответ.

6.

Решите неравенство:
x 1 0,
0 x 3 1;
1) ОДЗ:
log x 3 x 1 2;
x 1,
3 x 4.
3 x 4;
2) Переписываем неравенство в виде
log x 3 х 1 log x 3 ( x 3)2 ;
Решаем неравенство (х – 1 – (х – 3) 2)(х – 3 – 1) < 0;
(х – 1 – х 2 + 6 x – 9)(х – 4) < 0;
–( х 2 – 7 x + 10)(х – 4) < 0;
( х 2 – 7 x + 10)(х – 4) > 0; (х – 5)(х – 2)(х – 4) > 0;
ОДЗ
Ответ: 3 < x < 4; x > 5
–
+
/////////////////////////////////
○
2
–
//////////////////
+
/////////////////////////////////////////
○
○
○
х
3
4
5

7.

Решите неравенство: log x2 3 2 x 1
x 1,5,
3 2 х 0,
1) ОДЗ:
x 1,
2
0 x 1; х 0;
2) log 2 3 2 х 1 log 2 3 2 х log 2 x2
x
x
x
3 2 х x x 1 0; x
2
2
2
2 х 3 x 1 х 1 0;
х 3 х 1 x 1 х 1 0;
ОДЗ
+
+
+
//////////////////////
///////////////////////////////////////////////////
○
-3
Ответ: (- 3; - 1)
○
-1
○
0
○
1
○
1,5
х

8.

Решите неравенство: log x
x 3 0,
2
1) ОДЗ: x 3 x 0,
x 2 3 x 1;
2
3 х
x 3 1
3 13
x
,
x 3,
2
13 3
0 x
.
x( x 3) 0, х 3,
2
x( x 3) 0;
x 2 3 x 1 0;
2) log x2 3 х x 3 1 log 2 х 3 log 2 ( x2 3х)
x 3 х
x 3 х
2
2
х
3
x
3
х
x
3х 1 0;
2
2
x
2
х
3
x
3х 1 0;
13 3,6
3 13 3 13
х 3 х 1 x
х
0; ОДЗ
2
2
+
- //////////////////
+
+
///////////
///////////////////////
○
○
○0///////////////////////////
○ ○
13 3 1
-3
3 13
х
2
2
3 13
1;
Ответ: 0;
2

9.

15
2
Решите неравенство: log x
1 2x
15
0, 1 2 х 0, х 0,5, 0 x 0,5.
1) ОДЗ: 1 2 х
0 x 1; 0 x 1; 0 x 1;
15
2
2) log x
1 2x
∙ ( - 1);
1
15
1 log x
2;
1 2x
15
2
log x
log
х
;
x
1 2x
1 2х
log x
log x х 2 ;
15
1 2х
2
х
х 1 0;
15
1 2 х 15х х 1 0
2
15
∙ ( - 15);

10.

1
1
2
15
х
2
х
1
х
1
0;
15
х
х
х 1 0
3
5
1
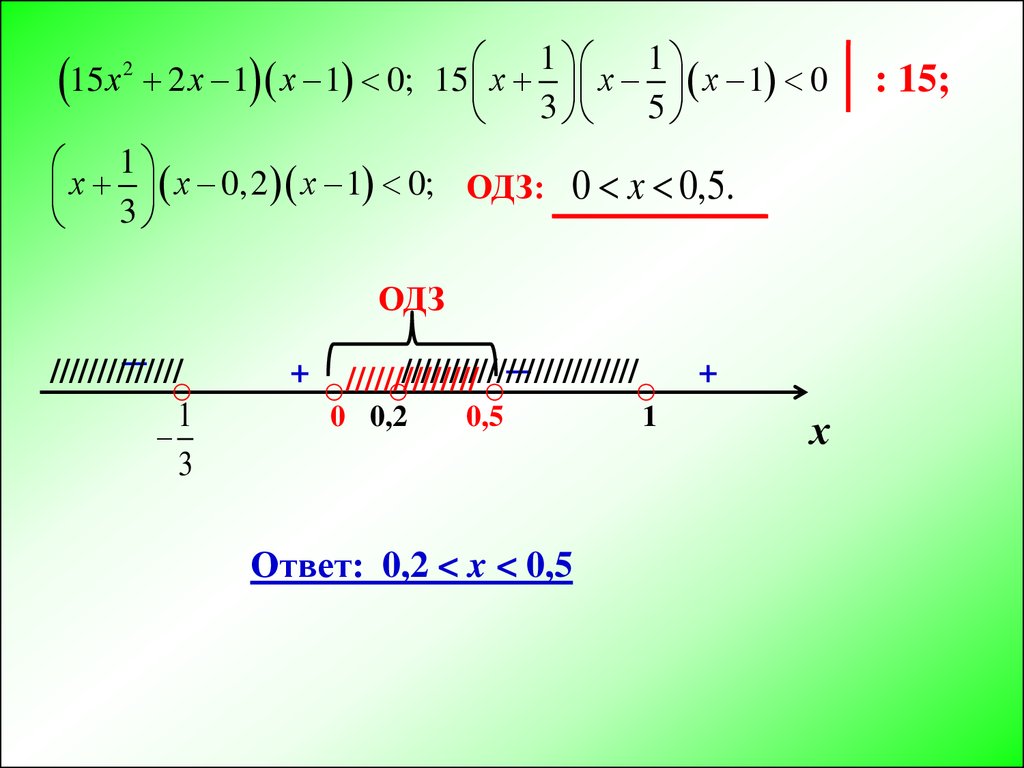
х х 0,2 х 1 0; ОДЗ: 0 x 0,5.
3
ОДЗ
─
//////////////
○
1
3
+
/////////////////////////
─
○//////////////
○
○
0 0,2
0,5
Ответ: 0,2 < x < 0,5
○
1
+
х
: 15;

11.

1) Решите неравенство: log3 x
Ответ:
3 13
;0
2
2) Решите неравенство:
1 2
Ответ: ;
5 7
1
1
x
3 5
0;
2
3 5
2;
2
log 2 x 5 х 1 log 3 x 7 х 1
1
; .
2
15 х 2 2
2
2
11 х
0