Similar presentations:
Определители
1.
ЛЕКЦИЯТЕМА:
«ОПРЕДЕЛИТЕЛИ»
1
2.
ПЛАН1.
2.
3.
4.
5.
6.
Определение, порядок определителя
Миноры и алгебраические
дополнения
Свойства определителей
Вычисление определителей: итоги
Понятие обратной матрицы.
Алгоритм построения (нахождения)
обратной матрицы
Матричные выражения и матричные
уравнения
2
3.
ИЗ ИСТОРИИ НАУКИШвейцарский математик Крамер (G. Cramer,
1704–1752) заложил основы теории определителей,
хотя и не предложил для них удобного
обозначения (это сделал в 1841 году А. Кэли).
В 1772 году Вандермонд (A.T. Vandermonde,
1735–1796) опубликовал обширное исследование
определителей, один из которых носит теперь его
имя.
Систематическое изложение этой теории
принадлежит Бине (J.F.M. Binet, 1786–1856) и
Коши (A.L. Cauchy, 1789–1857). Их труды по
теории определителей относятся к периоду 1812–
1815гг.
3
4.
Габриэль КрамерGabriel Cramer
1704–1752
Швейцарский
математик, ученик
и друг Иоганна
Бернулли,
один из
создателей
линейной
алгебры.
4
5.
Определитель (или детерминант) — одно изосновных понятий линейной алгебры
Это многочлен, комбинирующий элементы
квадратной матрицы таким образом, что его
значение сохраняется при транспонировании и
линейных комбинациях строк или столбцов.
ОПРЕДЕЛИТЕЛЬ ХАРАКТЕРИЗУЕТ
СОДЕРЖАНИЕ МАТРИЦЫ.
В частности, если в матрице есть линейнозависимые строки или столбцы, то определитель
равен нулю.
Определитель играет ключевую роль в решении в
общем виде систем линейных уравнений, на его
основе вводятся базовые понятия.
5
6.
СПЕЦИАЛЬНЫЕ ВИДЫОПРЕДЕЛИТЕЛЕЙ
Определитель
Вронского
(Вронскиан)
Определитель Вандермонда
Определитель Грама
Определитель Якоби (Якобиан)
Циркулянт
6
7.
1. ОПРЕДЕЛЕНИЕ. ПОРЯДОК ОПРЕДЕЛИТЕЛЯОпределение.
ОПРЕДЕЛИТЕЛЬ
(детерминант) n-го порядка,
составленный из элементов квадратной
матрицы (n*n) есть алгебраическая
сумма n! («эн факториал») слагаемых
или число, которое находится по
определённым правилам.
Замечание.
Квадратная матрица,
определитель которой равен нулю,
называется вырожденной (или
особенной)
7
8.
Для обозначения определителя квадратнойматрицы используется символ:
a11 a12 ... a1n
a 21 a 22 ... a 2 n
A
det A
. . . .
a a ... a
nn
n1 n 2
a11 a12 ... a1n
a 21 a 22 ... a 2 n
.
.
. .
a n1 a n 2 ... a nn
т.е. элементы матрицы заключаются в прямые
вертикальные чёрточки.
Определитель матрицы А также может
обозначаться как: det(A), |А| или Δ(A).
Этот символ был введён в 19 веке английским
математиком Кэли
8
9.
Определители второго порядка.Определение: Определителем или
детерминантом второго порядка называется
ЧИСЛО
a11 a12
a21 a22
a11a22 a12 a21
Числа (элементы определителя)
образуют главную диагональ,
элементы определителя
побочную диагональ.
a
12
и
a
11
a21
и
a22
образуют
9
10.
Правило: Чтобы вычислить определительвторого порядка, надо из произведения
элементов главной диагонали вычесть
произведения элементов побочной диагонали.
Пример: Вычислить определитель
8 5
3 2
8 2 5 3 1
10
11.
Определители третьего порядка.Определение: Определителем или
детерминантом третьего порядка называется
ЧИСЛО
a11 a12 a13
a21 a22 a23
a31 a32 a33
a11a22a33 a12a23a31 a13a21a32 a13a22a31 a12a21a33 a11a23a32
11
12.
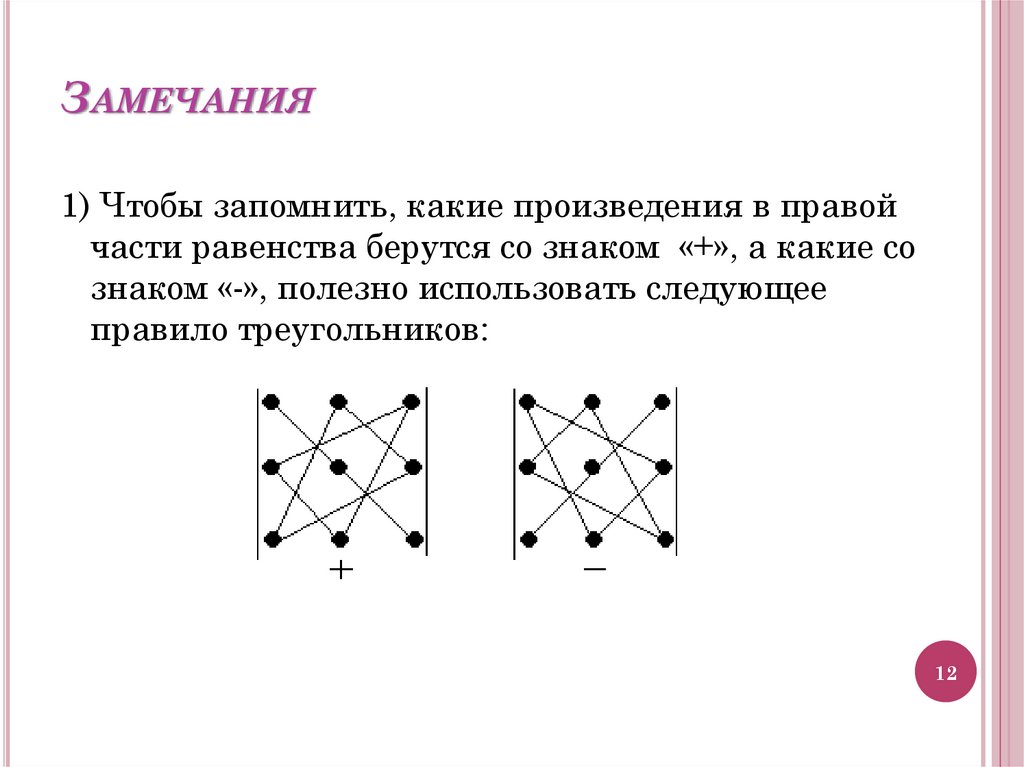
ЗАМЕЧАНИЯ1) Чтобы запомнить, какие произведения в правой
части равенства берутся со знаком «+», а какие со
знаком «-», полезно использовать следующее
правило треугольников:
12
13.
2) Второй способ вычисления определителяфактически совпадает с первым и
называется способом Саррюса
Суть его состоит в том, что справа от определителя
приписывают первый и второй столбец и
произведения элементов на главной диагонали и на
диагоналях, ей параллельных, берут со знаком
«плюс»,
а произведения элементов побочной диагонали и
диагоналей, ей параллельных, со знаком «минус»
13
14.
a11 a12 a13 a11a21 a22 a23 a21
a31 a32 a33 a31
a12
a22
a32
a11a22 a33 a12 a23a31 a13a21a32 a13a22 a31 a12 a21a33 a11a23a32
3) Определитель 4-го порядка есть алгебраическая
сумма 4!=4*3*2*1=24 слагаемых!
Как вычисляются определители, имеющие порядок
выше 3-го?
УДОБНЫМ И ЭФФЕКТИВНЫМ способом
вычисления определителей и третьего и более
высокого порядков является метод
РАЗЛОЖЕНИЯ ОПРЕДЕЛИТЕЛЯ ПО СТРОКЕ
ИЛИ СТОЛБЦУ
14
15.
1Пример. Вычислить определитель 4
7
2 3
0
6
8
9
с помощью правила (способа)Саррюса.
Решение
1
4
7
2 3 1
2
0
6 4
0
8
9 7
8
1 0 9 ( 2) 6 ( 7) 3 4 8 3 0 ( 7) 1 6 8 ( 2) 4 9 204
15
16.
2. МИНОРЫ ИАЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ
Определение: Минором M ij некоторого
элемента a ij называется определитель, который
получается из данного определителя
вычеркиванием i-ой строки и j -ого столбца, на
пересечении которых расположен этот элемент.
Пример.
1) Составить миноры M11 и M 23 определителя 3-го
порядка
a11 a12 a13
a21 a22 a23
a31 a32 a33
16
17.
Минор элемента a11 есть ОПРЕДЕЛИТЕЛЬ 2-ГОПОРЯДКА, который получается путём
зачёркивания 1-й строки и 1-го столбца исходного
ОПРЕДЕЛИТЕЛЯ 3-ГО ПОРЯДКА
a11 a12 a13
a22
a21 a22 a23 M
11
a32
a31 a32 a33
a23
a33
a22a33 a23a32
Аналогично находим минор элемента
a11 a12 a13
a11
a21 a22 a23 M 23
a31
a31 a32 a33
a12
a32
a23
a11a32 a12 a31
17
18.
2) Вычислить миноры M11 и M 23 определителя1
3
4
0
2
1
2
3 4
Решение
M 11
1
2
3 4
M 23
1 ( 4) ( 3)( 2) 10
1
0
4
3
( 1) ( 3) 0 4 3
18
19.
Определение: Алгебраическим дополнением Aijкакого-либо элемента a ij определителя есть
минор M ij этого элемента, взятый со знаком ( 1) i j :
Aij ( 1)
i j
M ij
Пример. Для приведенного выше определителя 3-го
порядка
1 0
2
3
4
1
2
3 4
записать и вычислить алгебраические дополнения
и A
23
A11
19
20.
РЕШЕНИЕ1
Дан определитель 3
4
0
2
1
2
3 4
Согласно определению находим
A11 ( 1)
1 1
A23 ( 1)
2 3
1
2
3 4
1
0
4
3
1 ( 4) ( 3)( 2) 10
( 1) ( 3) 0 4 3
1 1
A11 ( 1) M11 10 10
2 3
A23 ( 1) M 23 ( 1) 3 3
20
21.
ЗАМЕЧАНИЕАлгебраическое дополнение элемента a ij
совпадает с его минором , если сумма его индексов
i+j
чётна, и является противоположным числом
к минору, если сумма его индексов нечётна
Алгебраическое дополнение используется для
вычисления определителей
21
22.
3. СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙОпределитель обладает рядом свойств, которые
лежат в основе практических способов их
вычислений
Время, которое затрачивается на вычисление
определителя, зависит не только от вашего опыта,
но и ОТ ЗНАНИЙ СВОЙСТВ ОПРЕДЕЛИТЕЛЕЙ:
процесс решения вполне реально сократить до
считанных секунд, а иногда и сразу увидеть
результат!
Свойства определителей выполняются для
определителей любого порядка. Для экономии
времени и места рассмотрим эти свойства на
определителях второго порядка
22
23.
1. Величина определителя не изменится, если егостроки и столбцы поменять местами:
a11 a12
a 21 a 22
a11 a 21
a12 a 22
.
Для доказательства используем определение
a11 a 21
a11a 22 a 21a12 .
a12 a 22
2. Перестановка двух столбцов или двух строк
определителя равносильна умножению его на (–1):
a11 a12
a21 a22
a12 a11
a22 a21
или
a11 a12
a21 a22
a21 a22
a11 a12
23
24.
3. Умножение всех элементов одного столбца илиодной строки определителя на любое число
равносильно умножению определителя на это
число :
a11 a12
a11 a12
a11 a12
a11 a12
или
.
a21 a22
a21 a22
a21 a22
a21 a22
Пример.
10 4
5 2
5 2
2
2 3
2 3 (5 6) 6.
9 3
93
31
4. Если определитель имеет две одинаковые строки
или два одинаковых столбца, то он равен нулю:
a11 a12
a11 a12
a11a12 a12 a11 0, или
a11 a11
a21 a21
a11a21 a11a21 0.
24
25.
5. Если все элементы некоторого столбца илинекоторой строки определителя равны нулю, то и
сам определитель равен нулю:
0
0
a21 a22
0 a22 0 a21 , или
a11 0
a21 0
a11 0 0 a21.
6. Если элементы двух столбцов или двух строк
определителя пропорциональны, то определитель
равен нулю
1 2
Пример.
8 8 0.
- 4 -8
25
26.
7. Если каждый элемент некоторого столбца(строки) определителя представляет собой сумму
двух слагаемых, то определитель может быть
представлен в виде суммы двух определителей, из
которых один в данном столбце (строке) имеет
первые из упомянутых слагаемых, а другой –
вторые. Элементы, стоящие на остальных местах, у
всех трех определителей одни и те же.
a a
'
11
''
11
a a
'
21
a a
'
31
''
21
''
31
a12 a13
'
11
a a12 a13
a22 a23 a
a32 a33
'
21
''
11
a
a22 a23 a
a31 a32 a33
a12 a13
''
21
a22 a23
''
31
a32 a33
a
26
27.
8. Если к элементам некоторого столбца(строки) определителя прибавить
соответствующие элементы другого столбца
(строки), умноженный на любой общий
множитель , то величина определителя не
изменится.
a11 a12 a12 a13
a11 a12 a13
a21 a22 a22 a23 a21 a22 a23
a31 a32 a32 a33
a31 a32 a33
27
28.
9. Определитель равен сумме произведенийэлементов какого-нибудь столбца или строки
на их алгебраические дополнения
a11 A11 a 21 A21 a31 A31 ,
a11 A11 a12 A12 a13 A13 ,
a12 A12 a 22 A22 a32 A32 ,
a 21 A21 a 22 A22 a 23 A23 ,
a13 A13 a 23 A23 a33 A33 ,
a31 A31 a32 A32 a33 A33 .
10. Сумма произведений элементов какого-нибудь
столбца или строки определителя на
алгебраические дополнения соответствующих
элементов другого столбца или строки равна нулю
28
29.
КАКИЕ СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙПОЛЕЗНО ЗНАТЬ?
1) Величина определителя не меняется при
транспонировании. Свойство запоминаем.
2) Любая парная перестановка строк
(столбцов) меняет знак определителя на
противоположный. На практике лучше не
использовать
3) Из строки (столбца) определителя можно
вынести множитель (и внести его обратно).
Используем там, где это выгодно.
4) Если строки (столбцы) определителя
пропорциональны, то он равен нулю.
Определитель с нулевой строкой (столбцом)
равен нулю.
29
30.
ПРИМЕР. ВЫЧИСЛИТЬИСПОЛЬЗУЯ СВОЙСТВО
ОПРЕДЕЛИТЕЛЬ,
9.
6 -2 1
7 4 -1
-3 5 1
30
31.
ЗОЛОТОЕ ПРАВИЛО ВЫЧИСЛЕНИЙОПРЕДЕЛИТЕЛЯ
Определитель выгоднее
раскрывать по ТОЙ строке
(столбцу), где:
1) нулей побольше
2) числа поменьше
3) использовать
правило
-
знаков -
-
-
31
32.
РЕШЕНИЕ1. Выбираем строку или столбец: это третий
столбец
2. Записываем формулу вычисления
определителя
a13 A13 a23 A23 a33 A33
6 -2 1
1 3
7 4 - 1 ( 1) 1
-3 5 1
7
4
-3 5
( 1)
2 3
( 1)
6
-2
-3
5
( 1)
3 3
1
6 -2
7
4
(35 12) (30 6) (24 14) 47 24 38 109
32
33.
ЗамечаниеМожно упростить запись, если
использовать правило знаков:
6 -2 1
7 4 -1 1
-3 5 1
7
4
-3 5
( 1)
6
-2
-3
5
1
6 -2
7
4
(35 12) (30 6) (24 14) 47 24 38 109
33
34.
4. ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ (ИТОГИ)1. Значение определителя второго порядка находим
по определению:
a11 a12
a11a22 a12 a21
a21 a22
2. Определитель третьего порядка вычисляем,
используя свойство 9, разложив данный
определитель по строке или столбцу
3. Для вычисления определителей высоких порядков
(выше третьего) используют метод ПОНИЖЕНИЯ
ПОРЯДКА
34
35.
4. Если в определителе все числа, расположенныениже или выше главной диагонали, или все числа
кроме элементов главной диагонали равны нулю,
то он равен произведению элементов главной
диагонали.
Например,
1 2 3
1
0 0 1 0 0
0 4 0 3 4 0 0 4 0 24
0 0 6
2 5 6 0 0 6
1
0
2 1
6 0 12
2 0 0
35
36.
5. ОПРЕДЕЛИТЕЛЬ РАВЕН НУЛЮ,если две строки (столбца) определителя
пропорциональны (как частный случай –
одинаковы)
Пример.
4 2 2
2 1
5 7
1 0
3
или
4 2 2
2 1
5 7
2 1 1
1 2 2 1 1 0
3
5 7
3
6. Определитель с нулевой строкой (столбцом)
равен нулю
36
37.
5. ПОНЯТИЕОБРАТНОЙ МАТРИЦЫ
Определение:
Если A – КВАДРАТНАЯ
НЕВЫРОЖДЕННАЯ МАТРИЦА, то
обратной для нее называется матрица,
обозначаемая A-1 и удовлетворяющая
условию
1
1
A A A A E
Матрицы A и A-1 называются
взаимообратными
37
38.
Обратнаяматрица определяется
единственным образом по формуле
A11
1
1
1
T
A
A
A12
det A
det A
A13
A21
A22
A23
A31
A32
A33
A11 A21 A31
T
Здесь A A12
транспонированная
A22 A32
A
A
A
23
33
13
i j
A
(
1
)
M ij
матрица алгебраических дополнений ij
соответствующих элементов исходной матрицы
38
39.
АЛГОРИТМ ПОСТРОЕНИЯ (НАХОЖДЕНИЯ)ОБРАТНОЙ МАТРИЦЫ
1. Убедиться, что исходная матрицы не является
вырожденной, т.е. убедиться, что det A 0
2. Найти алгебраические дополнения исходной матрицы
Aij ( 1)i j M ij
3. Составить ПРИСОЕДИНЁННУЮ матрицу, элементами
которой являются найденные алгебраические дополнения
A11
*
A A12
A
13
A21
A22
A23
A31
A32
A33
39
40.
4. Записать обратную матрицуA11
1
1
A
A12
det A
A13
A21
A22
A23
A31
A32
A33
5.
Проверить правильность решения, т.е.
убедиться, что выполняется равенство:
1
или
A A E
1
A A E
40
41.
6. МАТРИЧНЫЕВЫРАЖЕНИЯ
Матричное выражение состоит из матриц,
связанных операциями сложения, умножения,
возведения в степень, транспонирования и др.
Пример матричного выражения:
2 A B T (C D) 1 5F 3
Продумайте и запишите порядок действий над
матрицами A, B, C , D, F для нахождения
значения этого выражения
Замечание.
Если матричное выражение
имеет смысл, то результат его вычисления
является матрицей.
41
42.
МАТРИЧНЫЕ УРАВНЕНИЯМатричное равенство, содержащее неизвестную
матрицу, называется матричным уравнением
Например, простейшие из них вида
A 3X B
A X B
X A B
A X 2X E
A X B C
42
43.
ЗАМЕЧАНИЕВыполнены
все требования, предъявляемые
к размерам матриц, входящих в матричные
уравнения
Решить матричное уравнение – это значит
найти неизвестную матрицу
43
44.
РАССМОТРИМ РЕШЕНИЕ МАТРИЧНОГОУРАВНЕНИЯ ВИДА
A X B
Решение
A X B
1
1
A A X A B
1
E X A B
1
X A B
44
45.
ПРИМЕР. РЕШИТЬ УРАВНЕНИЕ2 1 1 1
X
1 3 4 3
Решение
Задано уравнение вида X A B
После умножения СПРАВА это уравнение на
1
матрицу A
получаем, что
X B A
1
2 1
1. Найдём матрицу, обратную к матрице A
1 3
по формуле
A
1 A
1
11
A
det A A12
A22
21
45
46.
Вычислим определитель матрицы A:2 1
2 3 ( 1) 1 7 0
det A
1 3
Найдём миноры и алгебраические дополнения
матрицы A:
M 11 3
M 12 1
M 21 1 M 22 2
Составим
A11 3 A12 1
A21 1
A22 2
обратную матрицу
1
A
1 3 1
A
7 1 2
1
46
47.
2. Найдём неизвестную матрицу1
X B A :
1 1 1 3 1
X
7 4 3 1 2
1 1 3 1 ( 1) 1 1 1 2 1 2 3
X
7 4 3 3 ( 1) 4 1 3 2 7 9 10
1 2 3
X
7 9 10
3. Проверка
1 2 3 2 1 1 1
7 9 10 1 3 4 3
47
48.
1 2 2 3 1 2 ( 1) 3 3 1 17 9 2 10 1 9 ( 1) 10 3 4 3
1 7 7 1 1
7 28 21 4 3
1 1 1 1
верно
4 3 4 3
48
49.
МАТЕМАТИКИ ШУТЯТВычислить определитель
12.09.2021
49













































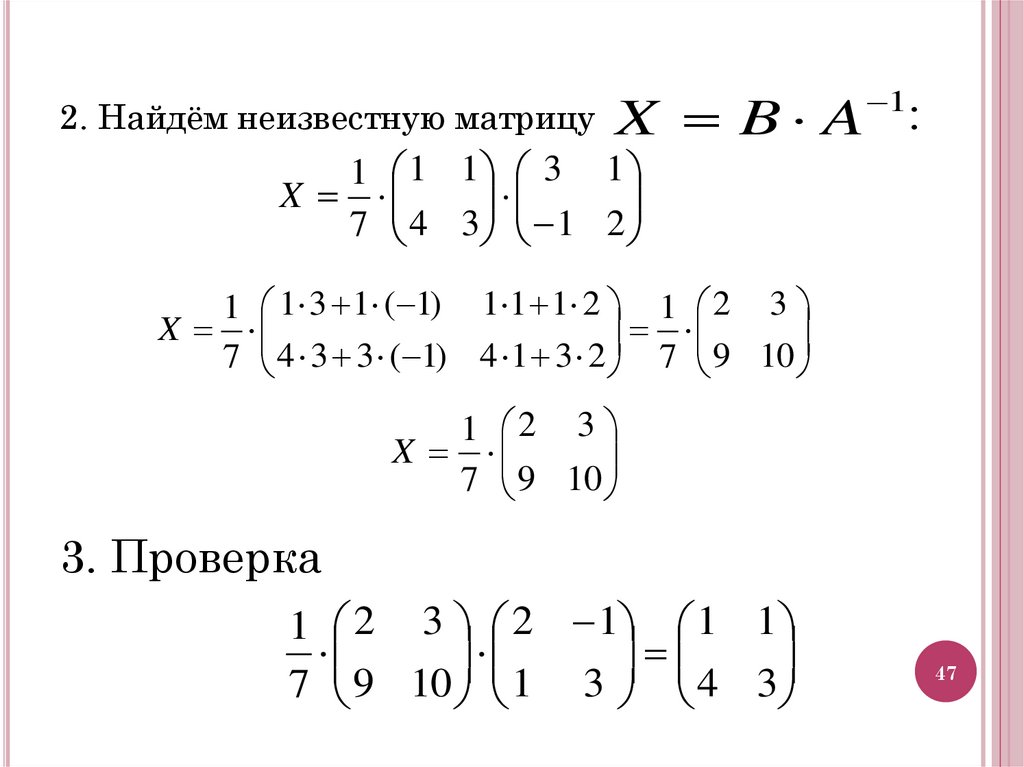
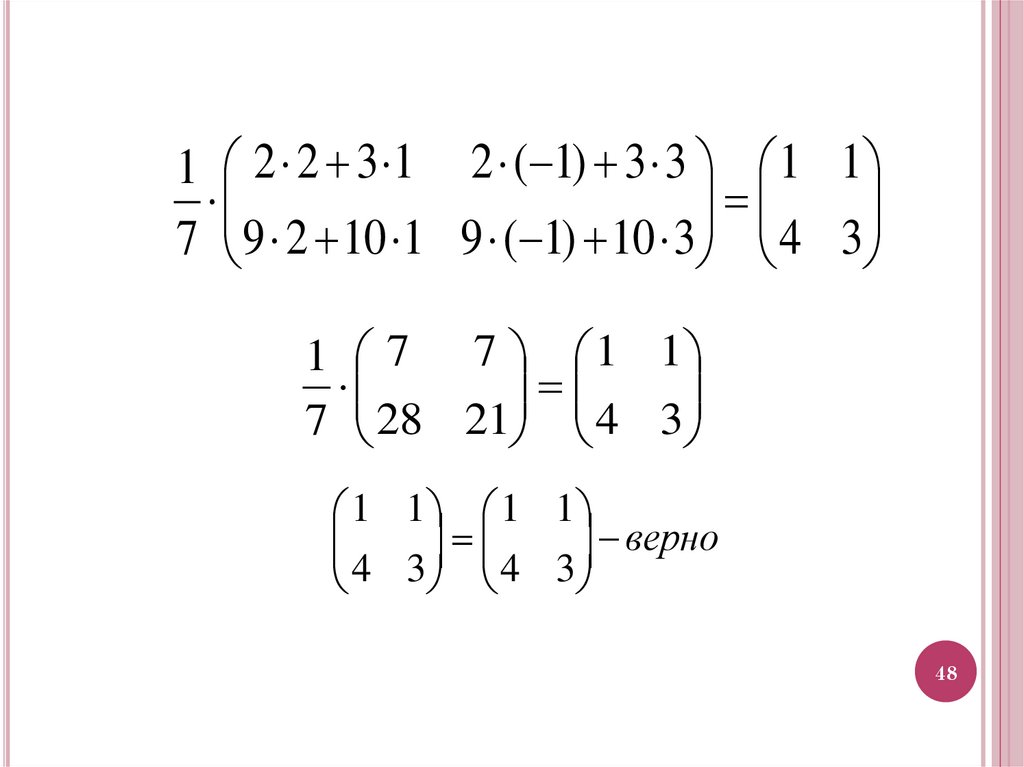

 mathematics
mathematics








