Similar presentations:
Корни натуральной степени из числа и их свойства
1.
2.
Корнем n – й степени из действительногочисла a (n – натуральное число) называют
такое действительное число x, при возведении
которого в степень n получается число a.
n
Это число обозначают: x=
a
a - подкоренное выражение
n - показатель корня
Если a 0, n = 2,3,4,5,…, то
n
n
n
1) a 0; 2) ( a ) = a;
Неотрицательное значение корня n –й степени из
неотрицательного числа называется арифметическим корнем.
3.
Операция извлечения корня является обратнойпо отношению к возведению в соответствующую
степень.
Возведение в степень
5² = 25
10³ = 1000
0,3⁴ = 0,0081
n
Извлечение корня
25
=
5
3
1000
=
10
4
0,0081 = 0,3
Иногда выражение a называют радикалом от
латинского слова radix – «корень».
Символ - это стилизованная буква r.
4.
Пример 1:3
7
4
Вычислить: а) 49; б) 0,125; в) 0 ; г) 17
5.
Корнем нечётной степени n из отрицательногочисла a (n=3,5,…) называют такое отрицательное
число, которое при возведении в степень n даёт в
результате число a.
Корень чётной степени имеет смысл (т.е.
определён)
только
для
неотрицательного
подкоренного выражения; корень нечётной
степени имеет смысл для любого подкоренного
Подобные
выражения.
корни
3
125 3 ( 5)( 5)( 5) 5
3
125 3 5 5 5 5
4
4
16 4
16 2
6.
1.Корень n-степени (n=2,3,4,5, …) из произведениянеотрицательных чисел равен произведению
корней n-степени из этих чисел:
=
Пример:
=
= 2*3=6
7.
2. Чтобы извлечь корень из дроби, нужно извлечькорень из числителя и знаменателя отдельно и
первый результат разделить на второй:
=
Пример:
=
=
8.
3. Если a≥0, n=2,3,4,5,… и k – любое натуральноечисло, то справедливо равенство:
Пример:
9.
4. Если a≥0, n и k - натуральные числа, большие1, то справедливо равенство:
Пример:
10.
5. Если показатели корня и подкоренноговыражения умножить или разделить на одно и
то же отличное от нуля число, то значение корня
не изменится:
Пример:
11.
6. Чтобы извлечь корень из степени, показателькоторой делится на показатель корня, нужно
показатель степени разделить на показатель
корня:
Пример:
12.
Приближенные значения корней умели находитьеще жители древнего Вавилона около 4 тысяч лет
назад. Не имея вычислительных машин, люди
применяли формулу, автор которой неизвестен:
Пример:
13.
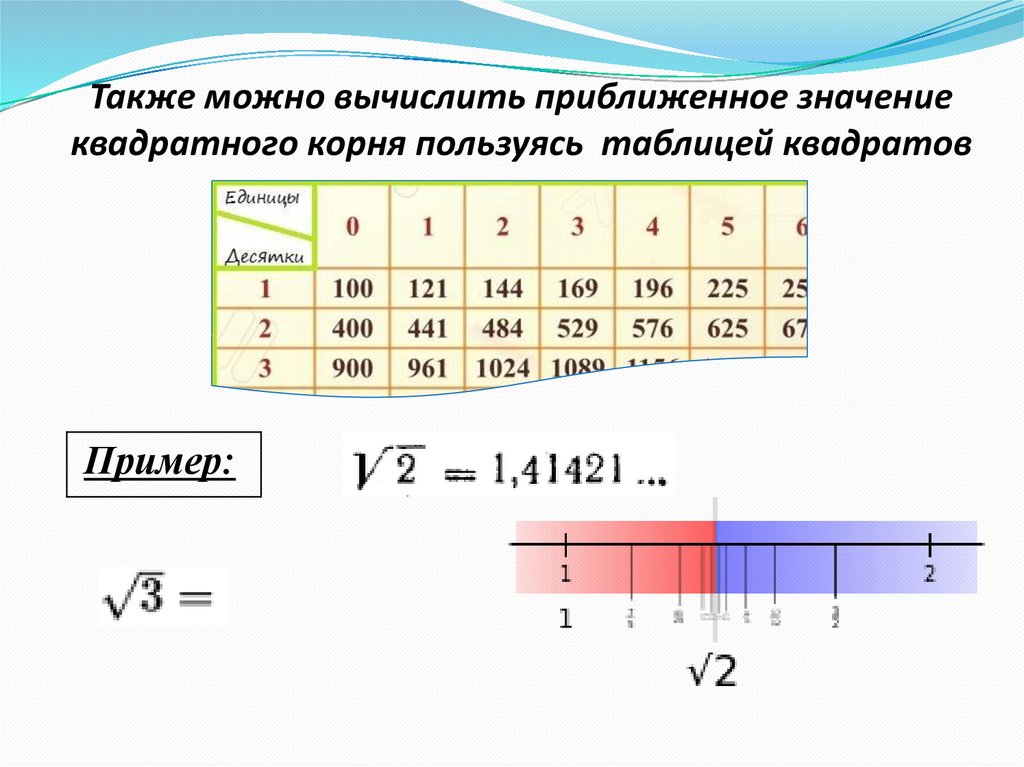
Также можно вычислить приближенное значениеквадратного корня пользуясь таблицей квадратов
Пример:









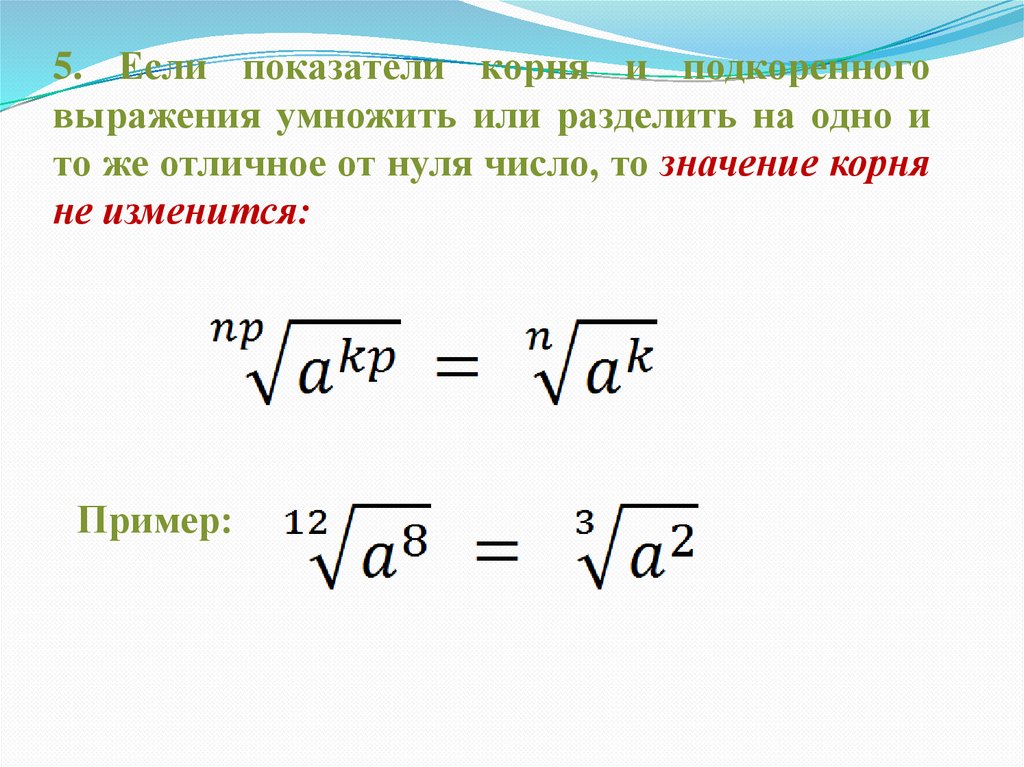





 mathematics
mathematics








