Классические распределения частиц идеального газа

1.

ГЛАВА II. МОЛЕКУЛЯРНАЯ
ФИЗИКА И
ТЕРМОДИНАМИКА
§7. Классические
распределения частиц
идеального газа
О. И. Лубенченко
НИУ МЭИ
Кафедра физики им. В. А. Фабриканта
2020

2.

§7. Распределения молекул
I. Функция распределения
Пусть имеется термодинамическая система из N частиц.
ξ — ФВ, характеризующая частицу. Вероятность того, что величина ξ будет
иметь значение ξi:
N
Pi
i
N
Ni — количество частиц, для которых ξ = ξi
Условие нормировки:
Среднее значение ξ:
P 1
Nξ
Pξ
i
ξ
i i
i i
N
Если ξ изменяется непрерывно, то вероятность того, что ξ = (ξ, ξ + dξ)
dP f ξ dξ
f(ξ) — функция распределения вероятности (плотность
вероятности)
f ξ
dP
dξ
2

3.

§7. Распределения молекул
ПРИМЕР
Распределение Гаусса
Распределение Гаусса — функция вида
f ξ Ae
3
f(ξ)
α ξ ξ 0
2
ξ0 — постоянная
α — положительная постоянная
A находят из условия нормировки
0
ξ0
По такому закону распределяются результаты серии большого числа
случайных измерений.
Свойства функции распределения
• Определённость и непрерывность во всей области определения ξ(a, b)
• Дифференцируемость во всей области определения
• Интегрируемость во всей области определения
b
Условие нормировки (нормируемость):
f ξ dξ 1
a
ξ

4.

§7. Распределения молекул
4
Зная функцию распределения, можно найти среднее значение любого
параметра, зависящего от ξ.
Вероятность того, что ξ принимает значение от ξ1 до ξ2:
ξ2
P ξ 1 , ξ 2 f ξ dξ
ξ1
Среднее значение ξ:
b
ξ ξf ξ dξ
a
b
Среднее значение квадрата ξ:
ξ 2 ξ 2 f ξ dξ
a
b
Среднее значение функции φ(ξ):
φ φ ξ f ξ dξ
a
Наиболее вероятное значение ξ:
df ξ
dξ
0
ξ ξ вер
ξвер

5.

§7. Распределения молекул
5
II. Распределение молекул идеального газа по скоростям (распределение
Максвелла)
Рассмотрим идеальный газ из N частиц. Случайная ФВ ξ — это модуль
скорости v молекул идеального газа. Найдём функцию распределения f(v).
vz
Рассмотрим подпространство фазового пространства
dv
— пространство скоростей (vx, vy, vz).
Плотность ИТ равна Nf(v).
v
Количество ИТ в сферическом слое радиуса v
толщиной dv: dN Nf v 4π v2d v
vy
O
Вероятность попадания ИТ в этот слой:
dN
vx
dP
f v 4π v2d v
N
Плотность вероятности F v
dP
f v 4π v2
dv
Так как все направления равноправны, f v φ1 v x φ2 v y φ3 vz
Функции φ1, φ2, φ3 одинаковы: φ1 = φ2 = φ3 = φ.

6.

§7. Распределения молекул
ln f v ln φ v ln φ v ln φ v
x
y
6
z
1 df v v
1 dφ vx
f v d v vx φ vx d vx
v
vx
v2x v2y v2z
vx
2vx
2 v2x v2y v2z
f v
const α
v f v
α v2x
ln φ vx
const
2
vx
v
φ vx
f v
v f v vx φ vx
v
1
1
f v x
φ vx
f v v φ vx
φ v y
f v
v f v v yφ v y
φ vz
f v
v f v vz φ vz
dφ vx
1
α
vx φ vx d vx
φ vx Ae
α v2
x
2
φ v y Ae
dφ vx
φ vx
α v2y
2
α v x d v x
φ vz Ae
α v2z
2

7.

§7. Распределения молекул
f v A3e
φ vx d vx
φ v y dv y
α 2 2 2
v x v y vz
2
A3e
α v2
2
A e
α v2x
2
d vx 1
A
3
2
α
f v
e
2π
2
φ vz d vz 1
m0 v2x
7
α v2
2
1 3
kT
3 2
v2x
kT
m0
v
2
x
2
v
x φ vx d vx
α
φ vx
m0
e
2πkT
m v2
0 x
2kT
3
2
m
f v 0 e
2πkT
α
2π
m0 v2
2kT
3
2
m0
kT
m0 v2
2
2kT
m
F v 0 4π v e
2πkT
— функция распределения
Максвелла

8.

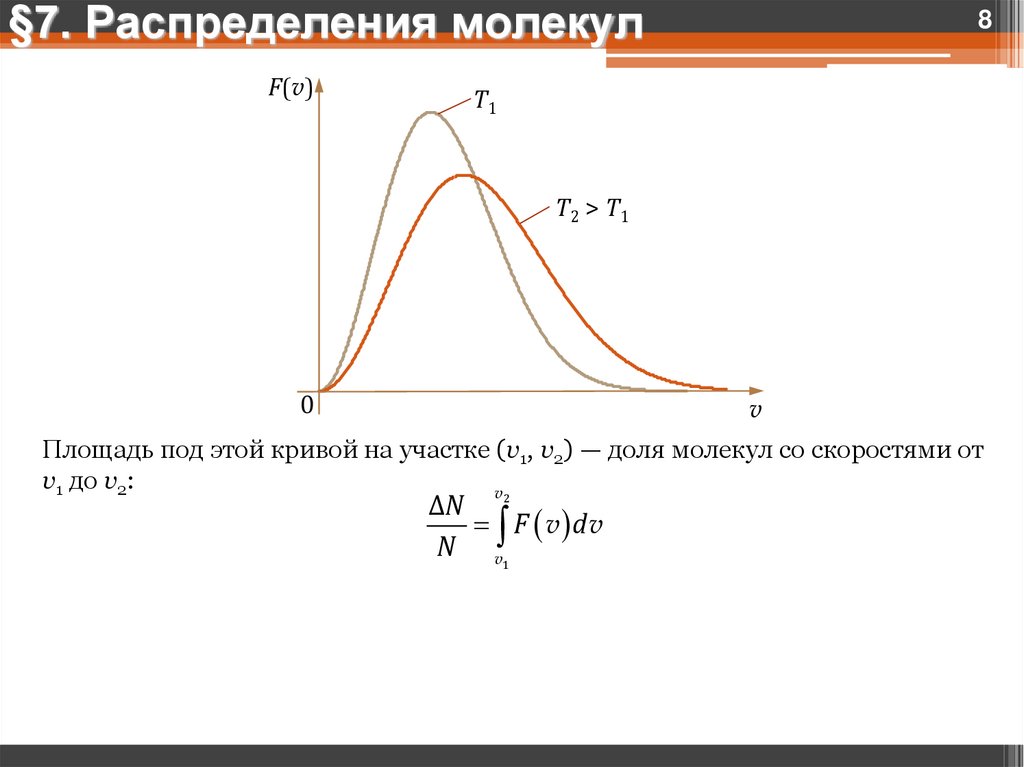
§7. Распределения молекул
F(v)
8
T1
T2 > T1
0
v
Площадь под этой кривой на участке (v1, v2) — доля молекул со скоростями от
v1 до v2:
v
ΔN 2
F v dv
N v1

9.

§7. Распределения молекул
9
Наивероятнейшая скорость молекулы идеального газа — скорость,
соответствующая максимуму функции распределения F(v):
dF v
dv
0
v vвер
2vверe
vвер
2
m0 vвер
2kT
v
2
вер
m0 2vвер
e
2kT
2
m0 vвер
2kT
0
2kT
2RT
m0
μ
Средняя скорость молекулы идеального газа:
v vF v d v
v
0
8kT
8RT
πm0
πμ
Средняя квадратичная скорость молекулы идеального газа:
v2 v2F v d v
0
3kT
m0
vкв
3kT
3RT
m0
μ
vвер v vкв

10.

§7. Распределения молекул
10
F(v)
0
vвер v vкв
v
III. Распределение молекул идеального газа по энергиям
Число молекул с кинетическими энергиями поступательного движения от ε до
ε + dε:
dNε NF ε dε
Эти энергии соответствуют скоростям молекул от v до v + dv: dNε NF v d v
F ε dε F v d v
m0 v2
ε
2
v
2ε
m0
dv
F ε F v
dε
dv
2 1
1
dε
m0 2 ε
2m0 ε

11.

§7. Распределения молекул
3
2
2ε
m
F v 0 4π e
m0
2πkT
F ε
m03 2 23 π
32
2 π
32
kT
32
ε
m 2ε
0
2kT m0
e
12
3
2
ε
m0 8π 2kT
εe
2πkT m0
ε
kT
12
0
m0 2 m
F ε
2
π kT
11
32
ε
2
εe
π kT
32
ε
kT
F(ε)
0
εвер
ε
kT
εвер
(доказать самостоятельно)
2
ε
εe
ε
kT

12.

§7. Распределения молекул
12
IV. Барометрическая формула
Рассмотрим столб идеального газа (молярная масса µ) в однородном
гравитационном поле (ускорение свободного падения g) при постоянной
температуре T (изотермическая атмосфера). Найдём зависимость давления и
концентрации газа от высоты.
Выделим тонкий слой газа толщиной dh на высоте h.
T
dh
Давление этого слоя
dp ρgdh
p
g ρ — плотность газа
h
p0
pV
mRT
μ
p
mRT
μV
ρRT
μ
pμ
ρ
RT
ρ
0
pμg
dp
dh
RT
p
dp
μg
dh
p
RT
p
h
dp
μg
p p RT 0 dh
0
ln
p
μgh
p0
RT
p0 — давление столба газа на нулевом уровне
p p0e
μgh
RT
— барометрическая формула
ρ ρ0e
μgh
RT
n n0e
μgh
RT

13.

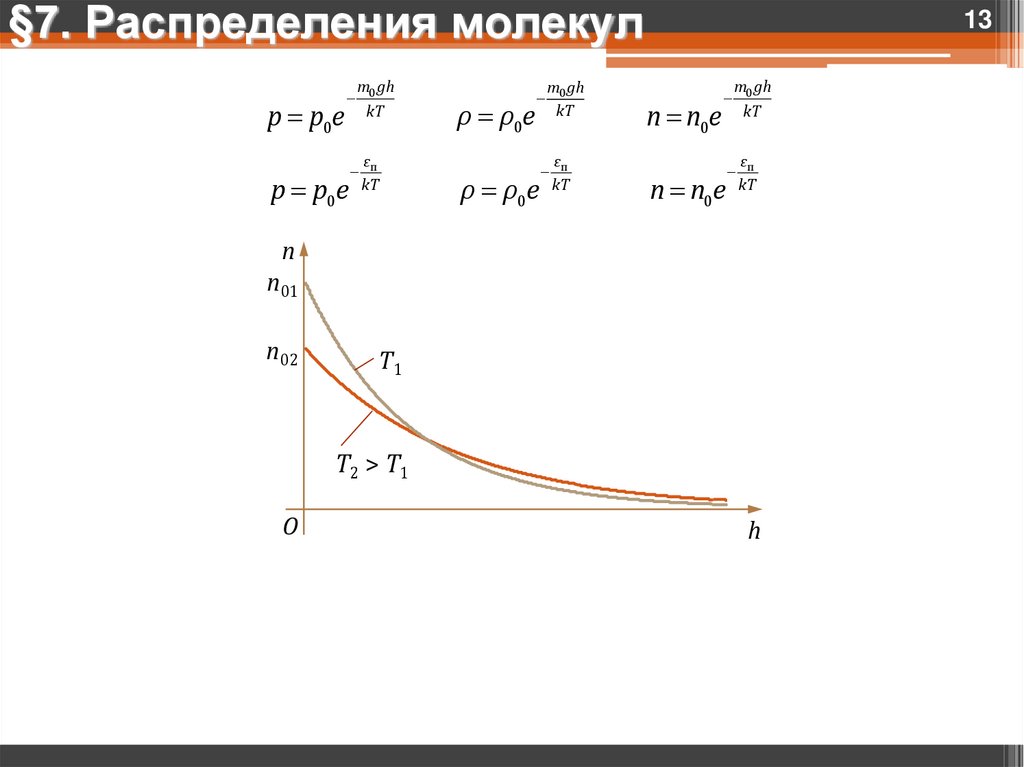
§7. Распределения молекул
p p0e
p p0e
m0 gh
kT
εп
kT
ρ ρ0e
ρ ρ0e
m0 gh
kT
εп
kT
13
n n0e
n n0e
m0 gh
kT
εп
kT
n
n01
n02
T1
T2 > T1
O
h

14.

§7. Распределения молекул
14
V. Распределение Максвелла-Больцмана
Распределение Больцмана: n n0e
εп
kT
εп — потенциальная энергия молекулы
n0 — концентрация молекул газа на нулевом уровне потенциальной энергии
3
2
Распределение Максвелла:
Распределение Больцмана:
ε
m0 kTк
dNεк N
e d v x d v y d vz
2πkT
dNεп n0e
εп
kT
3
2
dxdydz
ε ε
к п
m0
n0e kT d vx d v y d vz dxdydz
Закон Максвелла-Больцмана: dN
2πkT
— число частиц в элементе объёма фазового пространства
(dx, dy, dz, dvx, dvy, dvz)