Similar presentations:
Статистические распределения
1. Статистические распределения
12. Эргодическая гипотеза: среднее по ансамблю равно среднему по времени.
Рассмотрим систему, состоящую из n тел,движущихся со скоростями v1, v2 … vn.
v1 + v2 + v3 + ...
,
Скорость средняя по ансамблю: v =
n
где v1, v2 … vn измерены в
один момент времени.
v1 + v2 + v3
Скорость средняя по времени: v =
n
где v1, v2 … vn измерены для
одной молекулы в разные моменты времени.
+ ...
2
,
3. Распределение молекул по скоростям. (Распределение Максвелла)
dn функция распределения –f (v) =
доля
молекул,
ndv
приходящаяся на единичный интервал
скоростей вблизи некоторого значения
v, т.е. в интервале [v,v + dv].
dN
N n V f v
.
Ndv
Функция распределения – вероятность
того, что скорость молекул лежит в
единичном интервале вблизи
некоторого значения v.
3
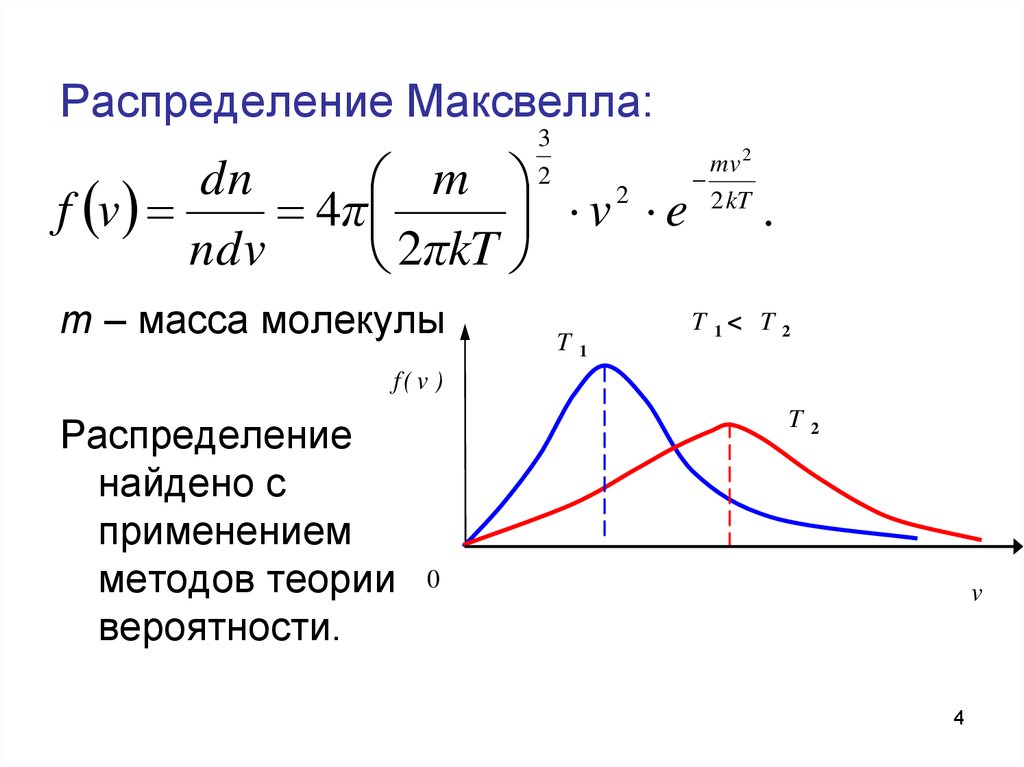
4. Распределение Максвелла:
32
dn
m
2
f v
4π
v e
ndv
2πkT
m – масса молекулы
T
mv 2
2 kT
.
T 1< T
2
1
f(v )
Распределение
найдено с
применением
методов теории
вероятности.
T
2
0
v
4
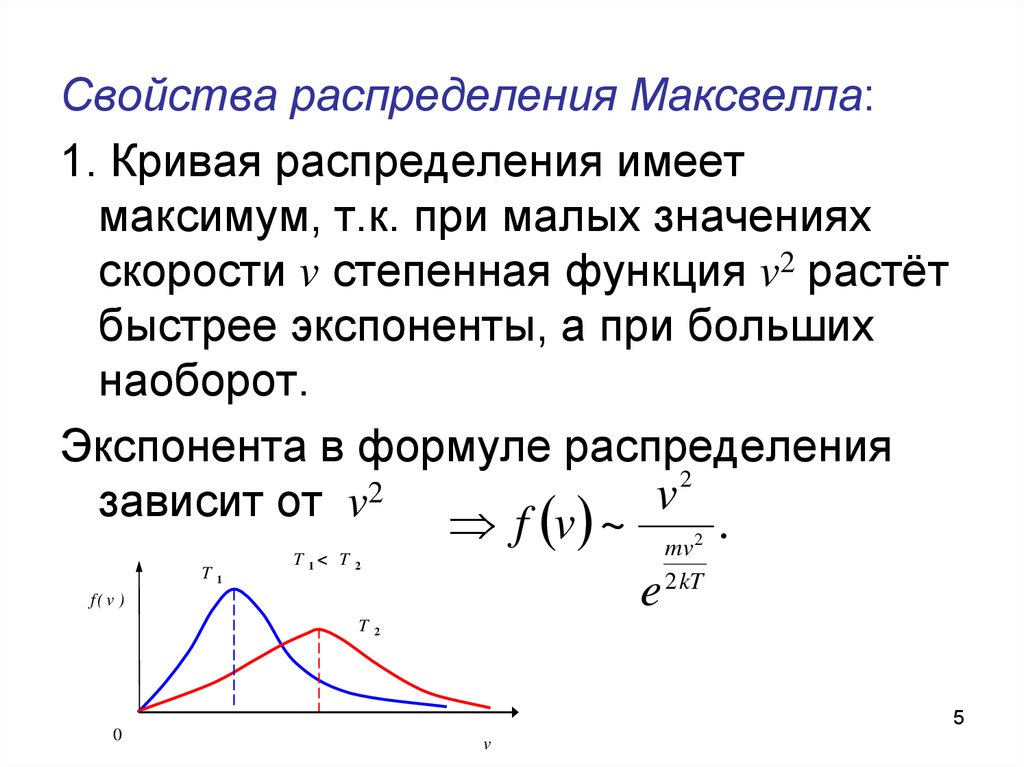
5. Свойства распределения Максвелла:
1. Кривая распределения имеетмаксимум, т.к. при малых значениях
скорости v степенная функция v2 растёт
быстрее экспоненты, а при больших
наоборот.
Экспонента в формуле распределения
2
2
v
зависит от v
f v ~
.
T
T 1< T
2
e
1
f(v )
T
0
mv 2
2 kT
2
5
v
6. Свойства распределения Максвелла:
2. При увеличении температуры Тмаксимум распределения смещается в
сторону более высоких скоростей и
понижается, т.к. площадь под кривой не
меняется.
n
0
0
0
0
dn f v ndv n n f v dv f v dv 1
T
T 1< T
условие нормировки.
2
1
f(v )
T
0
2
v
6
7. Свойства распределения Максвелла:
TСвойства распределения Максвелла:
T 1< T
2
1
f(v )
T
2
0
v
3. Доля молекул, приходящихся на
единичный интервал скоростей вблизи
v = 0 и v = ∞, равна нулю.
Связано это с тем, что в соответствии с
теорией вероятности молекулы при
столкновении не могут либо только
отдавать, либо только получать
энергию.
7
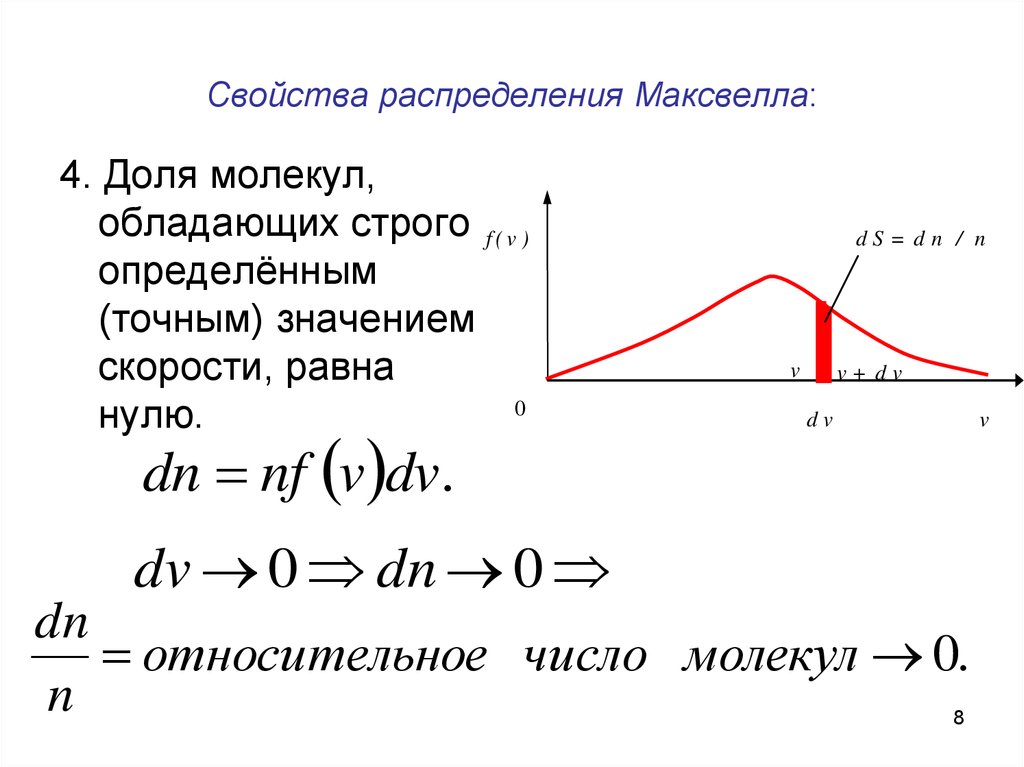
8. Свойства распределения Максвелла:
4. Доля молекул,обладающих строго f ( v )
определённым
(точным) значением
скорости, равна
0
нулю.
dn nf v dv .
dS= dn / n
v
v+ dv
dv
v
dv 0 dn 0
dn
относительное число молекул 0.
n
8
9. Свойства распределения Максвелла:
5. Распределение Максвелла поскоростям справедливо для молекул не
только идеального газа, но и для
реального газа, жидкости, твёрдого
тела.
6. Если систему молекул поместить в
силовое поле, то это силовое поле не
влияет на распределение молекул по
скоростям.
9
10. Опыт Штерна (1888 -1970 гг.)
Первое экспериментальноеопределение v молекул и
подтверждение
распределение Максвелла.
Pt + Ag – платиновая нить,
покрытая серебром.
1, 2, 3 – коаксиальные
цилиндры,
в цилиндре 2 сделана
диафрагма (щель).
10
11. Опыт Штерна
Платиновая нить нагреваетсятоком до t ~ 12350 C, при этом атомы серебра
испаряются и через щель в цилиндре 1 и
диафрагму в цилиндре 2 попадают на
внутреннюю поверхность цилиндра 3, давая
изображение щели – полосу О.
При вращении цилиндров 2 и 3 с одинаковой
угловой скоростью ω атомы серебра оседают
на некотором расстоянии от О, давая
расплывчатое изображение щели. Толщина
осаждённого слоя соответствует
распределению Максвелла.
11
12. Опыт Штерна
OO' Rt.(1)R
t .(2)
v
R 2
OO '
.
v
12
13. Скорости газовых молекул
1. Средняя скорость (средняяарифметическая скорость).
dN
в интервале
f v
dN N f v dv
от v до v + dv.
Ndv
vdN N f v vdv.
0
0
Сумма всех скоростей: vi vdN N f v vdv.
13
14. Скорости газовых молекул
Средняя скорость:N
v
v
i 1
N
i
N f v vdv
0
N
v f v dv.
0
3
2
m
2
f v 4π
v e .
2πkT
8kT kN A R;
8RT
v v
.
m mN A M
M
mv 2
2 kT
14
15. Скорости газовых молекул
2. Средняя квадратичная скорость.N
vкв
v ; v
2
v
2
v
2
2
dN v
0
N
v
2
v
i 1
N
N
2
i
; vкв
N f v dv
i 1
N
.
v f v dv.
2
0
N
3
2
v
2
i
m
2
f v 4π
v e
2πkT
0
mv 2
2 kT
.
15
16.
32
m 4
v 4π
v e
2πkT 0
2
( x e
4
0
ax 2
mv 2
2 kT
dv
5
2
3
m
dx
πa ;a
)
8
2kT
3
2
5
2
m 3 m
4π
π
2πkT 8 2kT
4π 3 π m
3
2
kT
2
8π
3 5
2 2
3kT
.
m
16
17. Средняя квадратичная скорость.
vкв3kT
3RT
.
m
M
17
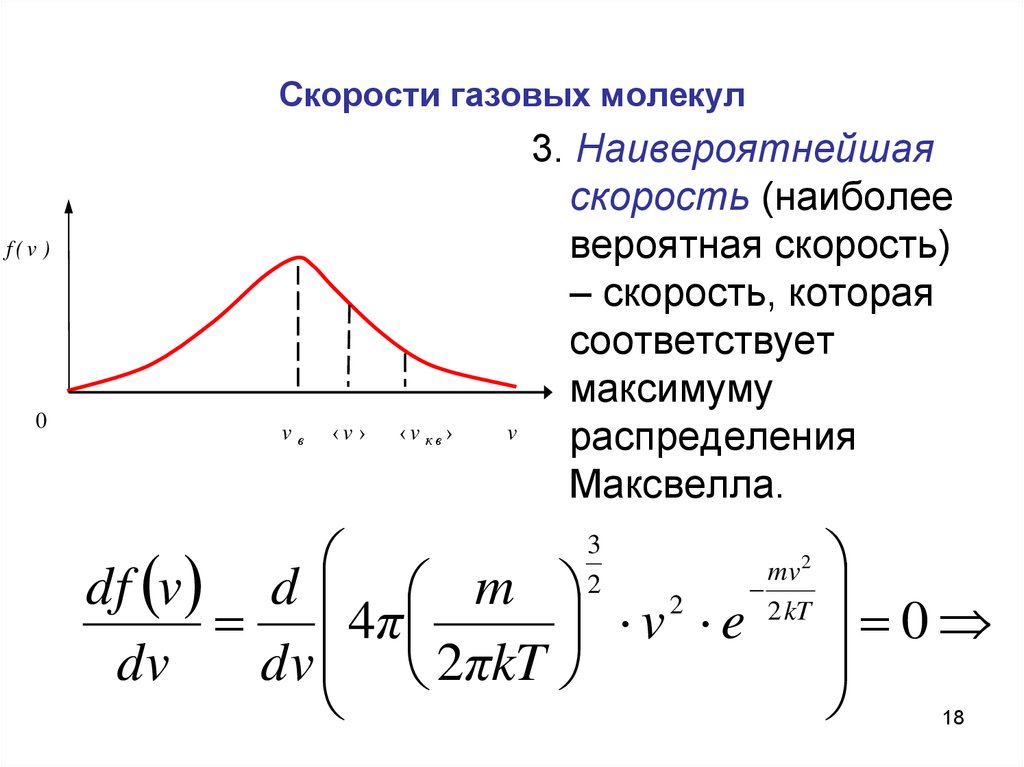
18. Скорости газовых молекул
f(v )0
vв
‹v ›
‹v кв›
v
3. Наивероятнейшая
скорость (наиболее
вероятная скорость)
– скорость, которая
соответствует
максимуму
распределения
Максвелла.
mv
df v d m
2
2 kT
4π
v e
dv
dv 2πkT
3
2
2
0
18
19. 3. Наивероятнейшая скорость
df v d 2v e
dv
dv
2v e
v e
mv 2
2 kT
mv 2
2 kT
mv
2mv 2 kT
2
v
e
2kT
mv 2
2 kT
2
mv
2
0
kT
2kT
2 RT
vв
.
m
M
2
19
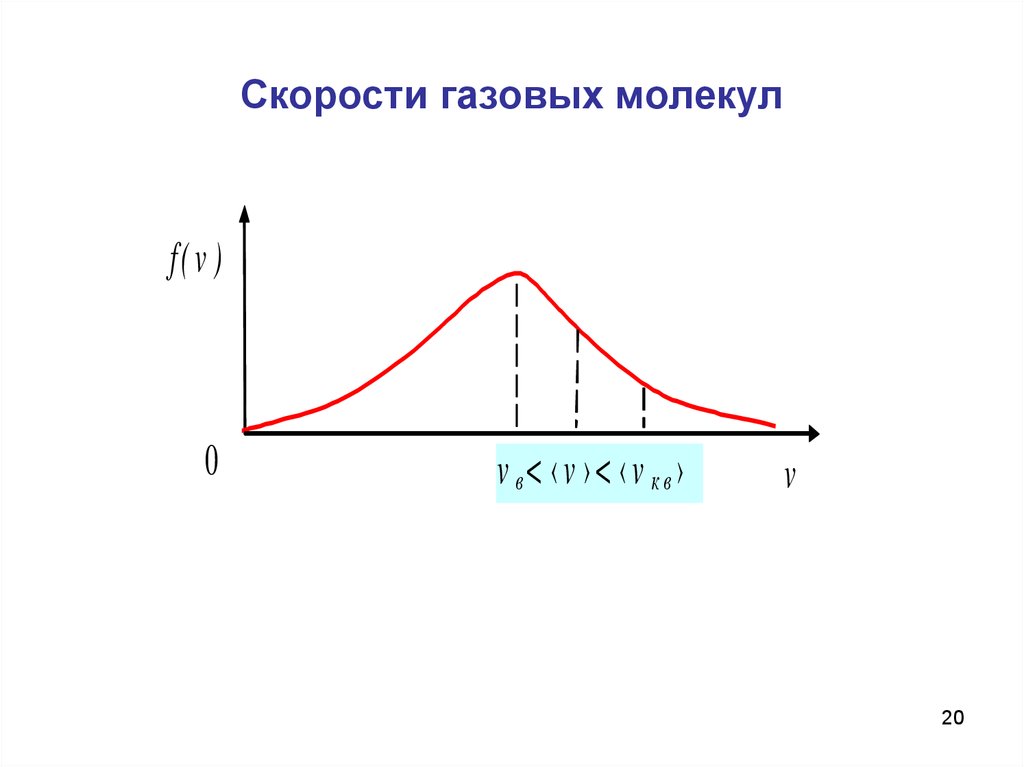
20. Скорости газовых молекул
f( v )0
v в< ‹v ›< ‹v кв›
v
20
21. Распределение молекул по импульсам и кинетическим энергиям
p dv 1p mv v ;
.
m dp m
dN
dN
f v
f v dv.
Ndv
N
dN
dN
f p
f p dp.
Ndp
N
dN
dv
f v dv f p dp f p f v .
N
dp
21
22. Распределение молекул по импульсам и кинетическим энергиям
dvf p f v .
dp
3
2
m
2
f v 4π
v e
2πkT
mv 2
2 kT
.
Делаем замену переменных:
22
23.
32
1
m 2
f p 4π
v e
2
π
kT
m
mv 2
2 kT
f v
3
2
dv
dp
m v
4π
e
2πmkT m
2
3
2
2
m 2v 2
2 mkT
1 mv
4π
e
m
2πmkT
3
2
p2
2 mkT
p2
3
2
1
2
4π
p
e
2πmkT
p2
2 mkT
.
23
24. Распределение молекул по импульсам и кинетическим энергиям
2 Ек dvmv
2 d Ек
1
Ек
v
;
.
2
m dЕк
m dЕк
2mЕк
2
dN
dN
f v
f v dv.
Ndv
N
dN
dN
f Е к
f Ек dЕк .
NdЕк
N
dN
dv
f v dv f Ек dЕк f Ек f v
.
N
dЕк
24
25.
dvf Ек f v
.
dЕк 3
mv
2
m
2
2 kT
f v 4π
v
e
.
2πkT
2
2 Ек
v
.
m
dv
1
.
dЕк
2mЕк
2 Ек
f Ек 4π
3 e
2πkT
2
kT Ек e
π
3
2
1
2
Ек
kT
.
Ек
kT
25
26. Распределение молекул по потенциальным энергиям (Распределение Больцмана)
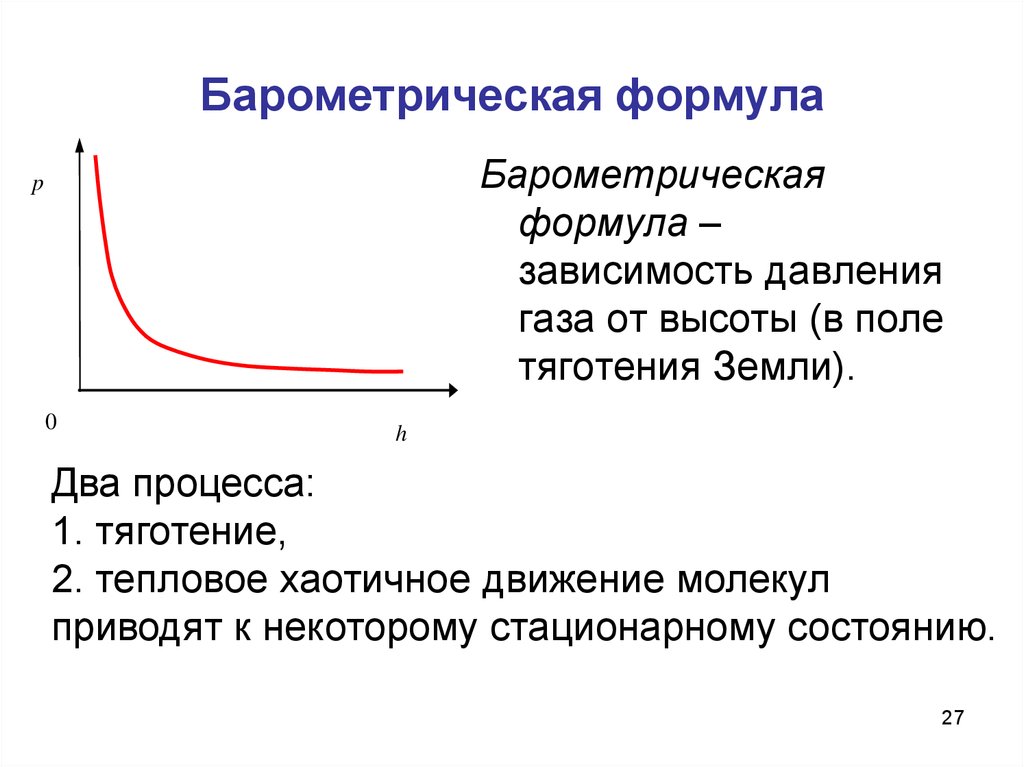
2627. Барометрическая формула
Барометрическаяформула –
зависимость давления
газа от высоты (в поле
тяготения Земли).
p
0
h
Два процесса:
1. тяготение,
2. тепловое хаотичное движение молекул
приводят к некоторому стационарному состоянию.
27
28. Барометрическая формула
Предположим:1) идеальный газ, m = const,
2) поле тяготения однородно, g = const,
3) T = const.
dh
dF mn
g Sdh
(1)
mед .V
dV
сила давления столба воздуха высотой
dh сечением S.
m – масса молекулы.
n – концентрация молекул.
h
S
28
29. Барометрическая формула
dFdp
mngdh.(2)
S
Знак «–» отражает то, что с увеличением h
давление p падает.
p
p nkT .(3) n
.
kT
mpg
dp
mgdh
dp
dh.(4)
.(5)
kT
p
kT
p
h
dp
mgdh
p
mgh
p p 0 kT ln p kT .(6) mgh
0
0
p p0 e
kT
.(7)
29
30. Применение: прибор для измерения высоты над поверхностью земли – высотомер (альтиметр).
p p0 emgh
kT
.(7)
Применение: прибор для измерения высоты
над поверхностью земли – высотомер
(альтиметр).
Для концентрации молекул.
p nkT ,
n
n0
p0 n0 kT .(8)
Уравнение (7).
0
h
n n0 e
mgh
kT
.(9)
30
31. Распределение молекул по потенциальным энергиям (Распределение Больцмана)
mgh E p (h) (1)n n0 e
n n0 e
mgh
kT
Ep (h)
kT
потенциальная энергия
в поле тяготения.
.
.(2) распределение Больцмана.
Больцман показал, что распределение такого
вида справедливо для любого внешнего
U
поля.
n n0 e
kT
, (3)
n0 – концентрация молекул с нулевой потенциальной
энергией U = 0.
31
32. Опыт Перрена (1870 – 1942 гг.) Определение числа Авогадро
32
4
1
Основан на распределении молекул
по высоте.
Под микроскопом исследовалось
броуновское движение частиц,
которые распределялись по
высоте подобно молекулам газа в
поле тяготения.
1 – предметное стекло,
2 – покровное стекло,
3 – микроскоп,
4 – эмульсия шариков диаметром
доли микрон (частицы гуммигута
– млечного сока деревьев).
32
Плотность жидкости примерно равна плотности шариков.
33. Опыт Перрена
n1 n0 em mж gh1
kT
, (1)
m – масса шарика,
mж – масса объёма жидкости, вытесненной шариком.
m mж gh2
n
1
kT
e
n2 n0e
(2).
n2
n1 m mж g h2 h1
ln
n2
kT
m mж g h1 h2
kT
.(4)
k
m m g h
ж
n1
T ln
n2
2
.(3)
h1
.(5)
33
34. Опыт Перрена. Определение числа Авогадро
km m g h
ж
2
h1
.(5)
n1
T ln
n2
ж
ж
m mж ( ж )V V
m
.
R
R kN A N A .
k
1
N A 6,8 10
.
Получил
моль
1
23
Точное значение:
N A 6,02 10
.
моль
23
34
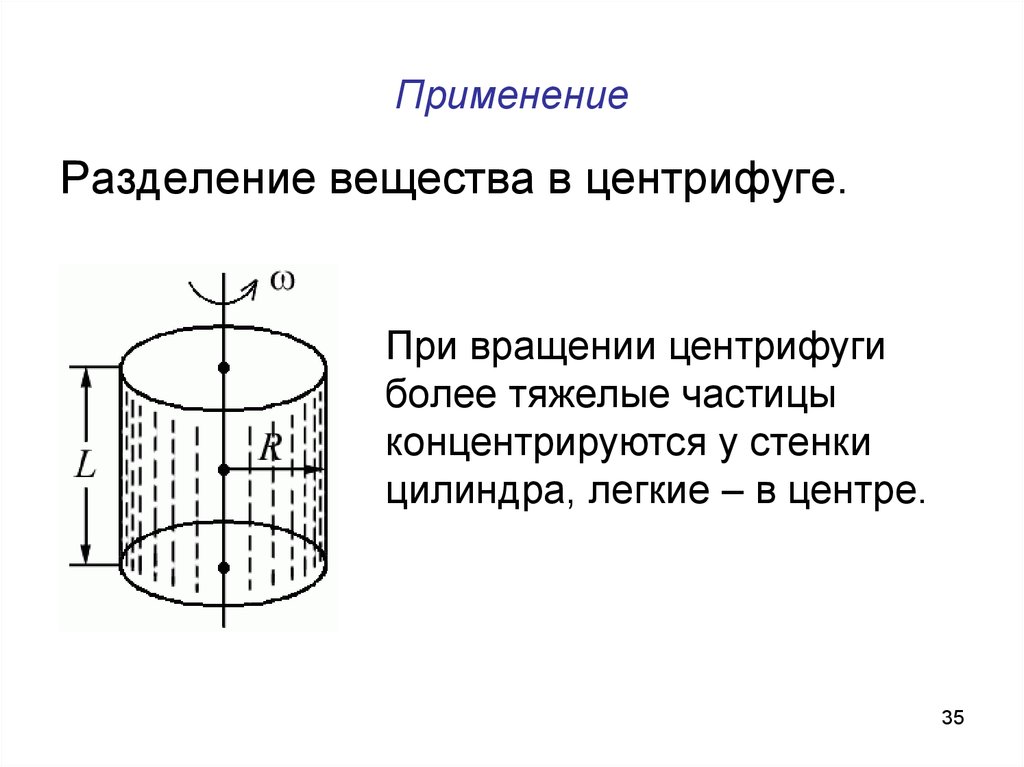
35. Применение
Разделение вещества в центрифуге.При вращении центрифуги
более тяжелые частицы
концентрируются у стенки
цилиндра, легкие – в центре.
35
36. Закон равномерного распределения энергии по степеням свободы
Степени свободы – число независимыхкоординат, определяющих положение и
конфигурацию системы в пространстве.
36
37. 1. Одноатомный газ имеет три степени свободы,
yт.к. может двигаться в 3-х
направлениях.
Следовательно, обладает
3 поступательными
степенями свободы.
x
z
Молекула –материальная точка.
Энергии вращательного движения нет
J
0; т.к . J 0.
2
2
37
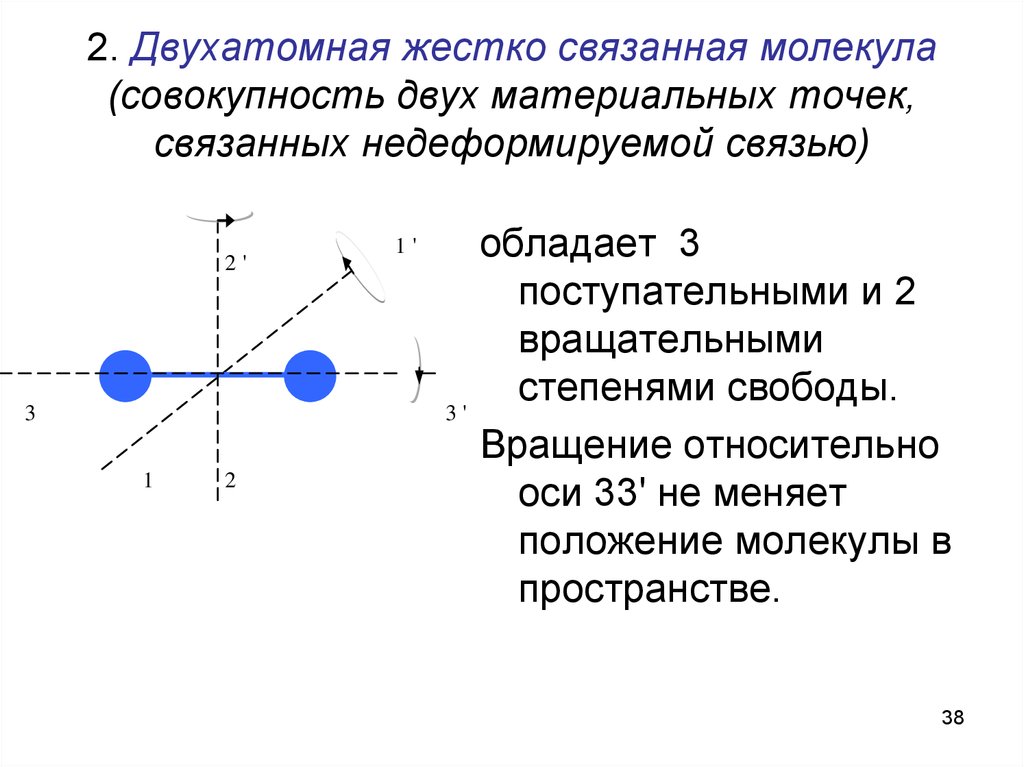
38. 2. Двухатомная жестко связанная молекула (совокупность двух материальных точек, связанных недеформируемой связью)
2'3
1'
3'
1
2
обладает 3
поступательными и 2
вращательными
степенями свободы.
Вращение относительно
оси 33' не меняет
положение молекулы в
пространстве.
38
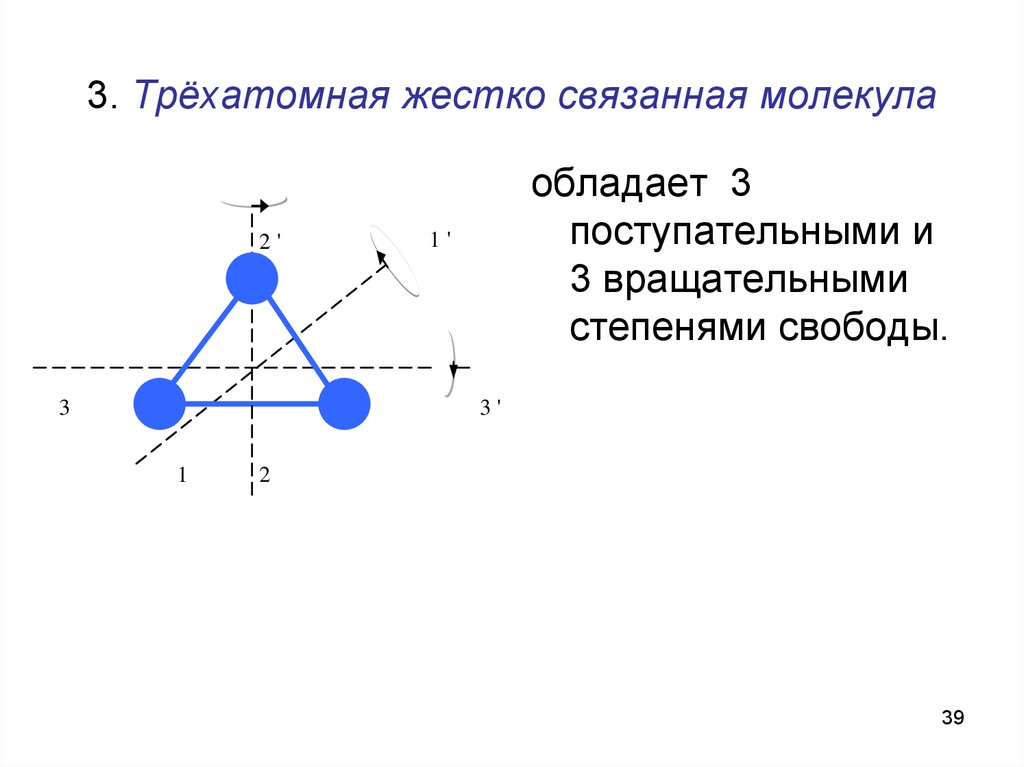
39. 3. Трёхатомная жестко связанная молекула
2'3
обладает 3
поступательными и
3 вращательными
степенями свободы.
1'
3'
1
2
39
40. Закон равномерного распределения энергии по степеням свободы (закон Больцмана):
если система частиц находится в состояниитермодинамического равновесия, то средняя
кинетическая энергия хаотического движения
молекул, приходящаяся на 1 степень свободы
поступательного и вращательного
1
движения, равна
2
kT .
Для реальных молекул, не обладающих
жёсткими связями между молекулами,
необходимо учитывать также степени свободы
40
колебательного движения.
41. На колебательную степень свободы
приходится не только кинетическаяэнергия, но и потенциальная, причём
среднее значение кинетической энергии
равно среднему значению
1
kT .
потенциальной энергии и равно
2
Следовательно, средняя суммарная
энергия молекулы: i kT ,
2
i = iпоступат. + iвращат. + 2iколеб.
41
42.
В идеальном газе взаимная потенциальнаяэнергия молекул E p 0 , т.к. молекулы
между собой не взаимодействуют, то
рассматривается только кинетическая
энергия, и
• для 1 моля газа внутренняя энергия равна
сумме кинетических энергии NA молекул:
i
i
U m N A Eк kTN A RT.
2
2
• Для произвольной массы m газа:
i
m i
U υ RT
RT ,
2
M2
υ – количество вещества.
42












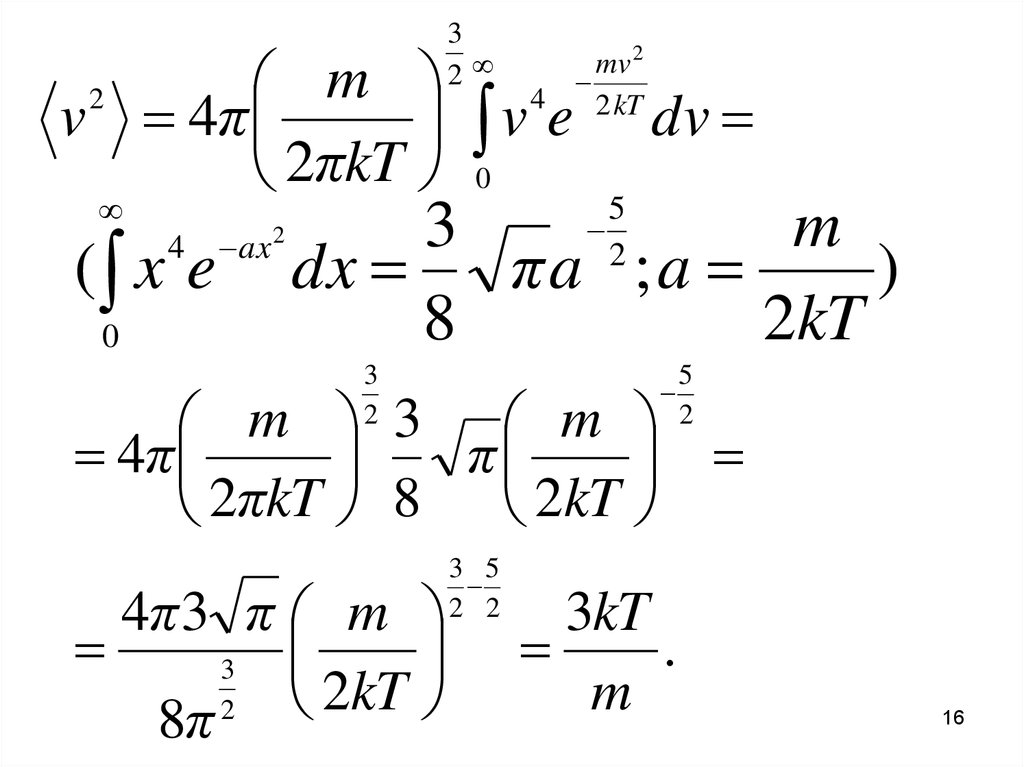






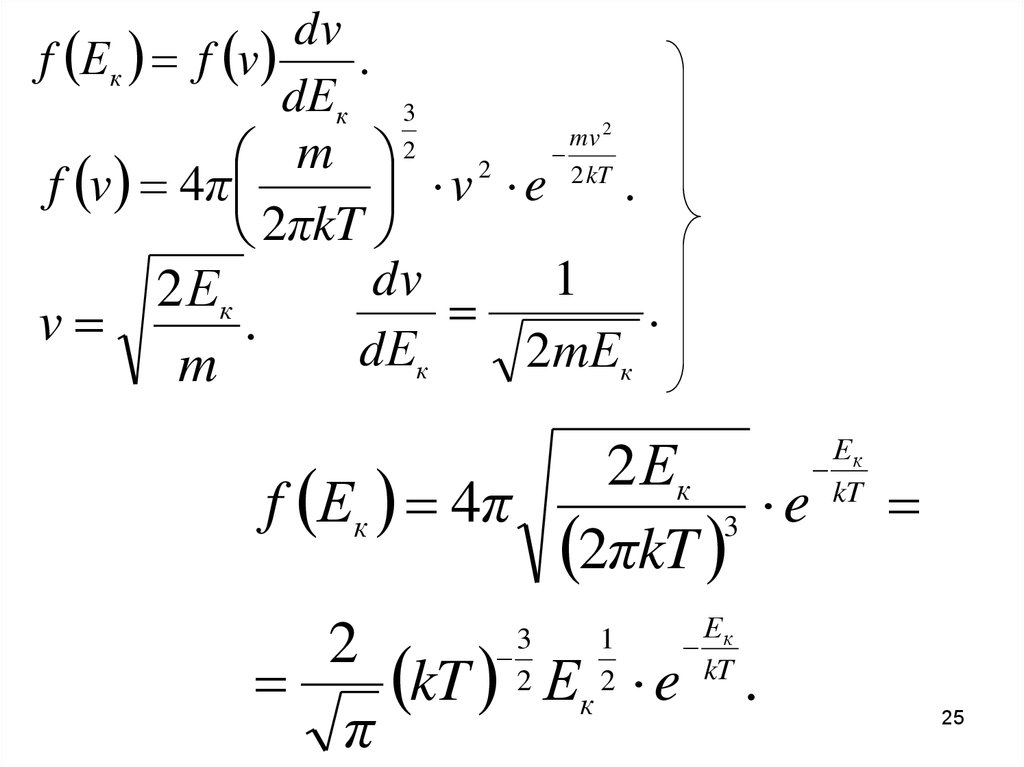













 physics
physics








