Similar presentations:
Распределение газовых молекул по скоростям и энергиям
1.
РАСПРЕДЕЛЕНИЕ ГАЗОВЫХ МОЛЕКУЛ ПОСКОРОСТЯМ И ЭНЕРГИЯМ
1. Скорости газовых молекул. Опыт Штерна
2. Вероятность события. Понятие о распределении
молекул газа по скоростям
3. Функция распределения Максвелла
4. Барометрическая формула
5. Распределение Больцмана
6. Закон распределения Максвелла-Больцмана
2.
1. Скорости газовых молекул. Опыт ШтернаВ средине XIX века была сформулирована
молекулярно-кинетическая теория, но тогда не было
никаких
доказательств
существования
самих
молекул.
Вся
теория
базировалась
на
предположении о движении молекул, но как
измерить скорость их движения, если они невидимы.
3. Теоретики первыми нашли выход. Из уравнения молекулярно-кинетической теории газов известно, что Отсюда среднеквадратичная скорость равна
Теоретики первыми нашли выход. Из уравнениямолекулярно-кинетической теории газов известно,
2
что
mυкв 3
kT
2
2
Отсюда среднеквадратичная скорость равна:
3kT
υкв
.
m
P RT
ρ
μ
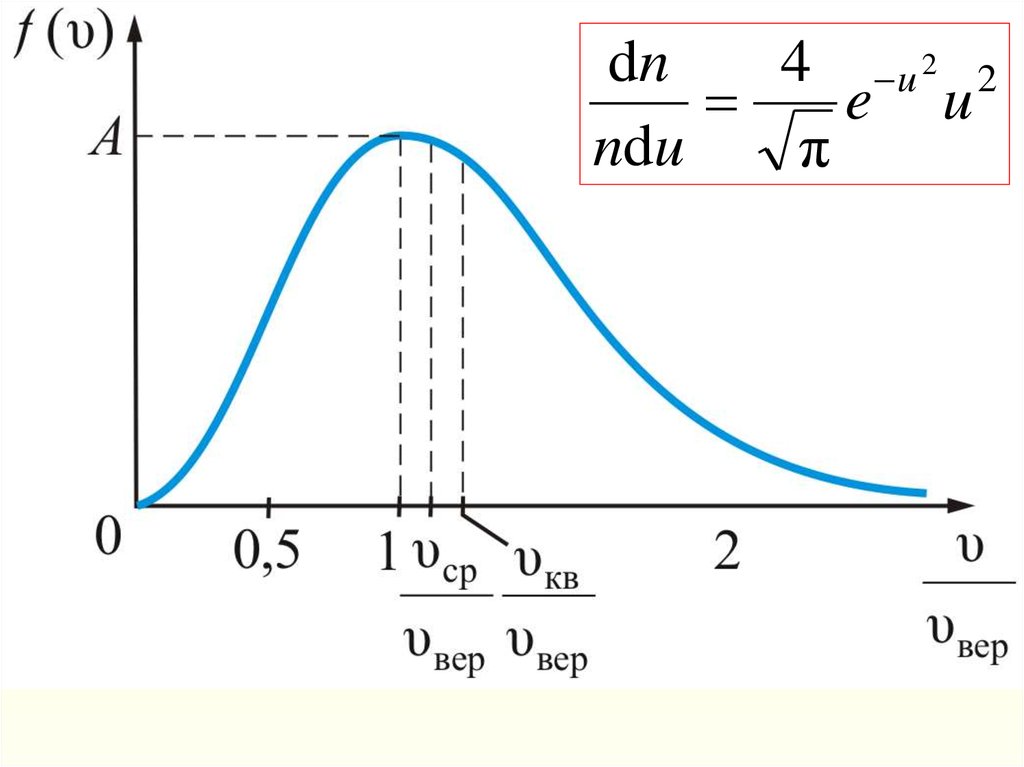
3kN AТ
3RT
υ кв
.
mN A
μ
3P
υкв
,
ρ
4. Например, при плотности азота, равной 1,25 кг/м3, при t = 0 С и , скорости молекул азота . Для водорода:
Например, при плотности азота, равной1,25 кг/м3, при t = 0 С и P 1 атм , скорости
молекул азота υ N 2 500 м/с.
Для водорода: υ H 2 2000 м/с
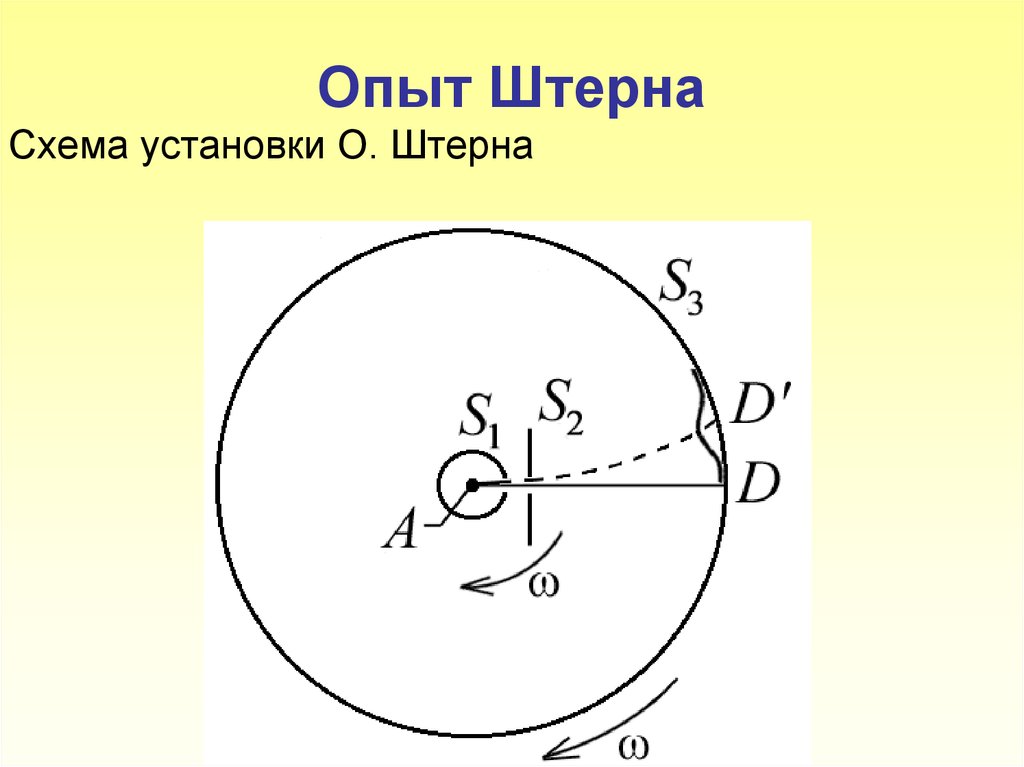
5. Опыт Штерна Схема установки О. Штерна
6. Платиновая нить А, покрытая снаружи серебром, располагается вдоль оси коаксиальных цилиндров S1, S3. Внутри цилиндров поддерживается низкое
Платиновая нить А, покрытая снаружисеребром,
располагается
вдоль
оси
коаксиальных цилиндров S1, S3.
Внутри
цилиндров поддерживается низкое давление
порядка10 3 10 4 Па.
При пропускании тока
через платиновую нить она разогревается до
температуры выше точки плавления серебра
(961,9 С). Серебро испаряется, и его атомы
через узкие щели в цилиндре S1 и диафрагме S2
летят к охлаждаемой поверхности цилиндра S3,
на которой они могут осаждаться. Если цилиндры
S1, S3 и диафрагма не вращаются, то пучок
осаждается в виде узкой полоски D на
поверхности цилиндра S3.
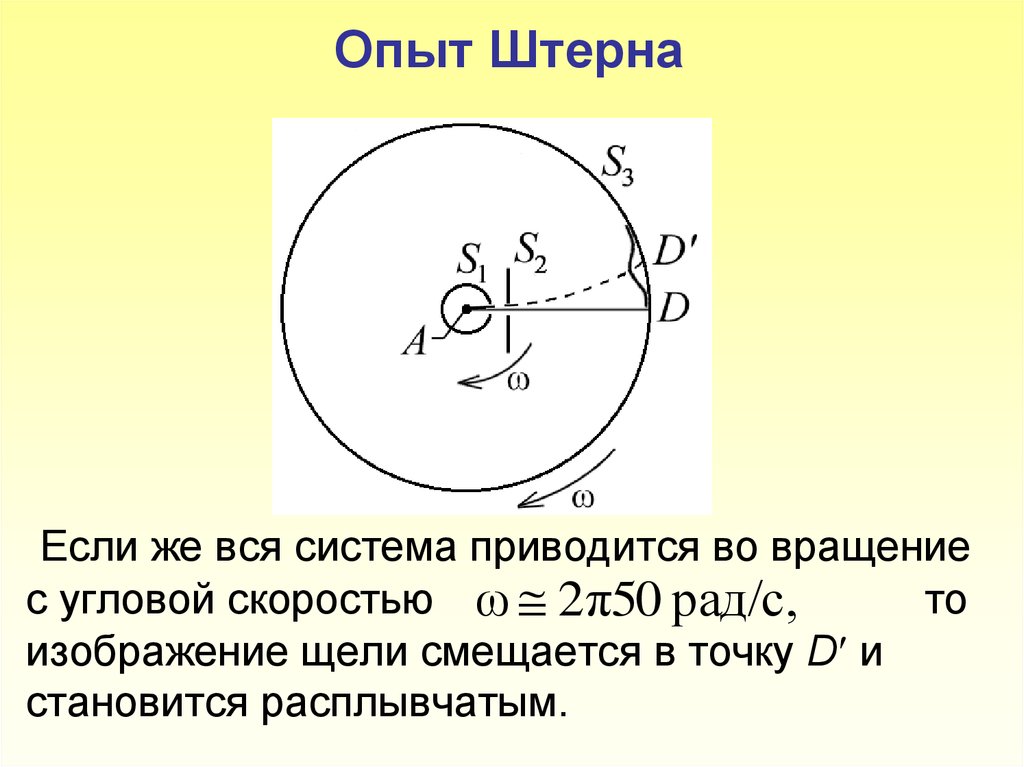
7. Опыт Штерна Если же вся система приводится во вращение с угловой скоростью то изображение щели смещается в точку D и становится расплывча
Опыт ШтернаЕсли же вся система приводится во вращение
с угловой скоростью ω 2π50 рад/с,
то
изображение щели смещается в точку D и
становится расплывчатым.
8. Пусть l – расстояние между D и D/, измеренное вдоль поверхности цилиндра S3, где – линейная скорость точек поверхности цилиндра S3, радиусом R;
Пусть l – расстояние между D и D/, измеренное вдольповерхности цилиндра S3, l υ t ,где
1
υ1 ωR – линейная скорость точек поверхности
цилиндра S3, радиусом R;
t S2 D / время прохождения атомами серебра
расстояния S D h .
2
Таким образом, имеем
l ωRh / υ, откуда
– можно определить величину скорости теплового
движения атомов серебра:
υэксп ωRh / l
9. Температура нити в опытах Штерна равнялась 1200С, что соответствует среднеквадратичной скорости молекул серебра В эксперименте получился
Температура нити в опытах Штерна равнялась1200 С, что соответствует среднеквадратичной
скорости молекул серебра
υкв 584 м/с
В эксперименте получился разброс значений
скорости от 560 до 640 м/с. Кроме того,
изображение щели D всегда оказывалось
размытым, что указывало на то, что атомы Ag
движутся с различными скоростями.
10. Ещё в XIX веке Дж. Максвелл утверждал, что молекулы, беспорядочно сталкиваясь друг с другом, как-то «распределяются» по скоростям, причём впо
Таким образом, в этом опыте были нетолько измерены скорости газовых молекул,
но и показано, что они имеют большой
разброс по скоростям. Причина – в
хаотичности теплового движения молекул.
Ещё в XIX веке Дж. Максвелл
утверждал, что молекулы, беспорядочно
сталкиваясь
друг
с
другом,
как-то
«распределяются» по скоростям, причём
вполне определённым образом.
11.
2. Вероятность события. Понятие ораспределении молекул газа по скоростям
С точки зрения атомно-молекулярного строения
вещества
величины,
встречающиеся
в
макроскопической физике, имеют смысл средних
значений, которые принимают некоторые функции от
микроскопических переменных системы.
Величины такого рода называются статистическими.
Примерами таких величин являются давление,
температура, плотность и др.
12.
Большое число сталкивающихся атомов и молекулобуславливает важные закономерности в поведении
статистических переменных, не свойственные
отдельным атомам и молекулам.
Такие закономерности называются вероятностными
или статистическими
13. Математическое определение вероятности: вероятность какого-либо события – это предел, к которому стремится отношение числа случаев, прив
Математическое определение вероятности:вероятность какого-либо события – это предел, к
которому стремится отношение числа случаев,
приводящих к осуществлению события, к общему
числу случаев, при бесконечном увеличении
последних:
n
P lim
n n
Здесь n число раз, когда событие произошло, а n
общее число опытов.
Отсюда следует, что Р может принимать значения от
нуля до единицы.
14. Молекулы движутся хаотически. Среди них есть и очень быстрые, и очень медленные. Благодаря беспорядочному движению и случайному характеру
Молекулы движутся хаотически. Среди них есть иочень быстрые, и очень медленные. Благодаря
беспорядочному движению и случайному характеру
их
взаимных
столкновений,
молекулы
определённым образом распределяются по
скоростям. Это распределение оказывается
однозначным и единственно возможным, и не только
не противоречит хаотическому движению, но именно
им и обусловлено.
15.
Будем искать число частиц ( n) скорости которыхлежат в определённом интервале значения скорости
υ ( т.е. от υ до υ Δυ ).
Здесь n – число молекул, попавших в этот интервал.
Для единицы объёма n должно быть пропорционально:
интервалу скорости υ,
концентрации молекул n,
самой скорости молекул υ.
Таким образом
Δn f ( υ)nΔυ
16.
n f ( )nЗдесь f ( ) – функция распределения молекул по
скоростям, n – концентрация молекул и
- интервал значений скоростей.
Перейдя к пределу, получим
dn f (υ)ndυ
Физический смысл f(υ) в том, что это отношение
числа молекул, скорости которых лежат в
определенном интервале скоростей, к общему числу
молекул в единичном интервале скоростей:
dn
dP
f ( )
nd d
17. Таким образом, f(υ) – имеет смысл вероятности, то есть показывает, какова вероятность любой молекулы газа в единице объёма иметь скорость, з
Таким образом, f(υ) – имеет смысл вероятности, тоесть показывает, какова вероятность любой молекулы
газа в единице объёма иметь скорость, заключённую в
единичном интервале, включающем заданную скорость υ.
В данном случае f(υ) называют плотностью
вероятности.
18.
3. Функция распределения МаксвеллаПусть
имеется
n
тождественных
молекул,
находящихся в состоянии беспорядочного теплового
движения при определенной температуре. После
каждого столкновения между молекулами, их
скорости меняются случайным образом.
В результате невообразимо большого числа
столкновений
устанавливается
стационарное
равновесное состояние, когда число молекул в
заданном
интервале
скоростей
сохраняется
постоянным.
19.
В результате каждого столкновения проекциискорости
молекулы
испытывают
случайное
изменение на υx, υy, υz, причем изменения каждой
проекции скорости независимы друг от друга.
Найдем в этих условиях, каково число частиц dn из
общего числа n имеет скорость в интервале
от
υ
до
υ dυ
20. Максвелл Джеймс Клерк (1831 – 1879) – английский физик. Работы посвящены электродинамике, молекулярной физике, общей статике, оптике, механике,
Распределение молекул идеального газа поскоростям впервые было получено знаменитым
английским ученым Дж. Максвеллом в 1860 году с
помощью методов теории вероятностей.
Максвелл Джеймс Клерк
(1831 – 1879) – английский
физик.
Работы посвящены
электродинамике, молекулярной
физике, общей статике, оптике,
механике, теории упругости.
Установил статистический закон,
описывающий распределение
молекул газа по скоростям.
21. Скорость – векторная величина. Для проекции скорости на ось х (x-ой составляющей скорости), имеем тогда или
Скорость – векторная величина. Дляпроекции скорости на ось х (x-ой
составляющей скорости), имеем
dnx f ( υ x )ndυ x ,
тогда
1
mυ 2x
2 2 kT
e
dnx
1 m
f (υ x )
ndυx
π 2kT
или
dnx
f (υ x )
ndυx
mυ2x
A1e 2 kT ,
mυ 2x
A1e 2 kT
,
22.
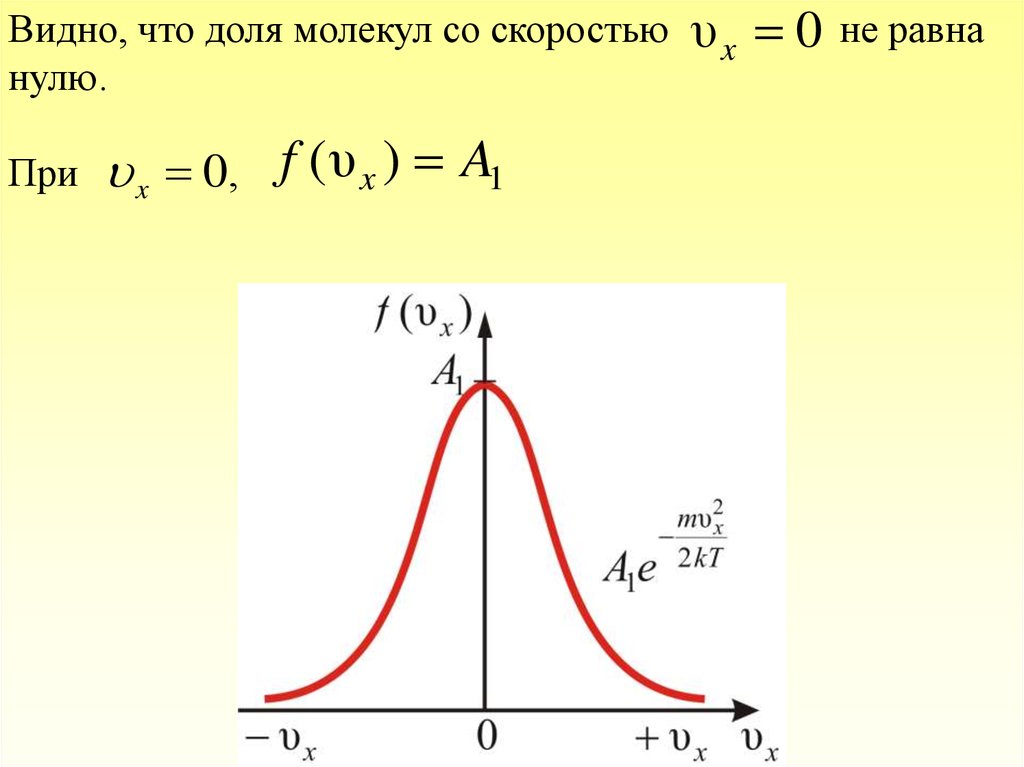
Видно, что доля молекул со скоростьюнулю.
При
x 0, f ( υ x ) A1
υx 0
не равна
23. Приведённое выражение и график справедливы для распределения молекул газа по x-ым компонентам скорости. Очевидно, что и по y–ым и z–ым комп
Приведённое выражение и графиксправедливы для распределения молекул газа
по x-ым компонентам скорости. Очевидно,
что и по y–ым и z–ым компонентам скорости
также можно получить:
dn y
ndυy
A1e
2
mυ y
2 kT
и
dnz
ndυz
mυ 2z
A1e 2 kT .
24. Вероятность того, что скорость молекулы одновременно удовлетворяет трём условиям: x – компонента скорости лежит в интервале от υх до ; y – к
Вероятность того, что скорость молекулыодновременно удовлетворяет трём условиям:
x – компонента скорости лежит в интервале
от υх до υ x dυ x ; y – компонента, в интервале
от υy до υ y dυ y ; z – компонента, в интервале
от υz до υ z dυ z будет равна произведению
вероятностей каждого из условий
(событий) в отдельности:
dnxyz
mυ 2
3 2 kT
A1 e
dυ x dυ y dυ z ,
n
2
2
2
2
где υ υ x υ y υ z
25. Или Этой формуле можно дать геометрическое истолкование: dnxyz – это число молекул в параллелепипеде со сторонами dυx, dυy, dυz, то есть в объёме
Илиdnxyz
n m
3/ 2
π 2kT
3/ 2
mυ 2
e 2 kT dυ
x dυ y dυ z .
Этой формуле можно дать геометрическое
истолкование: dnxyz – это число молекул в
параллелепипеде со сторонами dυx, dυy, dυz,
то есть в объёме dV dυ x dυ y dυ z
находящемся на расстоянии υ от начала
координат в пространстве скоростей.
26.
27.
Величина (dnxyz) не может зависеть от направлениявектора скорости. Поэтому надо получить функцию
распределения молекул по скоростям независимо от
их направления, то есть по абсолютному значению
скорости.
Если собрать вместе все молекулы в единице
объёма, скорости которых заключены в интервале от
υ до υ dυ по всем направлениям, и выпустить их,
то они окажутся через одну секунду в шаровом слое
толщиной dυ и радиусом υ
28.
29. Объём этого шарового слоя: Общее число молекул в слое:
Объём этого шарового слоя:dΩ 4πυ dυ
2
Общее число молекул в слое:
n m
dn 3 / 2
π 2kT
3/ 2
2
mυ
e 2 kT dΩ.
30. Отсюда следует закон Максвелла – распределение молекул по абсолютным значениям скоростей: где – доля всех частиц единичного объёма, скор
Отсюда следует закон Максвелла –распределение молекул по абсолютным
значениям скоростей:
dn
4 m
n
π 2kT
3/ 2
mυ 2
2
2
kT
e
υ dυ,
dn
где n – доля всех частиц единичного
объёма, скорости которых лежат в интервале
от υ до υ dυ.
31. При получаем плотность вероятности, или функцию распределения молекул по скоростям: Эта функция обозначает долю молекул единичного объём
При dυ 1получаем плотность
вероятности, или функцию распределения
молекул
по
скоростям:
3
mυ 2
2 2 kT 2
e
υ.
dn
4 m
f ( υ)
ndυ
π 2kT
Эта
функция
обозначает
долю
молекул
единичного
объёма
газа,
абсолютные скорости которых заключены
в
единичном
интервале
скоростей,
включающем данную скорость.
32.
Обозначим3
2
4 m
A
,
π 2кT
тогда получим:
2
f ( υ)
mυ
2
2
kT
Ae
υ.
33.
Выводы:f ( υ)
mυ 2
Ae 2kT υ2 .
- Вид распределения молекул газа по скоростям, для
каждого газа зависит от массы m и температуры Т газа и
не зависит от давления P и объёма V газа.
- В показателе степени стоит отношение, кинетической
энергии, соответствующей данной скорости υ к средней
энергии теплового движения молекул при данной
температуре: mυ 2
2kT
Значит распределение Максвелла характеризует
распределение молекул по значениям кинетической
энергии (показывает, какова вероятность при данной
температуре иметь такое значение кинетической энергии).
34. Рассмотрим пределы применимости классического описания распределения частиц по скоростям. Для этого воспользуемся соотношением неопред
Рассмотрим пределы применимостиклассического описания распределения частиц
по скоростям.
Для этого воспользуемся соотношением
неопределенностей Гейзенберга.
Согласно этому соотношению координаты и
импульс частицы не могут одновременно иметь
определенное значение. Классическое описание
возможно, если выполнены условия:
ΔxΔPx h,
ΔyΔPy h,
ΔzΔPz h.
35. Здесь – фундаментальная константа (постоянная Планка), определяющая масштаб квантовых (микроскопических процессов). Таким образом, если ч
34Дж с –
Здесь h 6,62 10
фундаментальная константа (постоянная
Планка), определяющая масштаб
квантовых (микроскопических процессов).
Таким образом, если частица
3
3
находится в объеме ,ΔxΔyΔz h / P то в
этом случае возможно описание ее
движения на основе законов классической
механики.
36.
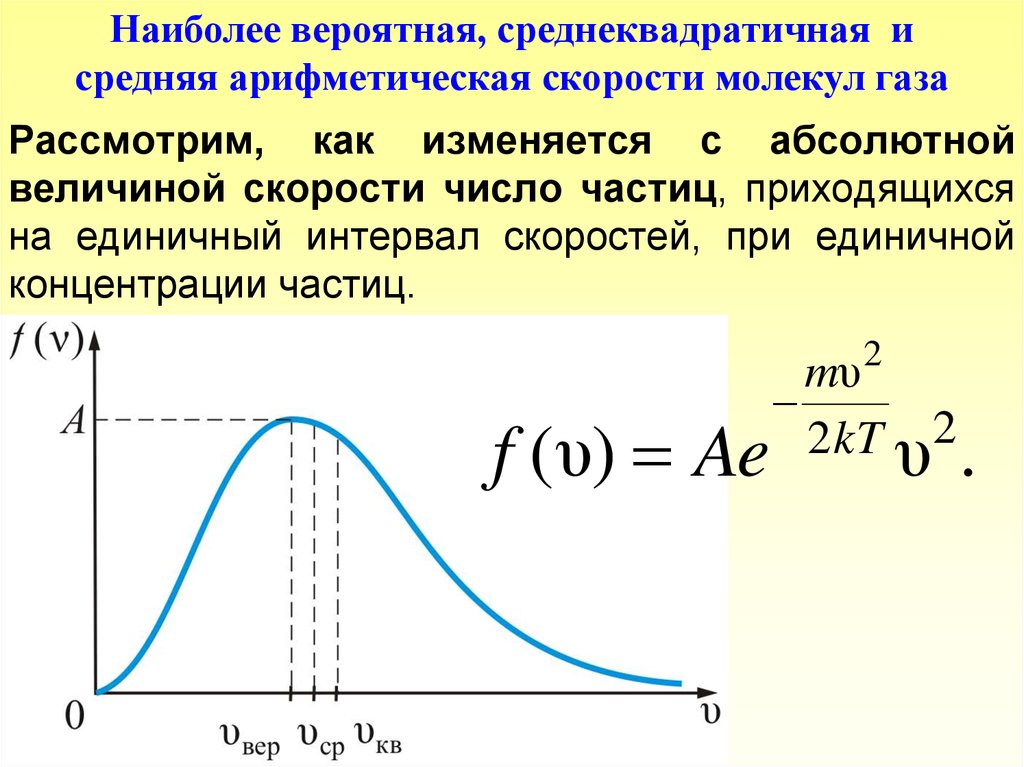
Наиболее вероятная, среднеквадратичная исредняя арифметическая скорости молекул газа
Рассмотрим, как изменяется с абсолютной
величиной скорости число частиц, приходящихся
на единичный интервал скоростей, при единичной
концентрации частиц.
2
f ( υ)
mυ
2
2
kT
Ae
υ.
37.
Из графика видно, что при «малых» υ , т.е. приmυ 2
1 , имеем f ( υ) ~ υ 2;
2kT
затем
f ( υ) достигает максимума А и далее
2
экспоненциально спадает
mυ
2 kT
f (υ) ~ e .
38.
Величина скорости, на которую приходится максимумзависимости f ( υ) называют наиболее вероятной
скоростью.
Величину этой скорости найдем из условия
равенства нулю производной
υ вер
2kT
m
df ( υ)
0
dυ
- наиболее вероятная скорость
одной молекулы.
Для одного моля газа:
υвер
2kN AT
2 RT
mNA
μ
2RT
υвер
μ
39.
Среднюю квадратичную скорость найдем используясоотношение :
2
mυкв 3
kT
2
2
3kT
υкв
m
3RT
υкв
μ
– для одной молекулы.
– для одного моля газа.
40. Средняя арифметическая скорость υср где – число молекул со скоростью от υ до . Если подставить сюда f(υ) и вычислить, то получим: – для одн
Средняя арифметическаяскорость υср
1
υср υn f ( υ)dυ,
n0
где nf (υ)dυ dn – число молекул со скоростью
от υ до υ dυ. Если подставить сюда f(υ) и
вычислить, то получим:
8kT
2,25kT
υ ср
– для одной молекулы.
πm
m
8RТ
2,25 RT
υ ср
– для одного моля газа.
πμ
μ
41.
υкв1,22
υвер
υср
υвер
1,13;
42. Формула Максвелла для относительных скоростей
Для решения многих задач удобно использоватьформулу Максвелла, где скорость выражена в
относительных единицах.
Относительную скорость обозначим через u:
υ
u
,
υвер
где
υ вер
2kT
m
43.
dn4 u 2 2
e u
ndu
π
Формула Максвелла для относительных
скоростей
Это уравнение универсальное.
В таком виде функция распределения не зависит ни от
рода газа, ни от температуры
44.
dn4 u 2 2
e u
ndu
π
45.
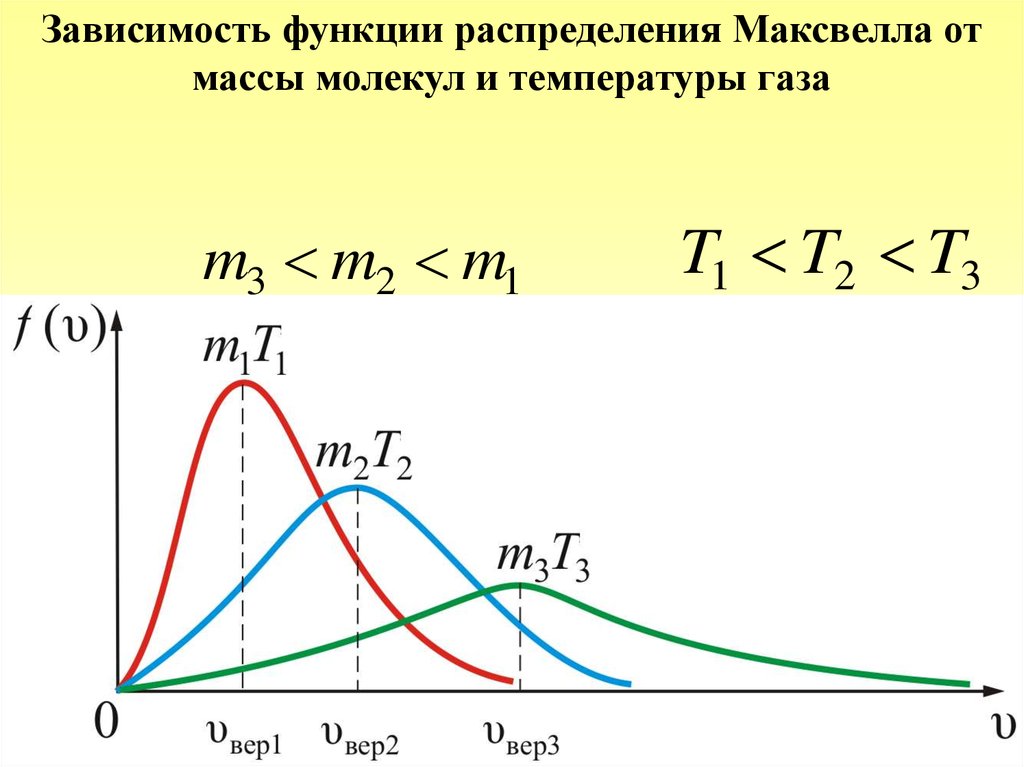
Зависимость функции распределения Максвелла отмассы молекул и температуры газа
m3 m2 m1
T1 T2 T3
46.
Площадь под кривой величина постоянная,равная единице ( f ( υ) const 1 ), поэтому важно
знать как будет изменяться положение максимума
кривой:
m
f ( υвер ) ~
,
T
υвер
T
~
.
m
Максвелловский закон распределения по скоростям
и все вытекающие следствия справедливы только
для
газа
в
равновесной
системе.
Закон
статистический и выполняется тем лучше, чем
больше число молекул.
47.
4. Барометрическая формулаАтмосферное давление на какой-либо высоте обусловлено
весом выше лежащих слоёв газа.
Пусть P – давление на высоте h, а P ΔP
– на высоте h Δh
Причём dh>0, dР < 0, так как на
большей высоте давление
меньше.
Разность давления P ( P dP)
равна весу газа, заключённого в
объёме цилиндра с площадью
основания равного единице и
высотой dh, P ρgh, ρ
плотность газа на высоте h,
медленно убывает с высотой.
48.
.P ρgh,
Pμ
ρ
– плотность газа на высоте h
RT
P ( P dP) ρgdh
dP
μg
μgP
dh
dP
dh
P
RT
RT
μgh
ln P
ln C
RT
С = Р0 – давление на высоте h 0
P
μgh
RT
P0e
- барометрическая формула
49.
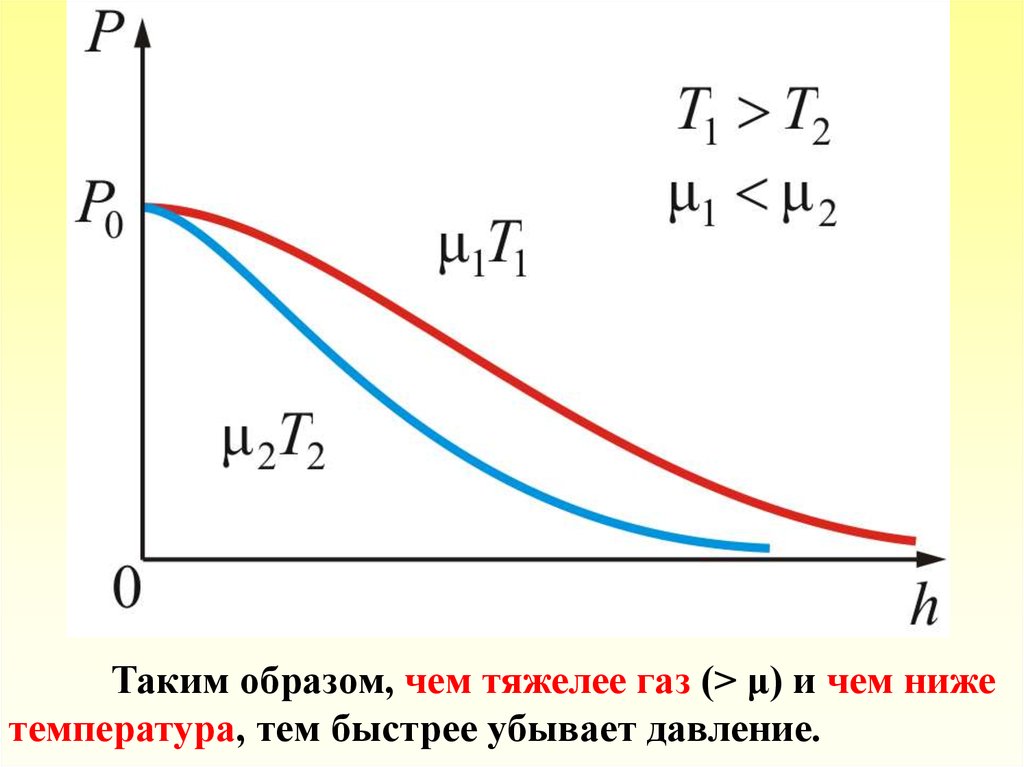
Из барометрической формулы следует, что P убывает свысотой тем быстрее, чем тяжелее газ (чем больше μ) и
чем ниже температура (например, на больших высотах
концентрация легких газов Не и Н2 гораздо больше чем у
поверхности Земли).
На рисунке изображены две кривые, которые можно
трактовать, либо как соответствующие разным μ (при
одинаковой Т), либо как отвечающие разным Т, при
одинаковых μ.
50.
Таким образом, чем тяжелее газ (> μ) и чем нижетемпература, тем быстрее убывает давление.
51.
5. Распределение БольцманаРаспределение
Больцмана
определяет
распределение частиц в силовом поле в условиях
теплового равновесия.
Пусть
идеальный
газ
находится
в
поле
консервативных сил, в условиях теплового
равновесия. При этом, концентрация газа будет
различной в точках с различной потенциальной
энергией, что необходимо для соблюдения условий
механического равновесия.
52.
Число молекул в единичном объеме n убывает судалением от поверхности Земли, значит и давление
тоже убывает.
P nkT
Если известно число молекул в единичном объеме,
то известно и давление, и наоборот. Давление и
плотность пропорциональны друг другу, поскольку
температура в нашем случае постоянна. Давление с
уменьшением высоты должно возрастать, потому что
нижнему слою приходится выдерживать вес всех
расположенных сверху атомов.
53.
Исходя из основного уравнения молекулярнокинетической теории:P nkT, заменим P и P0 вбарометрической формуле на n и n0 и получим
распределение Больцмана для молярной массы
газа:
μgh
n n0e
RT
,
где n0 и n число молекул в единичном объёме на
высоте h = 0 и h, соответственно.
54.
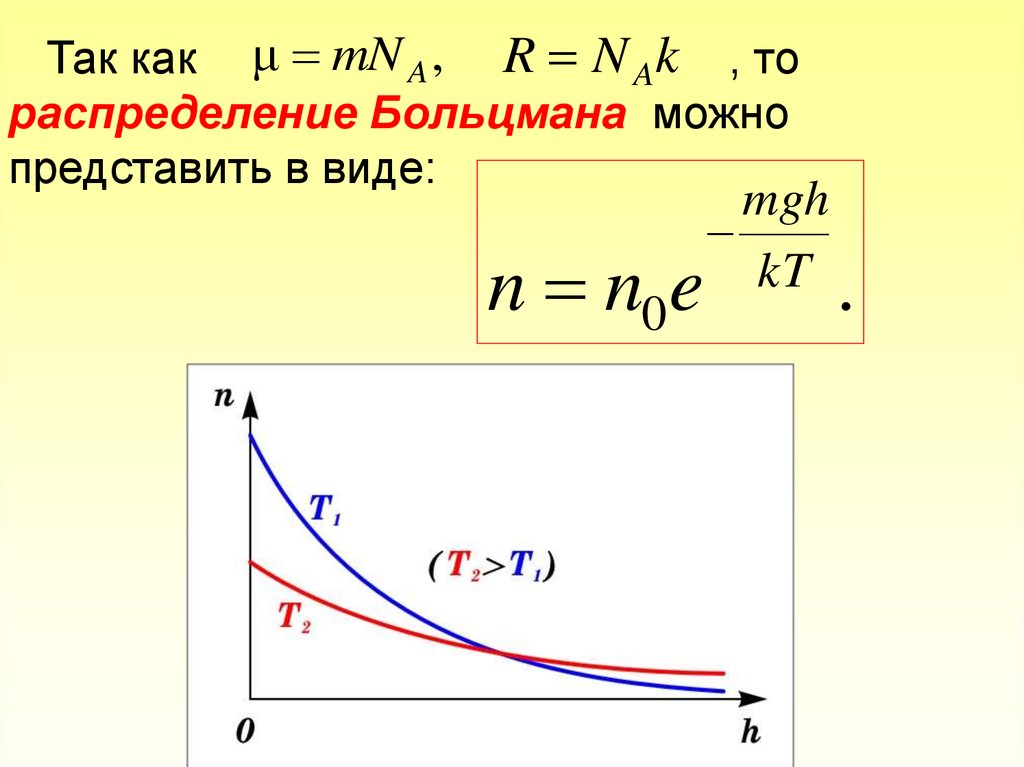
Так как μ mN A , R N Ak , тораспределение Больцмана можно
представить в виде:
n n0
mgh
kT
e
.
55.
С уменьшением температуры число молекул навысотах, отличных от нуля, убывает. При T=0
тепловое движение прекращается, все молекулы
расположились
бы
на
земной
поверхности.
При высоких температурах, наоборот, молекулы
оказываются распределёнными по высоте почти
равномерно, а плотность молекул медленно убывает
с высотой.
56.
Так как U mgh –потенциальная энергия,следовательно, распределение Больцмана
характеризует распределение частиц по значениям
потенциальной энергии:
U
n n0e
kT
– это закон распределения частиц по
потенциальным энергиям – распределение
Больцмана.
Здесь n0 – число молекул в единице объёма в там,
где U=0
57.
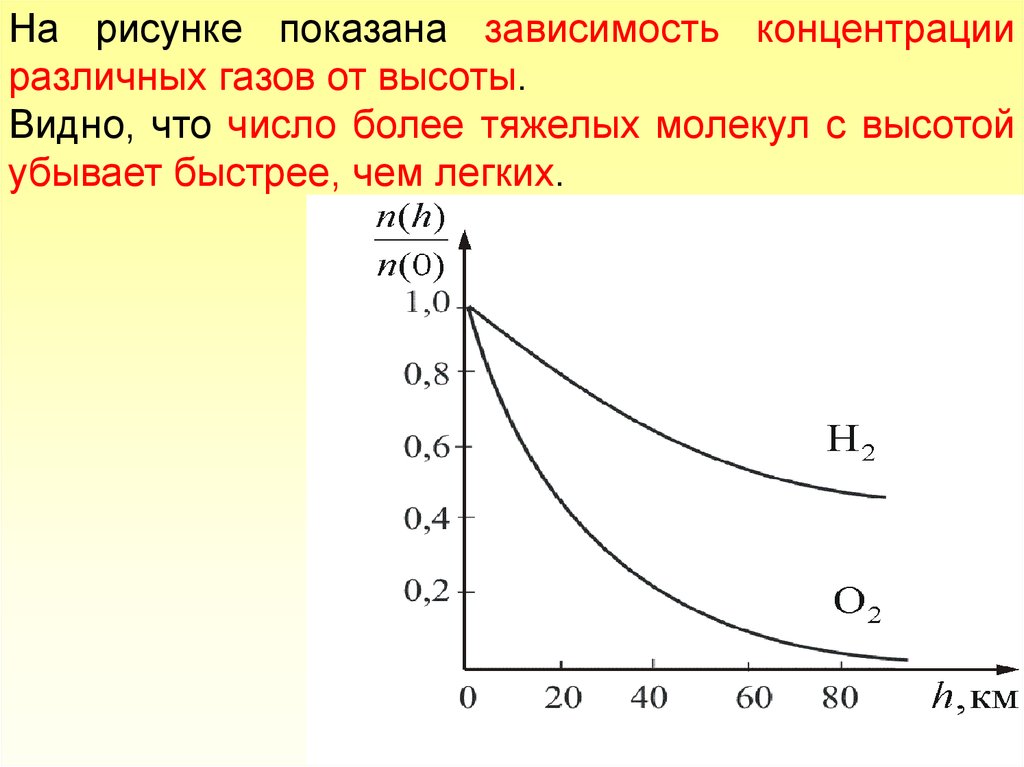
На рисунке показана зависимость концентрацииразличных газов от высоты.
Видно, что число более тяжелых молекул с высотой
убывает быстрее, чем легких.
58.
Можно получить отношение концентраций молекул вточках с U1 и U2
n1
e
n2
U 1 U 2
kТ
Больцман доказал, что соотношение справедливо
не только в потенциальном поле сил гравитации, но
и в любом потенциальном поле, для совокупности
любых одинаковых частиц, находящихся в состоянии
хаотического теплового движения.
59.
6. Закон распределения Максвелла-БольцманаИз выражения для распределения молекул по
скоростям
mυ2
3/ 2
4n m
2 kT υ 2 dυ.
dn( υ)
e
π 2kT
можно найти распределение молекул газа по
значениям кинетической энергии K. Для этого
2
перейдём от переменной υ к переменной К : K mυ
2
K
3 / 2 1 / 2 kT
K e dK
2n
kT
dn( K )
π
nf ( K )dK ,
где dn(K) – число молекул, имеющих кинетическую
энергию поступательного движения, заключённую в
интервале от K до К+dК
60. Отсюда получим функцию распределения молекул по энергиям теплового движения: Средняя кинетическая энергия молекулы идеального газа:
Отсюда получим функцию распределениямолекул по энергиям теплового движения:
K
3 / 2 1 / 2 kT
K e .
2
kT
f (K )
π
Средняя кинетическая K энергия
молекулы идеального газа:
3
K Kf K dK kT ,
2
0
61.
Итак, закон Максвелла даёт распределениечастиц по значениям кинетической энергии а
закон Больцмана – распределение частиц по
значениям потенциальной энергии.
Оба распределения можно объединить в единый
закон Максвелла-Больцмана, согласно которому,
число молекул в единице объёма, скорости которых
лежат в пределах от υ до υ+dυ равно:
dnU , K
4 m
n0
π 2kT
3/ 2
U K
2
kT
e
υ dυ.
62. Обозначим E=U+K – полная энергия. Тогда Это закон распределения Максвелла-Больцмана. Здесь n0 – число молекул в единице объёма в той точке, гд
Обозначим E=U+K – полная энергия.Тогда
dn n0
E
2
kT
Ae υ dυ.
Это закон распределения МаксвеллаБольцмана.
Здесь n0 – число молекул в единице объёма в
той точке, где U 0 ;
3/ 2
m
A
π 2kT .
63.
Потенциальнаяи
кинетическая
энергии,
а
следовательно и полная энергия Е, могут принимать
непрерывный ряд значений.
Если же энергия частицы может принимать лишь
дискретный ряд значений Е1, Е2 ... (как это имеет
место, например, для внутренней энергии атома), то
в этом случае распределение Больцмана имеет вид:
Ni ANe
Ei
kT
64. где Ni – число частиц, находящихся в состоянии с энергией Еi, а А – коэффициент пропорциональности, который должен удовлетворять условию: гд
где Ni – число частиц, находящихся всостоянии с энергией Еi, а А – коэффициент
пропорциональности, который должен
удовлетворять условию:
N
N
Νi A e
i 1
Ei
kT
N,
i 1
где N – полное число частиц в
рассматриваемой системе.
65. Тогда, окончательное выражение распределения Максвелла-Больцмана для случая дискретных значений будет иметь вид:
NiNe
e
Ei
Ei
kT
.
kT
























































 physics
physics








