Similar presentations:
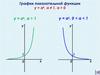
Показательные уравнения и неравенства
1.
64
g x = 2x-4
f x = 5x 2
-5
5
2.
Прикладноеиспользование
показательной
функции
Работу выполнили:
Горюнов Женя,
Парилова Варя
Мурзабекова Клара
3.
Цель:- НАГЛЯДНАЯ
ДЕМОНСТРАЦИЯ
ФУНКЦИОНАЛЬНЫХ ЗАВИСИМОСТЕЙ,
С ПОМОЩЬЮ КОТОРЫХ
МОЖНО ОПИСАТЬ
РЕАЛЬНЫЕ
СОБЫТИЯ
В ЖИЗНИ, ИСТОРИИ;
РАЗЛИЧНЫЕ ПРОЦЕССЫ В ХИМИИ,
ФИЗИКЕ,БИОЛОГИИ,АСТРОНОМИИ.
4.
Показательная функция очень частореализуется в физических,
биологических и иных законах. В
жизни нередко приходится встречаться
с такими фактами, когда скорость
изменения какой-либо величины
пропорциональна самой величине. В
этом случае рассматриваемая величина
будет изменяться по закону, имеющему
вид:
у=у0
x
а
5.
Графики убывающей ивозрастающей показательной
функции
Процессы органического роста или
органического затухания происходят по
закону показательной функции.
6.
Доказательство тому –распространение в Австралии
кроликов, которых там раньше не
было. Одна пара кроликов дает за
год приплод в 50 крольчат. Если бы
все они оставались в живых, то в
грубом приближении можно было
бы считать, что число кроликов
увеличивается в 25 раз каждый год.
7.
График размножения кроликов8.
Рост бактерий в идеальныхусловиях соответствует
процессу органического роста;
Закон органического роста
выражается формулой:
N = Nо
kt
e .
9.
радиоактивный распадвещества подчиняется процессу
органического затухания.
Когда радиактивное вещество
распадается, его количество
уменьшается.
m = m0(1/2)t/t0
10.
Законам органического ростаподчиняется рост вклада в
банке.
11.
А также законуорганического
роста подчиняется
восстановление
гемоглобина в
крови донора или
раненого.
12.
В природе и техникечасто можно
наблюдать процессы,
которые подчиняются
законам
выравнивания,
описываемым
показательной
функцией.
Например: все, наверное, замечали, что если
снять кипящий чайник с огня, то сначала он
быстро остывает, а потом остывание идет
гораздо медленнее. Дело в том, что скорость
остывания пропорциональна разности между
температурой чайника и температурой
окружающей среды. Чем меньше становится эта
разность, тем медленнее остывает чайник.
13.
Если сначала температура чайникаравнялась Т0, а температура воздуха Т1,
то через t секунд температура Т чайника
выразится формулой:
T=(T1-T0)e-kt + Т1
Где k – число, зависящее от формы
чайника, материала, из которого он
сделан, и количества воды, которое в
нем находится.
14.
При падении тел вбезвоздушном пространстве
скорость их непрерывно
возрастает. При падении тел в
воздухе скорость падения тоже
увеличивается, но не может
превзойти определенной
величины.
Рассмотрим задачу о падении парашютиста. Если считать, что сила
сопротивления воздуха пропорциональна скорости падения
парашютиста, то есть что F = kv, то через t секунд скорость
падения будет равна:
v= mg/k(1-e-kt/m)
где m – масса парашютиста. Через некоторый промежуток времени
e –kt/m станет очень маленьким числом, и падение станет почти
равномерным. Данная формула пригодна не только для изучения
падения парашютиста, но и для изучения падения капли дождевой
воды, пушинки и т.д.
15.
Барометрическая формула. Припостоянной температуре давление
воздуха изменяется с изменением
высоты над уровнем моря по
закону:
P=PoAn
Po – давление на уровне моря
Р – давление на высоте h
a – const, h – изменяется
16.
Рост народонаселения. Изменениечисла людей в стране на
наибольшем отрезке времени
описывается формулой:
N = Noeat
No – число людей, при t = 0
N – число людей в момент времени t
e, a – const
17.
Вывод:Мы проанализировали и изучили
литературу по истории развития
функции. Рассмотрели примеры
применения показательной функции в
науке, природе и технике. По закону
показательной функции описаны
процессы органического роста или
органического затухания, также ей
подчинены законы выравнивания.
18.
Блиц-опрос:10. Какое уравнение называется
показательным?
х
11. Решите уравнение: 3 1
х
1 49
7
6
х
-6
19.
Показательное уравнение – это уравнение, вкотором неизвестное содержится в показателе
степени.
Методы решения
показательных уравнений
Приведение степеней
к одному основанию
Метод
приведения к
квадратному уравнению
Вынесение
общего
множителя за скобки
Метод
почленного
деления
Функционально –
графический
20.
Указать способы решенияпоказательных уравнений.
Приведение к одному
основанию
1
Вынесение общего
множителя за скобки
5
3 x 1
5 5 5 31 36 216
x 1
1
1
x
27
81
2
3
9 3
4
x 1
x
x
x 1
54
6
2 x 1
3
7
8
4 3 2 4 0 4
x
x
2 x 2
8 3 3
2 x
x 1
9
1 3
x
1
3x
3
Замена переменного
(привед. к квадратному)
4
4 1 0
x 2
10
11
7
1
49 x 1
7
x 2
12
5 3 36
x
x
14 7 5
x
1 2 x
9 81
27
2 x
21.
Алгоритм решенияпоказательных уравнений
1. Уравниваем основания степеней во всех слагаемых,
содержащих неизвестное в показателе степени.
2. а) Если показатели степеней отличаются только
постоянным слагаемым, то выносим за скобки общий
множитель.
б) Если показатель одной из степеней по модулю
в 2 раза больше показателя другой, то вводим новую
переменную.
3. Графическое решение уравнения сводится к
построению графиков функций левой и правой
частей уравнения, нахождению по рисунку
примерного значения абсциссы точки пересечения
графиков. Если возможно, с помощью проверки
уточняется корень уравнения.
22.
Страничка ЕГЭРешите уравнения (Часть 1):
1)49
х 1
1
7
3)9
х
х
2)2
4 3
х
х
3
3 2
0
х 4
76
23.
Решение?
?
?показательных
уравнений
?
?
ЕГЭ (Часть 2)
?
?
24.
Решить показательноеуравнение:
3
16+х
4+х
4+х
8-х
4 5 = 540
2 4+х
3х
2
3
8-х
16+х
3
(2 )
5 = (2 3 5)
8+2х
3х
16-2х 24-3х 8-х
16+х
3
2
5 =2
3
5
8+2х-16+2х 16+х-24+3х 3х-8+х
2
3
5
=1
4х-8 4х-8 4х-8
2
3
5
= 1 54054 22 * 5
27
9
3
3
3
3
25.
(24х-8
* 3 * 5)
=1
4х-8
0
30
= 30
4х-8 = 0
4х = 8
Х = 2
26.
Подсказка к решению:Разложить
основания степеней в
обеих частях уравнения на
простые множители
Использовать правила действия
со степенями
Разделить обе части уравнения
27.
Решить самостоятельно:5х-1
2
3
Х+3
32
4х+1
7
3х+1
3
х-2
3х+3
= 504
х+2
625
Желаю успехов
при решении
уравнений!!!
х+7
= 600
28.
Страничка ЕГЭРешите уравнение (Часть 2):
16 х
3
4
4 х
5
3х
8 х
540
1.Основание степеней в обеих частях уравнения
разложите на простые сомножители.
2. Используйте правила действий со степенями.
29.
Блиц-опрос:1. Для чего необходимо знать свойства возрастания и
убывания функции?
2. Решите неравенства:
3
х
2 2
х
4
1 1
б.
3 3
а.
в. 3 -х
81
30.
Методы решенияпоказательных неравенств
Методы решения
показательных неравенств
Приведение степеней
к одному основанию
Метод
приведения к
квадратному
неравенству
Вынесение
общего
множителя за скобки
Метод
почленного
деления
Функционально –
графический
31.
Страничка ЕГЭ(Часть В)
1. Найдите число целых отрицательных решений
неравенства:
2х 1
1
5
125
2. Найдите наибольшее целое решение:
х
х
16 4 2 0
3. Найти наименьшее целое решение:
х
1 х 1
3
32.
Тест1 вариант
1.
Какие из данных функций
являются показательными:
а)у
х
2
3.
в)у
2
х
х 8
1
2 2
а)2
2.
х 1
б)4
6
в)0
Решите уравнение:
3
х 2
б) - 3 в)1
г)4
Найдите число целых
положительных решений:
3
г) -1
х
3 90
а)2
3.
3
б)у 5 - 3х
х
х - 1 г)у
х
3
х
в)у
х
32
а)2 б) - 3 в)0 г) -13
Укажите наибольшее целое
решение неравенства:
х
а)у
3-х
г)у 2 - 3х
Решите уравнение:
б)у
2.
2
2 вариант
1.
Какие из данных функций
являются показательными:
2х -9
а)5
1
27
б)2
в)7
г)4
33.
Итог урокаДля того, чтобы успешно сдать ЕГЭ, что нужно знать по данной
теме:
Определение показательной функции;
График показательной функции;
Свойства показательной функции;
Показательные уравнения;
Вид и метод их решения;
Показательные неравенства и методы их
решения.
Главное: применить свои знания на
практике.























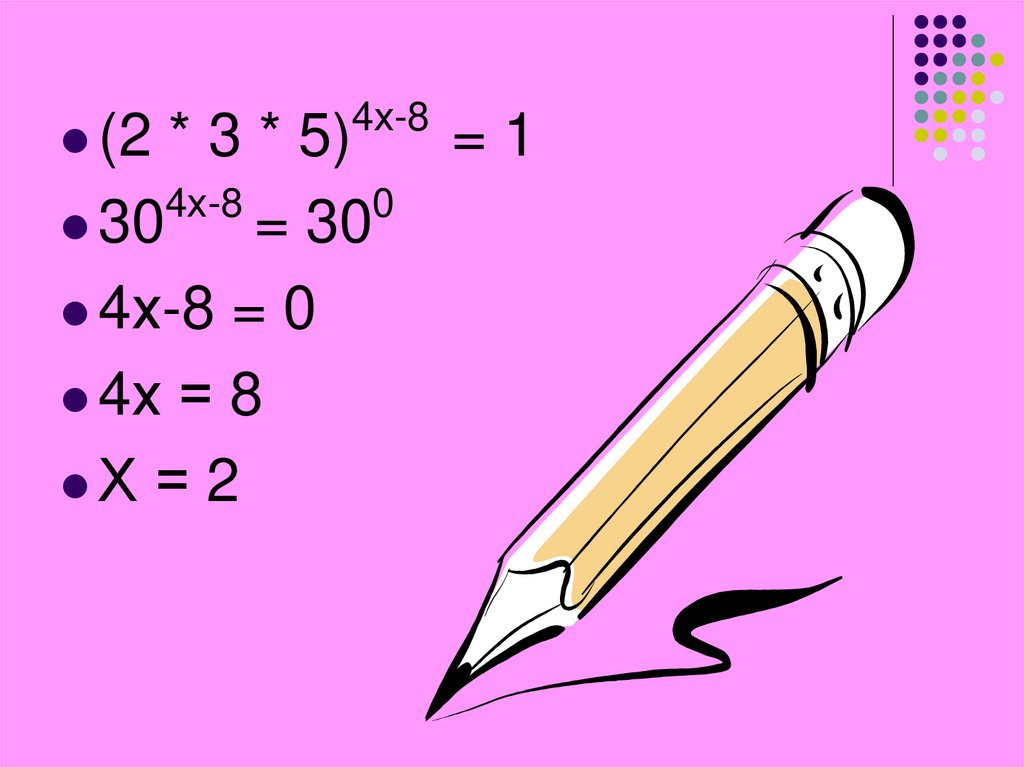







 mathematics
mathematics