Показательные уравнения и неравенства

1.

Показательные
уравнения и неравенства

2.

Разгадайте фамилию известного
французского математика, автора
крылатого выражения
«Мыслю, следовательно
существую»

3.

Мыслю, следовательно существую.

4.

Сопоставить ответы с буквами
1
5–Д
6-Р
8
2
3
4 – Е 3 –О
3 - Ж -3 Н
9
4
5
6
7
-3 – Е -1 – Д -1 – Е 1 – Й
3-Н 1-Н 2-А -1-К
10
11
-2 – М 2 – Р 1 – Н
2-А -2-А 0-Т
-2 – 2
-5

5.

Мыслю, следовательно существую.
Рене Декарт
6 (Р)
4 (Е)
- 3(Н)
- 3(Е)
- 1 (Д)
- 1 (Е)
- 1(К)
2 (А)
2(Р)
0 (Т)
(5)

6.

Какие из перечисленных функций являются
возрастающими, а какие убывающими?

7.

Какие из перечисленных функций являются
возрастающими, а какие убывающими?

8.

Какие функций являются возрастающими,
а какие убывающими?
Возрастающие
Убывающие
Основание Основание
больше больше нуля
и
меньше
единицы
единицы
а>1
0<а < 1

9.

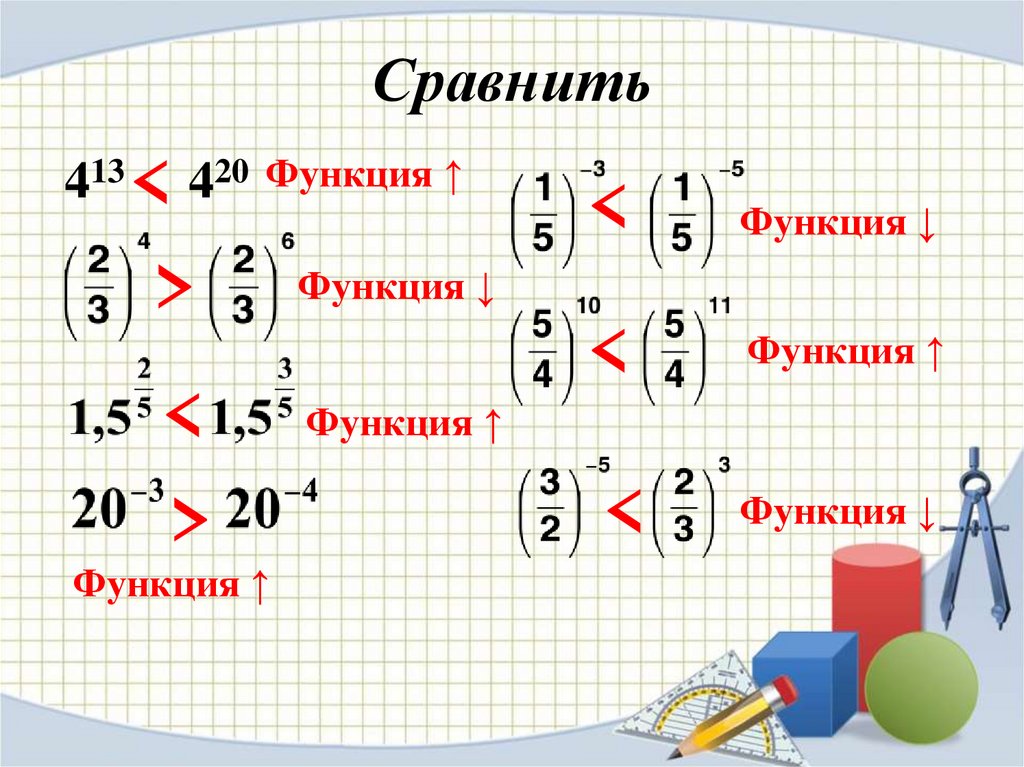
Сравнить
413 < 420
Функция ↑
>
<
>
Функция ↑
<
Функция ↓
<
Функция ↑
Функция ↓
Функция ↑
<
Функция ↓

10.

При а>1 функция возрастает
При 0<а<1 функция убывает

11.

Показательные неравенства
2
3
1

12.

Определение
Показательные
это
неравенства,
неравенства
в
–
которых
неизвестное содержится в показателе
степени.
Примеры:

13.

Простейшие показательные
неравенства – это неравенства вида:
где a > 0, a 1, b – любое число.

14.

Решение простейших показательных
неравенств
При решении простейших неравенств
используют свойства возрастания или
убывания показательной функции.
Знак неравенства
Сохраняется
Меняется

15.

Решения показательных
неравенств:
1. Способ уравнивания показателей.
2. Разложения на множители.
3. Введения новой переменной.

16.

Решите неравенство:

17.

Решите неравенство:

18.

Способ 2. Разложение на множители
3 > 1, ф-ция ↑

19.

Способ 3. Введение новой переменной
1
9
3>1, то ф- ция ↑
Ответ: 0 < х < 2.

20.

Показательные неравенства
2
3
1

21.

Решите неравенства
х € D (f)
3 > 1 ф-ия ↑
Ответ:
x
Ответ: х € D (f)
4
x
2
x

22.

Решите неравенство
5 >1 ф-ия ↑
-5
x

23.

Решите неравенство
7>1 ф-ия ↑
_
+
2
+
х1 = 2
х2 = 3
3
Ответ:

24.

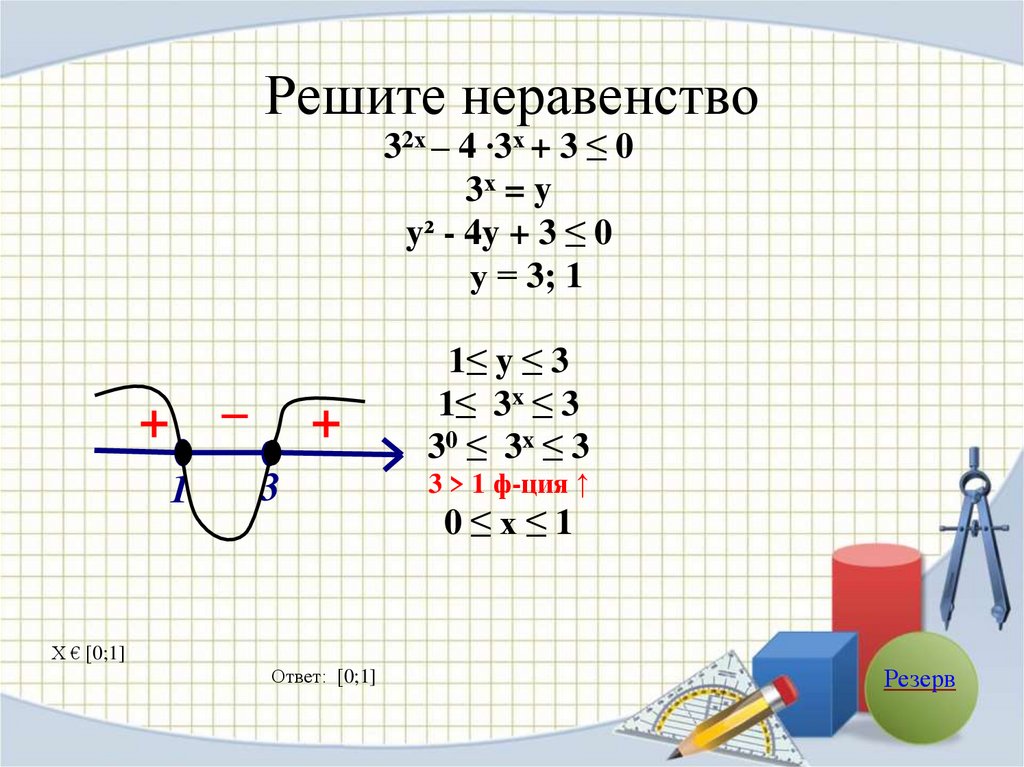
Решите неравенство
32х – 4 ∙3х + 3 ≤ 0
3х = y
y² - 4y + 3 ≤ 0
у = 3; 1
_
+
1
+
3
1≤ y ≤ 3
1≤ 3x ≤ 3
30 ≤ 3x ≤ 3
3 > 1 ф-ция ↑
0≤х≤1
Х € [0;1]
Ответ: [0;1]
Резерв

25.

Домашние задание
Рефлексия

26.

• Решите неравенство:
т. к. 7 > 1 ф-ия ↑
-1 ≤ х – 3 < 2
2≤х<5
Д.з

27.

• Решите неравенство:
т. к. 2 > 1 ф-ия ↑
10х + 15 < - 2
х < - 1,7
Д.з

28.

• Решите неравенство:
0,752 + 4х ≥ 0,751 – 8х
т. к. 0 < 0,75 < 1 ф – ия ↓
2 + 4х ≤ 1 – 8х
12х ≤ - 1
Д.з

29.

Сегодня на занятии
Я вспомнил……..
Я сделал ………
Я изучил……….
Я запомнил …………..
Я могу сделать ………

30.

Мыслю, следовательно
существую.
Рене Декарт

31.

Интернет-ресурсы
Циркуль: http://www.daviddarling.info/images/compasses.jpg
Карандаш:
http://www.proshkolu.ru/content/media/pic/std/3000000/2240000/22390937acd9447b354cc7e.gif
Угольник-транспортир:
http://p.alejka.pl/i2/p_new/25/38/duza-ekierka-geometryczna-z-uchwytem-rotring-14cm_0_b.jpg
Фон «тетрадная клетка»:
http://radikal.ua/data/upload/49112/4efc3/3bd0a3d6bb.jpg

32.

Спасибо за внимание!