Similar presentations:
Дифференцирование показательной функции
1.
Сычева Г.В.900igr.net
2.
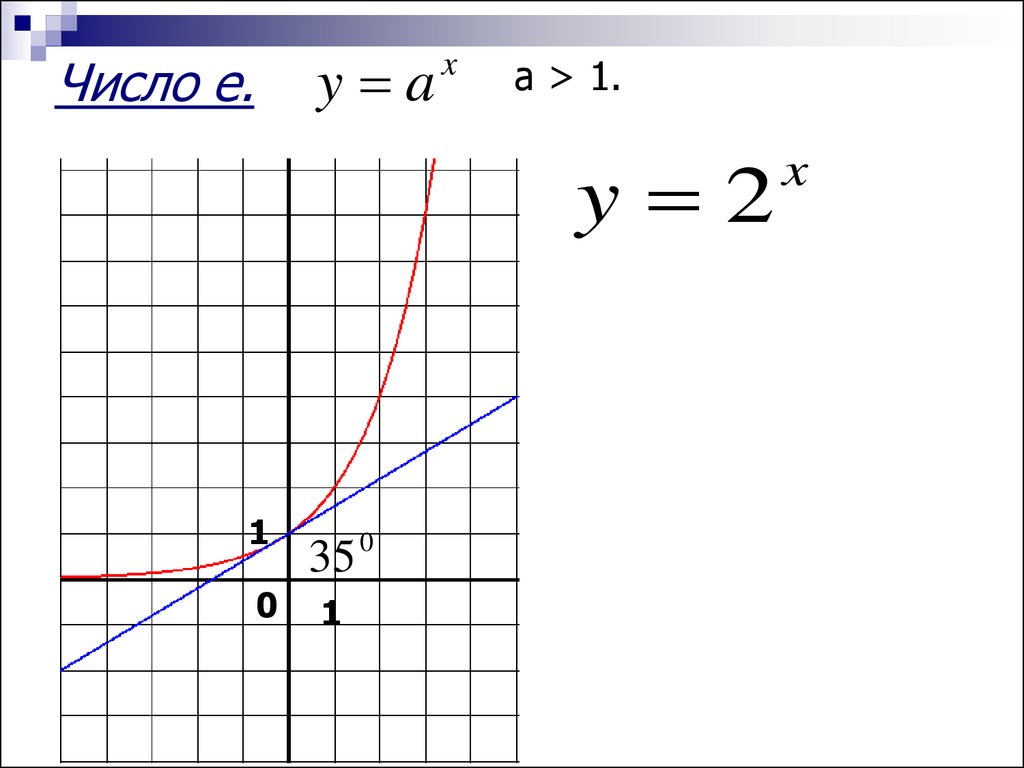
y aЧисло e.
x
а > 1.
y 2
1
0
35
1
0
x
3.
480 0
4545
0
y 3
x
y e
x
e = 2,7182818284590……
4.
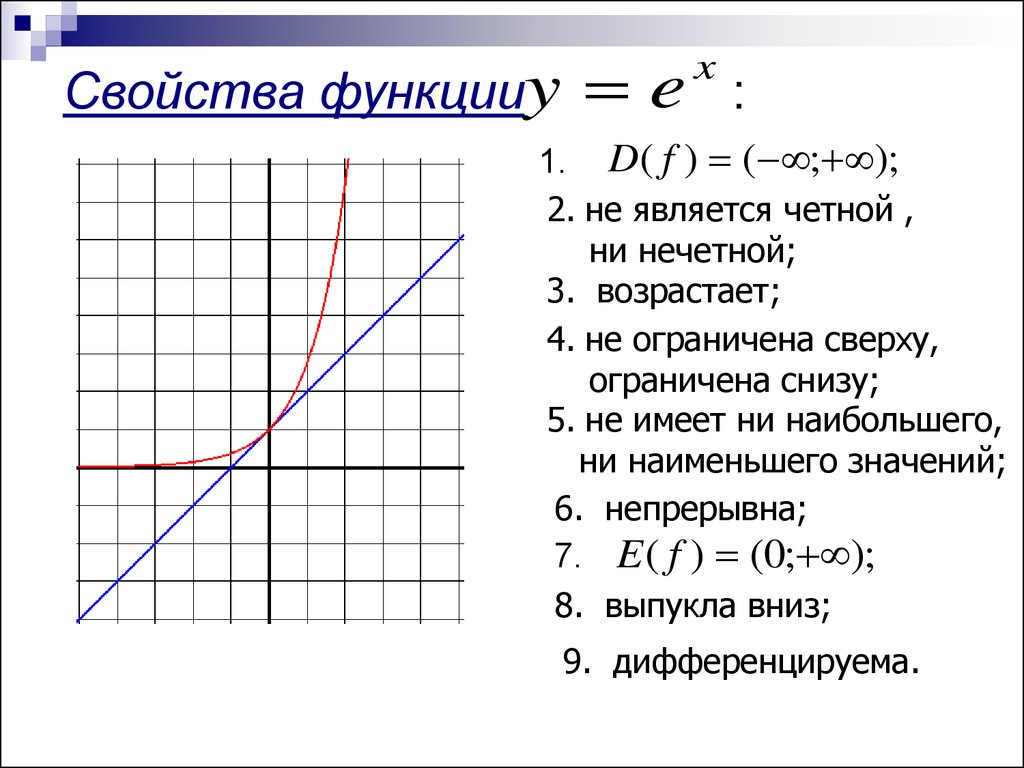
Свойства функцииye
x
:
1. D( f ) ( ; );
2. не является четной ,
ни нечетной;
3. возрастает;
4. не ограничена сверху,
ограничена снизу;
5. не имеет ни наибольшего,
ни наименьшего значений;
6. непрерывна;
7. E ( f ) (0; );
8. выпукла вниз;
9. дифференцируема.
5.
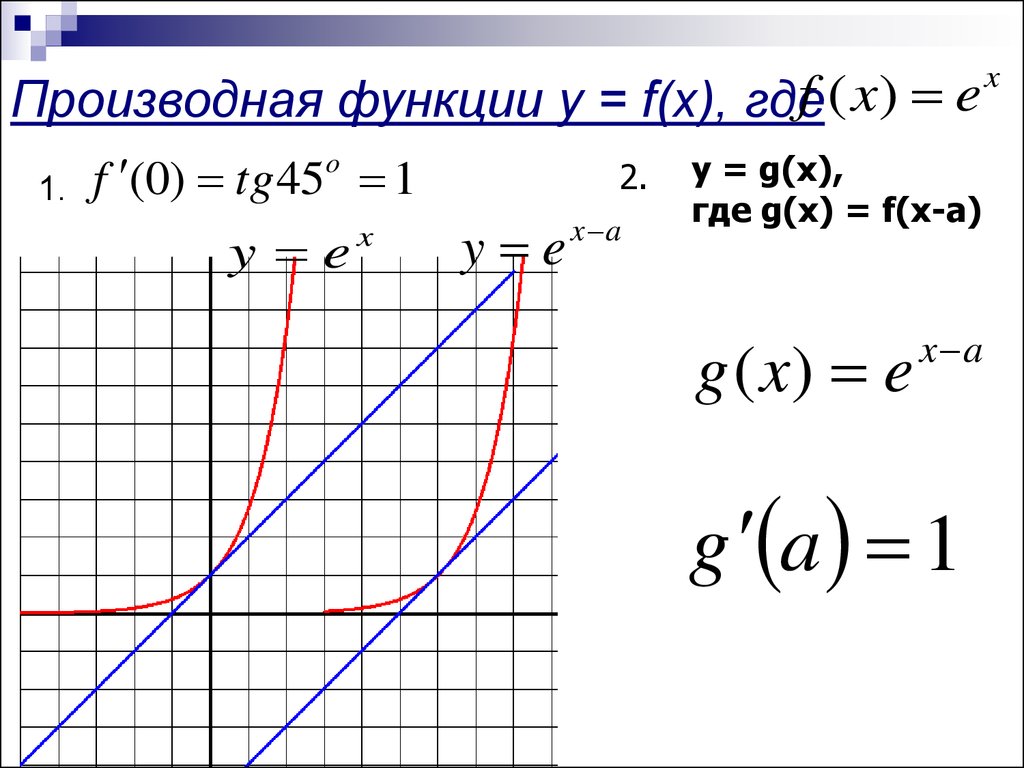
f ( x) eПроизводная функции y = f(x), где
1.
o
f (0) tg 45 1
y e
x
2.
y e
x a
y = g(x),
где g(x) = f(x-a)
g ( x) e
x a
g a 1
x
6.
f ( x) e e ex
a
x a
f a e g a
f x e g x
a
a
g a 1
e
x
e
x
e g ( x)
a
f a e
e
x
dx e C
x
a
7.
Пример 1. Провести касательную кx
графику функции y e в точке x=1.
Решение:
y f (a) f (a)( x a)
1) a=1
2) f(a)=f(1)=e
x
3) f ( x) e ;
f (a) f (1) e.
4) y=e+e(x-1);
y = ex
Ответ:
y=ex
8.
Пример 2.Вычислить значение производной
4 x 12
функции y e
в точке x=3.
Решение:
y (e
4 x 12
y 3 (e
Ответ:
) 4e
4 3 12
4
4 x 12
) 4e 4
0
9.
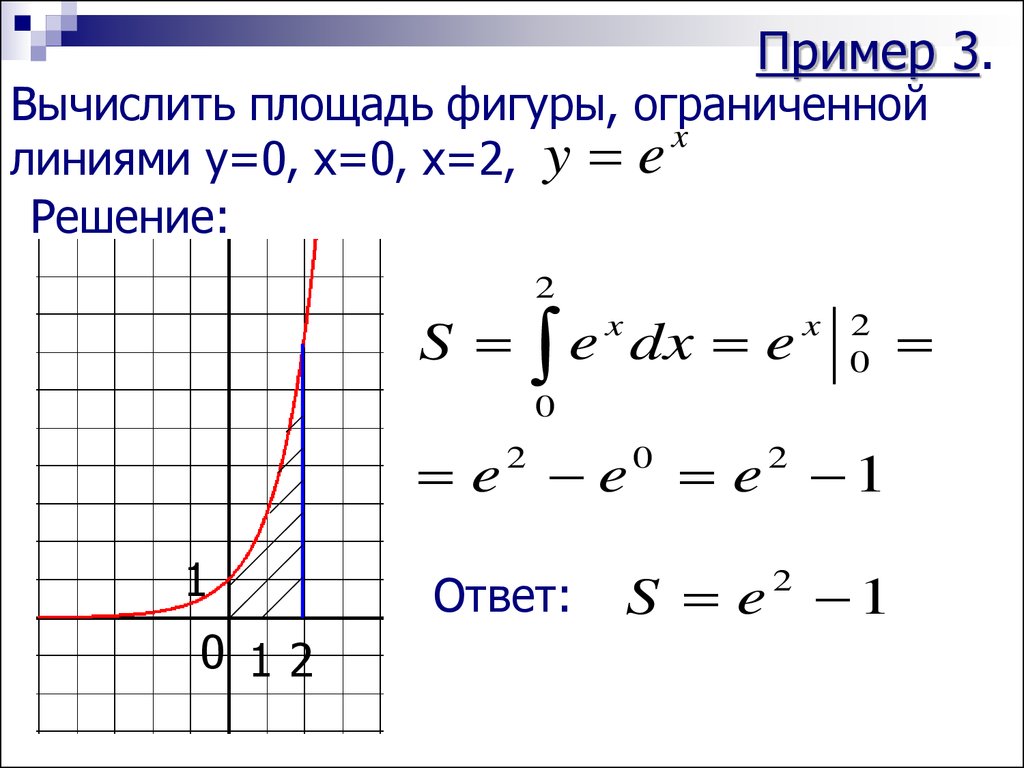
Пример 3.Вычислить площадь фигуры, ограниченной
x
линиями y=0, x=0, x=2, y e
Решение:
2
S
e
x
dx e
x 2
0
0
e e e 1
2
1
0 12
Ответ:
0
2
S e 1
2
10.
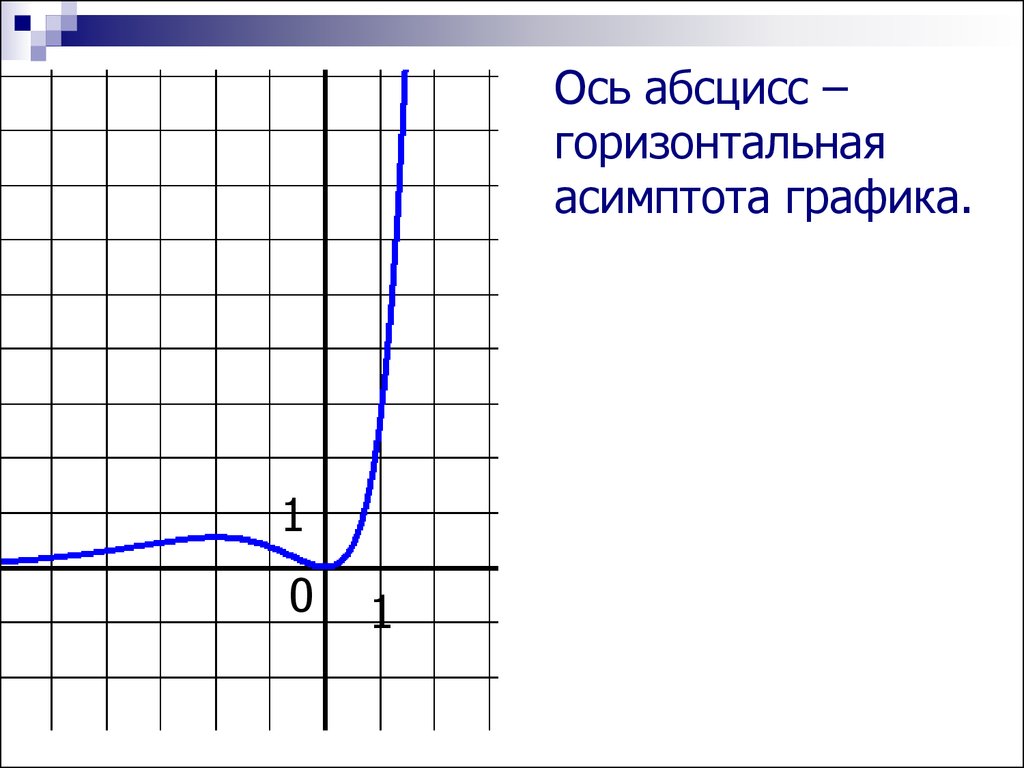
Пример 4.Исследовать на экстремум и схематически
2 x
изобразить график функции y x e
Решение:
1) D( f ) ;
2)
e
y ( x e ) x
2
x
2
2
2 xe x e xe x 2
x
2
x
x
x e
2
x
11.
3)y xe x 2
x
-
+
+
x
0
-2
4) x=-2 – точка максимума
y max y 2 2 e
2
2
x=0 – точка минимума
y min 0 e 0
2
0
4e
2
4
2 0,5
e
12.
Ось абсцисс –горизонтальная
асимптота графика.
1
0
1
13.
Решите упражнения:1620, 1623(a,б), 1624(а,б), 1628(а,б), 1629(а,б)
Решить дома: 1621, 1623(в,г), 1624(в,г),
1628(в,г), 1629(в,г), 1631.
14.
Натуральные логарифмы: log e 2 ln 2ln 1 0
ln e 1
ln e r
r
e
ln x
x
ln x
log a x
ln a
log e 7 ln 7
15.
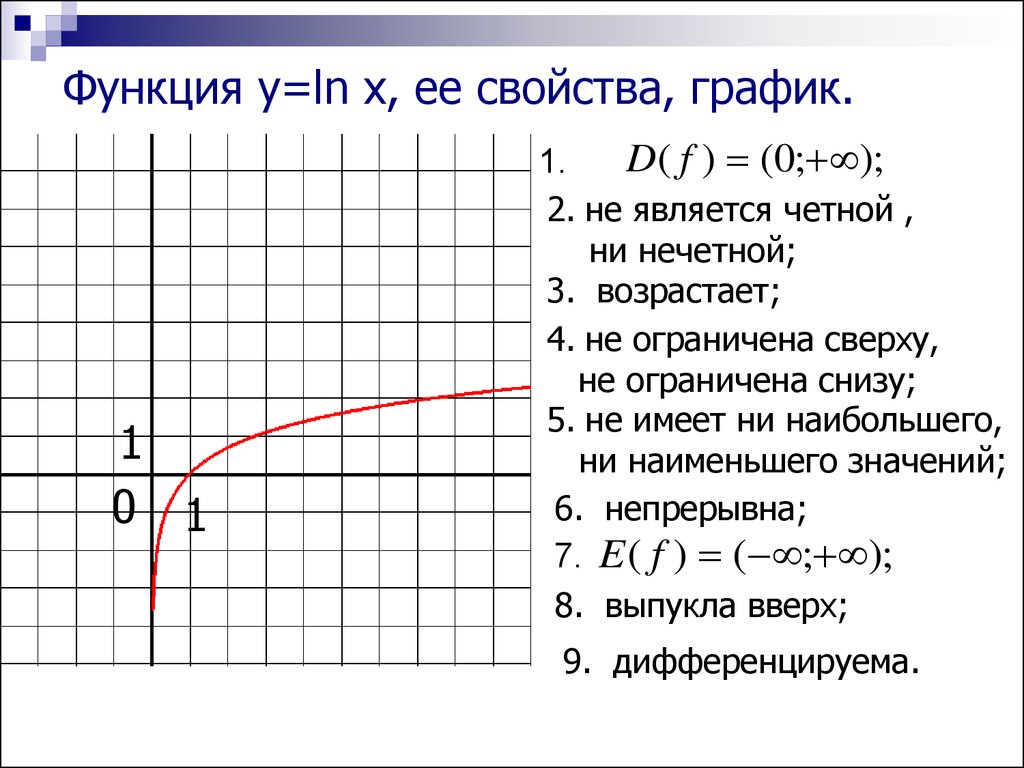
Функция y=ln x, ее свойства, график.1
0 1
D( f ) (0; );
1.
2. не является четной ,
ни нечетной;
3. возрастает;
4. не ограничена сверху,
не ограничена снизу;
5. не имеет ни наибольшего,
ни наименьшего значений;
6. непрерывна;
7. E ( f ) ( ; );
8. выпукла вверх;
9. дифференцируема.
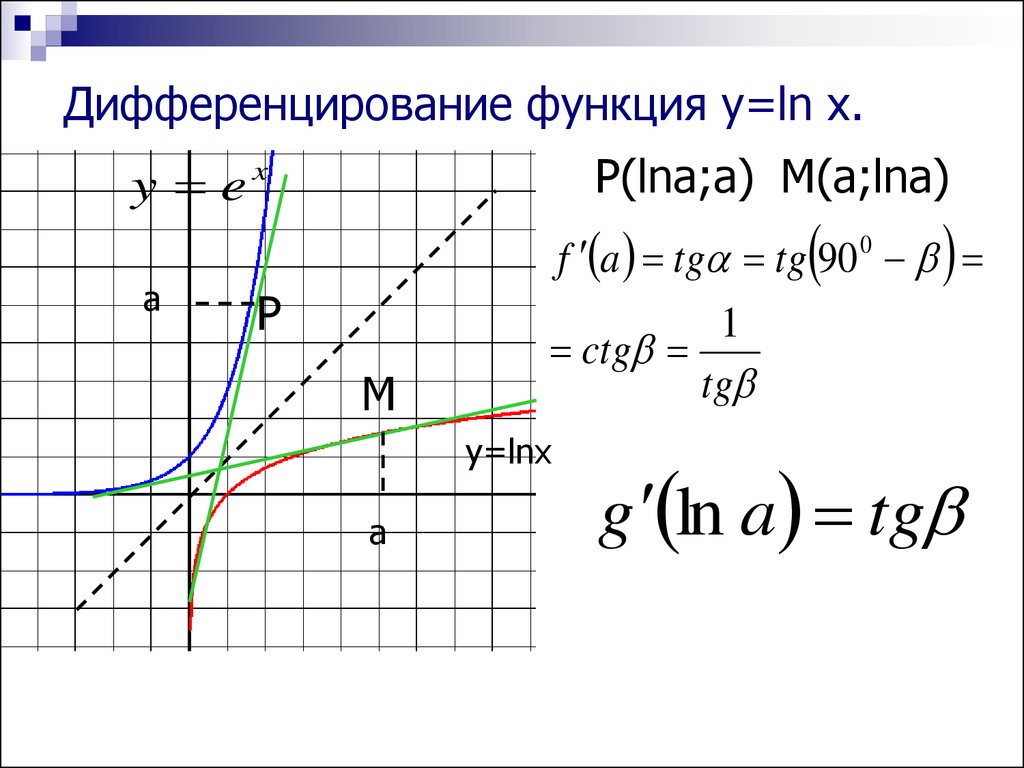
16.
Дифференцирование функция y=ln x.y e
a
P(lna;a) M(a;lna)
x
P
M
y=lnx
a
f a tg tg 90 0
1
ctg
tg
g ln a tg
17.
g ln a tgg x (e ) e
x
g ln a e
ln a
x
1
f a
tg
a
1
1
f a
tg a
1
f x
x
18.
1ln x
x
dx
ln
x
C
x
19.
Дифференцирование функции y ax
a e
x
x ln a
a e
x
x ln a
x ln a
x
(a ) (e ) ln a e
ln a a
ln a
(a ) a ln a
x
Например, 2
x
x
2 ln 2;
x
5
x
5 ln 5.
x
20.
Дифференцирование функцииy log a x
ln x
1
y (log a x)
ln x
ln a
ln a
1 1
1
ln a x x ln a
1
(log a x)
x ln a








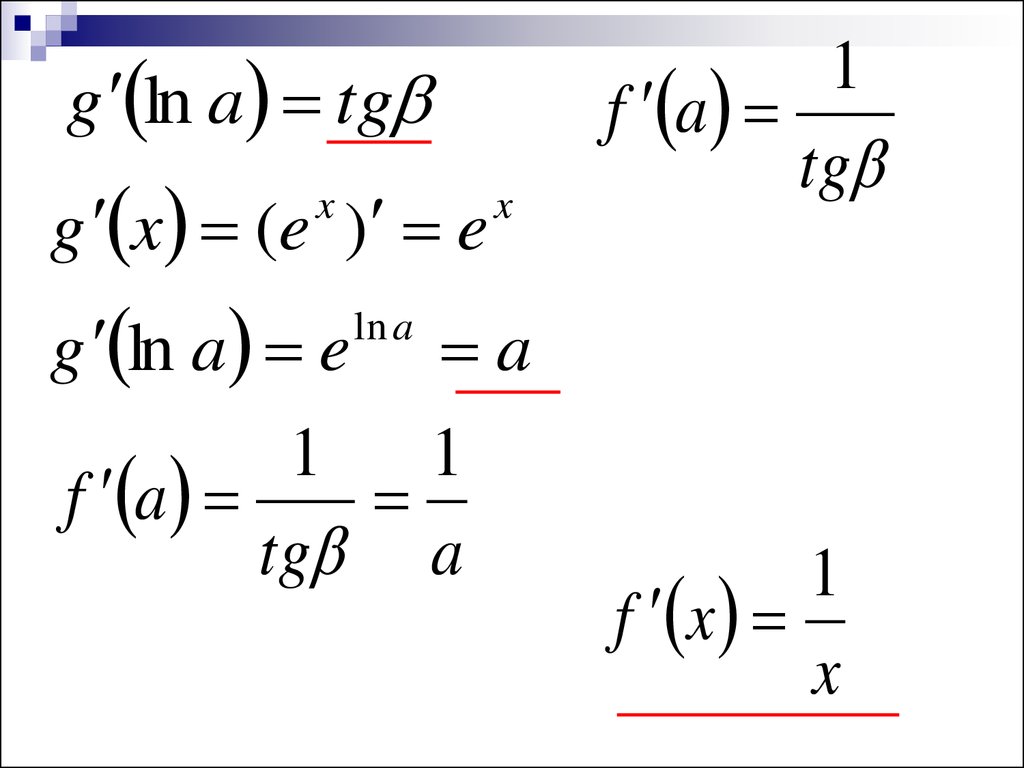



 mathematics
mathematics








