Дифференцирование функции одного аргумента. Производная

1.

2.

5. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ
ОДНОГО АРГУМЕНТА
5.1 Определение производной
5.2 Геометрический смысл производной
5.3 Связь между непрерывностью и
дифференцируемостью
5.4 Производные основных элементарных функций
5.5 Правила дифференцирования
5.6 Производная сложной функции
5.7 Производная обратной функции
5.8 Производная неявно заданной функции
5.9 Логарифмическое дифференцирование
5.10 Производная функции, заданной параметрически

3.

5.1 ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
Пусть функция y = f(x) определена в некотором интервале (a; b).
Аргументу
x придадим некоторое приращение x
x x (a; b)
:
Найдем соответствующее приращение функции:
y f ( x x) f ( x )
y
Если существует предел
f(x+ Δx )
y
f(x )
0
x
х
x+Δx
х
y
lim
x 0 x
то его называют производной
функции y = f(x) и обозначают
одним из символов:
y ;
f ( x);
dy
dx

4.

5.1 ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
Итак, по определению:
f ( x x) f ( x)
y lim
x 0
x
Функция y = f(x) , имеющая производную в каждой точке интервала (a; b),
называется дифференцируемой в этом интервале;
операция нахождения производной функции называется
дифференцированием.
Значение производной функции y = f(x) в точке x0 обозначается одним из
символов:
y ( x0 );
f ( x0 );
y x
0
Если функция y = f(x) описывает какой-либо физический процесс, то f (x)
есть скорость протекания этого процесса – физический смысл
производной.

5.

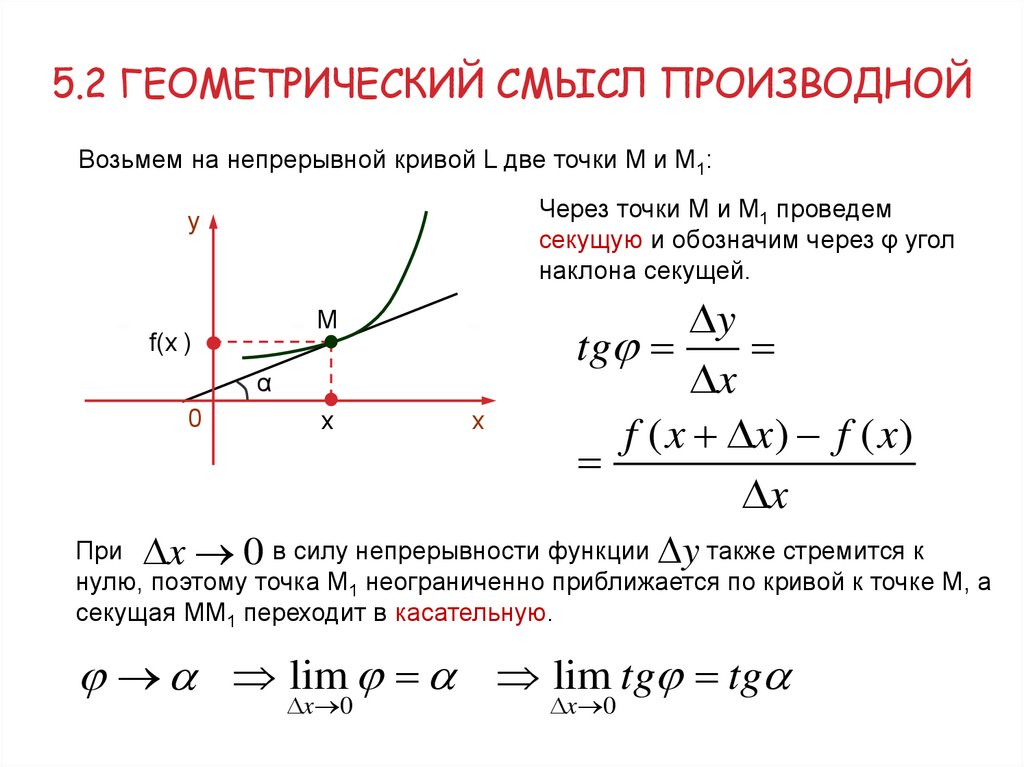
5.2 ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Возьмем на непрерывной кривой L две точки М и М1:
Через точки М и М1 проведем
секущую и обозначим через φ угол
наклона секущей.
y
М1
f(x+ Δx )
f(x )
α
0
y
М
М
x
φ
х
x+Δx
х
y
tg
x
f ( x x) f ( x)
x
При x 0 в силу непрерывности функции y также стремится к
нулю, поэтому точка М1 неограниченно приближается по кривой к точке М, а
секущая ММ1 переходит в касательную.
lim lim tg tg
x 0
x 0

6.

5.2 ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
f ( x x) f ( x)
lim
tg k y
x 0
x
Производная f (x) равна угловому коэффициенту касательной к графику
функции y = f(x) в точке, абсцисса которой равна x.
y
Если точка касания М имеет координаты (x0; y0 ), угловой коэффициент
касательной есть k = f (x0 ).
Уравнение прямой с угловым коэффициентом:
yy y00 кf ('(xx0-)(xx0 ) x0 )
Уравнение
Уравнение
касательной
нормали
Прямая, перпендикулярная касательной в точке касания, называется
нормалью к кривой.
f ' ( x0 )
kнорм
1
1
1
y y0
( x x0 )
kкас
f '( x0 )
f '( x0 )

7.

5.3 СВЯЗЬ МЕЖДУ НЕПРЕРЫВНОСТЬЮ И
ДИФФЕРЕНЦИРУЕМОСТЬЮ ФУНКЦИИ
Теорема
Если функция y = f(x) дифференцируема в некоторой точке, то она
непрерывна в ней.
Доказательство:
Пусть функция y = f(x) дифференцируема в некоторой точке х,
следовательно существует предел:
y
y
lim
f ( x)
f ( x) ( x)
x 0 x
x
где ( x ) 0 при x 0
По теореме о связи
функции, ее предела и
бесконечно
y 0
малой
y f ( x) x ( x) x lim
x 0
Функция y = f(x) – непрерывна.
функции
Обратное утверждение не верно: непрерывная функция может не иметь
производной.

8.

5.4 ПРОИЗВОДНЫЕ ОСНОВНЫХ
ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
Таблица производных (без вывода)
1. x n nx n 1
5. a x a x ln a
2. x 1
6. e x e x
1
1
3. 2
x
x
7. log a x
4.
x 2
1
x
1
8. ln x
x
1
x ln a

9.

5.4 ПРОИЗВОДНЫЕ ОСНОВНЫХ
ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
Таблица производных (без вывода)
9. sin x cos x
10. cos x sin x
11. tg x
1
cos 2 x
12. ctg x
1
sin 2 x
13. arcsin x
1
1 x2
1
14. arccos x
2
1 x
1
15. arctg x
1 x2
1
16. arcctg x
1 x2

10.

5.5 ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Пусть u(x) , v(x) и w(x) – дифференцируемые в некотором интервале (a; b)
функции, С – постоянная.
(C ) 0
(u v) u v
(u v) u v u v
u
u v u v
2
v
v
(C u ) C u
u u
C C
C C v
2
v
v

11.

5.6 ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ
Пусть даны функции y = f(u) и u = φ(x) , тогда y = f(φ(x)) – сложная
функция с промежуточным аргументом u и независимым аргументом x.
Теорема
Если функция u = φ(x) имеет производную
а функция y = f(u) имеет производную
yu
u x в точке x,
в соответствующей точке u ,
то сложная функция y = f(φ(x)) имеет производную
по формуле:
y x , которая находится
y x yu u x
Это правило остается в силе, если промежуточных аргументов несколько:
y f (u ); u (v); v g ( x) y f ( ( g ( x)))
y x yu uv v x

12.

5.6 ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ
Вычислить производную функции
y cos(ln12 x)
y (cos(ln12 x)) sin(ln12 x) (ln12 x)
sin(ln12 x) 12ln11 x (ln x)
1
12
11
sin ln x 12ln x
x

13.

5.7 ПРОИЗВОДНАЯ ОБРАТНОЙ ФУНКЦИИ
Пусть задана дифференцируемая функция y = f(x) и f (x) 0 , пусть
существует обратная функция
x f 1 y .
Из дифференцируемости f(x) следует её непрерывность, а значит и
непрерывность обратной функции, поэтому
x 0 y 0
1
1
1
x
x y lim
lim
x 0 y
y 0 y
y
y x
lim
x 0 x
x
1
x y
y x

14.

5.8 ПРОИЗВОДНАЯ НЕЯВНО ЗАДАННОЙ
ФУНКЦИИ
Если функция задана уравнением y = f(х) , разрешенным относительно y,
то говорят, что функция задана в явном виде.
Под неявным заданием функции понимают задание функции в виде
уравнения не разрешенного относительно y:
F ( x; y ) 0
Для нахождения производной неявно заданной функции необходимо
продифференцировать уравнение по х, рассматривая при этом y как
функцию от х, и полученное уравнение разрешить относительно
производной.
x 3 y 3 3 xy 0
( x 3 ) ( y 3 ) 3( xy ) 0
3 x 2 3y 2 y 3( x y xy ) 0
x 2 y 2 y y xy 0
y x2
y 2
y x

15.

5.9 ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ
В ряде случаев для нахождения производной целесообразно заданную
функцию сначала прологарифмировать, а затем результат
продифференцировать.
Такую операцию называют логарифмическим дифференцированием.
Типы функций, к которым применяют логарифмическое
дифференцирование:
1) функция, построенная при помощи нескольких операций произведения
и (или) деления
x3 4 3 2 x 3 e x
4
Например:
y
3x 2 5
2
2) степенно-показательная функция
Например:
y sin 2 x 1
cos x 2 1

16.

5.9 ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ
Для применения логарифмического дифференцирования необходимо
вспомнить свойства логарифмов:
1) ln a b ln a ln b
a
2) ln ln a ln b
b
3) ln a b b ln a
Найти производные следующих функций:
1)
x
y
3
4
3
3x
2 x 3
2
5
2) y sin 2 x 1
4
ex
2
cos x 2 1
в точке x 1

17.

5.10 ПРОИЗВОДНАЯ ФУНКЦИИ, ЗАДАННОЙ
ПАРАМЕТРИЧЕСКИ
Пусть функция y = f(x) задана параметрически уравнениями:
x f (t )
y g (t )
Выведем формулу для нахождения производной этой функции:
Пусть функция x = f(t) имеет обратную
t f 1 x ,
тогда
– сложная функция
y g t g f 1 x
y x g t x
g f
1
x x g t t f 1 x x
1
y t
y t t x y t
xt
xt
При выводе использовали:
производную сложной функции
производную обратной функции
требование x 0
t
yt
y x
xt

18.

5.10 ПРОИЗВОДНАЯ ФУНКЦИИ, ЗАДАННОЙ
ПАРАМЕТРИЧЕСКИ
Вычислить производные следующих функций, заданных
параметрически:
x t 2 4t 1
1)
y arctg 2t
x et cos t
2)
при t
t
y e sin t
y x
1
t 2 1 4t 2
y x 1

19.

ПРОДОЛЖЕНИЕ СЛЕДУЕТ...