Similar presentations:
Дифференцирование показательной и логарифмической функции
1. Дифференцирование показательной и логарифмической функции
2.
Установлено, что е – иррациональное число, т. е.представляет собой бесконечную непериодическую
десятичную дробь:
е = 2, 7182818284590… ;
На практике обычно полагают, что е ≈ 2,7.
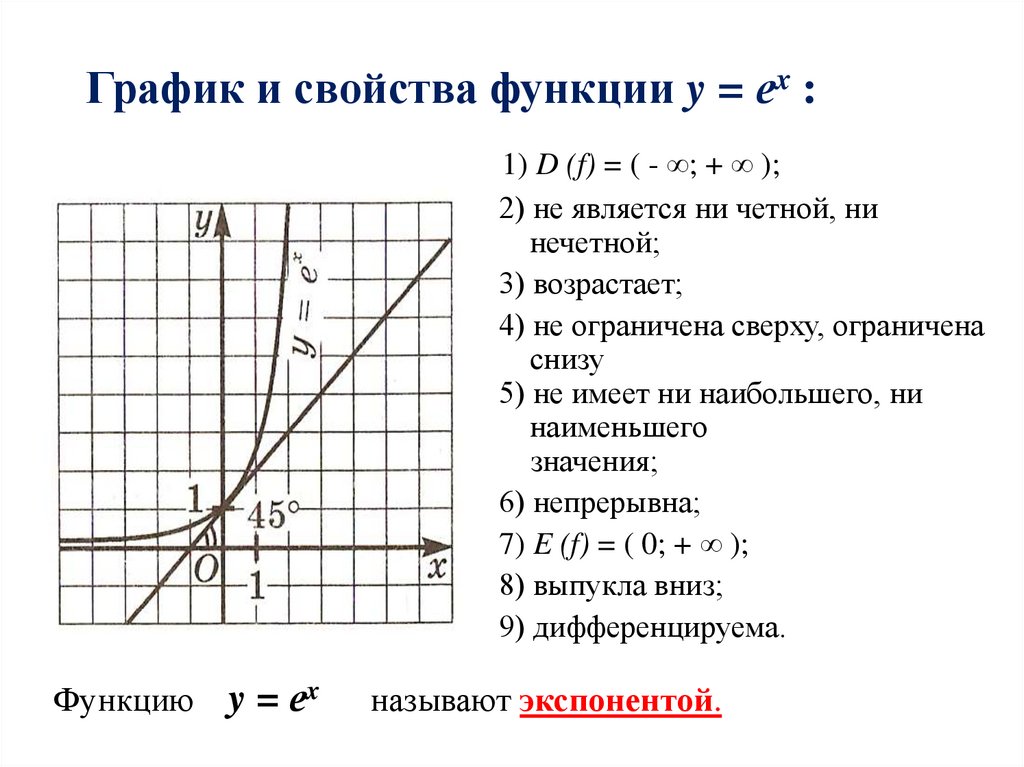
3. График и свойства функции y = еx :
1) D (f) = ( - ∞; + ∞ );2) не является ни четной, ни
нечетной;
3) возрастает;
4) не ограничена сверху, ограничена
снизу
5) не имеет ни наибольшего, ни
наименьшего
значения;
6) непрерывна;
7) E (f) = ( 0; + ∞ );
8) выпукла вниз;
9) дифференцируема.
Функцию y = еx
называют экспонентой.
4.
В курсе математического анализа доказано,что функция y = еx имеет производную в
любой точке х:
x
(e )
=
x
e
(е5х)' = 5е5х
(ех-3)' = ех-3
(е-4х+1)' = -4е-4х-1
5.
Пример 1.Вычислить значение производной функции
в точке x = 3.
y e 4 x 12
Решение:
y (e
4 x 12
y 3 (e
Ответ:
) 4e
4 3 12
4
4 x 12
) 4e 4
0
6.
Если основанием логарифма служит число е, тоговорят, что задан натуральный логарифм. Для
натуральных логарифмов введено специальное
обозначение ln (l – логарифм, n – натуральный).
log e 2 ln 2
ln x log e x
ln1 0;
ln е 1;
ln е r;
r
log e 7 ln 7
x;
ln x
log a x
.
ln a
е
ln x
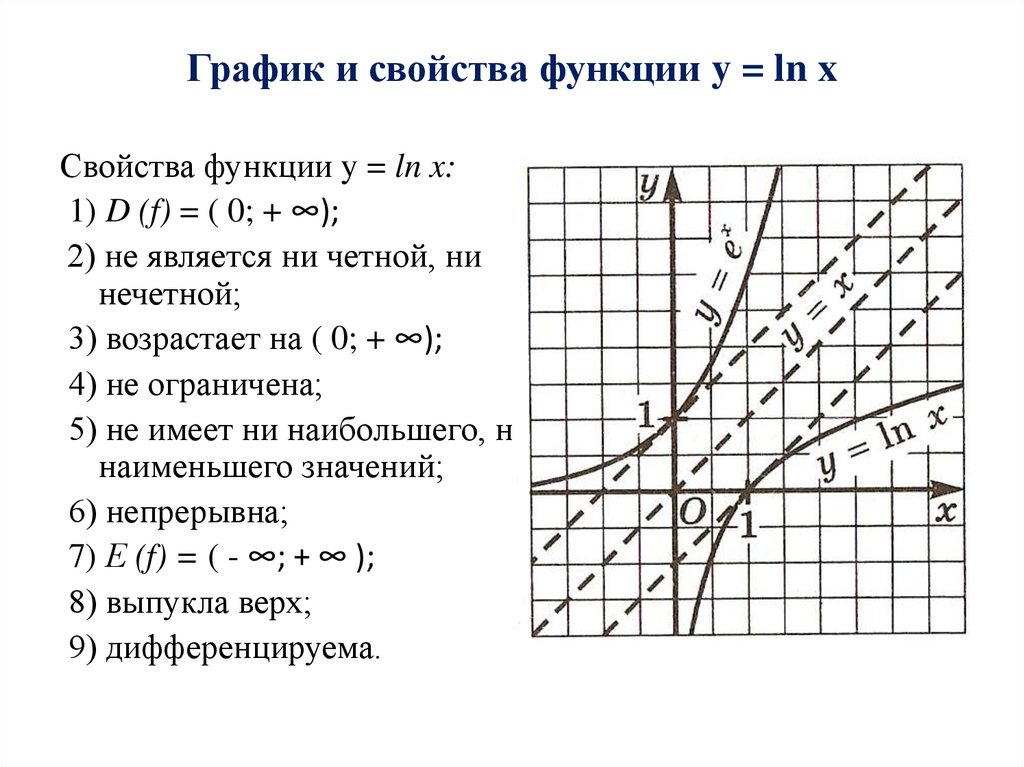
7. График и свойства функции y = ln x
Свойства функции y = ln x:1) D (f) = ( 0; + ∞);
2) не является ни четной, ни
нечетной;
3) возрастает на ( 0; + ∞);
4) не ограничена;
5) не имеет ни наибольшего, ни
наименьшего значений;
6) непрерывна;
7) Е (f) = ( - ∞; + ∞ );
8) выпукла верх;
9) дифференцируема.
8.
(a ) a ln a1
ln x
x
x
x
1
(log a x)
x ln a
9.
Пример 2:Вычислить значение производной функции
в точке x = -1.
y ln 3x 5
Решение:
y ' ln 3 x 5
1
3
3
;
3x 5 3x 5
3
f ' 1
1,5.
3 ( 1) 5
Ответ: 1,5







 mathematics
mathematics








