Числовые ряды

1.

Числовые ряды

2.

Определение числового ряда
Рассмотрим некоторую числовую
последовательность u1, u2 , u3 ,...,u n ,...
Составим из членов этой
последовательности бесконечную сумму
u1 u2 u3 ... un ...
Определение. Выражение (1)
u1 u 2 ... u n ...
.
un
n 1
называется числовым рядом,
член ряда.
u n - общий

3.

Примеры
n
(
1
)
• Рассмотрим ряд1-1+1-1+…+
+…
• Очевидно, сумма четного числа его
членов равна нулю, а нечетного –
единице. Такой ряд не имеет суммы.

4.

Примеры
Известно, что геометрическая
прогрессия со знаменателем, меньшим
единицы, a n a1 a 2 .. a n ...
n 1
сходится, если a n 1.

5.

Понятие сходящегося ряда
Опр. Конечные суммы S1 u1 , S2 u1 u2
S3 u1 u2 u3 ,..., Sn u1 u2 ... un ...
называются частичными суммами ряда (1).
Опр. Если существует конечный lim S n S ,
n
то числовой ряд называется сходящимся, а
число S - суммой ряда. Если lim S n равен
n
бесконечности или вообще не существует, то
ряд расходится.

6.

Пример сходящегося ряда
1
Показать, что ряд
n 1 n n 1
найти его сумму.
Общий член ряда
un
сходится и
1
1
1
n n 1 n n 1
.
1 1
1
1 1
Тогда u1 1 , u 2 , u3 ,…
2 3
3 4
2
1 1 1 1 1
S n u1 u 2 u3 ... un 1 ...
2 2 3 3 4
1
1
1
1
1
, lim 1
1
n n 1
n 1 n n 1

7.

Свойства сходящихся рядов
1) Сходящиеся ряды можно почленно
складывать, т.е.
u n v n (u n v n .)
n 1
n 1
n 1
2) Постоянный множитель можно
вынести за знак ряда, т. е.
cu n c u n .
n 1
n 1

8.

Свойства сходящихся рядов
От сходящегося ряда можно отбросить
конечное число членов или наоборот
прибавить конечное число слагаемых и
при этом сходимость ряда не
изменится.

9.

Гармонический ряд
1
Исследуем ряд , называемый
гармоническим. n 1 n
Для решения задачи запишем гармонический
ряд в развернутом виде:
1
1 1 1 1 1 1
1
1
1
...
...
...
2 3 4 5 6 7
16
32
n 1 n
и наряду с ним рассмотрим ряд с меньшими
членами
1 1 1 1 1 1 1 1
1
1
1
1 ...
...
...
2
4
4
8
8
8
8 16
16
32
32

10.

Продолжение
Найдем частичные суммы второго ряда:
1
S2 1 ;
2
1 1 1
1
S4 1 1 2 ;
2 4 4
2
1 1 1
1
S8 1 1 3 ;
2 2 2
2
S16
1 1 1 1
1
1 1 4
2 2 2 2
2
1
S2n 1 n
.
2
Итак,гармонический ряд расходится, т. к. его
сумма больше суммы вспомогательного
ряда.

11.

Признаки сходимости ряда
Необходимое условие сходимости ряда.
Если ряд
Если же
un
n 1
сходится, то
lim u n 0.
n
lim u n 0 , то ряд расходится.
n

12.

Пример расходящегося ряда
n
Пример 1. Ряд
n 1 5n 1
расходится, так
как
n
1
lim un lim
0
n
n 5n 1
5
.

13.

Знакоположительные
ряды

14.

Признак сравнения.
vn.
Пусть даны ряды u n и
n 1
n 1
Если ряд с большими членами
сходится, то сходится и ряд с меньшими
членами. Если же ряд с меньшими
членами расходится, то расходится и
ряд с большими членами.

15.

Признак сравнения в
предельной форме
Если существует конечный и
un
отличный от нуля lim
A
n vn
n 1
n 1
ряды u n и vn сходятся или
расходятся одновременно.
, то

16.

Примеры
В качестве рядов для сравнения берут
гармонический ряд 1 , который
n 1
n
1
2
n
n 1
1
или p ,о
n 1 n
расходится, и ряд
которых известно, что первый сходится,
а второй при p 1сходится, а при p 1
расходится.

17.

Примеры
Исследовать на сходимость ряды
1
а) 2
и б) 1
.
n 1
n 4
n 1
n
Найдем предел отношения
членов
1
данного ряда и ряда 2 ,с которым
n 1 n
сравниваем
данный
ряд.
1 n2
lim 2
1. Ряд сходится.
n ( n 1) 1

18.

Примеры
1
n
Ряд
сравниваем с
n 1
1
гармоническим рядом n .
n 1
1
1
n n
Так как
, то данный ряд
расходится вместе с гармоническим
рядом.

19.

Признак Даламбера
u n 1
Если существует конечный lim
n un
то
1)при 1 ряд u n , где un 0 ,
n 1
сходится,
2)при 1 ряд расходится,
3)при 1 признак ответа не дает.

20.

Примеры
Исследовать на сходимость ряд
Так как
2n
un n
e
, то un 1
2( n 1)
e n 1
2n
n
e
n 1
и
un 1
2( n 1)e n
n 1 1
n 1 1
lim
lim n 1
lim
lim
n u
n
n en
e 2n
e n n
e
n
Так как
1
1,
e
то данный ряд сходится.
.

21.

Признак Коши
Если существует конечный lim un тоe,
n
1)при
ряд
, где
,
un
e 1
un 0
сходится,
n 1
2)при
ряд расходится,
3)при e 1 признак ответа не дает.
n
e 1

22.

Примеры
3n 1
n 2
n 1
n
Ряд
исследуем с помощью
признака Коши.
n
Вычислим
n
3
n
1
3
n
1
un n
n 2
n 2
3n 1
lim un lim
3 1
n
n n 2
Тогда
и ряд согласно признаку Коши
расходится.
n
.

23.

Интегральный признак
Пусть члены ряда un
n 1
положительны и un un 1 при n N .
Пусть функция f (x) при x n имеет
значения f n u n , положительна и
монотонно убывает при x 1 .Тогда
числовой ряд сходится или расходится
вместе с несобственным интегралом
f x dx
1

24.

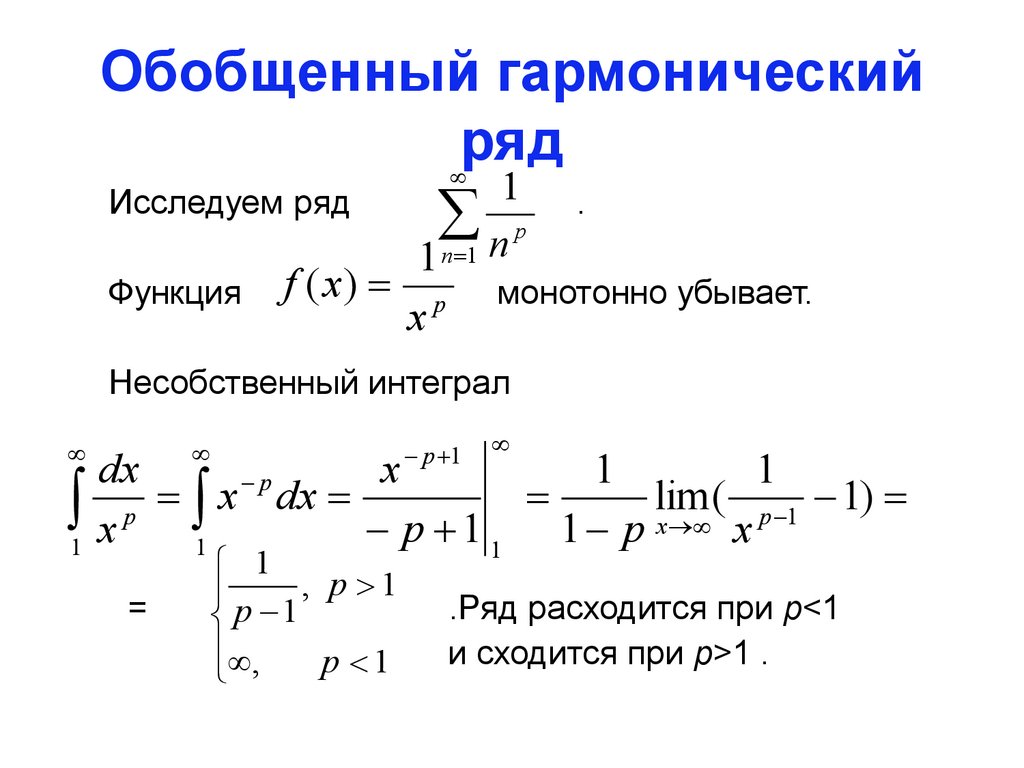
Обобщенный гармонический
ряд
Исследуем ряд
Функция
f ( x)
1
p
1 n 1 n
x
.
монотонно убывает.
p
Несобственный интеграл
p 1
dx
x
1
1
p
( p 1 1)
1 x p 1 x dx p 1 1 p lim
x x
1
=
1
, p 1
p 1
,
p 1
.Ряд расходится при p<1
и сходится при p>1 .

25.

Пример
Исследовать на сходимость ряд
1
n 2 n ln n
1
. Члены ряда un
n ln n
положительны и монотонно убывают.
1
Функция f ( x )
, очевидно, также
x ln x
положительна при x 2 и монотонно
убывает.

26.

Продолжение
2
b
b
dx
dx
d (ln x )
lim
lim
lim 2 ln x
b
x ln x b 2 x ln x b 0 ln x
lim 2 ln b 2 ln 2 .
b
Несобственный интеграл, а вместе с
ним и числовой ряд расходятся.
b
2

27.

Знакопеременные ряды

28.

Признак Лейбница
Пусть
члены знакочередующегося ряда
n 1
n 1
u
u
u
u
...
(
1
)
u n ...
(
1
)
u
1
2
3
4
n
n 1
удовлетворяют условиям:
1) u1 u 2 u3 ... u n ...
lim un 0.
и 2) n
Тогда знакочередующийся ряд
сходится, причём его сумма S не
превосходит его первого члена, т.е. .S u1

29.

Примеры
Исследовать
на сходимость ряды:
n
1
n 1
n 1
1) ( 1) n 1, 2) ( 1) n 2 .
n 1
n 1
1) члены знакочередующегося ряда
1
1
1
1
u1 , u2 , u3 ,.., un 1
,..
2
3
4
n 1
монотонно убывают и
1
lim un lim
0
n
n n 1
.
Согласно признаку Лейбница ряд
сходится.

30.

Примеры
n
n 2
2) общий член ряда ( 1)
n 1
не стремится к нулю, так как
n
lim
1
n n 2
n 1
Следовательно, ряд расходится
согласно необходимому признаку.

31.

Достаточный признак сходимости
знакопеременного ряда
Если сходится ряд
n 1
знакопеременный ряд
сходится.
un , то
un
n 1
также

32.

Абсолютно сходящийся ряд
Определение.
Если сходится ряд un , то
n 1
знакопеременный ряд называется
абсолютно сходящимся.

33.

Условно сходящийся ряд
Определение.
Если сходится ряд un , а
n 1
ряд un расходится, то
n 1
знакопеременный ряд u n
n 1
называется условно сходящимся.

34.

Пример
1
n2
Ряд ( 1)
абсолютно сходится, т.к.
n 1
1
ряд из модулей его членов 2
1
n 1 n
сходится. Ряд ( 1) n 1 сходится
условно, т.к. он согласно признаку
Лейбница сходится, но
ряд из модулей
1
его членов, т.е. ряд
n 1 n 1
расходится вместе с гармоническим
рядом .
n 1
n 1
n 1

35.

Остаток ряда и его оценка
Определение. Если числовой ряд
сходится, то разность Rn S S n
называется n-м остатком ряда. Таким
образом, Rn u n 1 u n 2 ...
представляет собой сходящийся ряд.
Rn lim ( S S n ) S S 0 .
При этом lim
n
n
Теорема. Если знакочередующийся ряд
сходится, то Rn u n 1 .