Similar presentations:
Ряд Тейлора функции многих переменных. Лекция 19
1. Здравствуйте!
Лекция №192.
Ряд Тейлора функции многих переменныхОпять-таки, для простоты вывода, рассмотрим функцию двух
переменных f ( x , y ) и получим для нее ряд Тейлора относительно
точки (х0, у0).
Напомним, что разложение в ряд Тейлора функции f ( x ) одной
переменной имеет вид:
f ( x0 )
f ( x 0 )
f ( x ) f ( x0 )
( x x0 )
( x x 0 ) 2 ...
1!
2!
А теперь рассмотрим f ( x, y ) и зафиксируем аргумент у. Тогда
разложение f ( x , y ) около точки х0 будет иметь вид
f x ( x 0 , y )
f xx ( x 0 , y )
f ( x , y ) f ( x0 , y )
( x x0 )
( x x 0 ) 2 ... (1)
1!
2!
А теперь, когда в правой части х0 фиксировано, разложим
оставшиеся функции в ряд Тейлора по у относительно точки у0:
3.
f ( x0 , y ) f ( x0 , y 0 )f y ( x 0 , y 0 )
f x ( x 0 , y ) f x ( x 0 , y 0 )
( y y0 )
1!
f xy ( x 0 , y 0 )
1!
f yy ( x 0 , y 0 )
2!
( y y 0 ) 2 ... ,
( y y 0 ) ... ,
f xx ( x0 , y) f xx ( x0 , y0 ) ... .
Подставим все это в (1) и соберем слагаемые с одинаковыми
степенями (х – х0) и (у – у0). Тогда получим
1
f ( x , y ) f ( x 0 , y 0 ) f x ( x 0 , y 0 )( x x 0 ) f y ( x 0 , y 0 )( y y 0 )
1!
1
f xx ( x 0 , y 0 )( x x 0 ) 2 2 f xy ( x 0 , y 0 )( x x 0 )( y y 0 ) f yy ( x 0 , y 0 )( y y 0 ) 2 ..
2!
4.
В общем случае функции f ( x ) отx ( x1 , x 2 , ..., x n ) ряд Тейлора имеет вид
1 n f ( x0 )
f ( x) f ( x0 )
( xi xi( 0 ) )
1! i 1 xi
п
переменных
1 n 2 f ( x0 )
( xi xi( 0 ) )( x j x (j0 ) ) ...
2! i , j 1 xi x j
5.
Безусловный экстремум функции многих переменныхРассмотрим вопрос о нахождении экстремума функции f ( x ) от
п переменных x ( x1 , x 2 , ..., x n ) .
Определение. Говорят, что в точке х0 функция f ( x ) имеет
локальный максимум (минимум), если существует такой шар
R ( x 0 , ) с центром в точке х0 и радиуса > 0, что
x R ( x 0 , ) x x 0 f ( x ) f ( x 0 ) f ( x ) f ( x 0 ) .
Термины «локальный максимум» и «локальный минимум»
объединяют в один термин «локальный экстремум»
6.
Необходимое условие экстремума.Пусть в точке x 0 ( x10 , x 20 , ..., x n0 ) функция f ( x ) имеет, скажем,
локальный максимум. Будем отходить от точки х0 меняя лишь
координату х1. Тогда
f ( x1 , x 20 , ..., x n0 ) f ( x10 , x 20 , ..., x n0 ) ,
то есть f ( x ) имеет локальный максимум по координате х1. Но тогда,
как это изучалось для функции одной переменной, в точке х0 должно
выполняться условие
f x ( x10 , x 20 , ..., x n0 ) 0 .
Аналогично можно рассуждать и в отношении всех остальных
переменных. Рассматривая переменную хi, запишем
f ( x10 ,..., x i0 1 , x i , x i0 1 ..., x n0 ) f ( x10 ,..., x i0 1 , x i0 , x i0 1 ..., x n0 ) ,
откуда следует, что f x ( x10 , x 20 , ..., x n0 ) 0
1
i
7.
Таким образом, в точке локального экстремума должно выполнятьсяусловие
f ( x 0 )
f ( x 0 )
f ( x 0 )
0;
0 ; …;
0.
(2)
x1
x 2
x n
Эти условия дают систему п уравнений с п неизвестными x1 , x2 , ..., xn .
Решая ее, найдем точки, «подозрительные» на экстремум, то есть
точки, где может быть локальный максимум или минимум.
Заметим, что необходимые условия локального экстремума (2)
можно коротко записать так: в точке локального экстремума должно
выполняться условие
grad f ( x 0 ) 0 .
8.
Достаточные условия локального экстремума.Пусть выполнены условия (2). Во-первых, это еще не означает,
что в точке х0 имеет место локальный экстремум. Во-вторых, даже
если там и имеется локальный экстремум, то надо установить его
тип – максимум это или минимум. Ответить на этот вопрос
помогают достаточные условия экстремума.
Для их вывода напомним сначала некоторые сведения из курса
алгебры по вопросу о положительной и отрицательной
определенности матрицы.
Пусть имеется симметричная квадратная матрица A a ij , в
которой п строк и п столбцов. Пусть, далее, 1 , 2 , ..., n есть
произвольные числа. Тогда выражение
Q
n
a
i , j 1
ij
i j
называется квадратичной формой, соответствующей матрице А.
9.
Матрица А называется положительно определенной матрицей, еслиQ > 0 когда хотя бы одно из чисел 1 , 2 , ..., n отлично от нуля и
Q = 0 может быть тогда и только тогда, когда все i 0 . Если при тех
же условиях Q < 0, то матрица А называется отрицательно
определенной. Если 1 , 2 , ..., n такие, что Q > 0 и 1 , 2 , ..., n
такие, что Q < 0, то матрица А называется неопределенной.
10.
Для определения типа матрицы Акритерий Сильвестра. Пусть
a11 a12 a13
a 21 a 22 a 23
A a 31 a 32 a 33
a n1 a n 2 a n 3
существует так называемый
a1 n
a2 n
a3 n .
a nn
11.
Рассмотрим ее минорыA1 a11; A2
a11
a11
a12
a12
a11
, A3 a 21 a 22
a 22
a 31 a 32
a12 a13 a1 n
a 21
a 22
a 23
a2 n
An a 31
a 32
a 33
a3 n .
a 21
a13
a 23 ; … ;
a 33
a n 1 a n 2 a n 3 a nn
Если выполнено условие
A1 0 ; A2 0 ; A3 0 ; …; An 0 ,
то матрица А положительно определенная. Если выполнено условие
A1 0 ; A2 0 ; A3 0 ; …,
то есть все нечетные миноры меньше нуля, а все четные – больше
нуля, то матрица А отрицательно определенная. Во всех остальных
случаях расстановки знаков и матрица А неопределенная.
12.
Конкретизируем теперь вид матрицы А. Пусть элементыматрицы А имеют вид
2 f ( x0 )
a ij
,
(3)
x i x j
где все производные вычисляются в точке х0 предполагаемого
экстремума.
Теорема. Если матрица А положительно определенная, то в
точке х0 локальный минимум.
Если матрица А отрицательно определенная, то в точке х0
локальный максимум.
Если матрица А неопределенная, то в точке х0 нет ни локального
максимума, ни локального минимума.
Доказательство. Мы докажем эту теорему не слишком строго.
Разложим f ( x ) в ряд Тейлора в окрестности точки х0. Обозначая
x i x i0 x i и вспоминая, что в точке х0 имеет место f x i ( x0 ) 0 ,
получим
1 n
f ( x) f ( x0 ) aij xi x j ... ,
2 i , j 1
где аij определены в (3).
13.
Пусть теперь матрица A a ijn
Тогда
a x x
i , j 1
ij
i
j
положительно определенная.
0 , когда хотя бы одно из x i 0 . Но тогда, по
крайней мере в некоторой окрестности точки х0, будет выполнено
условие f ( x ) f ( x 0 ) и в точке х0 будет локальный минимум.
Если же матрица А отрицательно определенная, то
n
a x x
i , j 1
ij
i
j
0 , и, по крайней мере в некоторой окрестности точки х0,
будет выполнено условие f ( x ) f ( x 0 ) и в точке х0 будет локальный
максимум.
Если же матрица А неопределенная, то x i такие, что
n
a x x
j
0 , и тогда f ( x ) f ( x 0 ) , но и x i такие, что
a x x
j
0 , и тогда f ( x ) f ( x 0 ) . Поэтому в данном случае в
i , j 1
n
i , j 1
ij
ij
i
i
точке х0 нет ни максимума, ни минимума.
14.
В заключение еще раз отметим, что мы пренебреглиследующим членом в разложении f ( x ) в ряд Тейлора. Поэтому
все эти рассуждения верны лишь в некоторой окрестности точки х0
и наши возможные минимум и максимум являются лишь
локальными.


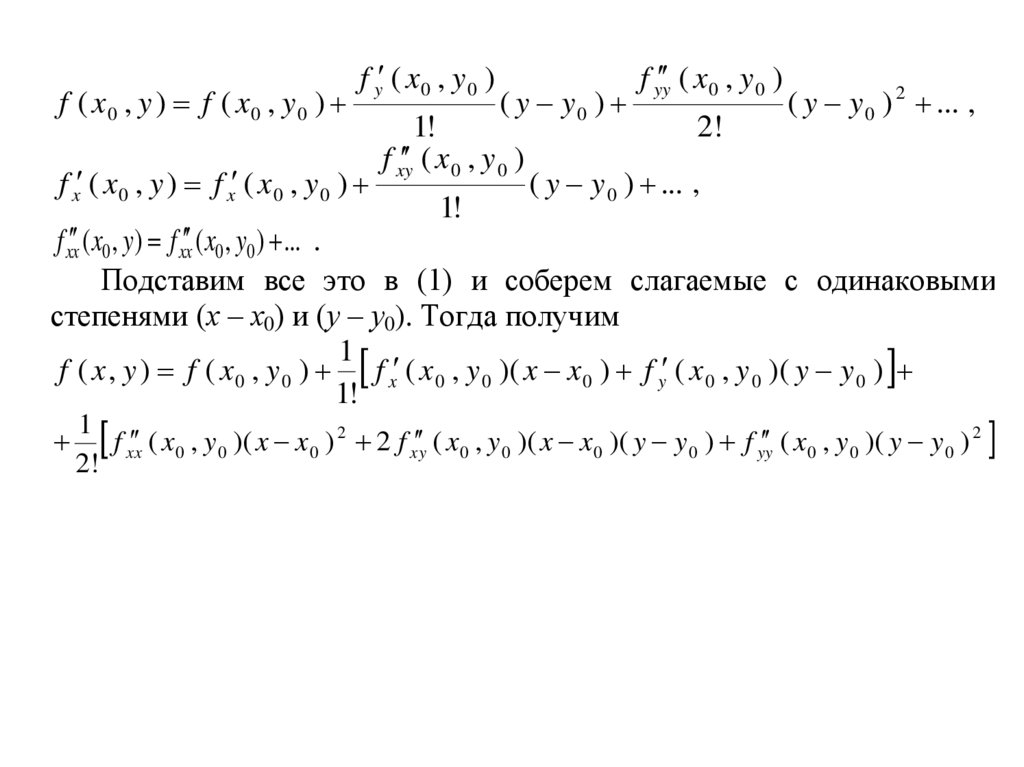











 mathematics
mathematics








