Функции многих переменных. Лекция 16

1. Здравствуйте!

Лекция №16

2. Функции многих

переменных

3.

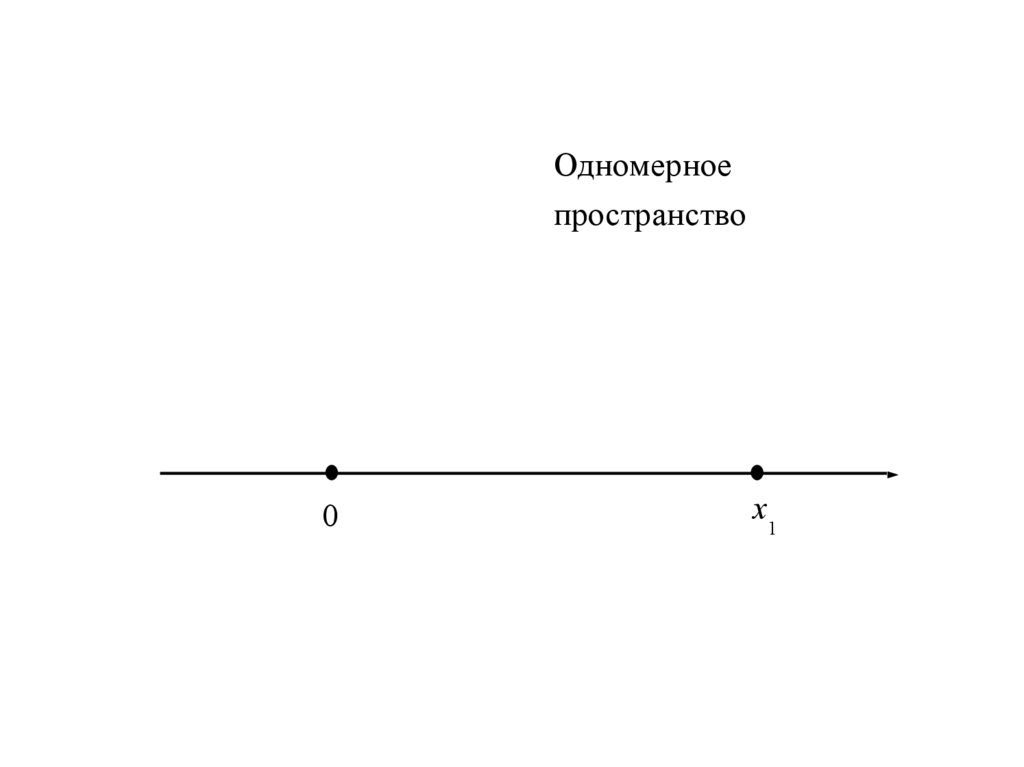
Одномерное
пространство
0
x1

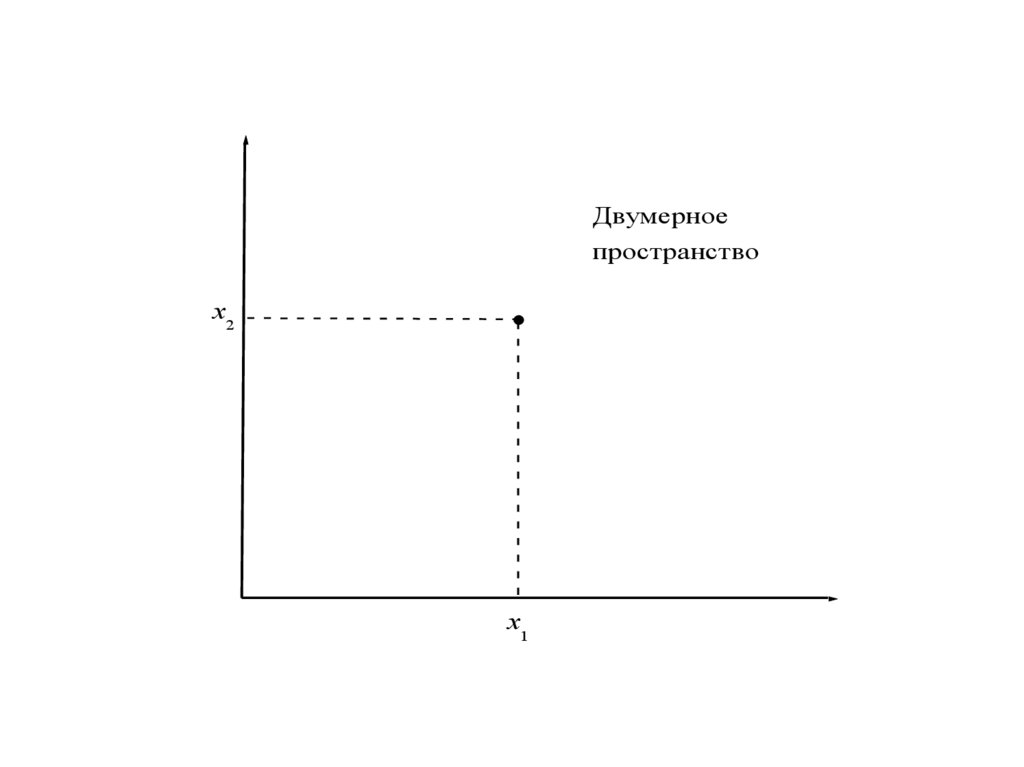
4.

Двумерное
пространство
x2
x1

5.

x3
Трехмерное
пространство
( x1, x2, x3 )
x2
x1

6.

В п-мерном пространстве точка – это совокупность п
вещественных чисел ( x1 , x 2 , x 3 ,... , x n ) , которые называются
координатами точки п-мерном пространстве. Для сокращения
записи, мы в дальнейшем будем часто точку обозначать одной
буквой х, но надо всегда помнить, что это сокращенное
обозначение подразумевает следующее
x ( x1 , x 2 , x 3 ,... , x n ) .

7.

Расстояние между двумя точками.
Пусть имеются две точки – x ( x1 , x 2 , x 3 ,... , x n ) и
y ( y1 , y 2 , y 3 ,... , y n ) . Эвклидовым расстоянием между этими
точками называется величина
d ( x, y )
n
( x
i 1
i
yi ) 2 .
Так как других расстояний в данном курсе не будет, то слово
«эвклидово» мы будем опускать.
Это расстояние обладает следующими свойствами:
1. d ( x , y ) 0 ; d ( x , y ) 0 x y (то есть i 1, n x i y i ).
2. d ( x , y ) d ( y , x ) .
3. Неравенство треугольника:
z d ( x , y ) d ( x , z ) d ( z , y ) .

8.

Области в п-мерном пространстве
Определение. Областью в п-мерном пространстве называется
любое множество точек из этого пространства.
1. Замкнутый параллелепипед – это множество точек х,
координаты которых удовлетворяют соотношению
a i x i bi , i 1, n .
Он обозначается символом
[a1, b1; a2 , b2 ; a3 , b3 ;... an , bn ] .
Точка с координатами
a n bn
a1 b1 a 2 b2 a 3 b3
,
,
,
...
,
2
2
2
2
называется центром параллелепипеда, величины bi a i , i 1, n –
сторонами параллелепипеда.

9.

2. Открытый параллелепипед – это множество точек х,
координаты которых удовлетворяют соотношению
a i x i bi , i 1, n .
Он обозначается символом
(a1, b1; a2 , b2 ; a3 , b3 ;... an , bn ) .
3. Замкнутый шар – это множество точек х, координаты
которых удовлетворяют соотношению
n
0 2
2
(
x
x
)
r
.
i i
i 1
Он обозначается символом R[ x 0 , r ]. Точка x 0 ( x10 , x 20 , x 30 ,... x n0 )
называется центром шара, величина r – его радиусом.

10.

4. Открытый шар – это множество точек х, координаты
которых удовлетворяют соотношению
n
0 2
2
(
x
x
)
r
i i
i 1
Он обозначается символом R ( x 0 , r ) . Шар R ( x 0 , ) O ( x 0 )
называется -окрестностью точки х0.
Теорема. Во всякий параллелепипед можно вписать шар и
наоборот – во всякий шар можно вписать параллелепипед.

11.

Доказательство.
1. Пусть дан параллелепипед
P [ a1 1 , a1 1 ; a 2 2 , a 2 2 ;... a n n , a n n ]
с центром в точке a ( a1 , a 2 ,..., a n ) и сторонами 2 1, 2 2, … , 2 п.
Рассмотрим шар с центром в точке а и радиусом
min( 1 , 2 , ..., n ) , то есть R [ a , ] .
Пусть x R[ a , ]. Это значит, что
n
2
2
(
x
a
)
.
j j
j 1
Но тогда i 1, n имеем
| xi ai | ( xi ai ) 2
n
( x
j 1
j
a j )2 i ,
и, следовательно, х Р. Это означает, что R [ a , ] P .

12.

2. Пусть дан шар R [ a , r ] . Возьмем r n и рассмотрим
параллелепипед
P [ a1 , a1 ; a 2 , a 2 ;... a n , a n ] .
Пусть х Р. Тогда i 1, n | x i a i | и мы имеем
n
n
r2
2
2
2
2
,
(
x
a
)
n
n
r
i
i
n
i 1
i 1
то есть x R [ a , r ]. Следовательно, P R[ a , r ].
Эта теорема позволяет переходить от шара к параллелепипеду и
обратно.

13.

Функции п переменных
Пусть в п-мерном пространстве задана какая-то область G.
Правило, которое каждой точке области G с координатами
x ( x1 , x 2 , x 3 ,... , x n ) ставит в соответствие число z, называется
функцией п переменных и обозначается символом z f ( x ) , или, в
полной форме записи, z f ( x1 , x 2 , x 3 ,... , x n ) .
Множество точек х, где это правило имеет смысл, называется
областью определения функции. Множество чисел z называется
областью значений функции.
Пусть z f ( x1 , x 2 , x 3 ,... , x n ) , а переменные хi в свою очередь
являются функциями m-мерных переменных t ( t1 , t 2 , ..., t m ) , то
есть
x i i ( t1 , t 2 , ..., t m ) , i 1, n .
Подставим в вместо хi эти функции. Тогда мы получим сложную
функцию, или суперпозицию функций
z f ( 1 ( t1 , t 2 , ..., t m ), 2 ( t1 , t 2 , ..., t m ), ..., n ( t1 , t 2 , ..., t m ))
F ( t1 , t 2 , ... , t m )

14.

Предел функции п переменных
Определение. Число А называют пределом функции f ( x ) при
x a ( a ( a1 , a 2 ,..., a n ) ), если
0 0 x | x i a i | i 1, n | f ( x ) A | ,
или
0 0 x d ( x , a ) | f ( x ) A | .
Геометрически это означает следующее. Пусть около значения
А мы взяли сколь угодно малый отрезок ( A , A ) . Тогда
найдется такой параллелепипед с центром в точке а и со сторонами,
равными 2 , что как только точка х попадет в этот параллелепипед,
так значение функции попадет в отрезок ( A , A )
Втрое определение отличается от первого тем, что вместо
параллелепипеда фигурирует шар с центром в точке а и радиусом ,
и попадание точки х внутрь этого шара приводит к тому, что
значение f(x) попадет в отрезок ( A , A ) .

15.

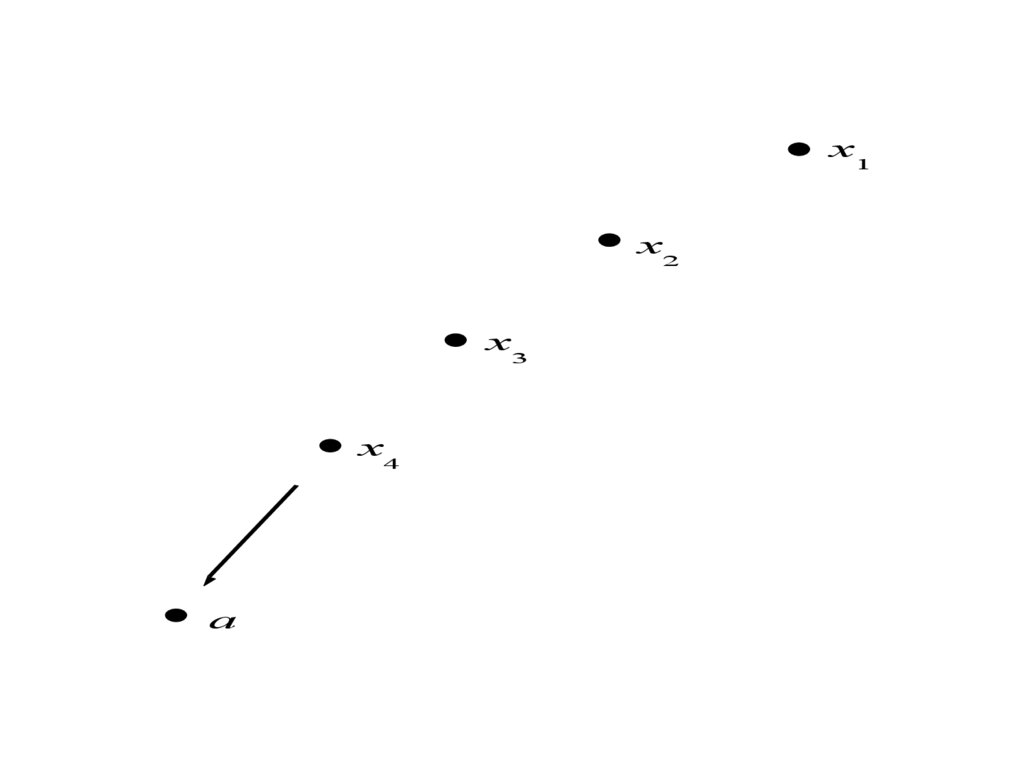
x1
x2
x3
x4
a

16.

Повторные пределы
Пусть задана функция f ( x, y) двух переменных х и у. Пусть
точка (х, у) стремится к точке с координатами (а, b), то есть (х, у)
(а, b). Это означает, что х а и у b.
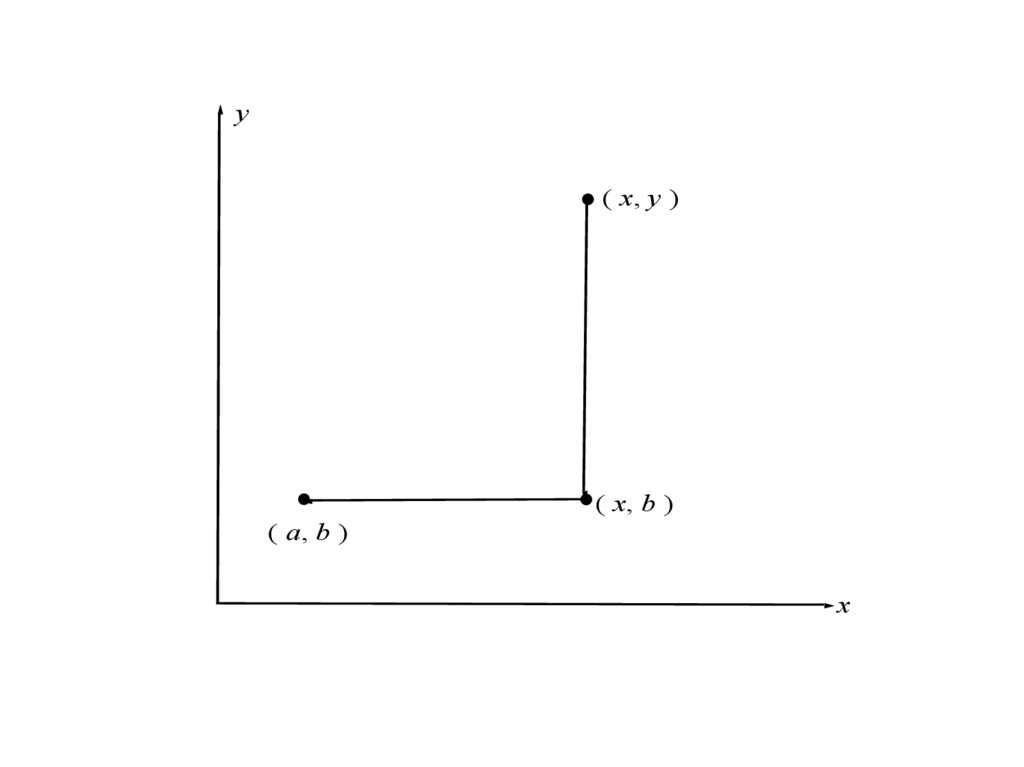
Будем подходить к точке (а, b) двумя путями. Первый путь
выглядит так: Сначала из точки (х, у) перейдем в точку (х, b),
двигаясь параллельно оси OY, а затем из этой точки перейдем в
точку (а, b), двигаясь параллельно оси OX. В приложении к
функции f ( x , y ) это означает, что сначала мы перешли к пределу
lim f ( x , y ) получив некоторую функцию ( x ) lim f ( x , y ) , а
y b
y b
затем уже нашли lim ( x ) , получив так называемый повторный
x a
предел lim lim f ( x , y ) .
x a y b

17.

y
( x, y )
( x, b )
( a, b )
x

18.

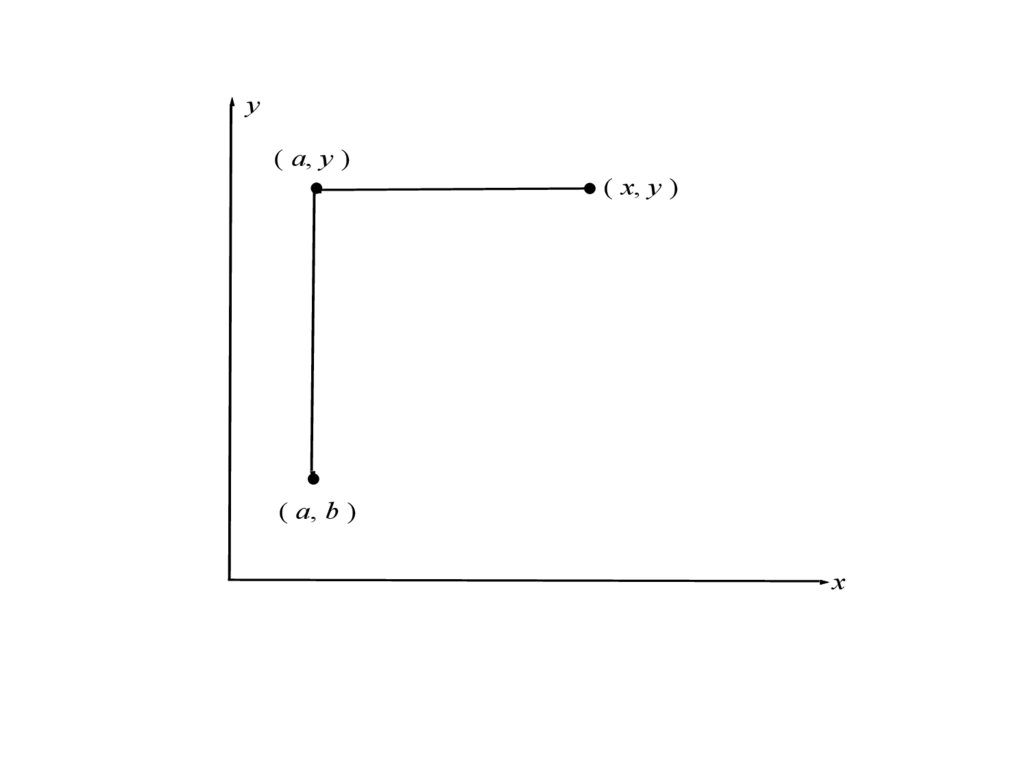
Теперь пойдем от точки (х, у) к точке (а, b) по такой
траектории: сначала перейдем в точку (а, у) двигаясь параллельно
оси ОХ. Тем самым мы найдем lim f ( x , y ) ( y ) , который будет
x a
функцией от у. Затем из точки (а, у), двигаясь параллельно оси OY,
перейдем в точку (а, b), вычисляя теперь уже lim ( y ) . Тем
y b
самым мы нашли другой повторный предел lim lim f ( x , y )
y b x a

19.

y
( a, y )
( x, y )
( a, b )
x

20.

Теорема. Если
1. Существует двойной предел
lim
( x , y ) ( a ,b )
f ( x, y );
2. у существует lim f ( x , y ) ( y ) ,
x a
то существует и повторный предел lim lim f ( x , y ) и он равен
y b x a
двойному пределу, то есть lim lim f ( x , y ) =
y b x a
lim
( x , y ) ( a ,b )
f ( x, y ).

21.

Доказательство.
Пусть A lim
( x , y ) ( a ,b )
f ( x , y ) . Это означает, что
0 0 x , y | x a | | y b | | f ( x , y ) A | .
Перейдем в этой строке к пределу х а. Тогда выписывать
неравенство | x a | не будет необходимости, так как x a 0 .
Далее, так как у существует lim f ( x , y ) ( y ) , то
x a
lim | f ( x , y ) A | | lim f ( x , y ) A | | ( y ) A | ,
x a
x a
и наша строчка кванторов примет вид
0 0 y | y b | | ( y ) A | .
По определению предела функции одной переменной это и
означает, что существует
lim ( y ) lim lim f ( x , y ) A.
y b
y b x a

22.

Следствие. Если к ограничениям теоремы добавить еще, что
3. х существует lim f ( x , y ) ( x ) ,
y b
то существуют оба повторных предела, и они равны друг другу
(так как оба они равны двойному пределу)
lim lim f ( x , y ) lim lim f ( x, y ) lim f ( x , y ) .
x a y b
y b x a
( x , y ) ( a ,b )
Через понятие предела обычным образом вводится понятие
непрерывности функции п переменных: функция f(x) называется
непрерывной в точке а, если lim f ( x ) f ( a ) . Все свойства
x a
непрерывных функций сохраняются и в случае функций п
переменных.