Функции многих переменных (лекция 8)

1. Лекция 8 Функции многих переменных

1

2. Понятие функции многих переменных

x1 , x 2 ,..., x n R - набор п действительных чисел
x ( x1 , x 2 ,..., x n ) - п-мерная точка (вектор)
R-n
п-мерное множество
• Если каждой точке ставится
в соответствие
x( x1 , x 2 ,...,
xn ) D
единственное число , то говорят, что
y задана
I
числовая функция n переменных:
y f ( x1 , x 2 ,..., x n )
- область определения
D Rn
- множество
значений функции
I R
2

3.

• Графиком функции n переменных называется nмерная гиперповерхность в пространстве R n 1 ,
каждая точка которой задается координатами
( x1 , x 2 ,..., x n , f( x1 , x 2 ,..., x n ))
• z=f(x,y) – совокупность точек (x,y,z),
( x, y ) D( z ), z f ( x, y )
3

4.

z=f(x,y)
y
O
x
(х,у)
D(x,y)
4

5.

z
O
x
f(x,y)
y
D(x,y)
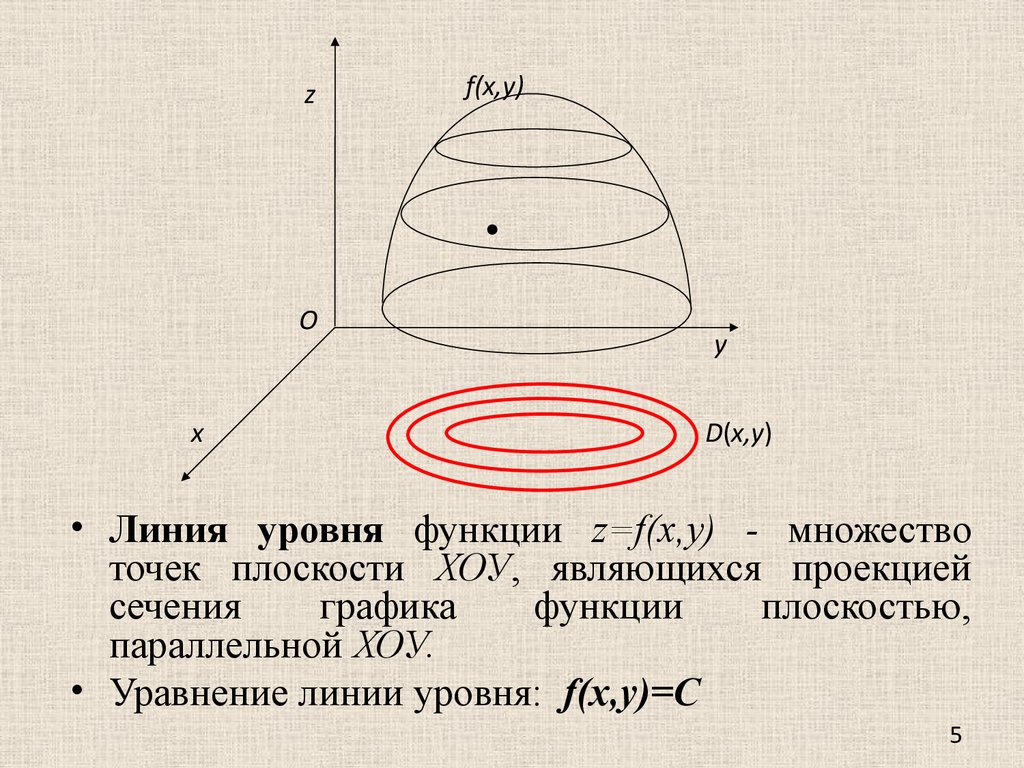
• Линия уровня функции z=f(x,y) - множество
точек плоскости ХОУ, являющихся проекцией
сечения
графика
функции
плоскостью,
параллельной ХОУ.
• Уравнение линии уровня: f(x,y)=С
5

6.

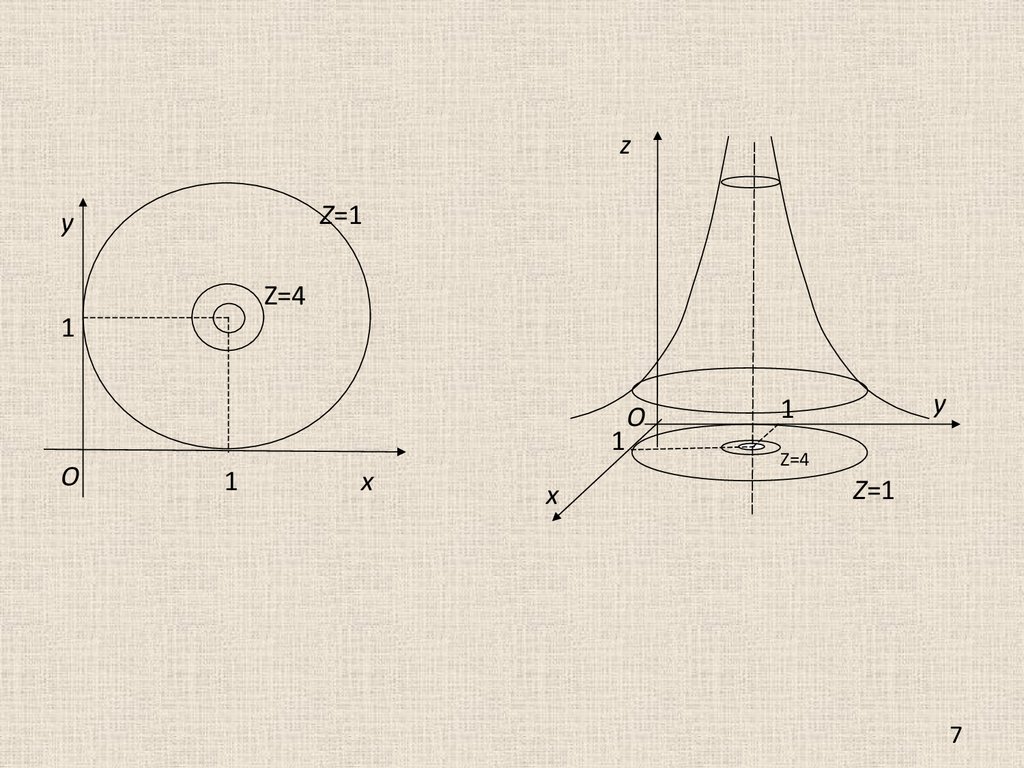
пример
Построить график функции двух переменных
D( z ) R 2 \ (1;1)
1
z
( x 1) 2 ( y 1) 2
;
Линия уровня: f(x,y)=с
;
При с=1:
.
При с=4:
.
При с=9:
1
1
2
2
( x 1) ( y 1)
( x 1) 2 ( y 1) 2 1
;
1
4
1
4
2
2
( x 1) ( y 1)
( x 1) 2 ( y 1) 2
1
9
2
2
( x 1) ( y 1)
1
( x 1) ( y 1)
9
2
2
6

7.

z
Z=1
y
Z=4
1
1
O
1
x
x
O
y
1
Z=4
Z=1
7

8. Предел функции многих переменных

• .
Число А называется пределом функции двух
переменных z=f(x,y) при х х0 , y y 0
и обозначается lim f ( x, y ) A,
x x0
y y0
,
если для любого положительного числа ε найдется
положительное число δ, такое, что если точка (x,y) удалена
от точки (x0,y0) на расстояние меньше δ, то величины f(x,y)
и А отличаются меньше чем на ε.
x2 4y
3
lim
x 1
2 xy 1
y 2
x2 y2
( x y )( x y )
x y
0
lim 2
lim
lim
1
x 2 x 2 x xy 2 y
x
2
x
2
0 y 2 ( x 2)( x y ) y 2 x 2
y 2
8

9. Непрерывность функции многих переменных

• Если функция z=f(x,y) определена в точке (x ,y ) и
имеет в этой точке предел, равный значению
функции lim f ( x, y ) f x , y ,
0
0
0
0
x x0
y y0
то она называется непрерывной в данной точке.
9

10. Частные производные функции многих переменных

• Рассмотрим функцию двух переменных z=f(x,y).
Положим y=y0, получим функцию одной переменной х.
Пусть она имеет производную в точке (х0, у0):
f x x0 , y0
f x 0 x , y 0 f x 0 , y 0
x
x 0
lim
- частная производная по переменной х.
z x x0 , y0 , f x0 , y0 , z x , y
0
0
x
x
x z f x 0 x, y 0 f x 0 , y 0
- частное
xz
x 0 x
f x x0 , y 0 lim
приращение по переменной х.
f y x0 , y0 lim
y 0
yz
y
10

11. Частные производные высших порядков

2z
f xx x, y
2
x
2z
f yy x, y
2
y
2z
f xy x, y
x y
2 z
f yx x, y
y x
11