Similar presentations:
Векторные неявные функции
1.
Векторные неявные функцииПредположим, что n функций yi i x1 ,
решение системы n функциональных уравнений
Fi x1 ,
, xm , y1 ,
, xm , i 1, n ищутся как
, yn 0, i 1, n .
(3.18)
Теорема о векторной неявной функции. Пусть функции
Fi x1 ,
, yn , i 1, n
, xm , y1 ,
непрерывно дифференцируемы в некоторой окрестности точки
N0 x10 ,..., xm0 , y10 ,..., yn0
Тогда если i 1, n Fi N 0 0 и
окрестности точки M 0 x10 ,
, xm0
m
F1 ,
y1 ,
m n
, Fn
, yn
.
N0 0 , то в некоторой
система уравнений (3.18) определяет
единственный набор функций
Fi x1 ,
, xm , y1 ,
, yn 0, i 1, n ,
являющихся решением системы (3.18), причем эти функции непрерывно
дифференцируемы в рассматриваемой окрестности точки M 0 .
1
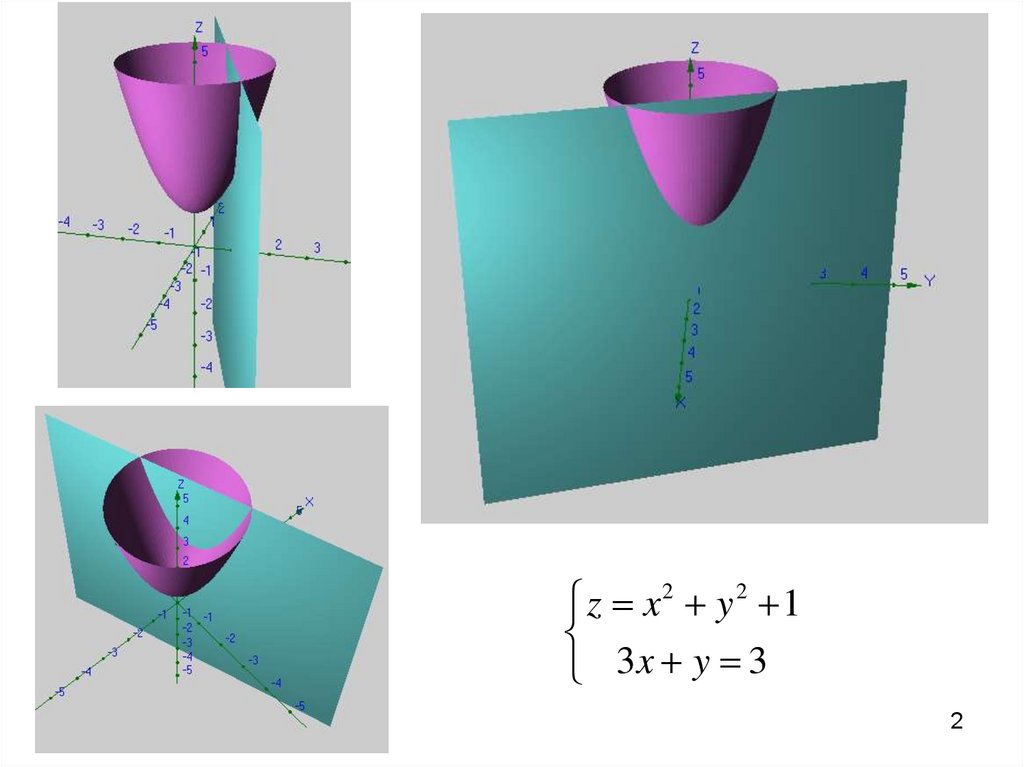
2.
z x2 y 2 13x y 3
2
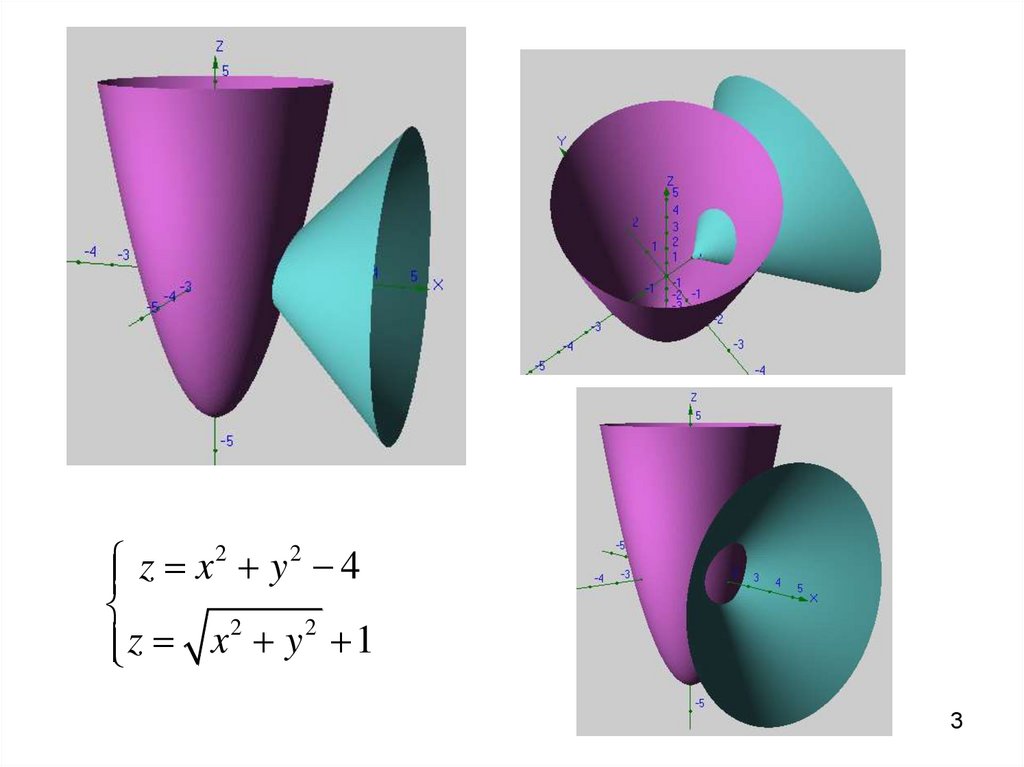
3.
z x 2 y 2 42
2
z
x
y
1
3
4.
45.
Вычисление частных производных неявно заданной векторной функцииПодставим функции (3.17) в систему (3.18), решением которой эти функции являются, и
продифференцируем получившиеся тождества по xl , l 1, m . Получим линейную систему
F1 y1
y x
1 l
F2 y1
y
x
1 l
Fn y1
y x
1 l
F1 yn F1
0,
yn xl xl
F2 yn F2
0,
yn xl xl
(3.19)
Fn yn Fn
0.
yn xl xl
F1 , , Fn
y
y1 y2
,
, , n . Определитель этой системы – якобиан
,
xl xl
xl
y1 , , yn
согласно условию, отличен от 0 в окрестности рассматриваемой точки N 0 . Следовательно, система
(3.19) имеет единственное решение, определяемое формулами Крамера:
относительно n неизвестных
yk
xl
F1 , F2 , , Fn
y1 , y2 , , yk 1 , xl , yk 1 ,
F1 , F2 , , Fn
y1 , y2 , , yn
, yn
, k 1, n. .
В случае необходимости вычисления производной более высокого порядка ее вычисляют
рекуррентно как производную от производной, имеющей порядок на единицу меньше, учитывая, что
5
y1 ,..., yn являются функциями переменных x1 ,..., xm .
6.
Зависимость функцийПусть n функций yi i x1 ,
емы в некоторой области A
m
, xm , i 1, n определены и дифференциру-
. Говорят, что одна из этих функций, например
yk , зависит в области A от остальных функций, если сразу для всех точек
x1 ,
, xm области A
yk y1 ,
, yk 1 , yk 1 ,
, yn ,
(3.21)
где – некоторая функция, определенная и дифференцируемая в соответствующей области B
m 1
Функции y1 , y2 ,
изменения своих аргументов.
, yn называют зависимыми в области A , если одна из
этих функций (безразлично какая) зависит в области A от остальных.
Если же не существует дифференцируемой функции такой, что сразу для
всех точек области A справедливо тождество вида (3.21), то функции y1 , y2 ,
, yn
называют независимыми в области A .
6
7.
Необходимое условие зависимости функций.Пусть в области A
m
заданы n непрерывно дифференцируемых функций:
y1 1 x1 , , xm ,
(3.22)
yn n x1 ,
, xm ,
где n m . Если система функций (3.22) зависима в области A , то в любой точке A
ранг матрицы Якоби этой системы меньше n .
Пусть n зависит от 1 , …, n 1 : n 1 x , , n 1 x , x A , где
y1 ,..., yn 1 – непрерывно дифференцируемая функция. Тогда
yn n 1 yk
.
j 1, m
x j k 1 yk x j
Эта формула показывает, что n -я строка матрицы Якоби
y1 x
x1
yn x
x1
y1 x
xm
yn x
xm
(3.23)
в каждой точке x A является линейной комбинацией остальных строк этой матрицы,
а значит, ранг матрицы Якоби меньше n в каждой точке x A .
7
8.
89.
y1 xx1
yn x
x1
y1 x
xm
yn x
xm
Следствие 1. Если m n и система функций yi i x1 ,
то якобиан
(3.23)
, xm , i 1, n зависима в области A ,
y1 ,..., yn
равен 0 во всех точках области A .
x1 ,..., xn
Следствие 2. Если система функций yi i x1 ,
, xm , i 1, n зависима в области A ,
то градиенты grad y1 , …, grad yn этих функций линейно зависимы в каждой точке области A .
Следствие 3 (достаточное условие независимости функций). Если хоть один определитель
n -го порядка, составленный из элементов матрицы (3.23), отличен от нуля в области A , то в этой
области функции y1 ,..., yn независимы.
Теорема 3.5. Пусть у функциональной матрицы (3.23)
1) некоторый минор r -го порядка отличен от нуля в точке M 0 x10 ,
, xm0 ;
2) все миноры r 1 -го порядка равны нулю в некоторой окрестности точки M 0 x10 ,
, xm0 .
Тогда r функций, представленных в указанном миноре r -го порядка, независимы в окрестности
точки M 0 , каждая из остальных функций зависит в этой окрестности от указанных r функций.
9
З а м е ч а н и е . Если r min n, m , то второе условие теоремы следует опустить.
10.
Локальный условный (относительный) экстремумПусть A
m
– открытое множество, f : A
. Для натурального s m пусть
i : A , i 1, s – заданные функции. Если
Q x x A, i x 0, i 1, s ,
то говорят, что множество Q определяется s уравнениями связи
1 x 0, 2 x 0,
, s x 0 .
(3.24)
Функция f имеет в точке x 0 Q локальный относительный максимум при
условиях (3.24), если существует окрестность этой точки, в которой
x Q f x f x 0 .
Локальный относительный максимум называется строгим, если в последнем
выражении неравенство будет строгим.
Аналогично определяются понятия локального относительного минимума и
строго локального относительного минимума. Все эти понятия описываются также
общим термином локальный относительный (или условный) экстремум.
10
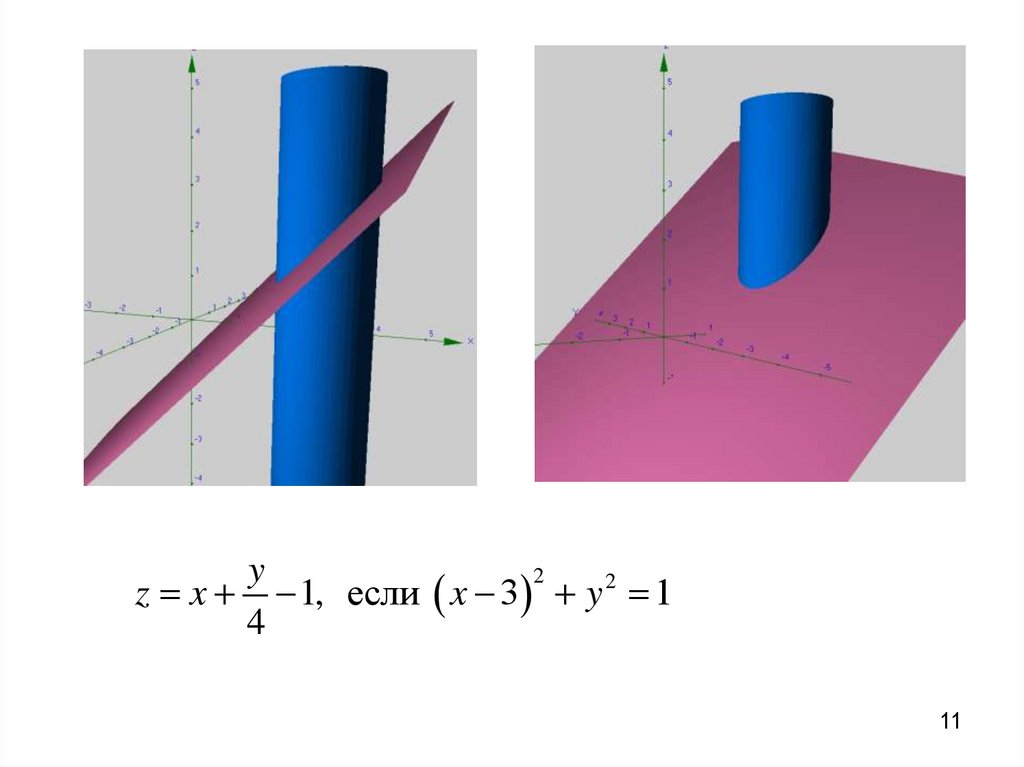
11.
y2
z x 1, если x 3 y 2 1
4
11
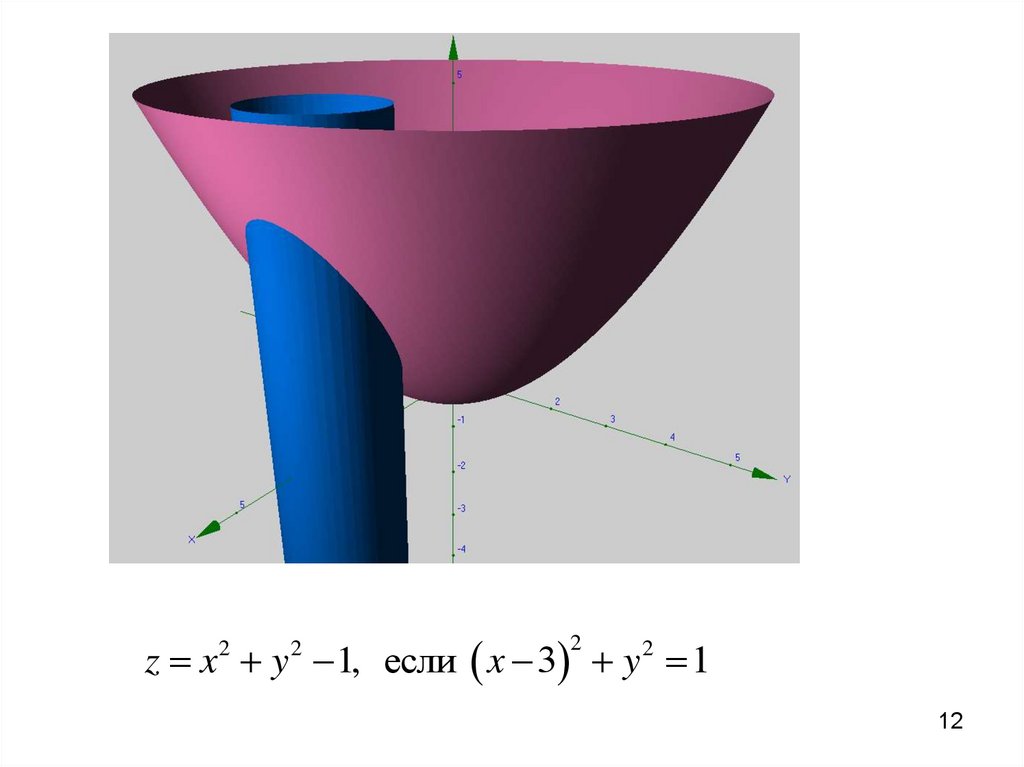
12.
z x y 1, если x 3 y 2 12
2
2
12
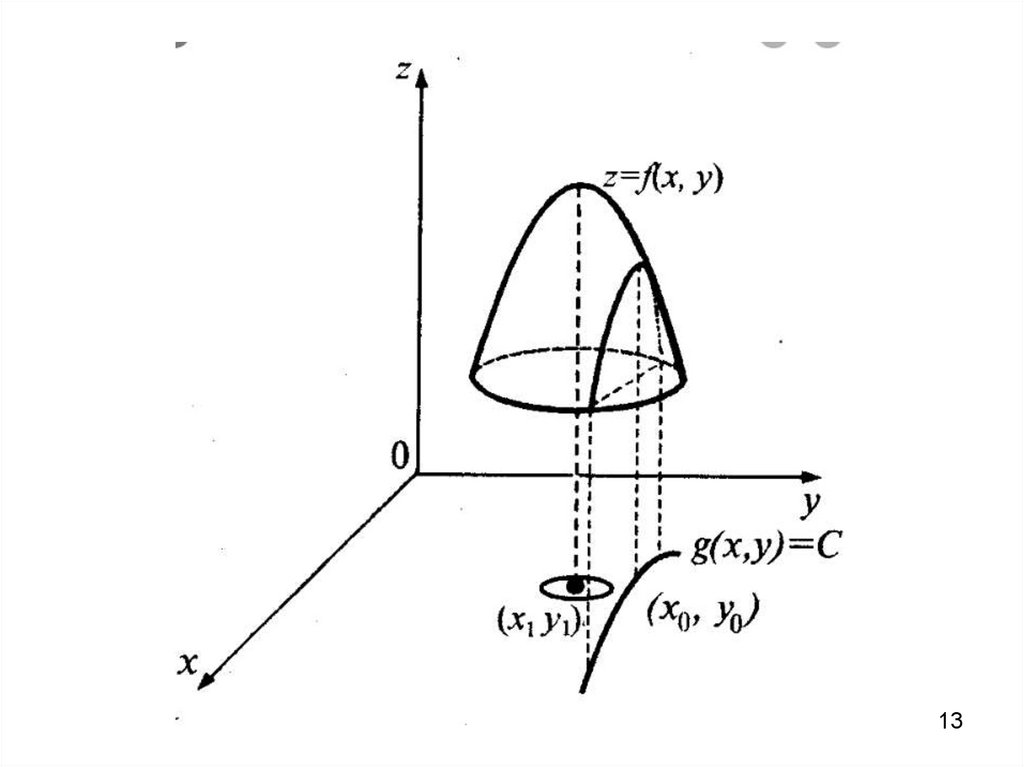
13.
1314.
Нахождение условного экстремума1. Если уравнения связи
1 x 0, 2 x 0,
, s x 0 .
(3.24)
могут быть аналитически разрешены относительно каких-либо s переменных,
то, подставляя полученные выражения в функцию f x , получим функцию
m s переменных, локальный экстремум которой совпадет с условным
экстремумом исходной функции при заданных уравнениях связи. Такой метод
нахождения условного экстремума называется методом исключений.
2. Если аналитически решить систему (3.24) не удается, то используется
метод Лагранжа, основанный на следующих двух теоремах.
14
15.
Пусть Am
– открытое множество, f C 1 A , i 1, s i C1 A , s m .
Необходимое условие локального относительного экстремума.
Если x 0 A – точка локального относительного экстремума функции f при ограничениях
s m
i x1 ,
i
имеет ранг s в точке x 0 , то i , i 1, s ,
, xm 0 , i 1, s и матрица
x
j i 1 j 1
такие, что точка x 0 – критическая точка функции Лагранжа
F f 1 1 2 2
s s .
Достаточное условие локального относительного экстремума.
s
Пусть x – критическая точка функции Лагранжа F f i i для некоторого набора
0
i 1
s m
i
чисел i , i 1, s , удовлетворяющая уравнениям связи и матрица
имеет ранг s
x
j i 1 j 1
m m
2 F
0
в точке x . Тогда, если квадратичная форма с матрицей
является положительно
x x
i j i 1 j 1
(отрицательно) определенной с учетом уравнений связи, то x 0 – точка относительного
локального минимума (максимума) для f .
15
16.
Метод Лагранжа нахождения условного экстремума функции f : Aпри условиях связи 1 x 0, 2 x 0,
, s x 0 .
s
1. Составив функцию Лагранжа F x f x i i x определить все критические
точки x10 ,
i 1
, xm0 s ,..., xm0 этой функции из системы m s уравнений
i x1 ,..., xm 0, i 1, 2,..., s;
F
x x1 ,..., xm 0, i 1, 2,..., m
i
относительно m s неизвестных x1 , x2 ,..., xm , 1 , 2 ,..., s .
2. Во всех критических точках исследовать второй дифференциал функции Лагранжа с
учетом заданных условий связи. Для этого сначала вычислить d 2 F в точке x10 , , xm0 s ,..., xm0 ,
считая все аргументы x1 , x2 ,..., xm независимыми переменными, а затем dxm s 1 ,
в полученном выражении заменить линейными функциями dx1 ,
, dxm s в точке x10 ,
, dxm
, xm0 s
согласно уравнениям связи.
2
3. Если выражение d F в рассматриваемой точке является знакоопределенной
квадратичной формой, то эта точка является точкой условного экстремума функции f .
2
З а м е ч а н и е : Без учета условий связи выражение d F в точке условного экстремума в
18
общем случае может быть знакопеременной квадратичной формой.
17.
Лемма 3.7. Если непрерывная в области D функция u x, y, z принимает внекоторой точке x0 , y0 , z0 границы D области D значение u0 такое, что
x, y, z D u0 u x, y, z ,
то это значение является супремумом данной функции в области D .
Так как функция u x, y, z непрерывна в области D , то
0 0 x1 , y1 , z1 D
x0 , y0 , z0 , x1 , y1 , z1 u x0 , y0 , z0 u x1 , y1 , z1 .
С учетом выбора точки x0 , y0 , z0 последнее неравенство можно переписать в
виде 0 u x0 , y0 , z0 u x1 , y1 , z1 . Точка
x0 , y0 , z0
является граничной
точкой области D , следовательно, в любой её -окрестности существует точка
x1 , y1 , z1 D . Отсюда получаем, что
0 x1, y1, z1 D u x0 , y0 , z0 u x1, y1, z1 ,
т.е. u0 sup u x, y, z .
x , y , z D
З а м е ч а н и е . Аналогичное утверждение можно сформулировать и для
20
инфимума функции u x, y, z в области D .













 mathematics
mathematics








