Similar presentations:
Электромагнитные волны. Курс лекций
1.
Вы приходите на экзамен по физике и встречаете это. Ваши действия?2.
Оглавление1)Электромагнитные волны
2)ЭМВ. Свойства
3)Интерференция
4)Дифракция Фраунгофера
5)Дифракция Френеля
6)Распространение ЭВМ в диэлектрической среде
7)Двойное лучепреломление
8)Тепловое излучение. Формула Планка
9)Корпускулярные свойства ЭМВ. Взаимодействие ЭМВ с
веществом
10)Ядерная модель атома. Свойства микрочастиц
11)Уравнение Шредингера
12)Простейшие случаи движения микрочастиц
3.
Лекция 3.1. Электромагнитныеволны
•Уравнения Максвелла(2,3)
•Решения системы уравнений Максвелла (4,5,6)
•Волновое уравнение(7,8)
•Поперечность волн Е и Н (9)
•Связь между волнами Е и Н (10,11)
•Свойства волновых решений уравнений Максвелла(12)
•Параметры электромагнитной волны (13)
•Поляризация (14, 15,16)
•Стоячие электромагнитные волны (17)
•Энергия электромагнитной волны(18,19)
3
4.
Уравнения Максвелла в интегральнойформе
4
5.
Уравнения Максвелла в дифференциальнойформе и их асимметрия
5
6.
Решения системы уравнений Максвелла6
7.
Решения неоднородной и однороднойсистем УМ
7
8.
Поиск решения однородной с-мы УМ8
9.
Сведение уравнений Максвелла кволновому уравнению
9
10.
Волновое и общее решения с-мы УМ10
11.
Поперечность волн Е и Н11
12.
Связь между волнами Е и Н12
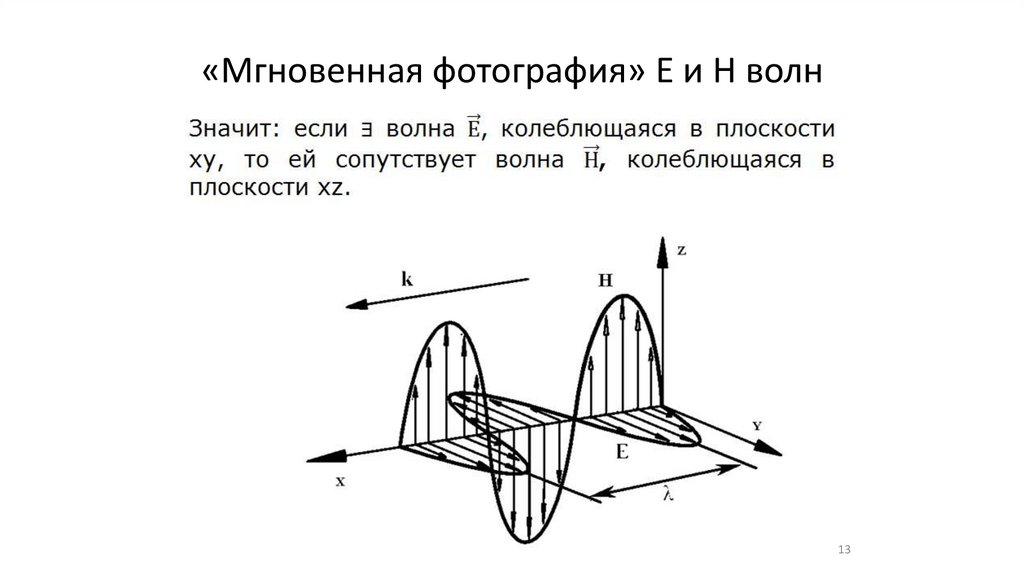
13.
«Мгновенная фотография» Е и Н волн13
14.
Свойства волновых решений уравненийМаксвелла
14
15.
Параметры электромагнитной волны15
16.
Поляризация16
17.
Поляризованные волны17
18.
Эллиптическая поляризация18
19.
Стоячие электромагнитные волны19
20.
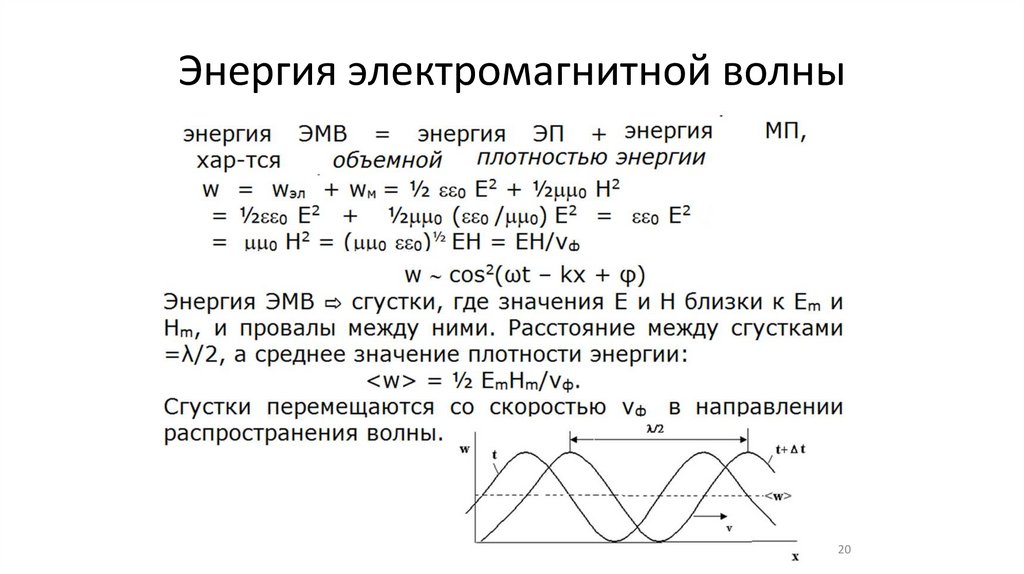
Энергия электромагнитной волны20
21.
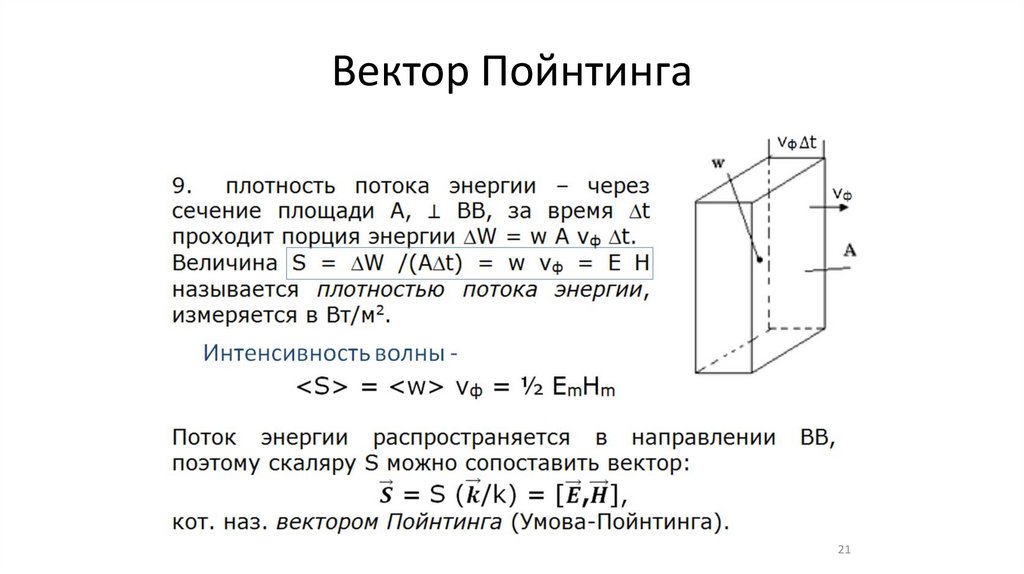
Вектор Пойнтинга21
22.
несодер
ен
приоб
раскр
жание
непол
ретён
ыто
матер
но,
ные
иала,
при
ранее
Допу
но
ответе
Чётко
щены
излож
допущ
и
грубы
ено
ены
прави
ефрагм
неточ
льно
ошибк
ентар
ности,
даны
и
в не
но,
наруш
опред
опред
всегда
ена
елени
елени
после
после
яях,и
доват
доват
раскр
доказ
ельно
ельно
ыто
ательс
Практ
сть
содер
тва
ическ
излож
жание
или
ие
ения.
.вывод
навык
Допу
Твёрд
ы
и
щены
ые
форму
слабы
небол
практ
л
не
еьшие
ическ
прове
Допу
неточ
ие
дены
щены
ности
навык
Нет
ошибк
при
и.
практ
и
при
вывод
Полно
Критерии оценки
отлично
хорошо
удовлетворительно
неудовлетворительно
22
23.
Лекция 3.2. Электромагнитныеволны. Свойства.
•Импульс бегущей волны. Давление (2,3,4)
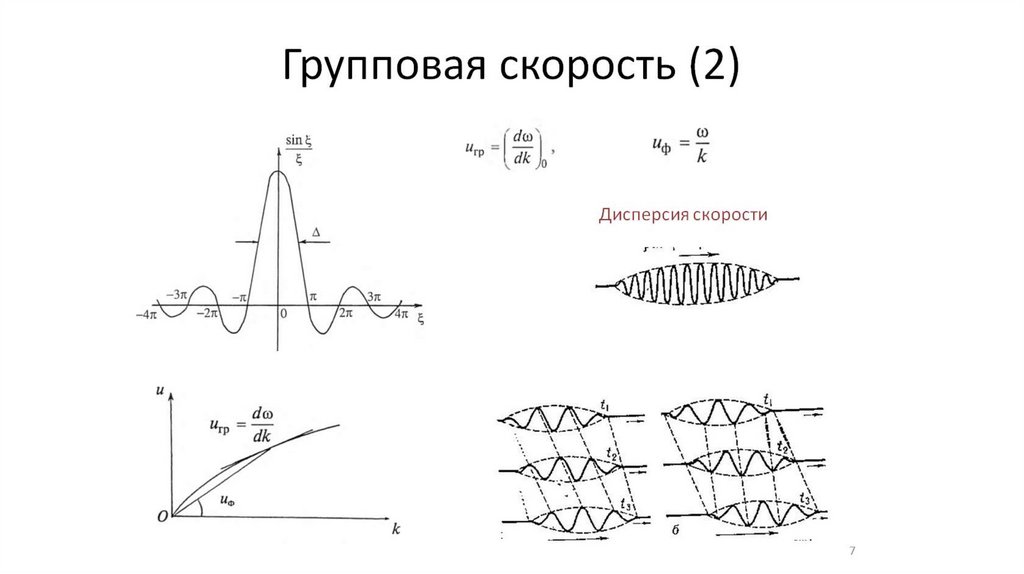
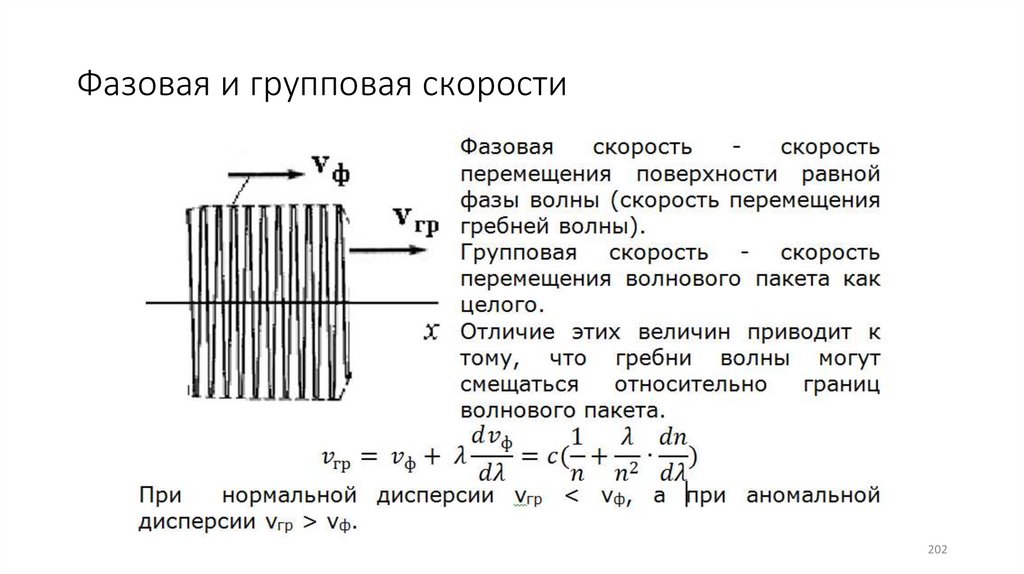
•Фазовая и групповая скорости (5,6,7)
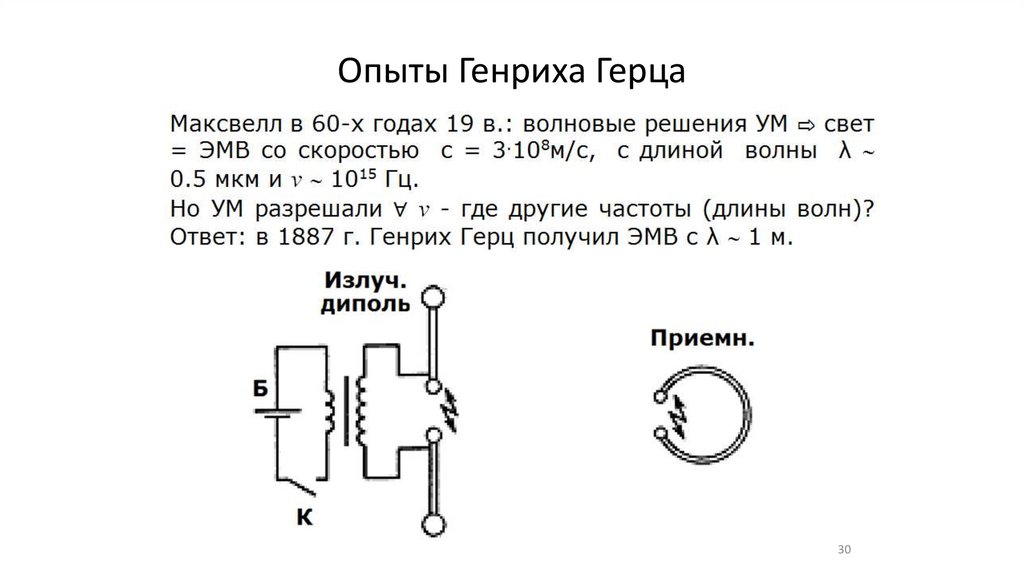
•Опыты Генриха Герца (8,9)
•Диапазоны ЭМВ(10,11)
•Излучение осциллирующего диполя (12, 13,14,15,16)
•Геометрическая оптика и оптические приборы (17,18)
•Прямолинейное распространение света (19)
•Независимость световых лучей(20)
23
24.
25.
26.
27.
28.
29.
30.
Опыты Генриха Герца30
31.
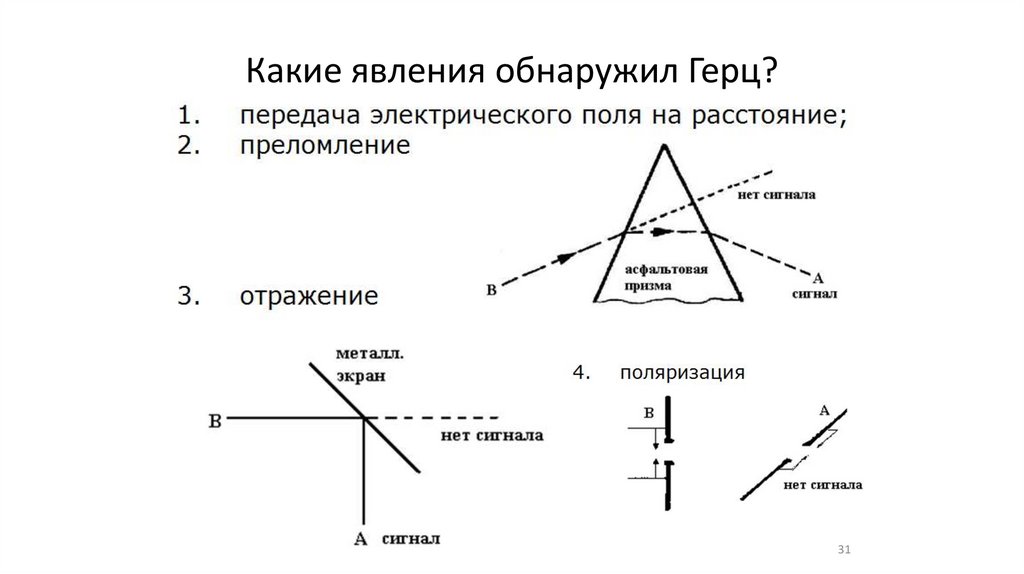
Какие явления обнаружил Герц?31
32.
Диапазоны ЭМВ32
33.
Шкала ЭМВ33
34.
Излучение осциллирующего диполя(1)34
35.
Излучение осциллирующегодиполя(2)
Сферическая волна, W = const
E 2 S const E 2 4 r 2 const
Em r
k ( pr )
r3
sin
Em pm 2
r
E grad E
E0
r
2 E
p 2
t
2 p
t 2
35
36.
Свойства излучения диполя36
37.
Причина ЭМ излучения37
38.
Геометрическая оптика и оптическиеприборы
38
39.
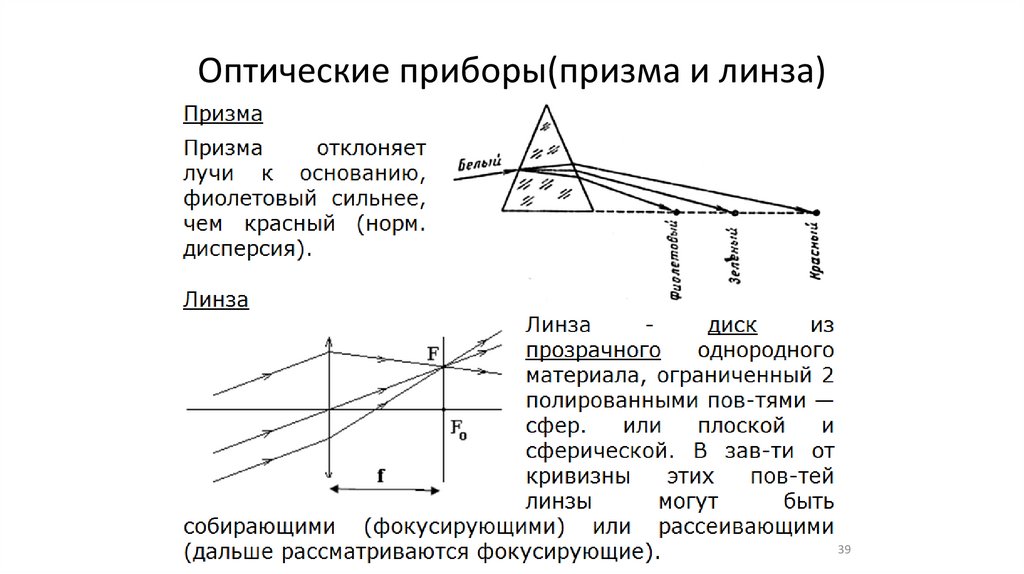
Оптические приборы(призма и линза)39
40.
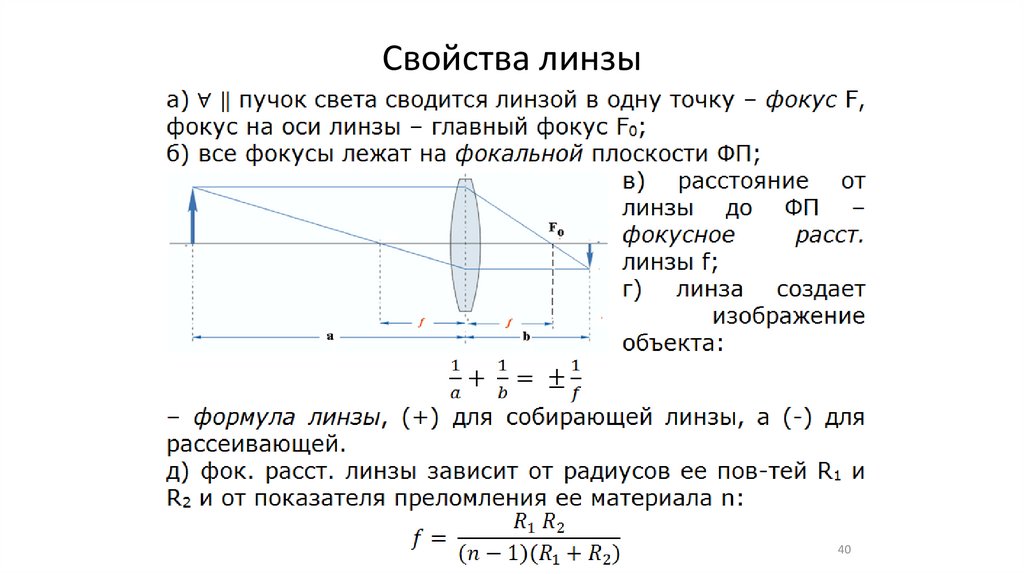
Свойства линзы40
41.
Прямолинейное распространение света41
42.
Независимость световых лучей42
43.
Лекция 3.3. Интерференция•Сложение волн от 2-х источников в одной точке(2,3,4)
•Интерференция(5)
•Опыт Юнга(6,7,8,9,10)
•Временная когерентность(11,12)
•Пространственная когерентность(13,14)
•Радиус и длина когерентности(15)
•Разновидности интерферометров(16,17,18,19)
•Отражение от тонкой пленки(20,21)
•Кольца Ньютона (22,23,24)
43
44.
Сложение волн от 2-х источников водной точке
44
45.
Сложение 2 волн в одной точке45
46.
Интенсивность суммарной волныдвух источников
46
47.
Интерференция47
48.
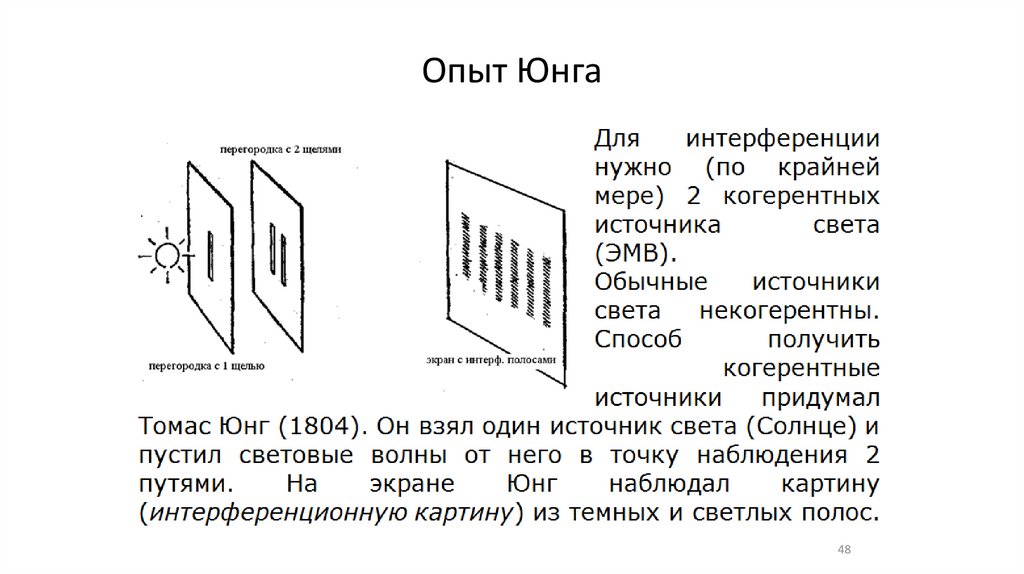
Опыт Юнга48
49.
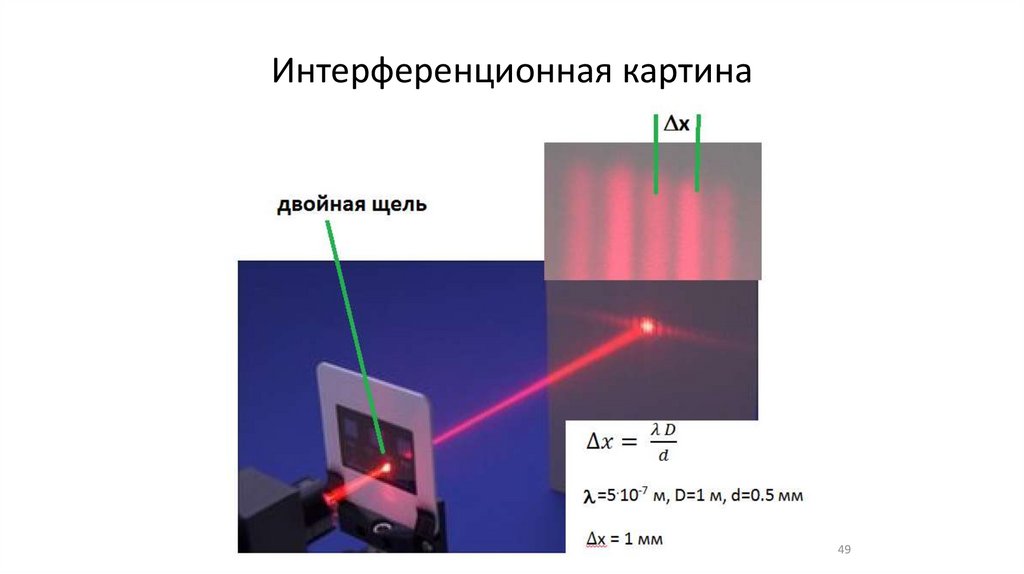
Интерференционная картина49
50.
Интерференционная картина в беломсвете
50
51.
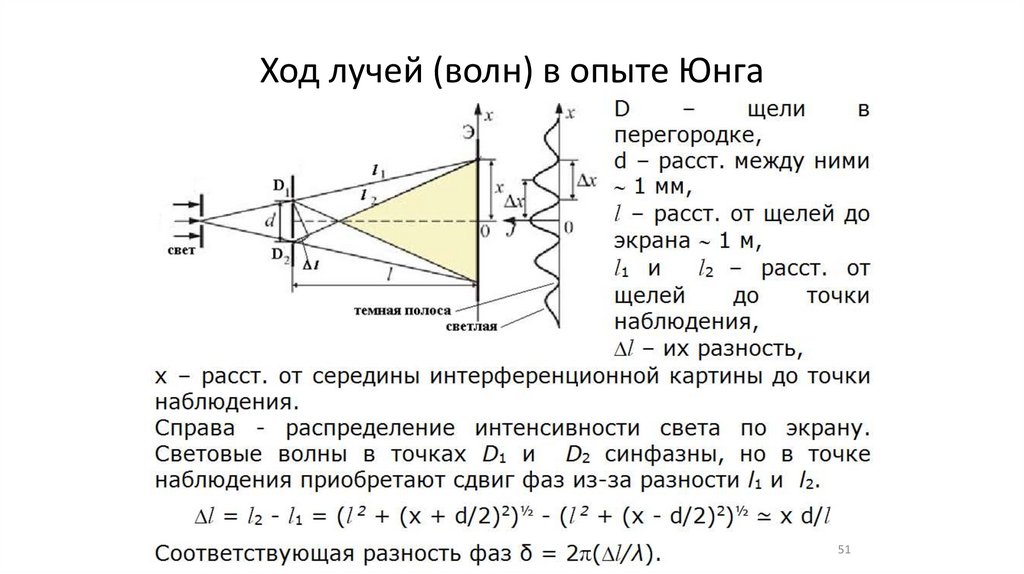
Ход лучей (волн) в опыте Юнга51
52.
Интерференционные полосы52
53.
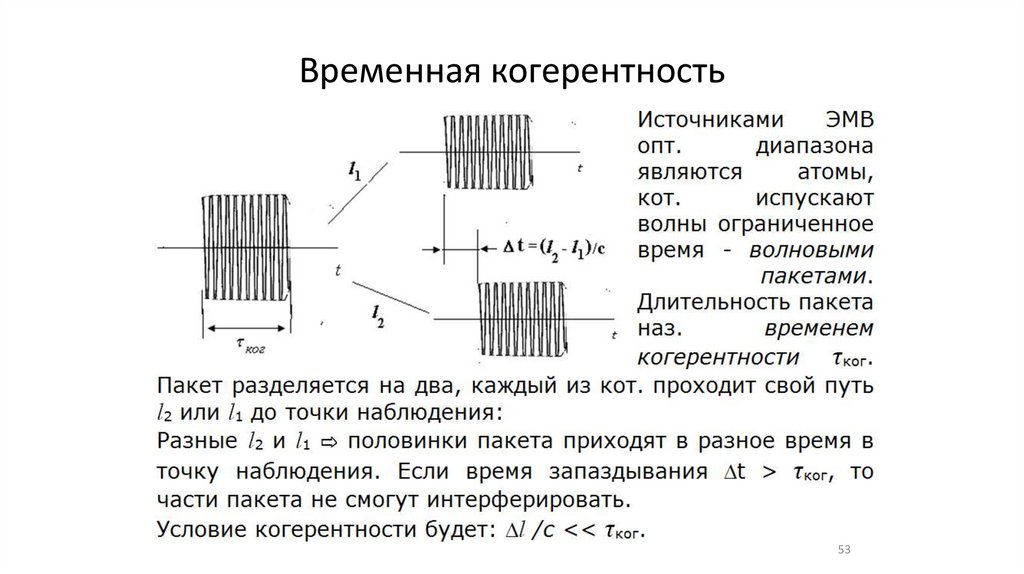
Временная когерентность53
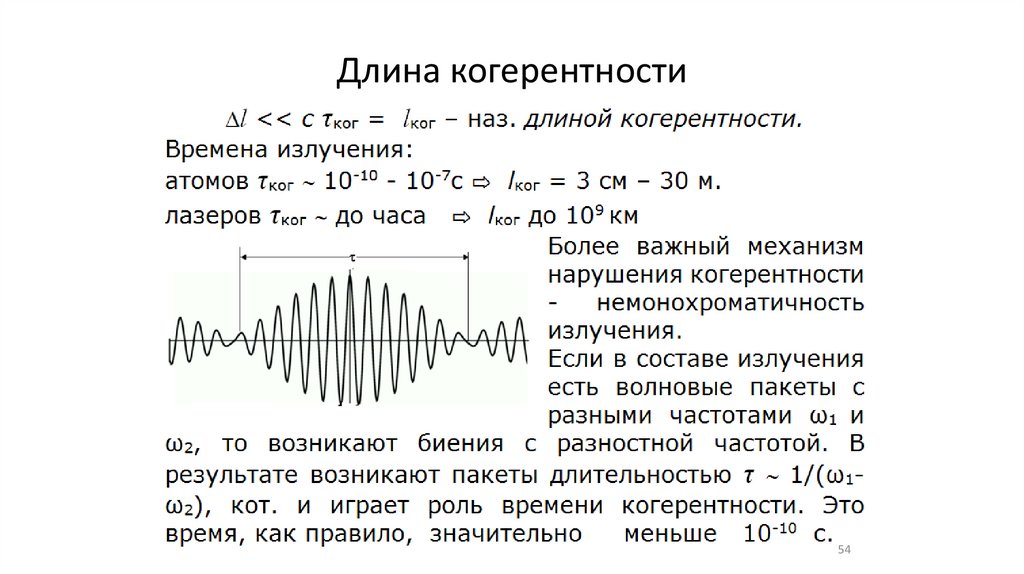
54.
Длина когерентности54
55.
Источник света конечных размеров55
56.
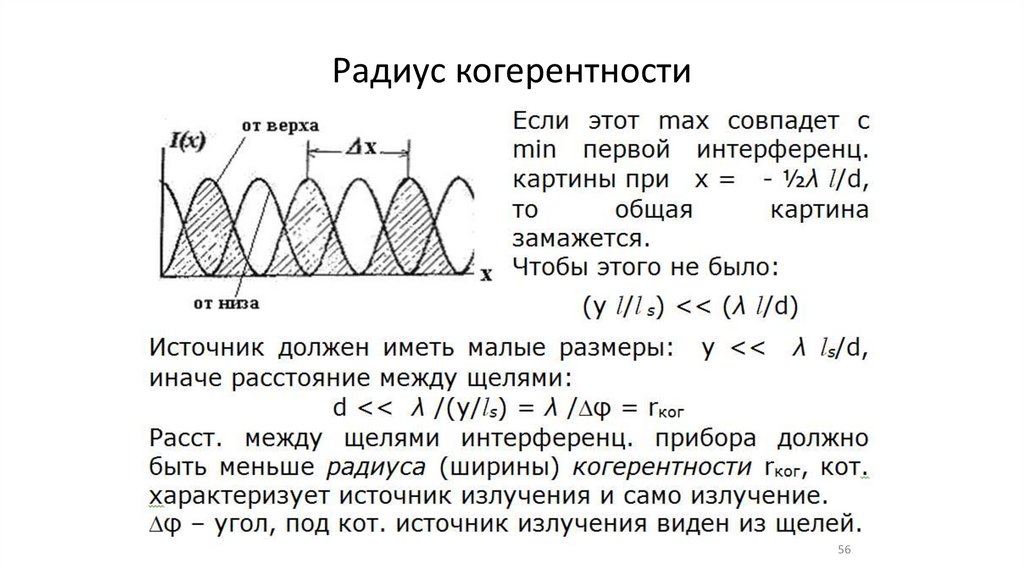
Радиус когерентности56
57.
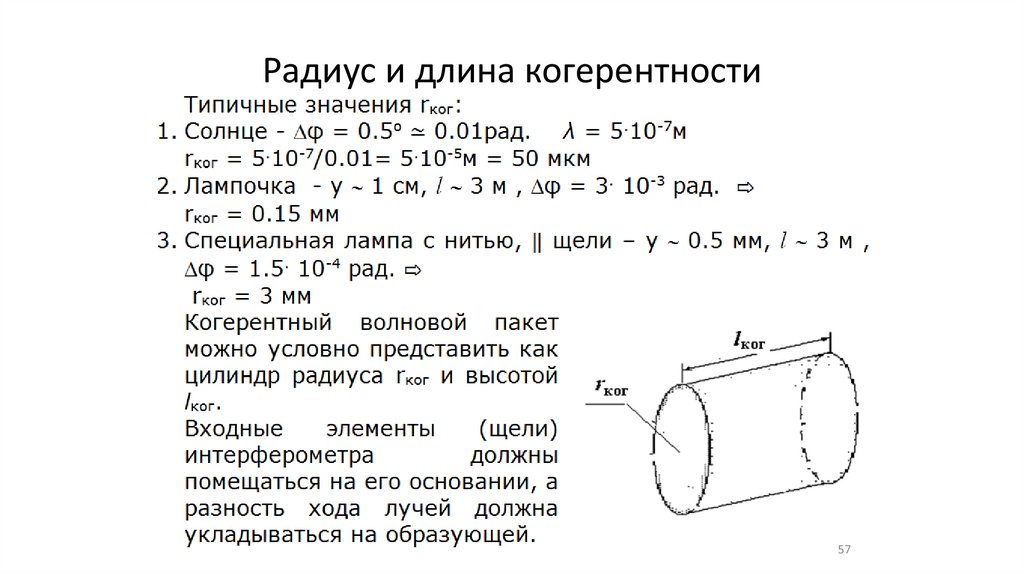
Радиус и длина когерентности57
58.
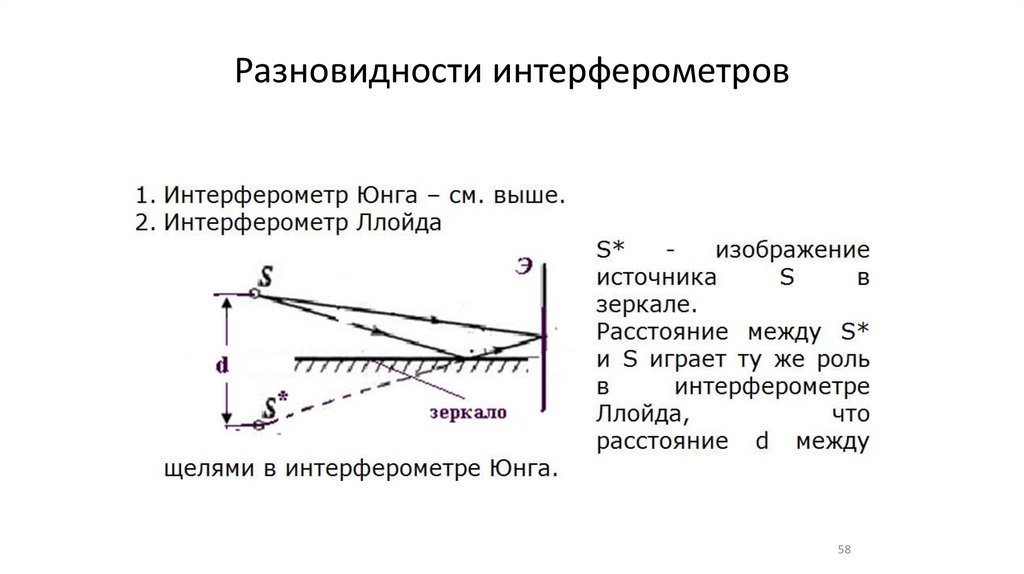
Разновидности интерферометров58
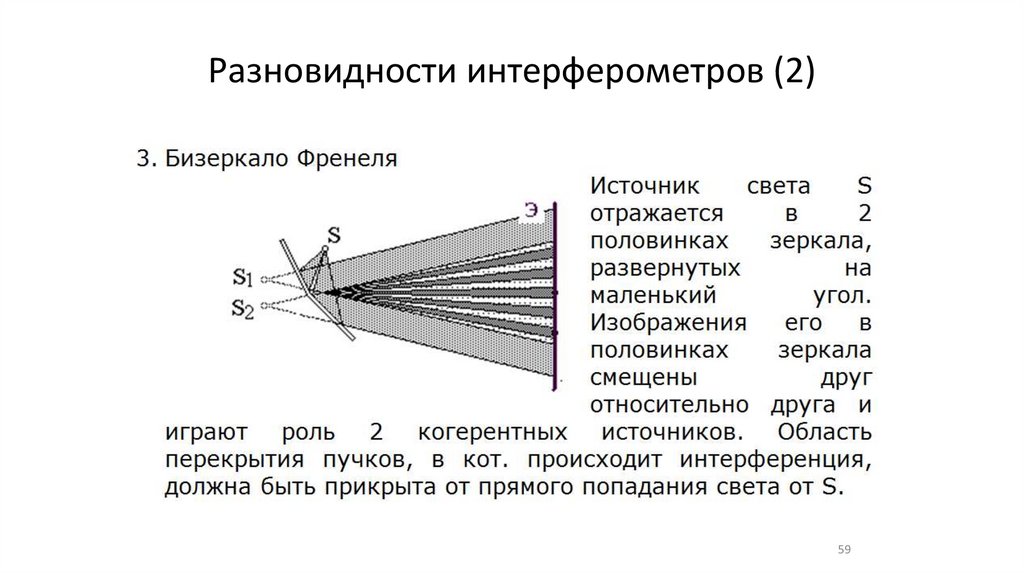
59.
Разновидности интерферометров (2)59
60.
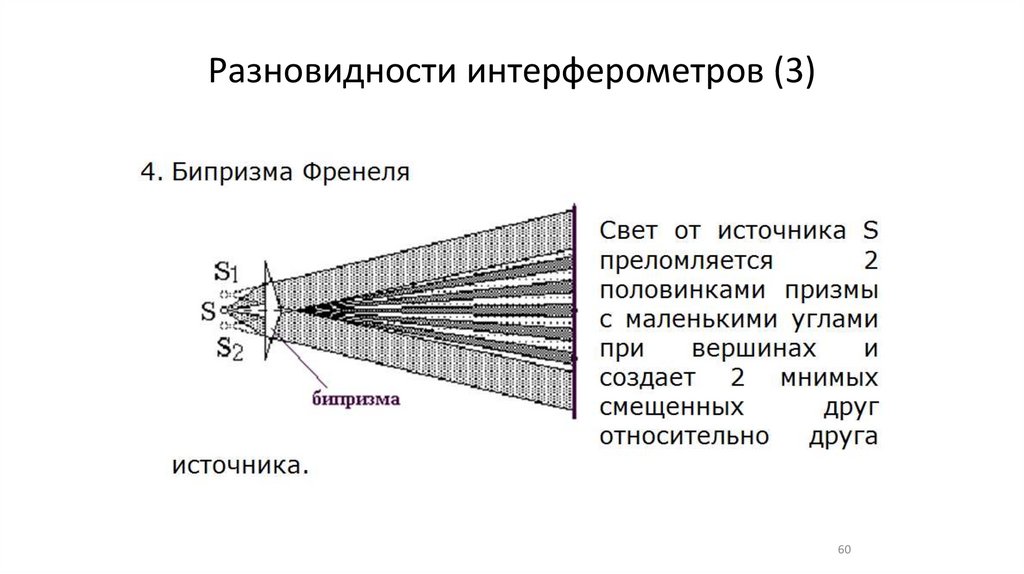
Разновидности интерферометров (3)60
61.
Разновидности интерферометров (4)61
62.
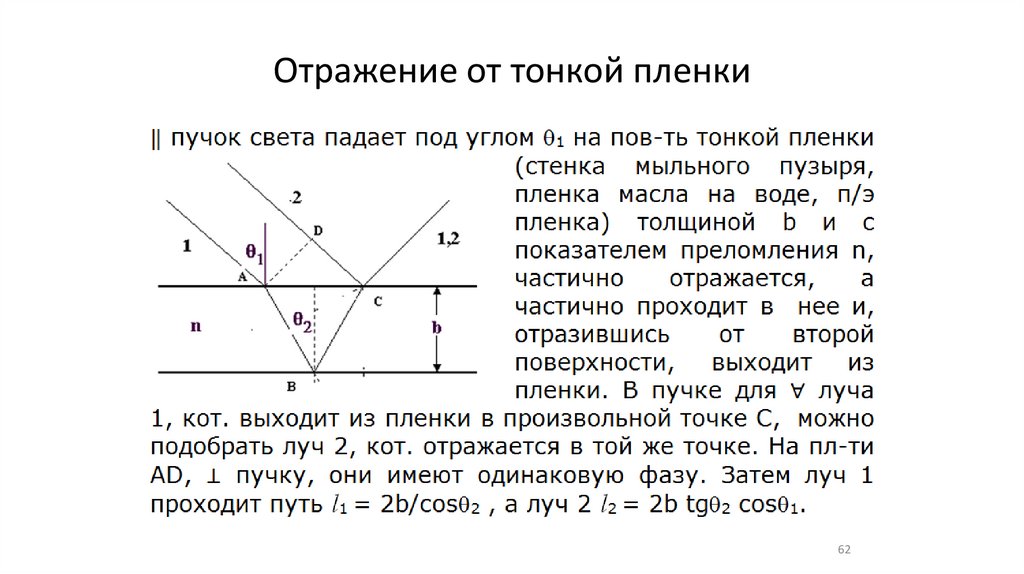
Отражение от тонкой пленки62
63.
Max и min интерференции63
64.
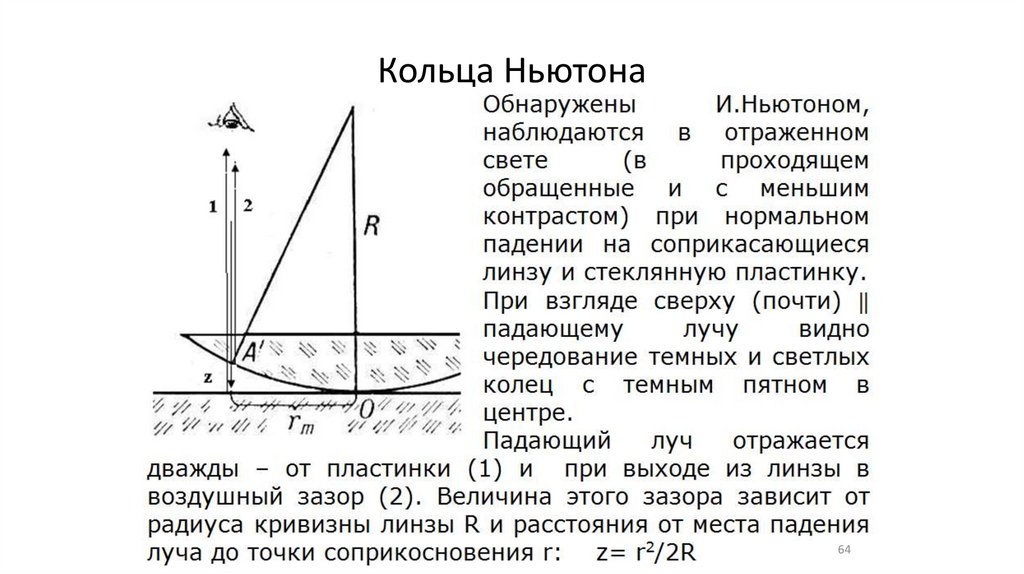
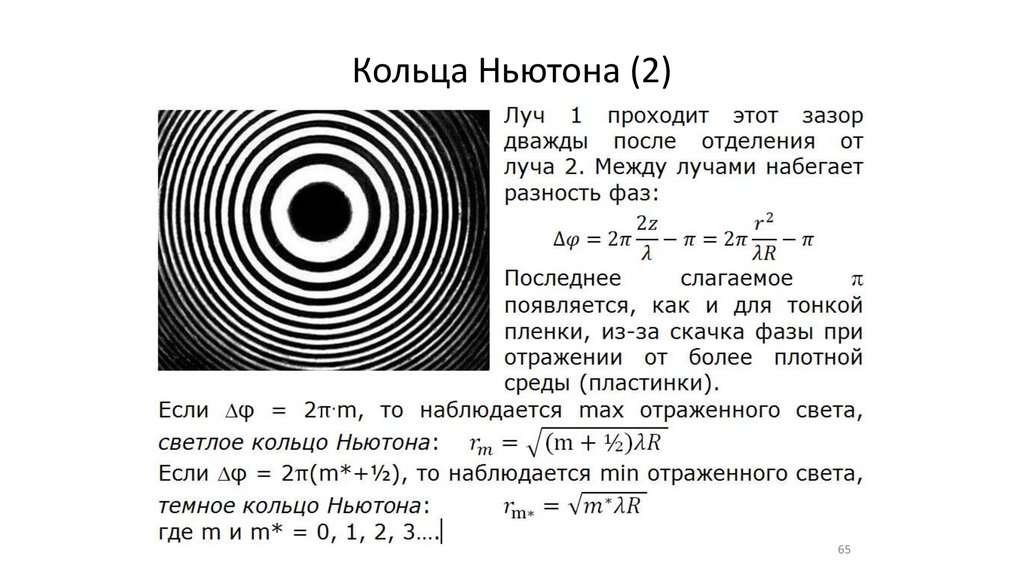
Кольца Ньютона64
65.
Кольца Ньютона (2)65
66.
Кольца Ньютона (3)66
67.
Лекция 3.4. ДифракцияФраунгофера
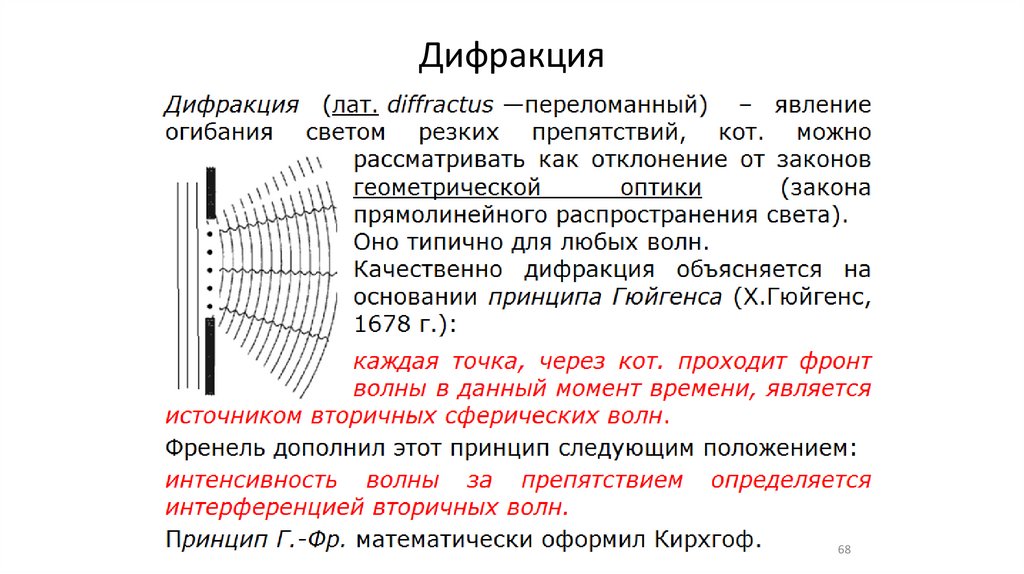
•Дифракция(2,3)
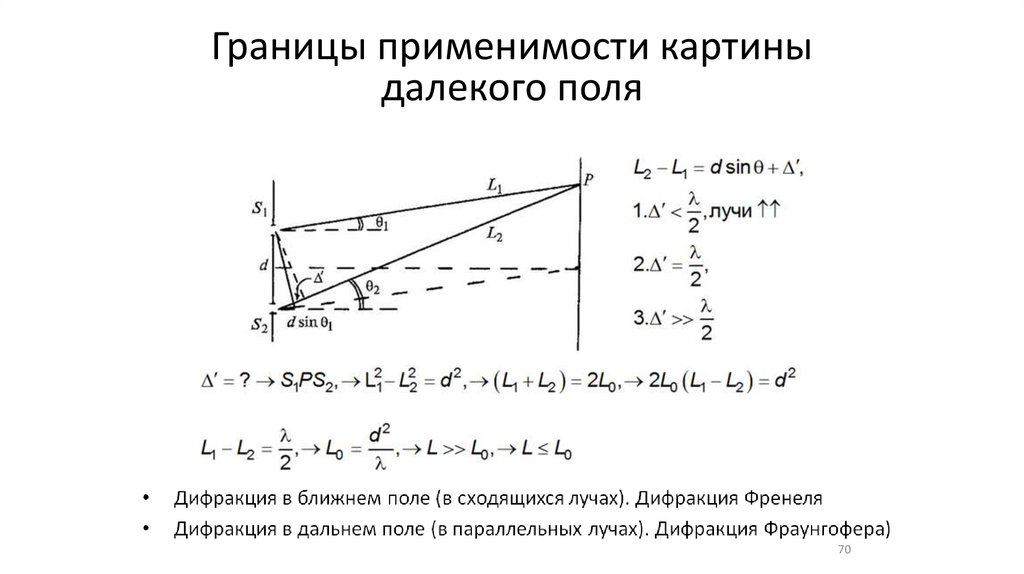
•Границы применимости картины далекого поля (4,5)
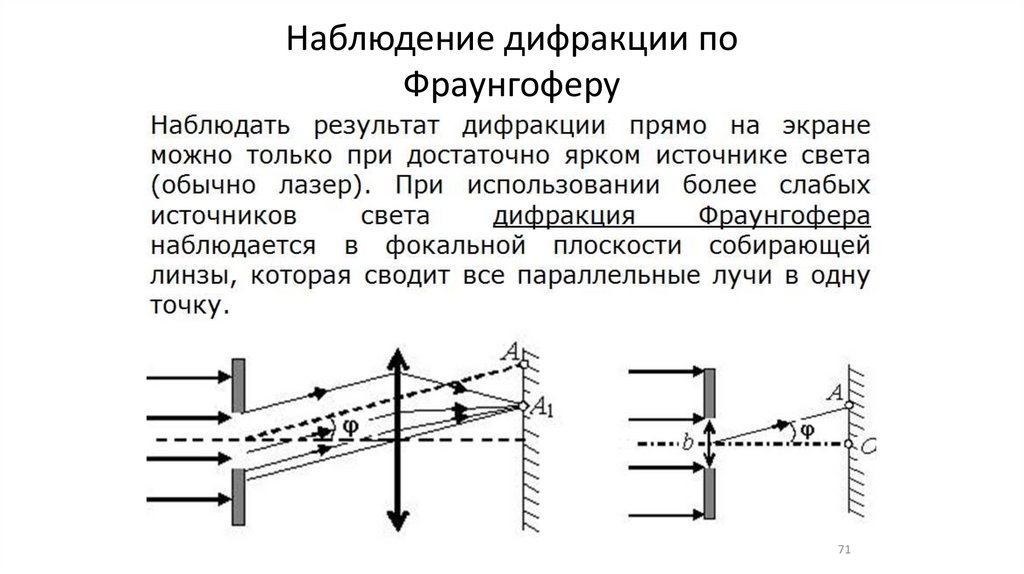
•Дифракция от одной щели (6,7)
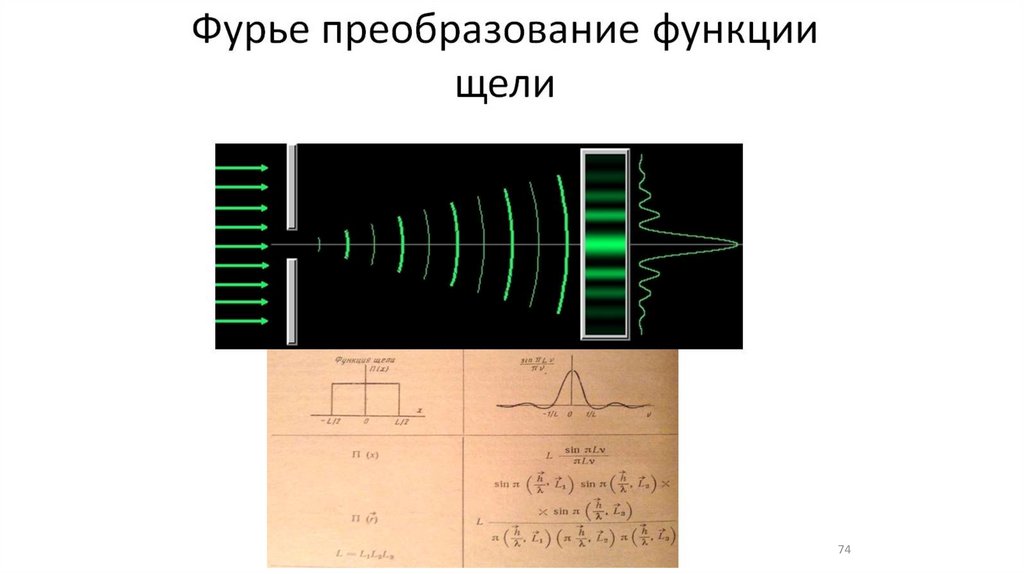
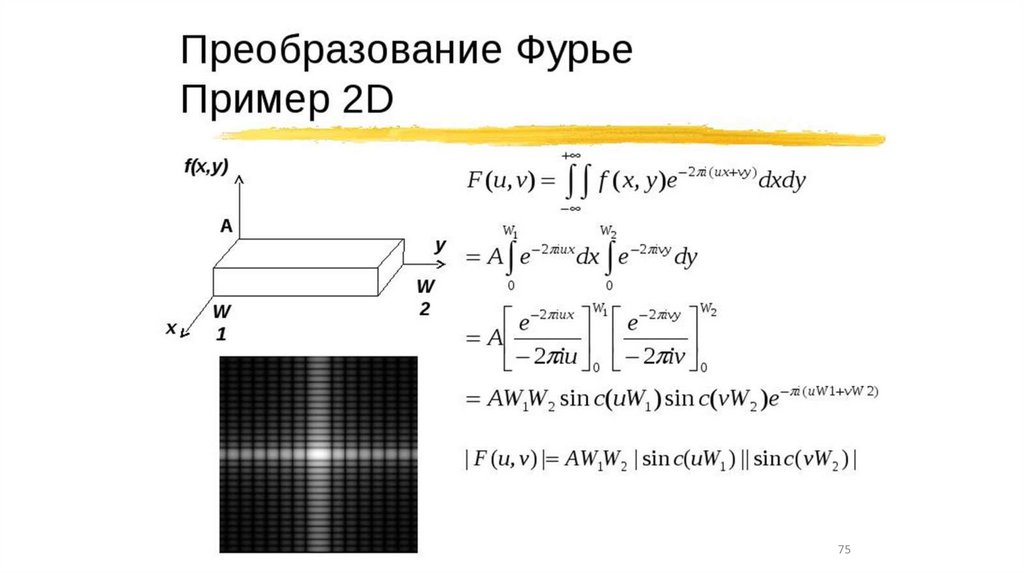
•Фурье преобразование функции щели (8,9,10)
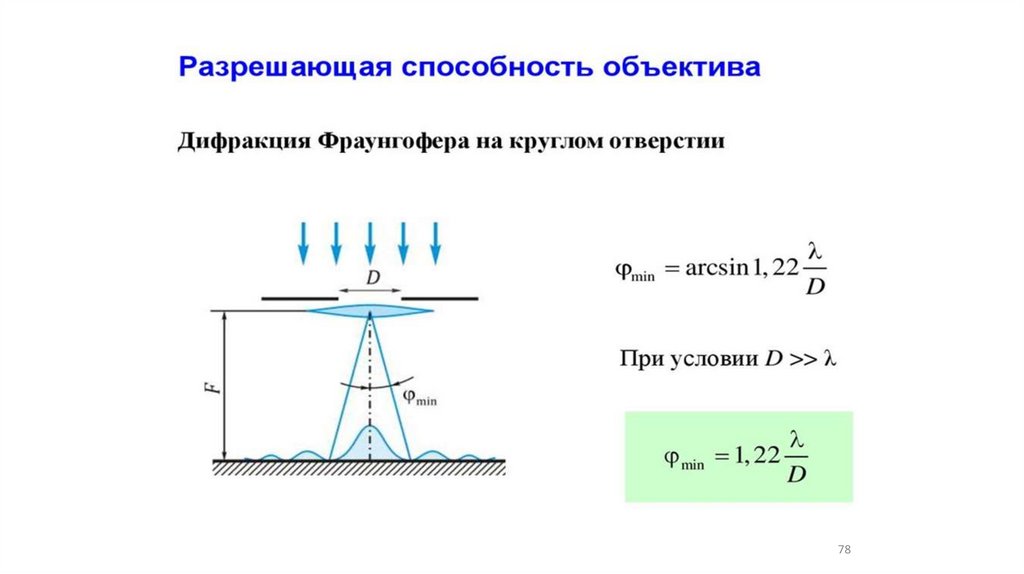
•Дифракция Фраунгофера на круглом отверстии (11,12)
•Дифракция на двух щелях (13,14)
•Дифракция на симметричной системе из N щелей(15,16)
•Дифракционная решетка (17,18,19,20)
•Свойства дифракционной картины от дифракционной
решетки(21,22,23, 24, 25)
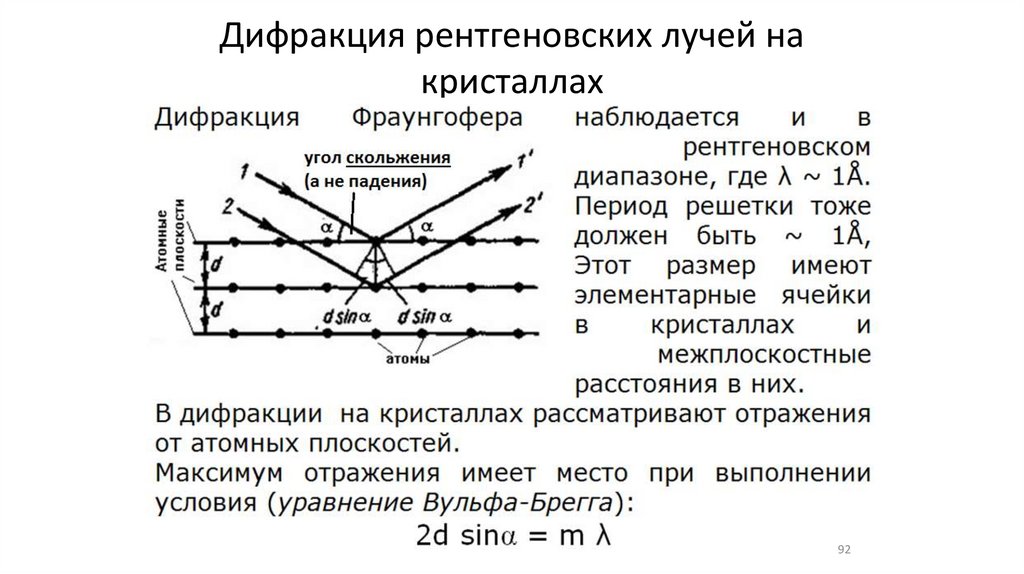
•Дифракция рентгеновских лучей на кристаллах(26)
67
68.
Дифракция68
69.
6970.
Границы применимости картиныдалекого поля
70
71.
Наблюдение дифракции поФраунгоферу
71
72.
Дифракция на одной щели72
73.
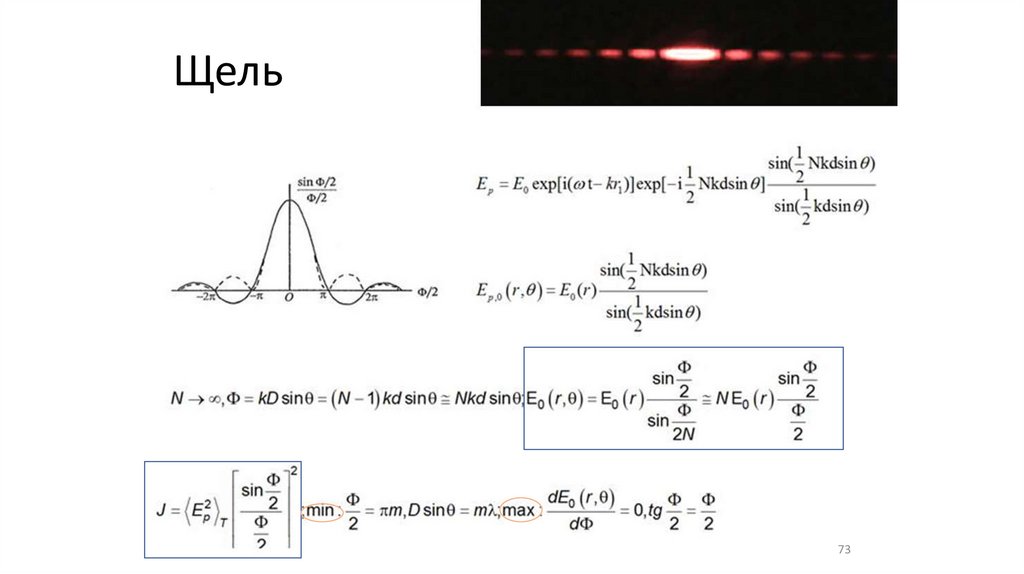
Щель73
74.
7475.
7576.
7677.
7778.
7879.
Дифракция на двух щелях+
79
80.
Дифракционная картина от двухщелей
80
81.
Дифракция на симметричнойсистеме из N щелей
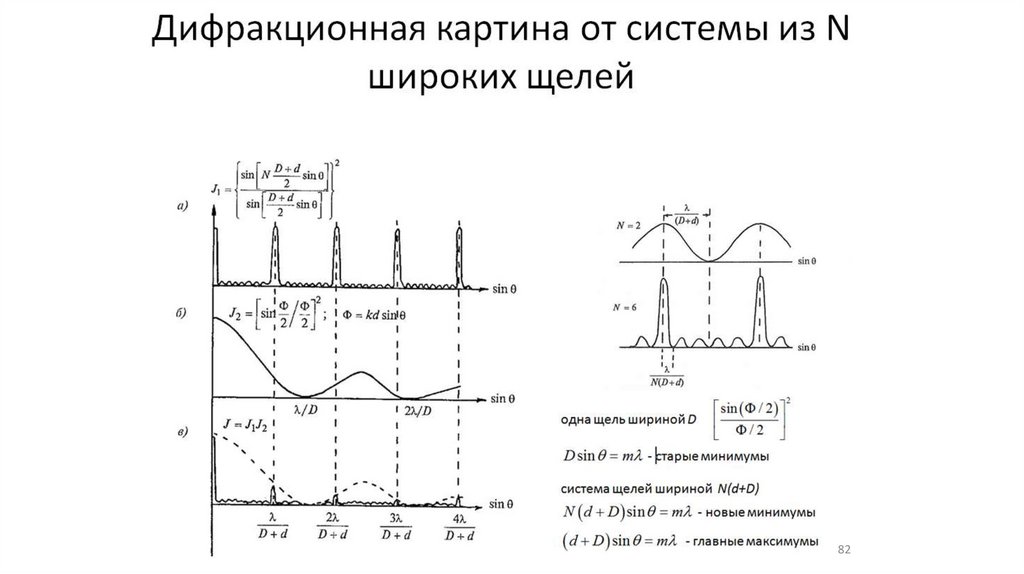
81
82.
8283.
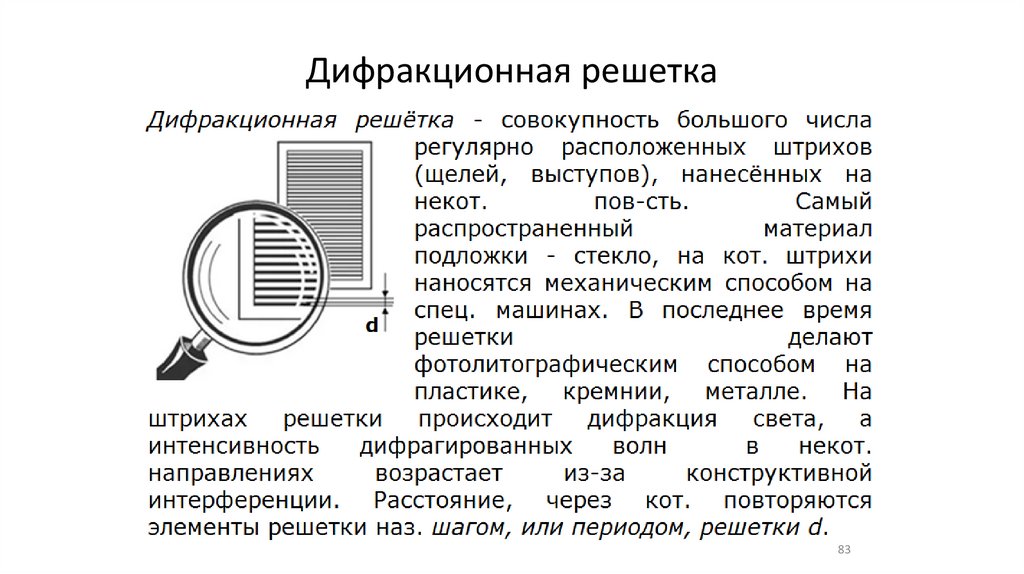
Дифракционная решетка83
84.
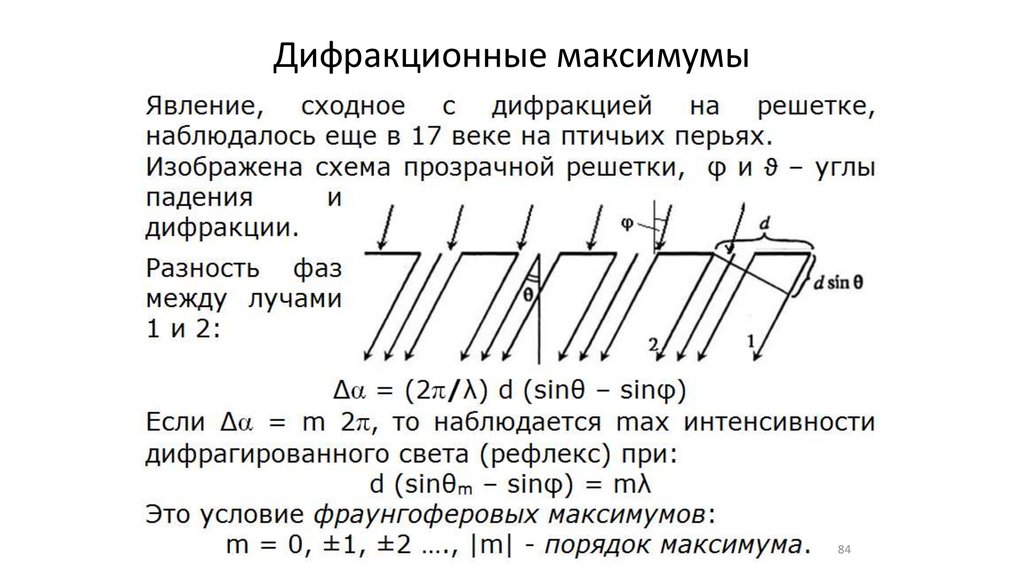
Дифракционные максимумы84
85.
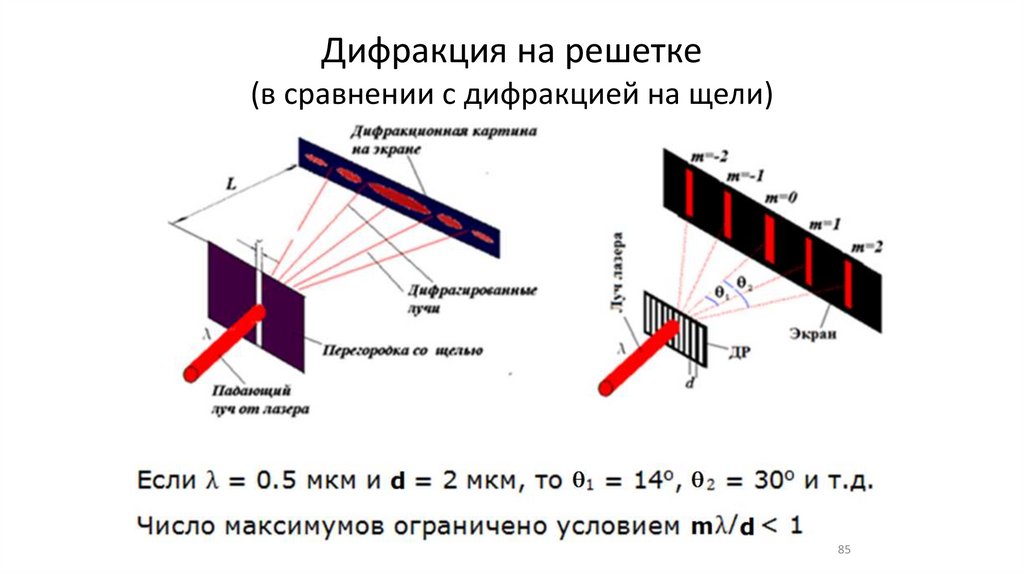
Дифракция на решетке(в сравнении с дифракцией на щели)
85
86.
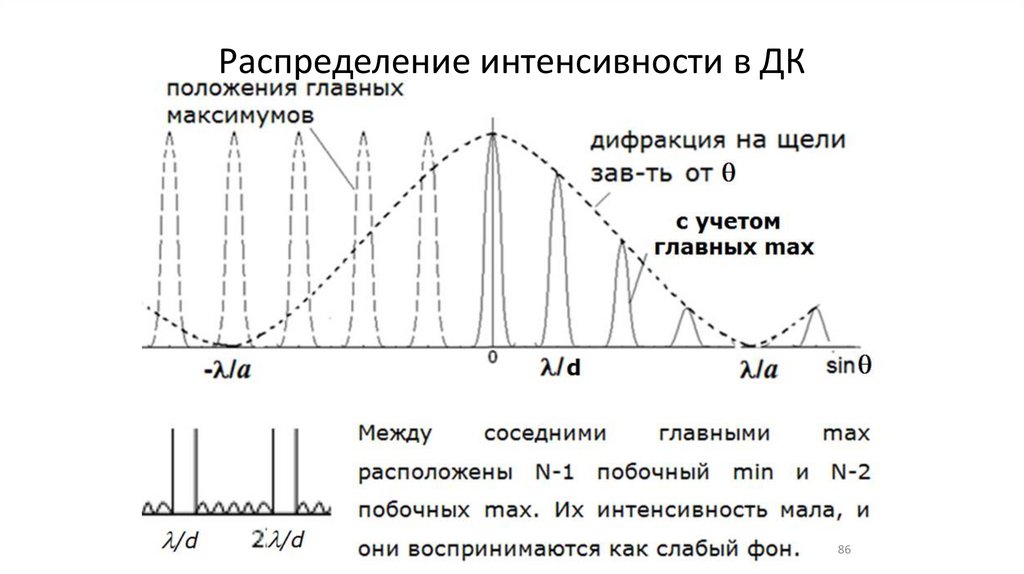
Распределение интенсивности в ДК86
87.
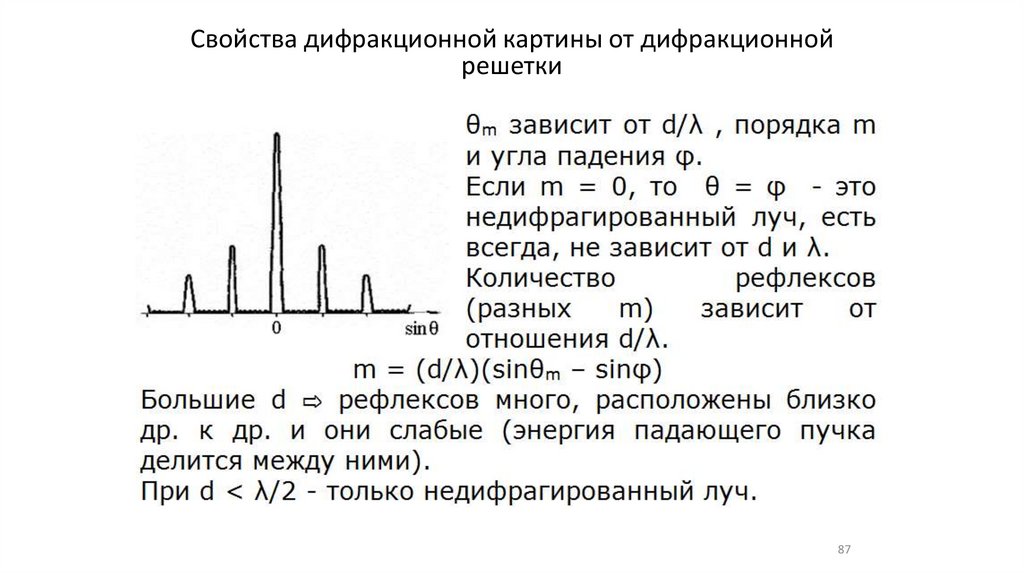
Свойства дифракционной картины от дифракционнойрешетки
87
88.
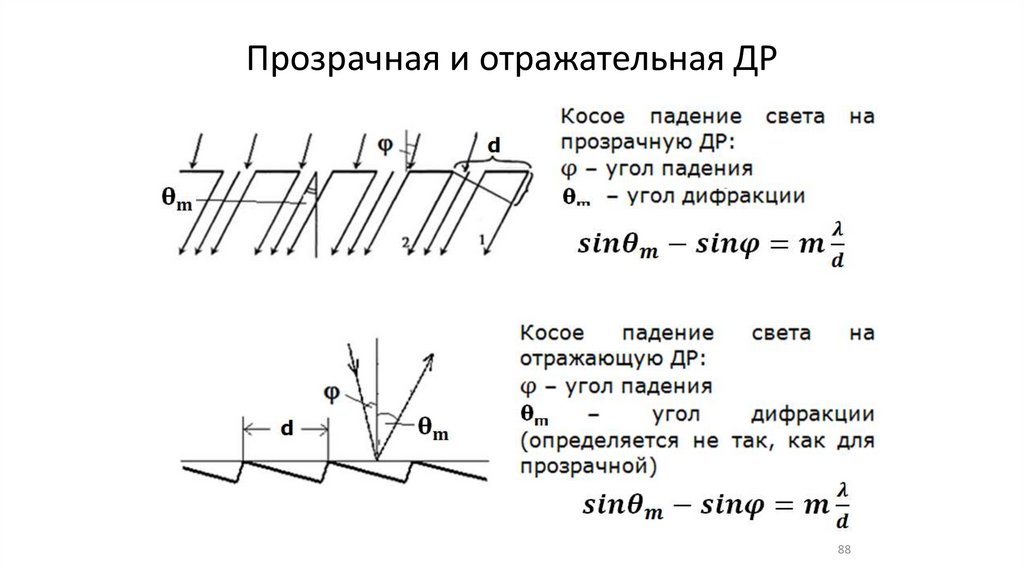
Прозрачная и отражательная ДР88
89.
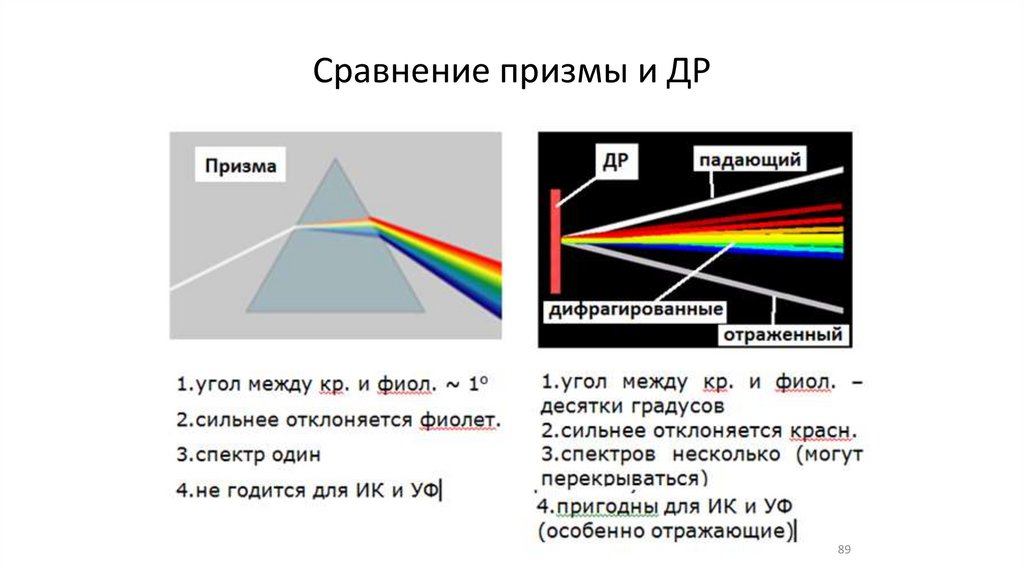
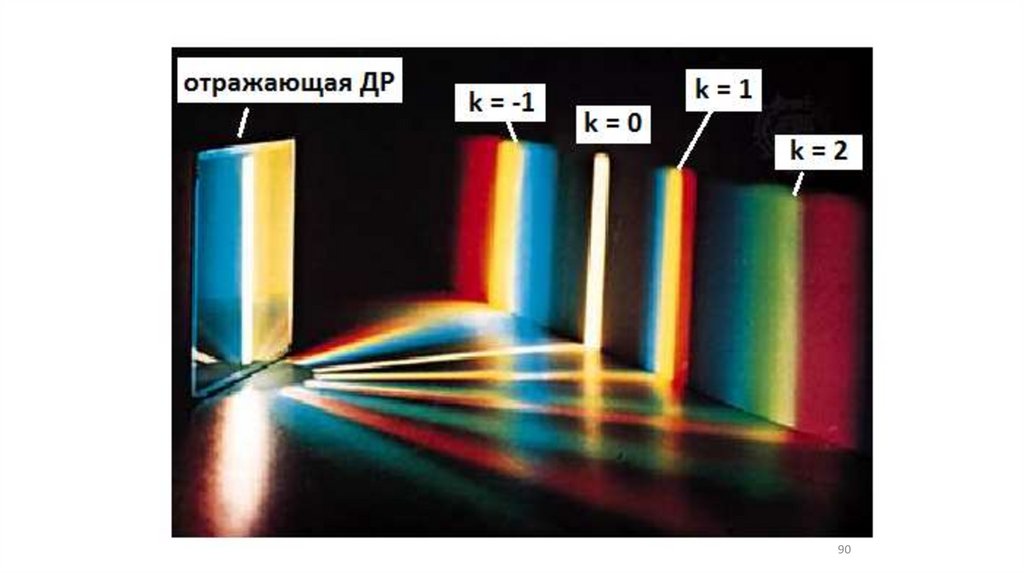
Сравнение призмы и ДР89
90.
9091.
9192.
Дифракция рентгеновских лучей накристаллах
92
93.
Лекция 3.5 ДифракцияФренеля
o5.1 Характеристики спектральных приборов (2,3)
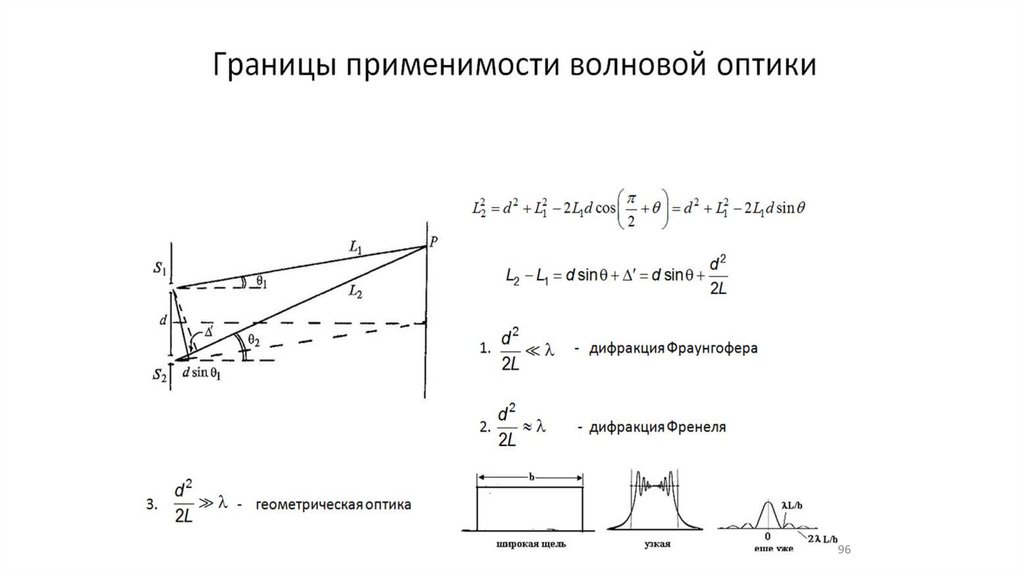
o 5.2 Границы применимости в волновой оптике (4)
o 5.3 Дифракция Френеля (5,6)
I.
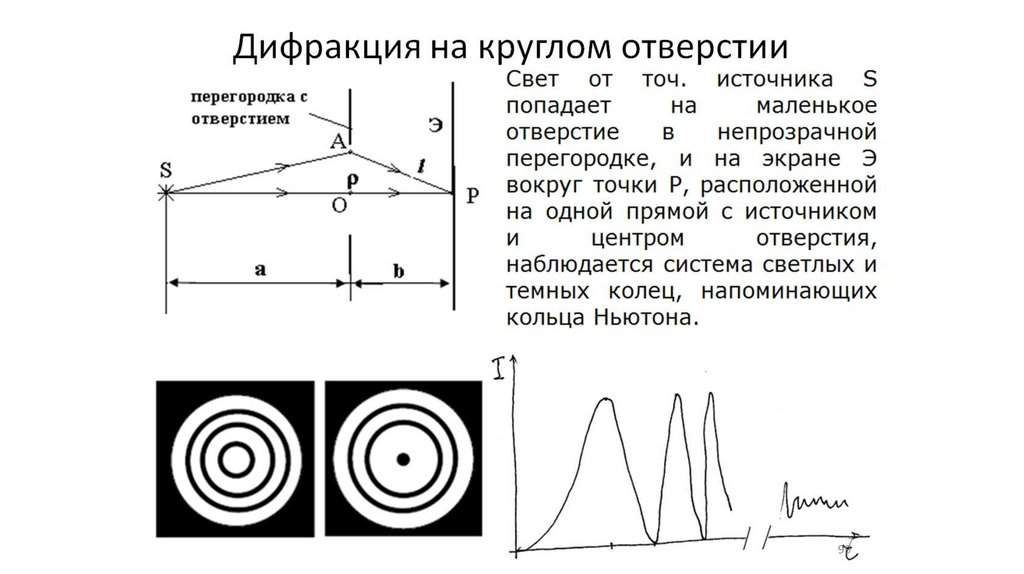
Дифракция на круглом отверстии (7 -10)
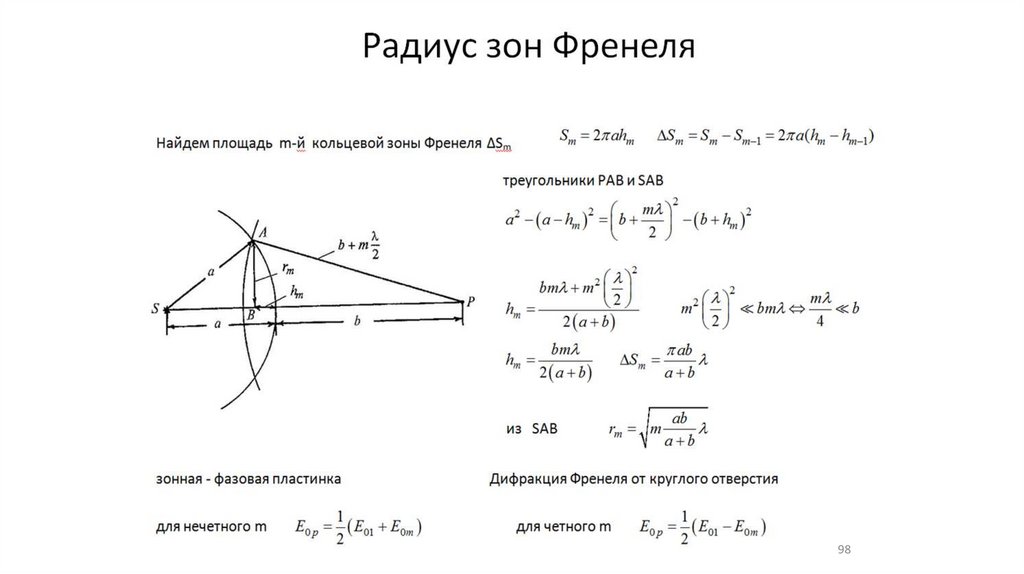
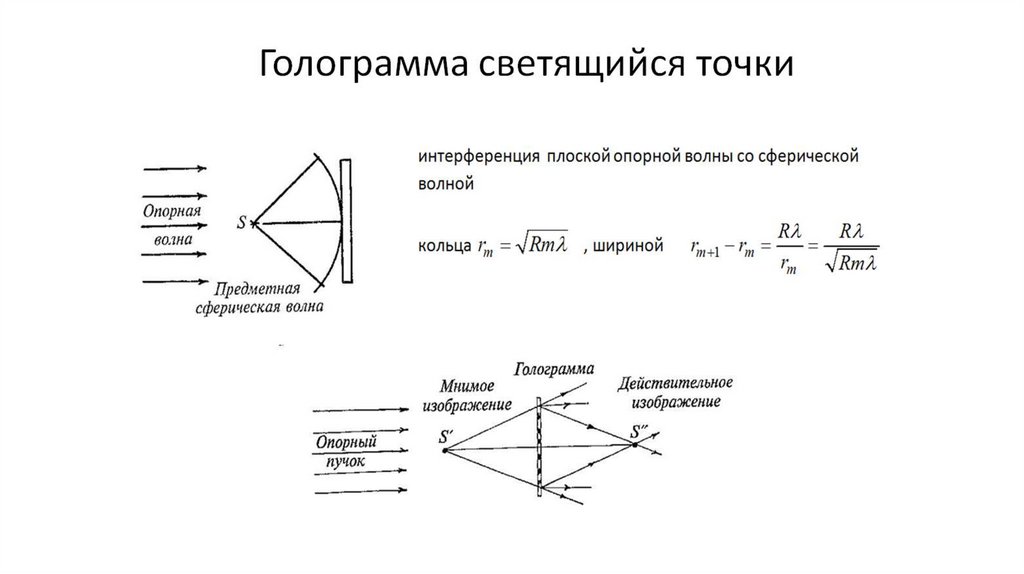
II. Зоны Френеля (11 -17)
III. Зонная пластинка Френеля (18)
IV. Дифракция на круглом диске (19,20)
93
94.
9495.
9596.
9697.
9798.
9899.
99100.
100101.
101102.
Круговая диаграмма Френеля102
103.
Зоны Френеля103
104.
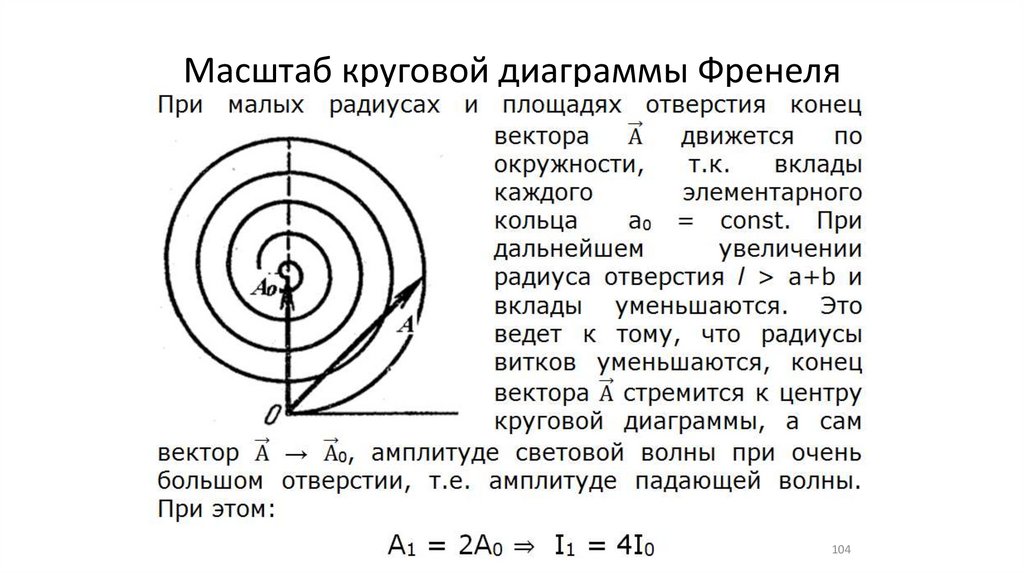
Масштаб круговой диаграммы Френеля104
105.
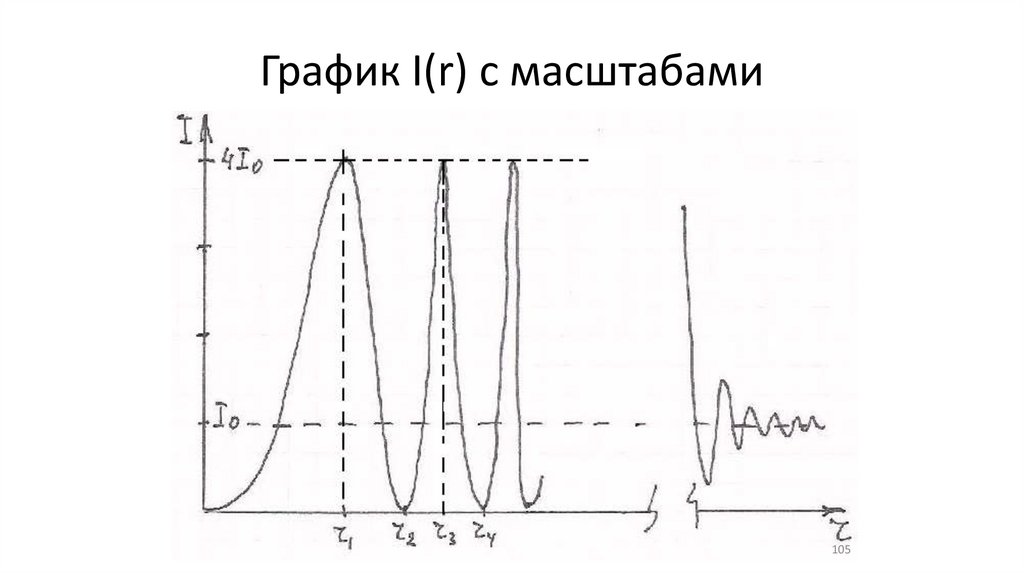
График I(r) с масштабами105
106.
Изменение числа зон Френеля вотверстии
106
107.
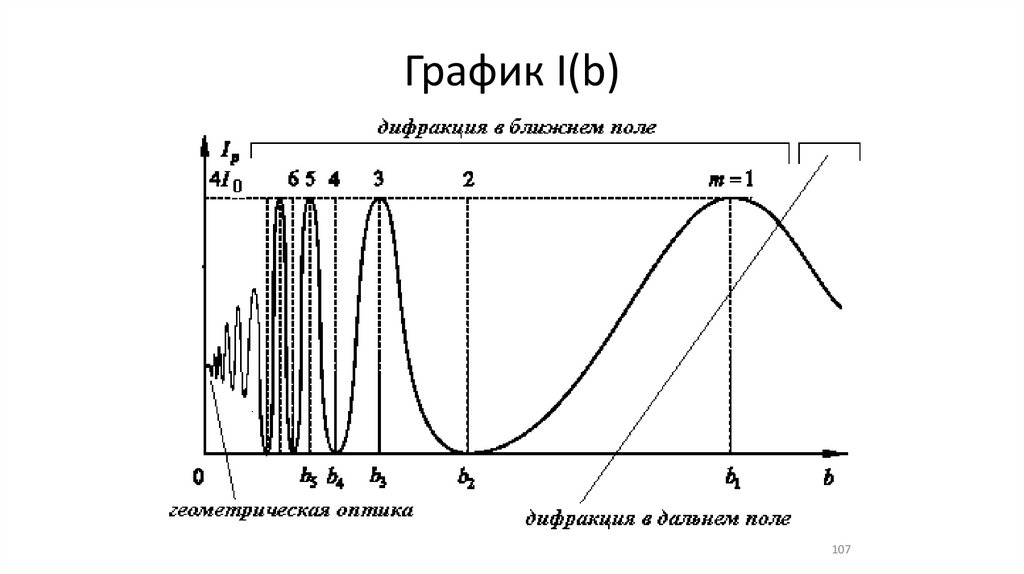
График I(b)107
108.
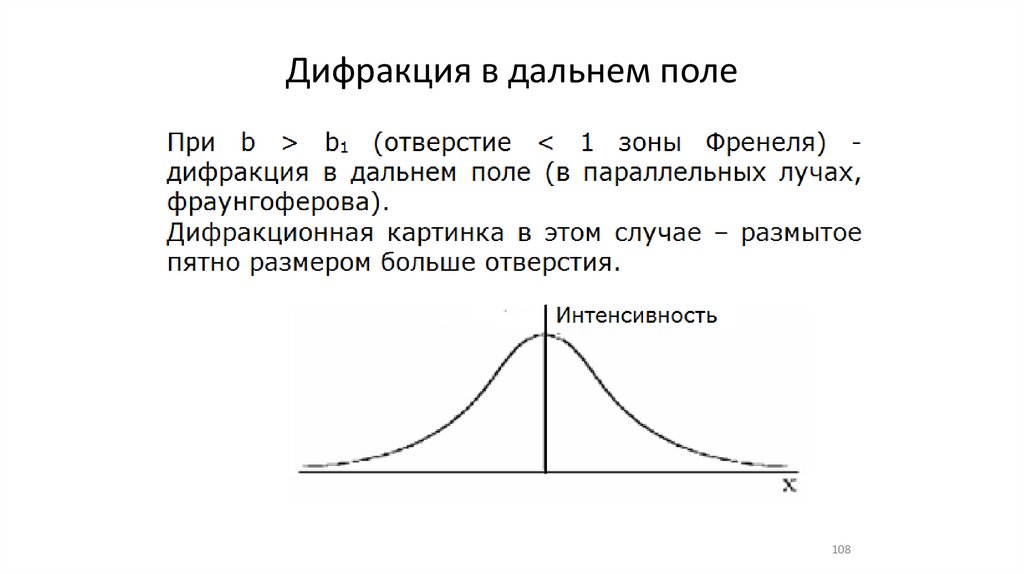
Дифракция в дальнем поле108
109.
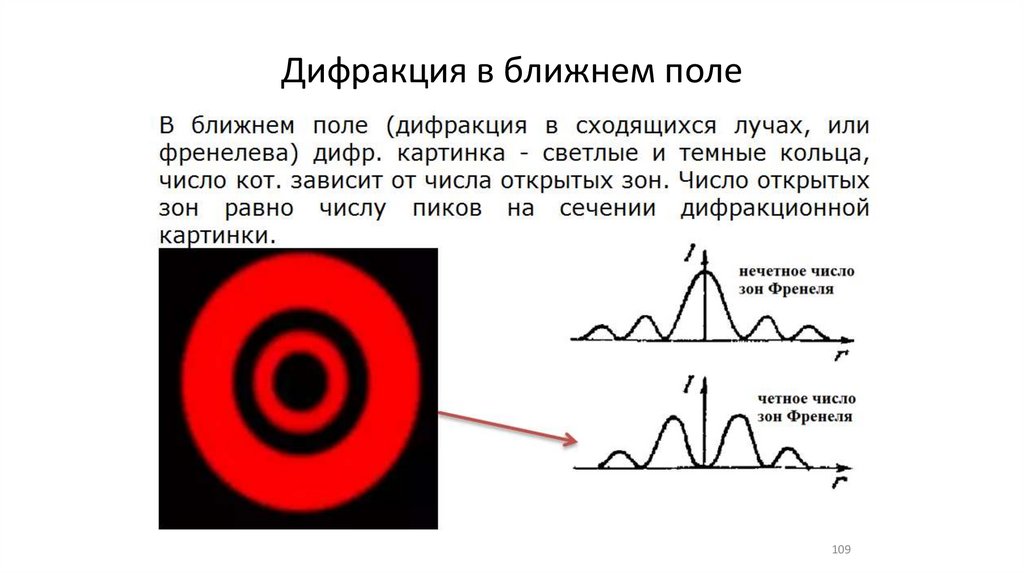
Дифракция в ближнем поле109
110.
Зонная пластинка Френеля110
111.
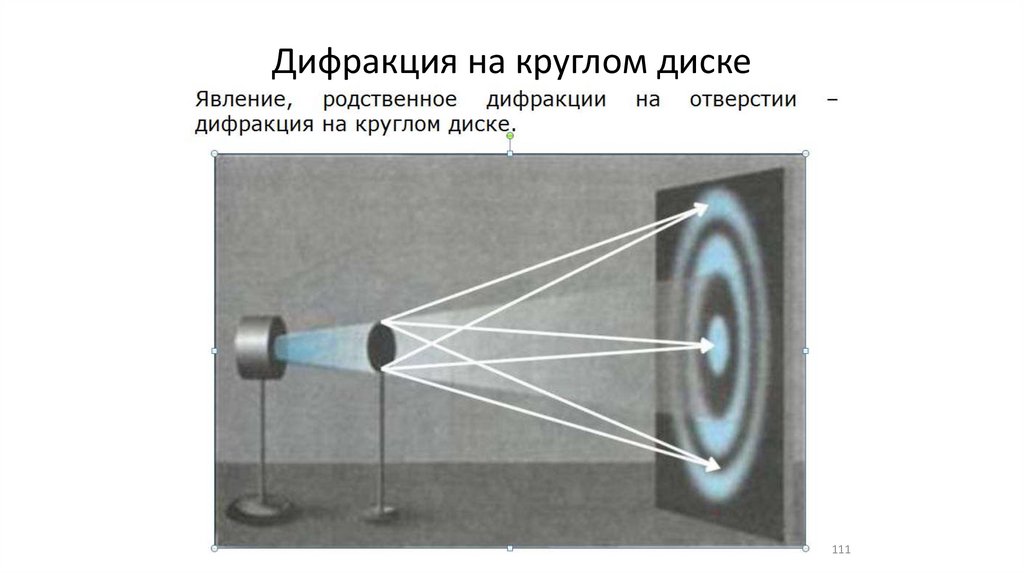
Дифракция на круглом диске111
112.
Пуассоново пятно112
113.
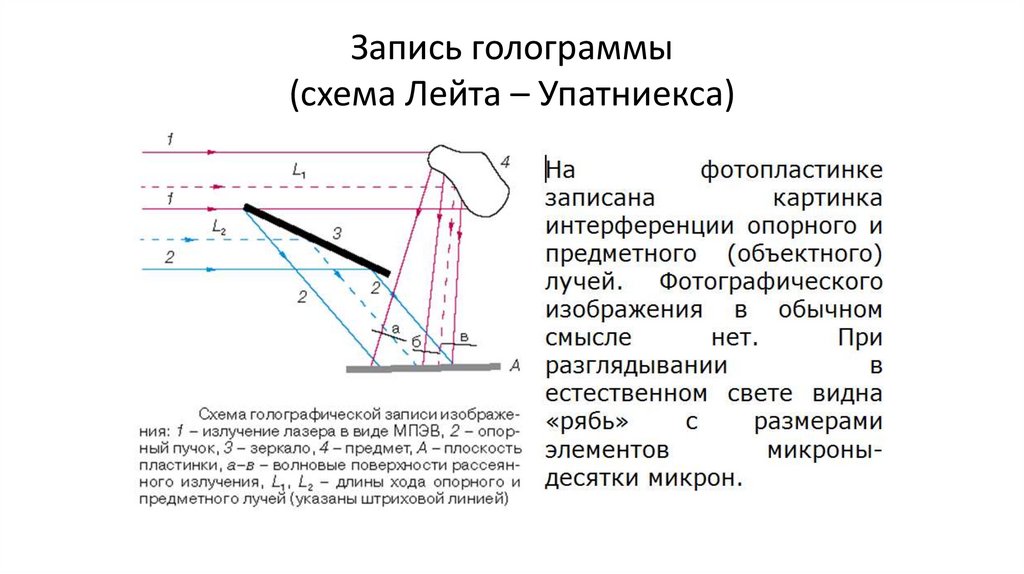
Запись голограммы(схема Лейта – Упатниекса)
114.
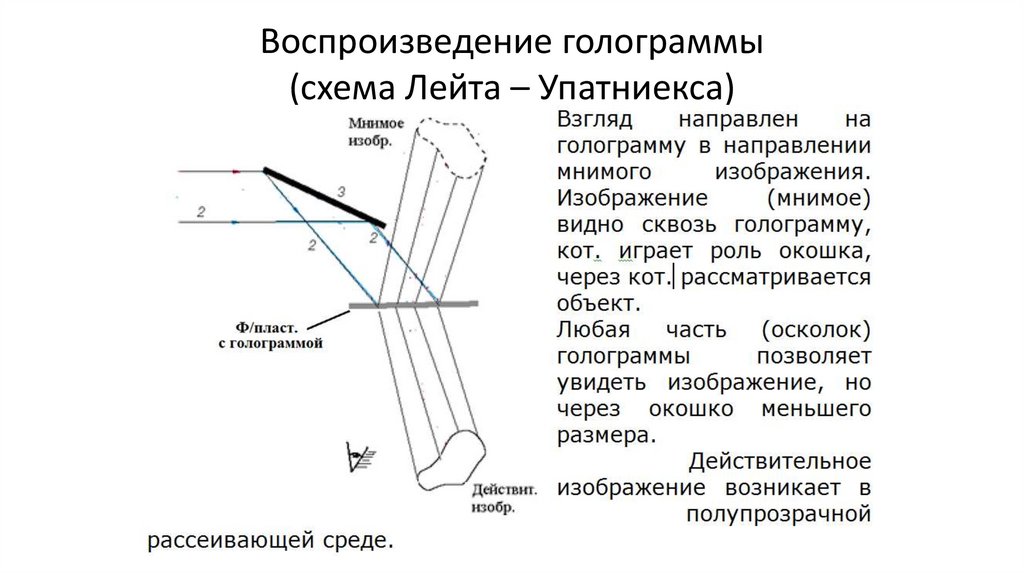
Воспроизведение голограммы(схема Лейта – Упатниекса)
115.
116.
Лекция 3.6 Распространениеэлектромагнитной волны в
диэлектрической среде
•Взаимодействие ЭМВ с веществом (2)
•Распространение ЭМВ в изотропной диэлектрической среде (3)
•Дисперсионное уравнение (4)
•Законы отражения и преломления света (5)
•ЭМВ на границе раздела 2 сред (6,7,8,9,10)
•Законы отражения и преломления (11, 12)
•Формулы Френеля (13,14,15,16,17,18)
•Коэффициенты отражения и пропускания (19,20,21)
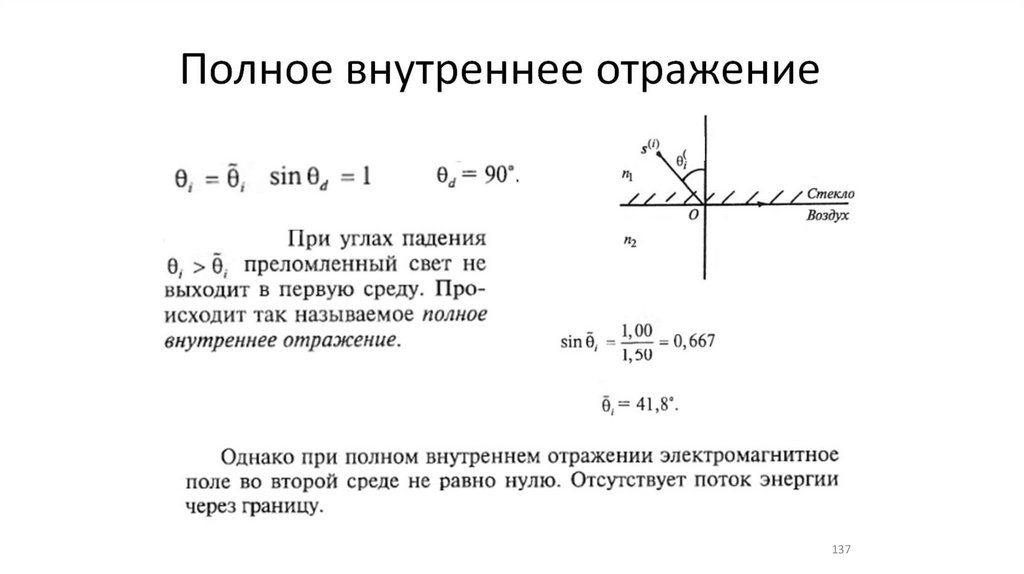
•Полное внутреннее отражение (22)
116
117.
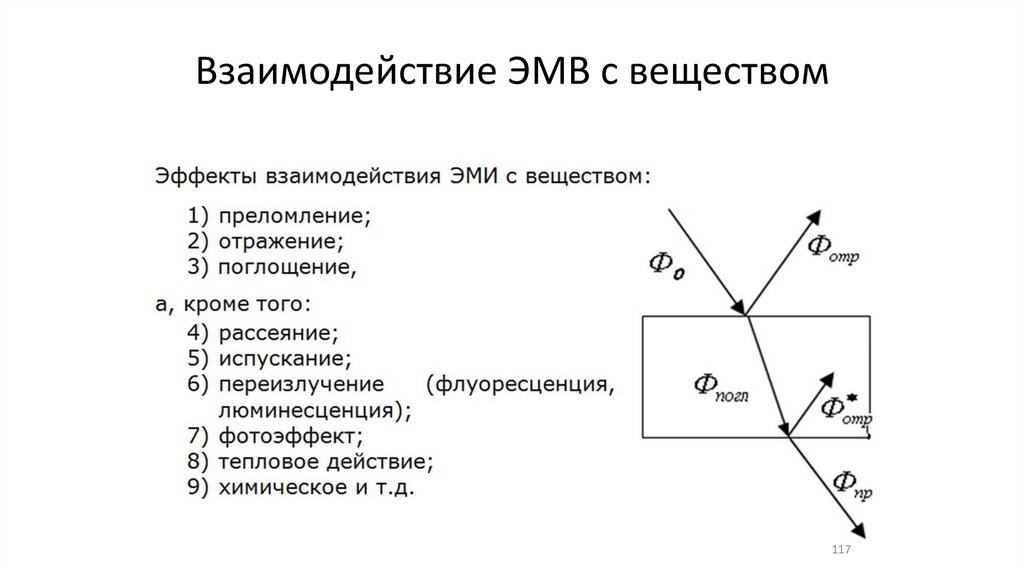
Взаимодействие ЭМВ с веществом117
118.
118119.
119120.
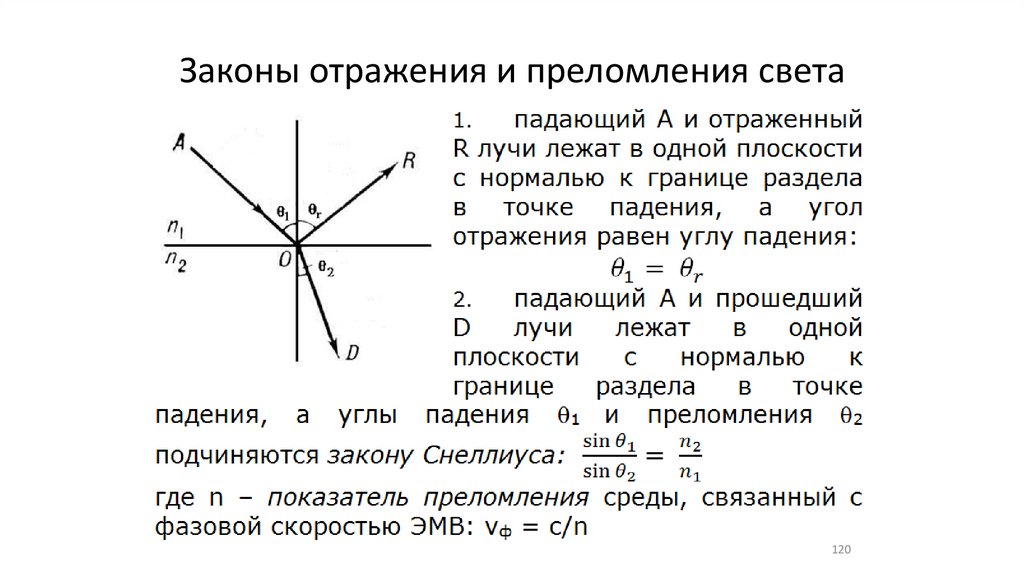
Законы отражения и преломления света120
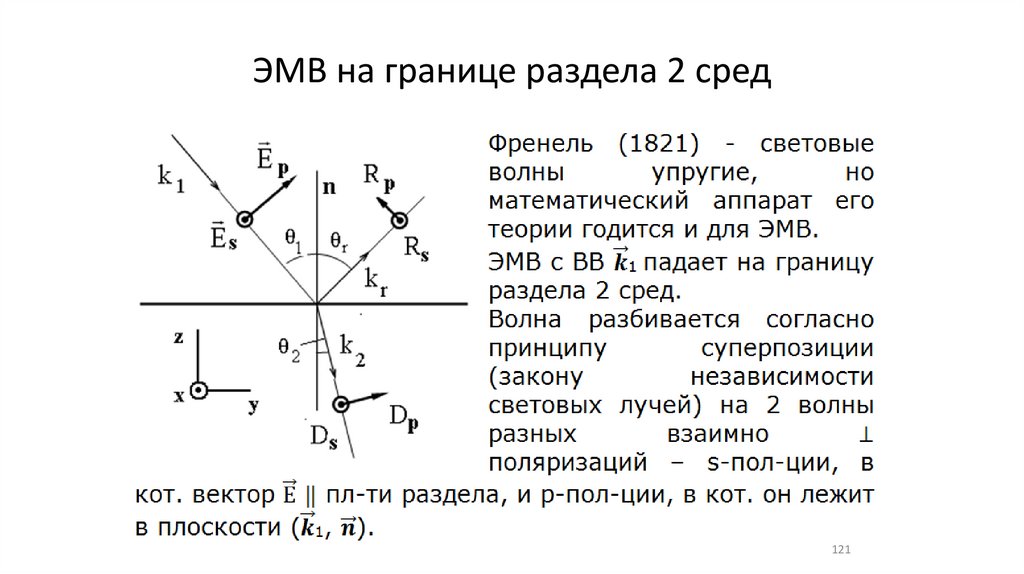
121.
ЭМВ на границе раздела 2 сред121
122.
ЭМВ на границе раздела 2 сред (2)122
123.
Уравнения электрических компонент волн123
124.
ЭМВ на границе раздела 2 сред (3)124
125.
Плоскость падения125
126.
Законы отражения и преломления126
127.
Свойства решений127
128.
128129.
129130.
Формулы Френеля130
131.
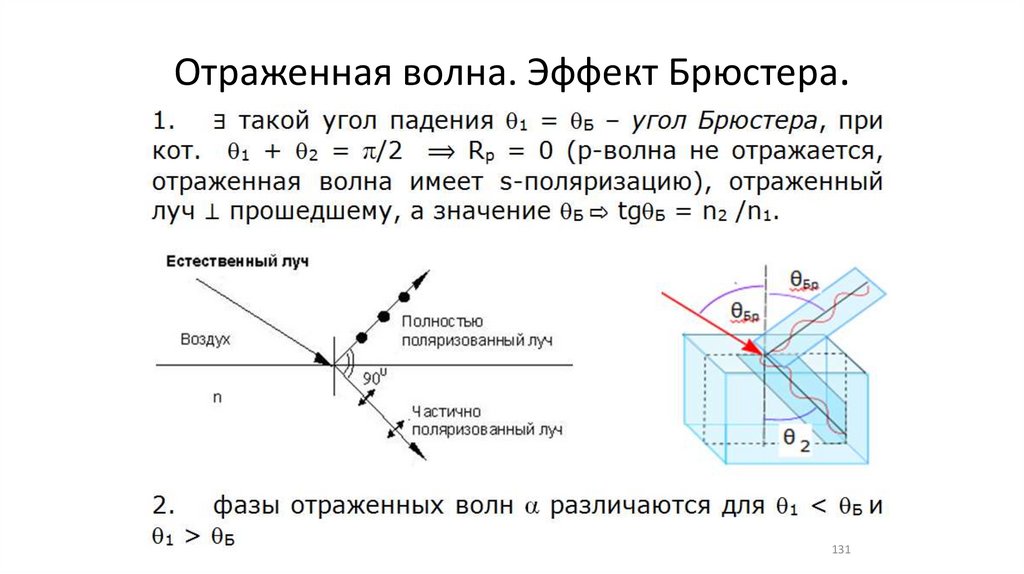
Отраженная волна. Эффект Брюстера.131
132.
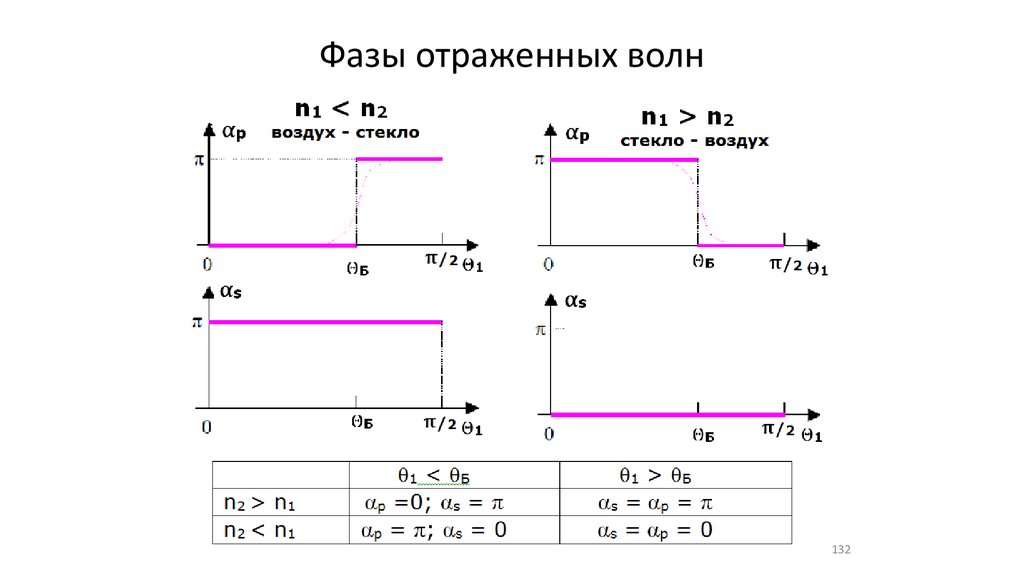
Фазы отраженных волн132
133.
133134.
134135.
135136.
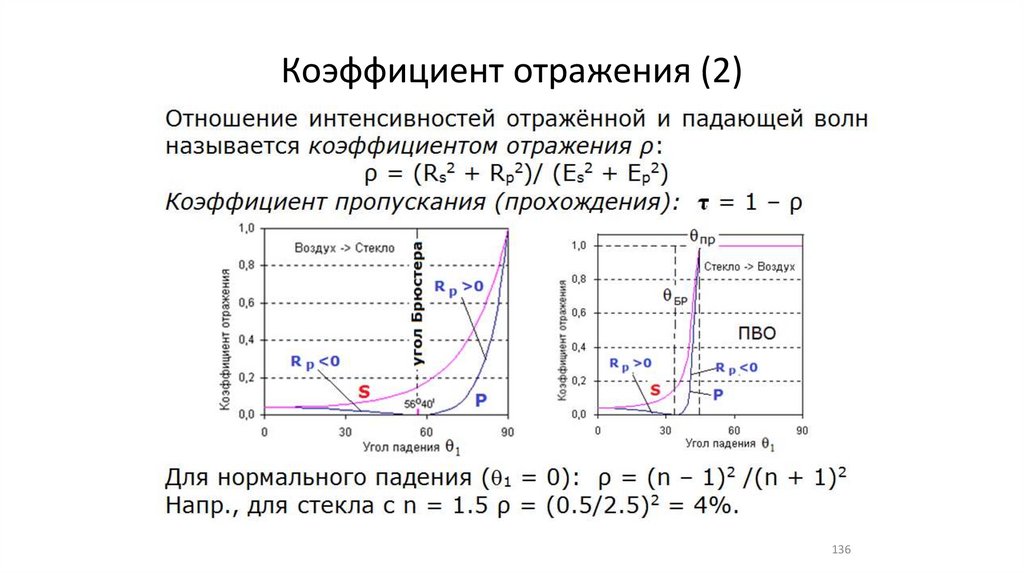
Коэффициент отражения (2)136
137.
137138.
Лекция 3.6 Распространениеэлектромагнитной волны в диэлектрической
среде
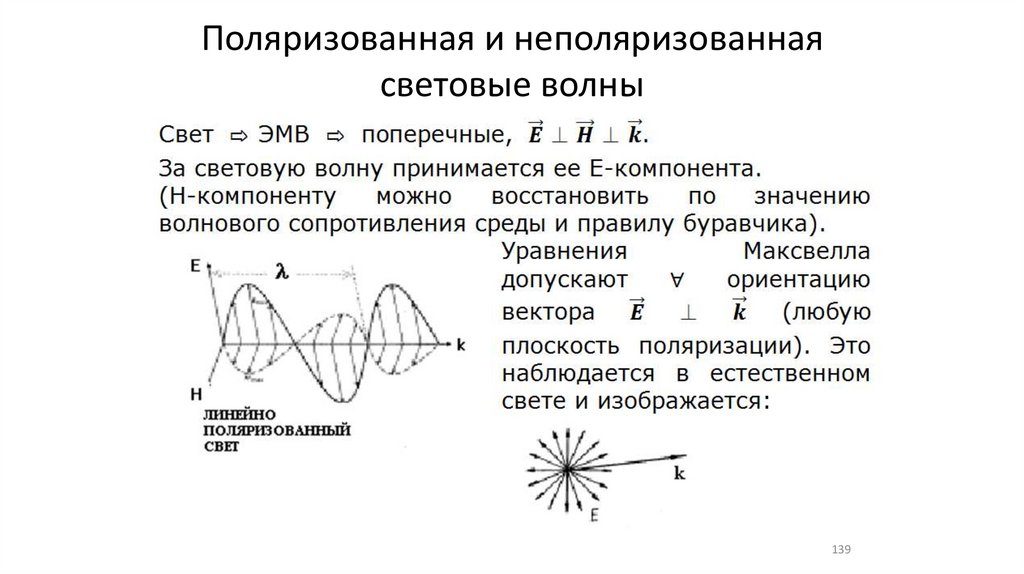
•Поляризованная и неполяризованная световые волны (2)
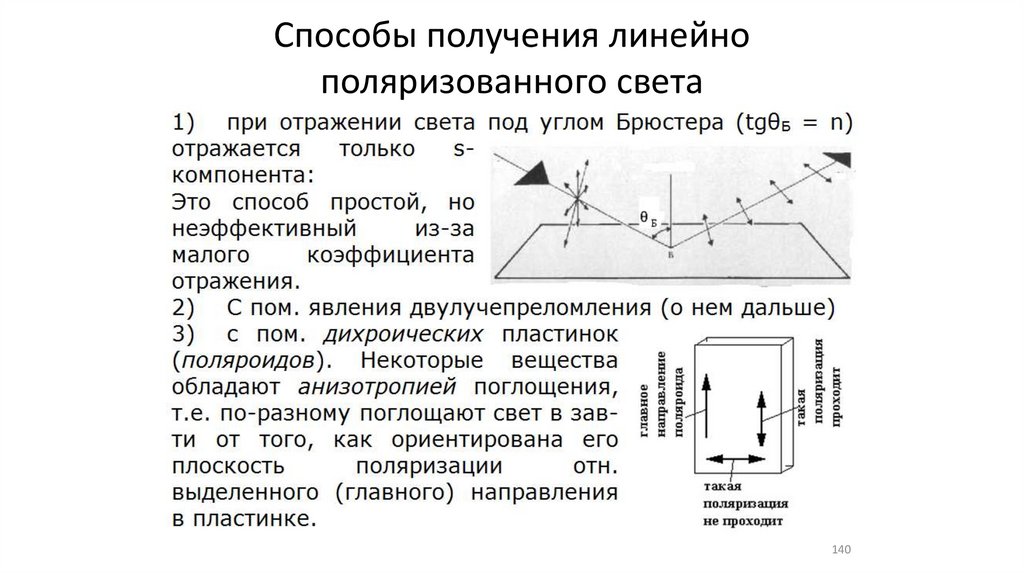
•Способы получения линейно поляризованного света (3)
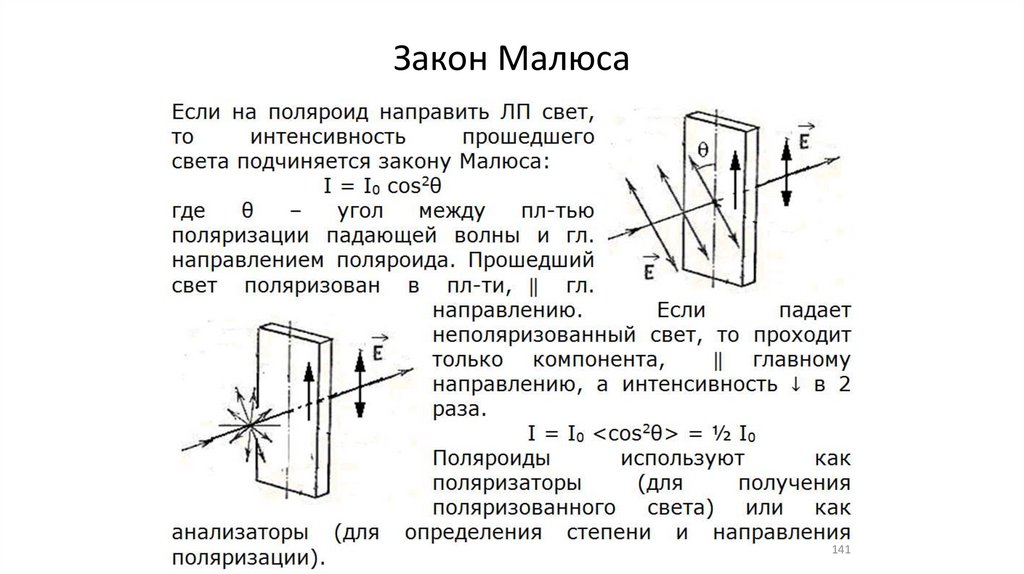
•Закон Малюса (4)
•Двулучепреломление (ДЛП) (5)
•Распространение волн в диэлектрической среде (6,7,8)
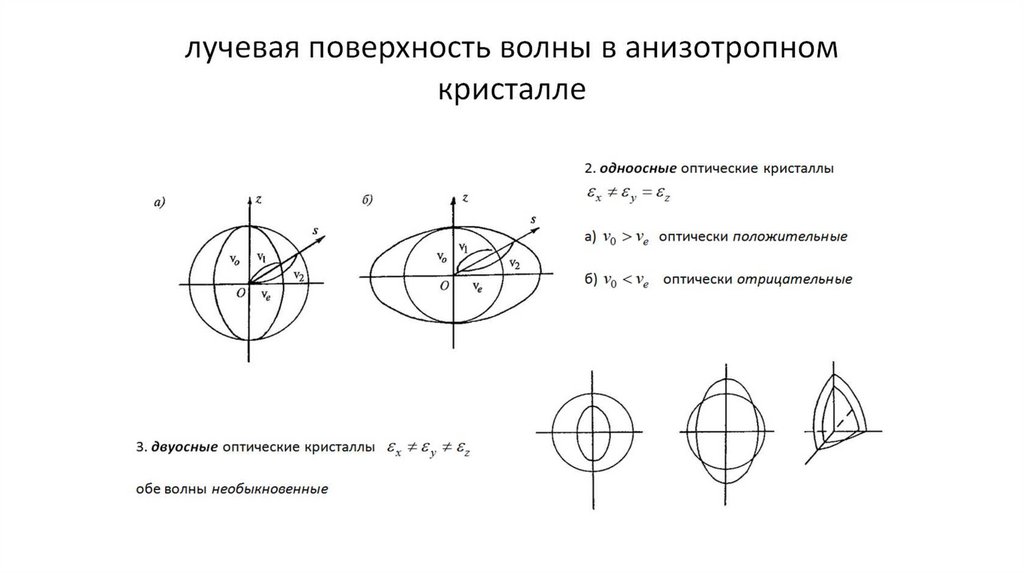
•Одноосные оптические кристаллы (9)
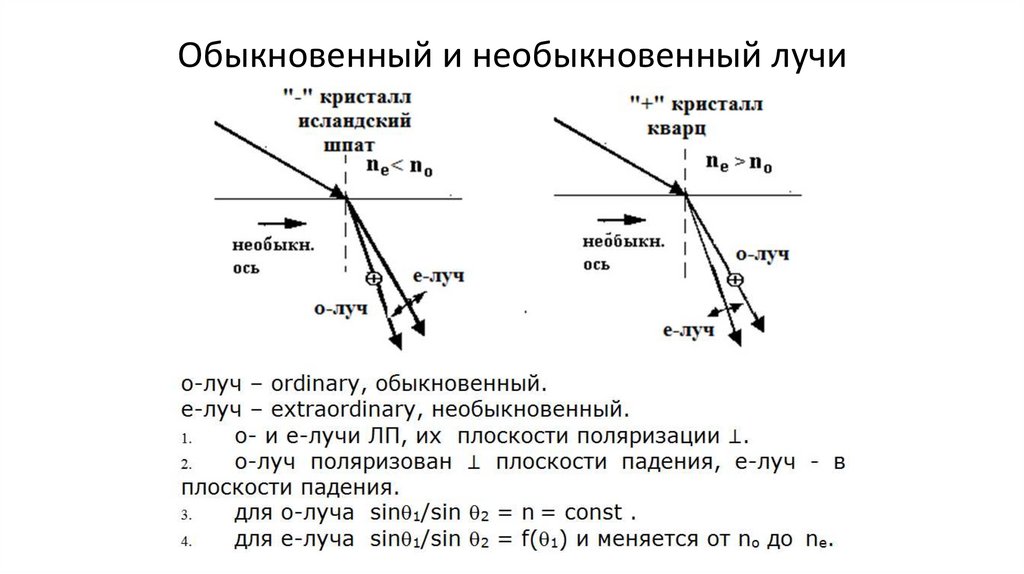
•Обыкновенный и необыкновенный лучи (10,11)
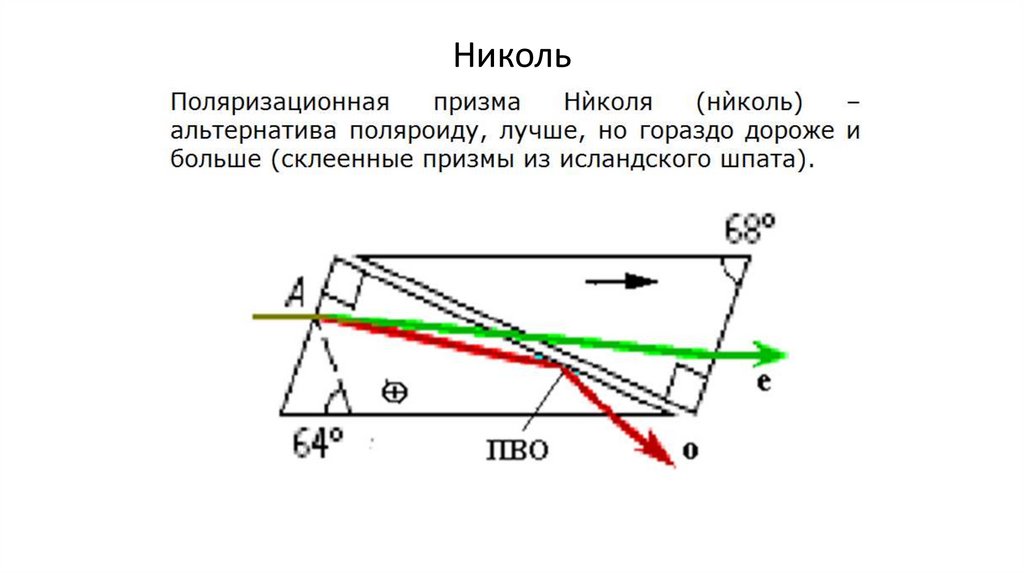
•Николь (12)
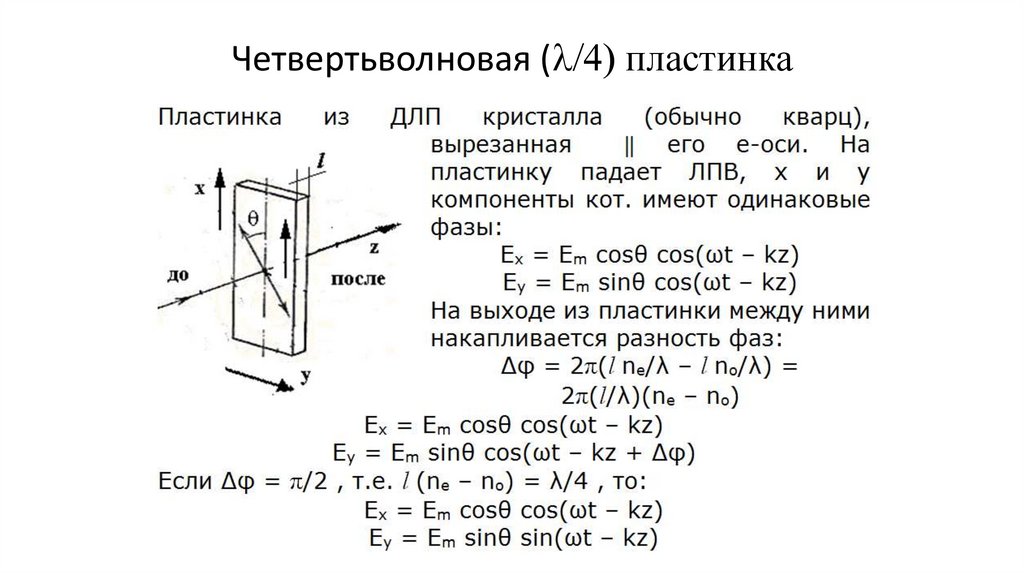
•Четвертьволновая (l/4 пластинка (13,14, 15,16)
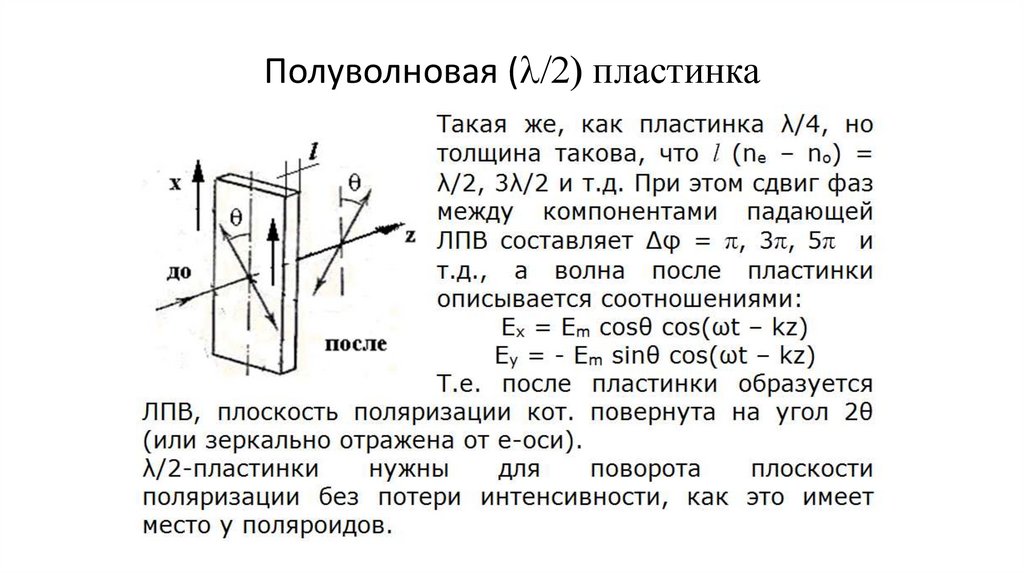
•Полуволновая (l/2 пластинка (17)
•искусственное ДЛП (18)
•Электрооптические эффекты (19, 20)
•Тензооптический эффект (21,22)
•Оптическая активность (23)
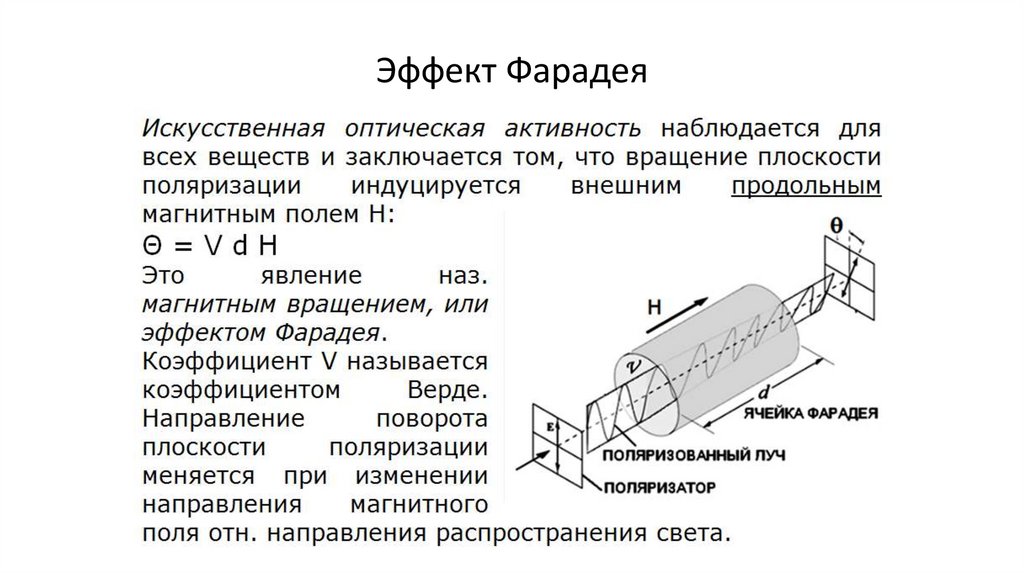
•Эффект Фарадея (24)
139.
Поляризованная и неполяризованнаясветовые волны
139
140.
Способы получения линейнополяризованного света
140
141.
Закон Малюса141
142.
Двулучепреломление (ДЛП)143.
144.
144145.
145146.
147.
148.
Обыкновенный и необыкновенный лучи149.
Николь150.
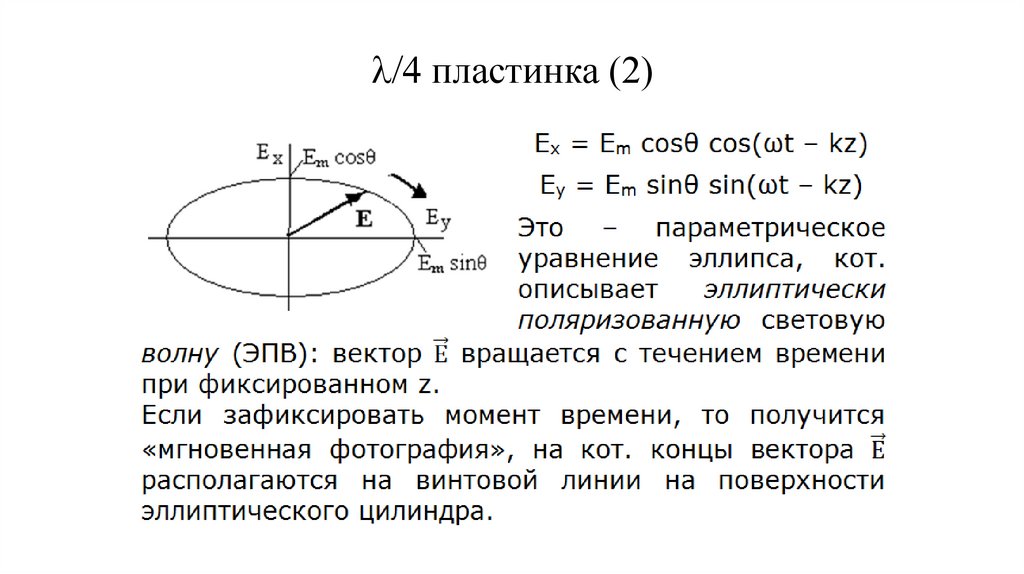
Четвертьволновая (l/4 пластинка151.
l/4 пластинка (2)152.
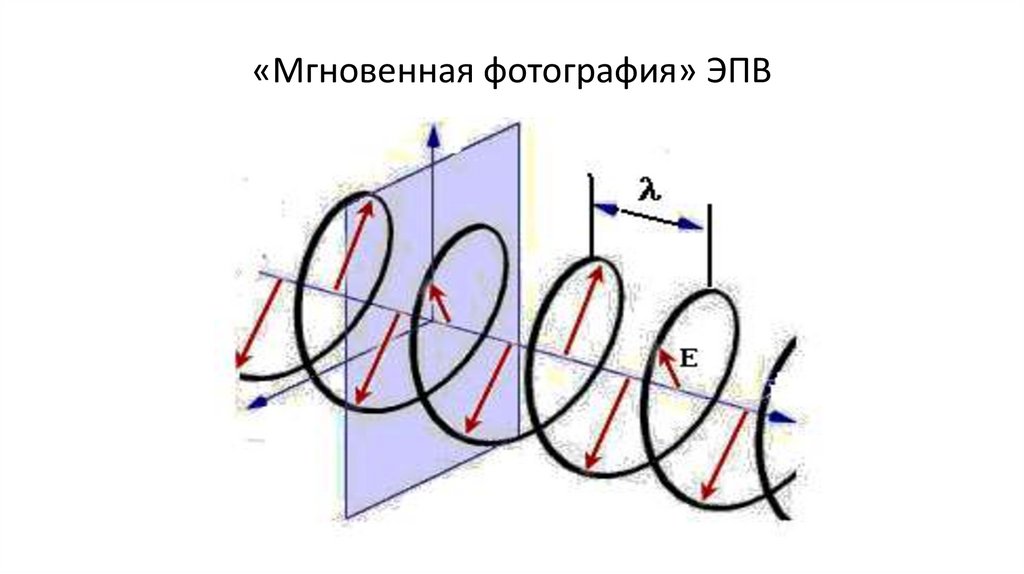
«Мгновенная фотография» ЭПВ153.
l/4 пластинка (3)154.
Полуволновая (l/2 пластинка155.
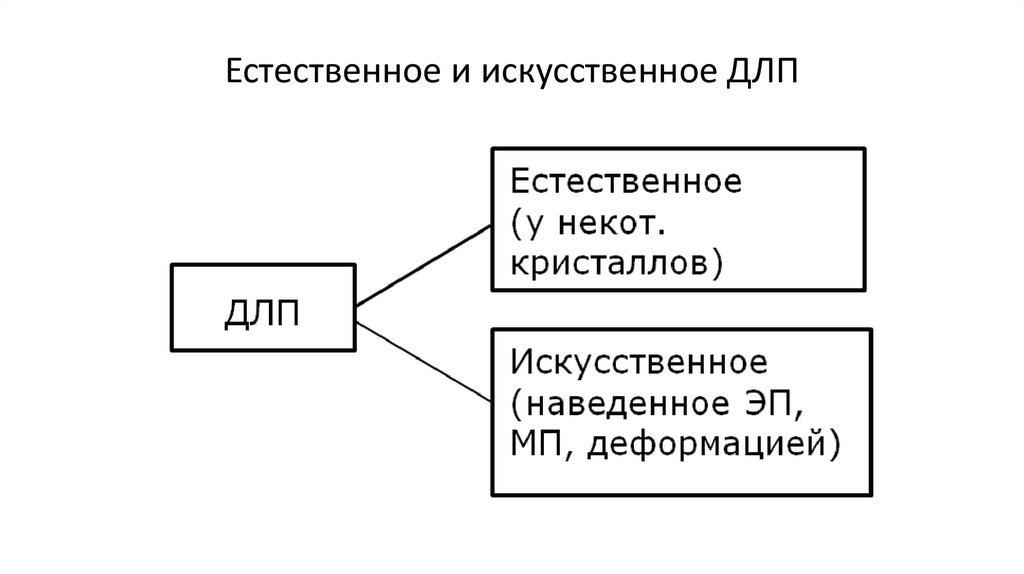
Естественное и искусственное ДЛП156.
Электрооптические эффекты. ЭффектПоккельса.
157.
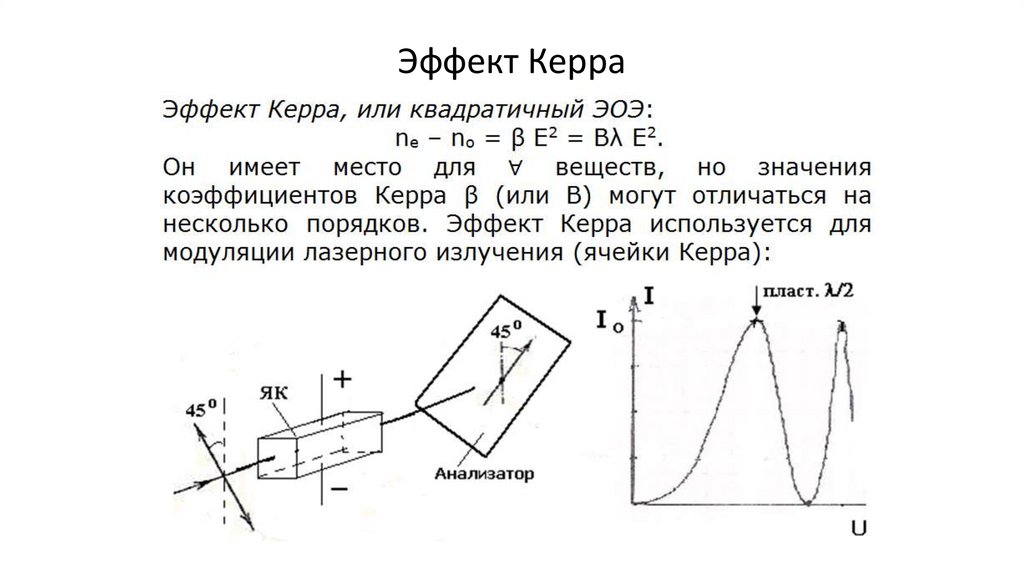
Эффект Керра158.
Тензооптический эффект159.
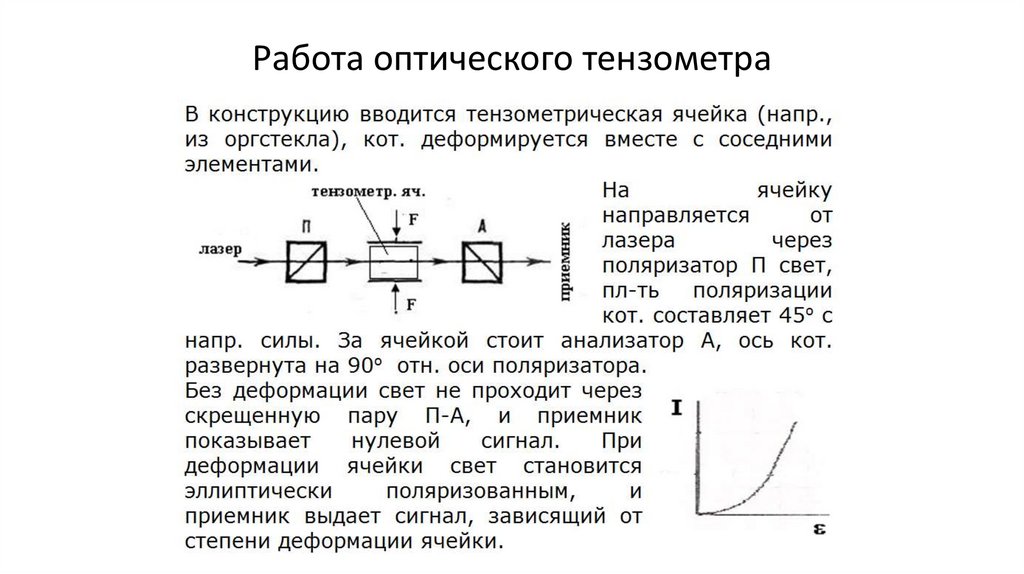
Работа оптического тензометра160.
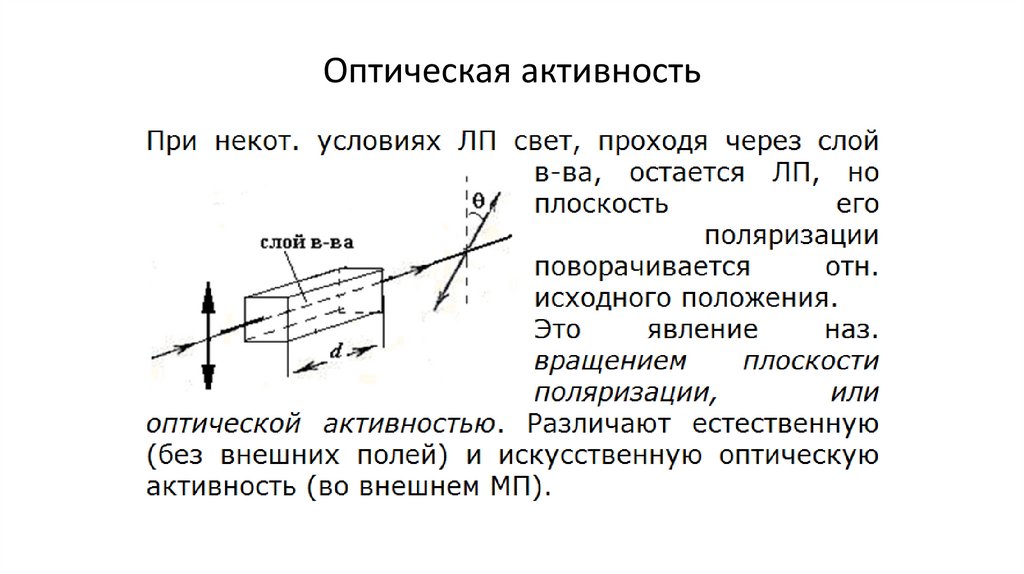
Оптическая активность161.
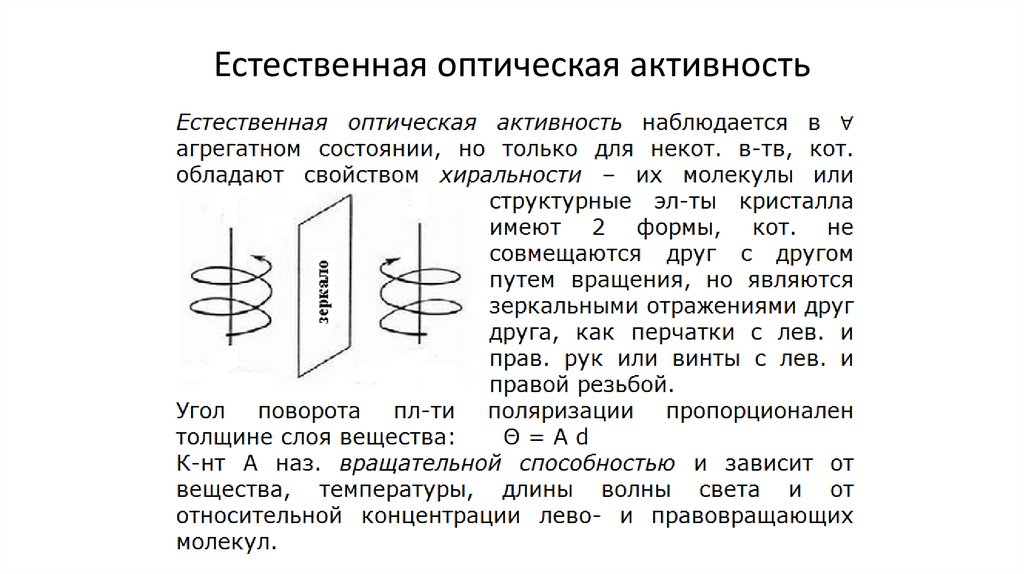
Естественная оптическая активность162.
Эффект Фарадея163.
Лекция 3.8 Тепловоеизлучение. Формула Планка.
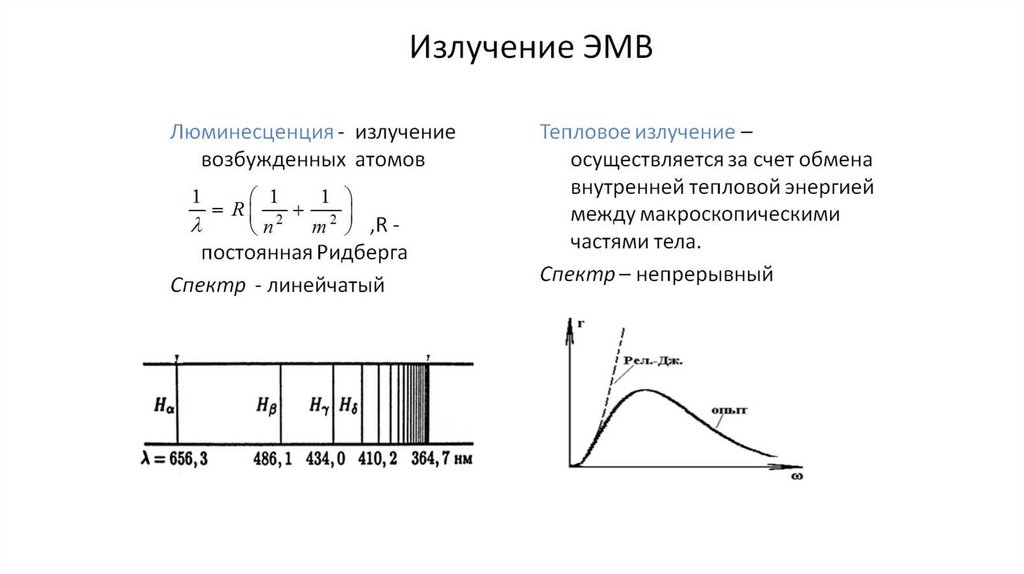
•Излучение электромагнитных волн (2,3)
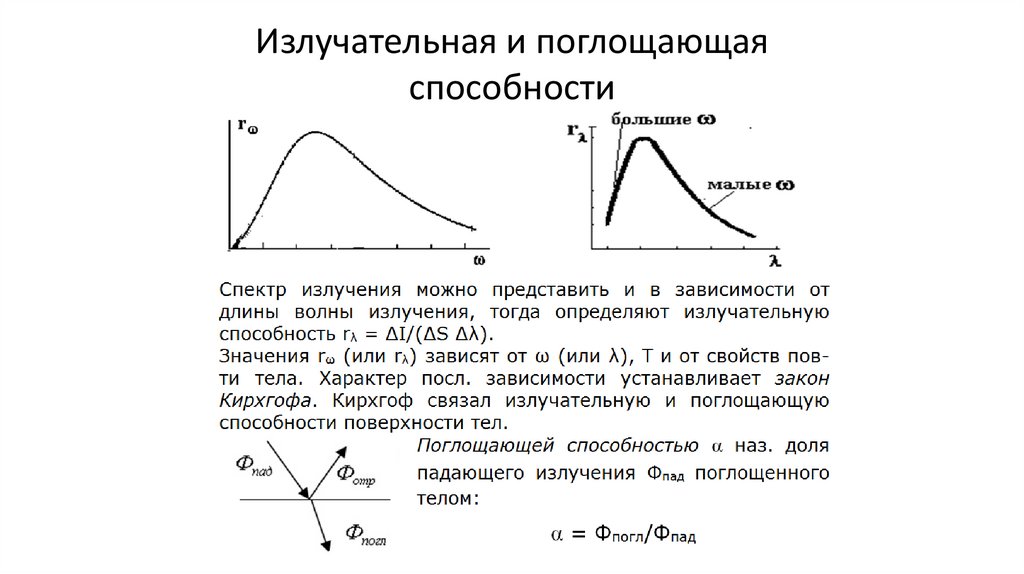
•Излучательная и поглощающая способности. Закон Кирхгофа (4,5)
•Абсолютно черное тело (6)
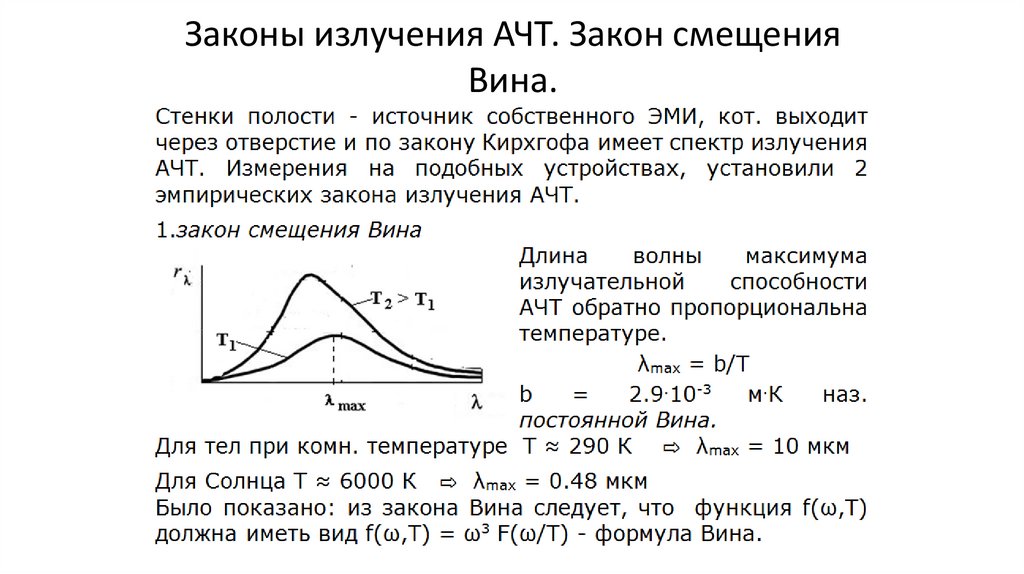
•Законы излучения АЧТ. Закон смещения Вина. Закон СтефанаБольцмана.(7,8,9)
•Формула Релея-Джинса (10,11)
•Гипотеза Планка и его формула (12 -15)
•Постоянные Планка. Кванты. (16)
•Фотоэффект (17,18,19)
•Рентгеновское излучение (20,21)
•Опыт Боте (22)
164.
165.
Тепловое ЭМ излучение166.
Излучательная и поглощающаяспособности
167.
Закон Кирхгофа168.
Абсолютно черное тело169.
Законы излучения АЧТ. Закон смещенияВина.
170.
Законы излучения АЧТ.Закон Стефана-Больцмана.
171.
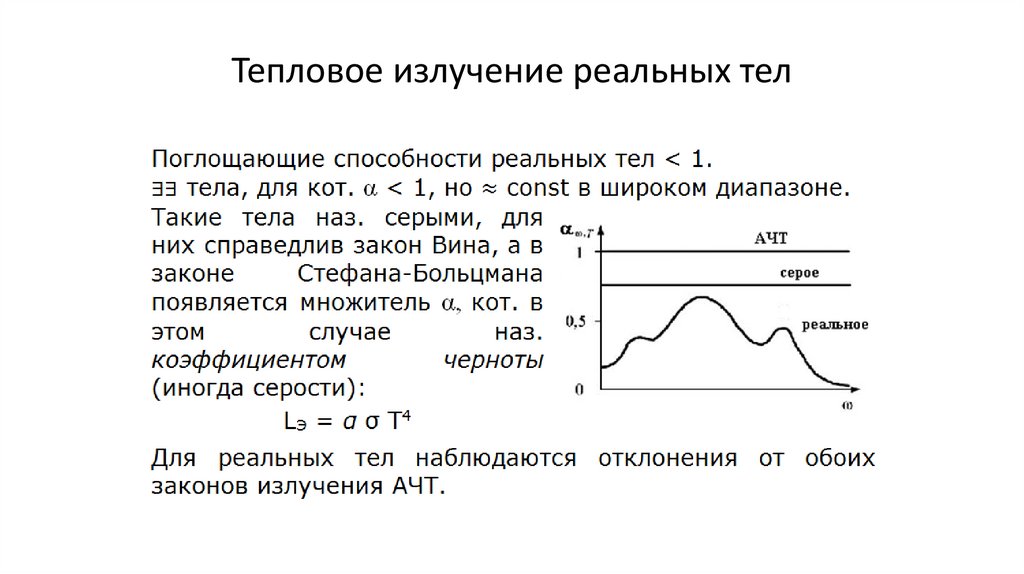
Тепловое излучение реальных тел172.
Формула Релея-Джинса173.
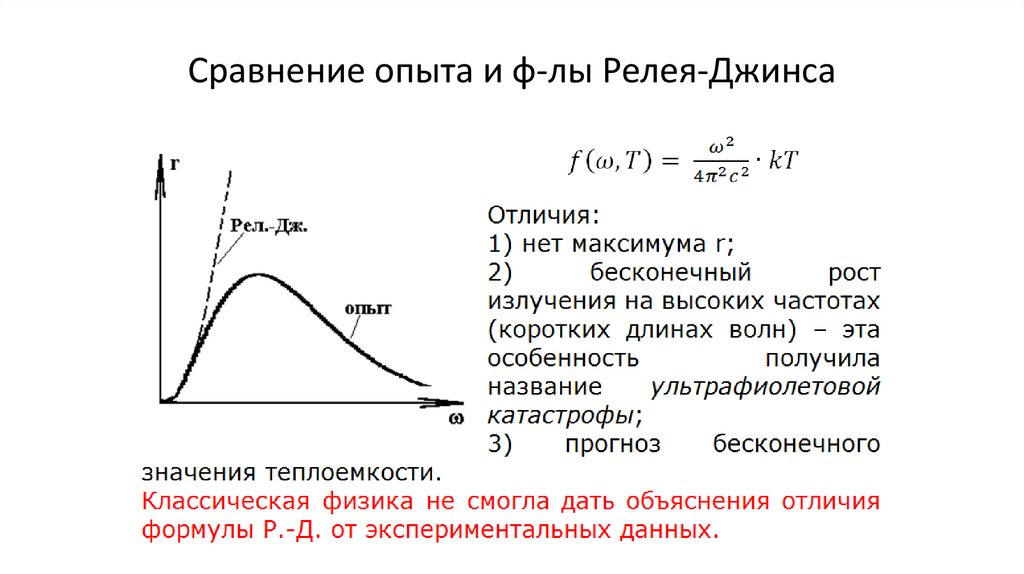
Сравнение опыта и ф-лы Релея-Джинса174.
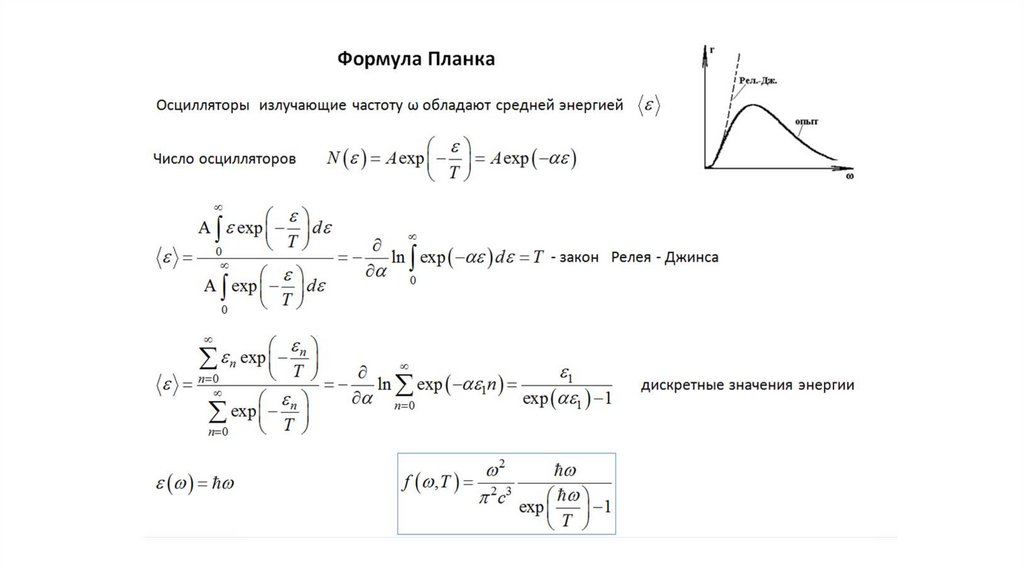
Гипотеза Планка и его формула175.
176.
177.
178.
Постоянные Планка. Кванты.179.
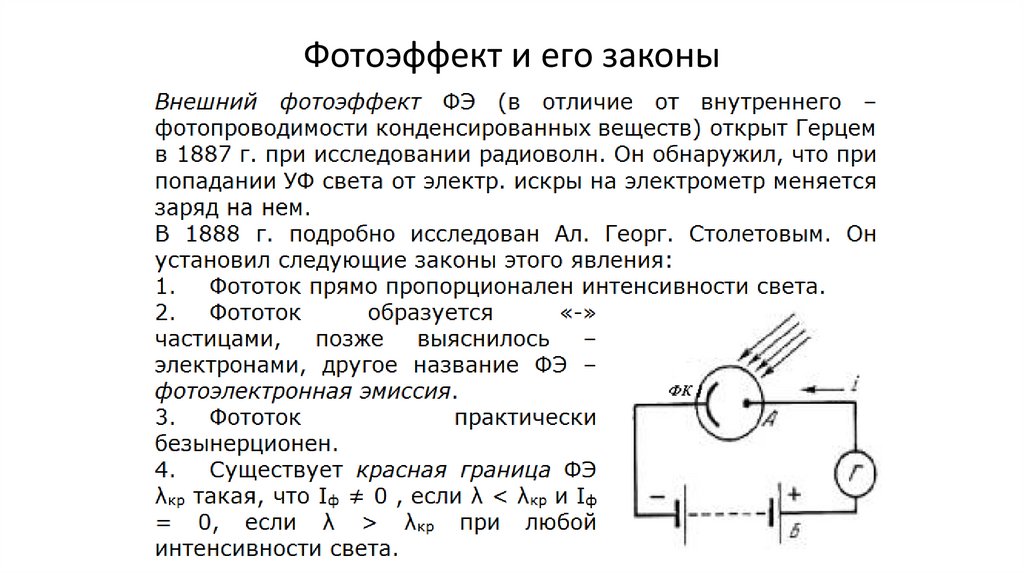
Фотоэффект и его законы180.
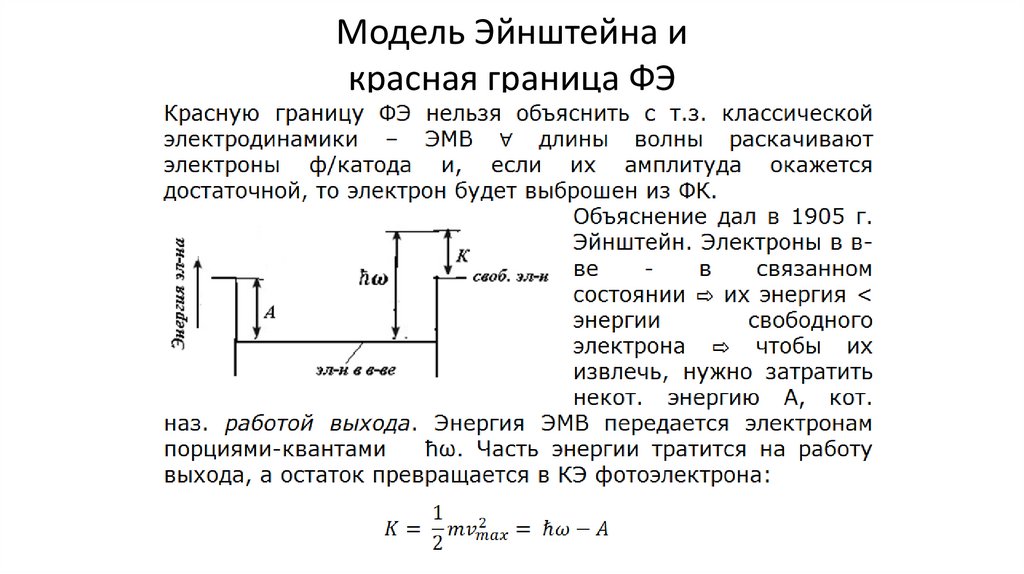
Модель Эйнштейна икрасная граница ФЭ
181.
Физический смысл соотношенияЭйнштейна
182.
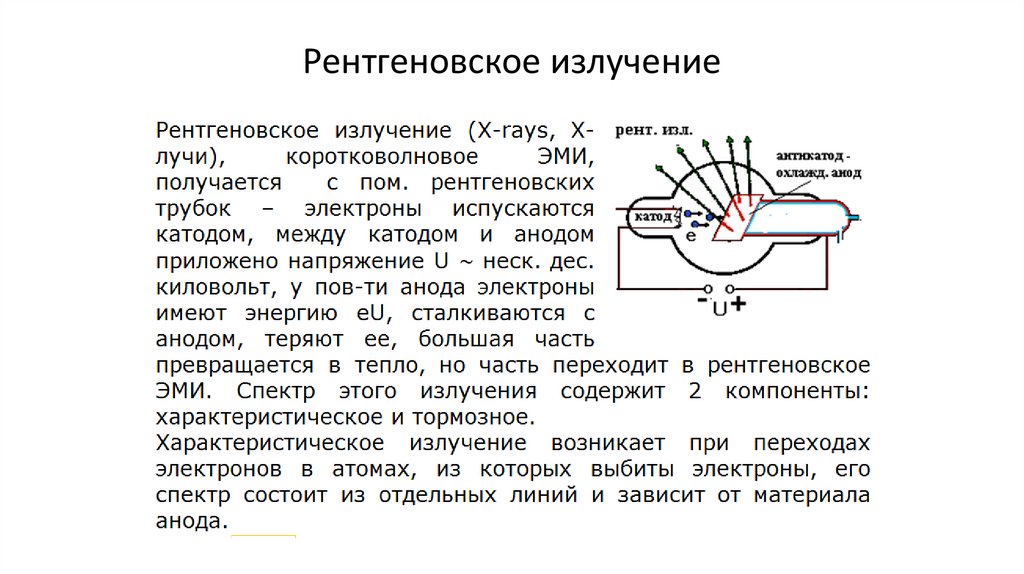
Рентгеновское излучение183.
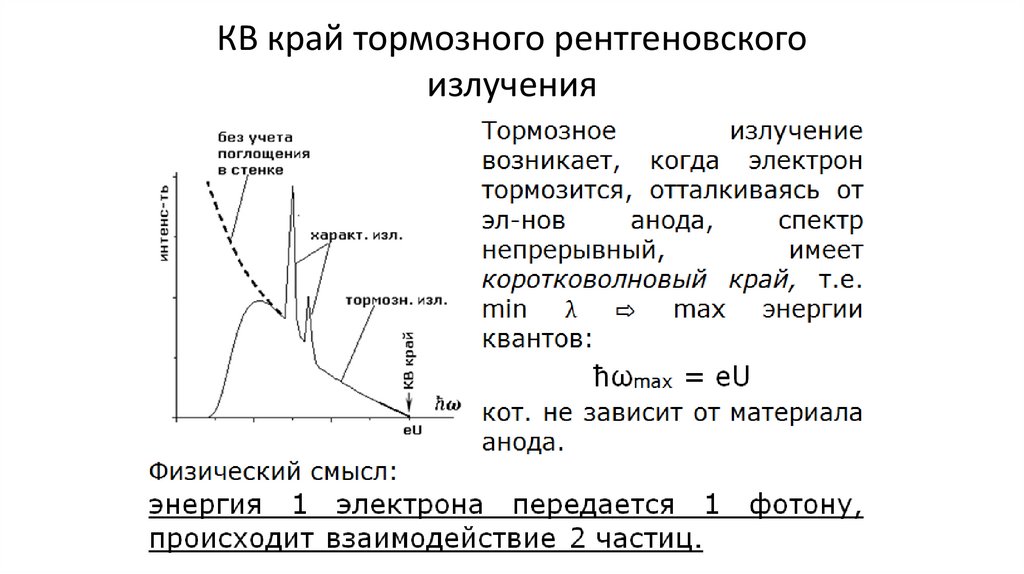
КВ край тормозного рентгеновскогоизлучения
184.
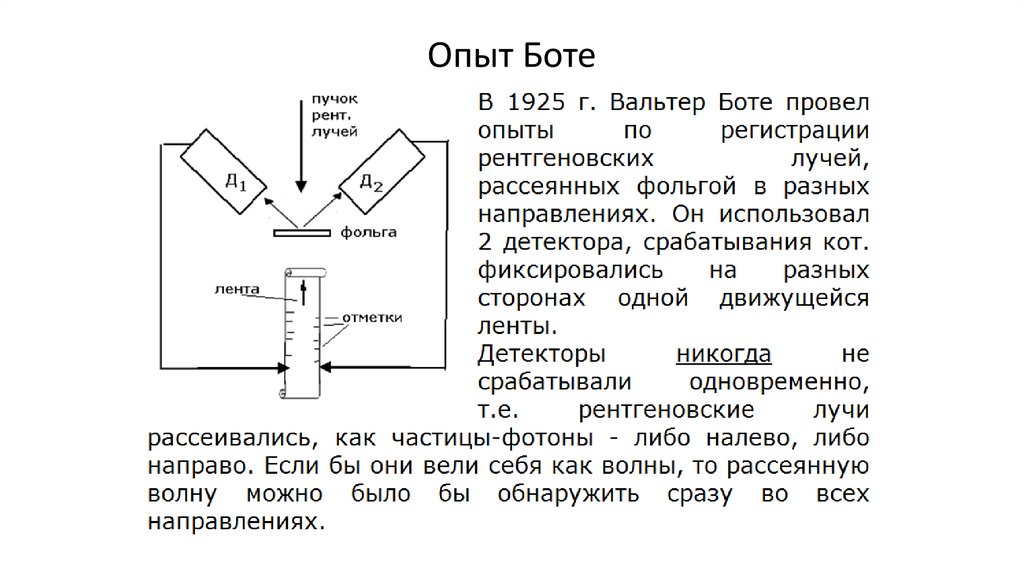
Опыт Боте185.
Лекция 3.9. Корпускулярные свойстваэлектромагнитных волн . Взаимодействие ЭМВ с
веществом
9.1. Корпускулярные свойства электромагнитных волн
1.
2.
Эффект Комптона (2,3, 4,5)
Импульс фотона (6)
9.2. Взаимодействие ЭМВ с веществом (14,15)
1.
2.
3.
Вывод формулы Планка по Эйнштейну (7, 8, 9, 10,11)
Поглощение и усиление света в среде(12,13)
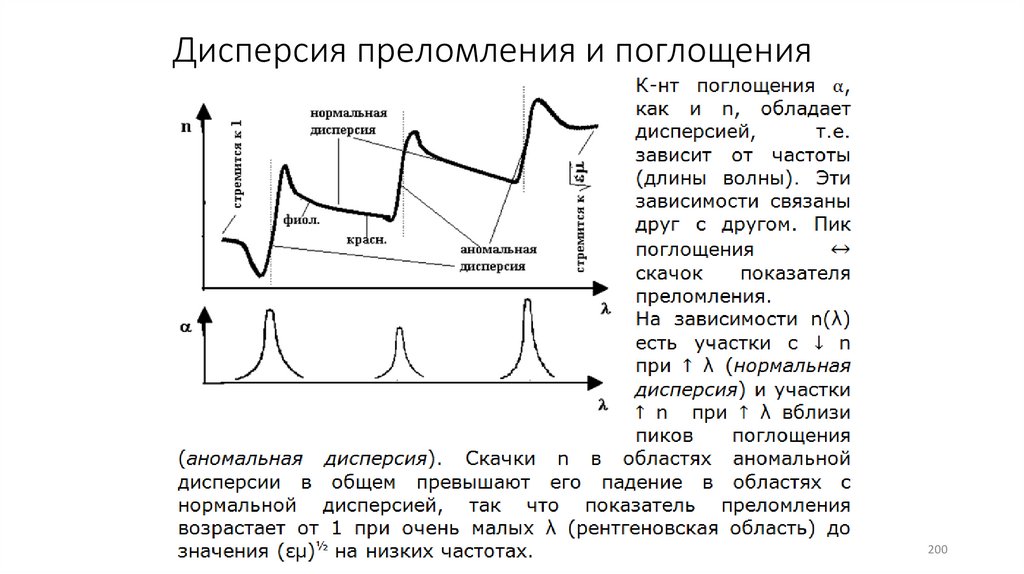
Дисперсия преломления и поглощения (16, 17, 18,19)
9.3. Излучение ЭМВ . Линейчатые спектры (20,21)
1.
Линейчатый спектр атома водорода (22,23)
185
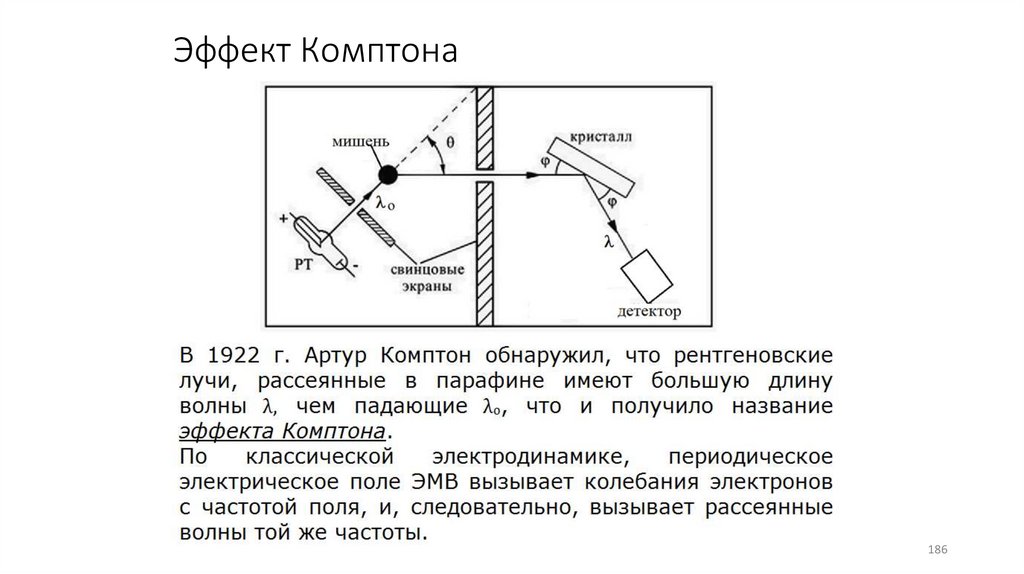
186.
Эффект Комптона186
187.
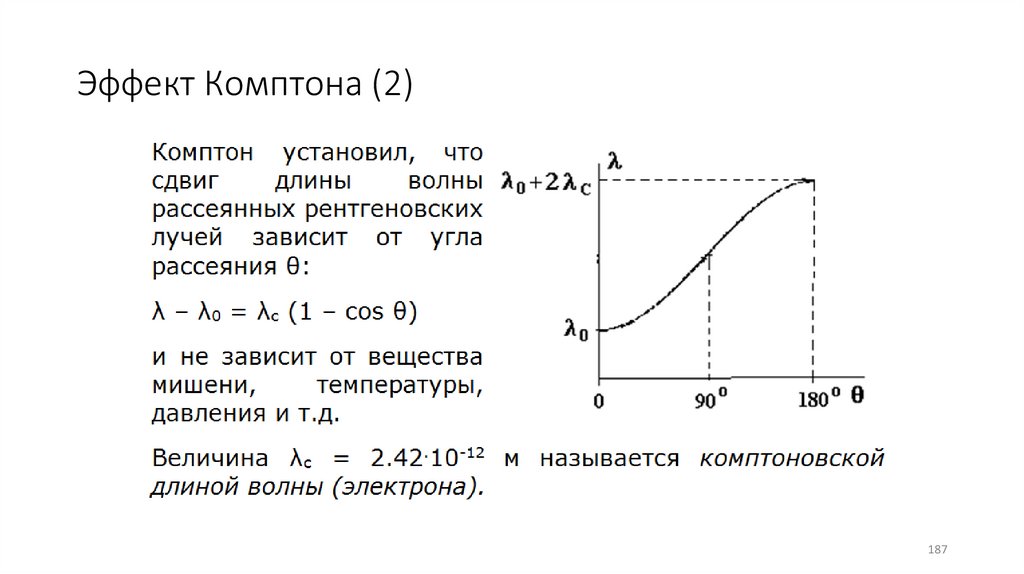
Эффект Комптона (2)187
188.
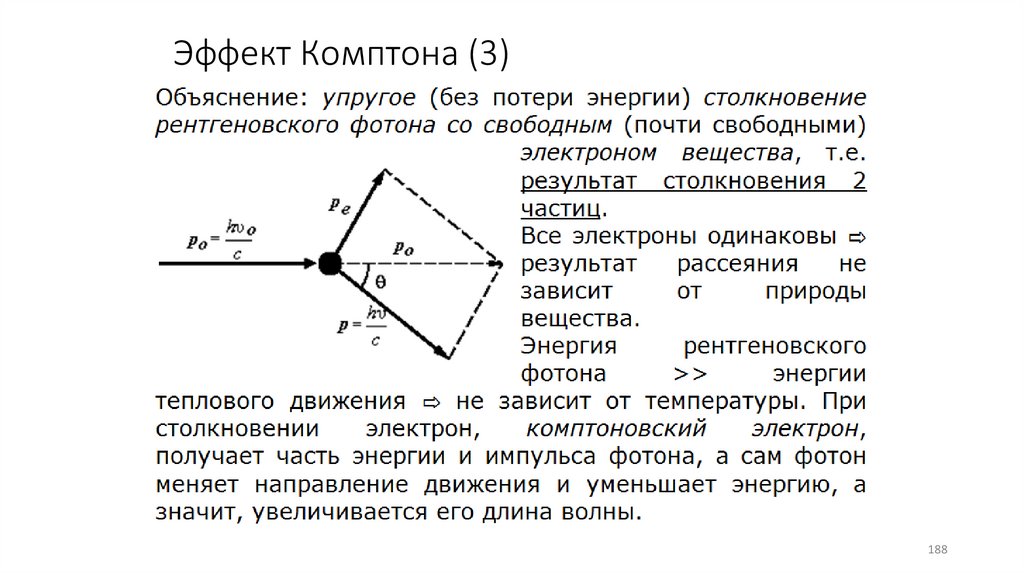
Эффект Комптона (3)188
189.
Эффект Комптона (4)189
190.
Импульс фотонаИмпульс фотона = масса фотона ⤫ скорость света =
= (энергия фотона/квадрат ск. света) ⤫ скорость света =
= энергия фотона/ скорость света
p = ℎν/c = ℎ/λ
Решение уравнений:
λ – λ0 = (h/mc) (1 – cosθ)
λс = h/mc = 2.42.10-12 м
• Эффект Комптона: корпускулярное свойство ЭМВ – фотон переносит
порцию импульса.
190
191.
Вывод формулы Планка по Эйнштейну191
192.
Радиационные процессы, связанные с испусканием илипоглощением излучения
192
193.
Радиационные процессы, связанные с испусканием илипоглощением излучения
193
194.
Вынужденное (стимулированное)излучение
194
195.
Вывод формулы Планка по Эйнштейну (2)195
196.
Поглощение и усиление света в среде196
197.
Коэффициент поглощения197
198.
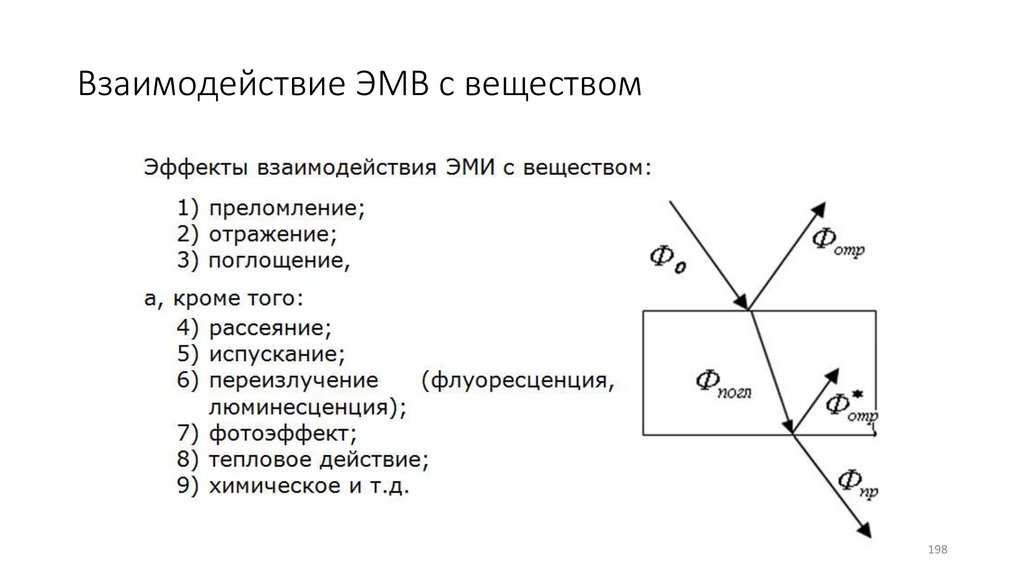
Взаимодействие ЭМВ с веществом198
199.
Преломление, отражение, поглощение199
200.
Дисперсия преломления и поглощения200
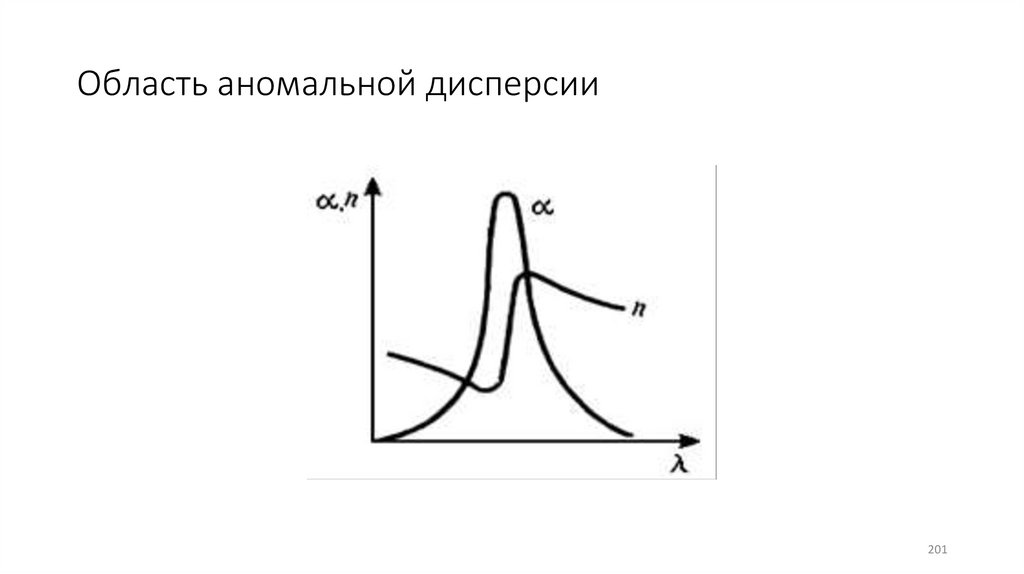
201.
Область аномальной дисперсии201
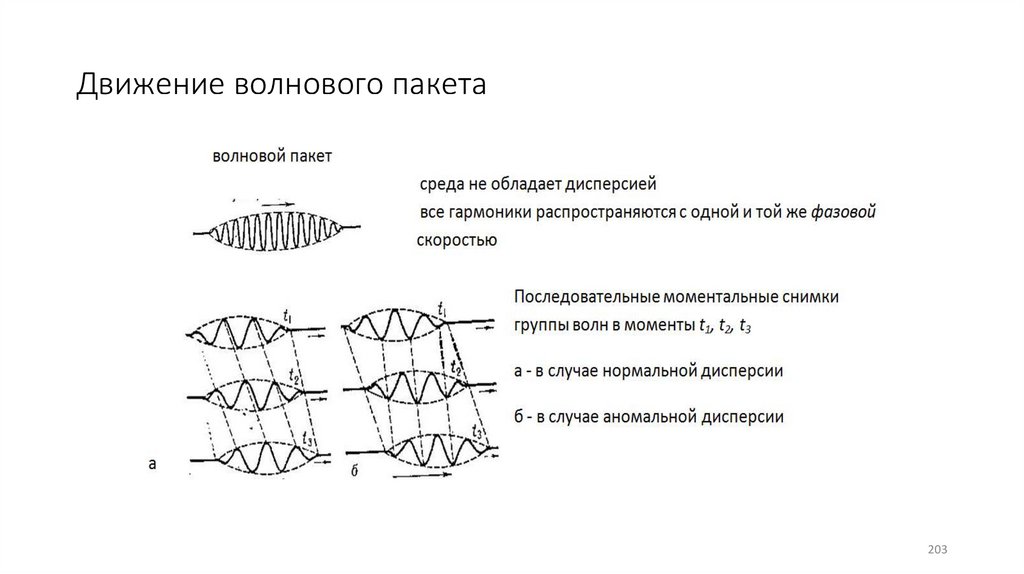
202.
Фазовая и групповая скорости202
203.
Движение волнового пакета203
204.
Корпускулярно-волновой дуализм204
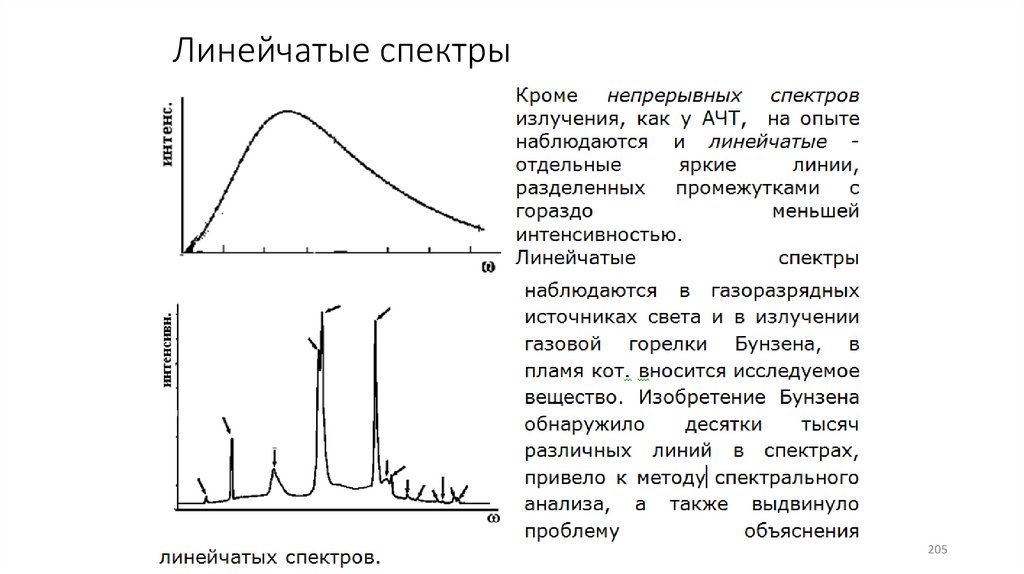
205.
Линейчатые спектры205
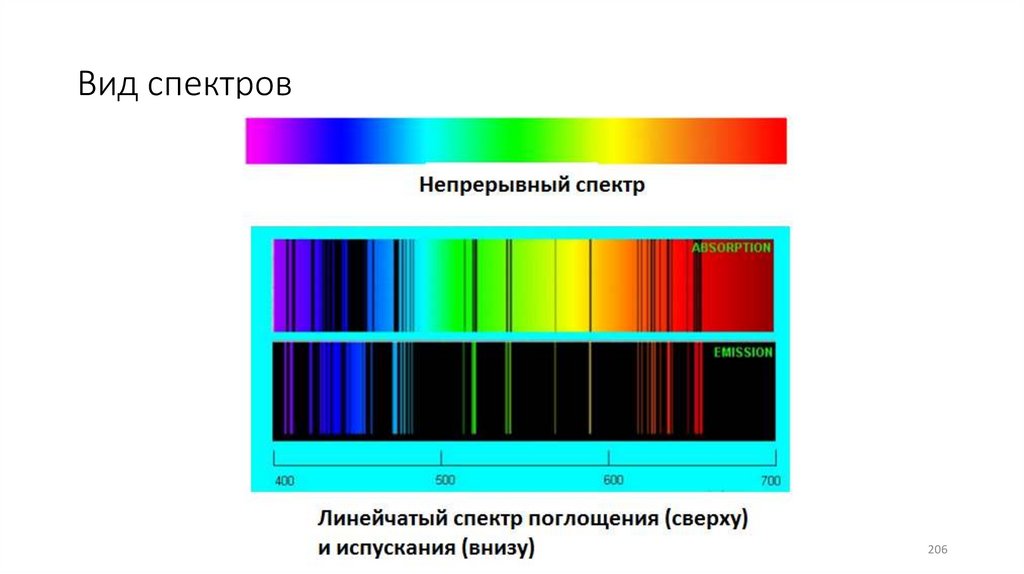
206.
Вид спектров206
207.
Линейчатый спектр атома водорода207
208.
Другие спектральные серии208
209.
Лекция 10. Ядерная модель атома. Волновыесвойства микрочастиц.
10.1. Ядерная модель атома
1.
Спектры (2,3)
2.
3.
4.
Модель Томсона(4,5,)
Опыт Резерфорда(6,7)
Модель Бора(8 - 13)
10.2. Волновые свойства микрочастиц
1.
2.
3.
4.
Гипотеза де-Бройля(14,15,16)
Эффект Рамзауэра и Таунсенда (17)
Опыт Дэвиссона – Джермера (18,19)
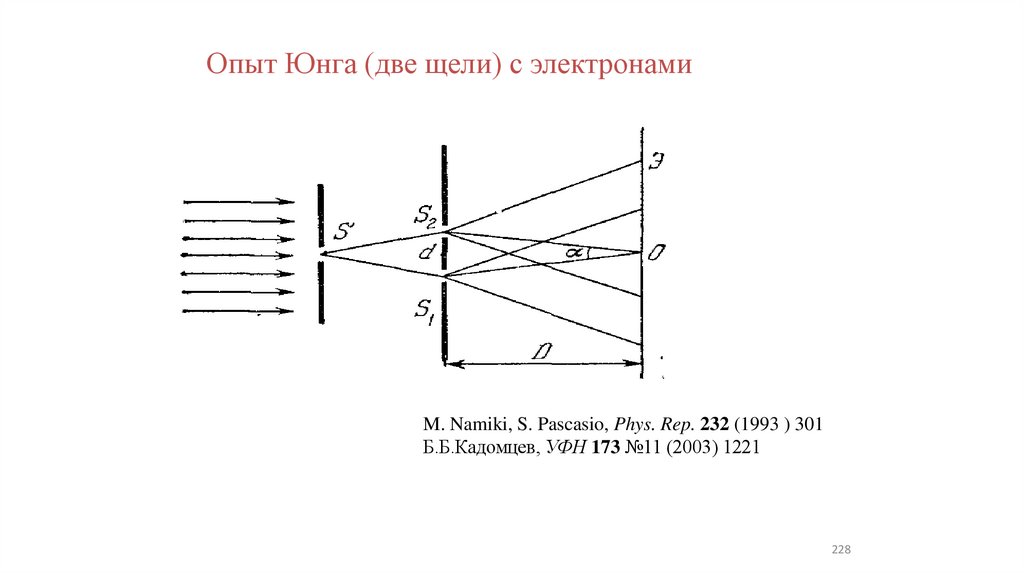
Опыт Юнга (две щели) с электронами (20 – 25)
209
210.
Линейчатый спектр атома водорода210
211.
Другие спектральные серии211
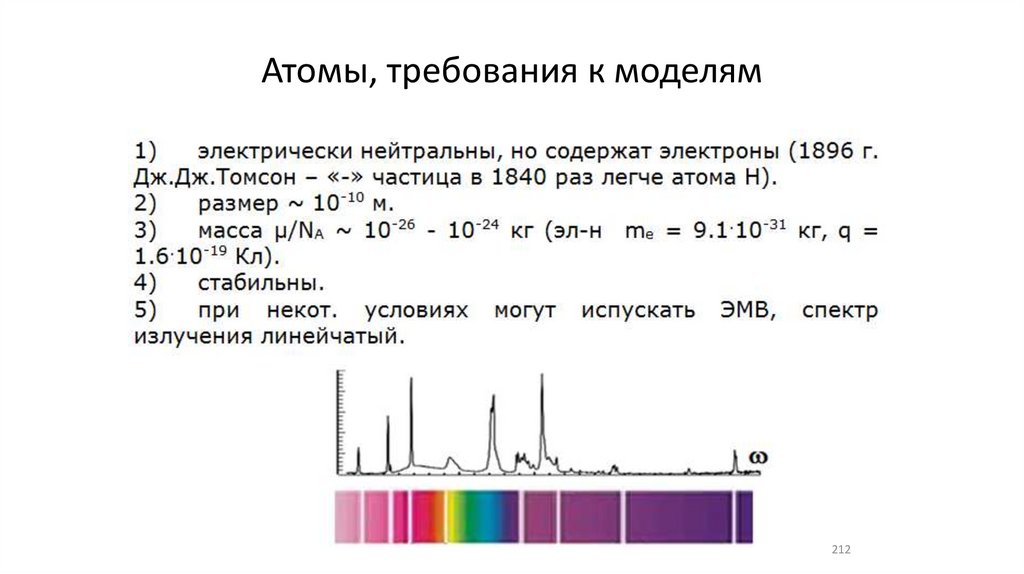
212.
Атомы, требования к моделям212
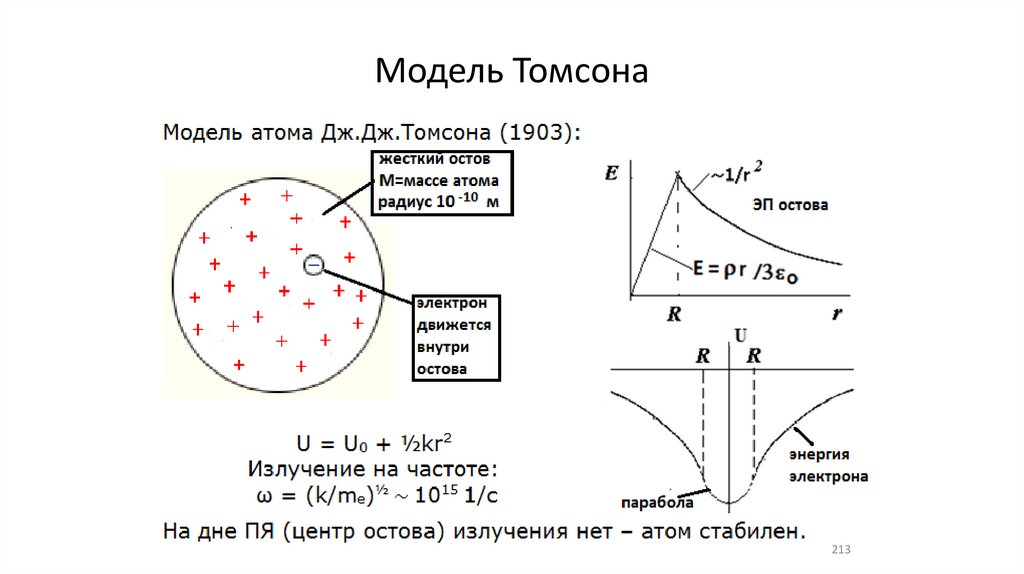
213.
Модель Томсона213
214.
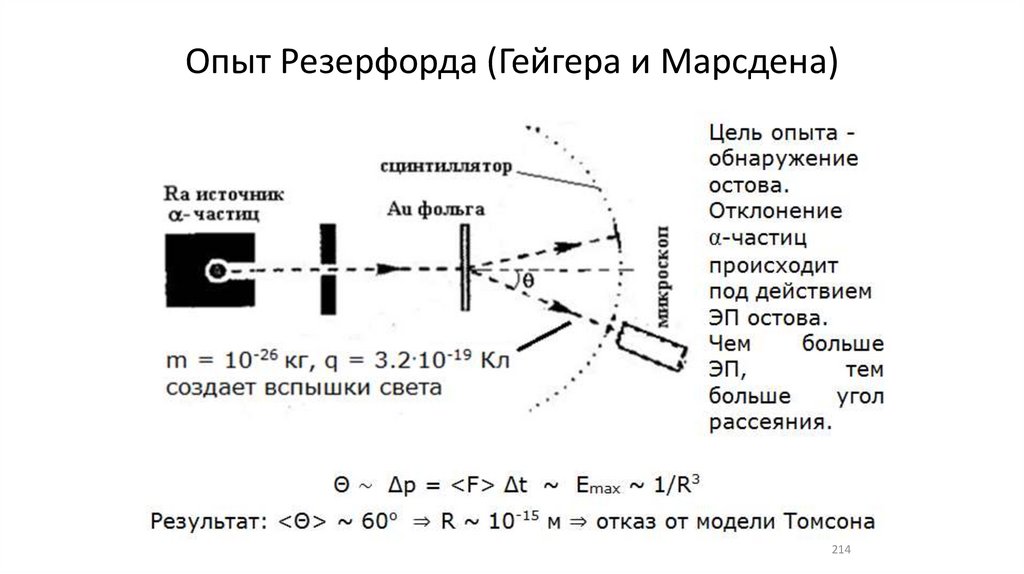
Опыт Резерфорда (Гейгера и Марсдена)214
215.
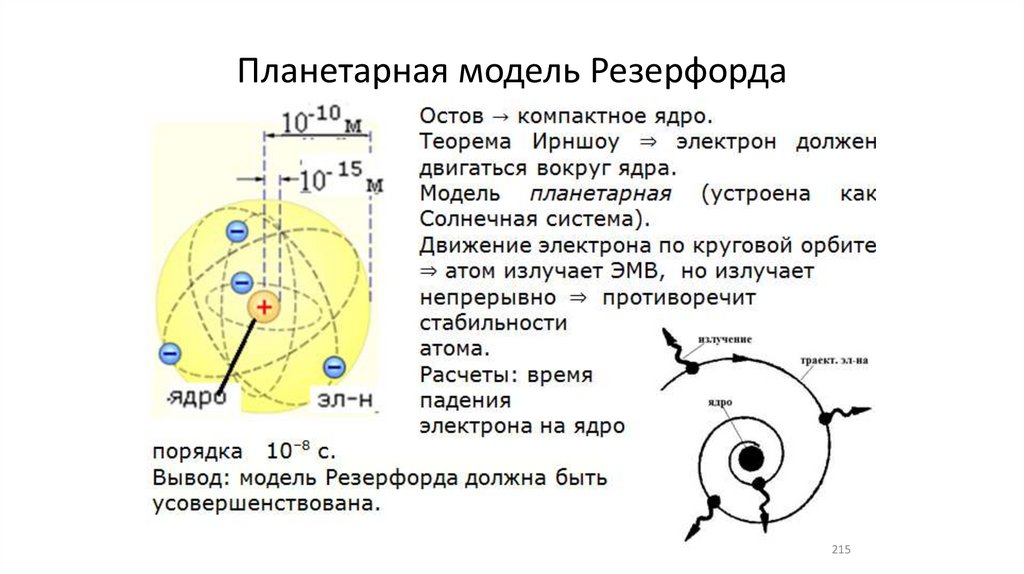
Планетарная модель Резерфорда215
216.
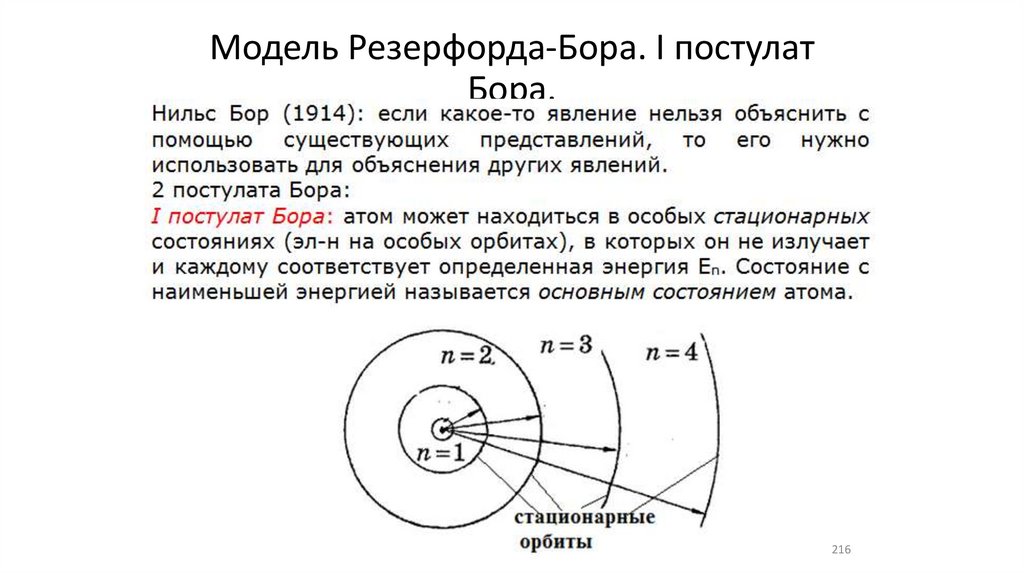
Модель Резерфорда-Бора. I постулатБора.
216
217.
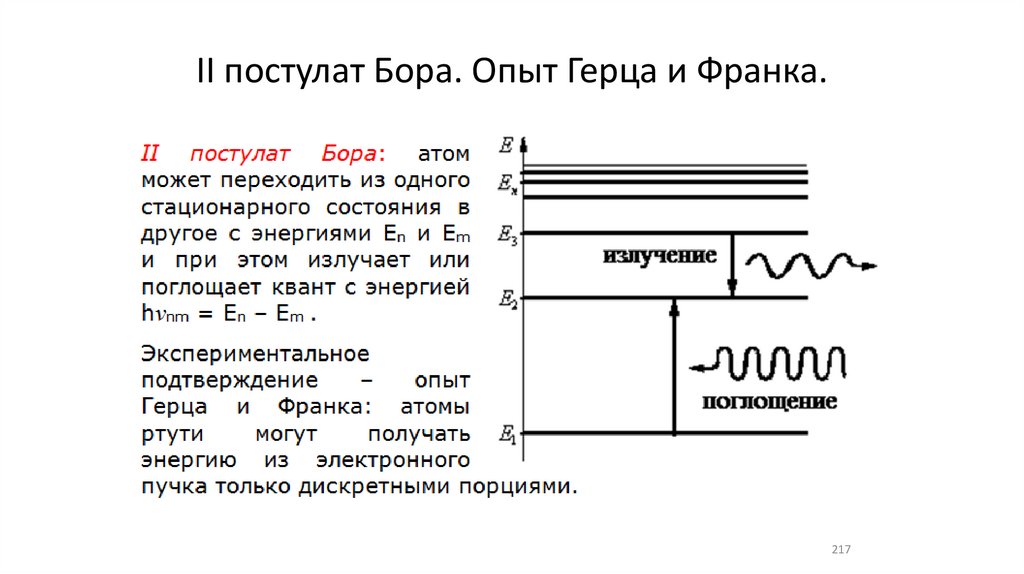
II постулат Бора. Опыт Герца и Франка.217
218.
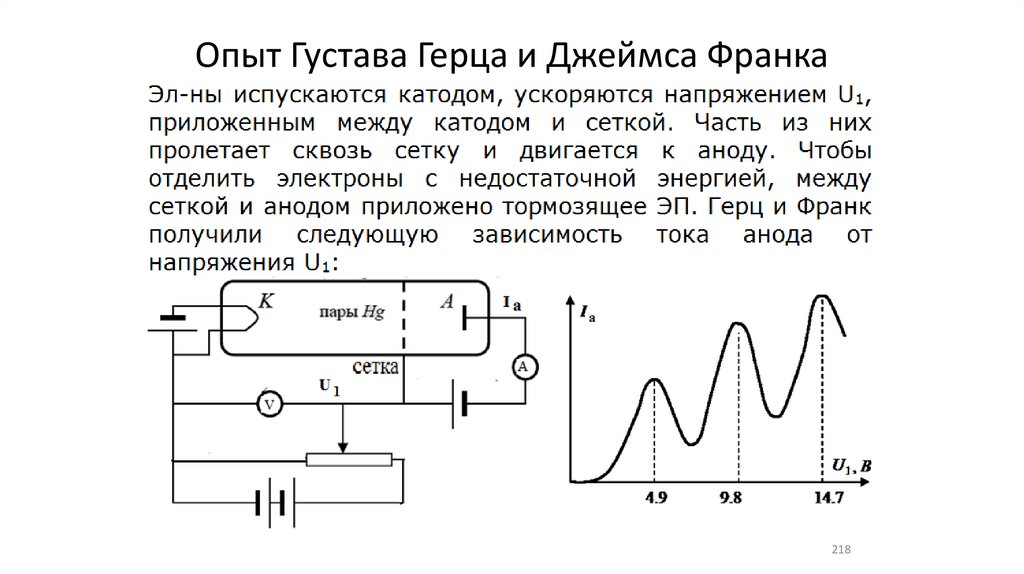
Опыт Густава Герца и Джеймса Франка218
219.
Интерпретация опыта Франка-Герца219
220.
Стационарные состояния атома Н поБору
220
221.
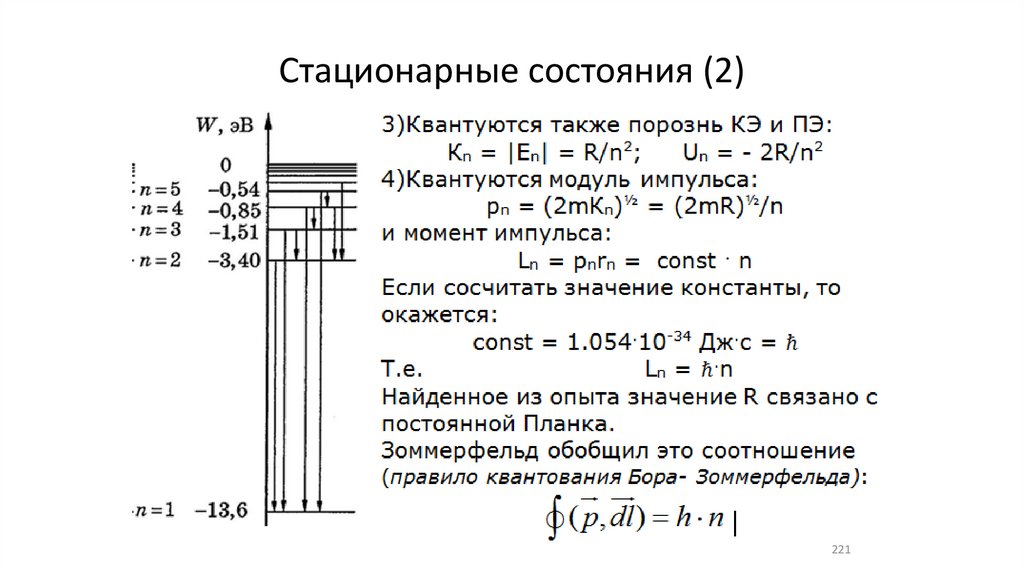
Стационарные состояния (2)221
222.
Гипотеза де-Бройля222
223.
Гипотеза де-Бройля (фазовая и групповаяскорости)
223
224.
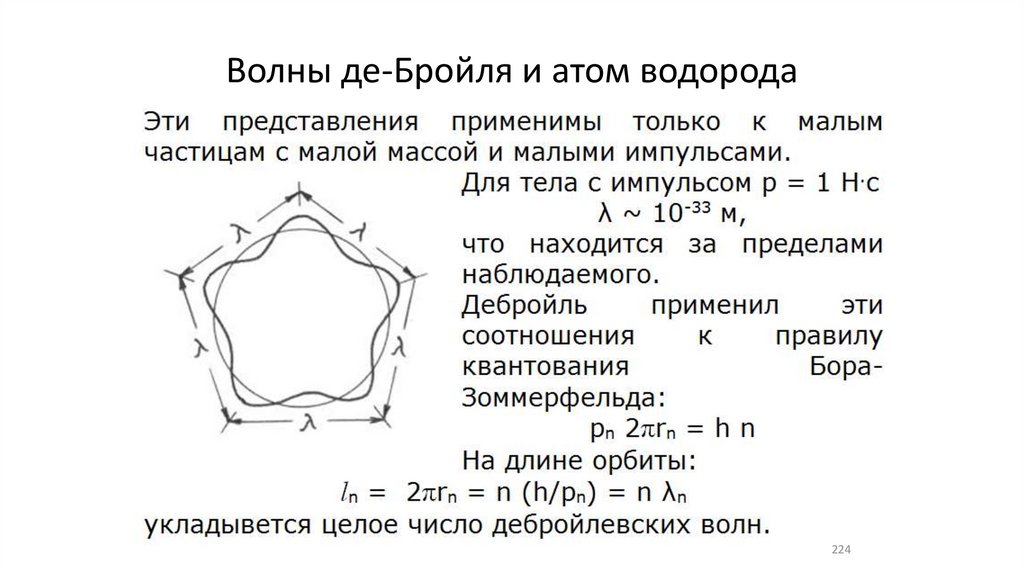
Волны де-Бройля и атом водорода224
225.
Эффект Рамзауэра и ТаунсендаКогда длина волны электрона имеет порядок
диаметра атома инертного газа, наблюдается
явление дифракции
Строение тиратрона ТГ30,1/1.3
1.Коробчатая сетка; 2. Катод;
3,5. Пластины со щелями; 4. Сетка;
6. Анод.
Экспериментальная ВАХ,
демонстрирующая практически
полное исчезновение рассеяния
электронов вблизи энергии 1 эВ
226.
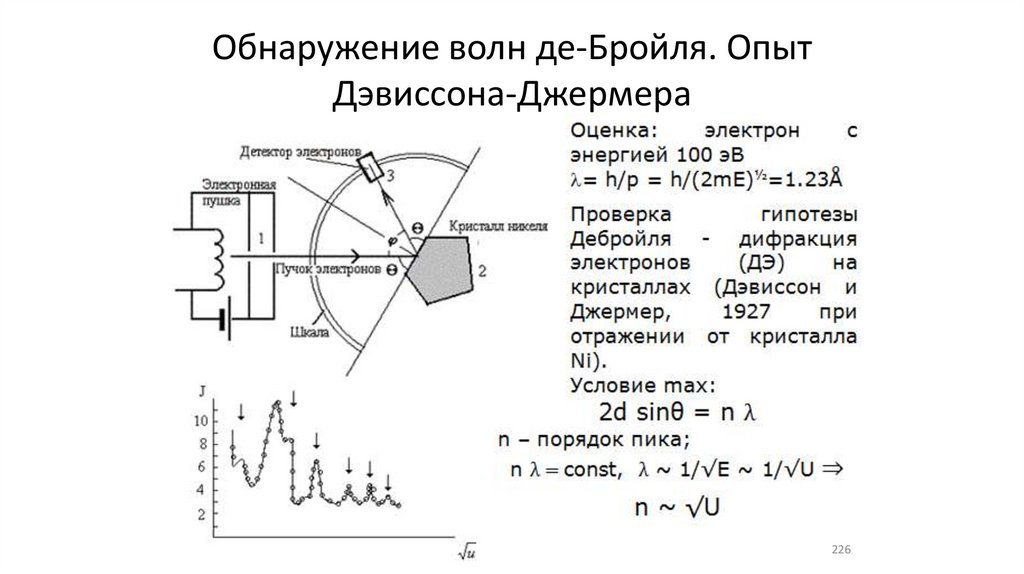
Обнаружение волн де-Бройля. ОпытДэвиссона-Джермера
226
227.
Результаты опыта Д.-Дж.227
228.
Опыт Юнга (две щели) с электронамиM. Namiki, S. Pascasio, Phys. Rep. 232 (1993 ) 301
Б.Б.Кадомцев, УФН 173 №11 (2003) 1221
228
229.
229230.
230231.
231232.
232233.
Уравнение Шредингера233
234.
УШ для свободной частицы (U =0)234
235.
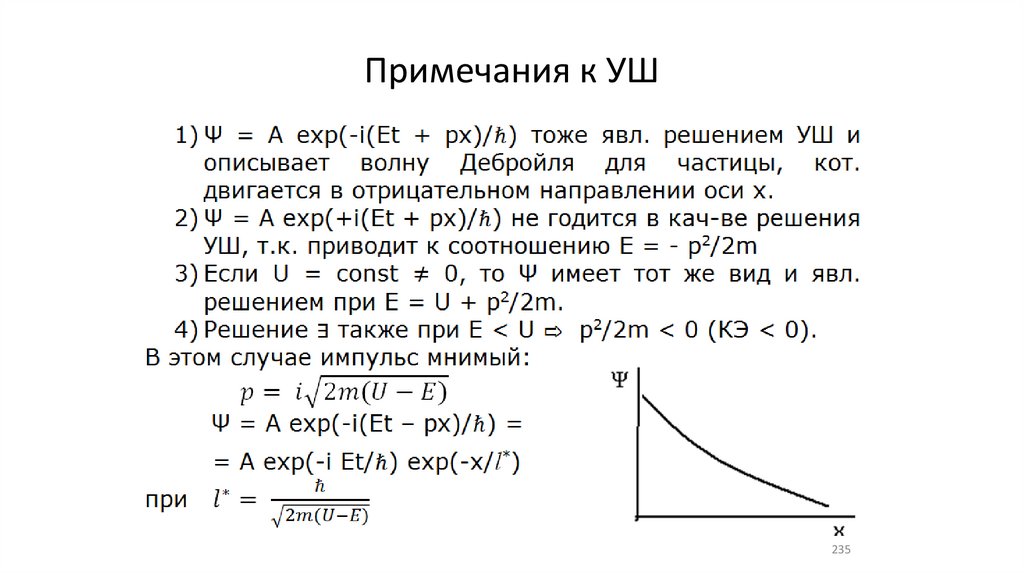
Примечания к УШ235
236.
Смысл волновой функции (волныДебройля)
236
237.
Лекция 11. Уравнение Шредингера11.1. Уравнение Шредингера
1.
2.
3.
Уравнение Шредингера (2,3)
Волновая функция (5,8)
Нестационарное уравнение Шредингера(6,7)
11.2. Динамические переменные
1.
2.
Постулаты квантовой механики (9)
Операторы динамических переменных (10-13)
11.3. Соотношение неопределенностей
1.
2.
3.
Условие одновременной измеримости различных динамических
переменных(14)
Соотношение неопределенностей(15-17)
Примеры(17-21)
237
238.
Уравнение Шредингера238
239.
Уравнение Шредингера для свободнойчастицы (U =0)
239
240.
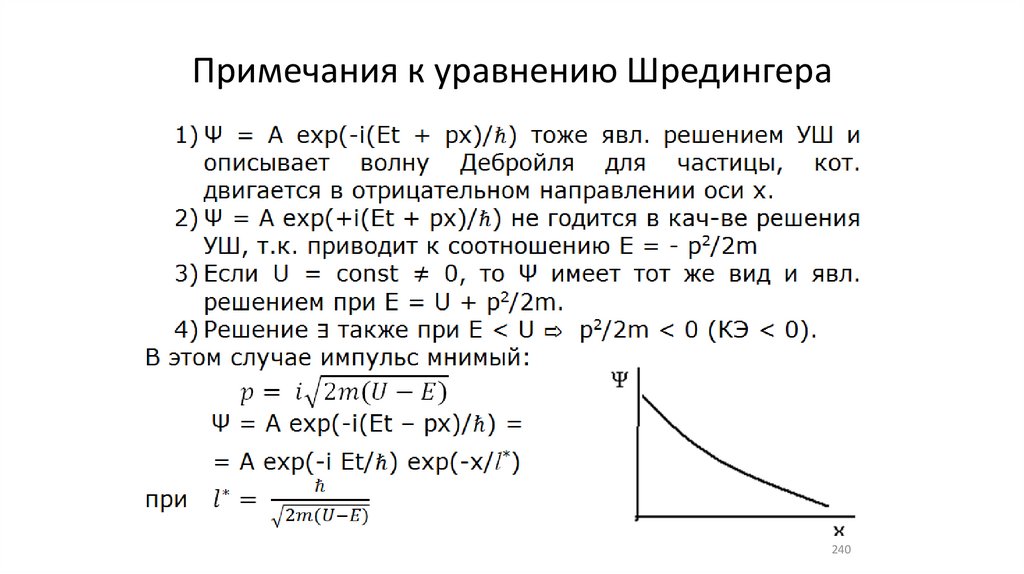
Примечания к уравнению Шредингера240
241.
Физический смысл волновой функции241
242.
Нестационарное уравнение Шредингера242
243.
Плотность заряда и плотность тока243
244.
Принцип суперпозиции состояний244
245.
Постулаты квантовой механики245
246.
Средние значения динамическихпеременных
246
247.
Вид операторов важнейшихдинамических переменных (1)
247
248.
Вид операторов важнейших динамическихпеременных (2)
248
249.
Вид операторов важнейших динамическихпеременных (3)
249
250.
Условие одновременной измеримостиразличных динамических переменных
250
251.
Соотношение неопределенностей251
252.
Соотношение неопределенностейГейзенберга.
253.
Соотношение неопределенностей междупроизвольными физическими величинами
253
254.
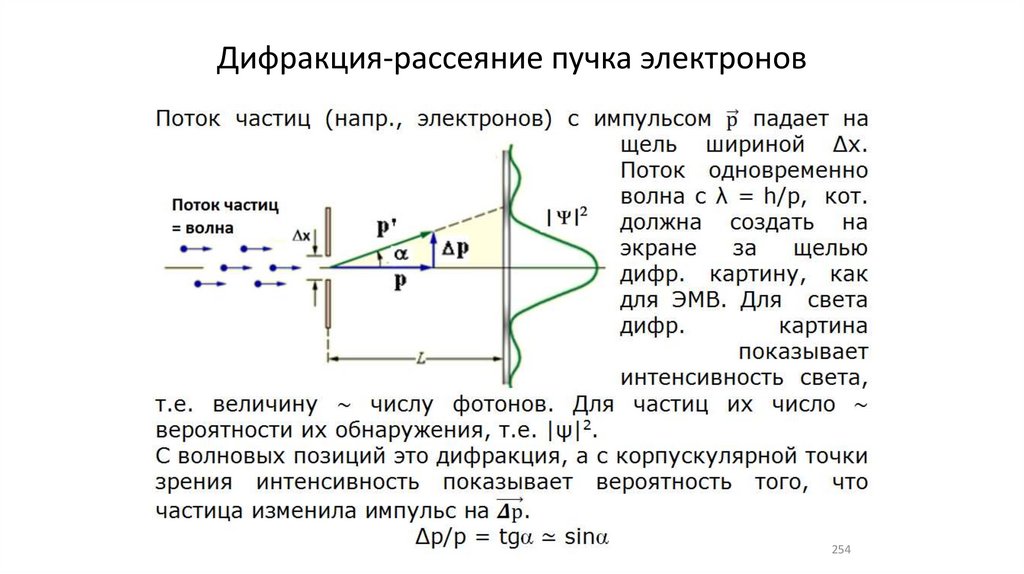
Дифракция-рассеяние пучка электронов254
255.
Дифракция-рассеяние пучка электронов (2)255
256.
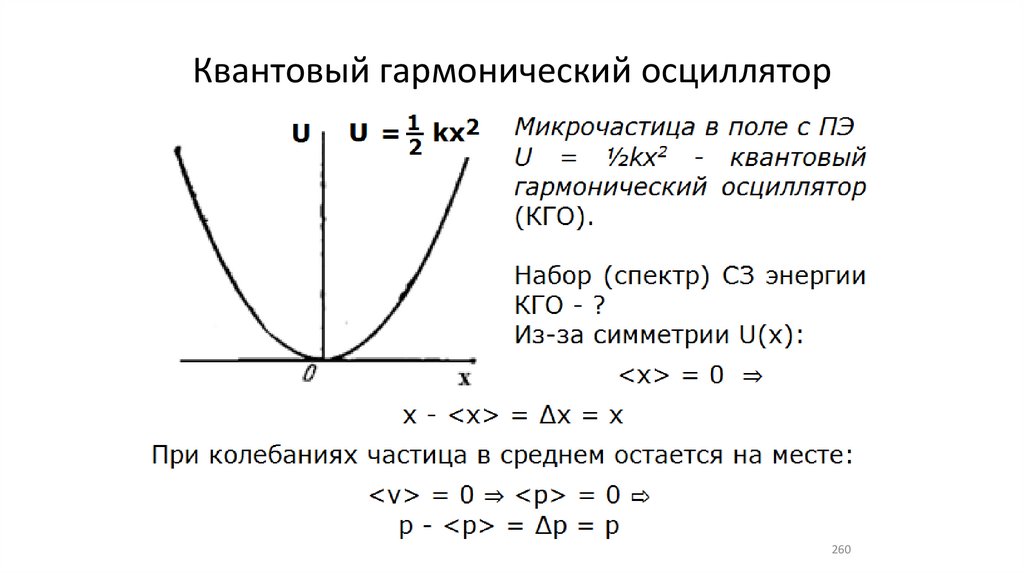
Квантовый гармонический осциллятор256
257.
Нулевые колебания квантового гармоническогоосциллятора
257
258.
Лекция 3.12 Простейшие случаи движениямикрочастиц
12.1. Соотношение неопределенностей
1.
2.
Энергия квантового гармонического осциллятора (2-5)
Нулевые колебания и спектр энергий гармонического осциллятора
(6,7,8)
12.2. Стационарное уравнение Шредингера
1.
2.
3.
Стационарное уравнение Шредингера и задача Штурма-Лиувилля (9,10)
Свободное движение частицы(11-15)
Одномерная прямоугольная потенциальная яма с бесконечными
стенками (16-19)
12.3. Микрочастица и потенциальный барьер
1.
2.
3.
4.
Микрочастица и потенциальный барьер (20-24)
Туннельный эффект (25)
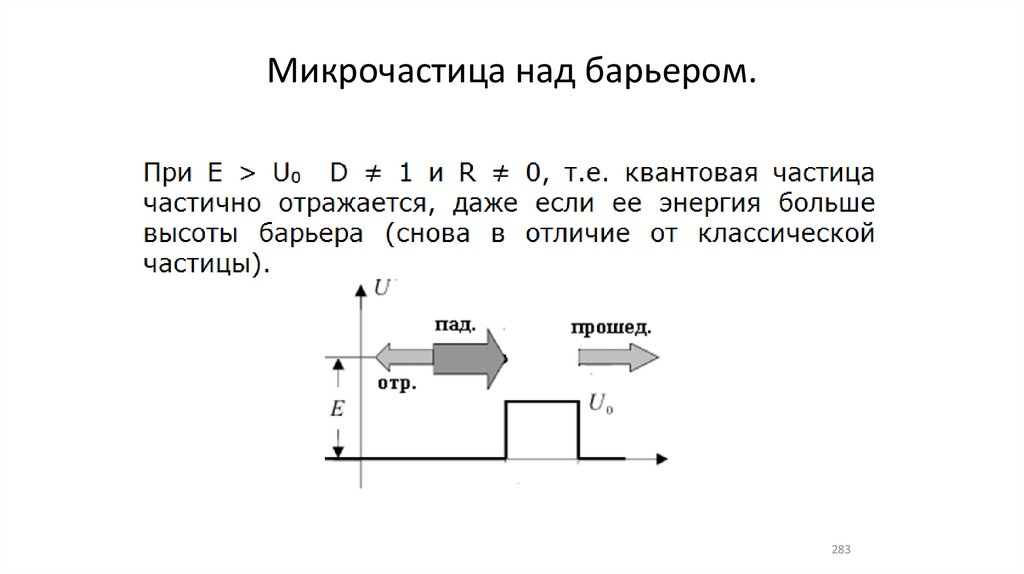
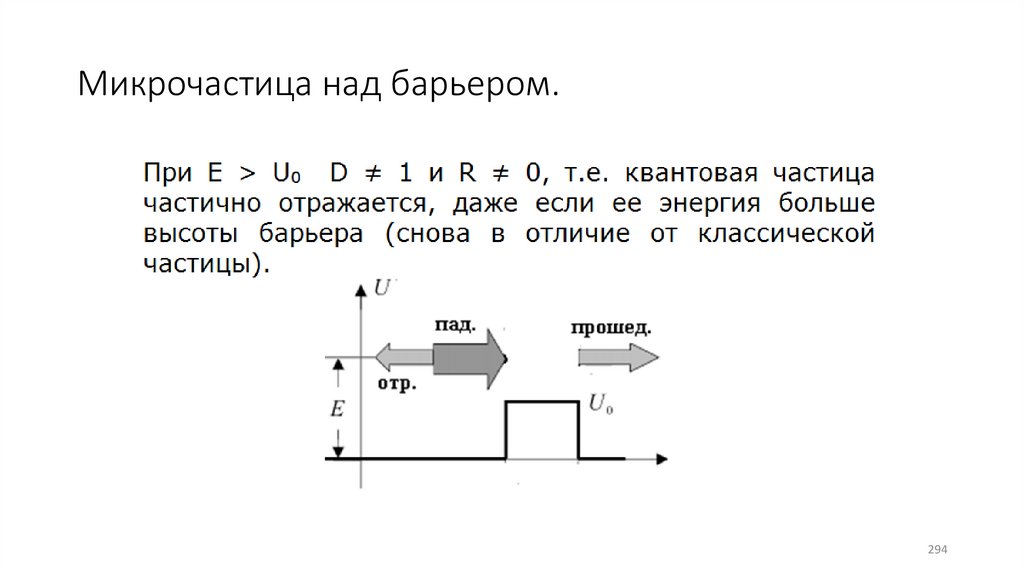
Микрочастица над барьером (26)
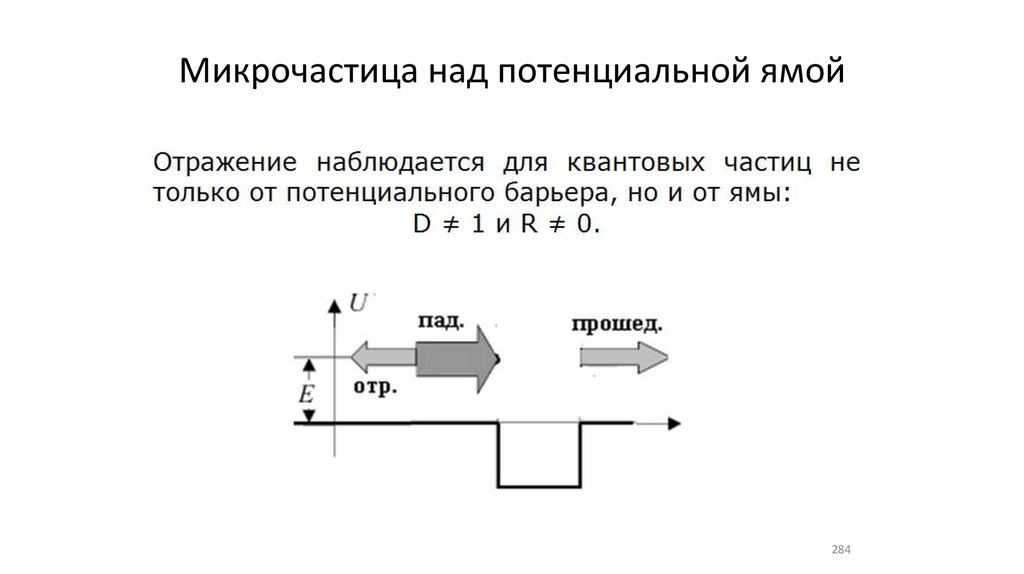
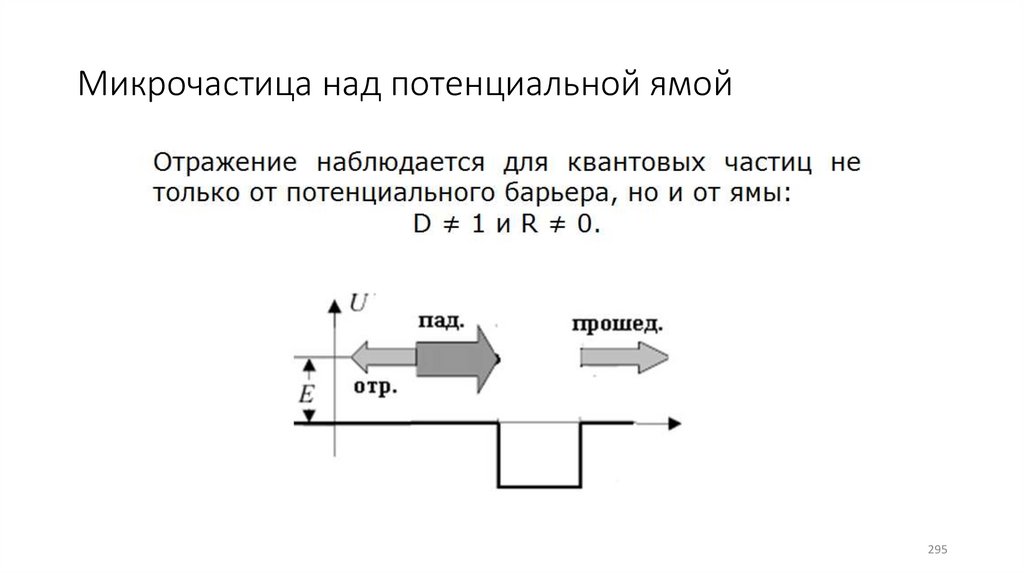
Микрочастица над потенциальной ямой (27)
258
259.
Соотношения неопределенностей.260.
Квантовый гармонический осциллятор260
261.
Энергия квантового гармоническогоосциллятора
261
262.
Минимальная энергия квантовогогармонического осциллятора
262
263.
Минимальное значение энергии квантовогогармонического осциллятора.
263
264.
Нулевые колебания и спектр энергийгармонического осциллятора
264
265.
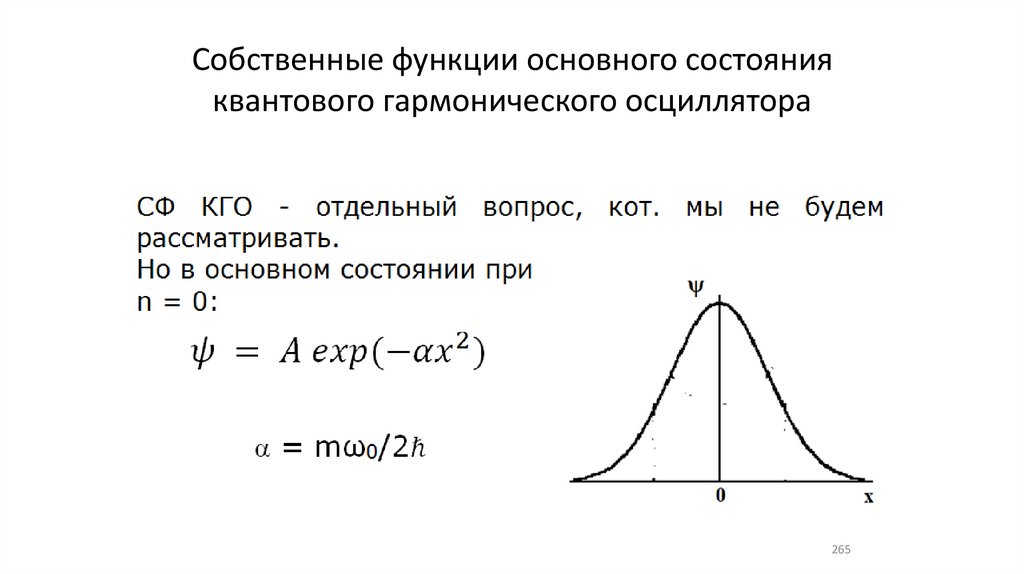
Собственные функции основного состоянияквантового гармонического осциллятора
265
266.
Стационарное уравнение Шредингера266
267.
Стационарное уравнение Шредингера изадача Штурма-Лиувилля
267
268.
Свободное движение частицы. Нахождение волновыхфункций
268
269.
Нормировка на длину периодичности269
270.
Непрерывный спектр270
271.
Плотность заряда и плотность тока271
272.
Свободное движение частицы в трехмерном случае272
273.
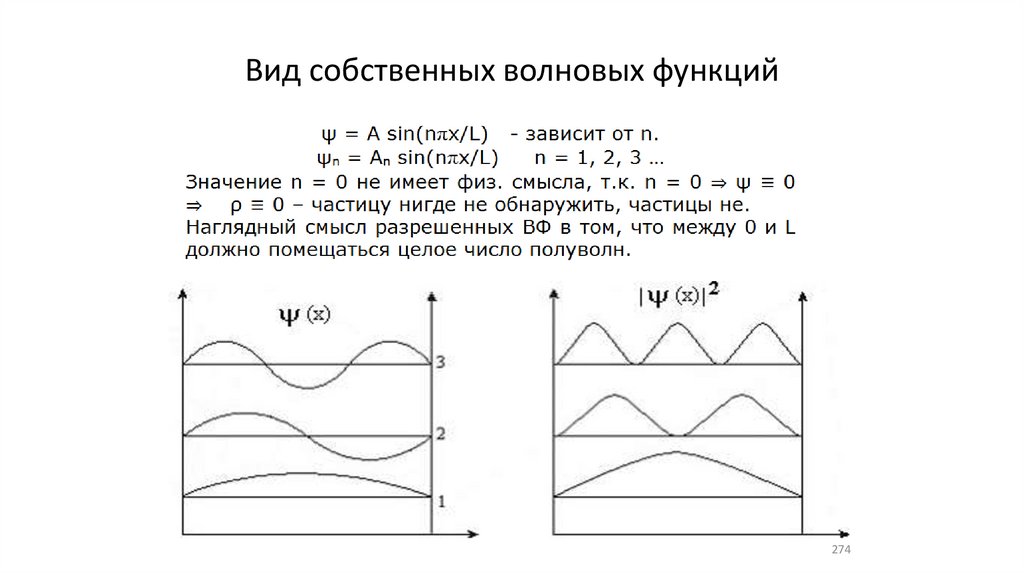
Одномерная прямоугольная потенциальнаяяма с бесконечными стенками
273
274.
Вид собственных волновых функций274
275.
Собственные значения275
276.
Примеры частицы в ПЯ• Молекула в газе - m = 10-26 кг и L = 10-2 м ⇒
Е = 5.10-38 Дж = 3.10-19 эВ
• Электрон в куске металла - m = 10-30 кг и
L = 10-2 м ⇒
Е = 5.10-34 Дж = 3.10-15 эВ
• Электрон в атоме - m = 10-30 кг и
L = 10-10 м ⇒
Е = 5.10-18 Дж = 30 эВ
276
277.
Микрочастица и потенциальный барьер277
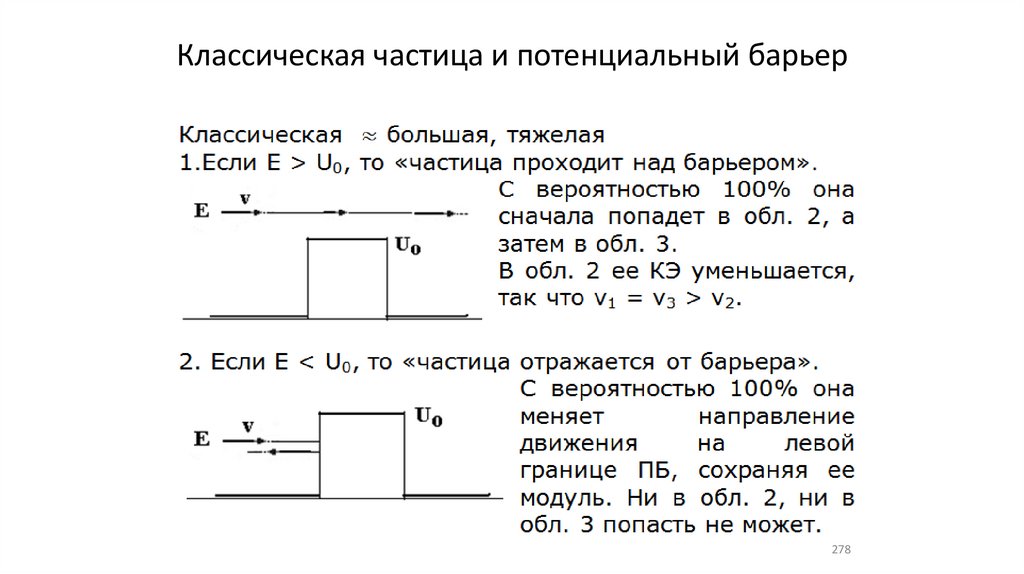
278.
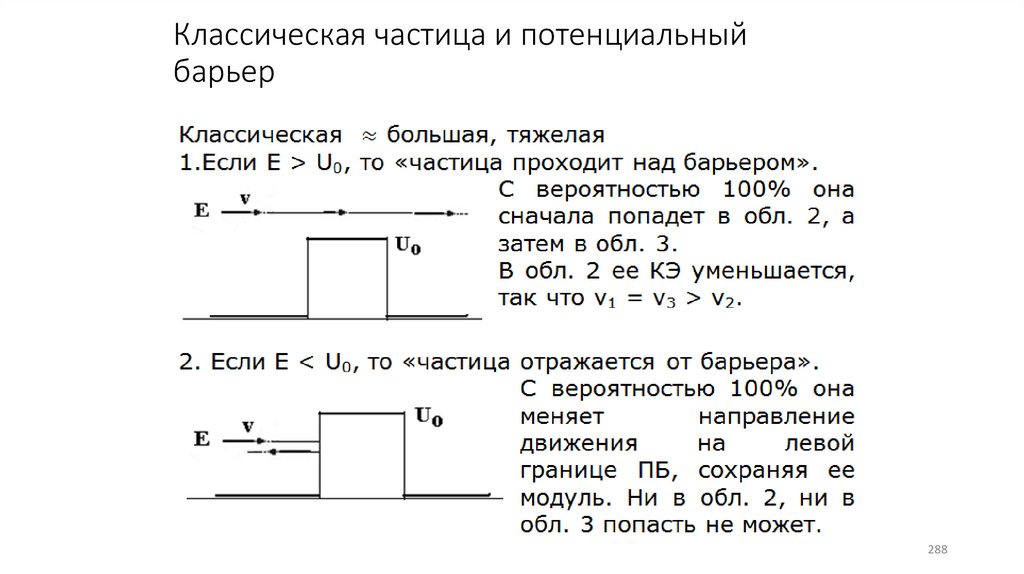
Классическая частица и потенциальный барьер278
279.
Микрочастица слева от потенциальногобарьера
279
280.
Микрочастица в области барьера280
281.
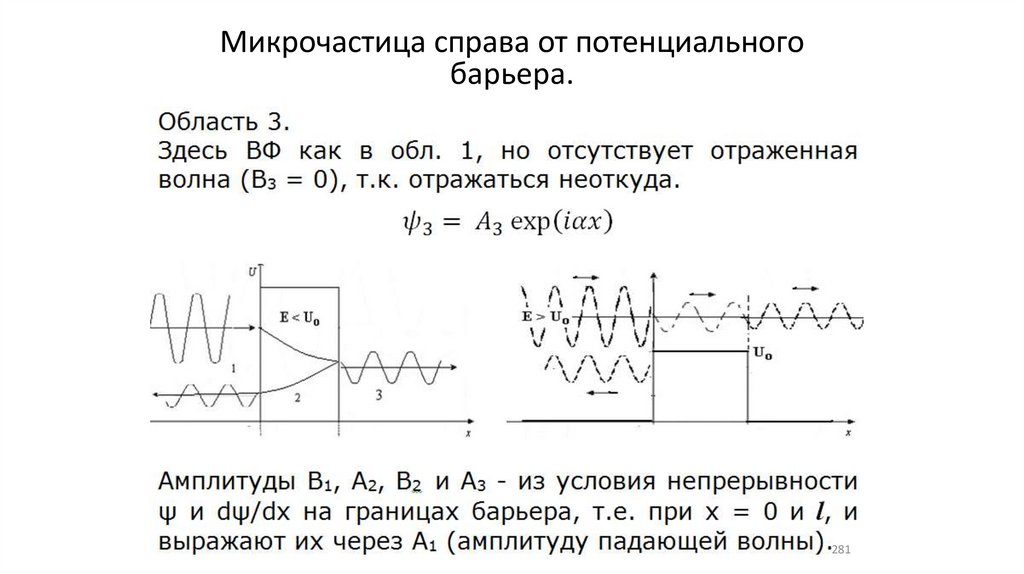
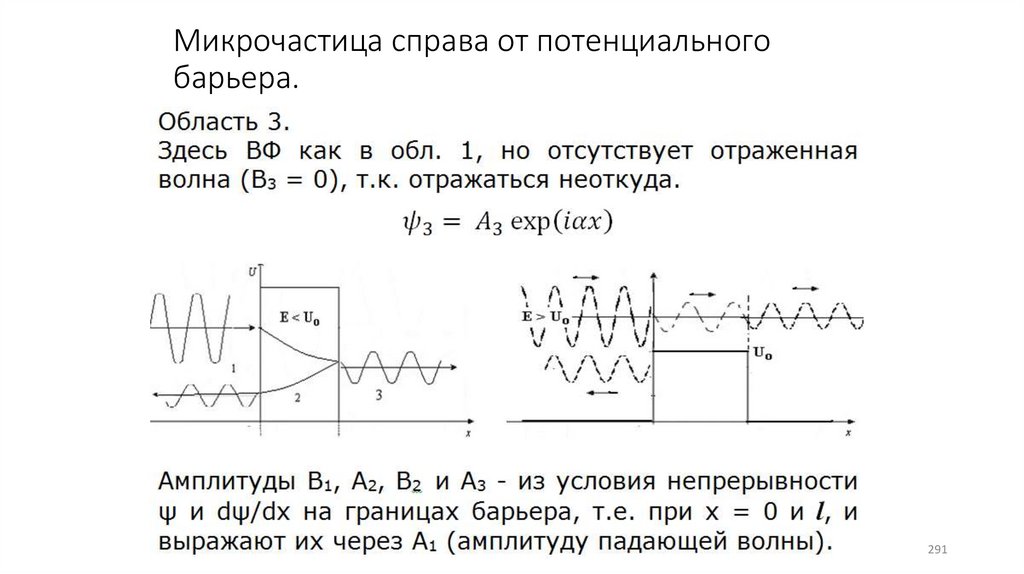
Микрочастица справа от потенциальногобарьера.
281
282.
Микрочастица в области барьера.Туннельный эффект.
282
283.
Микрочастица над барьером.283
284.
Микрочастица над потенциальной ямой284
285.
Лекция 3.13. Движение микрочастиц впотенциальном поле
13.1. Микрочастица и потенциальный барьер
1.
2.
3.
4.
Микрочастица и потенциальный барьер (3-7)
Туннельный эффект.(8)
Микрочастица над барьером (9)
Микрочастица над потенциальной ямой (10)
13.2. Уравнение Шредингера для атома водорода (11)
1.
2.
3.
4.
5.
6.
7.
Уравнение Шредингера для атома Н в сферических координатах(12-14)
Уравнение для угловой части волновых функций (15,16)
Уравнение для радиальных волновых функций (17)
Собственные волновые функции и квантовые числа для атома водорода (18)
Модель Бора-Резерфорда и уравнение Шредингера (19)
Радиальные волновые функции (примеры) (20-23)
Спектры энергии атома водорода и водородоподобного иона (24)
285
286.
Свободное движение частицы.286
287.
Микрочастица и потенциальный барьер287
288.
Классическая частица и потенциальныйбарьер
288
289.
Микрочастица слева от потенциального барьера289
290.
Микрочастица в области барьера290
291.
Микрочастица справа от потенциальногобарьера.
291
292.
Микрочастица в области барьера.Туннельный эффект.
292
293.
Радиоактивныйраспад
294.
Микрочастица над барьером.294
295.
Микрочастица над потенциальной ямой295
296.
Уравнение Шредингера для атома водорода296
297.
Сферические координаты для решения уравнениеШредингера
297
298.
Уравнение Шредингера для атома Н в сферическихкоординатах
Δψ=(1/r2)∂∕∂r(r2∂ψ∕∂r)+(1/r2sinθ)∂∕∂θ(sinθ∂ψ∕∂θ)
+(1/r2sin2θ)∂2ψ∕∂φ2
ψ = R(r) Y(θ,φ)
(1/r2)∂∕∂r(r2∂R∕∂r)Y + (1/r2sinθ)∂∕∂θ(sinθ∂Y∕∂θ)R +
(1/r2sin2θ)∂2Y∕∂φ2R + (2m/ℏ2)(Е + (1/4πε0)(e2/r))RY = 0
Это уравнение нужно умножить на r2/RY:
(1/R)∂∕∂r(r2∂R∕∂r) + (2m/ℏ2)r2(Е + (1/4πε0)(e2/r)) =
= - (1/Y)((1/sinθ)∂∕∂θ(sinθ∂Y∕∂θ) + (1/sin2θ)∂2Y∕∂φ 2)
298
299.
Разделение на радиальную и угловую части(1/R)∂∕∂r(r2∂R∕∂r) + (2m/ℏ2)r2(Е + (1/4πε0)(e2/r)) =
= - (1/Y)((1/sinθ)∂∕∂θ(sinθ∂Y∕∂θ) + (1/sin2θ)∂2Y∕∂φ2)
ЛЧ зависит только от r, а ПЧ только от θ и φ. ⇨
обе они не зависят от этих переменных ⇨
это некоторая константа λ.
∂∕∂r(r2∂R∕∂r) + [(2m/ℏ2)r2(Е + (1/4πε0)(e2/r)) – λ]R = 0
(1/sinθ)∂∕∂θ(sinθ∂Y∕∂θ) + (1/sin2θ)∂2Y∕∂φ2)+λY = 0
УШ распалось на 2 отдельных ДУ, но с общим параметром λ.
Какие значения может принимать λ?
299
300.
Уравнение для угловой части волновыхфункций
(1/sinθ)∂∕∂θ(sinθ∂Y∕∂θ) + (1/sin2θ)∂2Y∕∂φ2)+λY = 0
Это ур-ние не содержит указаний на то, что оно
относится к атому Н – нет ни вида ПЭ, ни массы
электрона, ни его заряда.
Это одно из стандартных ДУ математической физики.
Его решения - стандартные функции, зависящие от 2
целочисленных параметров l и m – сферические
гармоники Ylm.
Ylm(θ,φ) = A Plm(cosθ) eimφ
300
301.
Угловые волновые функцииYlm(θ,φ) = A Plm(cosθ) eimφ
Plm(cosθ) – присоединенные полиномы Лежандра,
полиномы степени l, их аргумент cosθ, а
коэффициенты (их можно найти в таблицах) зависят
от l и m.
Параметры сферических гармоник: 0 ≤ l < ∞;
-l≤
m ≤ l (т.е. их 2 l + 1 штука)
Решения ДУ для Y(θ,φ) существуют не всегда, а только
при значениях параметра λ = l (l + 1).
301
302.
Уравнение для радиальных волновых функций302
303.
Полная СВФ и квантовые числа для атома Н303
304.
Гамильтониан для движения частицы вцентрально-симметричном поле
305.
Модель Бора-Резерфорда и уравнение Шредингера305
306.
Обозначения электронов в атоме307.
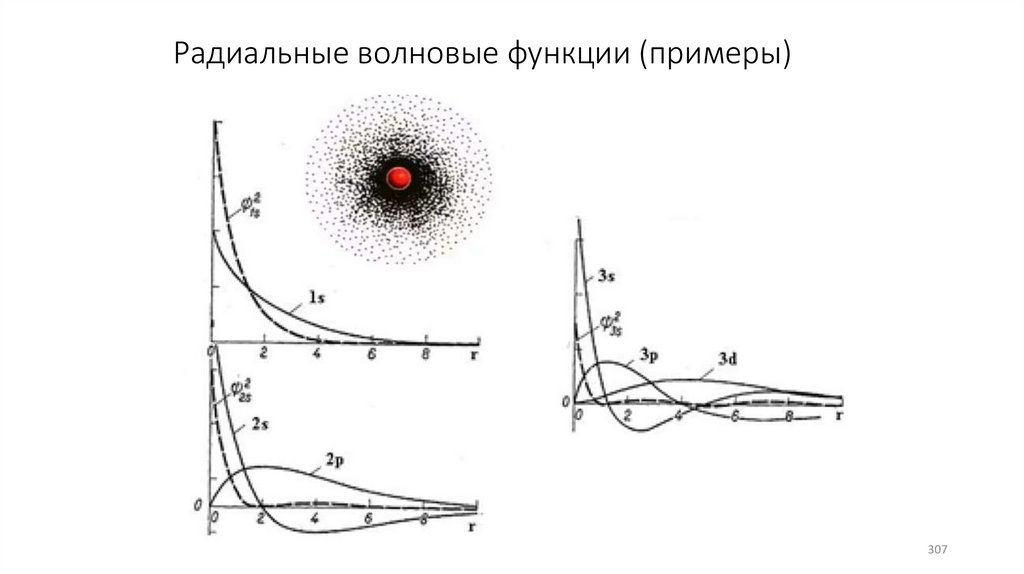
Радиальные волновые функции (примеры)307
308.
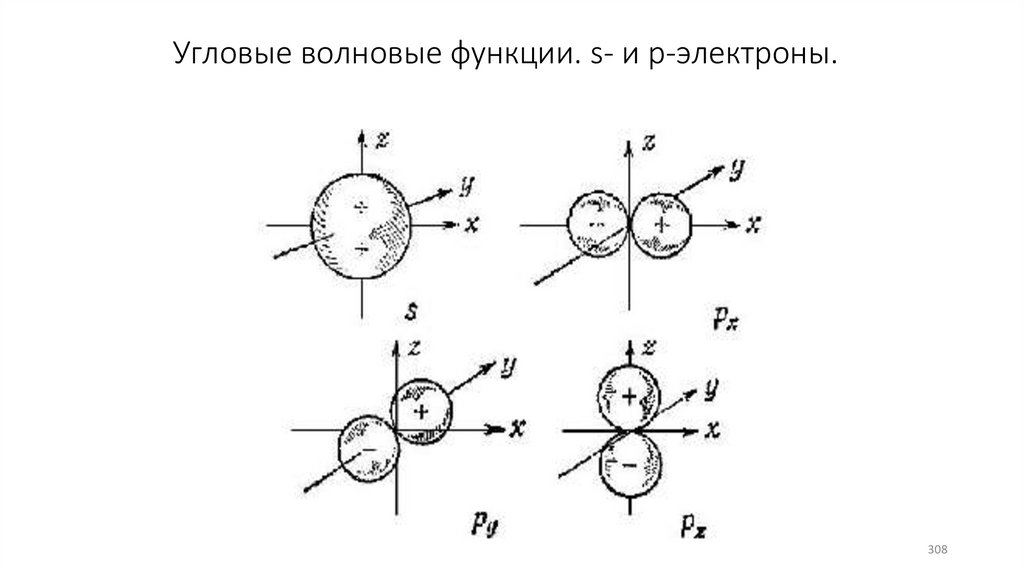
Угловые волновые функции. s- и р-электроны.308
309.
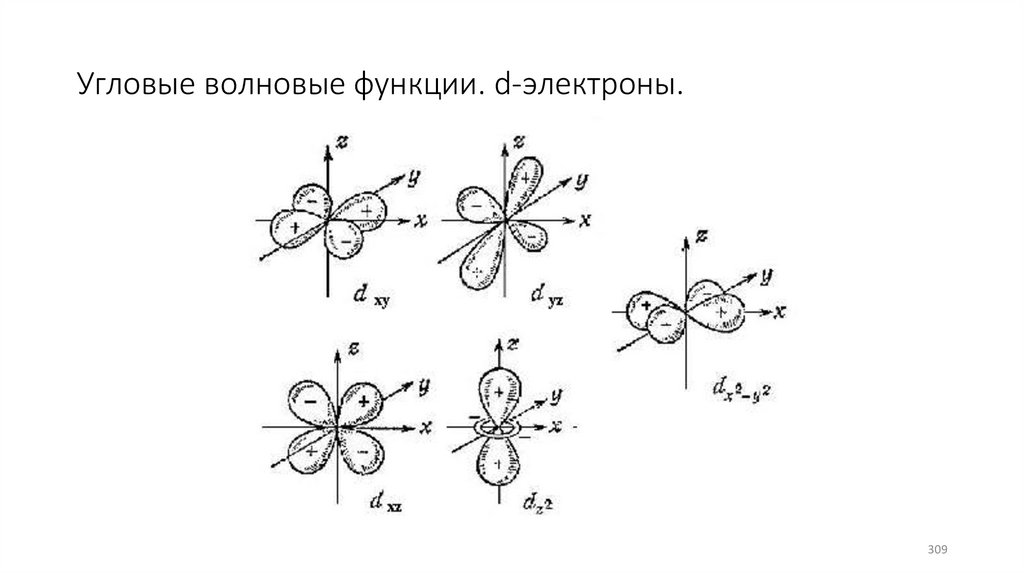
Угловые волновые функции. d-электроны.309
310.
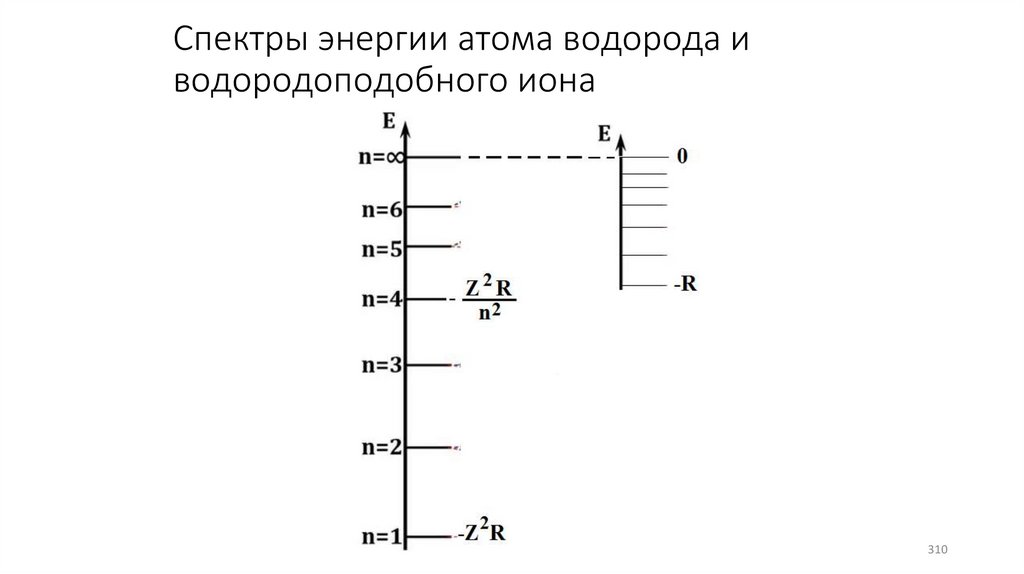
Спектры энергии атома водорода иводородоподобного иона
310
311.
Лекция 3.14: Строение атомов. Квантоваястатистика
14.1. Многоэлектронные атомы (2)
1.
2.
3.
Энергии электронов в МЭ атомах(3,4)
Характеристическое рентгеновское излучение(5 - 7)
Рентгеновский спектр поглощения(8)
14.2. Квантовая статистика (9,10)
1.
2.
3.
4.
5.
6.
7.
8.
Бозоны и фермионы (11,12)
Распределение Ферми-Дирака (13,14)
Разрешенные и запрещенные зоны в кристаллах (15)
Плотность состояний электронов в разрешенной зоне (16)
Электроны в металле (17,18)
Концентрации электронов и дырок в полупроводниках (19,20)
Распределения Ферми-Дирака и Планка(21)
Распределение Бозе – Эйнштейна (22,23)
311
312.
Многоэлектронные атомы312
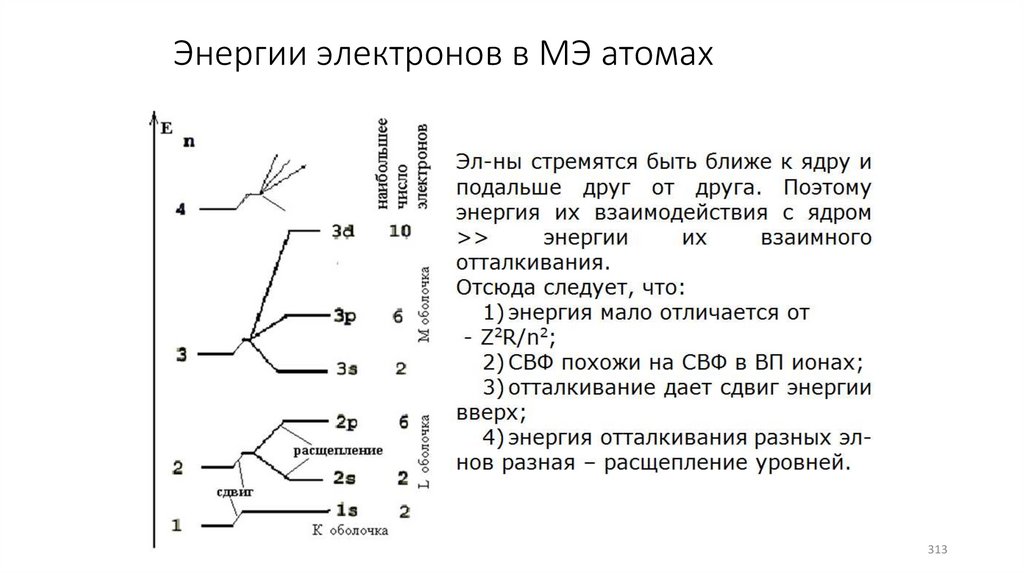
313.
Энергии электронов в МЭ атомах313
314.
Заполнение электронных оболочек314
315.
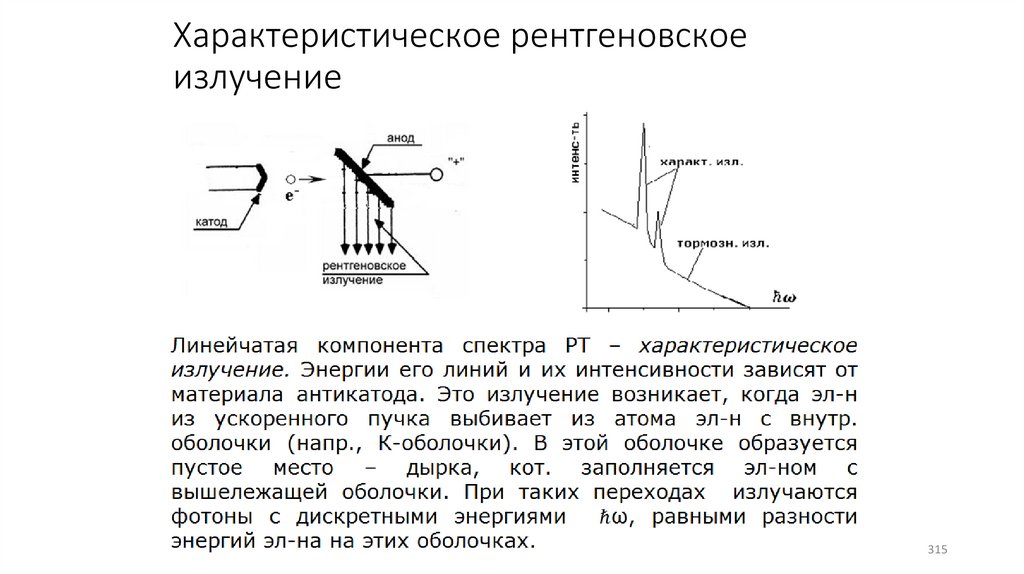
Характеристическое рентгеновскоеизлучение
315
316.
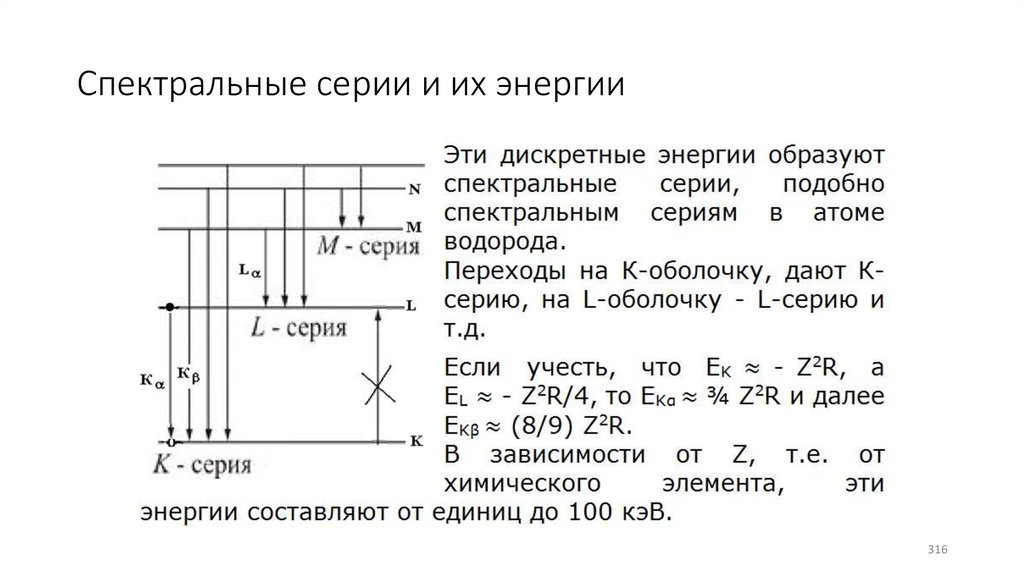
Спектральные серии и их энергии316
317.
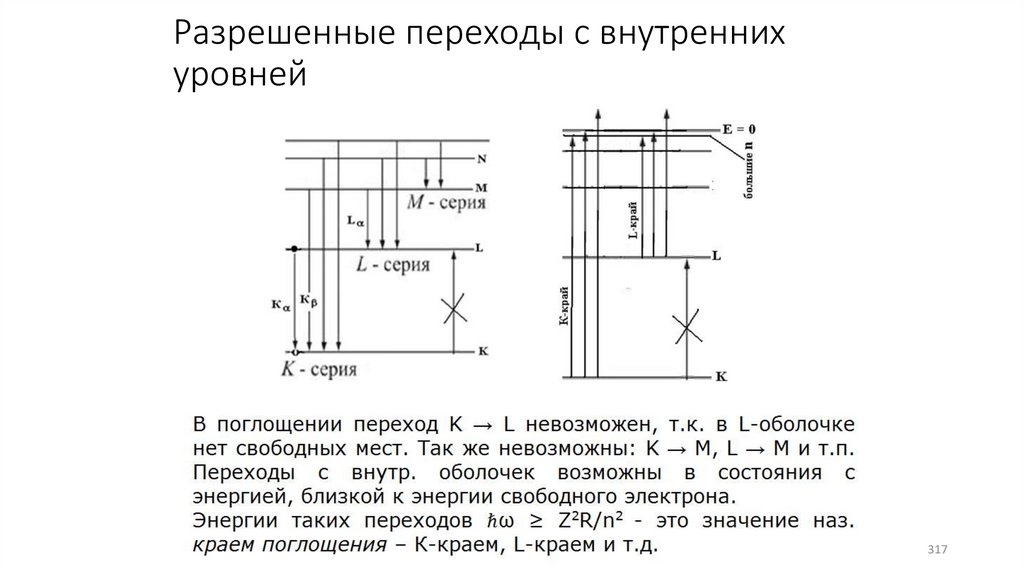
Разрешенные переходы с внутреннихуровней
317
318.
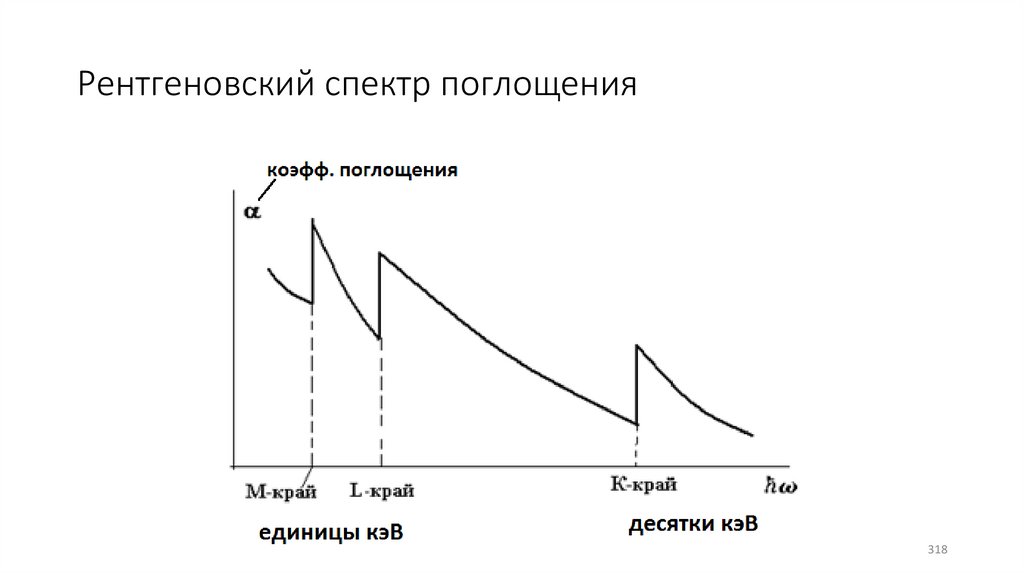
Рентгеновский спектр поглощения318
319.
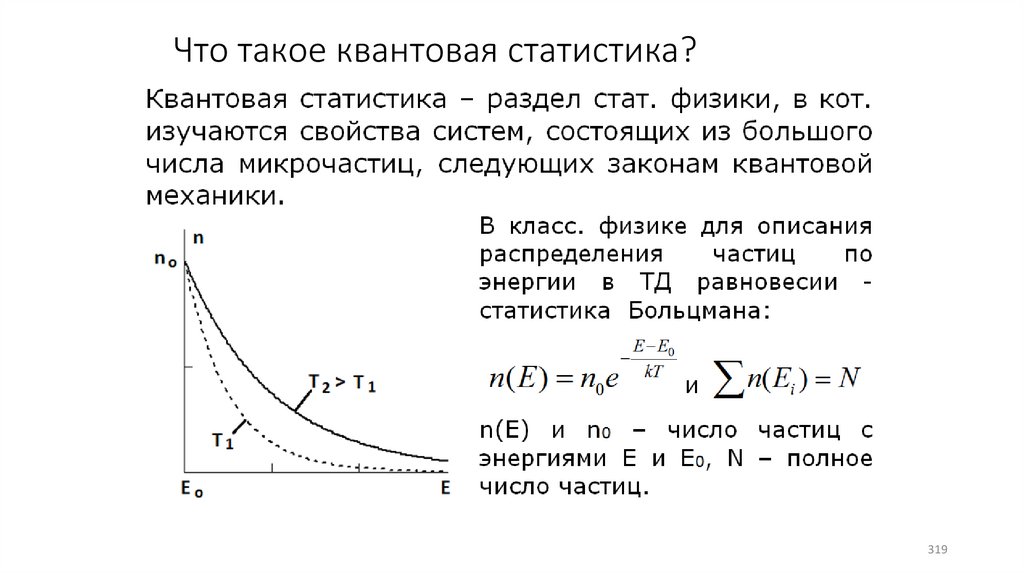
Что такое квантовая статистика?319
320.
Почему не Больцман?320
321.
Симметрия ВФ: бозоны и фермионы321
322.
Волновая функция двух бозонов322
323.
Фермионы – распределение ФермиДирака323
324.
Свойства функции Ферми324
325.
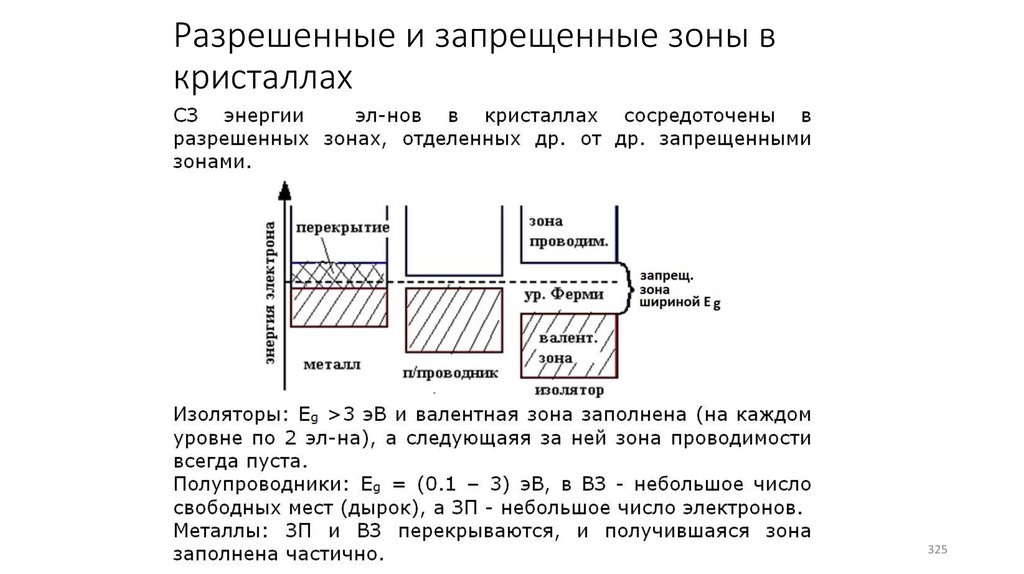
Разрешенные и запрещенные зоны вкристаллах
325
326.
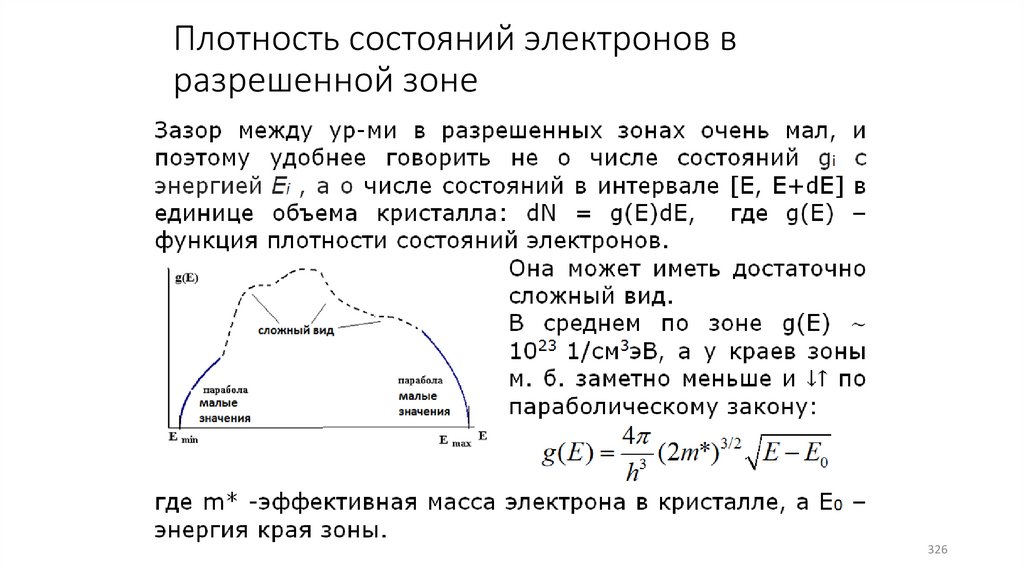
Плотность состояний электронов вразрешенной зоне
326
327.
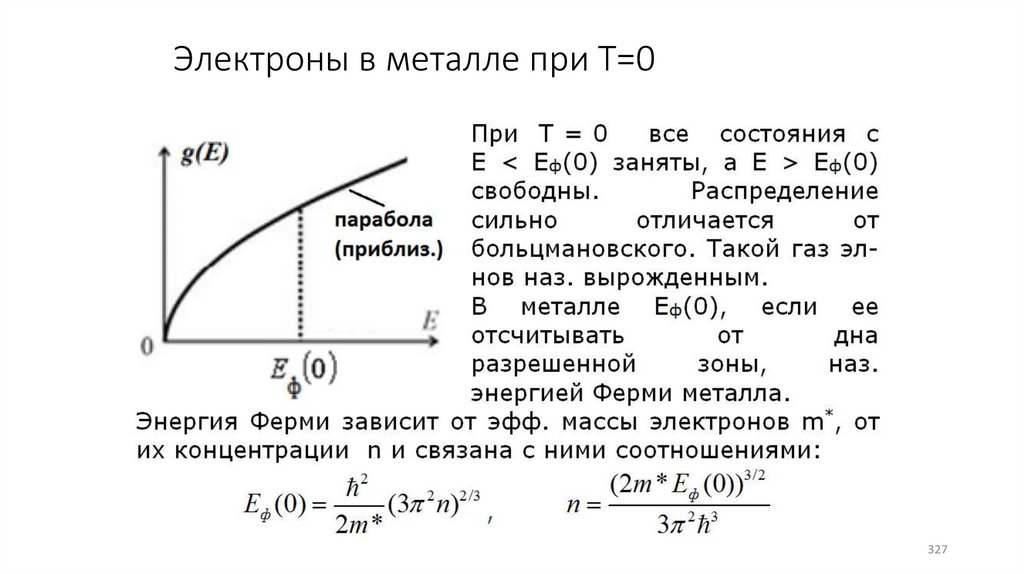
Электроны в металле при Т=0327
328.
Электроны в металле при Т > 0328
329.
Концентрация электронов в зонепроводимости полупроводника
329
330.
Концентрации электронов и дырок вполупроводниках
330
331.
Распределения Ферми-Дирака и Планка331
332.
Распределение Бозе-Эйнштейна332
333.
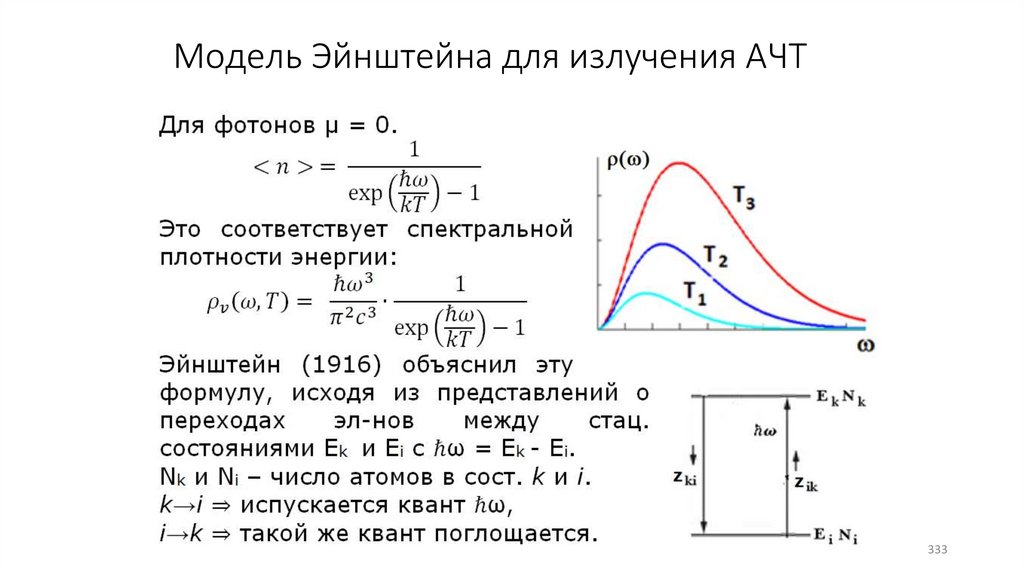
Модель Эйнштейна для излучения АЧТ333







































































































































































































 physics
physics








