Применение интеграла в физике и геометрии

1.

И4
Применение интеграла в физике
и геометрии

2.

1. Вычислите:
1 1
7 9
21
1 :1 =
∙
=
6 9
6 10 20
1 21 13 21 65−21 44 11
= = = 2,2
−
=
3 −
=
20
4 20
20 5
4 20
2,2: 2,2 = 1

3.

Повторение
Определение первообразной:
Свойство первообразной:
Определение неопределённого интеграла:
Определение определённого интеграла:
Геометрический смысл определённого интеграла:

4.

Определённый интеграл
Подстановка (замена переменной)
1 t4
2 4
Конечно мы делаем только
математическую запись:

5.

Неопределённый интеграл
Подстановка (замена переменной)
7
7
dt
2
7
x
1
t
6
t
2
7
x
dx
7 7 7 C 49 C
2 7x t
6
7dx dt
dt
dx
7

6.

Определённый интеграл
Подстановка (замена переменной)
5
5
x 2
sin
t
4
4
sin x cos xdx t dt 5 5
2
2
sin x t
5
5
sin sin
cos xdx dt
1 1 2
2 2
5
5
5 5 5
2

7.

Неопределённый интеграл
Подстановка (замена переменной)
xdx
3x 2 4
3x 2 4 t
6 xdx dt
dt
xdx
6
1
dt 1
2
ln
t
C
ln
3
x
4 C
6t 6
6

8.

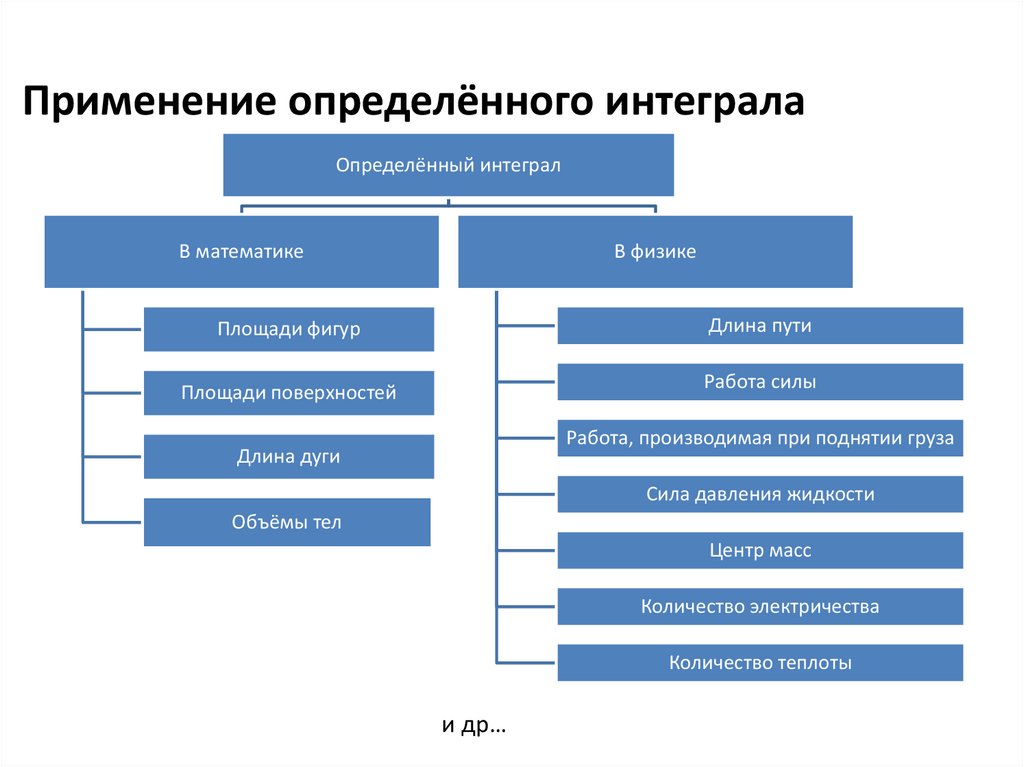
Применение определённого интеграла
Определённый интеграл
В математике
В физике
Длина пути
Площади фигур
Работа силы
Площади поверхностей
Работа, производимая при поднятии груза
Длина дуги
Сила давления жидкости
Объёмы тел
Центр масс
Количество электричества
Количество теплоты
и др…

9.

Применение определённого интеграла
Задача: Вычислите количество электричества,
протёкшего по проводнику за промежуток времени [3; 4],
если сила тока задана формулой: I(t)=3t2-2t.
q 3t 2 t dt t t
4
3
2
3
2
3 64 16 27 9 48 18 30 Кл
4

10.

Применение определённого интеграла
Задача: Вычислите работу А за промежуток
времени [1; 4], если мощность вычисляется
по формуле N( t )
4
6
t
4
6dt
A
6 2 t 12 4 12 1 12 Дж
1
t
1

11.

Домашнее задание
1. Вычислите:
x 2 dx
2. Найдите неопределённый интеграл: 3
dx
6x 1
3. Вычислите определённые интегралы:
1, 25
5 4x dx
6
1
6
cos
x ( sin x ) dx
0
4. Решите задачу:
Количество заражённых в начальный момент времени 7 человек. Закон
скорости заражения от 1 человека в зависимости от времени y=6x+1 за один
день. Сколько ожидается заражённых через 3 дня?

12.

Домашнее задание (ответы)
1. 2
2. Найдите неопределённый интеграл:
x 2 dx
1
3
dx
ln
6
x
1 C
6x 3 1 18
3. Вычислите определённые интегралы:
5 4x
5 4x dx
1, 25
7
6
1
28
1.25
1
1
28
7
cos
x
2
6
0 cos x ( sin x ) dx 7 0 7
4. Решите задачу: