Интегралы Фруллани

1. Здравствуйте!

Лекция №15

2.

Интегралы Фруллани
Пусть
1. функция f (x) определена и непрерывна при x 0 ;
2. существует конечный lim f ( x) f ( ) ;
3. 0 a b .
Тогда
x
0
f ( ax) f (bx )
b
dx f (0) f ( ) ln
x
a

3.

Рассмотрим следующий интеграл:
f ( ax) f (bx )
dx .
x
Имеем
f (ax) f (bx )
f (ax)
f (bx )
dx
dx
dx
x
x
x
В первом интеграле сделаем замену переменных z ax , во втором
z bx : получаем
a
b
f ( z)
f ( z)
dz
dz
z
z
a
b

4.

И теперь самое интересное. Посмотрите на области интегрирования
первого и второго интегралов :
a
b
b
a
a
b
У них есть общая часть отрезок [b , a ] . Подынтегральные функции
одинаковы, интегралы вычитаются следовательно, интегралы по
этой области сокращаются. Остается
b
b
f ( z)
f ( z)
dz
dz
z
z
a
a
А теперь срабатывает первая теорема о среднем
b
b
dz
dz
b
b
f ( ) f ( ) f ( ) ln f ( ) ln ,
z
z
a
a
a
a
где a b , a b .

5.

А теперь сделаем предельный переход при 0 , . Тогда
0 , и мы получаем
f (ax) f (bx )
f (ax) f (bx )
b
dx
lim
dx
f
(
0
)
f
(
)
ln
.
0
0
,
x
x
a
f ( ax) f (bx )
dx
называется интегралом
0
x
Полученная формула позволяет легко вычислять их.
Интеграл
Фруллани.

6.

Интегральные неравенства
Неравенство Гёльдера.
Выведем одно из важнейших неравенств математического
анализа неравенство Гёльдера.
Пусть p и q вещественные числа, такие, что
1. p 1, q 1:
1 1
2. (самое главное) 1.
p q
Прежде, чем выводить само неравенство, выведем некоторые
промежуточные формулы, чтобы потом не отвлекаться. Имеем
1
1 p 1
p
p
1
; ( p 1)q p ; q
; q 1
.
1
1
q
p
p
p 1
p 1
p 1

7.

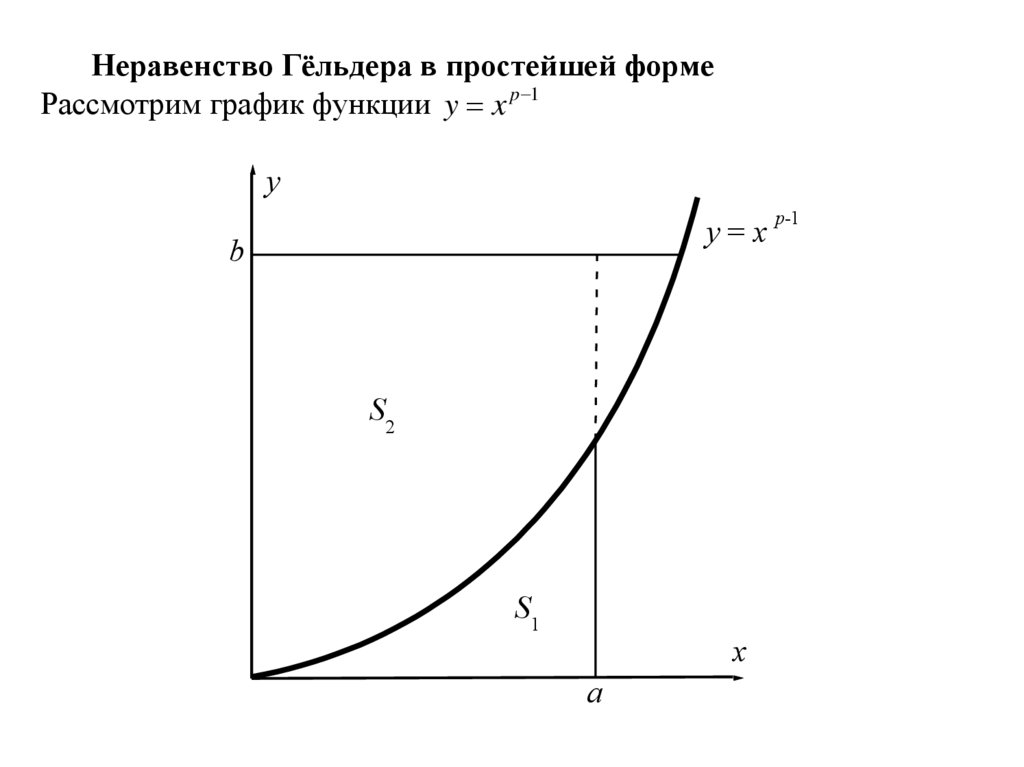
Неравенство Гёльдера в простейшей форме
Рассмотрим график функции y x p 1
y
y=x
b
S2
S1
x
a
p-1

8.

Сосчитаем площади областей, указанных на рисунке. Имеем
a
ap
p 1
S1 x dx .
p
0
Из уравнения y x p 1 , следует, что x y1 ( p 1) y q 1
вспомогательные формулы) и поэтому
b
bq
q 1
S 2 y dy .
q
0
Но, как видно из рисунка, S1 S2 ab , и поэтому
(см.
a p bq
ab
p q
При выводе этой формулы неявно предполагалось, что a 0 и b 0 .
Для произвольных а и b это неравенство можно записать в виде
| a | p | b |q
.
| ab |
p
q
Это и есть знаменитое неравенство Гёльдера.

9.

Неравенство Гёльдера для сумм
Пусть даны два набора чисел {x1 , x2 , x3 , , xn } и { y1 , y2 , y3 , , yn }.
Возьмем в неравенстве Гёльдера
| xi |
| yi |
и
.
a
b
1p
1
q
n
n
p
| xi |
| yi |q
i 1
i 1
Тогда неравенство Гёльдера даёт
| xi yi |
| xi | p
| yi |q
.
n
n
1 p
1q
n
n
p
q
p
q
p
|
x
|
q
|
y
|
i
i
| xi | | yi |
i 1
i 1
i 1
i 1

10.

Складывая все эти неравенства, получим
n
| x y |
i 1
1 p
p
i i
1q
q
|
x
|
|
y
|
i i
i 1
i 1
n
n
1 1
1,
p q
откуда
1 p
1q
p
q
x
y
|
x
y
|
|
x
|
|
y
|
,
i i
i i
i
i
i 1
i 1
i 1
i 1
что и представляет собой неравенство Гёльдера для сумм.
В случае р = 2 также и q = 2 неравенство Гёльдера принимает вид
n
n
n
n
n
n
n
n
x y | x y | x y
i 1
i i
i 1
i i
i 1
2
i
i 1
2
i
.

11.

Неравенство Гёльдера для интегралов
Пусть f (x) и g (x ) две функции, интегрируемые на [a,b].
Возьмем в неравенстве Гёльдера
| f ( x) |
| g ( x) |
и
.
a
b
1 p
1q
b
b
p
q
| f ( x) | dx
| g ( x) | dx
a
a
Тогда неравенство Гёльдера даёт
| f ( x) g ( x) |
| f ( x) | p
| g ( x) |q
.
b
b
1p b
1q
b
p
q
p
q
p
|
f
(
x
)
|
dx
q
|
g
(
x
)
|
dx
| f ( x) | dx | g ( x) | dx
a
a
a
a

12.

Интегрируя это неравенство, получим
b
| f ( x) g ( x) | dx
a
1 p
1q
1 1
1
p q
| f ( x) | p dx | g ( x) |q dx
a
a
откуда получаем
1 p b
1q
b
b
b
p
q
a f ( x) g ( x)dx a | f ( x) g ( x) | dx a | f ( x) | dx a | g ( x) | dx
что и представляет собой неравенство Гёльдера для интегралов.
В случае р = 2 также и q = 2 и неравенство Гёльдера принимает
вид
b
b
a
b
b
f ( x) g ( x)dx | f ( x) g ( x) | dx
a
Это
неравенство
Буняковского Коши Шварца.
b
b
f 2 ( x)dx g 2 ( x)dx .
a
a
называется
неравенством

13.

Неравенство Минковского
Неравенство Минковского для сумм.
Пусть даны два набора чисел {x1 , x2 , x3 , , xn } и { y1 , y2 , y3 , , yn }.
Тогда имеем
| xi | | yi | p | xi | | yi | | xi | | yi | p 1
| xi | | xi | | yi | | yi | | xi | | yi | .
Просуммируем эти выражения и к каждой сумме в правой части
применим неравенство Гёльдера. Тогда получим
1 p
1q
n
n
n
p
( p 1) q
p
|
x
|
|
y
|
|
x
|
|
x
|
|
y
|
i i
i
i
i
i 1
i 1
i 1
p 1
p 1
1 p
1q
( p 1) q
| yi | p | xi | | yi |
.
i 1
i 1
n
n

14.

Но (см. вспомогательные формулы) ( p 1)q p , и мы получаем
1 p
1 p
1q
n
n
n
n
p
p
p
p
|
x
|
|
y
|
|
x
|
|
y
|
|
x
|
|
y
|
i
i
i
i
i
i
i 1
i 1
i 1
i 1
1q
n
p
Деля обе части неравенства на | xi | | yi |
i 1
1 1
1 , получим неравенство
q p
1p
1p
и учитывая, что
1p
1p
p
p
p
p
|
x
y
|
|
x
|
|
y
|
|
x
|
|
y
|
i
i
i
i
i
i
i 1
i 1
i 1
i 1
которое и носит название неравенства Минковского. В частном
случае р = 2 оно принимает вид
n
n
n
xi yi
i 1
2
n
n
x
i 1
2
i
n
n
2
y
i,
i 1
которое Вы знаете еще со школы (длина стороны треугольника
меньше суммы длин двух других сторон).

15.

Неравенство Минковского для интегралов.
Пусть f (x) и g (x ) две функции, интегрируемые на [a,b].
Имеем, аналогично предыдущему,
| f ( x) | | g ( x) | p | f ( x) | | f ( x) | | g ( x) | p 1 | g ( x) | | f ( x) | | g ( x) | p 1
Интегрируя и применяя к каждому интегралу в правой части
неравенство Гёльдера для интегралов, получаем
1 p
1q
b
b
b
p
( p 1) q
p
|
f
(
x
)
|
|
g
(
x
)
|
dx
|
f
(
x
)
|
dx
|
f
(
x
)
|
|
g
(
x
)
|
dx
a
a
a
1 p
p
| g ( x) | dx
a
b
1q
( p 1) q
| f ( x) | | g ( x) |
dx .
a
b

16.

Принимая снова во внимание, что ( p 1)q p будем иметь
b
p
|
f
(
x
)
|
|
g
(
x
)
|
dx
a
1 p
1 p
1q
b
b
b
p
p
p
| f ( x) | dx | g ( x) | dx | f ( x) | | g ( x) | dx
a
a
a
1q
b
1 1
p
Деля на | f ( x) | | g ( x) | dx и снова учитывая, что 1 ,
q p
a
получим неравенство
b
p
| f ( x) g ( x) | dx
a
1 p
b
p
| f ( x) | | g ( x) | dx
a
1 p
1 p
1 p
b
b
p
p
| f ( x) | dx | g ( x) | dx
a
a
которое также носит название неравенства Минковского.

17.

В частном случае р = 2 оно принимает вид
b
b
( f ( x) g ( x)) dx
a
a
2
b
f ( x)dx
2
2
g
( x)dx .
a

18.

Неравенство Иенсена
Это неравенство мы выведем не очень строго.
Пусть
1. f (x) есть выпуклая на [a, b] функция:
b
2. p( x) 0 и
p( x)dx 1;
a
3. (x) непрерывная функция.

19.

Вспомним теперь неравенство Иенсена
n
n
f i xi i f ( xi )
i 1
i 1
и сделаем в нем следующие замены:
i p( xi ) xi , а xi заменим на ( xi ) . Тогда неравенство Иенсена примет
вид
n
n
f ( xi ) p ( xi ) xi p ( xi ) xi f ( ( xi )) .
i 1
i 1
Сделаем теперь в этом неравенстве предельный переход max xi 0 .
i
Тогда суммы перейдут в интегралы, и мы получим неравенство
b
b
f ( x) p ( x)dx f ( ( x)) p ( x)dx .
a
a
Это неравенство и называется неравенством Иенсена в интегральной
форме.

20. Конец третьей части