Similar presentations:
Криволинейные интегралы
1.
Криволинейные интегралыПусть L AB – плоская спрямляемая кривая
x t , y t , a t b , A a , a , B b , b ;
функции f M f x, y , P M P x, y , Q M Q x, y – определены на L .
Задав некоторое разбиение a, b точками a t0 t1 t2
tn b , получим
соответствующие разбиение кривой L n частичных дуг:
A0 A1 , A1 A2 , …, An 1 An , Ak tk , tk , k 0, n .
Выберем на каждой частичной дуге Ak 1 Ak произвольную точку
M k k , k x k , y k , tk 1 k tk .
Пусть lk – длина дуги Ak 1 Ak ( k 1, n ), а l max lk .
k
Составим интегральную сумму
n
1 f k , k lk ,
k 1
Составим две интегральные суммы
n
n
k 1
n
k 1
n
k 1
k 1
2 P k , k xk xk 1 P k , k xk ,
3 Q k , k yk yk 1 Q k , k yk .
1
2.
Составим интегральную суммуСоставим две интегральные суммы
n
n
1 f k , k lk ,
2 P k , k xk ,
k 1
n
k 1
3 Q k , k yk .
k 1
Число I называется пределом интегральной суммы i , i 1,2,3 при l 0 , если
0 0 такое, что разбиения кривой, если l , то i I .
Если существует предел интегральной суммы 1 2 , 3 при l 0 , то он
называется криволинейным интегралом первого (второго) рода от функции
f M f x, y по кривой L и обозначается символом:
или
f M dl f x, y dl ,
P M dx P x, y dx
L
AB
L
Q M dy Q x, y dy .
AB
AB
f M dl f x, y dl .
AB
AB
AB
P M dx Q M dy = P M dx Q M dy –
AB
AB
AB
общий криволинейный интеграл II рода.
2
3.
Для пространственной кривой КИ определяются аналогично:1. КИ1:
f M dl f x, y, z dl .
L
L
2. КИ2:
P M dx P x, y, z dx ,
AB
AB
Q M dy Q x, y, z dy ,
AB
AB
R M dz R x, y, z dz .
AB
AB
3. Общий КИ2:
P M dx Q M dy R M dz .
AB
3
4.
СУЩЕСТВОВАНИЕ КИ И СВЕДЕНИЕ ИХ К R1Теорема 6.1. Если кривая L AB , определяемая уравнениями
x t , y t , a t b , A a , a , B b , b ;
непрерывно дифференцируема и функции f x, y , P x, y и Q x, y
непрерывны на этой кривой, то справедливы следующие формулы,
сводящие КИ к обычным определенным интегралам (R1).
b
КИ1:
f x, y dl f t , t
AB
t t dt. (6.7)
2
2
a
b
КИ2:
P x, y dx P t , t t dt ,
AB
(6.8)
a
b
Q x, y dy Q t , t t dt .
AB
a
(6.9)
4
5.
Теорема 6.1.Если кривая L AB : x t , y t , a t b , A a , a , B b , b – непрерывно
дифференцируема и функции f x, y , P x, y и Q x, y непрерывны на ней, то
b
f x, y dl f t , t t t dt. (6.7)
AB
2
2
a
b
P x, y dx P t , t t dt ,
(6.8)
a
AB
R1, стоящие в правых частях формул, заведомо существуют (в силу непрерывности подынтегральных функций).
Разобьем a, b точками a t0 t1 t2
tn b на n частичных сегментов.
Учитывая, что длина параметрически заданной
дуги вычисляется по формуле
tk
lk
Учитывая, что по формуле НьютонаЛейбница
tk
t t dt
2
xk xk xk 1 tk tk 1 t dt , (6.11)
2
tk 1
tk 1
для интегральной суммы (6.2) получим
tk
1 f k , k
k 1
tk 1
n
для интегральной суммы (6.3) получим
t t dt , (6.10)
2
2
tk
2 P k , k t dt , (6.12)
k 1
tk 1
n
k tk 1 , tk .
(существование k обеспечивается непрерывностью t и t )
k tk 1 , tk
5
6.
Обозначим определенные интегралы, стоящие в правых частях формул (6.7) и (6.8), соответственночерез K1 и K2 . Тогда для сделанного выше разбиения можно записать:
n
tk
tk
n
K1 f t , t t t dt.
2
2
K 2 P t , t t dt.
(6.13)
k 1 tk 1
(6.14)
k 1 tk 1
Оценим разности
n
tk
n
1 K1 f k , k
k 1 tk 1
2 K 2 P k , k
k 1 tk 1
2
P t , t t dt . (6.16)
t t dt. (6.15)
f t , t
tk
2
Функции x t , y t непрерывны на a, b , а функции f x, y , P x, y непрерывны на L
f t , t , P t , t непрерывны на a, b .
Функции t и t непрерывны на a, b и не обращаются в нуль одновременно
t t непрерывна и достигает своего max и min на a, b , причем
2
2
t t 0
2
min
tk 1 ,tk
2
Условие l 0 в определении КИ можно заменить условием t 0 , где t max tk tk 1 , так как
k
tk
lk
tk 1
t t dt dt t t t ,
2
2
k
k 1
k
tk 1
t t max t t .
0 min
tk 1 ,tk
tk
2
2
2
tk 1 ,tk
2
6
7.
Отсюда, с учетом непрерывности f t , t и P t , t , получим, что0 0 такое, что при условии l выполняется
f k , k f t , t ,
P k , k P t , t ,
Следовательно,
n
tk
t t dt
1 K1
2
k 1 tk 1
b
2
t t dt l ,
2
2
tk
n
2 K 2 t dt
k 1 tk 1
n
6.17)
M dt M b a ,
(6.18)
k 1 tk 1
a
где l – длина кривой L .
tk
где M max t
a ,b
( t достигает максимума
на a, b , так как является непрерывной на a, b )
В силу произвольности получаем
lim 1 K1 .
l 0
lim 2 K 2 .
l 0
Тем самым одновременно доказано существование криволинейных интегралов, стоящих
в левых частях формул (6.7) и (6.8), и справедливость указанных формул.
7
8.
Замечания:1 . В случае кусочно-гладкой кривой L или кусочно-непрерывных вдоль кривой L функций
f x, y , P x, y и Q x, y КИ по этой кривой определяются как сумма соответствующих КИ по
всем участкам, для которых справедлива теорема.
2 . В случае непрерывно-дифференцируемой пространственной кривой L AB , определяемой
параметрическими уравнениями x t , y t , z t , a t b , для непрерывных на этой
кривой функций f x, y, z , P x, y, z , Q x, y, z и R x, y, z , аналогично доказывается, что
b
P x, y, z dx P t , t , t t dt ,
f x, y, z dl
AB
AB
b
Q x, y, z dy Q t , t , t t dt ,
a
AB
b
f t , t , t
a
t t t dt
2
2
a
b
2
R x, y, z dz R t , t , t t dt
AB
a
3 . Если КИ2 берется по прямой, перпендикулярной одной из осей, то соответствующий
интеграл равен нулю, т.е. если AB прямая и
1) AB Ox , то
P M dx 0 ; 2) AB Oy , то Q M dy 0 ; 3) AB Oz , то R M dz 0 ;
AB
AB
AB
4 . КИ по замкнутому положительно ориентированному контуру:
КИ1:
f M dl ,
L
КИ2:
P M dx Q M dy R M dz .
L
8
9.
СВОЙСТВА КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВВо всех свойствах предполагается существование интегралов.
1 . Линейность. Если , , то
f M g M dl f M dl g M dl ;
L
L
L
P M dx Q M dy P M dx Q M dy
P M P M dx Q M Q M dy
1
1
2
2
L
1
2
1
2
L
P1 M dx Q1 M dy P2 M dx Q2 M dy .
L
L
2 . Аддитивность. Если дуга AB составлена из двух дуг AC и CB , то
f M dl f M dl f M dl ;
AB
AC
CB
P M dx Q M dy P M dx Q M dy P M dx Q M dy.
AB
AC
CB
3 . Если M L f M g M , то f M dl g M dl .
L
L
9
10.
4 . Оценка модуля интеграла:f M dl f M dl .
L
L
5 . Теорема о среднем: f M dl l f M * , где l – длина кривой L .
L
Если f непрерывна, то M * L .
6 . Зависимость от направления обхода кривой:
– КИ1 не зависит;
– КИ2 меняет знак при изменении направления на кривой:
P M dx P x, y dx ,
AB
BA
Q M dy Q x, y dy ,
AB
BA
R M dz R x, y dz ;
AB
BA
P M dx Q M dy R M dz P M dx Q M dy R M dz .
AB
BA
В случае замкнутой кривой для КИ2 из двух возможных направлений
10
обхода всегда надо выбирать положительное.
11.
СВЯЗЬ МЕЖДУ КИ1 И КИ2Теорема 6.2. Если AB – простая непрерывно дифференцируемая кривая без
особых точек, а функции P и Q непрерывны на , то справедлива формула
Pdx Qdy P cos Q cos dl ,
(6.19)
где ( ) угол, составленный с осью Ox ( Oy ) касательной, направленной в сторону
возрастания параметра дуги.
– непрерывно дифференцируемая кривая без особых точек
можно представить параметрическими уравнениями
2
2
x t , y t , a t b , t , t 1 a, b , и t a, b t t 0 .
Касательный вектор в каждой точке кривой сонаправлен с вектором t , t
cos
t
t t
2
2
,
cos
t
t t
2
2
.
КИ2, стоящий в левой части равенства (6.19) преобразуется к виду
b
Pdx Qdy P t Q t dt .
a
К этому же интегралу преобразуется и КИ1, стоящий в правой части равенства (6.19),
если учесть, что
2
2
11
dl 2 dx 2 dy 2 t t dt 2
12.
Pdx Qdy P cos Q cos dl ,(6.19)
Замечания
1 . Для КИ1 и КИ2 по пространственной гладкой кривой, аналогично доказывается формула
Pdx Qdy Rdz P cos Q cos R cos dl ,
(6.20)
в которой P , Q и R – функции, непрерывные на кривой L , а cos ,cos ,cos –
направляющие косинусы касательной, направление которой отвечает направлению пути интегрирования.
2 . Формулы (6.19), (6.20) верны и в том случае, если кривая может быть
разбита конечным количеством точек на несколько участков, на каждом из
которых выполняются условия теоремы.
3 . Если изменить направление кривой в формулах (6.19), (6.20), то не только
интеграл слева (КИ2) изменит знак, но и ввиду изменения направления касательной угол изменится на , в связи с чем изменит знак и интеграл справа (КИ1).
12
13.
Формула Грина иее приложения
13
14.
Теорема 6.3. Пусть G – плоская область, ограниченнаяграфиками непрерывных функций y0 x и Y x и прямыми
x a и x b , причем x a, b y0 x Y x , а в G задана
функция P x, y , непрерывная на G вместе с производной
P
.
y
y
y Y x
R
S
y y0 x
F
Q
Тогда справедлива формула
P
G y dxdy L Pdx ,
a
b
в которой КИ2 берется по границе L области G в положительном ее направлении.
14
x
15.
Теорема 6.3. Пусть G – плоская область, ограниченнаяграфиками непрерывных функций y0 x и Y x и прямыми
y
x a и x b , причем x a, b y0 x Y x , а в G задана
функция P x, y , непрерывная на G вместе с производной
P
.
y
y Y x
R
S
y y0 x
F
Q
Тогда справедлива формула
P
G y dxdy L Pdx ,
a
b
x
в которой КИ2 берется по границе L области G в положительном ее направлении.
Учитывая, что P x, y dx 0 и P x, y dx 0 , так как FS Ox и RQ Ox , преобраFS
RQ
P
G y dxdy сначала к повторному, а потом к криволинейному,
получим требуемое соотношение:
зовав двойной интеграл
Y x
P x, y
P
d
xdy
dx
G y
a y x y dy a P x, Y x dx a P x, y0 x dx
0
b
b
b
P x, y dx P x, y dx P x, y dx P x, y dx
SR
FQ
SR
QF
Pdx Pdx Pdx Pdx Pdx .
FS
SR
RQ
QF
L
15
16.
Теорема 6.3. Пусть G – плоская область, ограниченнаяграфиками непрерывных функций y0 x и Y x и прямыми
x a и x b , причем x a, b y0 x Y x , а в G задана
функция P x, y , непрерывная на G вместе с производной
P
.
y
y
y Y x
R
S
y y0 x
F
Q
Тогда справедлива формула
P
G y dxdy L Pdx ,
a
b
x
в которой КИ2 берется по границе L области G в положительном ее направлении.
P
dxdy Pdx справедлива и для областей, которые можно
y
G
L
разбить прямыми параллельными оси Oy на конечное число таких «криволинейных трапеций».
З а м е ч а н и е 1 . Формула
16
17.
Теорема 6.3. Пусть G – плоская область, ограниченнаяграфиками непрерывных функций y0 x и Y x и прямыми
y
R
S
x a и x b , причем x a, b y0 x Y x , а в G задана
функция P x, y , непрерывная на G вместе с производной
y Y x
P
.
y
y y0 x
F
Q
Тогда справедлива формула
P
G y dxdy L Pdx ,
a
b
x
в которой КИ2 берется по границе L области G в положительном ее направлении.
y
Замечание
формулы
2 . Аналогично доказывается справедливость
Q
G x dxdy L Qdy
d
S
R
(6.22)
в предположении, что функция Q непрерывна в G
c
вместе
F
Q
x
Q
. При этом сначала за область G принимается криволинейная трапеция
x
вида, изображенного на рисунке. Затем формула обобщается, как и выше, на случай области, которая разлагается прямыми, параллельными оси Ox, на конечное число «криволиней17
ных трапеций» этого вида.
с производной
18.
Теорема 6.3. Пусть G – плоская область, ограниченнаяграфиками непрерывных функций y0 x и Y x и прямыми
y
x a и x b , причем x a, b y0 x Y x , а в G задана
функция P x, y , непрерывная на G вместе с производной
P
.
y
y Y x
R
S
y y0 x
F
Q
Тогда справедлива формула
P
G y dxdy L Pdx ,
a
(6.21)
b
x
в которой КИ2 берется по границе L области G в положительном ее направлении.
Q
G x dxdy L Qdy (6.22)
З а м е ч а н и е 3 . Формулы (6.21) и (6.22) справедливы для треугольников, а значит, и для
любого многоугольника. Поэтому предельным переходом, аппроксимируя границу конечнозвенными ломаными, можно получить справедливость формул (6.21) и (6.22) для любой
области, граница которой является кусочно-гладкой.
Теорема 6.4 (формула Грина). Если положительно ориентированная граница L
P Q
,
G , то
плоской области G является кусочно-гладкой кривой и P, Q,
y x
Q P
Pd
x
Qd
y
L
G x y dxdy
(6.23)
18
19.
Выражение площади с помощью криволинейных интеграловЕсли функции P и Q в формуле
Q P
Pdx
Qdy
L
G x y dxdy
подобрать так, чтобы
Q P
1 , то двойной интеграл приведется к площади
x y
фигуры G , и мы получим выражение этой площади с помощью того или иного КИ,
взятого по контуру L фигуры:
1) при Q x, P 0
dxdy xdy ;
G
2) при Q 0, P y
3) при Q
L
dxdy ydx ;
G
L
1
1
x, P y
2
2
dxdy
G
1
xdy ydx .
2L
З а м е ч а н и е . Из этих трех формул наиболее употребительной является последняя.
19
20.
Теорема 6.5. Пусть P x, y , Q x, y непрерывны в плоскойобласти G . Тогда следующие три условия эквивалентны:
1) Для любого замкнутого кусочно-гладкого контура L G
Pdx Qdy 0 .
L
2) A, B G КИ2 Pdx Qdy не зависит от кусочно-гладкой
AB
кривой AB G .
3) Выражение Pdx Qdy является в G полным дифференциалом, т.е. в области G существует первообразная функция
F M F x, y такая, что dF Pdx Qdy . При этом для любой
кусочно-гладкой кривой AB G имеет место равенство
Pdx Qdy F B F A .
AB
20
21.
Пусть функции P x, y , Q x, y непрерывны в плоской области G .1) Для любого замкнутого кусочно-гладкого контура L G
Pdx Qdy 0 .
L
2) A, B G КИ2 Pdx Qdy не зависит от кусочно-гладкой кривой AB G .
AB
1)=>2).
Пусть A и B – произвольные точки области G . Рассмотрим две кривые
AB 1 и AB 2 , лежащие в области G и соединяющие эти точки. Объединение
AB 1 BA 2 этих кривых – замкнутый контур, а значит,
Pdx Qdy 0 .
AB 1 BA 2
Учитывая аддитивность КИ2, получим
Pdx Qdy
AB 1 BA 2
Pdx Qdy Pdx Qdy 0 .
AB 1
AB 2
Следовательно,
Pdx Qdy Pdx Qdy .
AB 1
AB 2
21
22.
Пусть функции P x, y , Q x, y непрерывны в плоской области G .2) A, B G КИ2 Pdx Qdy не зависит от кусочно-гладкой кривой AB G .
AB
3) Выражение Pdx Qdy является в G полным дифференциалом, т.е. в области
G существует первообразная функция F M F x, y такая, что
dF Pdx Qdy .
При этом для любой кусочно-гладкой кривой AB G справедливо равенство
Pdx Qdy F B F A .
AB
2)=>3). Так как КИ2 Pdx Qdy , AB G не зависит от пути интегрироваAB
ния, он однозначно определяется заданием точек A x0 , y0 и B x1 , y1 и его можно
B
x1 , y1
A
x0 , y0
обозначить Pdx Qdy или
Pdx Qdy .
Если точку A x0 , y0 фиксировать, а точку B заменить произвольной точкой
M x, y области G , то полученный КИ2 есть функция от точки M в области G :
F M F x, y
x, y
Pdx Qdy .
x0 , y0
(6.26)
22
23.
Покажем, что функцияy
F M F x, y
x, y
B x1 , y1
Pdx Qdy
C x1 x, y1
x0 , y0
является первообразной для выражения Pdx Qdy .
A x , y
Для этого вычислим частные производные функx
ции F x, y в произвольной точке B x1 , y1 G .
Пусть x – произвольное приращение переменной x , достаточно малое для того, чтобы
отрезок BC , C x1 x, y1 принадлежал G . Тогда
0
F x1 , y1 Pdx Qdy
AB
x1 , y1
Pdx Qdy ,
x0 , y0
F x1 x, y1 Pdx Qdy
ABC
BC Oy
F x1 x, y1 F x1 , y1 Pdx Qdy
BC
0
x1 x , y1
Pdx Qdy .
x0 , y0
x1 x
Pdx P x, y dx ,
1
BC
x1
Согласно теореме о среднем
F x1 x, y1 F x1 , y1
P x1 x, y1 , 0 1 .
(*)
x
Пусть x 0 . В силу непрерывности P x, y правая часть (*) а с нею и левая, стремится
к P x1 , y1 . Следовательно,
F x, y
P x1 , y1 .
x x , y
1
Аналогично устанавливается, что
1
F x1 , y1
Q x1 , y1 .
y
23
24.
В силу произвольности выбора точки x1 , y1 , можем утверждать, чтоF
F
P,
Q.
x, y G
x
y
Так как частные производные непрерывны, то функция F x, y имеет дифференциал
F
F
dF
dx
dy Pdx Qdy , т.е. существование первообразной доказано.
x
y
Предположим теперь, что нам известна еще одна первообразная функция M для
выражения Pdx Qdy , т.е.
F
F
dF
dx
dy Pdx Qdy ,
d
dx
dy Pdx Qdy , F
x
y
x
y
Тогда
F
F
dF d 0
dx
y y dy
x
x
F
F
0 и
0 M G F M M C const .
x
y
Пусть M A , тогда
A C F A
Пусть теперь M B
x0 , y0
Pdx Qdy 0 C A F M M A .
x0 , y0
x1 , y1
0 0
Pdx Qdy F B B A x, y x , y .
AB
24
25.
Пусть функции P x, y , Q x, y непрерывны в плоской области G .3) Выражение Pdx Qdy является в G полным дифференциалом, т.е. в G
существует первообразная функция F M F x, y такая, что dF Pdx Qdy .
При этом для любой кусочно-гладкой кривой AB G имеет место равенство
Pdx Qdy F B F A .
AB
1) Для любого замкнутого кусочно-гладкого контура L G справедливо
равенство Pdx Qdy 0 .
L
3)=>1).
Для любого замкнутого контура начальная точка совпадает с конечной
Pdx Qdy F A F A 0 .
L
25
26.
З а м е ч а н и е . Функция F M F x, y может быть найдена по формулеF x, y
x, y
Pdx Qdy C .
x0 , y0
В качестве кривой, соединяющей точки x0 , y0 и x, y часто бывает
удобно брать ломаную, состоящую из двух отрезков, параллельных осям
координат. Например, если соединить точки x0 , y0 и x, y ломаной,
проходящей через
– точку x, y0 , то первообразную можно посчитать по формуле:
x , y0
x, y
x
y
x0 , y0
x , y0
x0
y0
F x, y Pdx Qdy C P x, y0 dx Q x, y dy C ,
– точку x0 , y , то для вычисления первообразной получим формулу:
x0 , y
x, y
y
x
x0 , y0
x0 , y
y0
x0
F x, y Qdy Pdx C Q x0 , y dy P x, y dx C .
26
27.
Плоская область G называется односвязной, если для любогозамкнутого контура, лежащего в этой области, ограниченная им
часть плоскости целиком принадлежит G .
Теорема 6.6. Если функции P x, y , Q x, y непрерывны вместе
со своими частными производными
P Q
,
в плоской односвязной
y x
области G , то каждое из условий 1), 2), 3) теоремы 6.5 эквивалентно
условию:
P Q
4)
в области G .
y
x
27
28.
Теорема 6.6. Если функции P x, y , Q x, y непрерывны вместе со своими частными произ-P Q
,
в плоской односвязной области G , то каждое из условий 1), 2), 3) теоремы 6.5
y x
P Q
эквивалентно условию:
4)
в области G .
y x
водными
3) => 4). Если F , для которой выполняется равенство dF Pdx Qdy
F
F
dx
dy , то
x
y
P F 2 F
Q F 2 F
,
.
y y x y x
x x y x y
P
Q
Так как по условию частные производные
и
непрерывны, непрерывными будут и сме y
x
2 F
2 F
шанные производные
и
, а значит, они будут равны.
x y y x
4) => 1). Рассмотрим в G произвольный кусочно-гладкий замкнутый контур L .
Область , ограниченная этим контуром, вложена в область G , ввиду ее односвязности,
а значит, для применима формула Грина:
Q P
Pdx
Qdy
L
x y dxdy .
Так как x, y G
Q P
P
Q
dxdy 0dxdy 0 . 28
, то Pdx Qdy
x y
y x , y x x , y
L
29.
xdy ydx, где L – замкнутый кусочно-гладкий контур,
2
2
x
y
L
П р и м е р 6 . 3 1 . Вычислим I
не проходящий через начало координат, пробегаемый в положительном направлении, если:
1) L не окружает начало координат; 2) L окружает начало координат.
P Q
y 2 x2
y
x
2
2
x
y
0.
Положим P 2
,
.
Тогда
при
Q
2
2
2
2
2
2
x y
x y
y x
x y
1. Если L не окружает O 0,0 , то выполнены все условия теоремы Грина
2. Применять т. Грина в исходной области нельзя, т.к. область,
ограниченная контуром L без O 0,0 , не будет односвязной.
Докажем, что интеграл не зависит от выбора кривой, окружающей
начало координат. Пусть l – другой кусочно-гладкий замкнутый
контур, окружающий O 0,0 . Контуры L и l ограничивают некоторую
I 0
y
L
G
l
x
область G , не содержащую O 0,0 , поэтому
формула
Грина
Pdx Qdy
Q P
G x y dxdy 0
Pdx Qdy Pdx Qdy .
L
l
2
xdy ydx x cos t
cos 2 t dt sin 2 t dt
y sin t
2 .
Следовательно, 2
2
2
2
x
y
cos
t
sin
t
0 t 2 0
L
29
30.
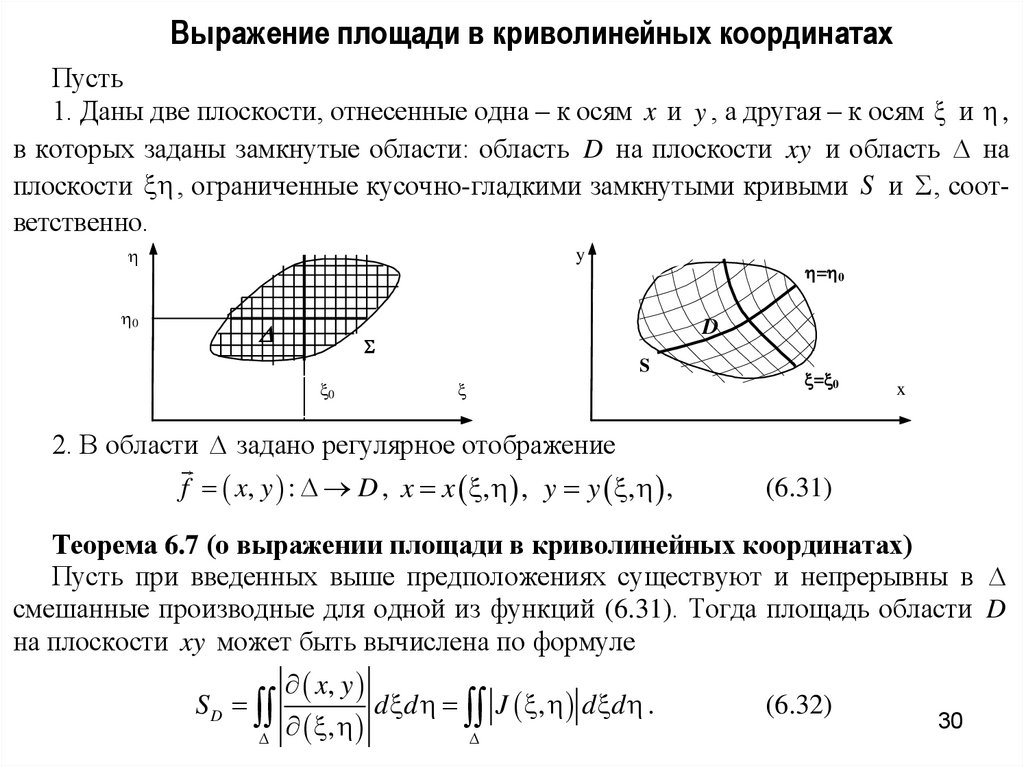
Выражение площади в криволинейных координатахПусть
1. Даны две плоскости, отнесенные одна – к осям x и y , а другая – к осям и ,
в которых заданы замкнутые области: область D на плоскости xy и область на
плоскости , ограниченные кусочно-гладкими замкнутыми кривыми S и , соответственно.
0
y
= 0
D
S
0
= 0
x
2. В области задано регулярное отображение
f x, y : D , x x , , y y , ,
(6.31)
Теорема 6.7 (о выражении площади в криволинейных координатах)
Пусть при введенных выше предположениях существуют и непрерывны в
смешанные производные для одной из функций (6.31). Тогда площадь области D
на плоскости xy может быть вычислена по формуле
x, y
S D
d d J , d d .
,
(6.32)
30
31.
0y
= 0
D
S
0
f x, y : D , x x , , y y , ,
= 0
x
(6.31)
Теорема 6.15 (о выражении площади в криволинейных координатах).
Пусть при введенных выше предположениях существуют и непрерывны в
смешанные производные для одной из функций (6.31). Тогда площадь области D
на плоскости xy может быть вычислена по формуле
x, y
d d J , d d .
,
S D
(6.32)
План доказательства:
1) используя формулу Грина, выразим площадь SD криволинейным интегралом,
взятым по контуру S области D ;
2) от криволинейного интеграла перейдем к определенному интегралу в xy ;
3) преобразуем определенный интеграл к криволинейному интегралу, взятому
по контуру области ;
4) пользуясь формулой Грина, заменим полученный криволинейный интеграл
31
двойным интегралом по области .
32.
1. Пусть t , t , t , или t параметрическое представление кривой , тогдаx x t , t x t , y y t , t y t
параметрическое представление кривой S . Пределы и изменения t выберем
так, чтобы при переходе от к кривая S описывалась в положительном
направлении.
2 y 2 y
Пусть существуют и равны (т.к. непрерывны) производные
,
. Тогда
2)
y
3)
y
y
y
S D xdy x t y t dt x t , t t t dt x d x d
S
1)
КИ 2
R1
R1
КИ 2
3. Контур S при изменении t от до описывается в положительном
направлении (так выбирали и ), но контур при этом может описывать как в
положительном, так и в отрицательном направлении, причем «+» – если при положительном обходе контура S контур также обходится в положительном
направлении, и «–» – в противном случае.
32
33.
yy
S D x d x d ,
«+» – если при положительном обходе контра S контур также обходится в
положительном направлении, и «–» – в противном случае.
y
y
4. Пусть P , x , Q , x . Тогда
Q x y
2 y
P x y
2 y
x
,
x
,
Q P x y x y
2 y
2 y x, y ô î ðì óëà Ãðèí à
x
x
,
3)
0
x, y
S D
d d .
,
x, y
,
непрерывен и J , 0 , то он сохраняет в области определенный знак.
Знак перед интегралом должен совпадать со знаком якобиана, так как в результате должно получиться положительное число.
4)
x, y
33
d d J , d d .
Следовательно, S D
,
При сделанных предположениях в области якобиан J ,
34.
x, yd d J , d d
,
S D
Замечание
1.
Выражение
(6.32)
x, y
d d J , d d
,
называют
элементом площади в криволинейных координатах.
З а м е ч а н и е 2 . Если определитель J , положительный, то положительные направления обхода контуров S и соответствуют друг другу по
формулам преобразования, если же определитель отрицательный, то положительному направлению на одном контуре соответствует отрицательное
направление на другом.
З а м е ч а н и е 3 . Если условия, при которых выведена формула (6.32),
нарушаются в отдельных точках или вдоль отдельных кривых площади
x, y
нуль, но при этом функциональный определитель
в области
,
сохраняет ограниченность, то формула (6.32) остается справедливой.
34
35.
З а м е ч а н и е 4 . Связь между производной и функциональным определителем.x, y
d d J , d d
,
S D
теорема
о среднем
J , S ,
(6.37)
.
где , , а S – площадь .
Сравним (6.37) с формулой Лагранжа f f f
Если x f – монотонная функция, то она задает биекцию между промежутком
и промежутком f x f (или f x f , если f x – убывает).
Обозначив длины этих промежутков через L и Ld , получим
Ld f L .
(6.38)
Ld
.
L
абсолютная величина производной является коэффициентом растяжения прямой
(в данной ее точке) при преобразовании ее в прямую x .
Если в (6.38) «сжимать» отрезок , в точку , то в получим f lim
SD
.
S
абсолютная величина функционального определителя является коэффициентом
растяжения плоскости (в данной ее точке) при преобразовании ее в плоскость36xy .
Если в (6.37) «сжимать» область в точку , получим J , lim
36.
Геометрический выводПусть регулярное отображение x x , , y y , преобразует плоскость
в плоскость xy .
Выделим на плоскости бесконечно малый прямоугольник П1П2 П3П4 со
сторонами d и d , параллельными осям и . Изображением этого прямоугольника в плоскости xy служит криволинейный четырехугольник PP
1 2 P3 P4 .
Координаты вершин прямоугольника П1П2 П3П4 имеют координаты
П1 , , П2 d , , П3 d , d , П4 , d .
Соответствующие вершины криволинейного четырехугольника П1П2 П3П4 :
P1 x , , y , ,
P2 x d , , y d , ,
P3 x d , d , y d , d ,
P3
y
P4
y
0
P2
P1
x
П4
П3
x
d
0
П1
d
П2
P4 x , d , y , d .
Если ограничиться членами первого порядка относительно d и d , то приближенно можно взять точки:
x
y
x
x
y
y
x
y
P1 x, y , P2 x d , y d , P3 x d d , y d d , P4 x d , y d ,
где все частные производные и функции x и y вычислены в точке , . Так как проекции отрезков P1 P2 и P3 P4
на обе оси соответственно равны, то сами отрезки эти равны и параллельны, так что с точностью до малых
высшего порядка четырехугольник PP
1 2 P3 P4 есть параллелограмм. Следовательно, его площадь (с точностью
до бесконечно малых высшего порядка) можно вычислить по формуле
x
x
d
d
x2 x1 x3 x2
x, y
d d .
y2 y1 y3 y2 y
y
,
d
d
Разлагая фигуру на плоскости прямыми, параллельными осям, на бесконечно малые прямоугольники
(и пренебрегая «неправильными» элементами у контура), мы одновременно разложим и фигуру D на плоскости xy
37
на криволинейные четырехугольники рассмотренного вида. Суммируя полученные выражения для их площадей,
получаем формулу (6.32).
37.
Замена переменных в двойных интегралахТеорема 6.8. Пусть выполняются все предположения теоремы (6.7) и функция
f x, y D . Тогда
f x, y dxdy f x , , y , J , d d .
(6.39)
D
Разобьем область с помощью некоторой сетки кусочно-гладких кривых
на части i , i 1,2,..., n . Тогда D соответствующими (тоже кусочно-гладкими)
кривыми разобьется на части Di . В каждой части Di выберем произвольно по
точке xi , yi и составим интегральную сумму
n
f xi , yi S Di ,
i 1
пределом которой при стремлении наибольшего из диаметров областей Di к 0
является интеграл f x, y dxdy .
D
i S Di J i , i S i , i , i – некоторая определенная точка области 38
i.
38.
nРассмотрим интегральную сумму f xi , yi J i , i S i .
i 1
дается теоремой о среднем, но точка x , y в области D
выбирается произвольно. Пусть x x , , y y , . Тогда
Точка i , i
i
i
n
i
i
f x i , i , y i , i
i 1
i
i
i
i
i
J , S .
i
i
i
В таком виде является интегральной суммой для интеграла
f x , , y , J , d d .
(*)
Интеграл (*) существует в силу непрерывности подынтегральной функции.
Если устремить диаметры всех областей i стремиться к 0, то по непрерывности функций x x , , y y , и диаметры всех областей Di будут стремиться к 0. Тогда сумма должна стремиться как к интегралу f x, y dxdy ,
D
так и к интегралу(*), так как является для обоих интегральной суммой.
Следовательно,
f x, y dxdy f x , , y , J , d d .
D
39
39.
З а м е ч а н и е 1 . Если условия, при которых выведена формулаf x, y dxdy f x , , y , J , d d ,
D
(6.39)
нарушаются в отдельных точках или вдоль отдельных кривых площади 0,
x, y
но при этом функциональный определитель
в области сохраняет
,
ограниченность, то формула (6.39) остается справедливой.
.
40
40.
Аналогия с определенным интегралом. Интеграл по ориентированной области.Формула замены переменных для R1:
b
a
f x dx f x x d .
Формула замены переменных для R2:
f x, y dxdy f x , , y , J , d d .
(*)
D
R1 берется по ориентированному промежутку ( a b или a b , а также
или ), а R2 берется по неориентированной области.
Для R2 можно перейти к ориентированным областям. В качестве площади
ориентированной области D берется ее обыкновенная площадь со знаком плюс,
если область ориентирована положительно, и со знаком минус – в противном
случае. Тогда (*) может быть написана для согласованно ориентированных
областей D и в виде
f x, y dxdy f x , , y , J , d d .
D
41







































 mathematics
mathematics








