ВКР: Исследование динамики итерирования полиномов второй степени и кусочно-линейных функций

1.

МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное
образовательное учреждение
высшего образования
«Костромской государственный университет»
(КГУ)
ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА
на тему:
«Исследование динамики итерирования полиномов второй
степени и кусочно-линейных функций»
Выполнил:
Коньков Павел
Владимирович
Магистрант 2 курса
направления
01.04.02 Прикладная
математика и информатика

2.

Актуальность
В настоящее время нелинейная динамика интенсивно развивается
и находит приложение в разных отраслях знаний от лингвистики
до нанотехнологий. В настоящей работе рассматривается два
семейства нелинейных функций, порождаемых квадратным
двучленом и тентообразной функцией.

3.

Цель, объект и предмет исследования
Цель –– исследование
исследование динамики
динамики итерирования
итерирования логистической
логистической ии
Цель
тентообразной функций.
функций.
тентообразной
Объект исследования
исследования –– нелинейная
нелинейная динамика.
динамика.
Объект
Предмет исследования
исследования –– сравнение
сравнение динамик
динамик итерированных
итерированных
Предмет
логистической ии тентообразных
тентообразных функций.
функций.
логистической

4.

Новизна
1. Адаптированы
Адаптированы алгоритмы
алгоритмы вычисления
вычисления константы
константы
1.
Фейгенбаума для
для логистической
логистической функции
функции ии тентообразной
тентообразной
Фейгенбаума
функции
функции
2. Выявлена
Выявлена связь
связь между
между кусочно-линейной
кусочно-линейной функцией
функцией ии
2.
множеством Кантора
Кантора
множеством
3. Разботано
Разботано многоэтапное
многоэтапное математико-информационное
математико-информационное
3.
задание
задание

5.

Задачи исследования
Задачи исследования:
исследования:
Задачи
1.Исследование
Исследование орбит
орбит точек
точек логистической
логистической ии
1.
тентообразной функций
функций
тентообразной
2.Разработать
Разработать алгоритм
алгоритм ии написать
написать программу
программу
2.
итерирования, вычисления
вычисления констант
констант Фейгенбаума,
Фейгенбаума, для
для
итерирования,
логистической ии тентообразной
тентообразной функций
функций различных
различных
логистической
средах
средах
3.Разработать
Разработать многоэтапное
многоэтапное математико-информационное
математико-информационное
3.
задание
задание

6.

Практическая значимость
Практическая значимость
значимость работы
работы заключается
заключается вв том,
том, что
что
Практическая
результаты исследования
исследования могут
могут быть
быть использованы
использованы при
при
результаты
изучениях нелинейных
нелинейных отображений
отображений ии построения
построения
изучениях
математических моделей.
моделей.
математических

7.

Переход к хаосу логистической
функции
На данном
данном этапе
этапе был
был подробно
подробно разобран
разобран переход
переход кк хаосу
хаосу логистической
логистической
На
функции. В
В нем
нем было
было выяснено,
выяснено, что
что при
при увеличении
увеличении значения
значения aa будет
будет
функции.
происходить бифуркация
бифуркация вв орбиту
орбиту длиной
длиной периода
периода 2.
2. Тем
Тем самым
самым мы
мы увидим
увидим
происходить
удвоение периода
периода уу данной
данной функции.
функции.
удвоение

8.

Символическая динамика
логистической функции
На данном
данном этапе
этапе было
было разобрано
разобрано понятие
понятие символической
символической динамики.
динамики.
На
Из чего
чего стало
стало понятно,
понятно, что
что это
это полезный
полезный метод
метод для
для понимания
понимания куда
куда попадет
попадет
Из
следующая точка
точка xxn+1
после выполнения
выполнения итераций:
итераций: слева
слева от
от максимума
максимума
следующая
n+1 после
(центра) (L),
(L), или
или справа
справа от
от максимума
максимума (R),
(R), либо
либо вв максимум
максимум функции
функции (C),
(C),
(центра)
где под
под максимумом
максимумом понимается
понимается глобальный
глобальный максимум
максимум функции
функции f(x)=a(1f(x)=a(1где
x)x на
на отрезке
отрезке [0;1].
[0;1].
x)x

9.

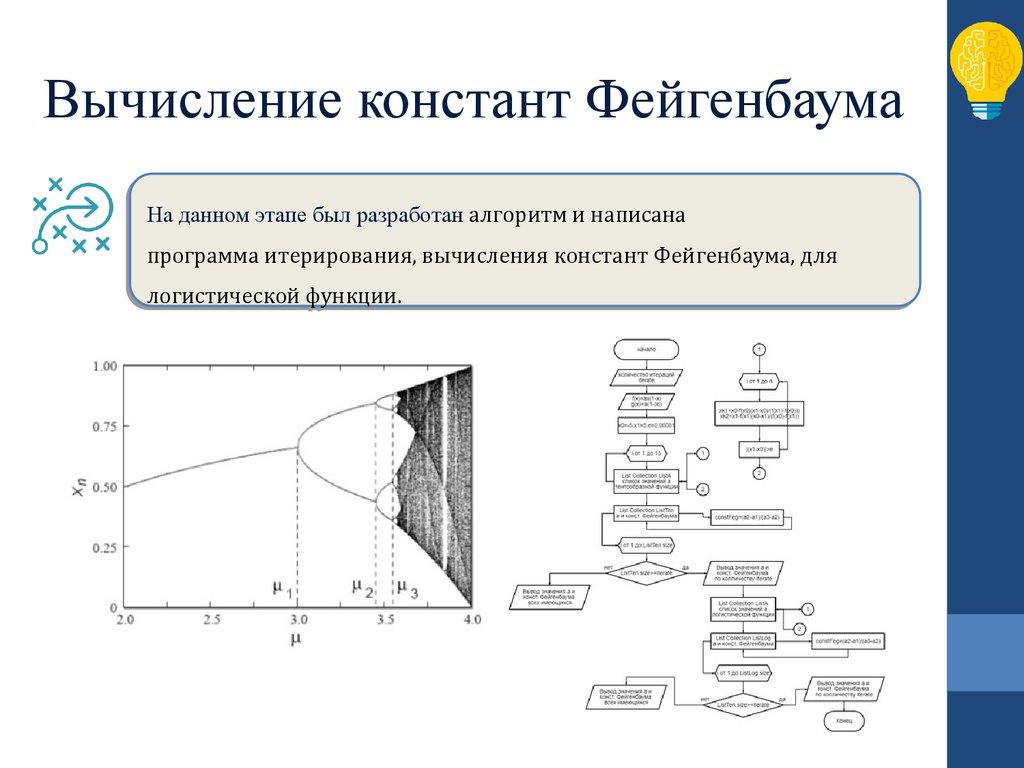
Вычисление констант Фейгенбаума
На данном
данном этапе
этапе был
был разработан
разработан алгоритм
алгоритм ии написана
написана
На
программа итерирования,
итерирования, вычисления
вычисления констант
констант Фейгенбаума,
Фейгенбаума, для
для
программа
логистической функции.
функции.
логистической

10.

Построение множества Кантора для
тентообразной функции
На данном
данном этапе
этапе был
был построен
построен алгоритм
алгоритм фрактальных
фрактальных множеств
множеств тентообразной
тентообразной
На
функции f(x),
f(x), каждое
каждое из
из которых
которых является
является множеством
множеством Кантора.
Кантора. Алгоритм
Алгоритм был
был
функции
реализован вв среде
среде MathCad.
MathCad.
реализован
Суть данного
данного алгоритма
алгоритма вв том,
том, что
что рассматривается
рассматривается точка
точка xx ии ее
ее сотая
сотая итерация
итерация .. Если
Если
Суть
то мы
мы закрашиваем
закрашиваем xx вв синий
синий цвет
цвет ии рассматриваем
рассматриваем другую
другую точку
точку x+h.
x+h. Множество
Множество
то
закрашенное вв синий
синий цвет
цвет ии даст
даст нам
нам множество
множество Кантора.
Кантора.
закрашенное

11.

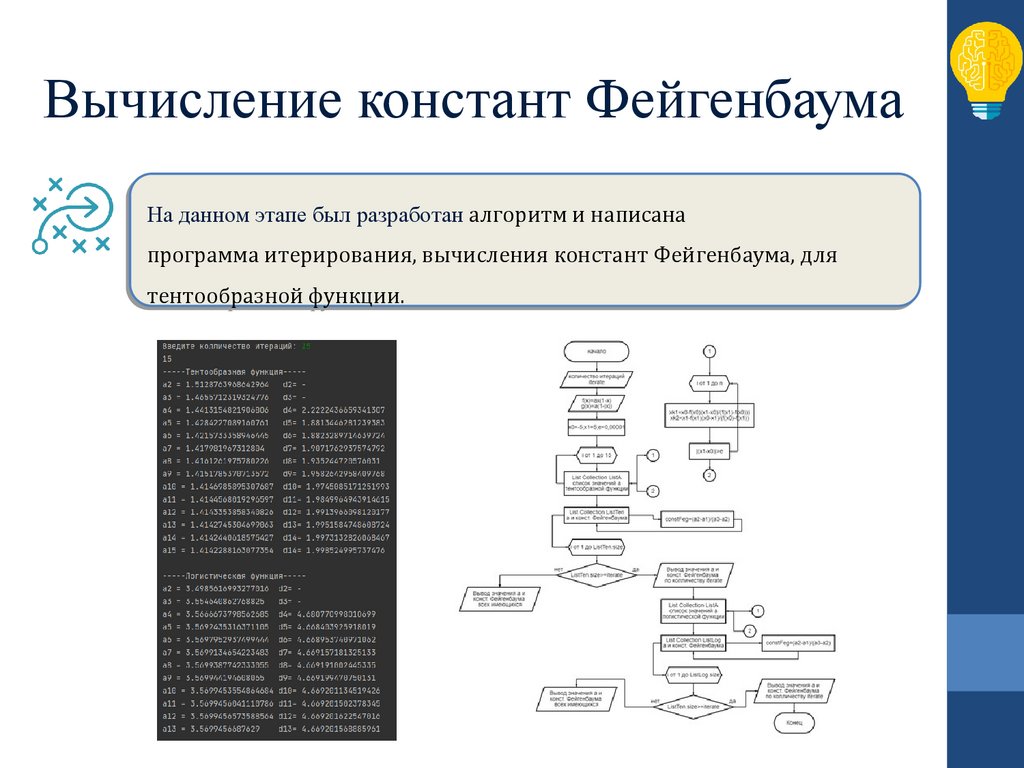
Вычисление констант Фейгенбаума
На данном
данном этапе
этапе был
был разработан
разработан алгоритм
алгоритм ии написана
написана
На
программа итерирования,
итерирования, вычисления
вычисления констант
констант Фейгенбаума,
Фейгенбаума, для
для
программа
тентообразной функции.
функции.
тентообразной

12.

Многоэтапное математикоинформационное задание
На данном
данном этапе
этапе было
было разработано
разработано
На
многоэтапное математикоматематикомногоэтапное
информационное задание
задание по
по
информационное
исследуемой теме.
теме. Оно
Оно состоит
состоит из
из
исследуемой
пяти этапов.
этапов. Данное
Данное ММИЗ
ММИЗ служит
служит
пяти
хорошим материалом
материалом для
для изучения
изучения
хорошим
данной темы
темы ии развития
развития
данной
креативности студентов.
студентов.
креативности