Неравенства второй степени с одной переменной

1. Решение неравенств второй степени с одной переменной.

2.

Цели урока:
ознакомление с понятием неравенства второй
степени с одной переменной
формирование навыков решения неравенств
второй степени с одной переменной на основе
свойств квадратичной функции
развитие интереса к предмету в процессе
нахождения решения проблемных ситуаций и
выполнения заданий творческого характера

3.

Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
-6
переменной х , при которых
функция принимает
значения,
- равные нулю,
- положительные значения,
- отрицательные значения.
у
-1
о
х

4.

Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
переменной х , при которых
функция принимает
значения,
- равные нулю,
- положительные значения,
- отрицательные значения.
у
о
х

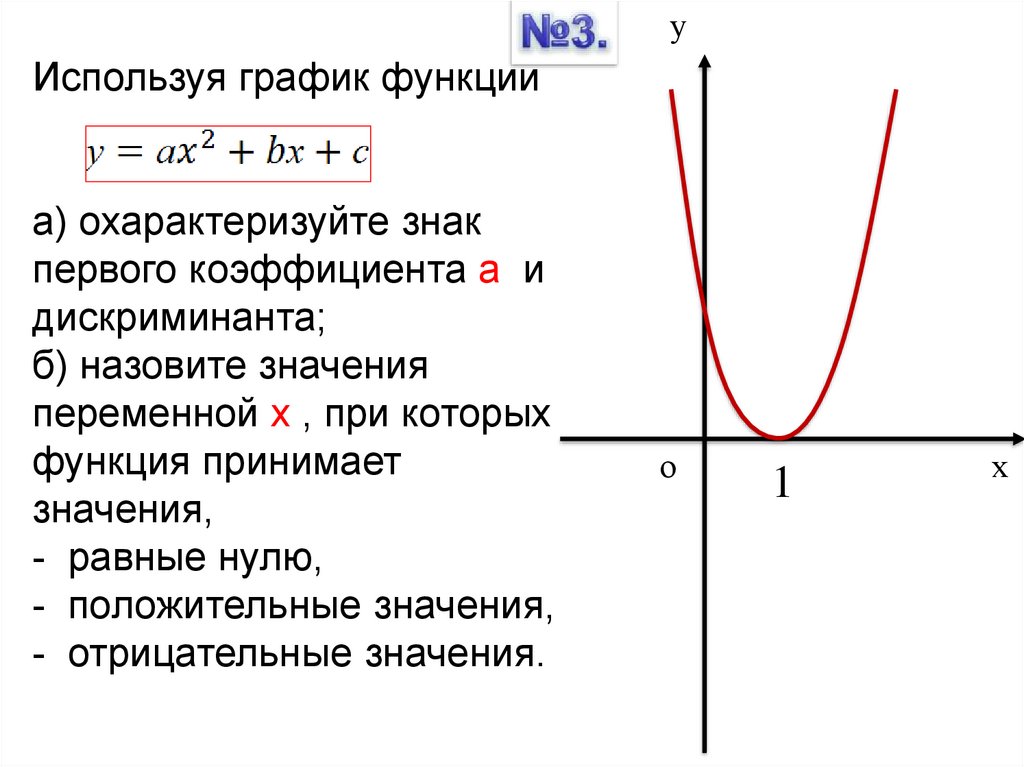
5.

у
Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
переменной х , при которых
функция принимает
значения,
- равные нулю,
- положительные значения,
- отрицательные значения.
о
1
х

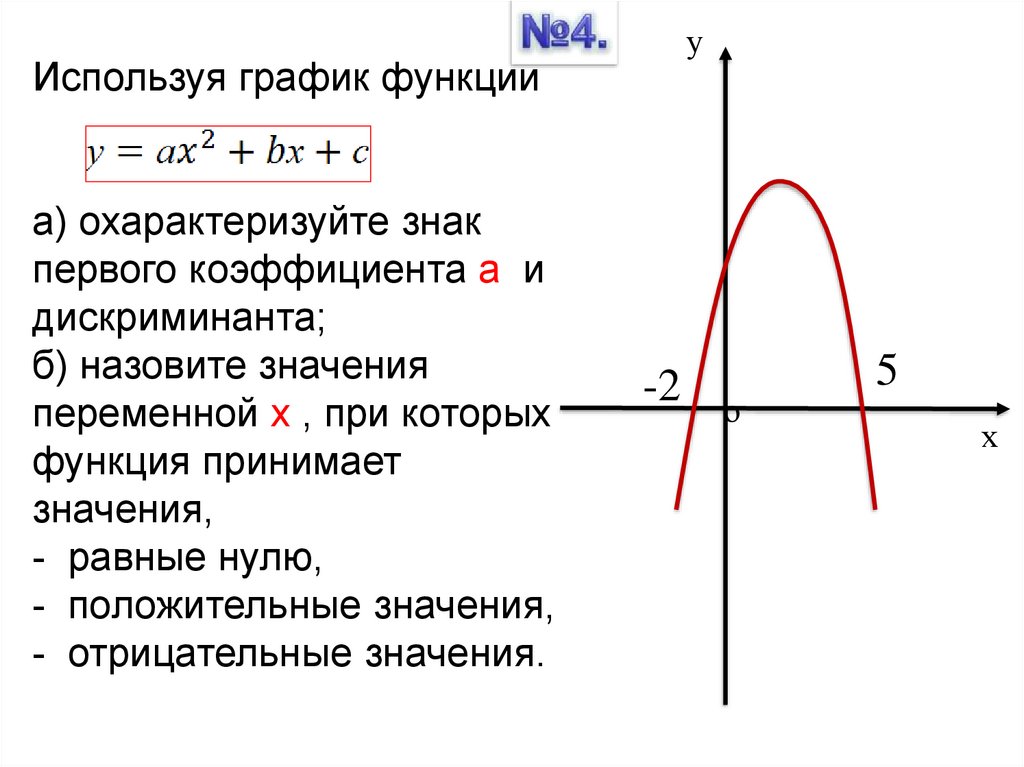
6.

у
Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
переменной х , при которых
функция принимает
значения,
- равные нулю,
- положительные значения,
- отрицательные значения.
-2
о
5
х

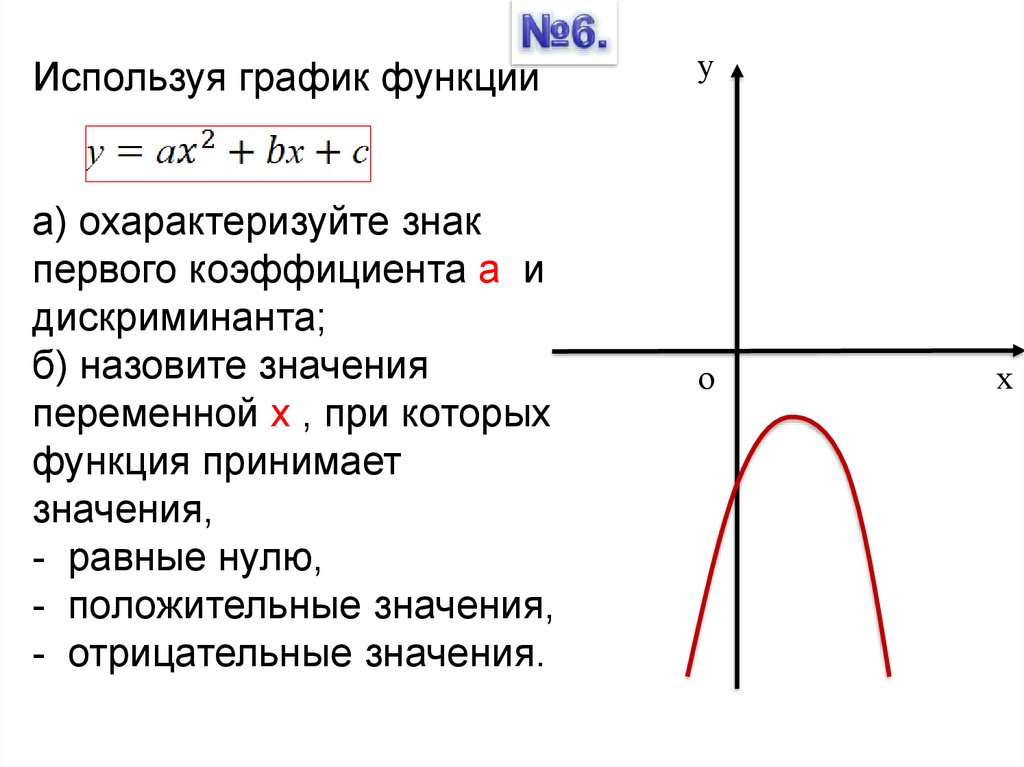
7.

у
Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
переменной х , при которых
функция принимает
значения,
- равные нулю,
- положительные значения,
- отрицательные значения.
-3
о
х

8.

Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
переменной х , при которых
функция принимает
значения,
- равные нулю,
- положительные значения,
- отрицательные значения.
у
о
х

9.

Пересекает ли ось ОХ график функции, заданной
уравнением:
(Если «да», то в каких точках?)
а)
б)
в)
г)
д)

10.

а) Да.
Ось ОХ пересекает график
функции, заданной уравнением
в двух точках с координатами
(4;0) и (-4;0)

11.

б) Да.
Ось ОХ пересекает график
функции, заданной уравнением
в одной точке с координаты
которой (-3;0)

12.

в) Да.
Ось ОХ пересекает график
функции, заданной уравнением
в одной точке с координаты
которой (5;0)

13.

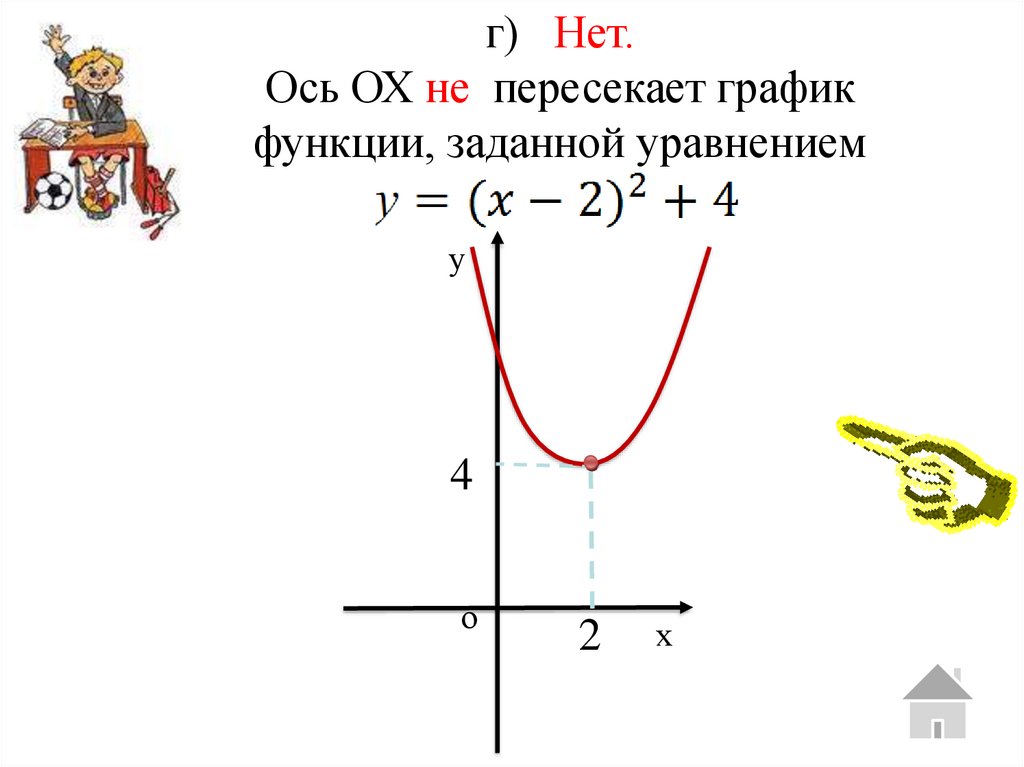
г) Нет.
Ось ОХ не пересекает график
функции, заданной уравнением
у
4
о
2
х

14.

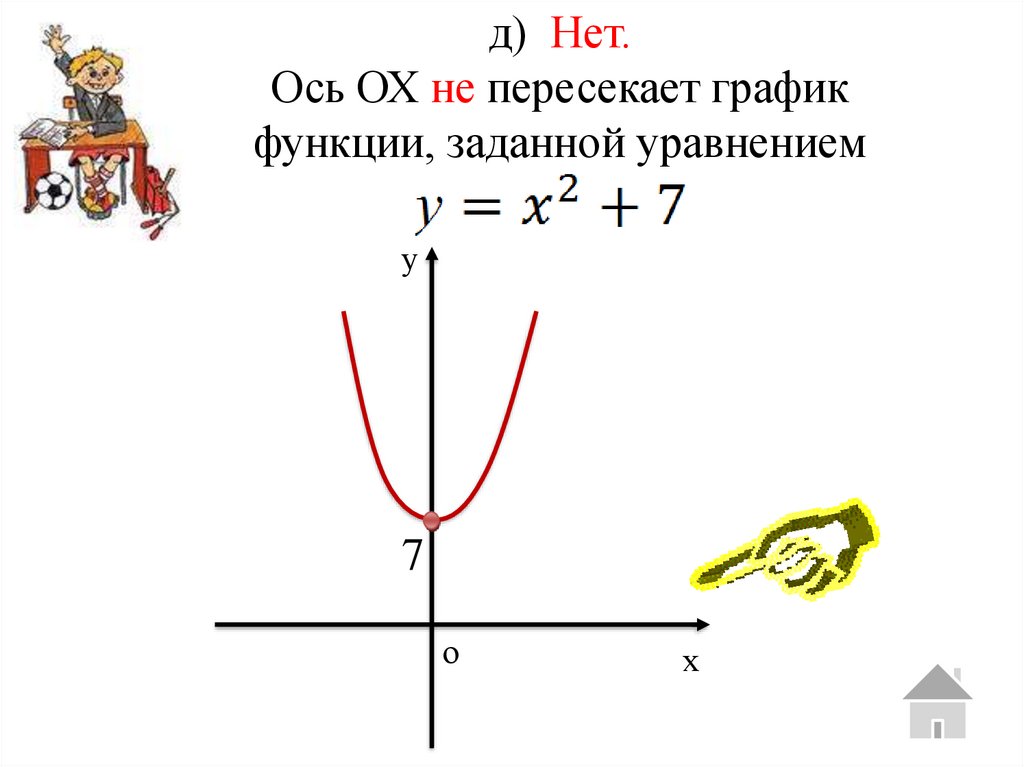
д) Нет.
Ось ОХ не пересекает график
функции, заданной уравнением
у
7
о
х

15.

Неравенства вида
aх2 + bх + с > 0 и
aх2 + bх + с < 0
где х - переменная,
а, в, с –некоторые числа,
причем
,
называют неравенствами
второй степени с одной
переменной.

16.

Современные знаки неравенств
появились лишь в XVII— XVIII вв.
Знаки < и > ввел английский математик
Томас Гарриот (1560—1621),
знаки ≥ и ≤ ввел французский
математик Пьер Буге (1698—1758).

17.

Алгоритм решения неравенств вида
ax2+bx+c>0 и ax2+bx+c<0
( см. схему стр.180)
Рассмотрим функцию
1. График функции – парабола,
ветви направлены вверх (т.к. а>0) или вниз (т.к.
2. Найдем нули функции.
3. На ось ОХ нанесем нули функции.
Построим эскиз графика.
4. Найдем значения переменной х, при которых
функция принимает нужные значения.
5. Записать ответ.
).

18.

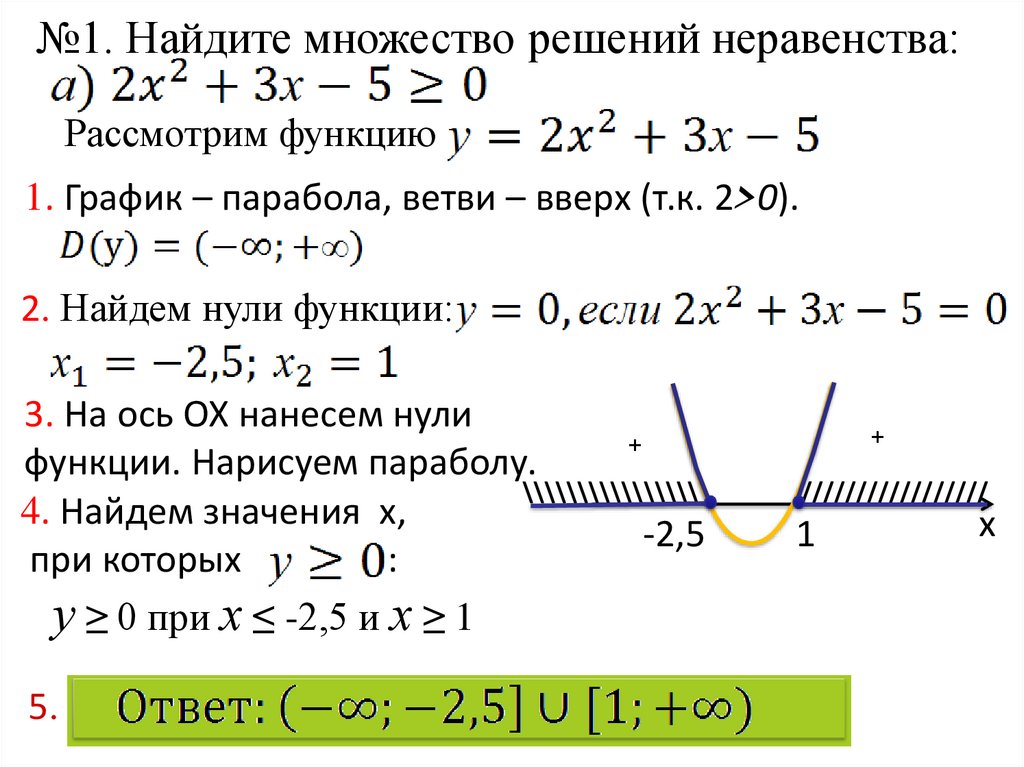
№1. Найдите множество решений неравенства:
Рассмотрим функцию
1. График – парабола, ветви – вверх (т.к. 2>0).
2. Найдем нули функции:
3. На ось ОХ нанесем нули
+
функции. Нарисуем параболу.
\\\\\\\\\\\\\\\\
4. Найдем значения х,
-2,5
при которых
:
у ≥ 0 при х ≤ -2,5 и х ≥ 1
5.
+
/////////////////
1
х

19.

Найдите множество решений неравенства:
Рассмотрим функцию
1. График функции – парабола, ветви – вниз (т.к.
).
2. Найдем нули функции:
+
3. На ось ОХ нанесем нули
функции. Нарисуем параболу.
4. Найдем значения х,
при которых
:
при -2 ≤ х ≤ 3
Ответ : 2;3
///////////
-2
3
х

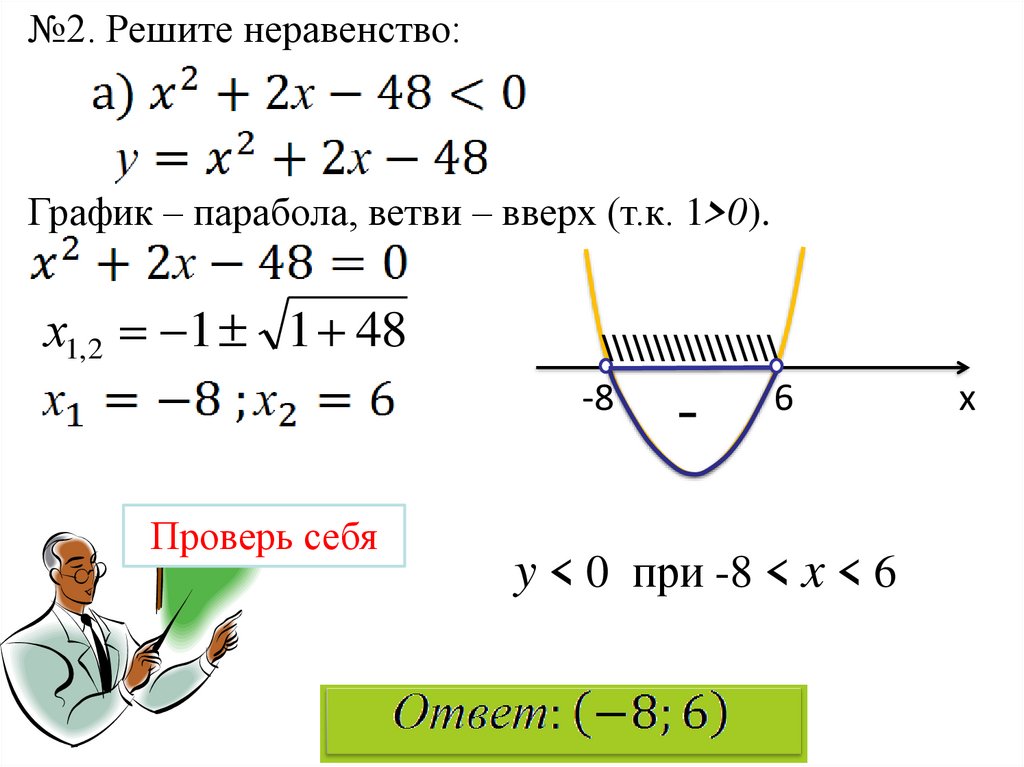
20.

№2. Решите неравенство:
График – парабола, ветви – вверх (т.к. 1>0).
х1,2 1 1 48
\\\\\\\\\\\\\\\\\
-8
Проверь себя
-
6
y < 0 при -8 < x < 6
х

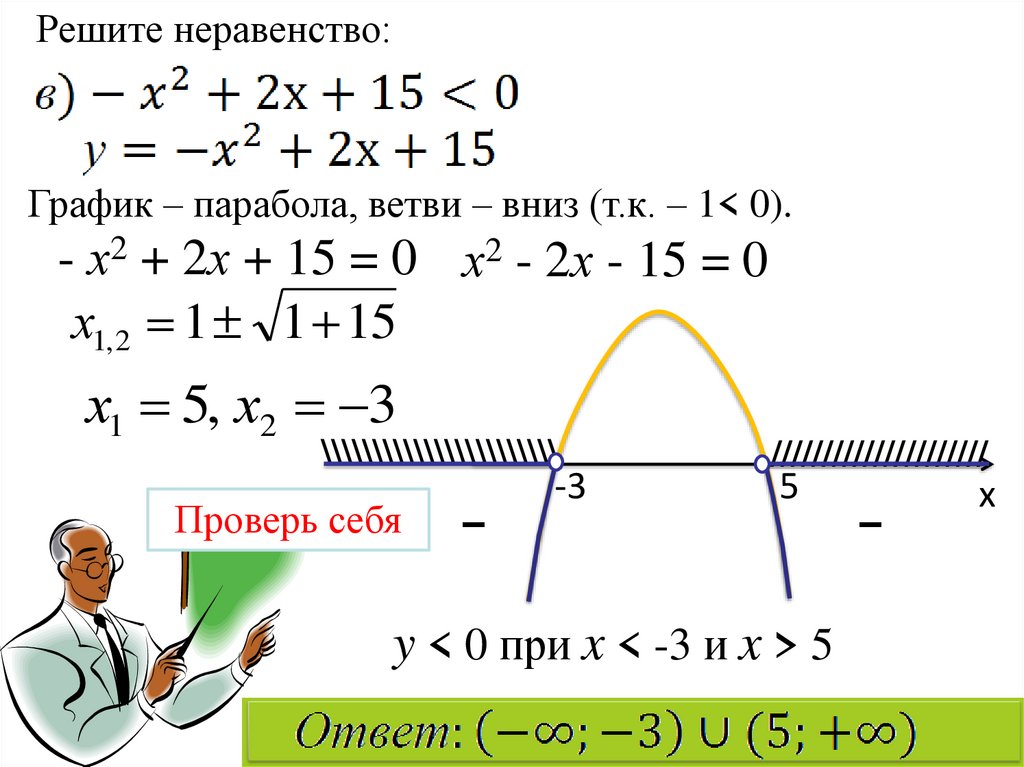
21.

Решите неравенство:
График – парабола, ветви – вниз (т.к. – 1< 0).
- х2 + 2х + 15 = 0 х2 - 2х - 15 = 0
х1,2 1 1 15
х1 5, х2 3
\\\\\\\\\\\\\\\\\\\\\\\
Проверь себя
-
-3
/////////////////////
5
y < 0 при x < -3 и x > 5
-
х

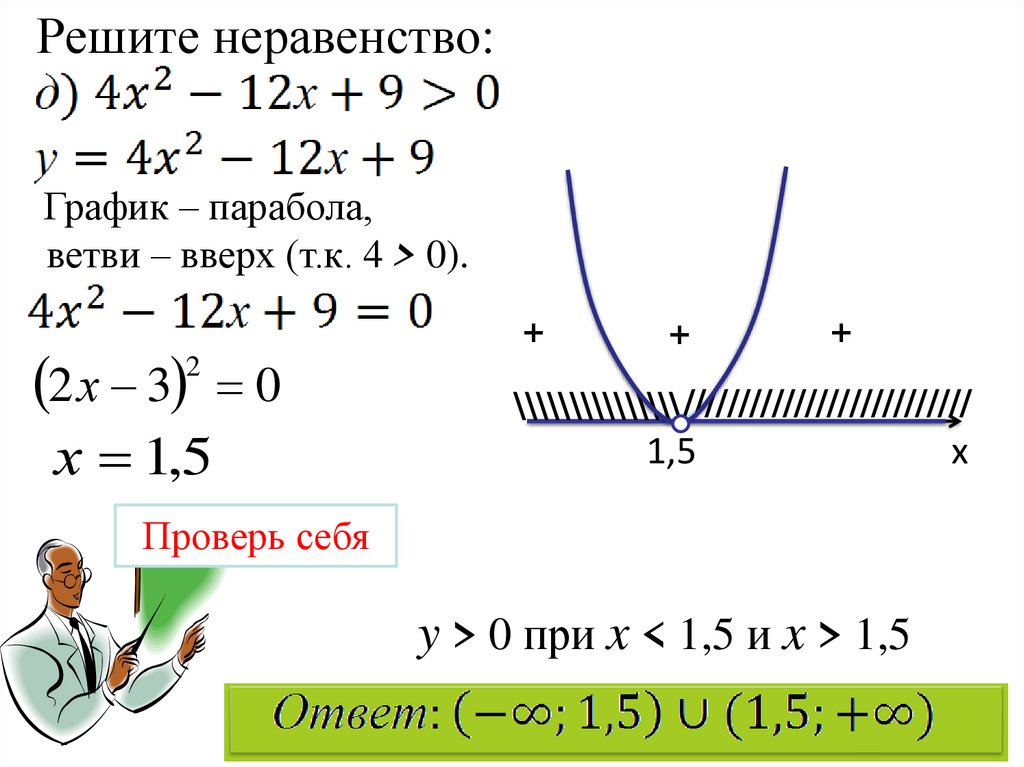
22.

Решите неравенство:
График – парабола,
ветви – вверх (т.к. 4 > 0).
2 х 3
2
0
х 1,5
+
+
+
\\\\\\\\\\\\\\\ //////////////////////////
1,5
х
Проверь себя
y > 0 при x < 1,5 и x > 1,5

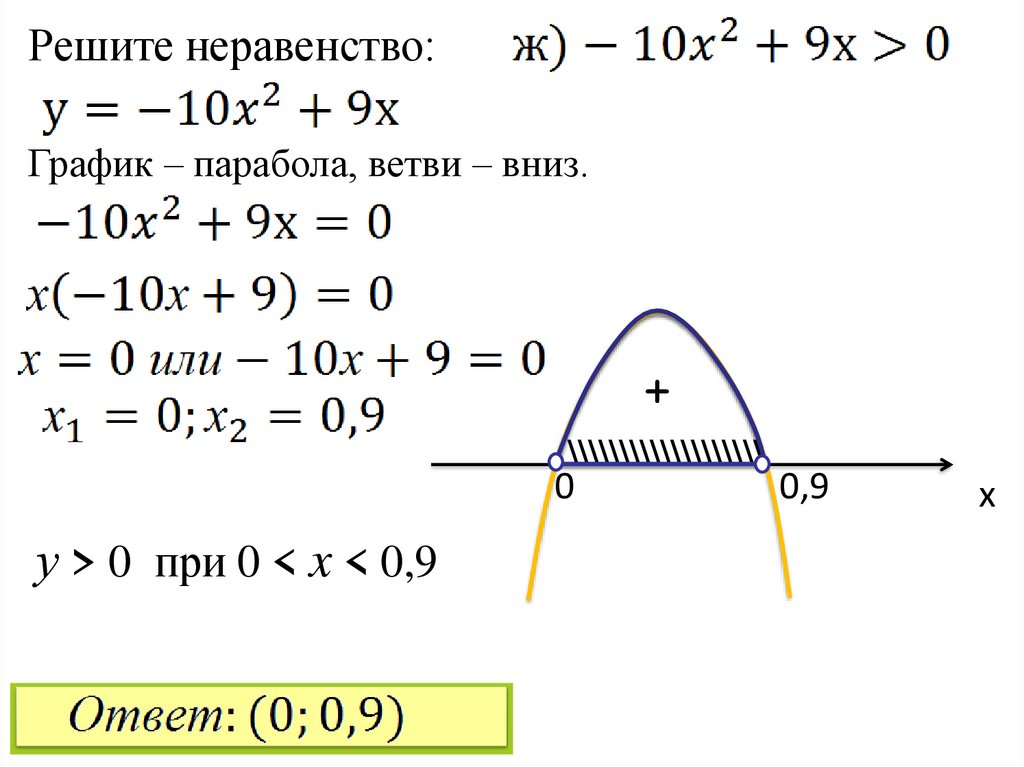
23.

Решите неравенство:
График – парабола, ветви – вниз.
+
\\\\\\\\\\\\\\\\\\\
0
у > 0 при 0 < x < 0,9
0,9
х

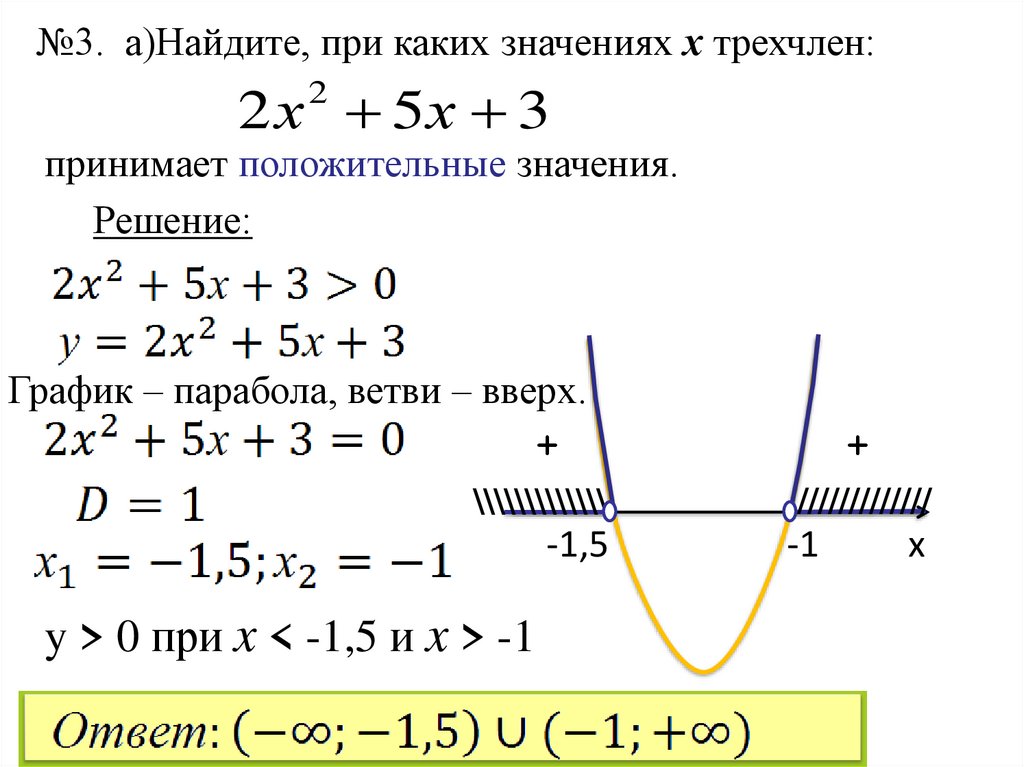
24.

№3. а)Найдите, при каких значениях х трехчлен:
2 х 5х 3
2
принимает положительные значения.
Решение:
График – парабола, ветви – вверх.
+
\\\\\\\\\\\\\
-1,5
y > 0 при x < -1,5 и x > -1
+
/////////////
-1
х

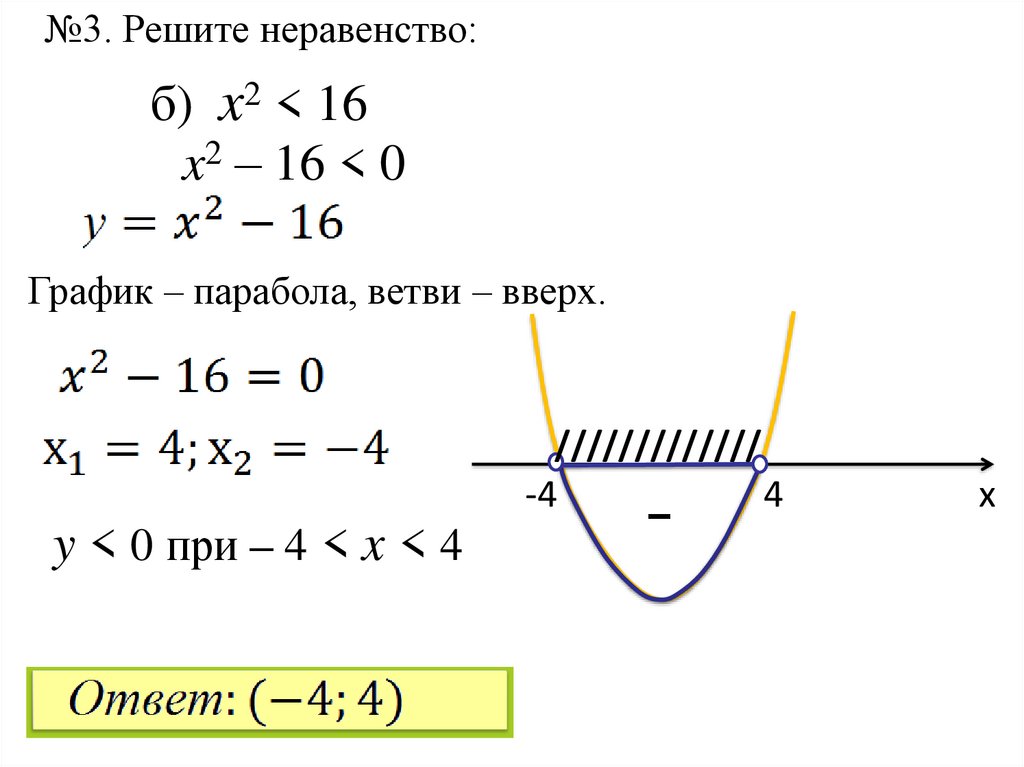
25.

№3. Решите неравенство:
б) x2 < 16
x2 – 16 < 0
График – парабола, ветви – вверх.
/////////////
-4
y < 0 при – 4 < x < 4
-
4
х

26.

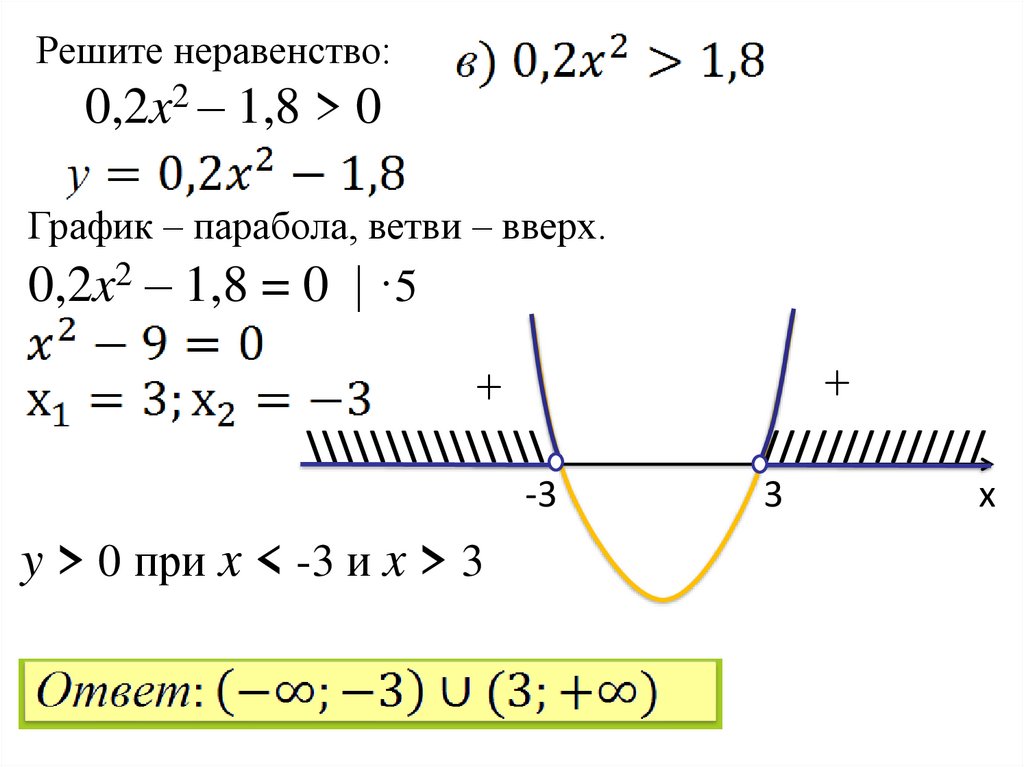
Решите неравенство:
0,2x2 – 1,8 > 0
График – парабола, ветви – вверх.
0,2x2 – 1,8 = 0 | ·5
+
+
\\\\\\\\\\\\\\\
-3
y > 0 при x < -3 и x > 3
//////////////
3
х

27.

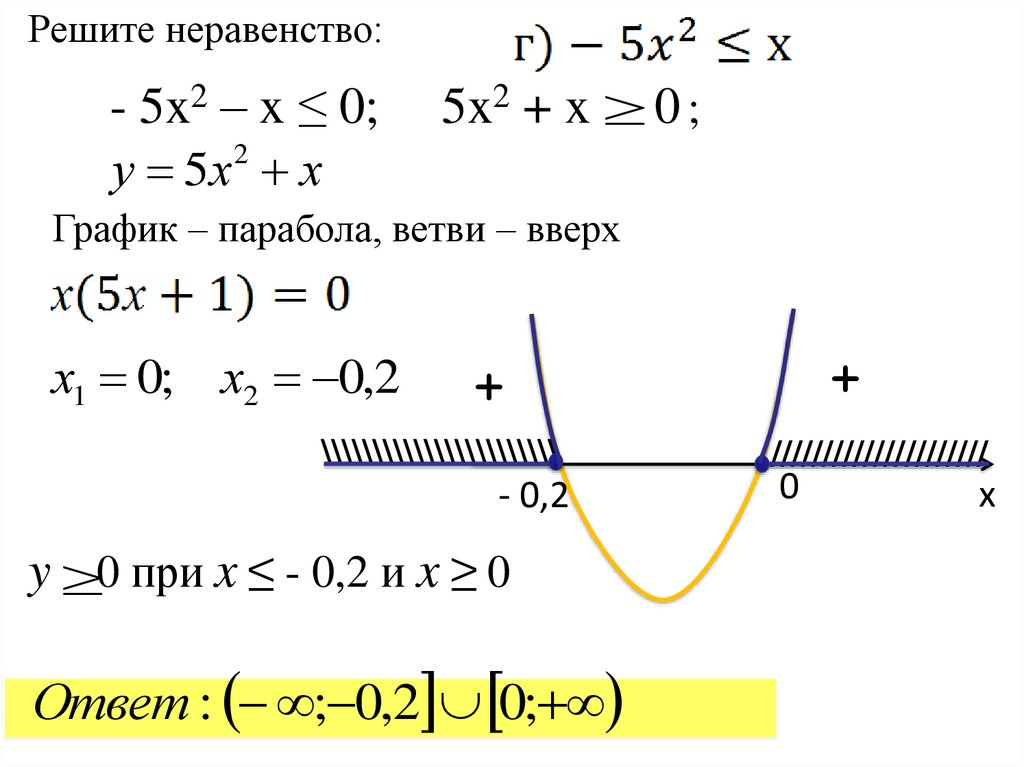
Решите неравенство:
- 5x2 – x ≤ 0;
5x2 + x 0 ;
у 5х х
2
График – парабола, ветви – вверх
х1 0; х2 0,2
+
+
\\\\\\\\\\\\\\\\\\\\\\\
/////////////////////
- 0,2
х
y 0 при x ≤ - 0,2 и x ≥ 0
Ответ : ; 0,2 0;
0

28.

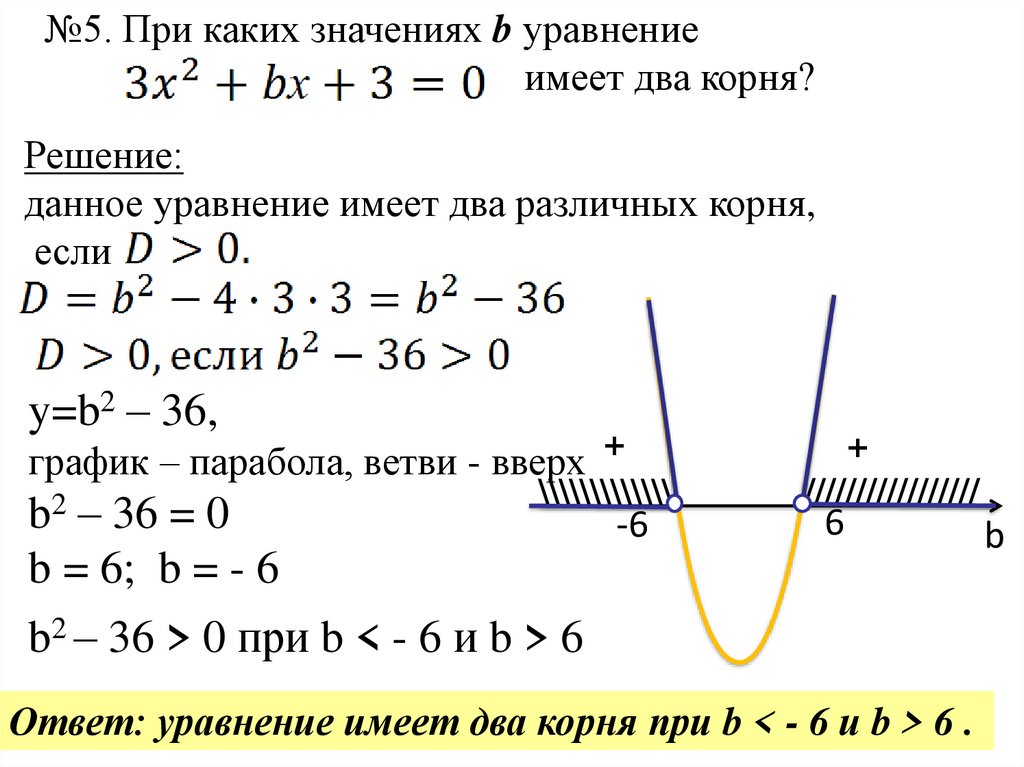
№5. При каких значениях b уравнение
имеет два корня?
Решение:
данное уравнение имеет два различных корня,
если
y=b2 – 36,
график – парабола, ветви - вверх +
– 36 = 0
b = 6; b = - 6
b2
\\\\\\\\\\\\\
-6
+
/////////////////
6
b2 – 36 > 0 при b < - 6 и b > 6
Ответ: уравнение имеет два корня при b < - 6 и b > 6 .
b

29.

30.

§41, учить алгоритм стр.180
№ 668, 669 (чет).