Решение неравенств второй степени с одной переменной

1. Решение неравенств второй степени с одной переменной.

Учитель математики
Юракова Наталия Петровна
МОУ школа№13 с углубленным изучением отдельных
предметов, г Жуковский
2009-2010 учебный год

2.

Цели урока:
ознакомление с понятием неравенства второй
степени с одной переменной
формирование навыков решения неравенств
второй степени с одной переменной на основе
свойств квадратичной функции
развитие интереса к предмету в процессе
нахождения решения проблемных ситуаций и
выполнения заданий творческого характера

3.

4.

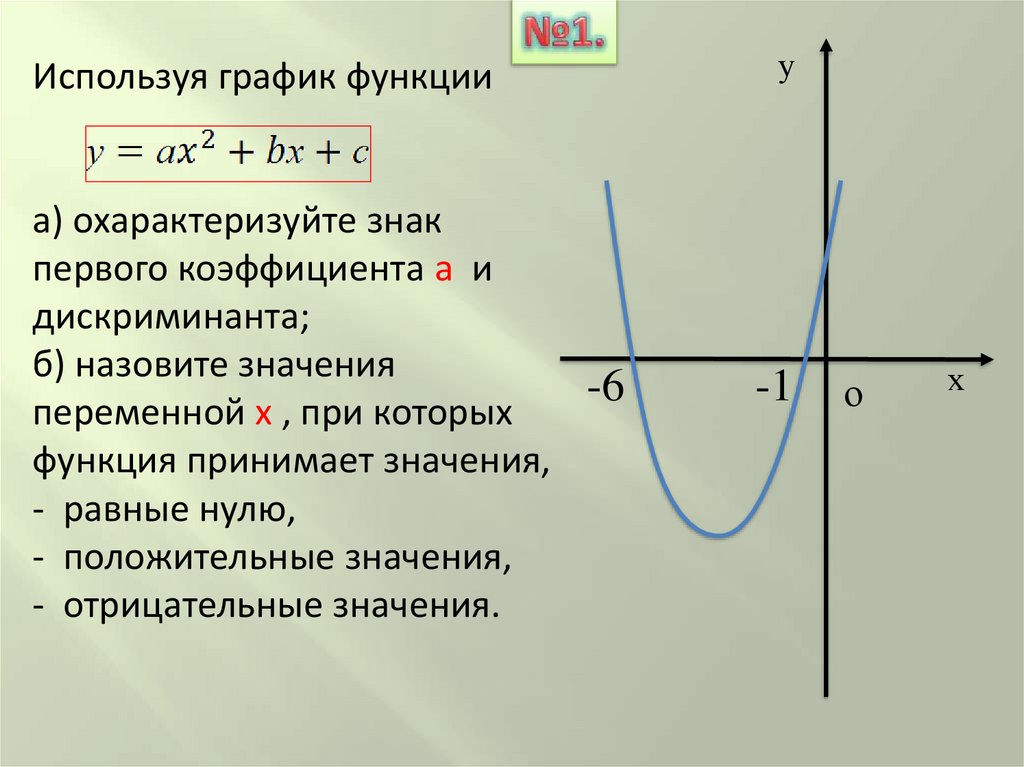
Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
-6
переменной х , при которых
функция принимает значения,
- равные нулю,
- положительные значения,
- отрицательные значения.
у
-1
о
х

5.

Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
переменной х , при которых
функция принимает значения,
- равные нулю,
- положительные значения,
- отрицательные значения.
у
о
х

6.

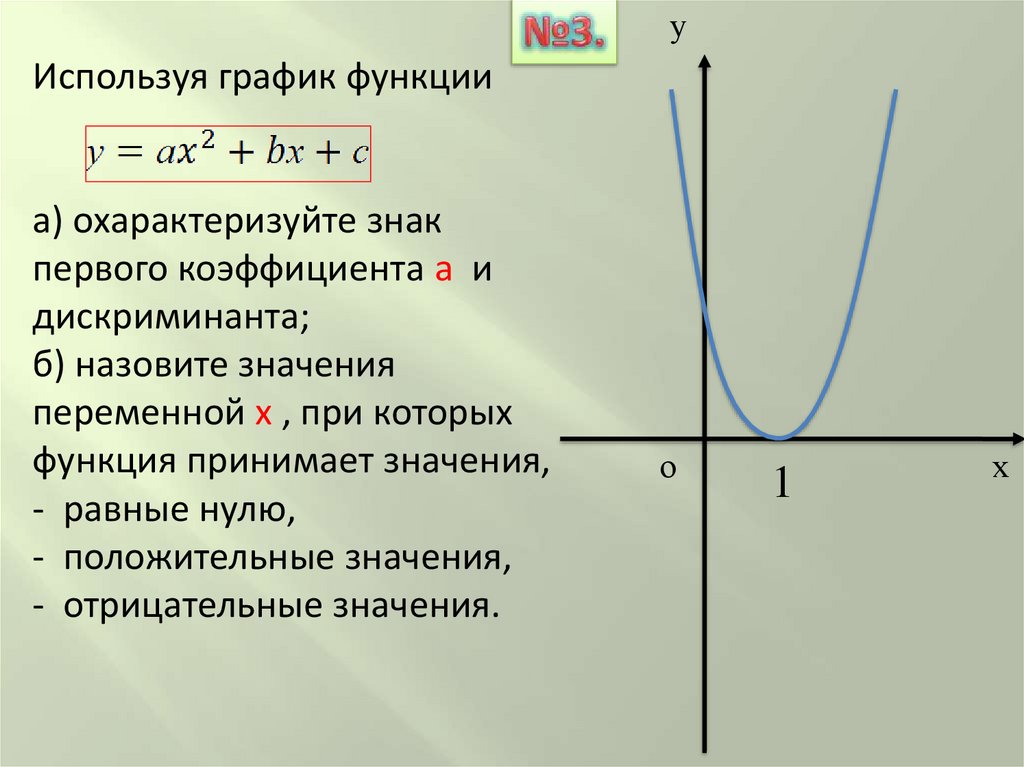
у
Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
переменной х , при которых
функция принимает значения,
- равные нулю,
- положительные значения,
- отрицательные значения.
о
1
х

7.

у
Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
переменной х , при которых
функция принимает значения,
- равные нулю,
- положительные значения,
- отрицательные значения.
-2
о
5
х

8.

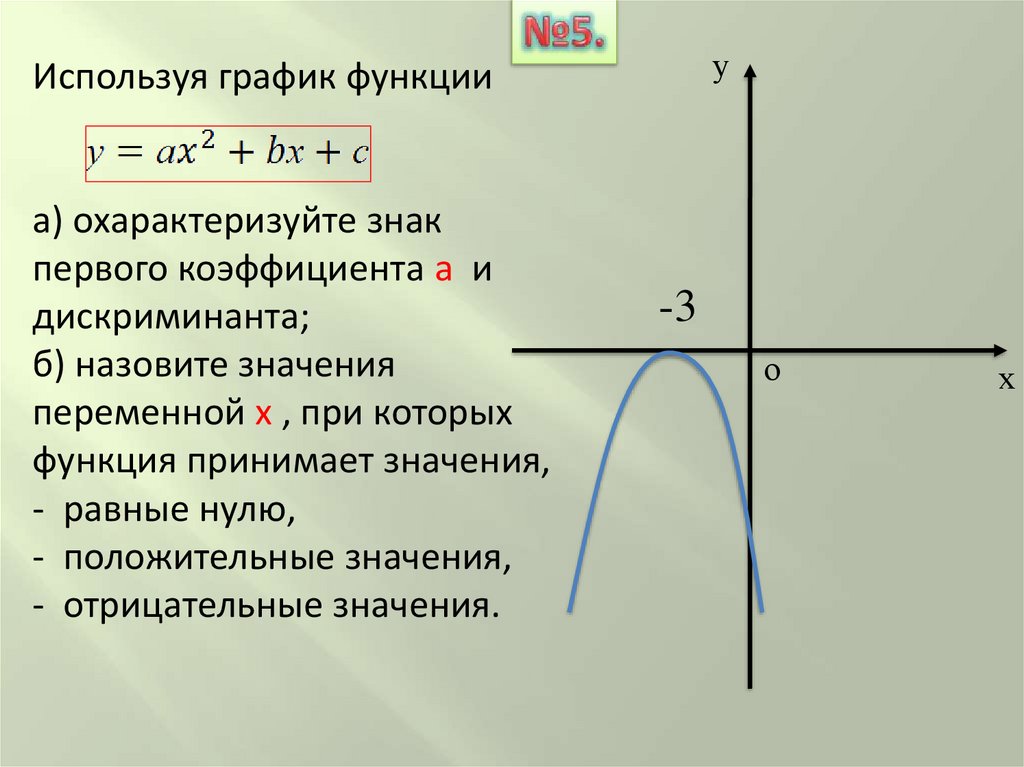
у
Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
переменной х , при которых
функция принимает значения,
- равные нулю,
- положительные значения,
- отрицательные значения.
-3
о
х

9.

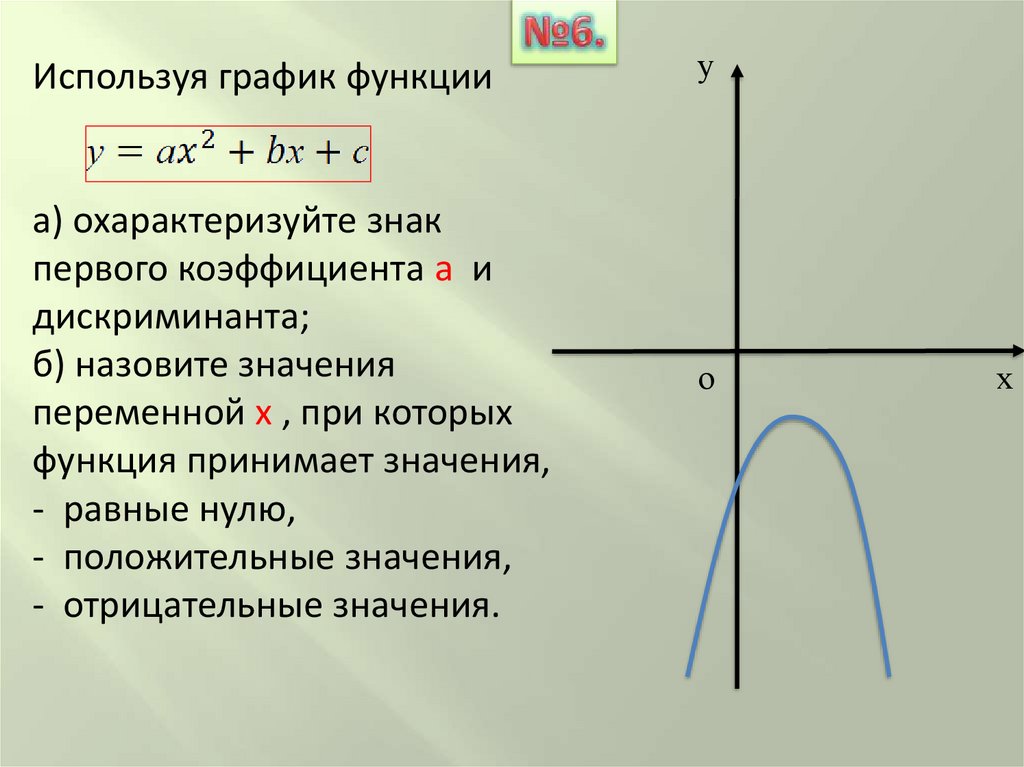
Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
переменной х , при которых
функция принимает значения,
- равные нулю,
- положительные значения,
- отрицательные значения.
у
о
х

10.

Пересекает ли ось ОХ график функции, заданной
уравнением:
(Если «да», то в каких точках?)
а)
б)
в)
г)
д)

11.

а) Да.
Ось ОХ пересекает график
функции, заданной уравнением
в двух точках с координатами
(4;0) и (-4;0)

12.

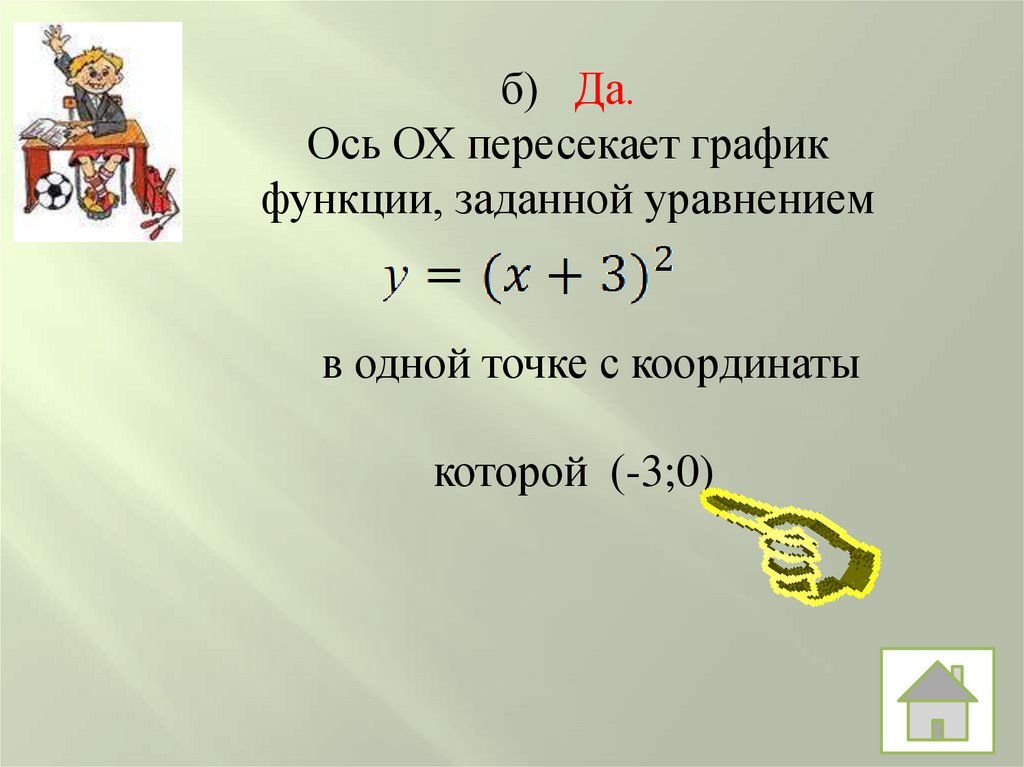
б) Да.
Ось ОХ пересекает график
функции, заданной уравнением
в одной точке с координаты
которой (-3;0)

13.

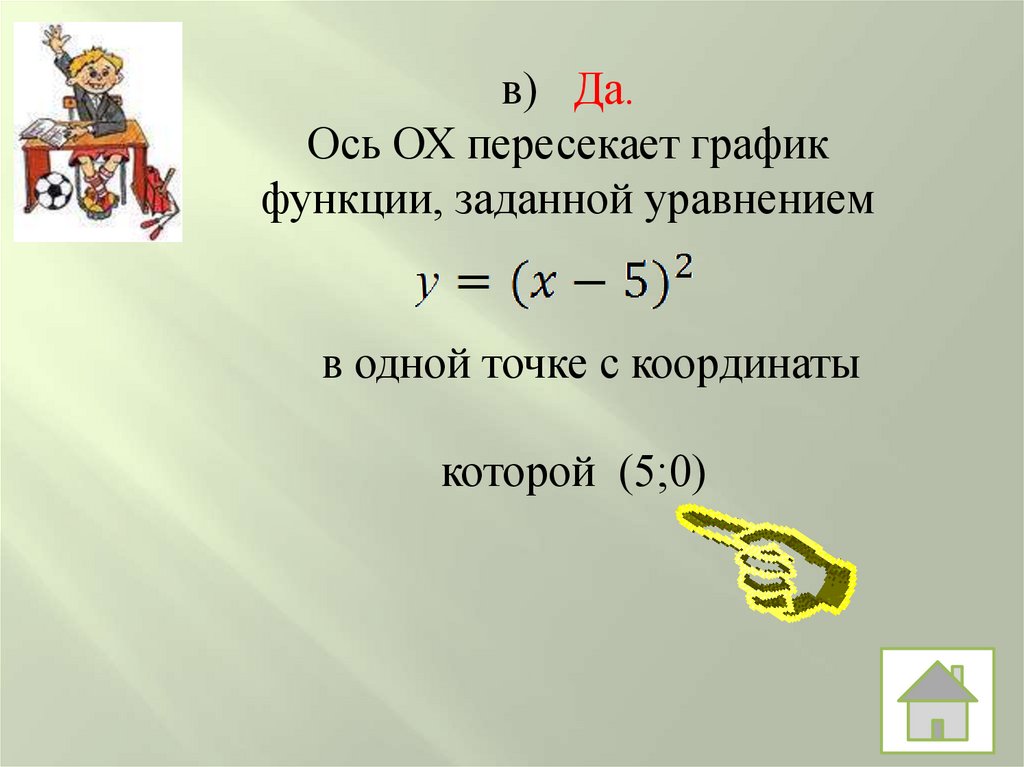
в) Да.
Ось ОХ пересекает график
функции, заданной уравнением
в одной точке с координаты
которой (5;0)

14.

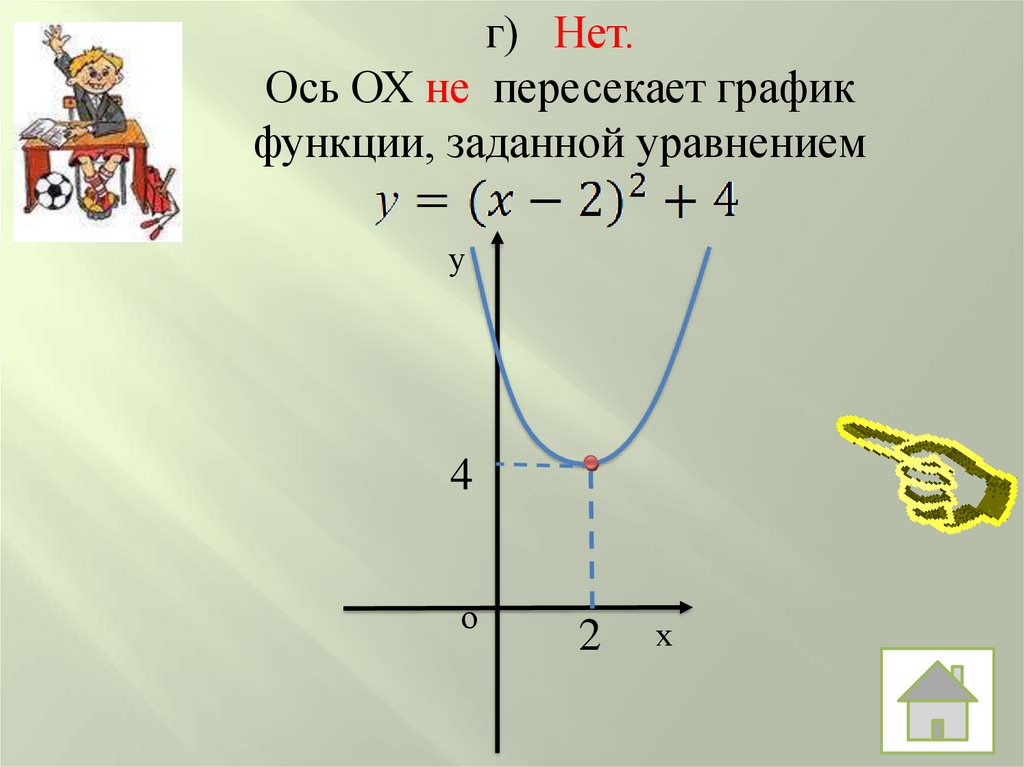
г) Нет.
Ось ОХ не пересекает график
функции, заданной уравнением
у
4
о
2
х

15.

д) Нет.
Ось ОХ не пересекает график
функции, заданной уравнением
у
7
о
х

16.

Неравенства вида
2
aх + bх + с > 0 и
aх2 + bх + с < 0
где х - переменная,
а, в, с –некоторые числа,
причем
,
называют неравенствами
второй степени с одной переменной.

17.

Алгоритм решения неравенств вида
ax2+bx+c>0 и ax2+bx+c<0
1. Рассмотрим функцию
2. Графиком функции является парабола ,
ветви которой направлены вверх (т.к. а>0)
/или вниз (т.к.
) /.
3. Найдем нули функции.
4. На область определения функции нанесем нули
функции. Нарисуем параболу.
5. Найдем значения переменной х, при которых у >0
/или у 0/.

18.

№305(а,б)
№304(а,в,д,ж)
№307(а)
№308(а,в,г)
№310(а)

19.

Найдите множество
решений неравенства:
1. Рассмотрим функцию
2. Графиком функции является парабола , ветви
которой направлены вверх (т.к. 2>0).
3. Найдем нули функции:
4. На область определения
функции нанесем нули функции.
\\\\\\\\\\\\\\\\
Нарисуем параболу.
-2,5
5. Найдем значения
переменной х, при которых
/////////////////
1
х

20.

Найдите множество
решений неравенства:
1. Рассмотрим функцию
2. Графиком функции является парабола , ветви ее
направлены вниз (т.к.
).
3. Найдем нули функции:
4. На область определения
функции нанесем нули
Функции. Нарисуем параболу.
5. Найдем значения переменной
х, при которых
///////////
-2
3
х

21.

Современные знаки неравенств
появились лишь в XVII— XVIII вв.
Знаки < и > ввел английский математик
Томас Гарриот (1560—1621),
знаки ≥ и ≤ ввел французский
математик Пьер Буге (1698—1758).

22.

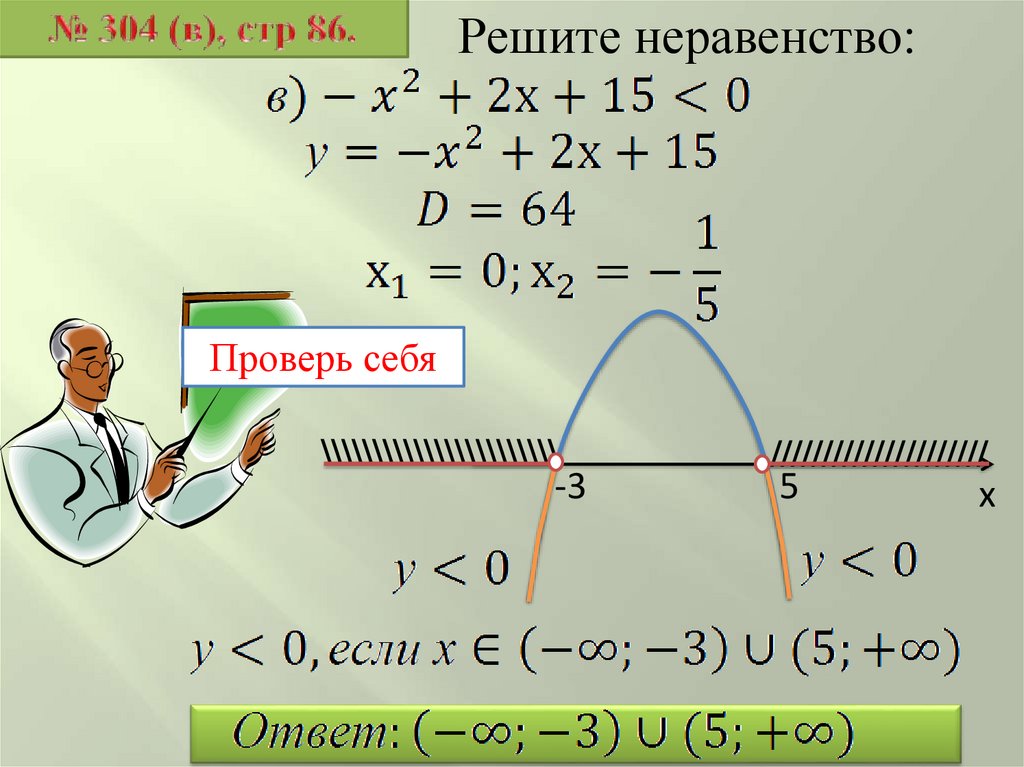
Решите неравенство:
\\\\\\\\\\\\\\\\\
-8
Проверь себя
6
х

23.

Решите неравенство:
Проверь себя
\\\\\\\\\\\\\\\\\\\\\\\
-3
/////////////////////
5
х

24.

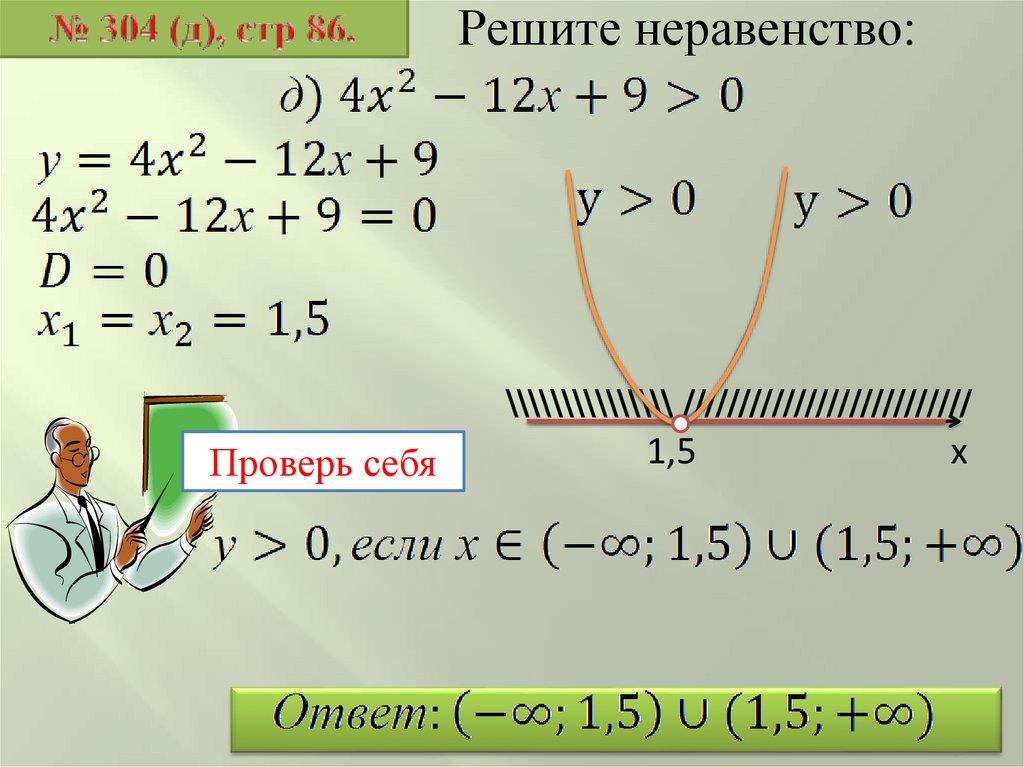
Решите неравенство:
Проверь себя
\\\\\\\\\\\\\\\ //////////////////////////
1,5
х

25.

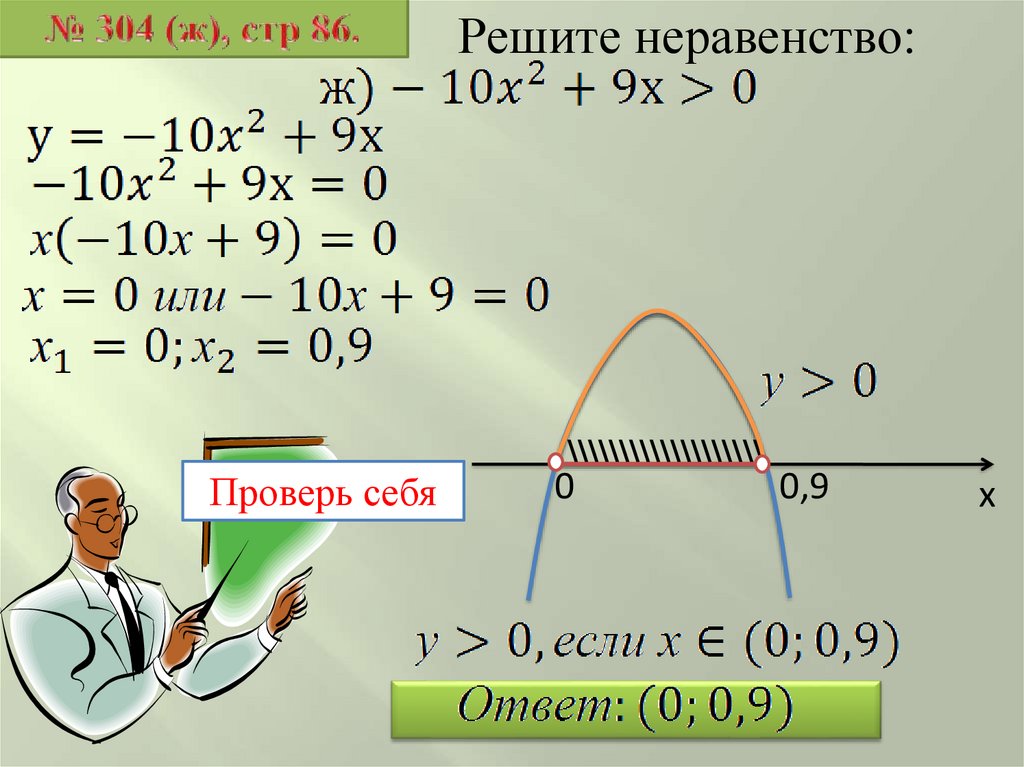
Решите неравенство:
Проверь себя
\\\\\\\\\\\\\\\\\\\
0
0,9
х

26.

27.

Найдите, при каких значениях х трехчлен:
принимает положительные значения.
Проверь себя
Решение:
\\\\\\\\\\\\\
-1,5
/////////////
-1
х

28.

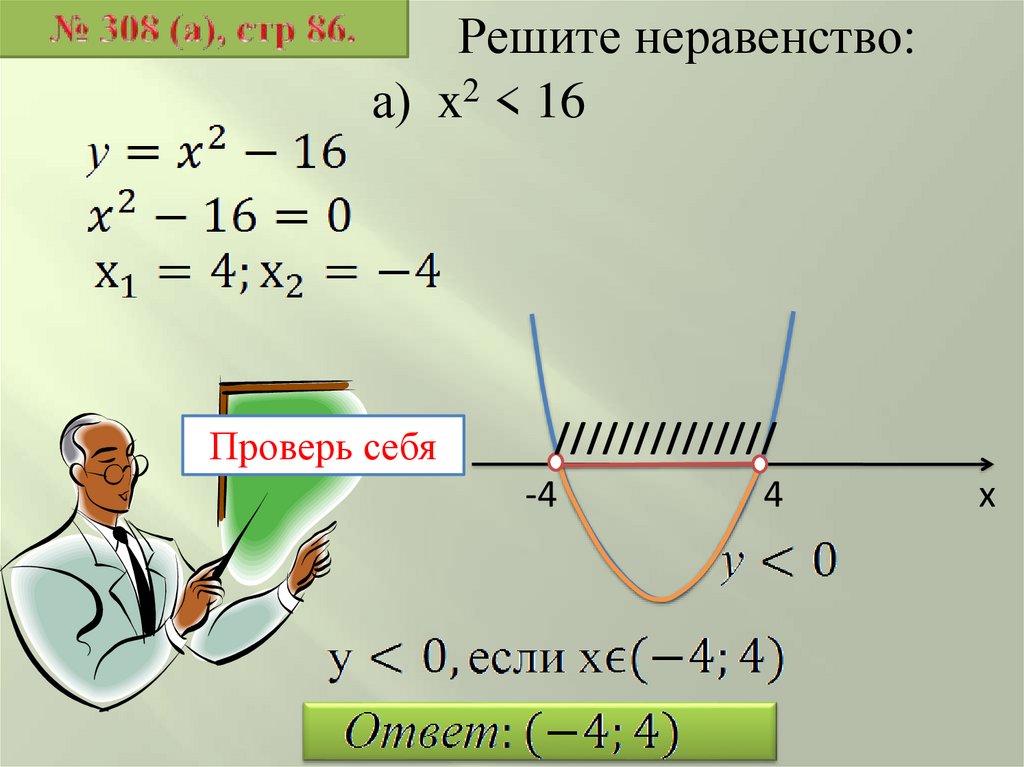
Решите неравенство:
а) x2 < 16
Проверь себя
//////////////
-4
4
х

29.

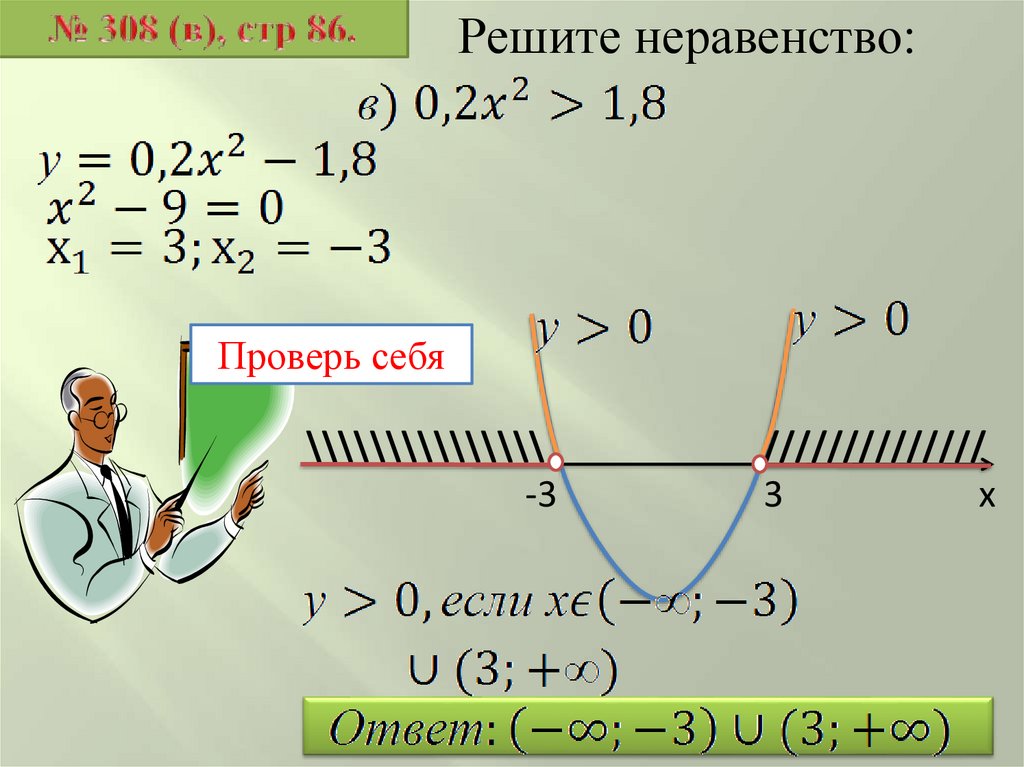
Решите неравенство:
Проверь себя
\\\\\\\\\\\\\\\
-3
//////////////
3
х

30.

Решите неравенство:
Проверь себя
\\\\\\\\\\\\\\\\\\\\\\\
-1/5
/////////////////////
0
х

31.

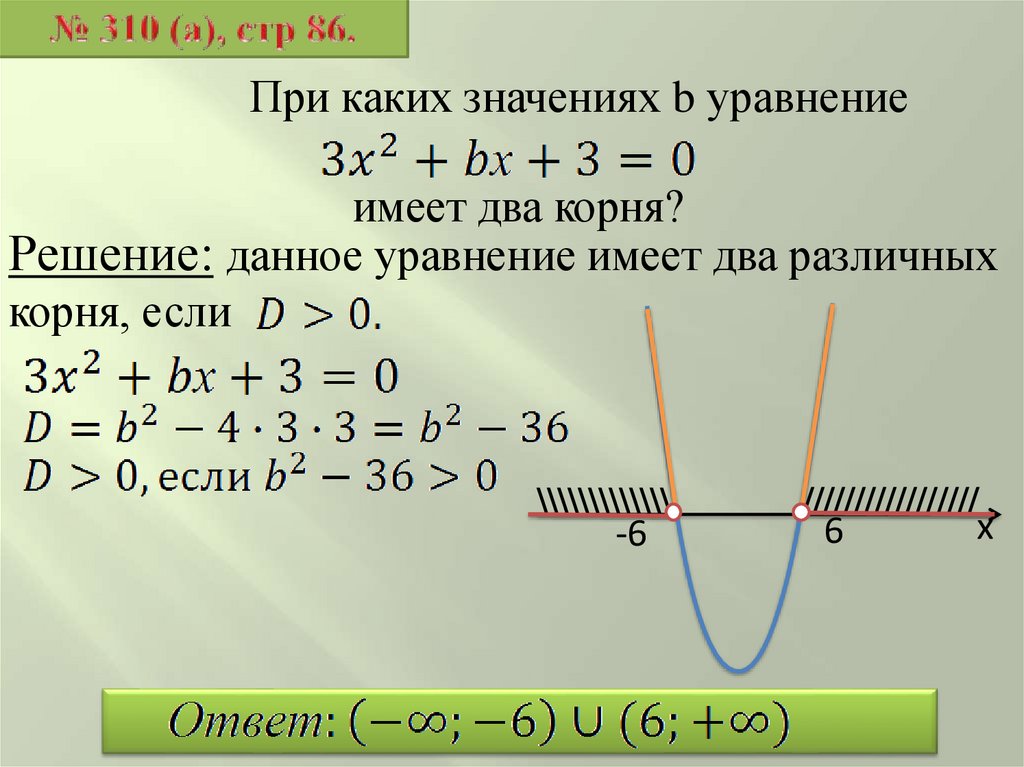
При каких значениях b уравнение
имеет два корня?
Решение: данное уравнение имеет два различных
корня, если
\\\\\\\\\\\\\
-6
/////////////////
6
х

32.

33.

•п. 14, стр 83-85
•вопрос 1, стр 93
•№ 304(б,з), 305(в),310(б);буклеты