Площадь боковой поверхности тела вращения. Лекция №11

1. Здравствуйте!

Лекция №11

2.

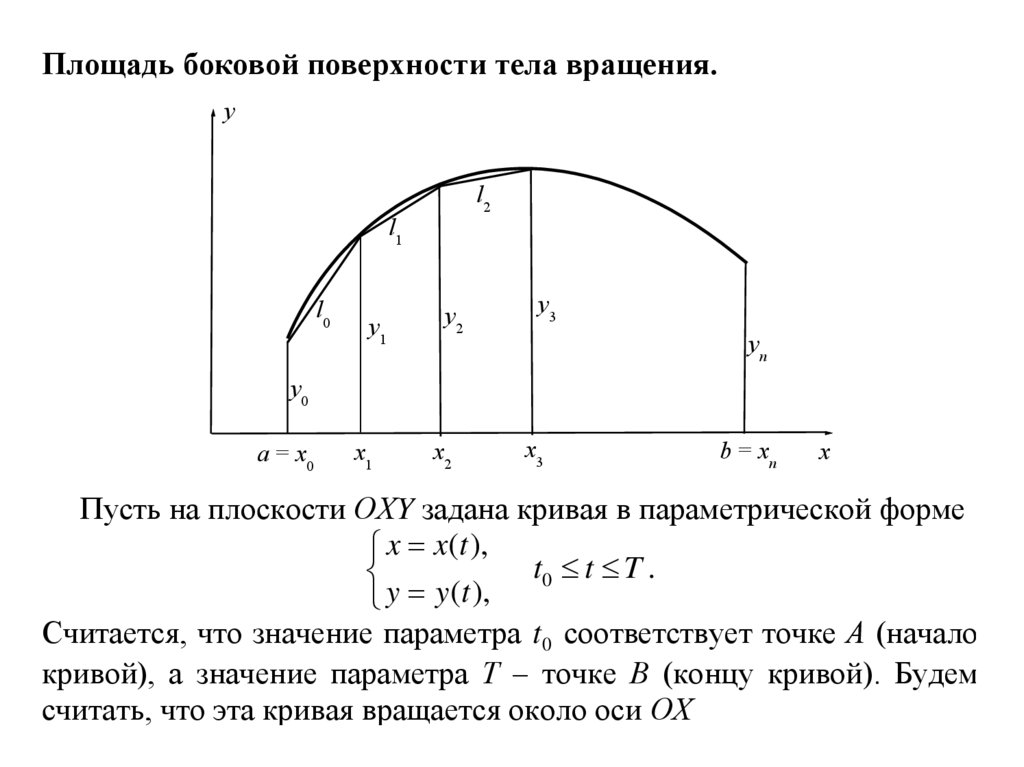
Площадь боковой поверхности тела вращения.
y
l2
l1
l0
y1
y2
y3
yn
y0
a = x0
x1
x2
x3
b = xn
x
Пусть на плоскости ОХY задана кривая в параметрической форме
x x(t ),
t0 t T .
y y (t ),
Считается, что значение параметра t0 соответствует точке А (начало
кривой), а значение параметра Т – точке В (концу кривой). Будем
считать, что эта кривая вращается около оси ОХ

3.

Разобьем отрезок [t0 , T ] на части t0 t1 t2 ... tn 1 tn T и пусть
max ti . Построим на каждом кусочке усеченный конус с
i
радиусами оснований yi и yi 1 и образующей li . Тогда площадь
y (ti ) y (ti 1 )
li , а
боковой поверхности этого конуса будет равна 2
2
суммарная площадь боковых поверхностей всех этих конусов будет
n 1
y (t ) y (ti 1 )
li . За определение величины площади
равна Q 2 i
2
i 0
боковой поверхности тела вращения примем величину P lim Q .
0
Вычислим ее.

4.

n 1
1. Рассмотрим величину Q1 2 y ( i )li , где ti i ti 1. Тогда
i 0
мы имеем
n 1
| Q Q1 | 2
i 0
y (ti ) y (ti 1 )
y ( i ) li
2
n 1
n 1
y (ti ) y ( i ) li y ( i ) y (ti 1 ) li .
i 0
i 0
Но, в силу равномерной непрерывности функции y (t ) разности
y(ti ) y( i ) и y( i ) y(ti 1 ) могут быть сделаны меньше любого
n 1
наперед заданного . Но тогда | Q Q1 | 2 li 2 s0 , где s0 –
i 0
длина дуги нашей кривой. Поэтому lim (Q Q1 ) 0 и P lim Q1.
0
0

5.

n 1
2. Пусть Q2 2 y ( i ) si , где si – длина дуги кусочка кривой. В
i 0
силу непрерывности кривой значения y (t ) ограничены по модулю
величиной М. Тогда имеем
n 1
0 | Q2 Q1 | 2 | y ( i ) | ( si li )
i 0
n 1
n 1
2 M ( si li ) 2 M s0 li 0
i 0
i 0
n 1
n 1
так как s0 lim li . Поэтому P lim Q2 2 lim y ( i ) si .
0
i 0
0
0
i 0

6.

3. Пользуясь первой теоремой о среднем, получаем
si
ti 1
( x ( ))2 ( y ( ))2 d ( x ( i ))2 ( y ( i ))2 ti .
ti
Так как ранее величина i в y ( i ) была произвольной, то возьмем ее
такой же, как и в выражении для si . Тогда
n 1
Q2 2 y ( i ) ( x ( i )) 2 ( y ( i )) 2 ti
i 0
и предельный переход дает
T
P lim Q2 2 y (t ) ( x (t ))2 ( y (t )) 2 dt .
0
t0

7.

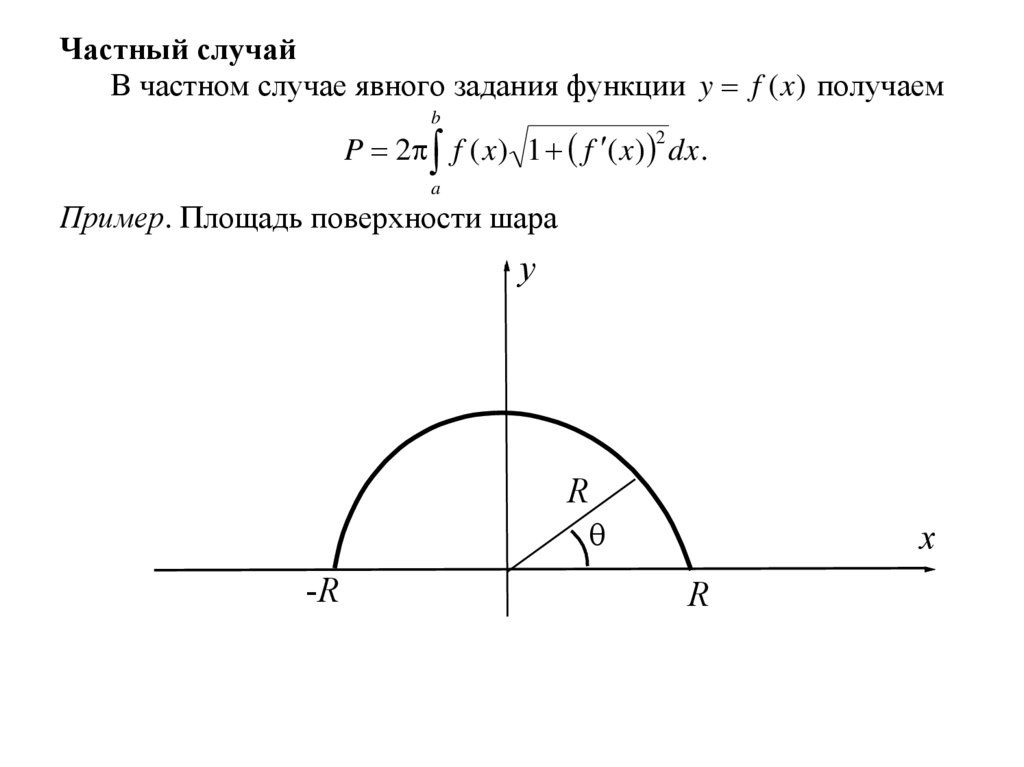
Частный случай
В частном случае явного задания функции y f (x) получаем
b
P 2 f ( x) 1 f ( x) dx .
2
a
Пример. Площадь поверхности шара
y
R
-R
x
R

8.

Как уже говорилось выше, шар получается вращением
полуокружности около оси ОХ. Параметрически полуокружность
задается уравнениями
x R cos ,
0 .
y R sin ,
Тогда x R sin , y R cos , ( x )2 ( y )2 R 2 и мы получаем
0
0
P 2 R sin Rd 2 R 2 sin d 4 R 2 .

9.

Интеграл Стилтьеса
Пусть на отрезке [a, b] заданы две функции f (x) и g (x ) .
Проделаем ту же процедуру, что и при построении интеграла
Римана.

10.

1. Разбиение отрезка на кусочки
Разобьем отрезок [a, b] произвольным образом на части
(кусочки) точками a x0 x1 x2 x3 ... xn 1 xn b (см. рис.).
Для единообразия, точку а будем называть точкой х0, а точку b
точкой хп.
0
x
a = x0
1
x
x1
2
x
x2
...
x3
Пусть g ( xi ) g ( xi 1 ) g ( xi ) и max xi .
i
xn-1
n-1
x
b = xn

11.

2. Составление интегральной суммы
На каждом из кусочков [ xi , xi 1 ] возьмем произвольно
некоторую точку i (она называется средней точкой, хотя, конечно,
не обязательно лежит на середине кусочка), так что [ xi i xi 1 ] и
составим сумму
n 1
f ( i ) g ( xi ) ,
i 0
которая называется интегральной суммой.

12.

3. Предельный переход
Наконец, перейдем к пределу lim .
0
Определение. Если lim существует и не зависит от
0
а) способа разбиения отрезка [a, b] на кусочки и от
б) способа выбора средней точки,
то он называется интегралом Стилтьеса от функции f (x) по
функции g (x ) на отрезке [a, b] и обозначается символом
b
f ( x)dg ( x) :
a
b
.
f ( x)dg ( x) = lim
0
a

13.

Свойства интеграла Стилтьеса
Приведем основные свойства интеграла Стилтьеса. Часть из них
приведем без доказательства.
b
1.
f ( x) f
1
2
f ( x ) d g ( x ) g
1
a
b
3.
b
a
a
( x) dg ( x) f1 ( x)dg ( x) f 2 ( x)dg ( x) .
a
b
2.
b
b
2
b
( x) f ( x)dg1 ( x) f ( x)dg 2 ( x)
a
a
b
k f ( x) d k g ( x) k k f ( x)dg ( x)
1
2
1 2
a
a
b
c
4. Если f ( x)dg ( x) , то c [a, b] f ( x)dg ( x) и
a
a
верно равенство
b
c
b
a
a
c
f ( x)dg ( x) = f ( x)dg ( x) + f ( x)dg ( x) .
b
f ( x)dg ( x)
c
и

14.

Заметим, что обратное вообще говоря неверно, то есть из
существования
c
b
a
c
f ( x)dg ( x) и f ( x)dg ( x) не следует существование
b
f ( x)dg ( x) .
a
5. Основное неравенство.
Пусть функция g (x ) определена на отрезке [a, b] . Разобьем этот
отрезок на части a x0 x1 x2 ... xn 1 xn b и введем величину
b
n 1
V g ( x) sup g ( x
a
k 0
k 1
) g ( xk ) ,
где супремум берется по всем возможным разбиениям отрезка [a, b]
на части. Эта величина называется вариацией (или изменением)
функции g (x ) на отрезке [a, b] . Если
b
V g (x) , то функция
a
называется функцией с ограниченной вариацией.
g (x )

15.

Основное неравенство на интеграл Стилтьеса имеет вид
b
b
f ( x)dg ( x) max | f ( x) | V g ( x)
x [ a , b ]
a
a
Доказательство. Имеем
n 1
n 1
f ( ) g ( x ) f ( ) g ( x
i 0
i
i
i 0
i
i 1
) g ( xi )
n 1
| f ( i ) | | g ( xi 1 ) g ( xi ) |
i 0
n 1
b
max | f ( x) | | g ( xi 1 ) g ( xi ) | max | f ( x) | V g ( x) .
x [ a , b ]
i 0
x [ a , b ]
a
Переходя к пределу 0 получим требуемое неравенство.

16.

6. Интегрирование по частям.
b
b
a
b
a
Если f ( x)dg ( x) , то g ( x ) df ( x) и верно соотношение
b
f ( x)dg ( x) f (b) g (b) f (a) g (a) g ( x)df ( x) .
a
a
Доказательство.
Вновь вернемся к рисунку, показывающему разбиение отрезка
[a, b] на кусочки
0
x
a = x0
Тогда имеем
1
x
x1
2
x
x2
x3
...
xn-1
n-1
x
b = xn

17.

n 1
n 1
n 1
i 0
i 0
i 0
f ( i ) g ( xi 1 ) g ( xi ) f ( i ) g ( xi 1 ) f ( i )g ( xi )
f ( 0 ) g ( x1 ) f ( 1 ) g ( x2 ) f ( 2 ) g ( x3 ) ... f ( n 1 ) g ( xn )
f ( 0 ) g ( x0 ) f ( 1 ) g ( x1 ) f ( 2 ) g ( x2 ) ... f ( n 1 ) g ( xn 1 )
f ( xn ) g ( xn ) f (b) g (b) f ( x0 ) g ( x0 ) f (a) g (a)
(переформируем суммы так, чтобы сомножители вида g ( xi ) стояли
перед скобками)
f (b) g (b) f (a ) g (a )
g ( x0 ) f ( 0 ) f ( x0 ) g ( x1 ) f ( 1 ) f ( 0 ) g ( x2 ) f ( 2 ) f ( 1 )
... g ( xn ) f ( xn ) f ( n 1 ) f (b) g (b) f (a) g (a) ,
где есть интегральная сумма для
b
g ( x)df ( x) ,
в которой точки i
a
стали точками разбиения, а точки xi – средними точками.

18.

Теперь после предельного перехода 0 и получим требуемое
соотношение
b
b
a
a
f ( x)dg ( x) f (b) g (b) f (a) g (a) g ( x)df ( x) .

19.

Вычисление интеграла Стилтьеса
Рассмотрим частные случаи.
1. g (x) .
Тогда g ( xi 1 ) g ( xi ) g ( i ) xi . Возьмем в интегральной сумме у
f ( i ) именно то i , которое получилось по формуле Лагранжа.
Тогда имеем
n 1
n 1
i 0
i 0
f ( i ) g ( xi ) f ( i ) g ( i ) xi .
Делая предельный переход 0 , получим
b
b
a
a
f ( x)dg ( x) f ( x) g ( x)dx ,
где первый интеграл понимается в смысле Стилтьеса, а второй – в
смысле Римана.

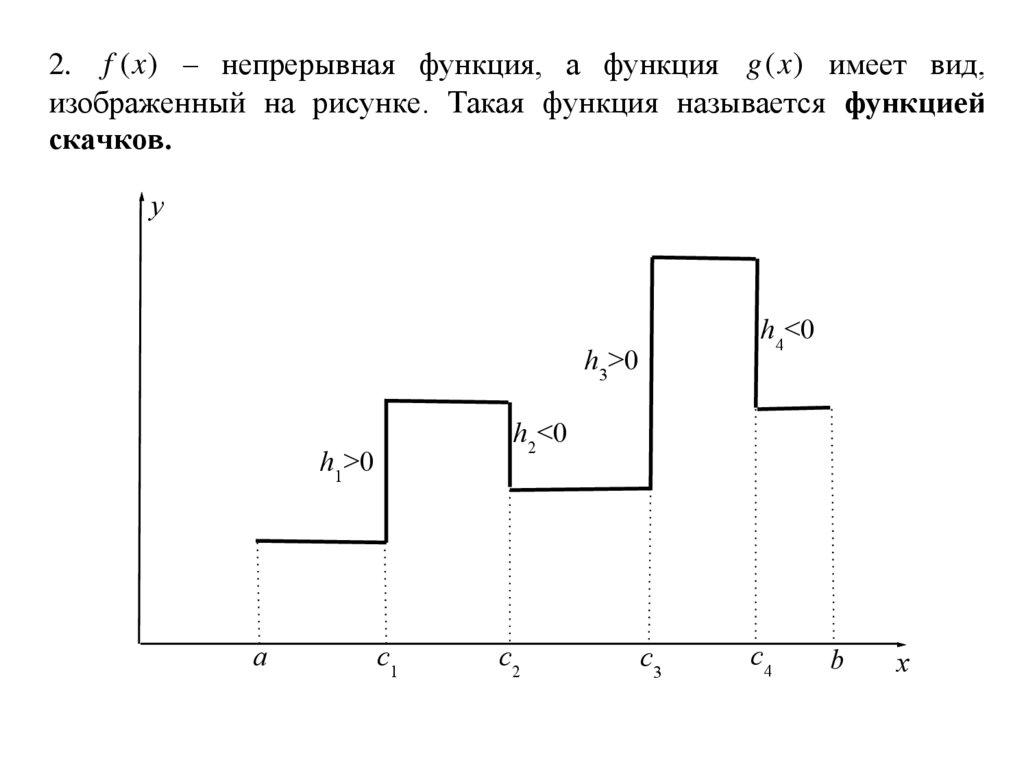
20.

2. f (x) – непрерывная функция, а функция g (x ) имеет вид,
изображенный на рисунке. Такая функция называется функцией
скачков.
y
h4<0
h3>0
h2<0
h1>0
a
c1
c2
c3
c4
b
x

21.

Разобьем отрезок [a, b] на части и пусть xi1 c1 xi1 1 , xi2 c2 xi2 1 ,
xi3 c3 xi3 1, …, xik ck xik 1. Тогда в интегральной сумме останутся
лишь слагаемые
f (cs ) g ( xi 1 ) g ( xi ) .
k
s
s 1
s
Но при предельном переходе 0 g ( xis 1 ) g ( xis ) hs и поэтому
b
k
f ( x)dg ( x) lim f (c )h .
a
0
s 1
s
s

22.

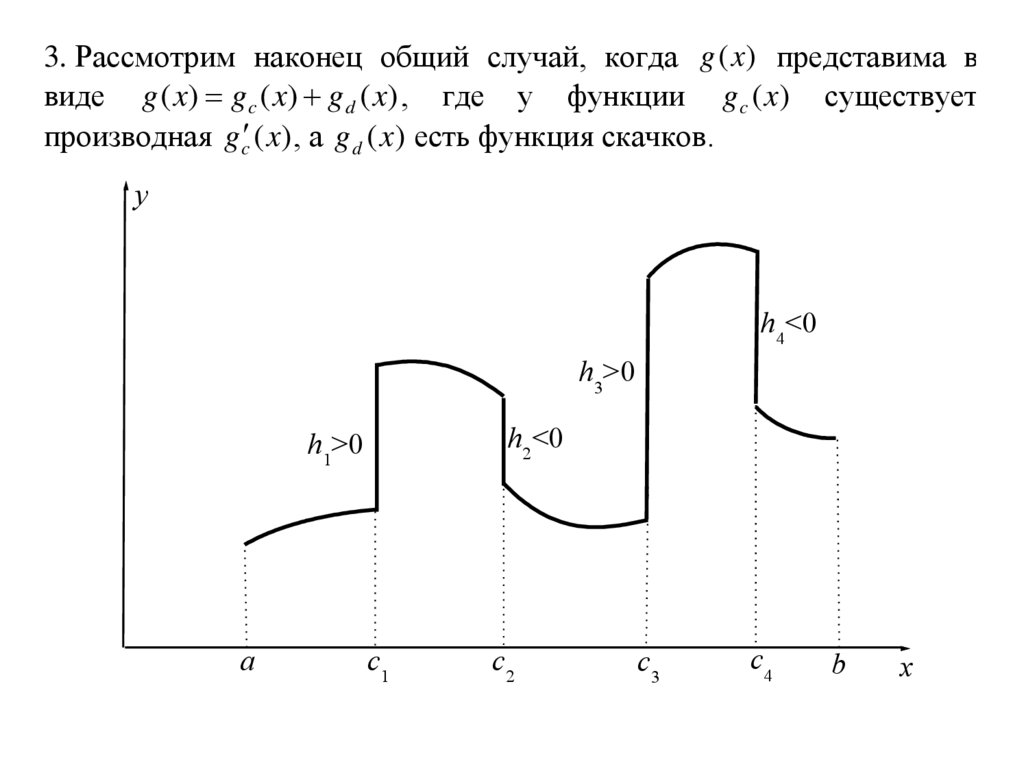
3. Рассмотрим наконец общий случай, когда g (x ) представима в
виде g ( x) gc ( x) g d ( x) , где у функции g c (x) существует
производная g c (x) , а g d (x) есть функция скачков.
y
h4<0
h3>0
h2<0
h1>0
a
c1
c2
c3
c4
b
x

23.

Тогда, по свойствам интеграла Стилтьеса
b
b
k
f ( x)dg ( x) f ( x) g ( x)dx f (c )h .
c
a
Этой формулой и
практических задач.
s 1
a
пользуются
чаще
s
всего
s
при
решении

24. Конец второй части