Замена переменных в определенном интеграле. Лекция №9

1. Здравствуйте!

Лекция №9

2.

Замена переменных в определенном интеграле
Теорема. Пусть
1. f (x) интегрируема на [a, b] ;
2. функция (t ) монотонно возрастает и ( ) a , ( ) b ;
3. t [ , ] (t ) .
Тогда
b
a
f ( x)dx f ( (t )) (t )dt .
Обратите внимание на пределы интегрирования во втором
интеграле.

3.

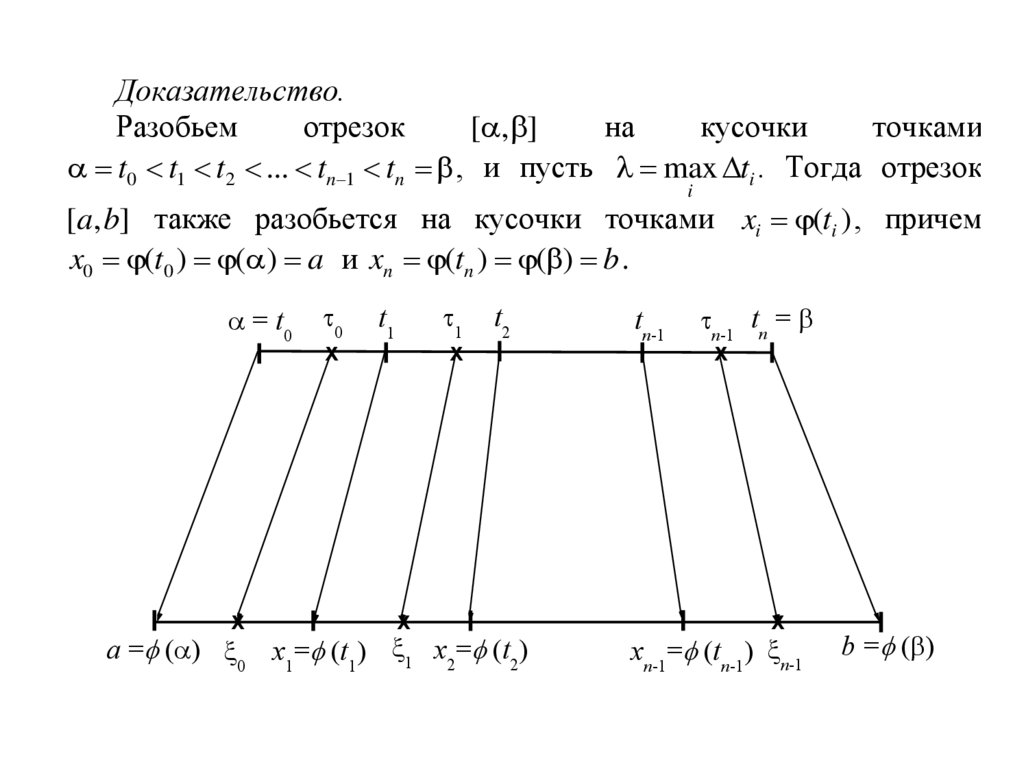
Доказательство.
Разобьем
отрезок
на
кусочки
точками
[ , ]
t0 t1 t2 ... tn 1 tn , и пусть max ti . Тогда отрезок
i
[a, b] также разобьется на кусочки точками xi (ti ) , причем
x0 (t0 ) ( ) a и xn (tn ) ( ) b .
= t0
x
0
1
t1
x
t2
x
x
a = ( ) 0 x1= (t1) 1 x2= (t2)
tn-1
n-1 tn =
x
x
xn-1= (tn-1) n-1
b = ( )

4.

Рассмотрим величины xi xi 1 xi . Для них, используя формулу
Лагранжа, имеем
xi xi 1 xi (ti 1 ) (ti ) ( i ) ti ,
где ti i ti 1.
Как говорилось в определении понятия определенного интеграла,
предел интегральной суммы не должен зависеть от выбора средней
точки. Возьмем поэтому i ( i ) . Тогда для интегральной суммы
получим
n 1
n 1
f ( ) x f ( ( )) ( ) t .
i 0
i
i
i 0
i
i
i

5.

Проделаем теперь предельный переход при max ti 0 . В силу
i
равномерной непрерывности функции (t ) на отрезке [ , ] , при этом
будет и max xi 0 . Мы получим
i
n 1
n 1
lim f ( i ) xi lim f ( ( i )) ( i ) ti ,
0
0
i 0
что и дает формулу
b
a
i 0
f ( x)dx f ( (t )) (t )dt .
Обратите внимание на следующие моменты:
1. В отличие от неопределенного интеграла здесь нет возврата к
переменной х.
2. Но зато во втором интеграле стоят другие пределы! И это есть тот
момент, о котором студенты, решая задачи, часто забывают. Так что НЕ
ЗАБЫВАЙТЕ МЕНЯТЬ ПРЕДЕЛЫ!

6.

Определенный интеграл как функция верхнего предела
Прежде, чем приступить к изучению данного раздела, обратите
внимание на следующее:
1. Неопределенный интеграл f ( x) dx это функция от х, а
b
определенный интеграл
f ( x)dx это число.
a
2. Значение определенного интеграла не зависит от того, какой
буквой обозначена переменная интегрирования, то есть
b
b
b
f ( x)dx f (t )dt f (u )du ...
a
a
.
Поэтому
если
в
процессе
a
выкладок переменная интегрирования вдруг будет обозначена
другой буквой не пугайтесь, это совершенно все равно.

7.

Объектом
исследования
данного
раздела
является
определенный интеграл с переменным верхним пределом
x
f (t )dt F ( x) ,
a
который представляет собой функцию от х.
Теорема 1. Пусть f (x) интегрируема на интервале [a, b] .
Тогда F (x ) есть непрерывная функция на этом интервале.

8.

Доказательство.
Так как f (x) интегрируема на интервале [a, b] , то она
ограничена на этом интервале, то есть существуют конечные т и
М, такие, что x [a, b] m f ( x) M . Тогда
F ( x x )
x x
x
x x
x x
a
a
x
x x
x
f (t )dt f (t )dt f (t )dt F ( x) f (t )dt.
Но, по первой теореме о среднем,
f (t )dt x ,
где m M .
x
Тогда
x x
lim
x 0
и
f (t )dt lim ( x) 0
x
x 0
x x
lim F ( x x) F ( x) lim
x 0
x 0
f (t )dt F ( x) ,
x
что и говорит о непрерывности функции F (x ) .

9.

Теорема 2. Пусть f (x) непрерывна на интервале [a, b] . Тогда
F ( x) f ( x) .
Доказательство.
В ходе доказательства теоремы 1 было получено соотношение
x x
F ( x x ) F ( x )
f (t )dt.
x
Но теперь f (x) непрерывна. Поэтому, по следствию из первой
теоремы о среднем, мы можем записать:
x x
f (t )dt f (c) x ,
x
где x c x x и при x 0 c x .

10.

Тогда имеем
и, наконец,
F ( x x) F ( x) f (c) x ,
F ( x x) F ( x)
f (c ) ,
x
F ( x x ) F ( x )
lim f (c) f ( x) .
x 0
c x
x
Таким образом, у каждой непрерывной функции существует
первообразная!
F ( x) lim

11.

Замечание.
b
~
Рассмотрим F ( x ) f (t ) dt , то есть определенный интеграл с
x
переменным нижним пределом. Но так как
b
x
~
F ( x) f (t )dt f (t )dt ,
x
b
то этот объект немедленно сводится к предыдущему. Получаем:
~
1. F ( x) непрерывная функция;
~
2. если f (x) непрерывна на интервале [a, b] , то F ( x) f ( x) .

12.

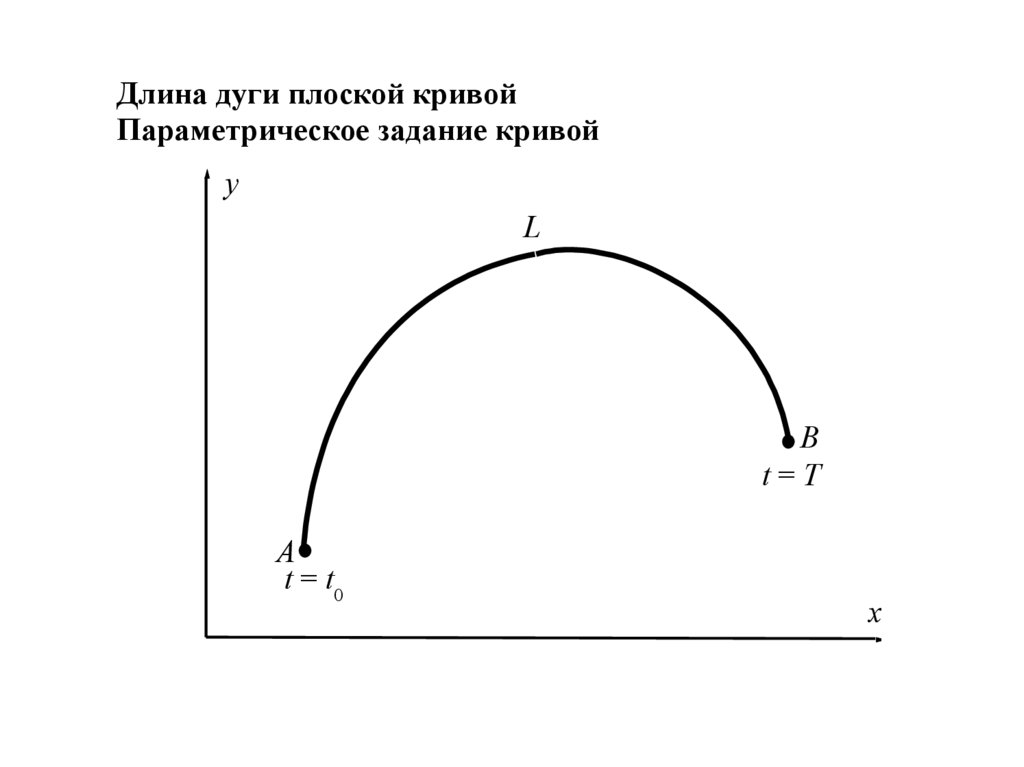
Длина дуги плоской кривой
Параметрическое задание кривой
y
L
B
t=T
A
t = t0
x

13.

Наиболее общим способом задания кривой на плоскости
считается так называемое параметрическое задание кривой, когда
кривая L задается системой уравнений
x x(t ),
t0 t T .
y y (t ),
Считается, что значение параметра t0 соответствует точке А
(начало кривой), а значение параметра Т – точке В (концу кривой).

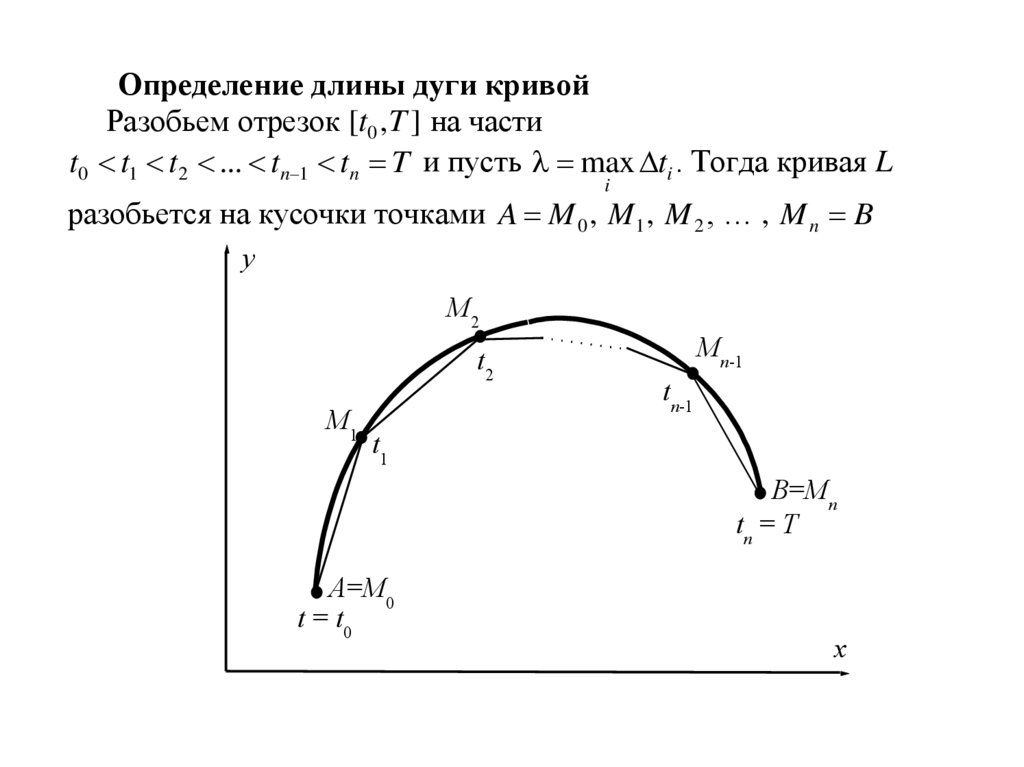
14.

Определение длины дуги кривой
Разобьем отрезок [t0 , T ] на части
t0 t1 t2 ... tn 1 tn T и пусть max ti . Тогда кривая L
i
разобьется на кусочки точками A M 0 , M 1 , M 2 , … , M n B
y
M2
t2
M1
Mn-1
tn-1
t1
B=Mn
tn = T
A=M0
t = t0
x

15.

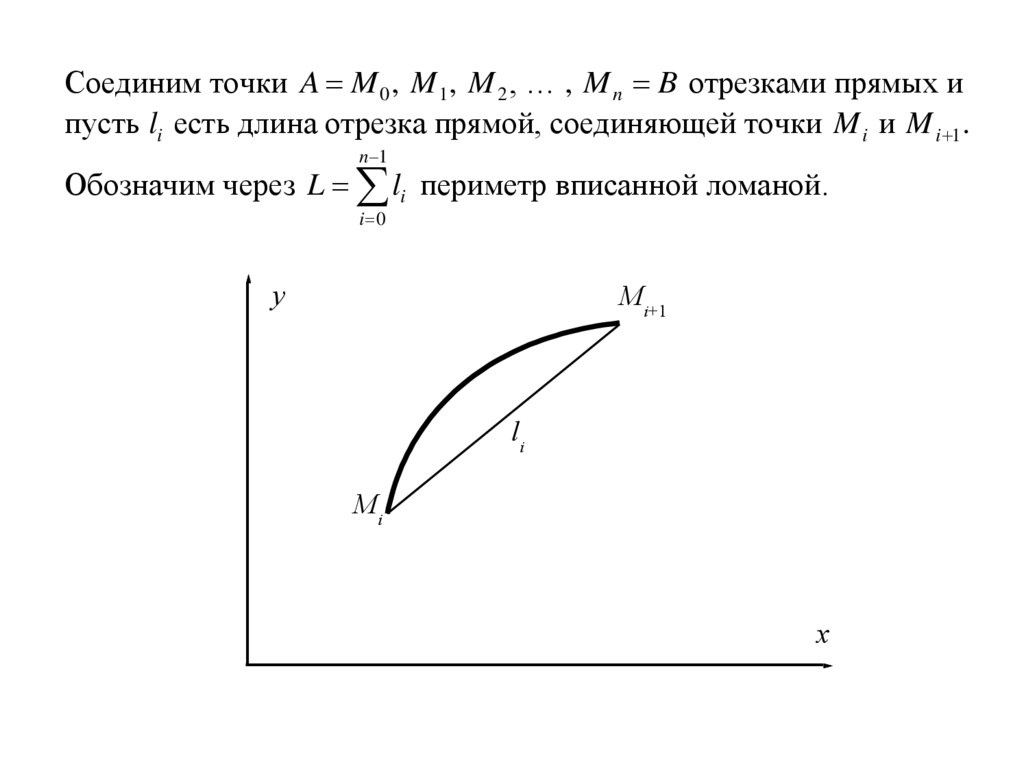
Соединим точки A M 0 , M 1 , M 2 , … , M n B отрезками прямых и
пусть li есть длина отрезка прямой, соединяющей точки M i и M i 1 .
n 1
Обозначим через L li периметр вписанной ломаной.
i 0
y
Mi+1
li
Mi
x

16.

Определение. Если существует lim L s и этот предел не
0
зависит от способа разбиения отрезка [t0 , T ] на части, то он
называется длиной дуги кривой АВ.
Вычисление длины дуги кривой
Теорема. Пусть функции x(t ) и y (t ) имеют на отрезке [t0 , T ]
непрерывные производные x (t ) и y (t ) . Тогда
T
s ( x (t )) 2 ( y (t )) 2 dt .
t0

17.

Доказательство.
Разобьем отрезок [t0 , T ] на части t0 t1 t2 ... tn 1 tn T и
пусть max ti . Тогда точка M i имеет координаты ( x(ti ), y (ti )) , а
i
точка M i 1 имеет координаты ( x(ti 1 ), y (ti 1 )) . Поэтому
li ( x(ti 1 ) x(ti ))2 ( y (ti 1 ) y (ti ))2
и поэтому
n 1
L ( x(ti 1 ) x(ti ))2 ( y (ti 1 ) y (ti ))2 .
i 0

18.

Используя два раза формулу Лагранжа, получаем
x(ti 1 ) x(ti ) x ( i ) ti , y(ti 1 ) y(ti ) y ( i ) ti .
Однако здесь возникает одна трудность – величины i и i разные.
Теперь имеем
n 1
L ( x ( i ))2 ( y ( i ))2 ti .
i 0
Наряду с этой величиной рассмотрим величину
n 1
L ( x ( i ))2 ( y ( i ))2 ti
i 0
и оценим разность между ними.

19.

Для этого выведем одно вспомогательное неравенство. Имеем
b 2 b12
b 2 b12
2
2
2
2
b b1 ,
a b a b1
2
2
2
2
b b1
a b a b1
так как
a 2 b 2 a 2 b12 b 2 b12 b b1
и поэтому
1
1
.
2
2
2
2
a b a b1 b b1

20.

Поэтому имеем
( x ( i ))2 ( y ( i ))2 ( x ( i ))2 ( y ( i ))2 y ( i ) y ( i )
и теперь
n 1
L L ( x ( i )) 2 ( y ( i ))2
i 0
n 1
( x ( i ))2 ( y ( i )) 2 ti y ( i ) y ( i ) ti .
i 0
Но, по предположению, y (t ) непрерывна на промежутке [t0 , T ] ,
следовательно, по теореме Кантора, она равномерно непрерывна на
этом промежутке. Это означает, что
0 0 ti y ( i ) y ( i ) .
Но тогда
n 1
n 1
i 0
i 0
L L y ( i ) y ( i ) ti ti (T t0 ) ,
и, в силу произвольности , это означает, что lim L L 0 .
0

21.

Но тогда
n 1
s lim L lim L lim ( x ( i )) 2 ( y ( i )) 2 ti
0
0
0
T
i 0
( x (t )) 2 ( y (t )) 2 dt .
t0