Методы вычисления определенных интегралов. (Лекция 9)

1.

Лекция 9.
Определенный интеграл. Общее определение.
Основные свойства. Основные методы вычисления
определенных интегралов.

2.

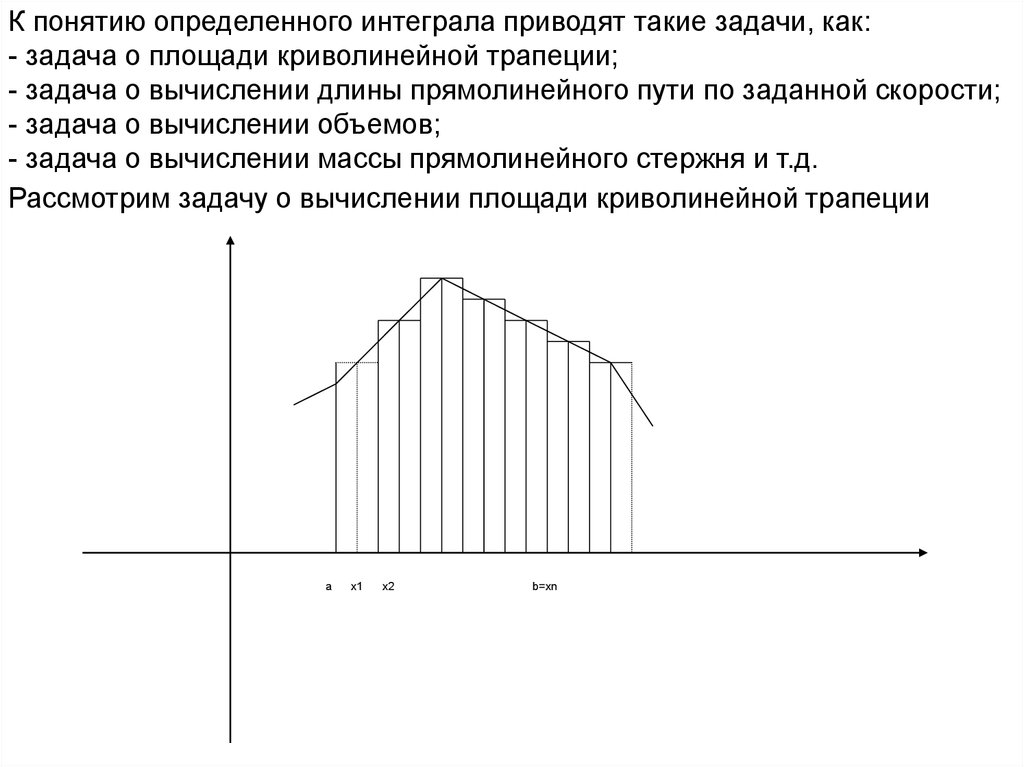
К понятию определенного интеграла приводят такие задачи, как:
- задача о площади криволинейной трапеции;
- задача о вычислении длины прямолинейного пути по заданной скорости;
- задача о вычислении объемов;
- задача о вычислении массы прямолинейного стержня и т.д.
Рассмотрим задачу о вычислении площади криволинейной трапеции
a
x1
x2
b=xn

3.

Рассмотрим криволинейную трапецию aABb, то есть плоская фигура,
ограниченная графиком функции y=f(x), отрезками аА, вВ, прямыми x=a,
x=b и осью ОХ.
Разобьем отрезок [a,b] точками a x0 x1 ... xn b
на n произвольных отрезков , то есть [a, x1 ][ x1 , x2 ]...[ xn 1 .b]
Длину каждого отрезка обозначим через xk , k 1,2,..., n На каждом отрезке
'
x k построим прямоугольник высотой f ( x k ) , где x k' [ x k 1 , x k ]
f ( x k' ) - значение функции в этой точке.
f ( x k' ) x k - площадь такого прямоугольника.
n
Составим сумму таких произведений S n f ( x k' ) x k(1) – интегральная сумма
k 1
для функции f(x) на отрезке [a,b]
Интегральная сумма (1) выражает площадь ступенчатой фигуры и
приближенно заменяет площадь криволинейной трапеции aABb
Функция y=f(x) – непрерывная и площадь построенной фигуры при
достаточно малых xk ”почти совпадает” с площадью рассматриваемой
криволинейной трапеции. Можно для [a,b] выбирать различные x k и
x k' [ x k 1 , x k ] и таким образом получать последовательность разбиений и
последовательность интегральных
сумм. Можно доказать, что существует
n
предел S переменной S n f ( x k' ) x k, когда n , а длина x 0
k 1
k

4.

то есть S lim n S n
n
lim xk f ( x k' ) x k
Предел S – площадь криволинейной
k 1
трапеции.
Определение
n
Предел S интегральной суммы S n f ( x k' ) x k для функции y=f(x) на отрезке
k 1
[a,b], когда число n отрезков неограниченно возрастает, а наибольшая
длина отрезка xk 0 называют определенным интегралом от функции
y=f(x) на отрезке [a,b].
b
Обозначение
f ( x)dx lim
a
n
xk
k 1
f ( x k' ) x k
(2)
a– нижний предел интегрирования;
b – верхний предел интегрирования;
[a,b] – отрезок интегрирования;
f(x) – подынтегральная функция;
x – переменная интегрирования.
Функцию f(x) интегрируема на отрезке [a,b], если для нее существует
предел (2).
Замечание
Если f(x) интегрируема на отрезке [a,b], то f(x) интегрируема и на [c, d ] [a, b]

5.

Таким образом, возвращаясь к задаче о площади криволинейной
трапеции, можно сказать, что она может быть вычислена с помощью
b
определенного интеграла S f ( x)dx
a
Из определения следует, что величина определенного интеграла не
зависит от обозначения переменной интегрирования
b
b
b
f ( x)dx = f ( y)dy =...= f (u)du
a
a
и т.д.
a
Формула Ньютона-Лейбница
Вычисление определенного интеграла основано на применении формулы
Ньютона-Лейбница.
Пусть f(x) – интегрируема на отрезке [a,b] и F(x) – одна из первообразных
функции f(x), то есть f(x)=F’(x). Тогда приращение первообразной на
отрезке [a,b], то есть F(b)-F(a) равно значению определенного интеграла
b
f ( x)dx F (b) F (a)
a
(1)
b
Другая форма записи f ( x)dx F ( x) ba - двойная подстановка от a до b
a
Таким образом, чтобы вычислить определенный интеграл, достаточно
найти одну из первообразных подынтегральной функции и вычислить ее
значение сначала при x=b, затем при x=a и из первого результата вычесть
второй.

6.

3
Пример 2 xdx x 2 13 9 1 8
1
3
Если F(x)= x c , тогда 2 xdx ( x 2 c) 13 9 c 1 c 8
2
1
Следовательно, от выбора первообразной значение интеграла не зависит.
Определенный интеграл с переменным верхним пределом
Пусть f(x0 непрерывна на отрезке [a,b]. Рассмотрим интеграл
x
f (t )dt (1), где
t [ a, x ] [ a, b]
a
(во избежании путаницы, переменная интегрирования обозначена другой
буквой)
Если F(x) – первообразная функции f(x), то есть F’(x)=f(x), то согласно
формуле Ньютона-Лейбница имеем
x
f (t )dt F ( x) F (a)
(2), отсюда
a
x
d
d
f
(
t
)
dt
[ F ( x) F (a)] F ' ( x) ( F (a))' f ( x) 0 f ( x)
dx a
dx

7.

Следовательно
Производная определенного интеграла с переменным верхним пределом
по этому пределу равна значению подынтегральной функции для этого
предела:
x
d
f (t )dt f ( x) (3)
dx a
x
Таким образом, интеграл Ф( х) f (t )dt (4)
a
является первообразной для подынтегральной функции f(x).
Отметим, что из формулы (2) следует, что Ф(а)=0, то есть Ф(х) есть та
первообразная для функции f(x), которая обращается в 0 при х=а.
x
Пример d 1 t 2 dt 1 x 2
dx 0
Рассмотрим определенный интеграл с переменным нижним пределом
b
f (t )dt , где x [a, b]
x
На основании формулы Ньютона-Лейбница имеем
b
d
d
f
(
t
)
dt
[ F (b) F ( x)] ( F (b))' F ' ( x) f ( x)
dx x
dx

8.

Таким образом, производная определенного интеграла с переменным
нижним пределом по этому пределу равна значению подынтегральной
функции для этого предела, взятому с обратным знаком.
Основные свойства определенного интеграла
При выводе основных свойств определенного интеграла исходим из
формулы Ньютона-Лейбница
b
f ( x)dx F (b) F (a) (1), где f(x) – непрерывна на отрезке [a,b] , f(x)=F’(x).
a
I.
Разобьем свойства определенного интеграла на группы.
А. Общие свойства
Величина определенного интеграла не зависит от обозначения
переменной интегрирования, то есть
b
b
a
a
b
f ( x)dx = f ( y)dy =...= f (u)du
a
II. Определенный интеграл с одинаковыми пределами интегрирования
равен 0, то есть
a
f ( x)dx
a
=F(a)-F(a)=0

9.

III. При перестановке пределов интегрирования определенный интеграл
меняет свой знак на обратный. Действительно, переставляя пределы
интегрирования, в силу формулы (1), получим
a
b
f ( x)dx F (a) F (b) [ F (b) F (a)] f ( x)dx
b
(2)
a
Б. Свойство аддитивности
IV. Если отрезок интегрирования [a,b] разбить на конечное число частичных
отрезков, то определенный интеграл, взятый по отрезку [a,b] равен сумме
определенных интегралов, взятых по всем частичным отрезкам.
Пусть [a, b, ] [a, c] [c, b] , где a c b
Полагая F’(x)=f(x)
a
c
b
b
a
c
f ( x)dx F (a) F (b) [ F (с) F (a)] [ F (b) F (c)] f ( x)dx f ( x)dx (3)
Замечание
Формула (3) справедлива, если с лежит вне отрезка [a,b] и f(x)
непрерывна на отрезках [a,c],[c,b].

10.

В. Свойства линейности
V. Постоянный множитель можно выносить за знак интеграла
Пусть F(x) – первообразная для f(x) на [a,b], где А – постоянная
величина, тогда AF(x) – первообразная для Af(x), так как
[AF(x)]’=AF’(x)=Af(x). Получаем
a
Af ( x)dx AF ( x) |
b
b
a
AF (b) AF (a) A[ F (b) F (a)] A f ( x)dx
b
a
VI. Определенный интеграл от алгебраической суммы конечного числа
непрерывных функций равен такой же алгебраической сумме
определенных интегралов от этих функций.
Рассмотрим алгебраическую сумму функций f(x)+g(x)-h(x) (4),
где f(x),g(x),h(x) – непрерывные функции.
F(x), G(x), H(x) – их первообразные, то есть F’(x)=f(x), G’(x)=g(x), H’(h)=h(x),
тогда F(x)+G(x)-H(x) – первообразная для f(x)+g(x)-h(x), так как
[F(x)+g(x)-H(x)]’=F’(x)+G’(x)-H’(x)=f(x)+g(x)-h(x)
Отсюда получаем
b
b
[
f
(
x
)
g
(
x
)
h
(
x
)]
dx
[
F
(
x
)
G
(
x
)
H
(
x
)]
|
a [ F (b) G(b) H (b)] [ F (a) g (a) H (a)]
a
b
b
b
a
a
a
[ F (b) F (a)] [G(b) G(a)] [ H (b) H (a)] f ( x)dx g ( x)dx h( x)dx

11.

Г. Свойства монотонности
VII. Если подынтегральная функция определенного интеграла непрерывна
и неотрицательна, а верхний предел интегрирования больше нижнего или
равен ему, то определенный интеграл также неотрицателен.
Пусть f ( x) 0 при a x b . Так как F’(x)=f(x) 0
, то F(x) – неубывающая функция. В таком случае при b 0 имеем
b
f ( x)dx F (b) F (a) 0
a
VIII. Неравенство между непрерывными функциями можно интегрировать
поэлементно при условии, что верхний предел интегрирования больше
нижнего.
Пусть f ( x) g ( x) при a x b , f(x),g(x) – непрерывные функции на
отрезке [a,b].
Так как g ( x) f ( x) 0 , то в силу свойств VI и VIII имеем
b
b
b
[ g ( x) f ( x)]dx g ( x)dx f ( x)dx 0
a
a
a
, отсюда
b
b
a
a
f ( x)dx g ( x)dx

12.

Замечание
Пусть f(x) – знакопеременная непрерывная функция на отрезке [a,b],
где b>a.
f ( x) 0, a x
f ( x) 0, x
f ( x) 0, x b
В силу свойства аддитивности IV и учитывая геометрический смысл
интеграла имеем
b
b
f ( x)dx f ( x)dx f ( x)dx f ( x)dx S
a
1
S 2 S 3 , S1 , S 2 , S 3
- площади
a
соответствующих криволинейных трапеций.
Таким образом, определенный интеграл, в общем случае при a<b
представляет собой алгебраическую сумму площадей, соответствующих
криволинейных трапеций, где площади трапеций, расположенных выше
оси ОХ, берутся со знаком +, а площади трапеций, расположенных ниже
оси ОХ, - со знаком -.

13.

Теорема о среднем
Теорема
Определенный интеграл от непрерывной функции равен произведению
длины отрезка интегрирования на значение подынтегральной функции
при некотором промежуточном значении аргумента.
Доказательство:
В силу формулы Ньютона-Лейбница имеем
b
f ( x)dx F (b) F (a) (1), где F’(x)=f(x)
a
Применяя к разности первообразных теорему о конечном приращении
функции получим ( f ( x) x f ' ( ) , где x
b
F(b)-F(a)=(b-a)F’(c)=(b-a)f(c), где a<c<b, отсюда f ( x)dx (b a) f (c) (2),
a
где a<c<b

14.

Геометрическая интерпретация
B
D
E
C
A
a
c
b
В формуле (2):
Левая часть – площадь криволинейной трапеции aABb
Правая часть – площадь прямоугольника с основанием b-a и высотой
f(c)
Таким образом, формула (2) геометрически означает, что можно
всегда подобрать на дуге AB такую точку С с абсциссой с, заключенной
между a и b, что площадь соответствующего прямоугольника aDEb с
высотой сС будет в точности равна площади криволинейной трапеции
aABb.

15.

Число f (c )
- называется средним значением функции f(x) на
отрезке [a,b].
Из (2) имеем 1
b
f ( x)dx
b a
(3)
a
Следствие
Пусть m min f ( x), a x b и M max f ( x), a x b . Так как
m f ( x) M , при a<b из (2) имеем
b
m(b a) f ( x)dx M (b a)
(4)
a
Интегрирование по частям в определенном интеграле
Пусть u(x) и v(x) непрерывные дифференцируемые функции на
отрезке [a,b]. Имеем d[u(x)v(x)]=v(x)du(x)+u(x)dv(x). Интегрируя, это
равенство в пределах от a до b и учитывая,
что du(x)=u’(x)dx и dv(x)=v’(x)dx находим
b
b
a
a
u ( x)v( x) |ba v( x)u ' ( x)dx u ( x)v' ( x)dx
Отсюда получаем формулу интегрирования по частям в определенном
интеграле
b
b
u( x)v' ( x)dx u(b)v(b) u(a)v(a) v( x)u' ( x)dx
a
a
(1)

16.

b
Для краткости употребляется выражение u (b)v(b) u (a)v(a) u ( x)v( x) | a
Пример
2
2
2
x
sin
xdx
{
u
x
;
du
dx
;
dv
cos
xdx
;
v
sin
x
}
x
sin
x
|
sin
xdx
2
sin
2
0
sin
0
cos
x
|
0
0
0
0
Замена переменной в определенном интеграле
Пусть дан определенный интеграл
b
f ( x)dx
(1), где f(x) непрерывна на отрезке [a,b].
a
Ввели новую переменную t, связанную с х соотношением x (t ), ( t ) (2)
(t ) непрерывная дифференцируемая функция на отрезке [ , ]
Если при этом
1. При изменении t от до переменная х меняется от a до b, то есть
( ) a, ( ) b (3)
2. Сложная функция f ( (t )) определена и непрерывна на отрезке [ , ]
b
Тогда справедлива формула
f ( x)dx f ( (t )) ' (t )dt
a
(4)

17.

Доказательство
Рассмотрим сложную функцию F ( (t )) , где F(x) – первообразная для f(x),
то есть F’(x)=f(x)
Применяя правило дифференцирования сложной функции, получим
d
F ( (t )) F ' ( (t )) ' (t ) f ( (t )) ' (t )
dt
Следовательно функция F ( (t )) - первообразная для функции f ( (t )) ' (t )
Отсюда, на основании формулы Ньютона-Лейбница, учитывая равенство
(3), получаем
b
f ( (t )) (t )dt F ( (t )) | F ( ( )) F ( ( )) F (b) F (a) f ( x)dx
a
Замечание
При вычислении определенного интеграла с помощью замены переменной
нет необходимости возвращаться к прежней переменной, достаточно
ввести новые пределы интегрирования по формулам (3).

18.

Пример
3
2
2
x
1
x
dx
{
t
1
x
;
x
t
1
;
dx
2
tdt
;
x
0
t
1
;
x
3
t
2
}
(
t
1) t 2tdt
2
0
1
t5 t3 2
31 1 8 1 62 14
11
2( ) |1 2(
)
7
5 3
5
3
5
3
15
Приложения определенного интеграла
Определенный интеграл можно применять в следующих задачах:
•вычисление площадей, ограниченных некоторыми линиями;
•вычисление длин дуг линий;
•вычисление объемов тел по известным площадям поперечных сечений;
•вычисление объемов тел вращения;
•вычисление поверхностей тел вращения;
•вычисление координат центра тяжести плоской фигуры;
•вычисление моментов инерции линии, круга, цилиндра и т.д.

19.

Площадь в прямоугольных координатах
Задача 1 Найти площадь S криволинейной трапеции aABb, ограниченной
анной непрерывной линией y=f(x), отрезком [a,b] ооси ОХ и двумя
вертикалями x=a и x=b, если f ( x) 0, x [a, b].
y
M
M’
A
B
y
dS
S
0
a
x
x’=x+dx
b
x

20.

Решение
На основании геометрического смысла определенного интеграла имеем
b
S ydx (1), где y=f(x) – данная функция
a
Рассмотрим другой способ обоснования формулы (1).
Будем рассматривать площадь S как переменную величину, образованную
перемещением текщей ординаты xM=y из начального положения aA в
конечное положение bB. Давая текущей абсциссе x приращение x dx
получим приращение площади S представляющее собой площадь
вертикальной полосы xMM’x’, заключенной между ординатами в точках x и
x' x x
Дифференциал площади dS есть главная линейная часть приращения S
при x 0 и очевидно равен площади прямоугольника с основанием dx и
высотой y. Поэтому dS=ydx (2)
Интегрируя
равенство (2) в пределах от x=a до x=b получаем формулу (1)
b
S ydx
В этом случае показано применение метода дифференциала , сущность
которого заключается в том, что сначала из элементарных соображений
составляется дифференциал искомой величины, а затем после
интегрирования в соответствующих пределах находится значение самой
искомой величины.
a

21.

Задача 2
Найти площадь обрасти, ограниченной двумя непрерывными линиями
y1 f1 ( x), y2 f 2 ( x), ( y2 y1 ) и двумя вертикалями x=a и x=b.
y
S
0
x
b
x
Решение.
Будем предполагать, что y1 f1 ( x), y2 f 2 ( x)
- неотрицательные функции на отрезке [a,b].
Искомую площадь S можно рассматривать, как разность площадей двух
криволинейных трапеций, ограниченных данными линиями. Поэтому
b
b
b
a
a
a
S y 2 dx y1dx ( y 2 y1 )dx
(3)

22.

Примеры
2
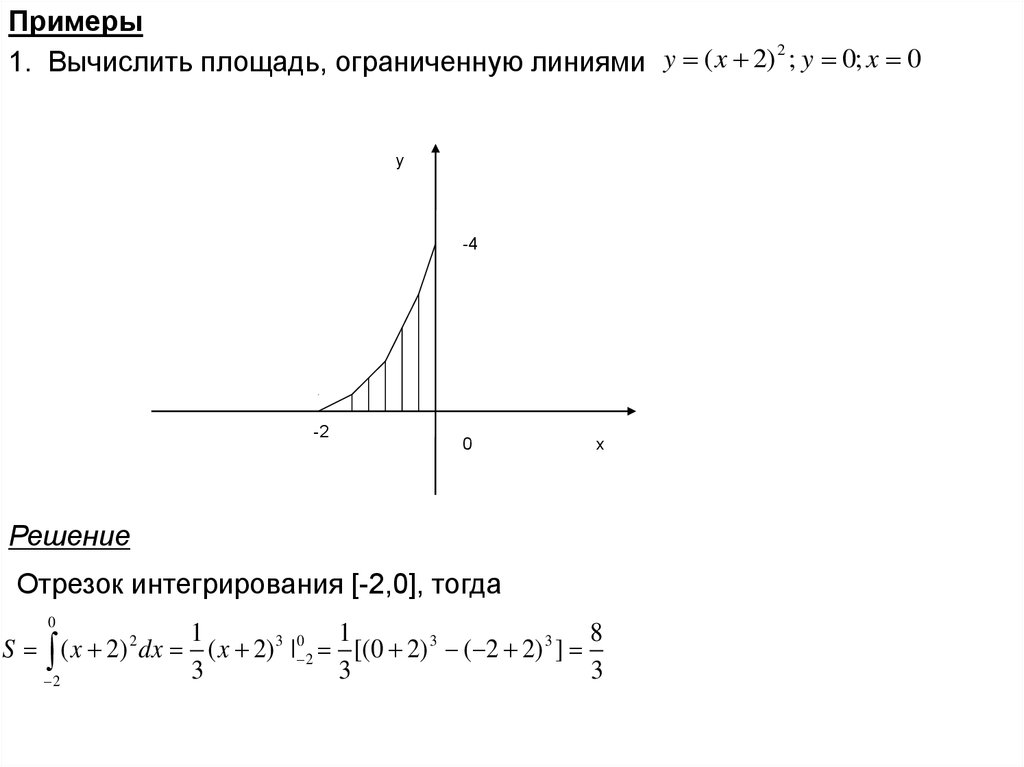
1. Вычислить площадь, ограниченную линиями y ( x 2) ; y 0; x 0
y
-4
-2
0
x
Решение
Отрезок интегрирования [-2,0], тогда
0
1
1
8
S ( x 2) 2 dx ( x 2) 3 |0 2 [(0 2) 3 ( 2 2) 3 ]
3
3
3
2

23.

2
2. Вычислить площадь, ограниченную линиями y x 2 x; y 0
y
2
0
x
Решение
0
1 3
8
4
2
2 2
S
|
(
x
2
x
)
dx
|
|
x
x
|
|
|
4
|
Отрезок интегрирования [0,2], тогда
0
2
3
3
3
3. Вычислить площадь, ограниченную графиком функции y=sinx на
отрезке [0;2 ] и ОХ.
Решение
Отрезок интегрирования [0;2 ] разбиваем на два отрезка и S S1 S 2
где S1 sin xdx cos x | 0 cos cos 0 1 1 2
0
2
S 2 | sin xdx | | cos x | 2 | | cos 2 cos | | 1 1 | 2
S S1 S 2=2+2+4

24.

2
4. Вычислить площадь, ограниченную параболой y x 1 и прямой
x+y=3.
y
y
-2
1
0
x
Решение
Отрезок интегрирования [ 2;1] , так как точки пересечения линий x1 2; x2 1
y x2 1
определяются при решении системы уравнений
x y 3
На основании формулы (3) находим
1
1
x2 x3 1
1
1
1
S [(3 x) ( x 1)]dx (2 x x )dx (2 x
) | 2 2(1 2) (1 4) (1 8) 4
2
3
2
3
2
2
2
2
2

25.

x2 y2
5. Найти площадь области, ограниченной эллипсом 2 2 1
a
b
В виду симметрии можно ограничиться вычислением ¼
площади.
y
y
b
a
x
0
Решение
Отрезок интегрирования [0; a ]
b 2
1
y
a x 2 ; S a 2 x 2 dx {x a sin t; dx a cos tdt; x 0 t 0; x a t }
a
4
2
0
a
2
2
2
b
ab
ab
1
ab ab
2
2
2
2
2
a
a
sin
a
a
cos
tdt
ab
cos
tdt
(
1
cos
2
t
)
dt
(
t
sin
2
t
)
|
0
0
a 0
2 0
2
2
2 2
4
Тогда
S ab.

26.

x a(t sin t )
6. Найти площадь, ограниченную первой аркой циклоиды
y a(1 cos t )
y
y
2a
0
2 a
Решение
Отрезок интегрирования [0;2 a ]
S
2 a
2
0
0
ydx dx a(1 cos t )dt; x 0 t 0; x 2 a; t 2 a(1 cos t )a(1 cos t )dt
2
a
2
x
(1 2 cos t cos t )dt a [(t 2 sin t ) |
2
0
a 2 (2 ) 3 a 2
2
2
0
2
1 cos 2t
1
1
dt ] a 2 [2 (t sin 2t ) |02 ]
2
2
2
0

27.

d
Площадь в полярных координатах
Задача Найти площадь S сектора OAB, ограниченного данной
непрерывной линией f ( ) и двумя лучами ; , где ,
- полярные координаты.
B
M’
M
dS
d
O
f ( )
, ,
A
x
Для решения задачи используется метод дифференциала.
Представим, что площадь S возникла в результате перемещения
полярного радиуса f ( ) при изменении угла ; (см. рисунок).
Если текущий полярный угол получает приращение d
то приращение площади S пл.OMM '
Дифференциал dS – главная линейная часть S при d 0 и dS=пл.OMN
(площадь кругового сектора OMN радиуса f ( ) с центральным углом d

28.

1
2
1
2
1
2
Поэтому dS MN OM d 2 d (1)
Это элемент площади в полярных координатах. Интегрируя (1) в пределах
1
; получим искомую площадь S
2 d где f ( )
- данная функция
2
Пример.
Найти площадь, ограниченную кардиоидой a(1 cos )
Составляя таблицу значений, получим
2
5
0
6
3
2
3
6
2a
a
0,5a
1,9 a
1,5a
0,1a
0

29.

Построим кривую
А
х
2а
1
1
S 2 d S 2 d a 2 (1 cos ) 2 d a 2 ( d 2 cos d cos 2 d )
2
20
0
0
0
0
0
1
1
1
3 2
a 2 (( sin ) | 0 (1 cos 2 )d ) a 2 ( 0 ( sin 2 ) | 0 )
a
20
2
2
2