Кусочная функция

Функция y = f(x).
y = f(x) - зависимость y от x по правилу f .
x – независимая переменная (аргумент)
y – зависимая переменная (функция)
f – правило зависимости (уравнение, график и т.д.)
1)Область определения функции – допустимые
значения аргумента (х).
ширина по Ох D(y)
2)Множество значений функции – соответствующие
значения функции (y).
высота по Оу
E(y)
Для каждого значения х – единственное значение у.

8.

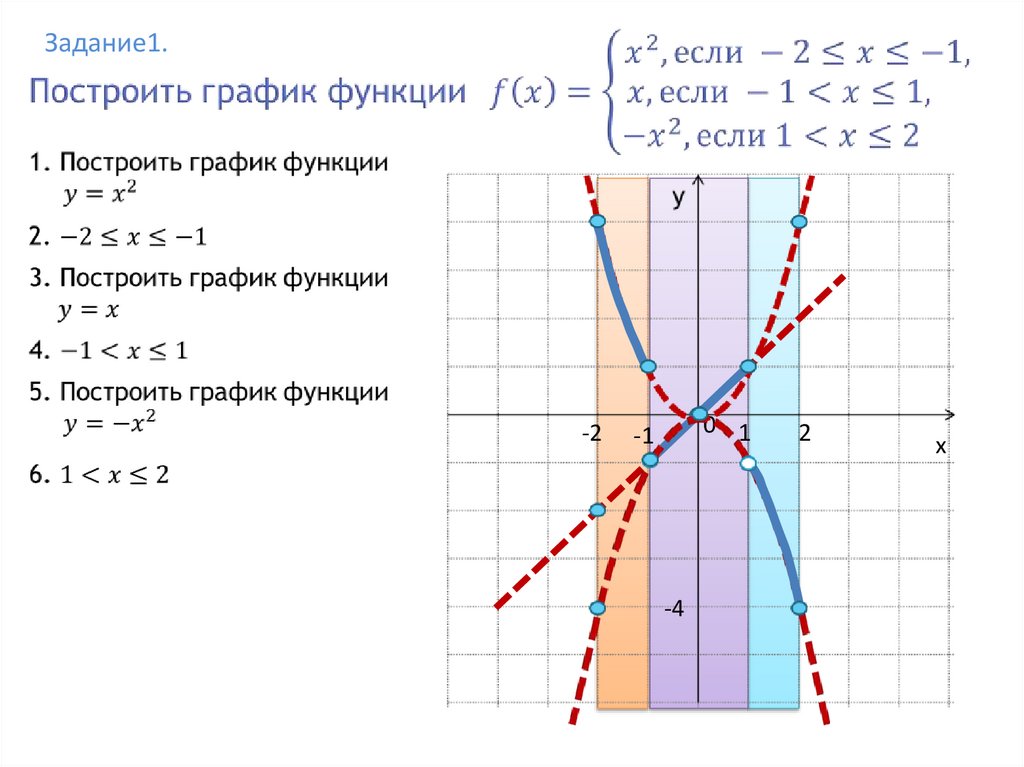
Задание1.
-2
0 1
-1
-4
2
x

9.

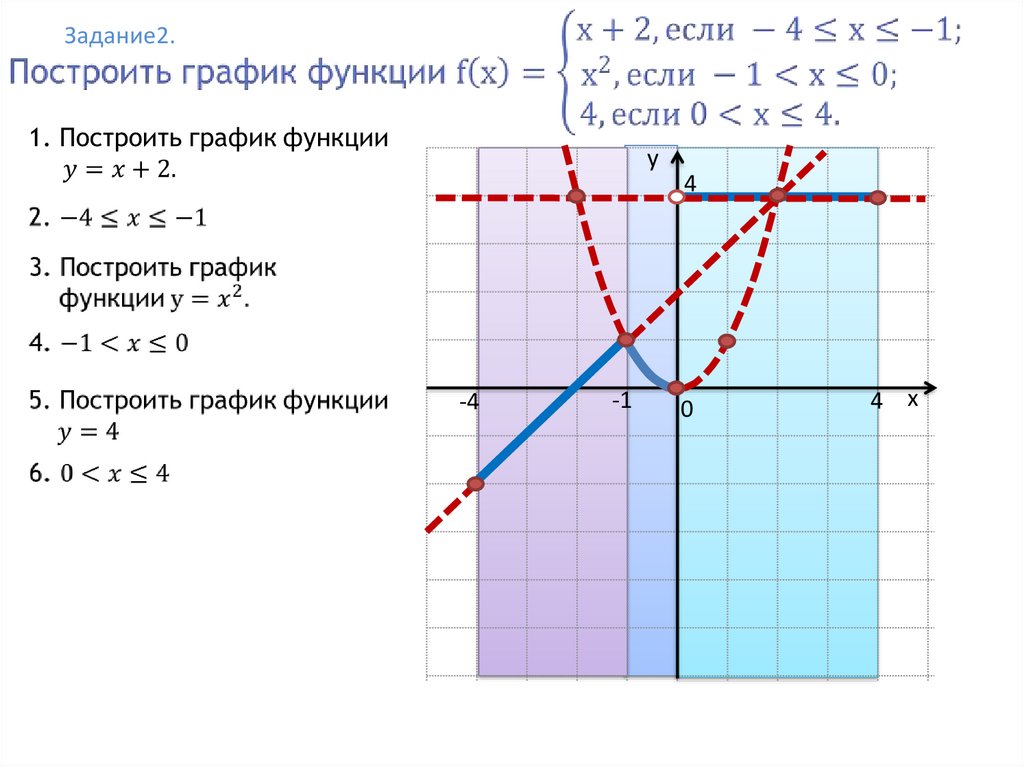
Задание2.
y
-4
-1
4
0
4 x

10.

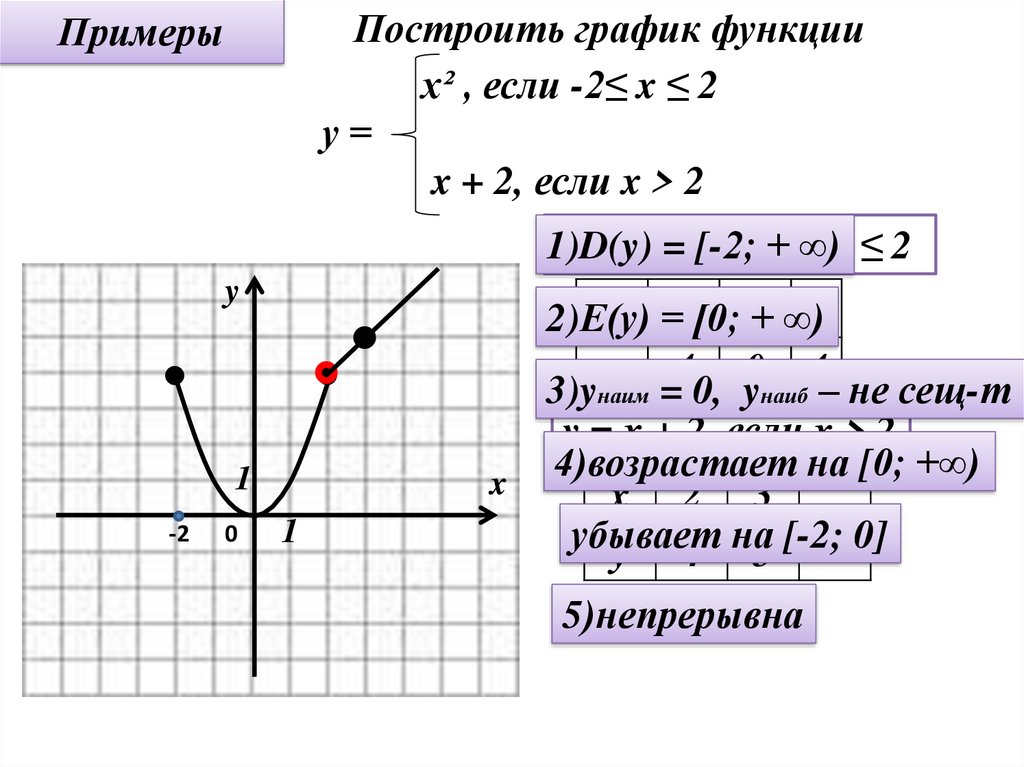
Построить график функции
x² , если -2≤ x ≤ 2
у=
x + 2, если x > 2
Примеры
1)D(y)
y = x² ,=если
[-2; -2≤
+ ∞)x ≤ 2
y
1
-2
0
1
x =-2[0; 0+ ∞)2
2)E(y)
y 4 0 4
3)yнаим = 0, yнаиб – не сещ-т
y = x + 2, если x > 2
4)возрастает на [0; +∞)
x
x 2 3
убывает
y 4 на
5 [-2; 0]
5)непрерывна

11.

Построить график и прочитать свойства
1)у ==- х²
, - 3≤ х ≤ 2
1)D(y)
[-3;2]ᴜ(2;+∞)
х -3 0 2
2)E(y) = [0;+∞)
у -9 0 -4
3)y2)у
наим = 0,
= 2х - 4 , х >2
y
yнаибх= не2существует
3
у 0 2 на [0;2] и
4)возрастает
на (2;+∞);
1
1 2
x
убывает на [-3;0]
5)разрывна в точке х = 2

12.

y
1 точка
прямая
нет точек
1 точка
x 0 2
y 0 2
1 точка
y = p – горизонтальная прямая
Ответ: при p = 1.
1
1
x

13.

Постройте график функции
f(x)=
2х²,если -1≤х≤1
2,если 1<х≤6
и опишите её свойства.

14.

f(x)=
2х²,если -1≤х≤1
2,если 1<х≤5
у=2х²
у
Х
0
±1
±2
8
У
0
2
8
6
5
4
3
2
1
-1 ≤ х ≤ 1
у=2
Х
1
6
У
2
2
1<х≤5
-3 -2 -1 0
х
1 2 3 4 5 6

15.

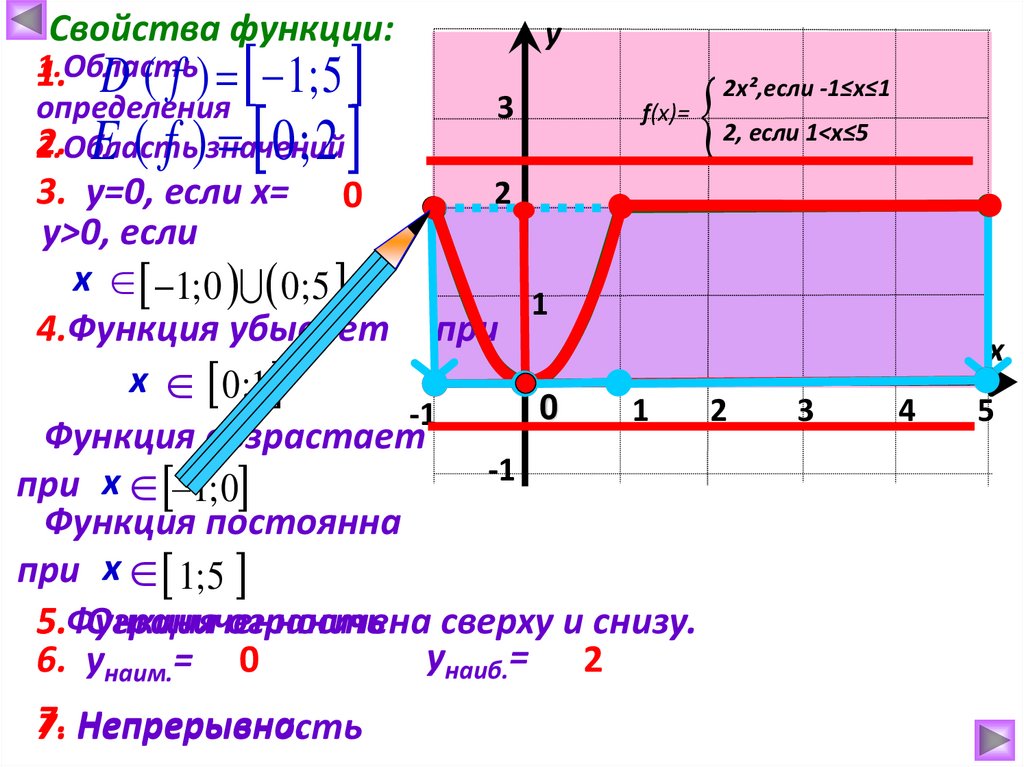
Свойства функции:
1.Область
1. D ( f ) 1; 5
определения
E ( f ) 0; 2
2.
2.Область
значений
у
3
f(x)=
2x²,если -1≤х≤1
2, если 1<х≤5
2
3. у=0, если х= 0
у>0, если
х 1; 0 0; 5
1
4.Функция убывает при
х 0 ;1
0
1
2
-1
Функция возрастает
-1
при х 1; 0
Функция постоянна
при х 1; 5
5.Функция
Ограниченность
ограничена сверху и снизу.
унаиб.= 2
6. унаим.= 0
7. Непрерывность
Непрерывна.
х
3
4
5

16.

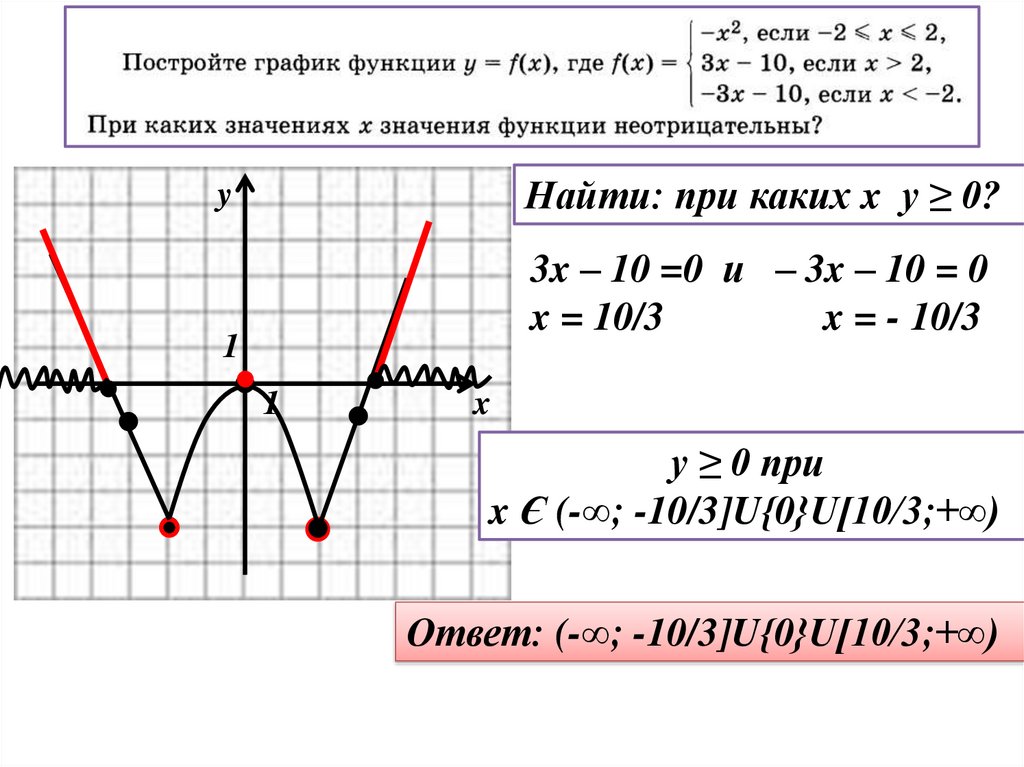
Найти: при каких x y ≥ 0?
y
3x – 10 =0 и – 3x – 10 = 0
x = 10/3
x = - 10/3
1
1
x
y ≥ 0 при
x Є (-∞; -10/3]U{0}U[10/3;+∞)
Ответ: (-∞; -10/3]U{0}U[10/3;+∞)

English Русский Rules