Similar presentations:
Кусочно-заданные функции
1.
2. способы задания функции:
табличный способ;графический способ;
аналитический способ;
словесный способ.
2
3. В процессе формирования определения понятия функции встречалась мысль о том, что на разных участках области определения она
может быть задана разными аналитическимивыражениями.
Понятие о кусочных функциях. На
различных участках числовой прямой
функция может быть задана разными
формулами. Например: y=f(x), где
f(x)=
х2, -3≤х≤-2
2х+8, -2<х≤0
такие функции назовём кусочными.
3
4. Чтобы построить график кусочной функции, нужно:
Построить в одной системе координатграфики входящих функций,
Провести прямые x=a1, x=a2, x=a3,… где aграничные точки,
На каждой составляющей области
определения (a1, an), где nєN выбрать тот
график, который соответствует входящей
функции на этой составляющей.
Выяснить значение функции в граничных
точках.
4
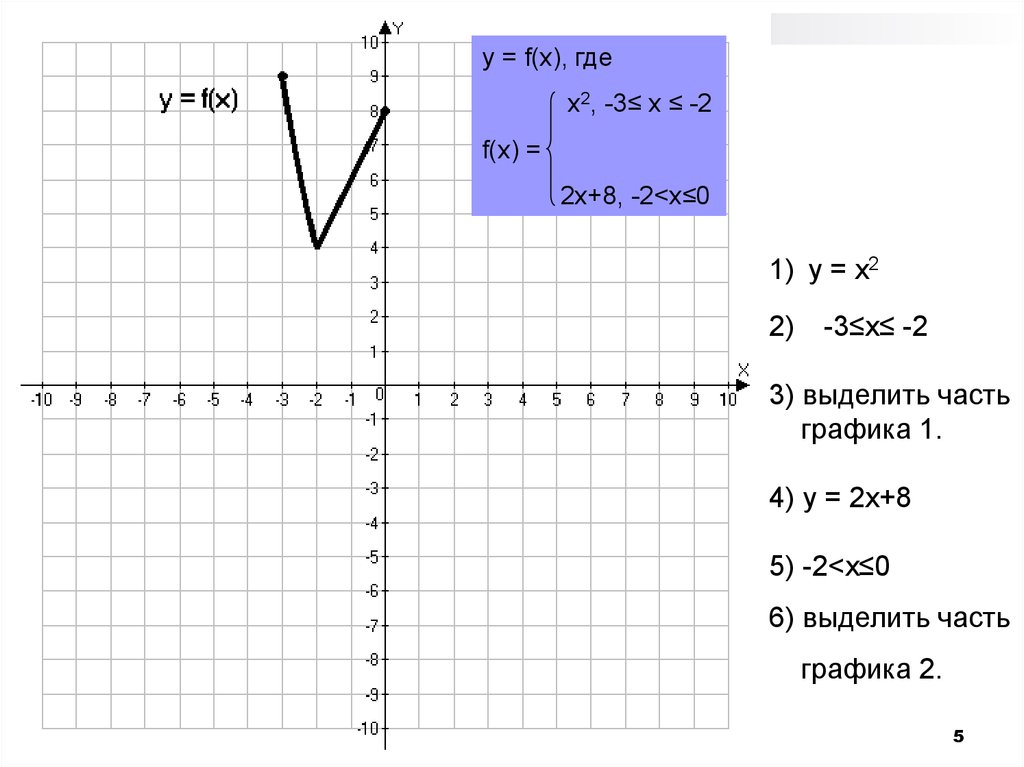
5.
y = f(x), гдеx2, -3≤ x ≤ -2
f(x) =
2x+8, -2<x≤0
1) y = x2
2)
-3≤x≤ -2
3) выделить часть
графика 1.
4) y = 2x+8
5) -2<x≤0
6) выделить часть
графика 2.
5
6. Для построения графиков функций можно использовать компьютерные программы 3D Grapher, Advanced Grapher.
Изменения графика мынаблюдаем при изменении
коэффициентов и значений
свободного члена. При
положительном значении а
(красный, синий), анализируя
график функции, видим, что
функция возрастает на всей
области определения.
Отрицательном значении а
(желтый), функция убывает на
всей области определения.
Движение графика вдоль оси ОУ
(зелёный, синий), происходит за
счет изменения значений с. При
записи коэффициента а дробным
числом – меняется угол наклона
прямой относительно оси ОХ
(синий).
6
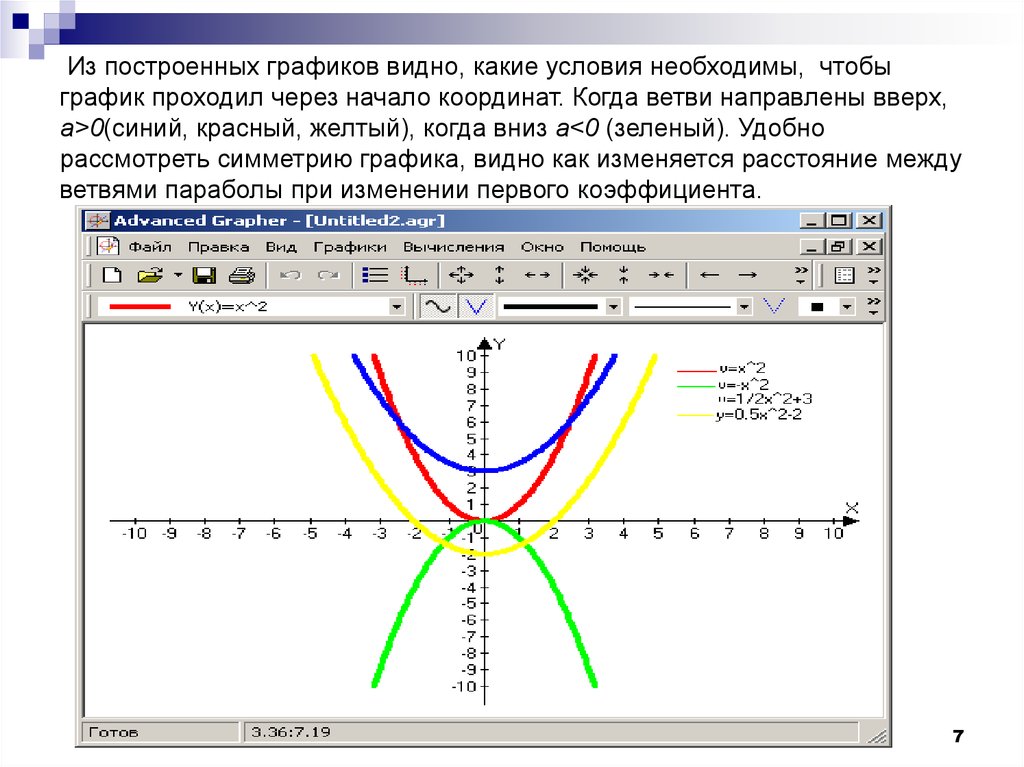
7. Из построенных графиков видно, какие условия необходимы, чтобы график проходил через начало координат. Когда ветви направлены
вверх,а>0(синий, красный, желтый), когда вниз а<0 (зеленый). Удобно
рассмотреть симметрию графика, видно как изменяется расстояние между
ветвями параболы при изменении первого коэффициента.
7
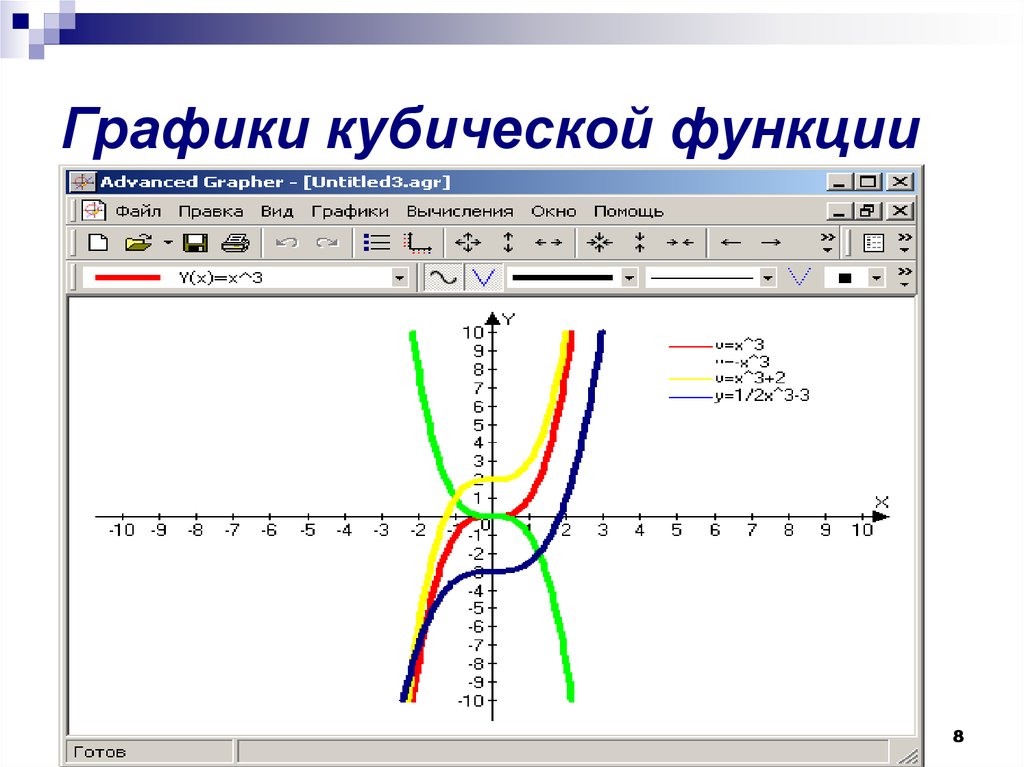
8. Графики кубической функции
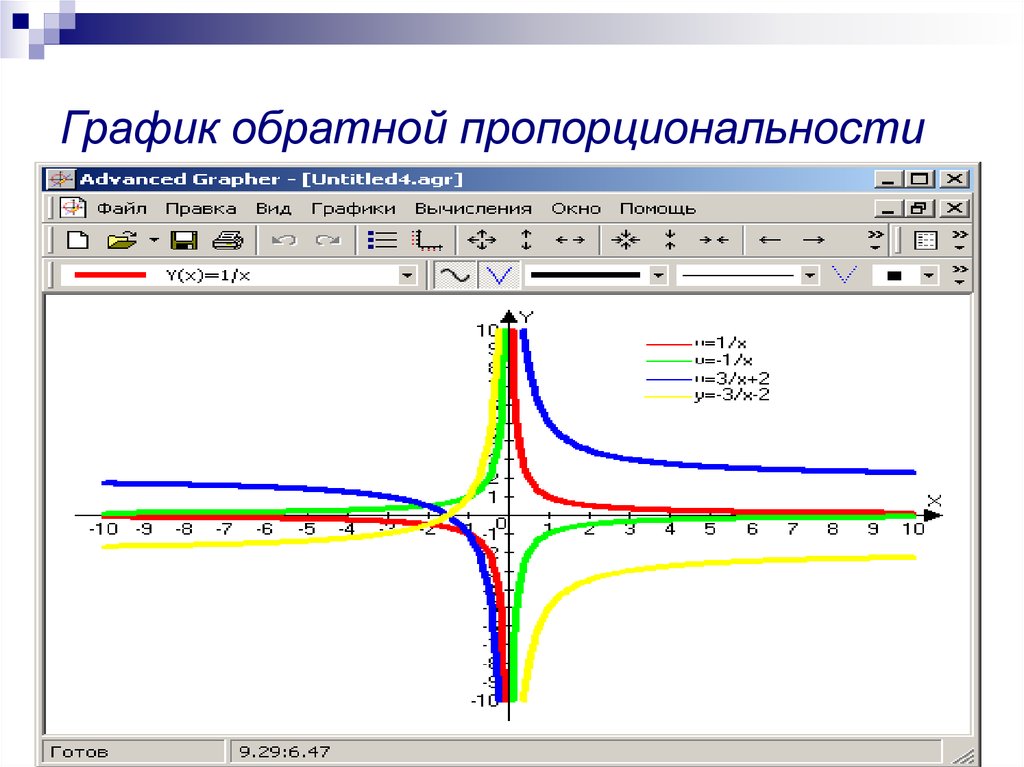
89. График обратной пропорциональности
910. С помощью программыAdvanced Grapher была построена функция -х2-4х-3, если x ≤ -1 f(x)= x+1, если -1<x ≤ 1 2/x, если х>1
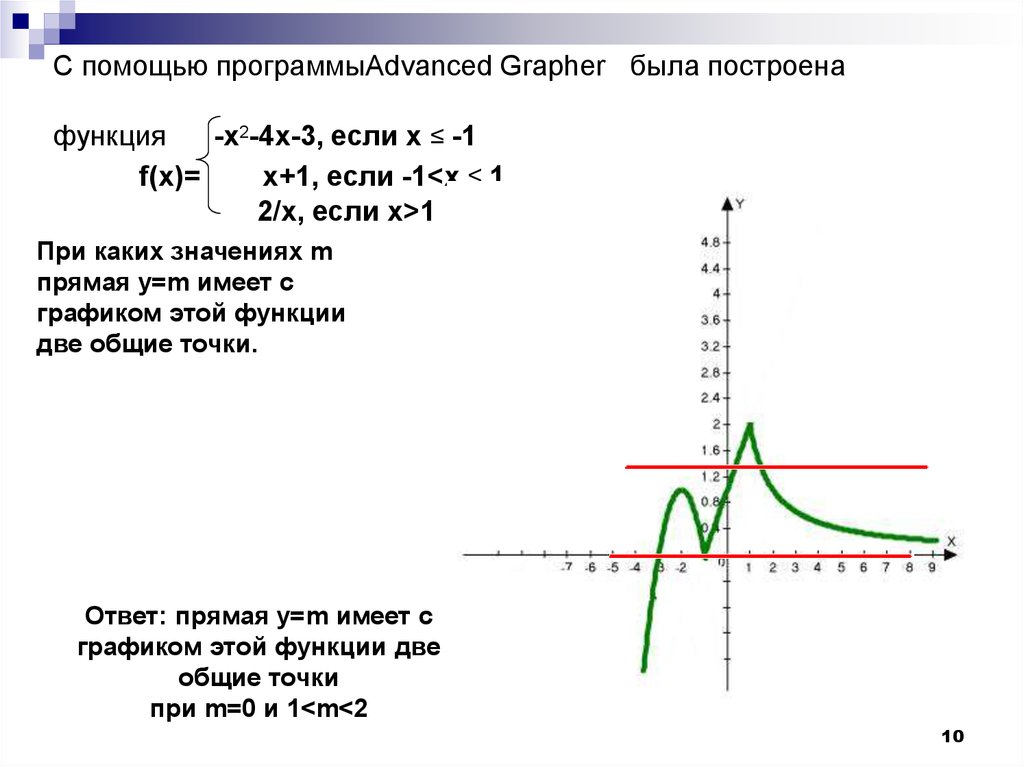
С помощью программыAdvanced Grapher была построенафункция
-х2-4х-3, если x ≤ -1
f(x)=
x+1, если -1<x ≤ 1
2/x, если х>1
При каких значениях m
прямая у=m имеет с
графиком этой функции
две общие точки.
Ответ: прямая у=m имеет с
графиком этой функции две
общие точки
при m=0 и 1<m<2
10
11. В математике широко используются задания в которых ученики строят точки по их координатам и последовательно соединяют, получая
при этом рисунок. Этот рисунок построен с помощьюпрограммы Advanced Grapher
Y
20
18
16
14
12
10
8
6
4
2
X
-20
-18
-16
-14
-12
-10
-8
-6
-4
-2
0
2
4
6
8
10
12
14
16
18
20
-2
-4
-6
-8
-10
-12
-14
-16
y=-1/18x^2+12, x [-12;12]
y=-1/8x^2+6,x [-4;4]
y=-1/8(x+8)^2+6 ,x [-12;-4]
y=-1\8(x-8)^2+6 , x [4;12]
y=2(x+3)^2-9, x [-4;0.3]
y=1.5(x+3)^2-10, x [-4;0.2]
-18
-20
11
12. Вывод. Использование компьютерных программ для построения графиков функций, изучение их свойств и закономерностей, дает за
минимальноеколичество времени рассмотреть большое количество примеров функций
разных видов. Данная работа предназначена в помощь учителям при
изучении функции, а также ученикам с целью заинтересовать
математикой, информатикой, показав возможности использования
технологий на уроках.
В школе широко используются задания на построение и исследование
графиков функций. Я предлагаю для изучения этих тем использовать
компьютерные программы: 3D Grapher, Advanced Grapher; и рассмотрев
предоставленные мной материалы, разработать свои аналогичные задания.
Эти задания можно дать в качестве домашней работы. Они будут особенно
полезны школьникам, обучающимся по программам с информатикоматематическим уклоном. Достоинство – простота выполнения, наглядность
результата, объемное цветное изображение позволяет привить интерес к
математике, развить эстетический вкус.
Работа способствует развитию познавательных интересов, повышению
информационной грамотности, фундаментальному математическому
образованию.
12







 mathematics
mathematics








