Сканирующая туннельная спектроскопия. Туннельные и дифференциальные туннельные ВАХ

1.

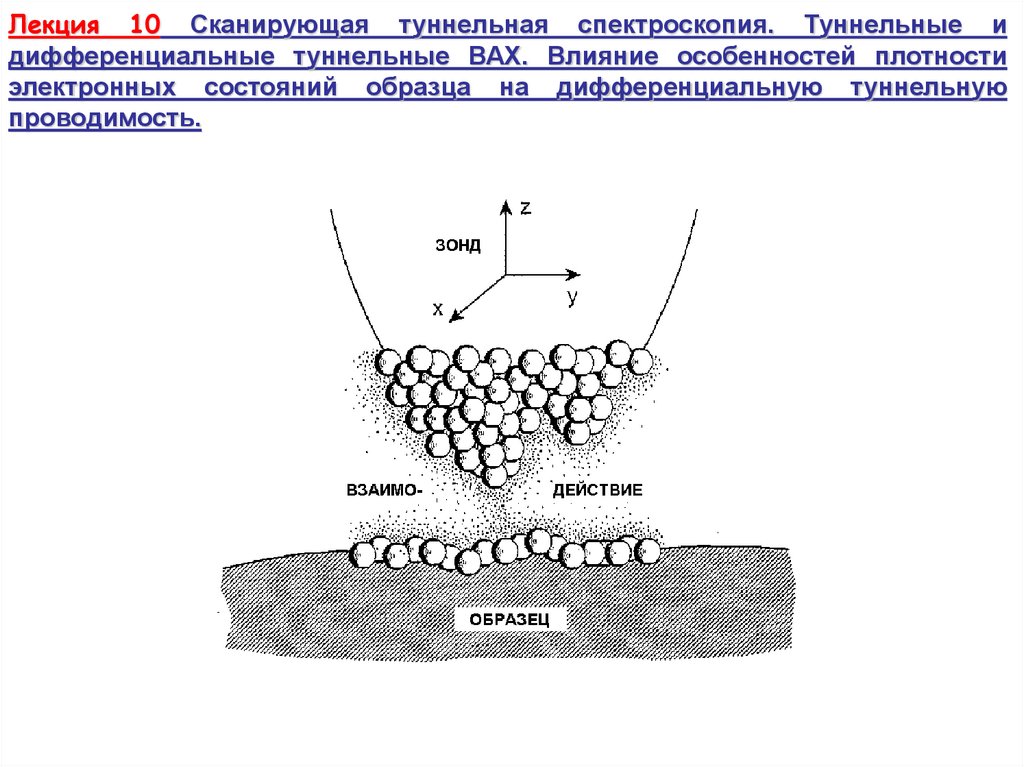
Лекция 10 Сканирующая туннельная спектроскопия. Туннельные и
дифференциальные туннельные ВАХ. Влияние особенностей плотности
электронных состояний образца на дифференциальную туннельную
проводимость.

2.

Физические основы СТМ
Туннелирование электрона через
потенциальный барьер:
одномерная задача для свободного электрона
Aeikx Be ikx ( x 0),
( x ) Ce x De x (0 x d ),
Feikx
( x d ),
2 d 2
V ( x) E 0
2
2m dx
k 2mE /
2m( E V0 ) /
Коэффициент пропускания
T F/A
Экспоненциальная зависимость
туннельного тока ширины барьера:
Обратная длина затухания к ~ 1 А-1
2
при
d 1/
16k 2 2 2 d
T 2
e
2
k
I B exp( Ad ) eV exp( Ad eV )
при увеличении ширины барьера (расстояния между зондом и образцом) на 1 Å
туннельный ток уменьшится в ~ 7 раз:
I d
exp 2 d
exp 2 d ~ e 2
I d d exp 2 (d d )

3.

Туннелирование электрона между металлами
Нет
контакта
V>0
V<0
V=0
2
I
s t eV T , d , eV f f eV d
2
T exp d 2m eV / 2 f
Если kT<< eV
I
2
EF
eV T , d , eV , d
s
t
E F eV
F
2
Если t const I
t s T , d , eV , d
E F eV
E

4.

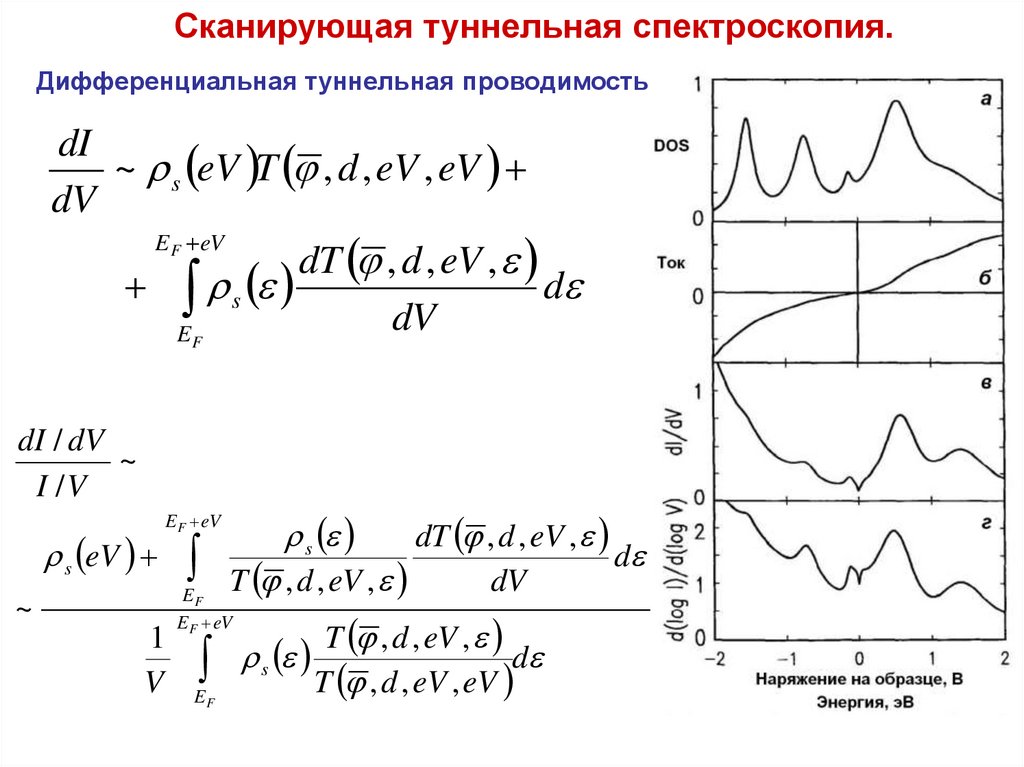
Сканирующая туннельная спектроскопия.
Дифференциальная туннельная проводимость
dI
~ s eV T , d , eV , eV
dV
dT , d , eV ,
s
d
dV
EF
E F eV
dI / dV
~
I /V
s eV
E F eV
~
1
V
dT , d , eV ,
d
T , d , eV ,
dV
EF
E F eV
EF
s
T , d , eV ,
s
d
T , d , eV , eV

5.

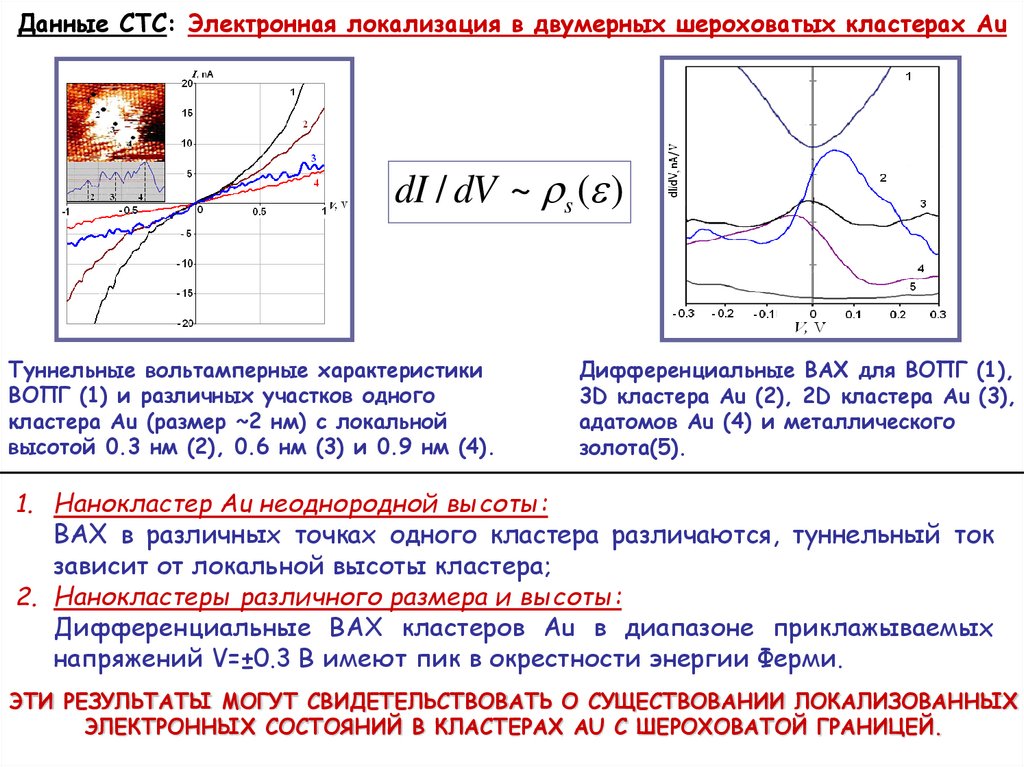
Данные СТС: Электронная локализация в двумерных шероховатых кластерах Аu
dI / dV ~ s ( )
Туннельные вольтамперные характеристики
ВОПГ (1) и различных участков одного
кластера Au (размер ~2 нм) с локальной
высотой 0.3 нм (2), 0.6 нм (3) и 0.9 нм (4).
Дифференциальные ВАХ для ВОПГ (1),
3D кластера Au (2), 2D кластера Au (3),
адатомов Au (4) и металлического
золота(5).
1. Нанокластер Au неоднородной высоты:
ВАХ в различных точках одного кластера различаются, туннельный ток
зависит от локальной высоты кластера;
2. Нанокластеры различного размера и высоты:
Дифференциальные ВАХ кластеров Au в диапазоне приклажываемых
напряжений V=±0.3 В имеют пик в окрестности энергии Ферми.
ЭТИ РЕЗУЛЬТАТЫ МОГУТ СВИДЕТЕЛЬСТВОВАТЬ О СУЩЕСТВОВАНИИ ЛОКАЛИЗОВАННЫХ
ЭЛЕКТРОННЫХ СОСТОЯНИЙ В КЛАСТЕРАХ AU С ШЕРОХОВАТОЙ ГРАНИЦЕЙ.

6.

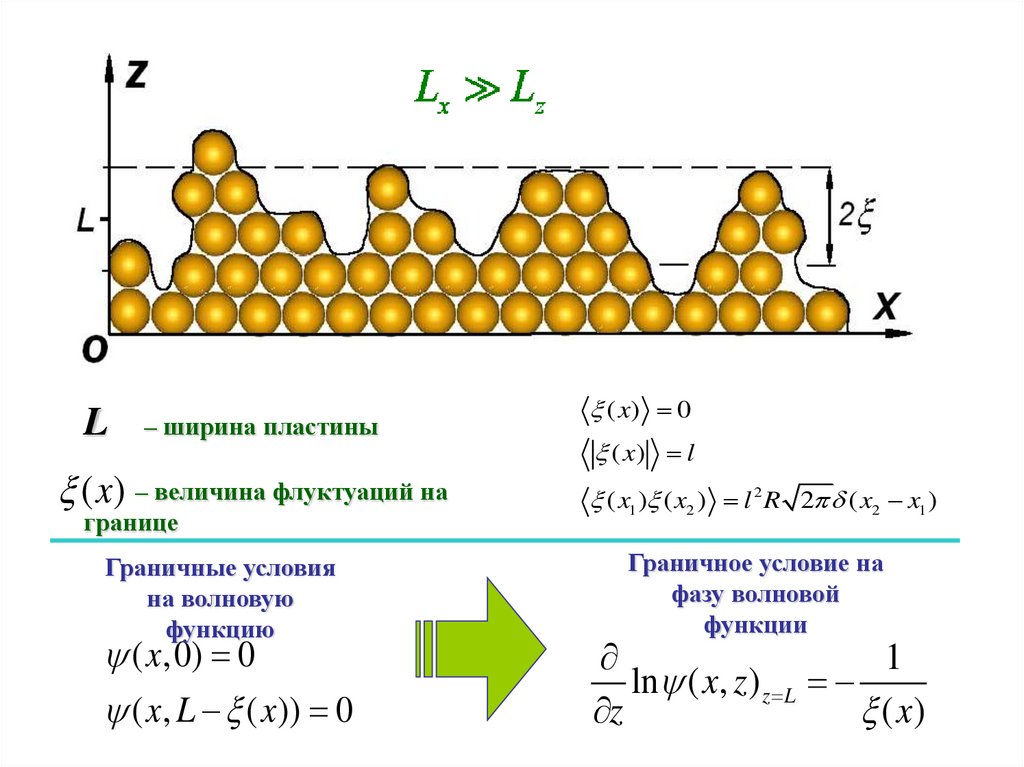
L
– ширина пластины
( x) – величина флуктуаций на
границе
Граничные условия
на волновую
функцию
( x,0) 0
( x, L ( x )) 0
( x) 0
( x) l
( x1 ) ( x2 ) l 2 R 2 ( x2 x1 )
Граничное условие на
фазу волновой
функции
1
ln ( x, z ) z L
z
( x)

7.

ПЕРЕХОД К ГЛАДКИМ ГРАНИЧНЫМ УСЛОВИЯМ
z 0 z L ( x)
Lz
X x, Z
L ( x)
Z 0
Z L
СООТВЕТСТВУЮЩЕЕ ПРЕОБРАЗОВАНИЕ ИМПУЛЬСОВ
Z x'
p x Px Pz
L
( x)
p z Pz 1
L
px pz Px Pz
( x ) R L
H V
Px Pz
2m 2m 2m 2m
2
2
2
2
! ! ! ВОЗМУЩАЮЩИЙ ПОТЕНЦИАЛ ! ! !
V
( x)
mL
2
z
P
Pz
j
L
V
( j)
x
( x) j
mL L
2

8.

ФЛУКТУИРУЮЩИЙ ПОТЕНЦИАЛ
V ( x) 0
j
2
2
4
V ( x)V ( x ) 2 D ( x x )
/
/
, где
D
l2R
2m L6
ПОЛУЧИМ УРАВНЕНИЕ НА ФАЗУ ВОЛНОВОЙ ФУНКЦИИ
2
2m
//
V ( x) E
/
/ ( 2
2m
2
E)
УРАВНЕНИЕ ФОККЕРА ПЛАНКА
2
P ( x, )
2 2m
2
m
P( x, )
2 E P ( x, ) D 2
x
2m
2m P ( )
J ( E ) 2 E 2 P ( ) D 2
2
2m
2
V ( x)

9.

СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ СОСТОЯНИЙ
ДЛЯ ОДНОМЕРНОЙ СИСТЕМЫ
N
( 1)
(E)
2
2
j l R /16
4 2
L2
1/ 3
0
2/3
3
2
3
dz
z
EmL 16 L
exp z
3 2 4 2
24
(2 ) j l R
z
N 2 D ( E ) N X ( E ) NY ( E )
dN 2 D ( E )
dE
j 1
total ( E )
ПЛОТНОСТЬ ЭЛЕКТРОННЫХ СОСТОЯНИЙ ДЛЯ ПЛЕНКИ ВЫСОТОЙ L
2 2 j 4l 2 R /16 1/ 3
d
total ( E )
L2
j 1 dE
0
z3
dz
EmL2 16 L3
exp
z
24
(2 )3 2 j 4l 2 R
z
2/3
2

10.

Локализация электронов в разупорядоченных поверхностных атомных слоях
ИЛО нанокластеров
Переход к гладким граничным
условиям приводит к появлению
случайного потенциала
h
U
( x) 0
( x) l
( x1 ) ( x2 ) l R 2 ( x2 x1 )
2
2 2 j,4l 2 R /16 1/ 3
d
2D (E)
dE
h2
R - радиус корреляций, l – средняя амплитуда
Плотность состояний в двумерной
системе с наличием
случайного
0
0
0
потенциала. ( R 1 A l 3 A h 15 A )
Штриховая
линия
соответствует
расчетной плотности состояний в
приближении двумерного свободного
электронного газа.
0
( j)
x
( x)
h
z
dz
Emh
exp
z
24
(2 )3
z
3
E( j)
2
16h
4 2
j l R
3
2
2/3
2

11.

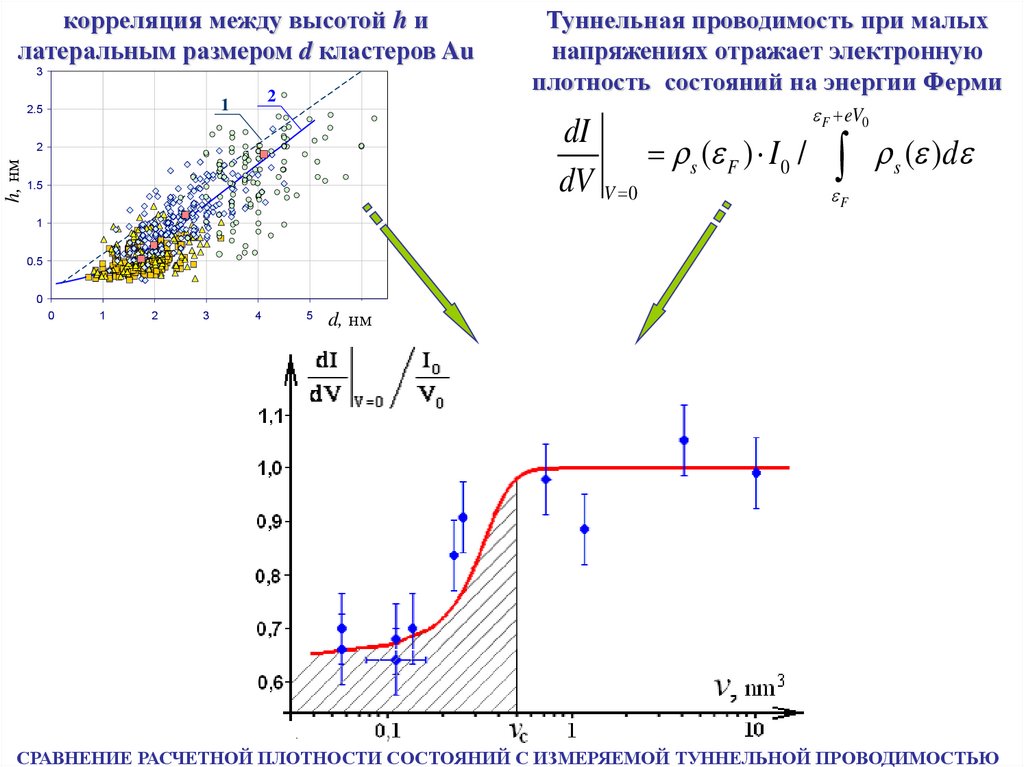
корреляция между высотой h и
латеральным размером d кластеров Au
3
2
1
2.5
dI
dV
2
h,
нм
h , нм
Туннельная проводимость при малых
напряжениях отражает электронную
плотность состояний на энергии Ферми
1.5
s ( F ) I 0 /
V 0
F eV0
s ( )d
F
1
0.5
0
0
1
2
3
4
5
6
l ,d,
нмнм
СРАВНЕНИЕ РАСЧЕТНОЙ ПЛОТНОСТИ СОСТОЯНИЙ С ИЗМЕРЯЕМОЙ ТУННЕЛЬНОЙ ПРОВОДИМОСТЬЮ

12.

dI
dV
s ( F ) I 0 /
V 0
F eV0
s ( )d
F
Заштрихованная область отвечает наличию локализованных
электронных состояний на энергии Ферми.