Spectroscopy_Russian_2022-1

1.

Введение в спектроскопию атомов, молекул и
кластров -1
О. С. Васютинский, [email protected]
Осенний семестр 2022 г.
Рекомендуемая литература
1. И. И. Собельман, Введение в теорию атомных спектров, Наука, 1977
2. М. А. Ельяшевич, Атомная и молекулярная спектроскопия, Физматгиз, 1962
3. Л. Д. Ландау, Е. М. Лифшиц, Теоретическая физика. Т. III
Квантовая механика. Нерелятивистская теория., Наука, 1974
4. Н. Ф. Степанов, Квантовая механика и квантовая химия, - М. Мир, Издательство
Московского университета, 2001.
5. G. Herzberg, Molecular Spectra and Molecular Structure.
I. Spectra of Diatomic Molecules, 2-nd ed., 1989
6. G. Herzberg, Molecular Spectra and Molecular Structure.
III. Electronic Spectra and Electrinic Structure of Polyatomic Molecules, 1988
7. W. Demtröder, Laser Spectroscopy, 1996
8. D. A. McQuarrie, J.D.Simon, Physical Chemistry: a Molecular Approach, 1997

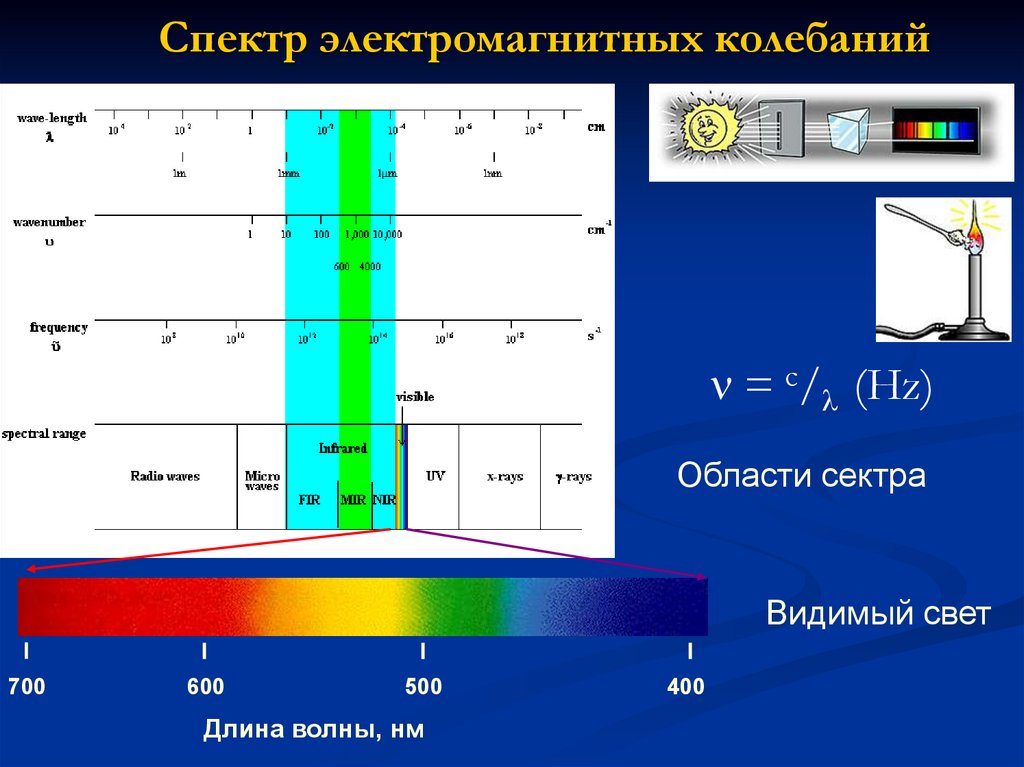
2. Спектр электромагнитных колебаний

= с/ (Hz)
Области сектра
Видимый свет
700
600
500
Длина волны, нм
400

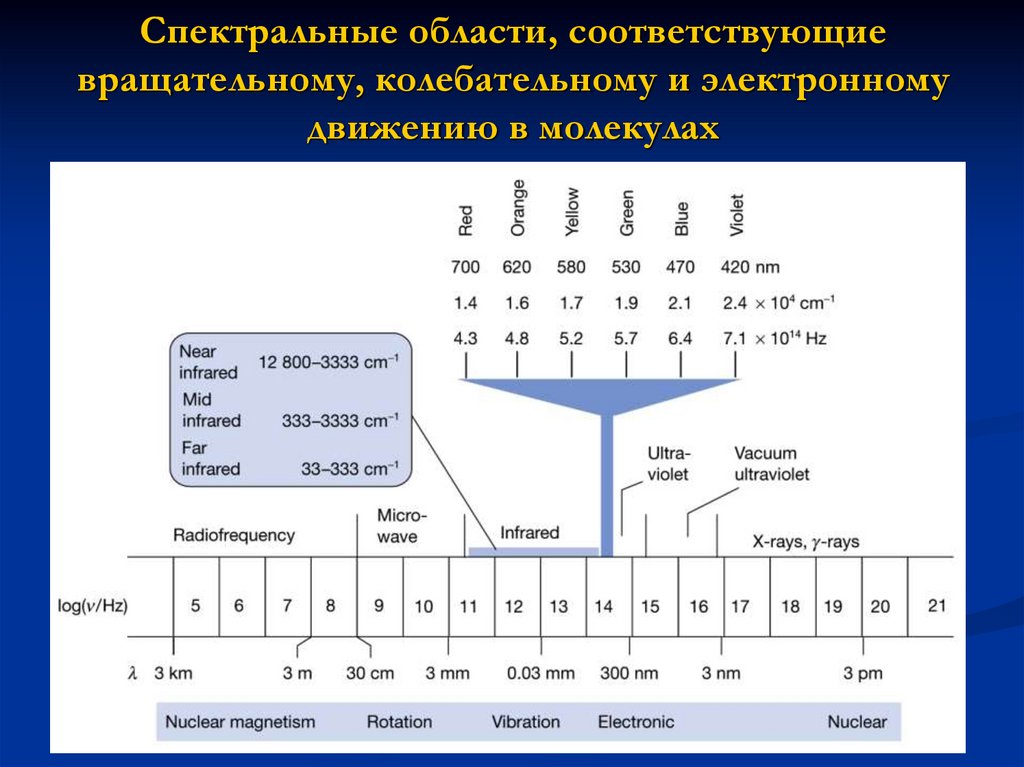
3. Спектральные области, соответствующие вращательному, колебательному и электронному движению в молекулах

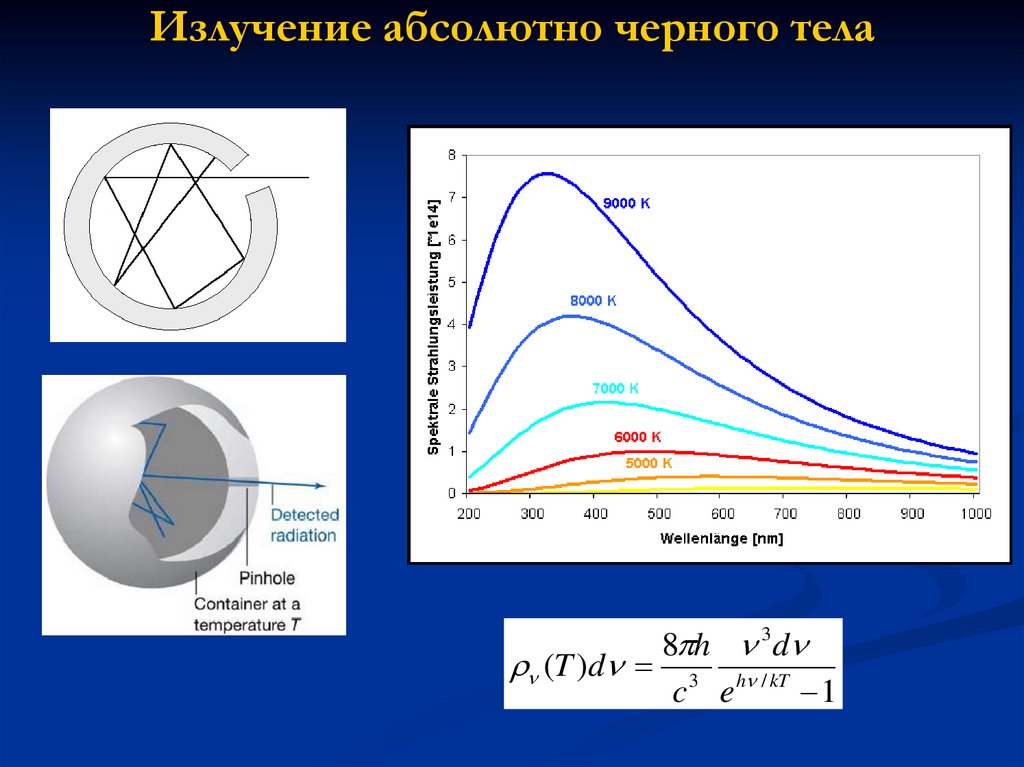
4. Излучение абсолютно черного тела

8 h 3d
(T )d 3 h / kT
c e
1

5.

Max (Karl Ernst Ludwig) Planck
В 1900 году Макс Планк впервые предположил, что энергия
электромагнитного излучения может излучаться и поглощаться только
определенными дискретными порциями, называемыми квантами энергии.
Элементарный квант энергии равен hν, где h – постоянная Планка.
h = 6,626176.10-34 Js
Нобелевская премия по
физике, 1918 г.
* 23. апреля 1858, Киль, Германия
+ 4. октября 1947, Гёттинген, Германия

6.

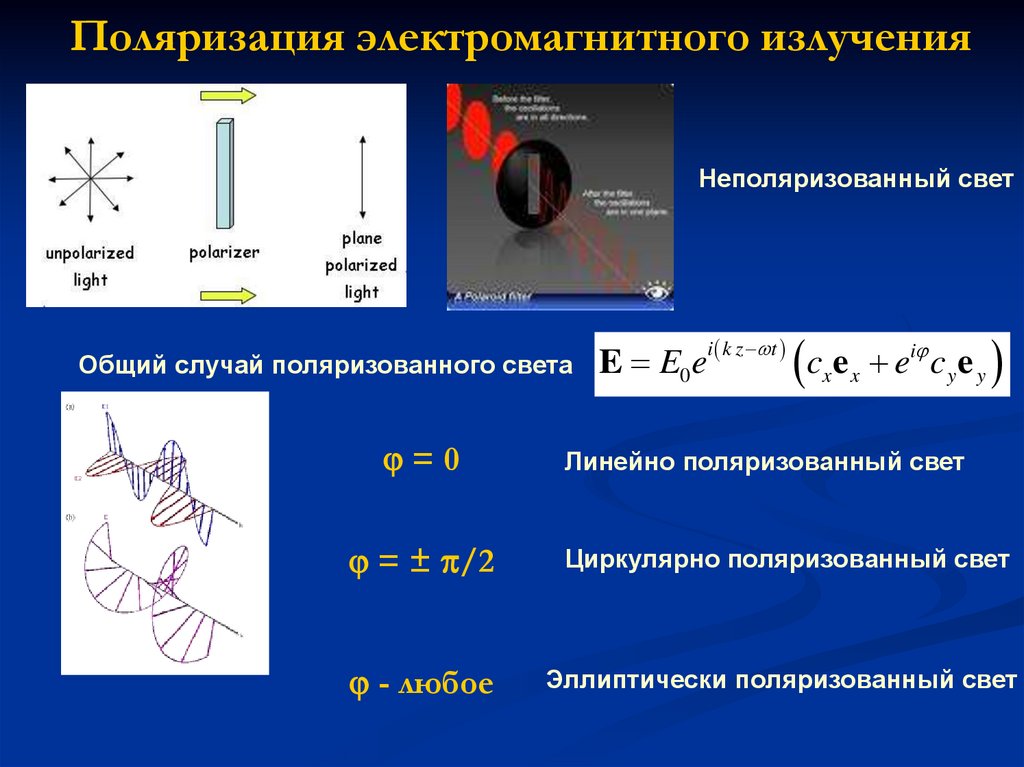
Поляризация электромагнитного излучения
Неполяризованный свет
Общий случай поляризованного света
=0
E E0e
i k z t
i
c
e
e
x x cye y
Линейно поляризованный свет
= ± /2
Циркулярно поляризованный свет
- любое
Эллиптически поляризованный свет

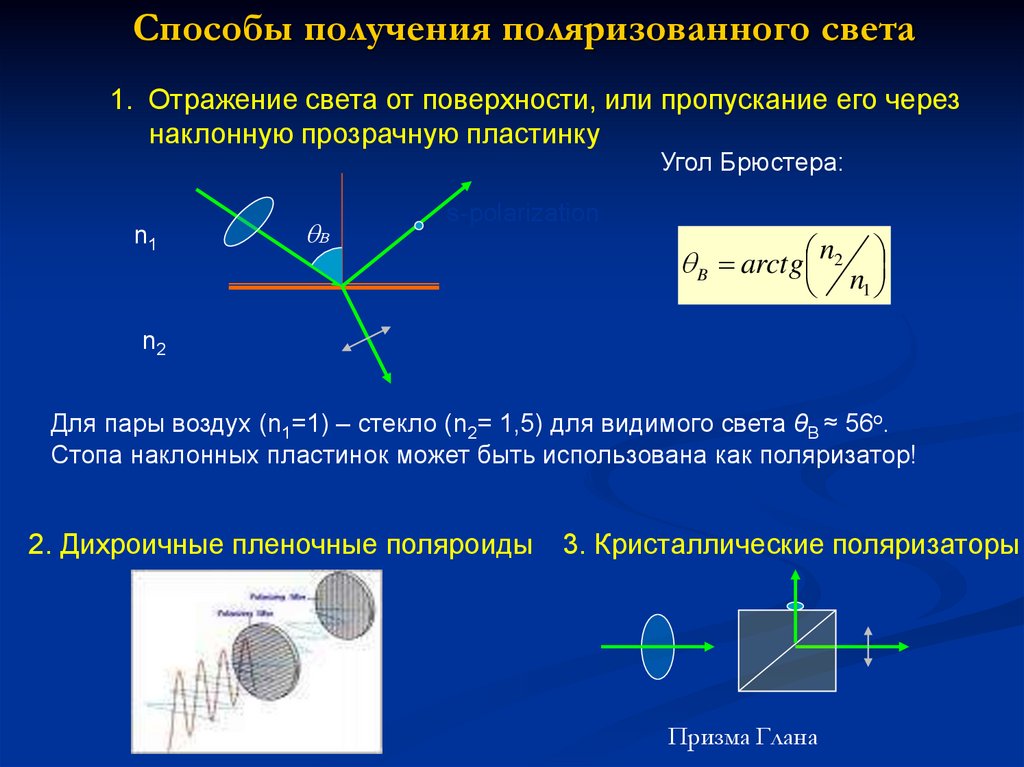
7. Способы получения поляризованного света

1. Отражение света от поверхности, или пропускание его через
наклонную прозрачную пластинку
Угол Брюстера:
n1
B
s-polarization
B arctg n2 n
n2
1
p-polarization
Для пары воздух (n1=1) – стекло (n2= 1,5) для видимого света θB ≈ 56o.
Стопа наклонных пластинок может быть использована как поляризатор!
2. Дихроичные пленочные поляроиды
3. Кристаллические поляризаторы
Призма Глана

8.

Способы получения эллиптическиполяризованного света
1. Фазовая пластинка: оптический элемент, преобразующий форму
Поляризации проходящего через него монохроматического луча света
E E0e
i k z t
c e e c e
i
x x
y y
d (n 0 n e ) / 2, / 4
Пластинка /2
=
Пластинка /4
= /2

9.

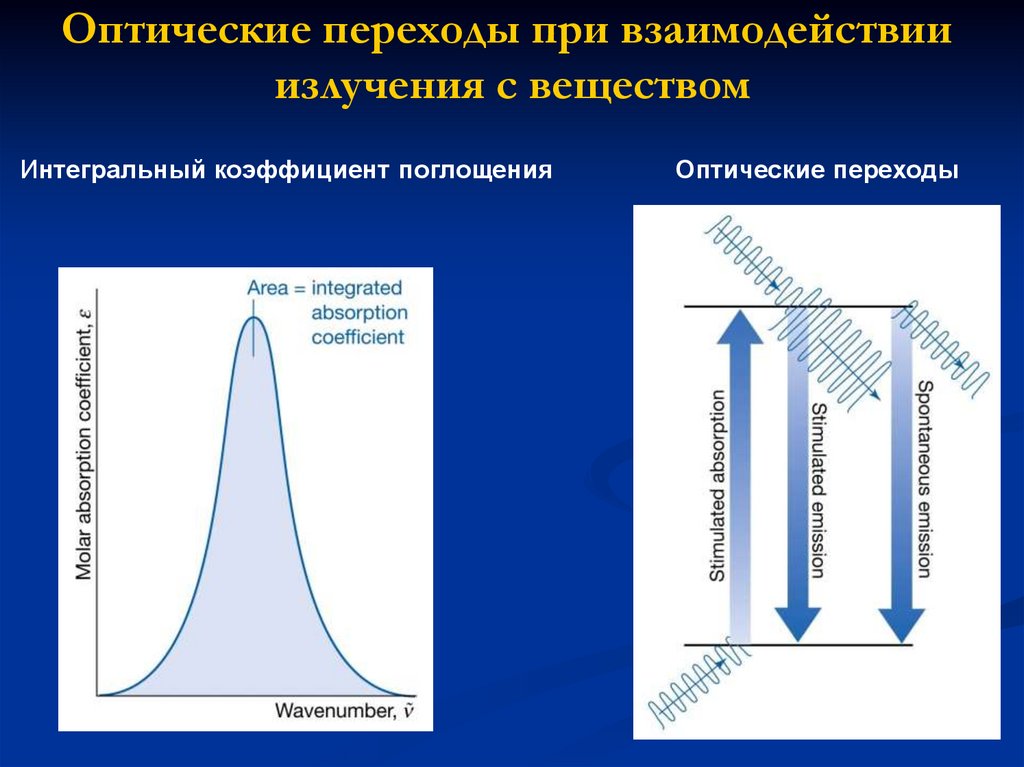
Оптические переходы при взаимодействии
излучения с веществом
Интегральный коэффициент поглощения
Оптические переходы

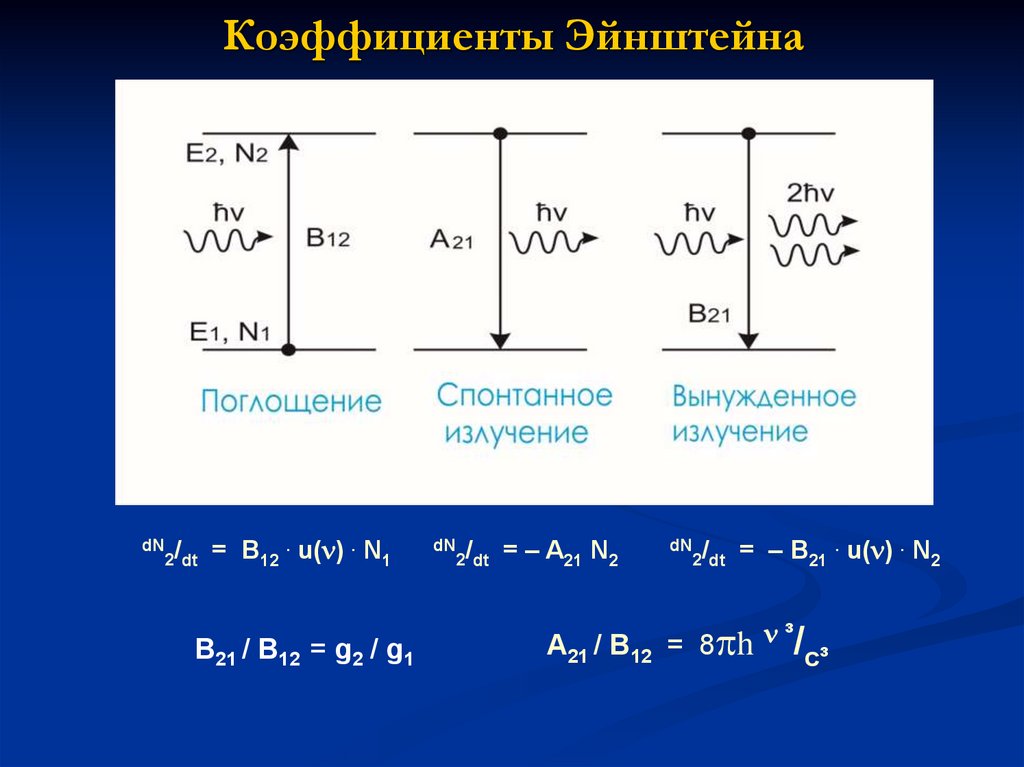
10. Коэффициенты Эйнштейна

dN /
2 dt
= B12 . u( ) . N1
B21 / B12 = g2 / g1
dN /
2 dt
= – A21 N2
dN /
2 dt
= – B21 . u( ) . N2
A21 / B12 = 8 h ³/c³

11. Albert Einstein

* 14. марта 1879 в г. Ульм, Вюртенберг,
Германия
† 18. апреля 1955 в г. Принстоне, Нью
Джерси, США
Нобелевская премия по физике, 1921
за объяснение фотоэффекта
Эйнштейн создал теорию
фотоэффекта, квантовую теорию
взаимодействия излучения с
веществом, специальную теорию
относительности, общую теорию
относительности.

12. Albert Einstein

13.

I0
Закон Ламберта-Бэра
I
c
·)─ Детектор
ℓ
Коэффициент прозрачности:
T = e- Nℓ = e-kℓ = e- ,
T = I / I0
где [cm2] сечение поглощения, N[cm-3] концентрация атомов или молекул в
образце, ℓ [cm] длина образца
Альтернативное выражение для коэффициента прозрачности:
T = 10- Cℓ,
где - [L mol-1 cm-1] коэффициент экстинкции, а
C [mol L-1] – молярная концентрация:
C
Количество молекул N
NAV
NA
где NA – число Авогадро, NA = 6.022 10-23 mol-1

14.

Приближение тонкого оптического слоя
I( ) = I0 [ 1 – ( ) N ℓ ]
Если проинтегрировать это выражение по частоте излучения в пределах
контура поглощения, предполагая, что интенсивность исходного излучения не
зависит от частоты, то вместо сечения поглощения = ( ) в нем возникает
интегральное сечение поглощения < (ν)>:
h 0
( ) d B12
c
где B12 - коэффициент Эйнштейна, а 0 – центр поглощения атомной
(молекулярной) линии. Таким образом, коэффициент Эйнштейна B12 может
быть определен непосредственно из эксперимента

15.

Однородное уширение спектральных линий
Принцип неопределенности для энергии:
E
Два главных процесса ответственны за конечное время жизни
квантовых состояний атомов и молекул:
1. Спонтанная эмиссия, интенсивность которой пропорциональна соответствующеми
коэффициенту Эйнштейна Anm. Согласно квантовой электродинамике, интенсивность
спонтанной эмиссии пропорциональна квадрату матричного элемента взаимодействия
атома/молекулы с электромагнитными модами вакуума.
2. Взаимодействие атома/молекулы в определенном квантовом состоянии с другими
частицами или полями. В газовой фазе это в основном неупругие столкновения с
окружающими частицами. В конденсированном состоянии – это обычно
взаимодействие с фононами (колебаниями кристаллической решетки).
Соответствующая форма спектральной линии описывается
формулой Лоренца:
I ( )
1
где
2
v v
2
0
2
2
= 1/2 - скорость
распада данного квантового
состояния и L =

16.

Однородное (Лоренцево) уширение
спектральных линий
Условия
νL (Hz)
νL (cm-1)
Естественные
времена жизни
Электронные
переходы в атомах и
молекулах
107
10-4
Естественные
времена жизни
Вращательные
переходы в
молекулах
10-4
10-15
Столкновительные
времена жизни
Газовая фаза,
атмосферное
давление
109
10-2
Столкновительные
времена жизни
Электронные
переходы в жидкой и
твердой фазе
1012
101

17.

Неоднородное уширение спектральных линий
Эффект Допплера заключается в сдвиге частоты детектируемого излучения когда
источник излучения движется относительно наблюдателя. Если источник излучения с
частотой ν0 движется со скоростью v в направлении на или от наблюдателя, то
наблюдатель детектирует частоту:
vZ
0 1
c
Молекулы в газе хаотически движутся во всех направлениях. В случае термического равновесия, распределение проекций скоростей молекул на направление
наблюдения, (ось Z), описывается известным распределением Максвелла:
m v 2Z
m
n( v Z ) dv Z
exp
dv Z
2 kT
2k T
При этом наблюдатель детектирует форму спектральной линии:
I ( )
4 ln 2
0 2
exp 4 ln 2
2
D
D
1
где
2 0
D
c
k T 2 ln 2
m
Для электронных переходов в видимой и близкой ультрафиолетовой части спектра
при температуре газа около 300 K, типичное допплеровское уширение составляет
около одного ГГц. Эта величина значительно больше естественного
уширения спектральных линий при тех-же условиях.

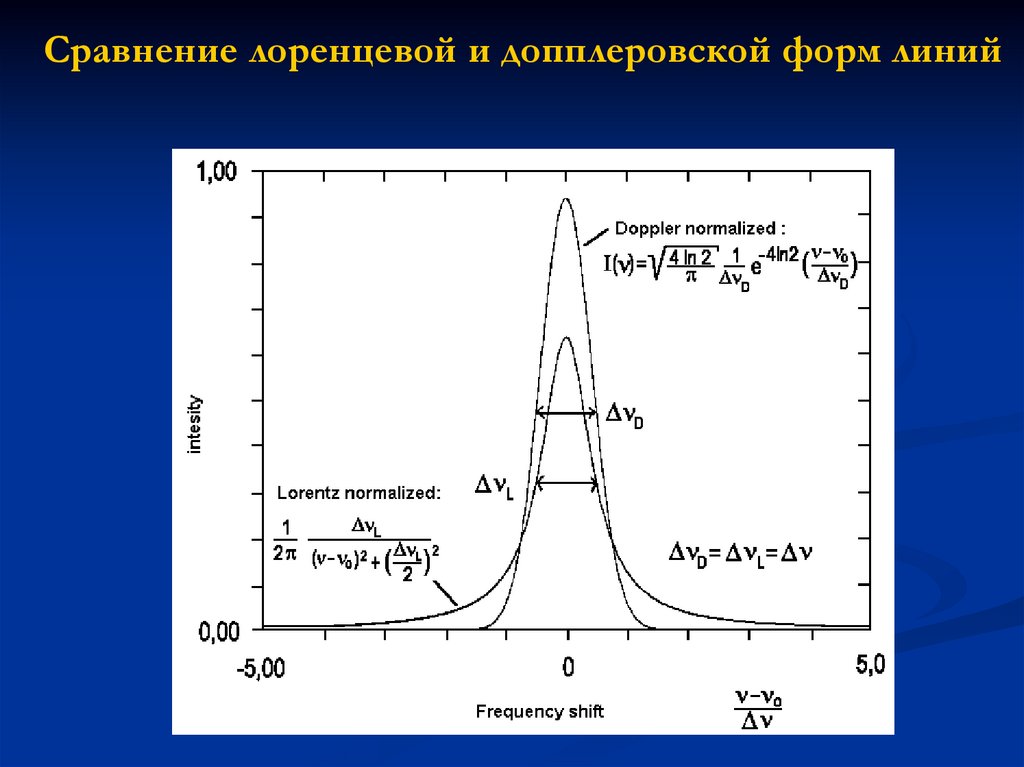
18.

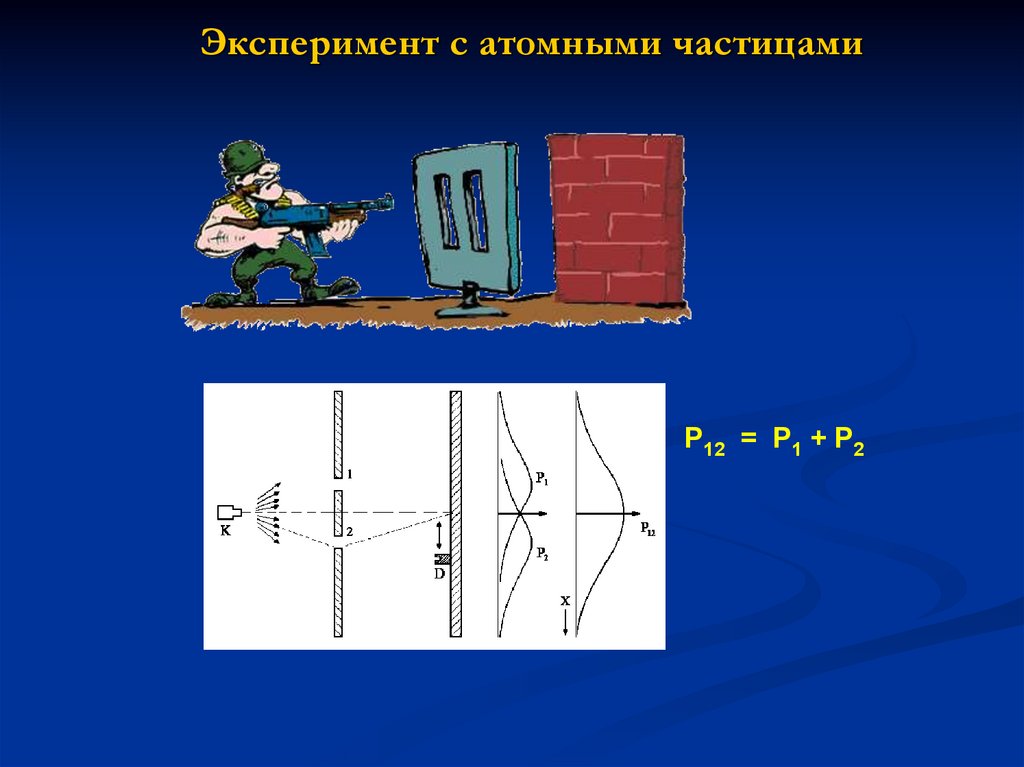
Сравнение лоренцевой и допплеровской форм линий

19. Эксперимент с атомными частицами

P12 = P1 + P2

20. Луи де Бройль (de Broglie): волновое поведение частиц

Диссертация де Бройля: “Recherches sur la
théorie des quanta“ в 1924 впервые
продемонстрировала взаимосвязь между
массой частицы m, ее скоростью v и
соответствующей длиной волны :
Wavelength:
D = h/mv
Louis Victor Pierre Raymond
duc de Broglie
* 15. Aug. 1892 in Dieppe, France
† 19. März 1987 in Paris, France
Nobelpreis 1929

21. Интерференция волн материи в пространстве

= A e i t+ikx - амплитуда вероятности
(волновая функция)
= E/ħ - круговая частота
k = 2 / = p/ħ - волновой вектор
Вероятность детектирования частицы
I = | |2
1+ 2
I = | 1+ 2|2
I = I1+I2+2(I1I2)½.cos
2
x
D
где фазовый сдвиг

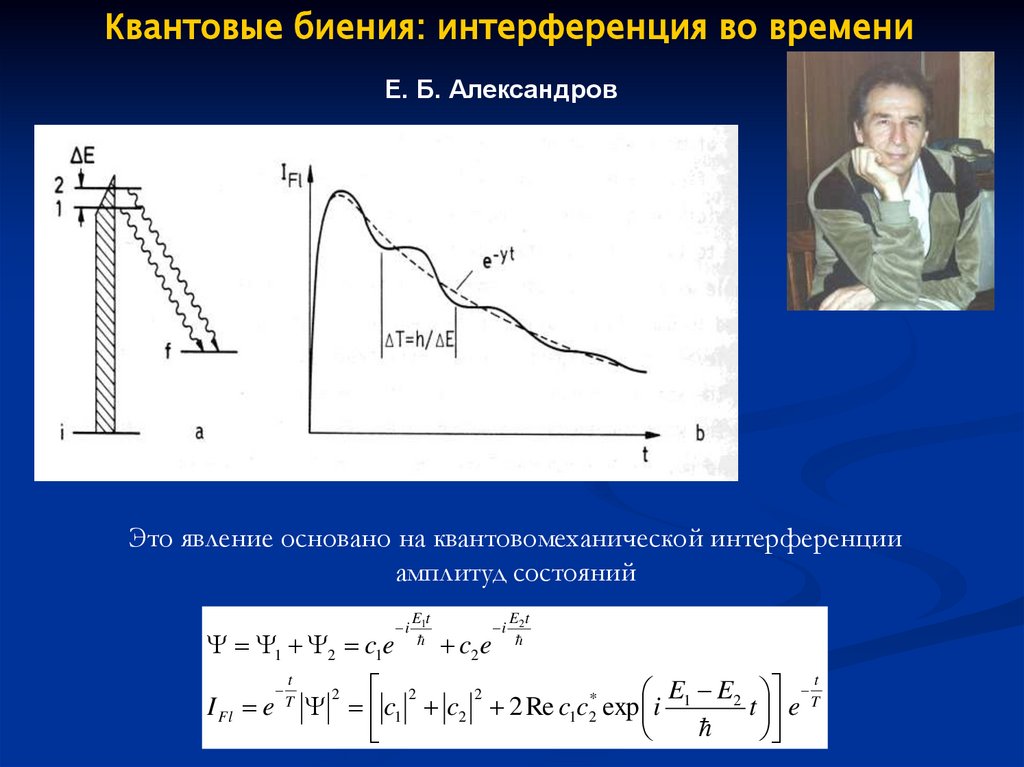
22.

Квантовые биения: интерференция во времени
Е. Б. Александров
Это явление основано на квантовомеханической интерференции
амплитуд состояний
1 2 c1e
I Fl e
t
T
i
E1t
c2 e
i
E2t
t
2
2
E1 E2 T
*
c1 c2 2 Re c1c2 exp i
t e
2

23. Парадокс: Кот Шредингера

Через одну минуту радиоактивное ядро
распадается с вероятностью 50% и
сопровождается выделением ядовитого газа.
В этот момент состояние радиоактивного
ядра описывается суперпозицией состояний:
|Ψn> = |1> + |2>. Однако это значит, что и
волновая функция Кота описывается
суперпозицией состояний:
|PsiК> = |Кот мертв> + |Кот жив>!
В то же время, если открыть коробку, то Кот
явно будет найден либо жив, либо мертв!
Вопрос состоит в том, в какой
момент времени система
перестает существовать, как
смешение двух состояний и
выбирает одно конкретное?

24. Уравнение Шредингера

Независящее от времени уравнение Шредингера :
[ h²/2m ²/ x² + V(x)] (x) = E (x)
( одномерное )
[ h²/2m + V(x,y,z)] (x,y,z) = E (x,y,z) ( трехмерное)
где – оператор Лапласа: = ²/ x² + ²/ y² + ²/ z²
Зависящее от времени уравнение Шредингера:
[ h²/2m ²/ x² + V] (x,t) = ih / t (x,t)
Нормировка волновой функции:
| (x,y,z)|2 dx dy dz = 1

25. Вычисление амплитуды вероятности (волновой функции)

1) Матричная алгебра
Werner Heisenberg
Nobelpreis 1932
Имеется три математически
эквивалентных путя вычисления
амплитуды вероятности
* 5. Dez. 1901
† 1. Feb. 1976
2) Дифференциальное уравнение,
Erwin Schrödinger
Nobelpreis 1933
* 12. Aug. 1887 in Erdberg, Wien
† 4. Jan. 1961 in Wien
3) Интегралы по траекториям
Richard Feynman; Nobelpreis 1965
* 11. Mai 1918 in Far Rockaway, New York
† 15. Feb. 1988 in Los Angeles

26.

Волновые функции и уровни энергии атома:
атом водорода
-
Гамильтониан:
+
H k Ek k
Сферические координаты
e2
2
2
2
2
2
2
x
y
z
2 2
Z e2
H
e
2 me
4 0 r
e2
1 2
2
r
,
2
r r r
1 2
1
,
sin
sin 2 2 sin
2
Волновые функции
k (r , , ) где k ≡ n, l, s, m , m
l
s
k (r , , ) Rnl (r ) l m ( , ) s m
l
где Rnl(r) – присоединенные полиномы Лагерра,
а Yl m(θ,Φ) – сферические гармоники
s

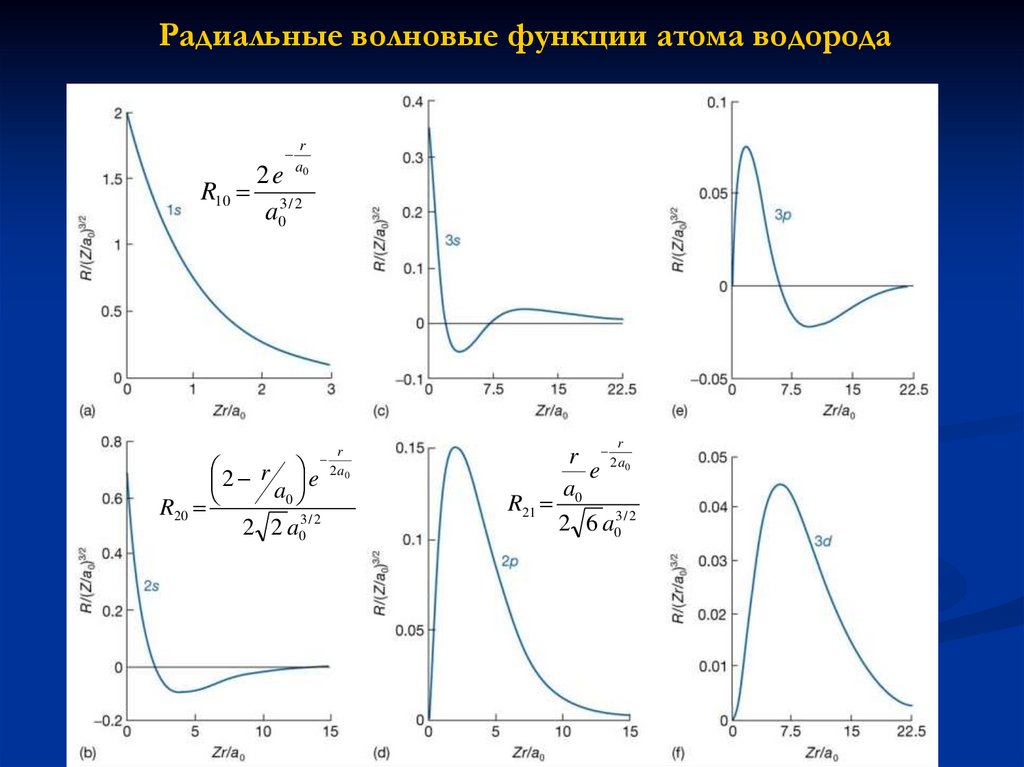
27.

Радиальные волновые функции атома водорода
R10
r
a0
2e
a03 / 2
2 r e
a0
R20
2 2 a03 / 2
r
2 a0
r
r 2 a0
e
a
R21 0 3 / 2
2 6 a0

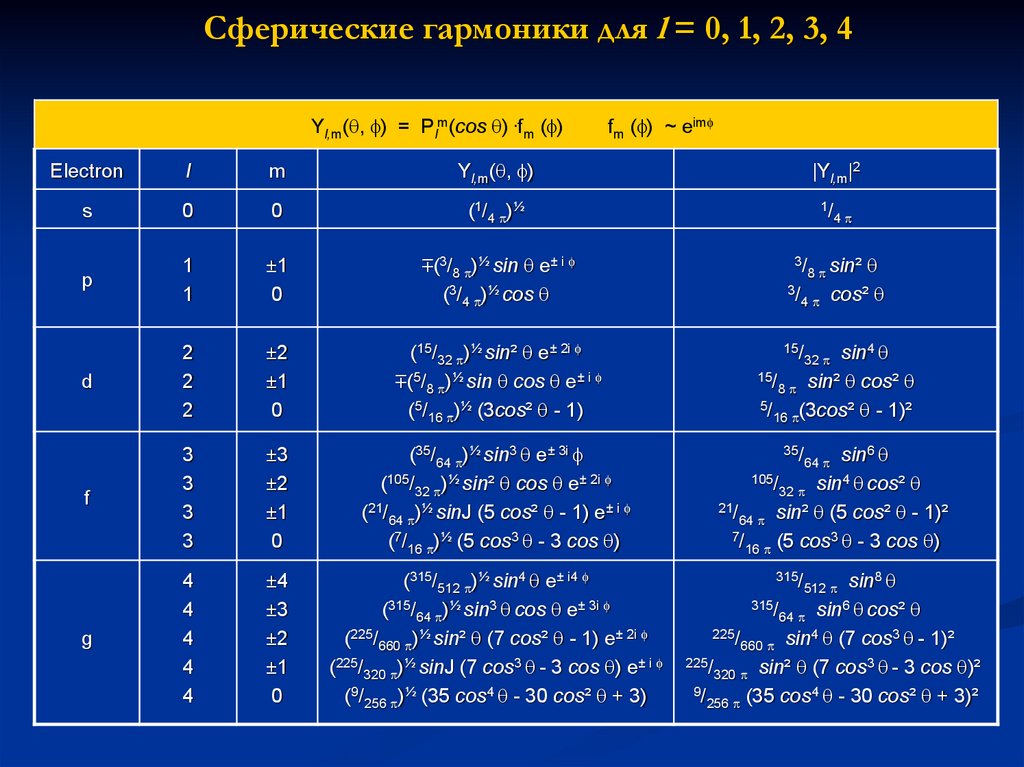
28. Сферические гармоники для l = 0, 1, 2, 3, 4

Yl,m( , ) = Plm(cos ) .fm ( )
fm ( ) ~ eim
Eleсtron
l
m
Yl,m( , )
|Yl,m|2
s
0
0
(1/4 )½
1/
p
1
1
±1
0
(3/8 )½ sin e± i
(3/4 )½ cos
d
2
2
2
±2
±1
0
(15/32 )½ sin² e± 2i
(5/8 )½ sin cos e± i
(5/16 )½ (3cos² - 1)
sin4
15/
8 sin² cos²
5/
16 (3cos² - 1)²
f
3
3
3
3
±3
±2
±1
0
(35/64 )½ sin3 e± 3i
(105/32 )½ sin² cos e± 2i
(21/64 )½ sinJ (5 cos² - 1) e± i
(7/16 )½ (5 cos3 - 3 cos )
sin6
105/
4
32 sin cos²
21/
64 sin² (5 cos² - 1)²
7/
3
16 (5 cos - 3 cos )
g
4
4
4
4
4
±4
±3
±2
±1
0
(315/512 )½ sin4 e± i4
(315/64 )½ sin3 cos e± 3i
(225/660 )½ sin² (7 cos² - 1) e± 2i
(225/320 )½ sinJ (7 cos3 - 3 cos ) e± i
(9/256 )½ (35 cos4 - 30 cos² + 3)
sin8
315/
6
64 sin cos²
225/
4
3
660 sin (7 cos - 1)²
225/
3
320 sin² (7 cos - 3 cos )²
9/
4
256 (35 cos - 30 cos² + 3)²
3/
3/
8 sin²
4
15/
35/
315/
4
cos²
32
64
512

29. Действительные волновые функции (линейные комбинации)

l
|ml|
Волновые функции
0
0
s = 1/(4p)½
0
pz = Y10 = (3/4 )½cosθ
1
px = -1/√2 (Y11 – Y1-1 ) = (3/4 )½sinθcos
1
py = i/√2 (Y11 + Y1-1 ) = (3/4 )½sinθsin
0
1
d3z²-r² = Y20 = (5/16 )½(3 cos²θ - 1)
dxz = -1/√2 (Y21 – Y2-1 ) = (15/4 )½sinθcosθcos
dyz = i/√2 (Y21 + Y2-1 ) = (15/4 )½sinθcosθsin
2
2
dx²-y² = 1/√2 (Y22 + Y2-2 ) = (15/16 )½sin²θcos2
dxy = – i/√2 (Y22 – Y2-2 ) = (15/16 )½sin²θsin2

30.

Угловые волновые функции атома водорода
s орбиталь:
l = 0 m= 0
pZ орбиталь:
l = 1 m= 0
l=2
pX орбиталь pY орбиталь
l = 1 m = ±1
dz² орбиталь: m=0
dxy орбиталь
dx²-y² орбиталь
dzx орбиталь dyz орбиталь

31. Niels Henrik David Bohr

* 7 октября 1885 в г. Копенгагене,
Дания
† 18 ноября 1962 в г. Копенгагене,
Дания
Нобелевская премия по
физике, 1925

32.

Уровни энергии атома водорода и водородо-подобного иона
Z2
En 2
2n
1 Hartree
n 1, 2, 3,
e2
4 0 a0
27,2 eV
0 – восприимчивость вакуума; 0 = 8.854·10-12 J-1 C2 m-1
e – заряд электрона; e = 1.602·10-19 C
a0 боровский радиус; a0 = 4 0ħ2/mee2 = 5.292·10-11 m
Квантовые числа
l = 0 … n – 1, орбитальный момент электрона
ml = - l … l , проекция орб. момента электрона на ось Z
s = ½, спин электрона
ms = -s… s, проекция спина электрона
j = l + s, полный электронный момент, j = |l - ½| … l + ½
Правила отбора для электрических
дипольных переходов:
l – l' = ± 1,
s - s' = 0,
ml – ml’ = 0, ±1
ms – ms’ = 0

33. Симметрия и законы сохранения

Обратимость времени → сохранение энергии
(т.е. замена t на –t не меняет уравнений движения)
Однородность пространства → сохранение импульса
Изотропия пространства →
сохранение момента количества движения

34.

N
1 2 N Z N N 1
H i
i 1 2
i 1 ri
i 1 j i ri j
Уравнение Шредингера для
многоэлектронного атома
H (r1 , r2 , rN ) E (r1 , r2 , rN )
N
1 2 N Z N N 1
H i
i 1 2
i 1 ri
i 1 j i ri j
Вариационный принцип
|H |
E0
|

35.

Многоэлектронные атомы
1. Каждый электрон атома движется в поле ядра и всех остальных электронов, которое
называется самосогласованным. Самосогласованное поле центрально-симметрично, но
не является кулоновским, соответствующее уравнение Шредингера не может быть решено
точно. Приближенные волновые функции и уровни энергии каждого из электронов
могут быть получены в результате решения системы уравнений Хартри-Фока.
2. Полученные одноэлектронные уровни энергии зависят от квантовых чисел n и l. Эти
уровни энергии заполняются по очереди всеми электронами, которые образуют электронную
конфигурацию данного атома. Заполнение осуществляется с учетом принципа Паули:
Два электрона не могут одновременно находиться в одном квантовом состоянии
Поэтому каждое s-состояние (l = 0) могут заселять не более двух электронов, каждое
p-состояние (l = 1) могут заселять не более 6 электронов, каждое d-состояние (l = 2) могут
заселять не более 10 электронов и т.д.
1 2
i U i (r ) i (ri ) i i (ri )
2
1 (r1 ) 2 (r2 ) N (rN )
i Rnl (ri )Ylm ( i , i )

36. Wolfgang Ernst Pauli

Нобелевская премия по
физике, 1945
* 25 апреля 1900 Вена, Австрия
† 15. декабря 1958 Цюрих, Швейцария

37.

Учет нецентрально-симметричной части
потенциала
1. Учет нецентрально-симметричной части потенциала, действующего на электрон,
приводит к расщеплению уровней энергии, соответствующей данной электронной
конфигурации атома, на термы, характеризующиеся моментами, описывающими
атом как целое.
2. Сложение моментов отдельных электронов по правилам квантовой механики дает
квантовые числа, которые характеризуют данное электронное состояние всего атома:
L – полный орбитальный момент атома, МL – проекция L на ось Z
S – полный спиновый электронный момент, MS – проекция S на ось Z
J – полный электронный момент атома: J=L+S, M J – проекция J на ось Z.
P = (-1)Σ li = ± 1 – четность состояния атома.
3. Если одной и той же конфигурации соответствуют несколько различных термов, то
терм, имеющий наименьшую энергию находится по правилу Гунда:
Наинизшую энергию в данной электронной конфигурации имеет терм с наибольшим
значением S и наибольшим (при данном S) значением L .

38.

Обозначения уровней энергии (термов) в
многоэлектронных атомах в приближении
LS связи.
2 S 1 o
J
L
2 S 1
LJ
- для нечетных состояний
- для четных состояний
L=0
S-состояние
L=1
P-состояние
L=2
D-состояние
S=0
Синглет
S=1
Триплет
Правила отбора для радиационных переходов в
многоэлектронных атомах
L – L'
S – S'
J – J'
MJ – MJ'
P
0, ± 1
0
0, ± 1
0, ± 1
+↔ –
J+J ≥1!

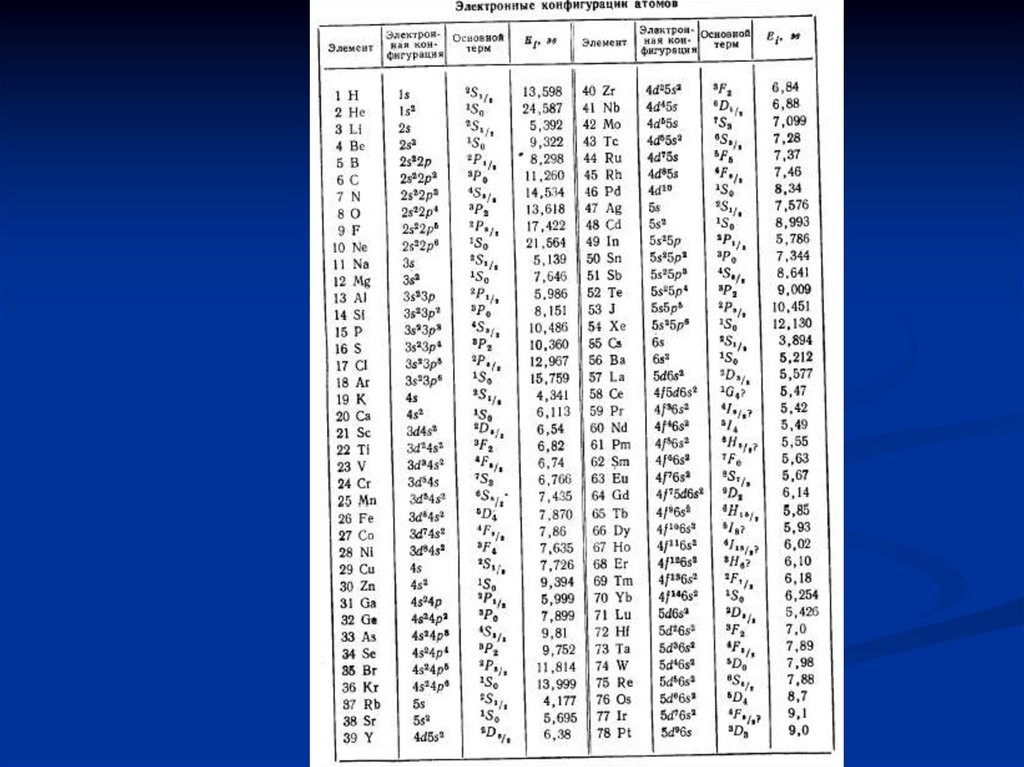
39.

Термы, соответствующие различным
электронным конфигурациям

40.

41.

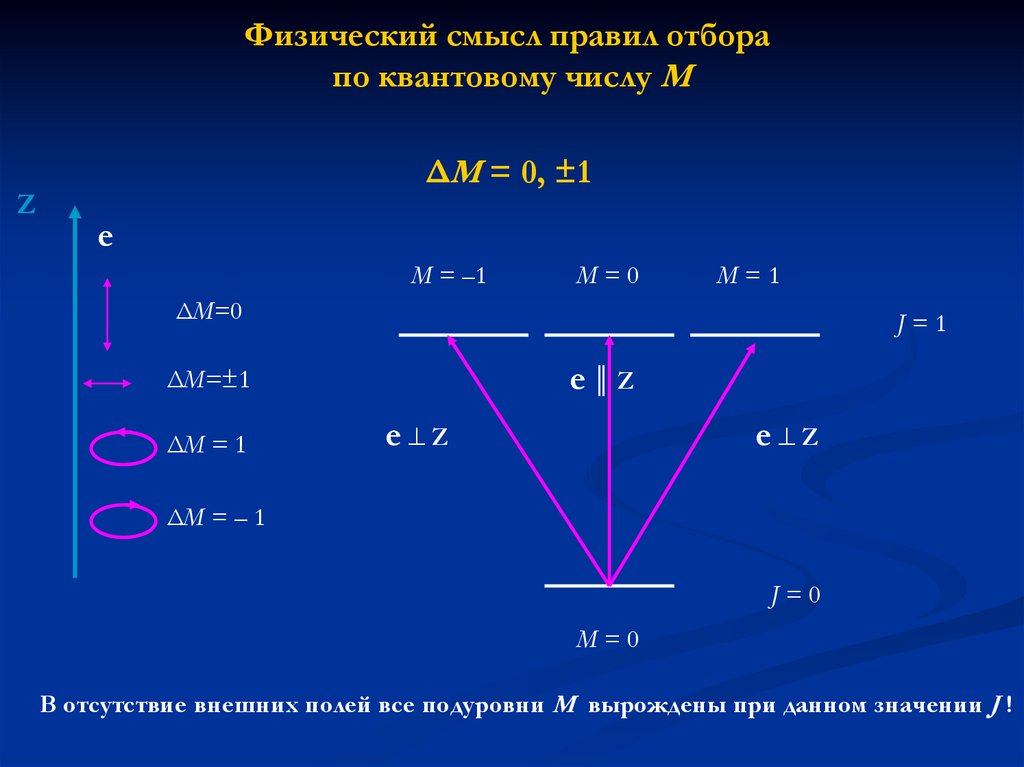
Физический смысл правил отбора
по квантовому числу М
Z
ΔM = 0, ±1
e
M = –1
M=0
M=1
ΔM=0
J=1
e║Z
ΔM=±1
ΔM = 1
e Z
e Z
ΔM = – 1
J=0
M=0
В отсутствие внешних полей все подуровни М вырождены при данном значении J !

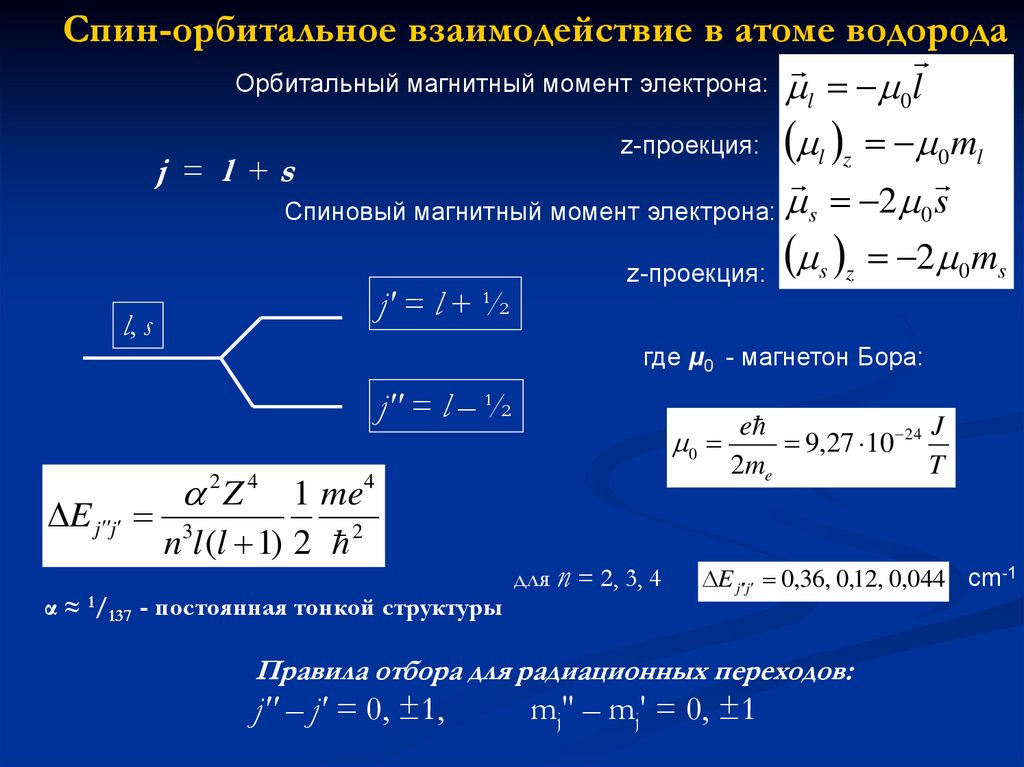
42.

Спин-орбитальное взаимодействие в атоме водорода
Орбитальный магнитный момент электрона: l
l
0
z-проекция: l z 0 ml
j = l +s
Спиновый магнитный момент электрона: s 2 0 s
s z 2 0 ms
z-проекция:
j' = l + ½
l, s
где μ0 - магнетон Бора:
j'' = l – ½
E j j
0
2 Z 4 1 me4
n3l (l 1) 2 2
α ≈ 1/137 - постоянная тонкой структуры
для n = 2, 3, 4
e
J
9,27 10 24
2me
T
E j j 0,36, 0,12, 0,044 cm-1
Правила отбора для радиационных переходов:
j'' – j' = 0, ±1,
mj'' – mj' = 0, ±1

43.

Тонкая структура спектральных линий
Тонкая структура обусловлена
спин-орбитальным взаимодействием
L'', S
J''max = L + S
J''+1
J''
J''min = |L'' – S|
А'' > 0
VSO = A L·S
L', S
J'max = L + S
J'+1
J'
J'min = |L' – S|
А' > 0
EJ = ½ A [ J (J+1) – S(S+1) – L(L+1)] → ΔEJ, J-1 = A J
правило интервалов Ланде

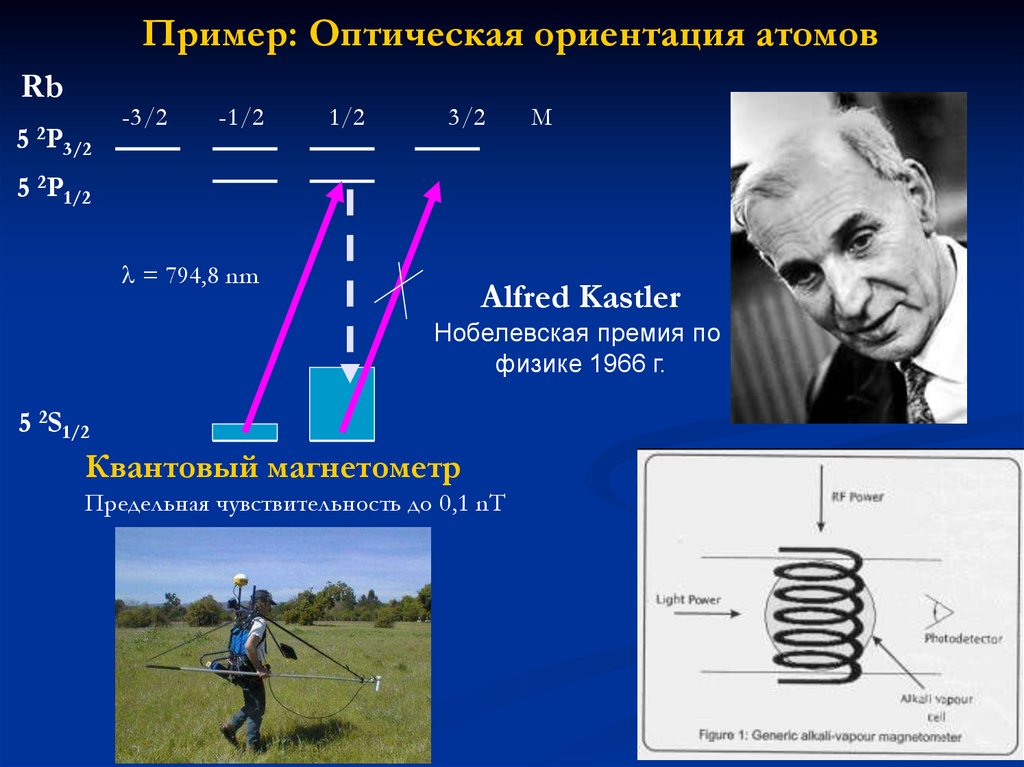
44.

Пример: Оптическая ориентация атомов
Rb
5 2P
-3/2
-1/2
1/2
3/2
М
3/2
5 2P1/2
= 794,8 nm
Alfred Kastler
Нобелевская премия по
физике 1966 г.
5 2S1/2
Квантовый магнетометр
Предельная чувствительность до 0,1 nT

45.

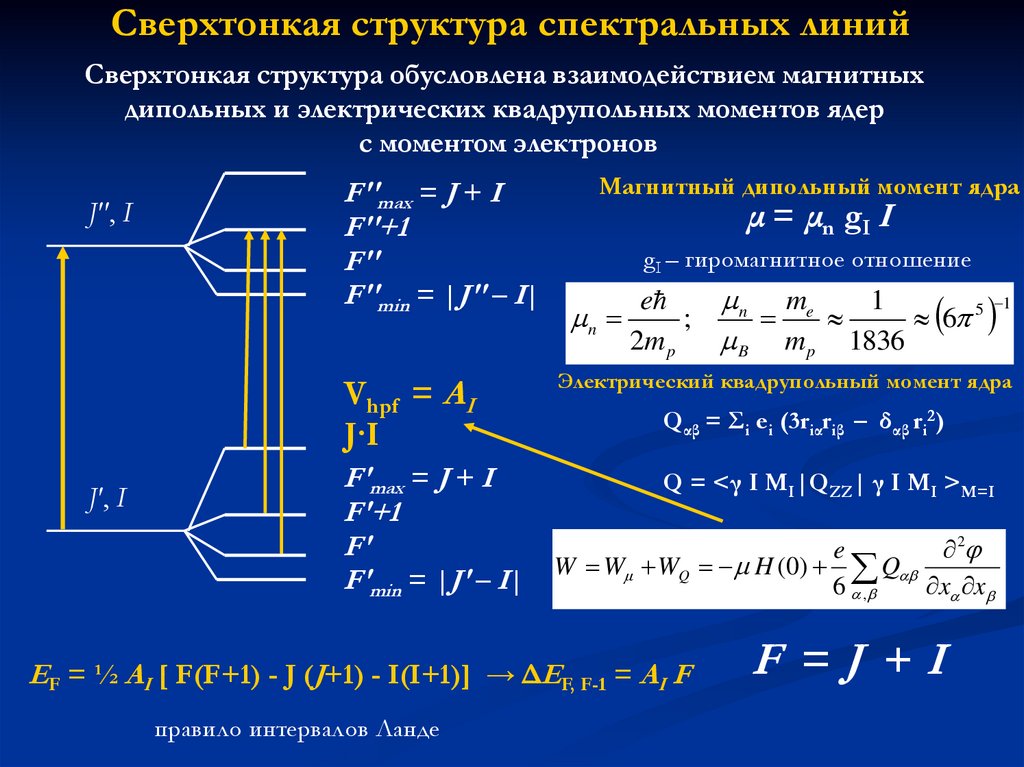
Сверхтонкая структура спектральных линий
Сверхтонкая структура обусловлена взаимодействием магнитных
дипольных и электрических квадрупольных моментов ядер
с моментом электронов
J'', I
F''max = J + I
F''+1
F''
F''min = |J'' – I|
Vhpf = AI
J·I
J', I
Магнитный дипольный момент ядра
μ = μn gI I
gI – гиромагнитное отношение
n
e
;
2m p
1
n me
1
6 5
B m p 1836
Электрический квадрупольный момент ядра
Qαβ = Σi ei (3riαriβ – δαβ ri2)
F'max = J + I
Q = <γ I MI|QZZ| γ I MI >M=I
F'+1
F'
e
2
Q
F'min = |J' – I| W W WQ H (0) 6
x x
,
EF = ½ AI [ F(F+1) - J (J+1) - I(I+1)] → ΔEF, F-1 = AI F
правило интервалов Ланде
F =J +I

46.

Пример: Квантовый стандарт частоты
87Rb
Предельная точность стандарта частоты f/f0 ≈ 10-9
f0 = 6834682612,8… Гц

47.

Атом во внешнем электрическом поле: эффект Штарка
WE = - E D = e E Σi ri
E J M E J M DZ J M E
2
J M DZ J M J M DZ J M
E J E J
J
0
ΔEγJM = E 2 [ AγJ + BγJ M2 ]
В результате при наложении однородного электрического поля уровень энергии атома γ J
расщепляется на компоненты:
|M| = J, J-1, …,
Для сильных электрических полей, когда штарковские
поправки к энергии становятся сравнимыми с
первоначальным расщеплением соседних уровней энергии
γ J и γ' J' , формула для расщепления уровней имеет вид:
2
2
E1, 2 E J M DZ J M
2
2
Т.е. при больших полях происходит переход квадратичного
эффекта Штарка в линейный!

48.

Johannes Stark
Нобелевская премия по
физике, 1919
* 14 апреля 1874 Шикенхофф, Германия
† 21 июня 1957 Траунштейн, Германия

49.

Поляризация излучения флуоресценции при
наблюдении эффекта Штарка
Z, E
e
M=1
M = –1
ΔM=0
M=0
ΔM=±1
e║Z
e Z
Je = 1
π - компонента
σ - компонента
e Z
σ - компонента
Jg = 0
M=0
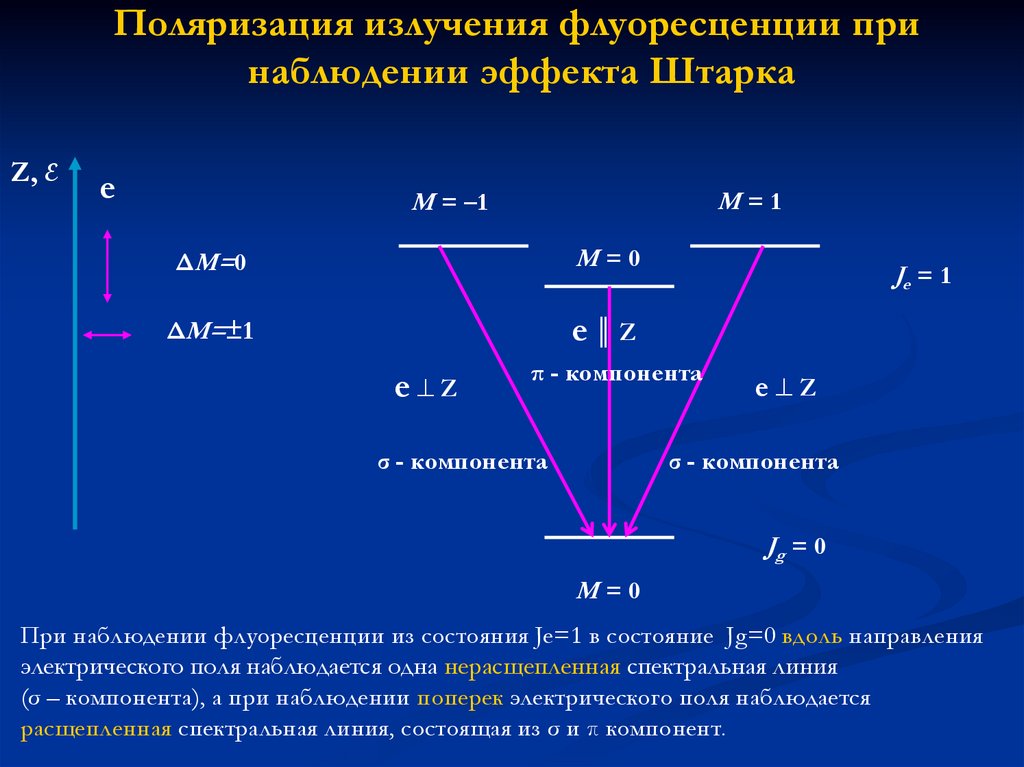
При наблюдении флуоресценции из состояния Je=1 в состояние Jg=0 вдоль направления
электрического поля наблюдается одна нерасщепленная спектральная линия
(σ – компонента), а при наблюдении поперек электрического поля наблюдается
расщепленная спектральная линия, состоящая из σ и π компонент.

50.

Атом во внешнем магнитном поле: эффект Зеемана
WВ = - μ ·В
μ = - μ0 g J,
где
e
0
2 me
-магнетон Бора, μ0 ≈ 9,2732 10-24 J/Т ,
μ0 ≈ 1,4 МГц/Гаусс,
g – гиромагнитное отношение
EB = < WB > = g μ0 BZ M
Т.е. в результате при наложении однородного магнитного поля уровень энергии атома в
состоянии |γ J расщепляется на 2J+1 компонент:
M = J, J-1, …, -J
Для случая LS связи
g 1
J ( J 1) L( L 1) S ( S 1)
2 J ( J 1)
Для случая чисто орбитального углового момента (S=0), g = 1
Для случая чисто спинового углового момента (L=0), g = 2

51.

Pieter Zeeman
Нобелевская премия по
физике, 1902
* 25 мая 1865 Зоннемар, Голландия
† 9 октября 1943 Амстердам, Голландия

52.

Поляризация излучения флуоресценции при
наблюдении эффекта Зеемана
M=1
Z, Н
M=0
e
M = –1
ΔM = 0
ΔM = ±1
e Z
J=1
e║Z
π - компонента
σ– - компонента
e Z
σ+ - компонента
J=0
M=0
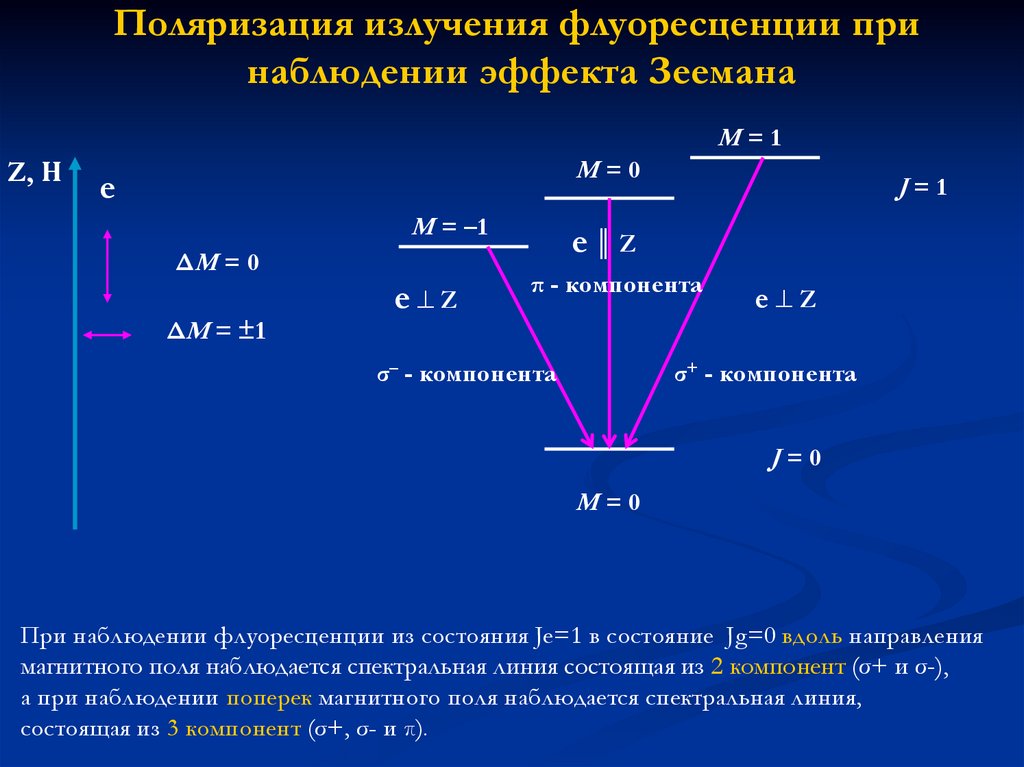
При наблюдении флуоресценции из состояния Je=1 в состояние Jg=0 вдоль направления
магнитного поля наблюдается спектральная линия состоящая из 2 компонент (σ+ и σ-),
а при наблюдении поперек магнитного поля наблюдается спектральная линия,
состоящая из 3 компонент (σ+, σ- и π).

53.

Pадиационыe переходы в атомах
Квантование поля электромагнитного излучения
Wfield n k 1
2
Согласно квантовой электродинамике, вероятность
радиационного перехода, сопровождающегося
эмиссией или поглощением фотона равна:
2
e 2
ikr
dWem
JM e k pe J M (nk 1)dO
3 2
2 c m
2
e 2
ikr
dWab
JM e k pe J M nk dO
3 2
2 c m
Разлагая экспоненту по степеням kr, можно получить выражения для
мультипольного излучения. Первый член этого разложения eikr = 1
описывает электрическое дипольное излучение (поглощение).

54.

Мультипольное излучение и поглощение
I. Электрическое дипольное излучение и поглощение
sp
DE
dW
2
3
JM
e
D
J
M
dO
k
3
2 c
2
4 2
dW 2 JM e k D J M I dO
c
D e ri
ind
DE
Правила отбора:
ΔJ = 0, ±1
ΔMJ = 0, ±1
ΔP ≠ 0 (+ ↔ −)
i
Если электрический вектор электромагнитной волны направлен вдоль оси Z, то
dWDE JM DZ ' J ' M '
2
Преобладает при радиационных переходах между электронными состояниями
атомов и молекул, имеющими противоположную четность. Эти переходы
в атомах наблюдаются как правило в видимом и ультрафиолетовом диапазонах
спектра. В молекулах электрическое дипольное излучение ответственно также за
колебательно-вращательные переходы, которые находятся в основном в
инфракрасном диапазоне спектра.

55.

II. Магнитное дипольное излучение и поглощение
Второй член разложения eikr = 1 + ikr описывает магнитное дипольное и
электрическое квадрупольное излучение (поглощение).
sp
DM
dW
2
3
JM
B
M
J
M
dO
k
3
2 c
2
4 2
dW 2 JM B k M J M I dO
c
e
l i 2si
M
2mc i
ind
DM
Правила отбора:
ΔJ = 0, ±1
ΔMJ = 0, ±1
ΔP = 0 (+ ↔ + или − ↔ − )
Если магнитный вектор в электромагнитной волне направлен вдоль оси Z, то
dWDM JM M Z ' J ' M '
2
WME
10 4
WDE
Преобладает при радиационных переходах между электронными состояниями
атомов, имеющими одинаковую четность: между состояниями тонкой
и сверхтонкой структуры, а также между чисто спиновыми состояниями
(магнитный резонанс). Эти переходы наблюдаются как правило в инфракрасном
и микроволновом диапазонах спектра, а для случая магнитного резонанса – в
области радиочастот.

56.

Двухатомная молекула: молекулярный ион H2+
Координатная система
Уравнение Шредингера:
H E
Гамильтониан:
2
2
1
e
1 1
ˆ
H
2 me
4 0 rA rB R
Вековое уравнение:
E ES
0
ES E
Волновые функции нулевого приближения
A H A B H B Кулоновский интеграл
A H B B H A
S A B
Обменный интеграл
Интеграл перекрытия
A
e
rA / a0
a
3 1/ 2
0
B
e rB / a0
a
3 1/ 2
0
Волновые функции молекулы
cA A cB B

57.

Молекулярный ион H2+ : Значения энергии и
волновые функции
E1
0
0
E2
1 S
1 S
Волновые функции: орбитали
N A (rA ) B (rB )
N A (rA ) B (rB )
Связывающая молекулярная орбиталь
A
e rA / a0
a
3 1/ 2
0
B
e rB / a0
a
3 1/ 2
0
Разрыхляющая молекулярная орбиталь
Нормировка
N
1
2(1 S ) 1/ 2

58.

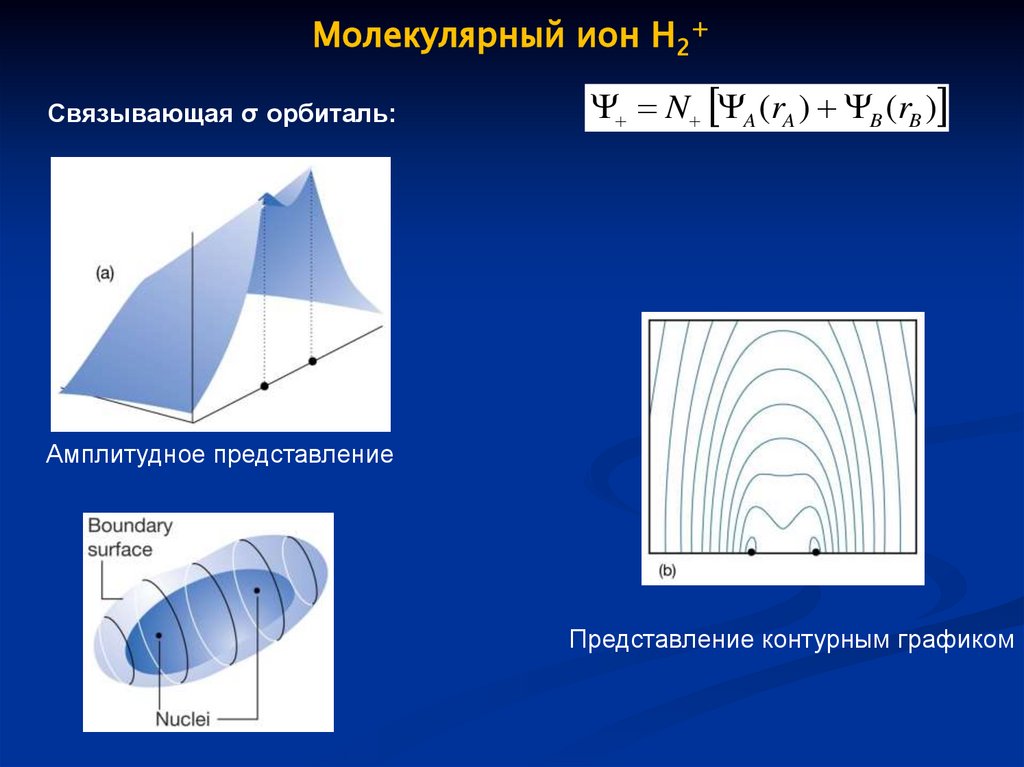
Молекулярный ион H2+
Связывающая σ орбиталь:
N A (rA ) B (rB )
Амплитудное представление
Представление контурным графиком

59.

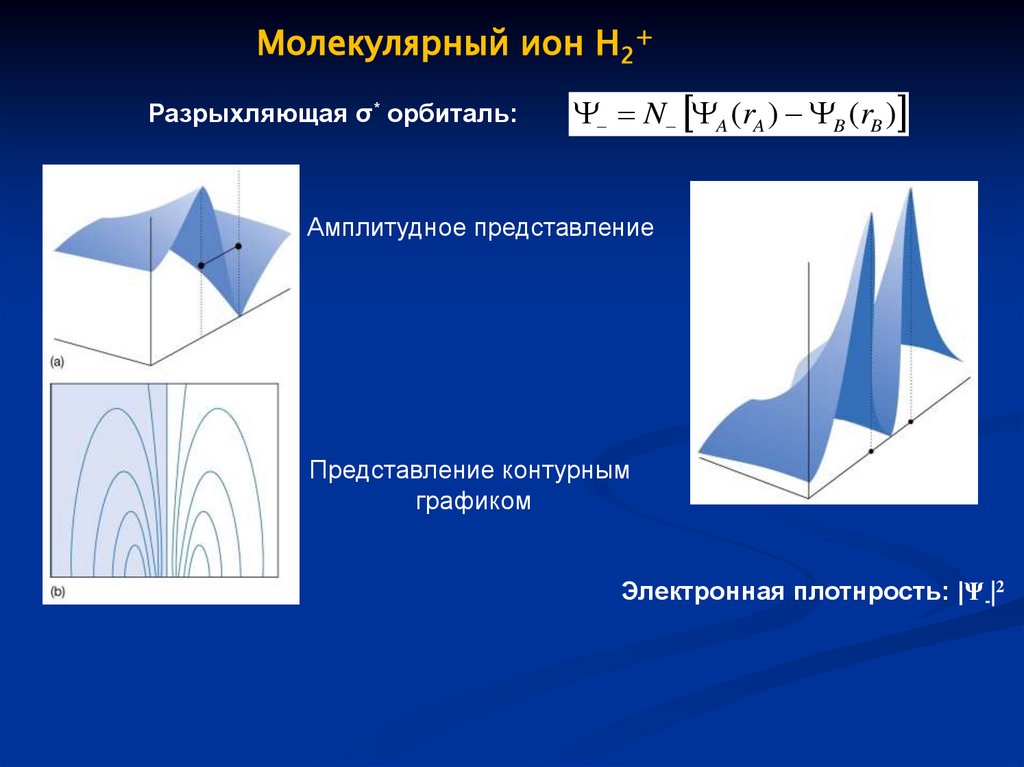
Молекулярный ион H2+
Разрыхляющая σ* орбиталь:
N A (rA ) B (rB )
Амплитудное представление
Представление контурным
графиком
Электронная плотнрость: |Ψ-|2

60.

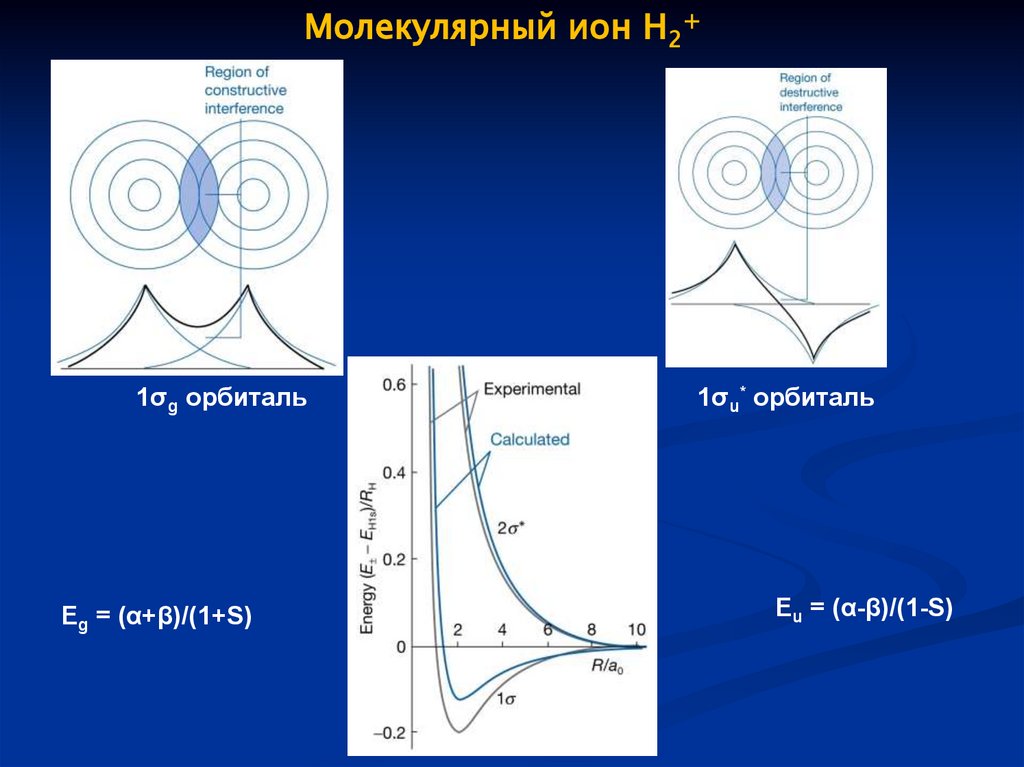
Молекулярный ион H2+
1σg орбиталь
Eg = (α+β)/(1+S)
1σu* орбиталь
Eu = (α-β)/(1-S)

61.

Линейные комбинации атомных орбиталей (LCAO):
Гомоядерные двухатомные молекулы
(q) ci i (q)
i
Волновая функция молекулы представляется
в виде суперпозиции всех атомных орбиталей
одинаковой симметрии
Типы симметрии одноэлектронной молекулярной орбитали
1. Проекция орбитального момента электрона
на ось молекулы: lz = ± ħ
= 0, 1, 2, 3,
орбиталь , , , , …
2. Инверсия электронной волновой функции молекулы в точке симметрии:
gerade
ungerade
g
u

62.

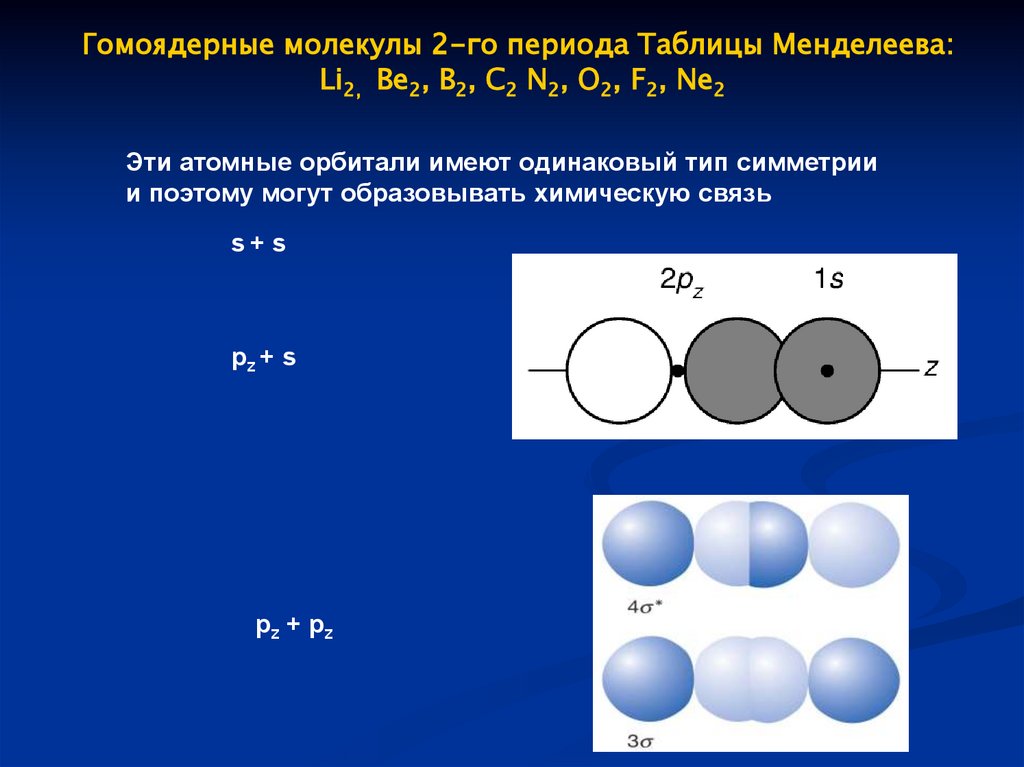
Гомоядерные молекулы 2-го периода Таблицы Менделеева:
Li2, Be2, B2, C2 N2, O2, F2, Ne2
Эти атомные орбитали имеют одинаковый тип симметрии
и поэтому могут образовывать химическую связь
s+ s
pz + s
p z + pz

63.

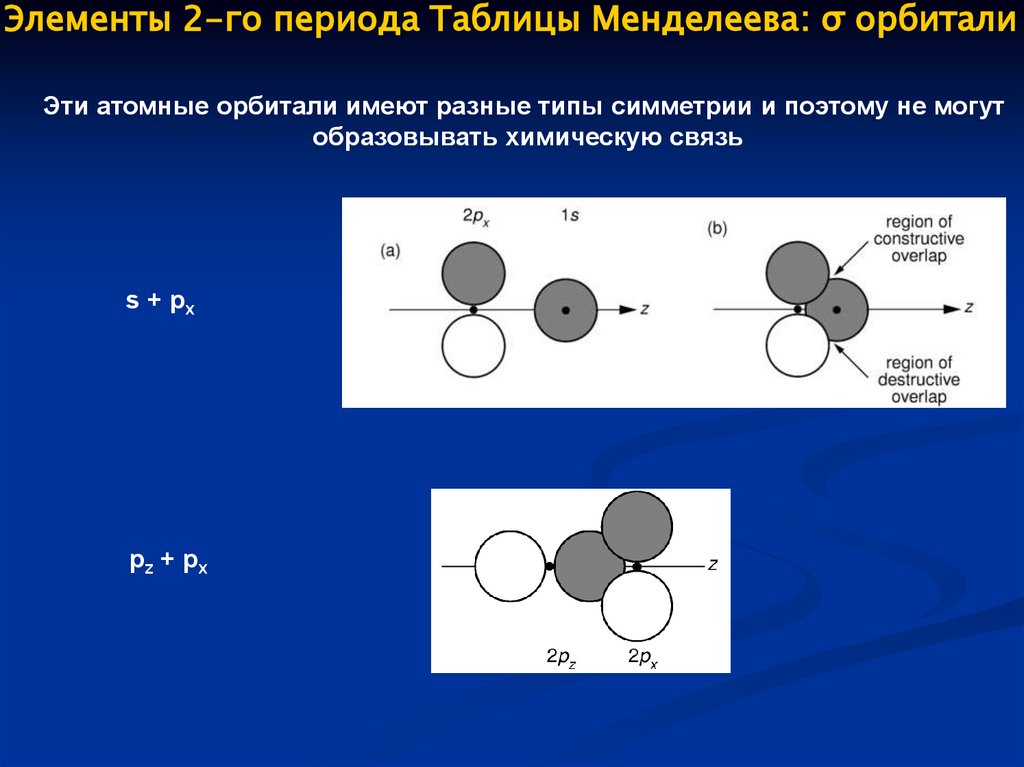
Элементы 2-го периода Таблицы Менделеева: σ орбитали
Эти атомные орбитали имеют разные типы симметрии и поэтому не могут
образовывать химическую связь
s + px
pz + px

64.

σ орбитали в молекулах 2-го периода Периодической таблицы:
В общем случае:
Ψσ = CA2s ΦA2s + CB2s ΦB2s + CA2pz ΦA2pz + CB2pz ΦB2pz
Ось Z параллельна межъядерной оси
Только 2s и 2pz атомные
орбитали могут быть
использованы для построения
молекулярных σ орбиталей!
Иногда атомные 2s и 2pz орбитали могут рассматриваться порознь, поскольку они
обладают разными энергиями. В этом случае две 2s орбитали (по одной от каждого
атома) перекрываются друг с другом, образуя пару g , u* молекулярных орбиталей,
а две 2pz атомные орбитали перекрывваются с друг другом, образуя другую пару g
, u* молекулярных орбиталей.

65.

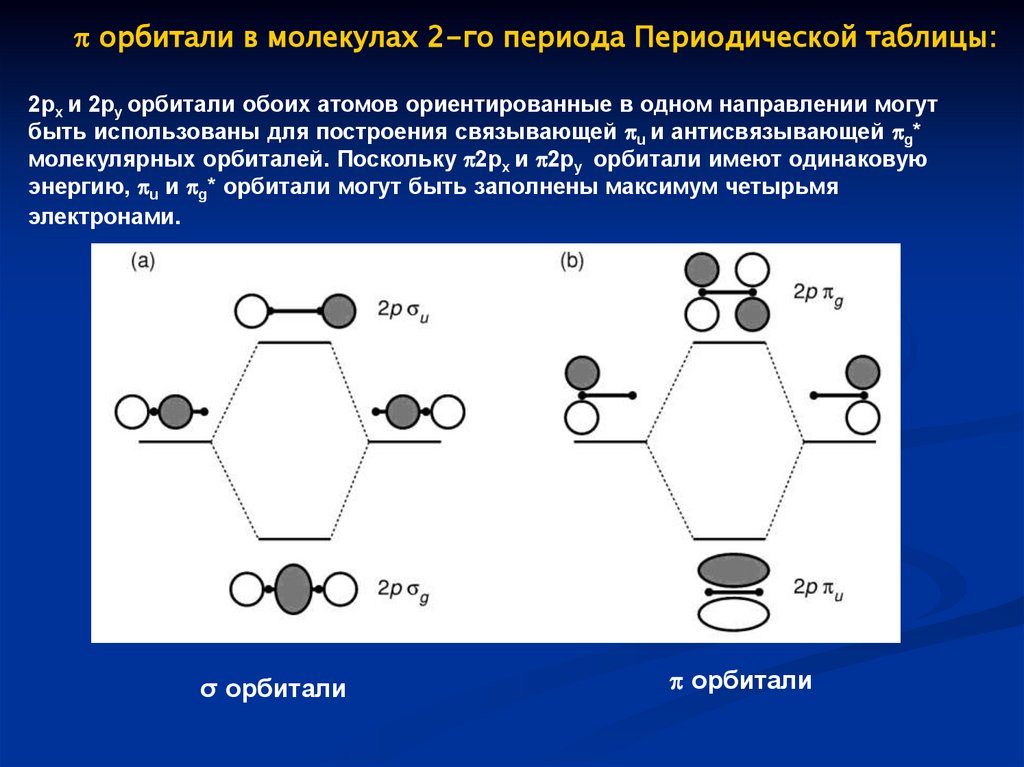
орбитали в молекулах 2-го периода Периодической таблицы:
2px и 2py орбитали обоих атомов ориентированные в одном направлении могут
быть использованы для построения связывающей u и антисвязывающей g*
молекулярных орбиталей. Поскольку 2px и 2py орбитали имеют одинаковую
энергию, u и g* орбитали могут быть заполнены максимум четырьмя
электронами.
σ орбитали
орбитали

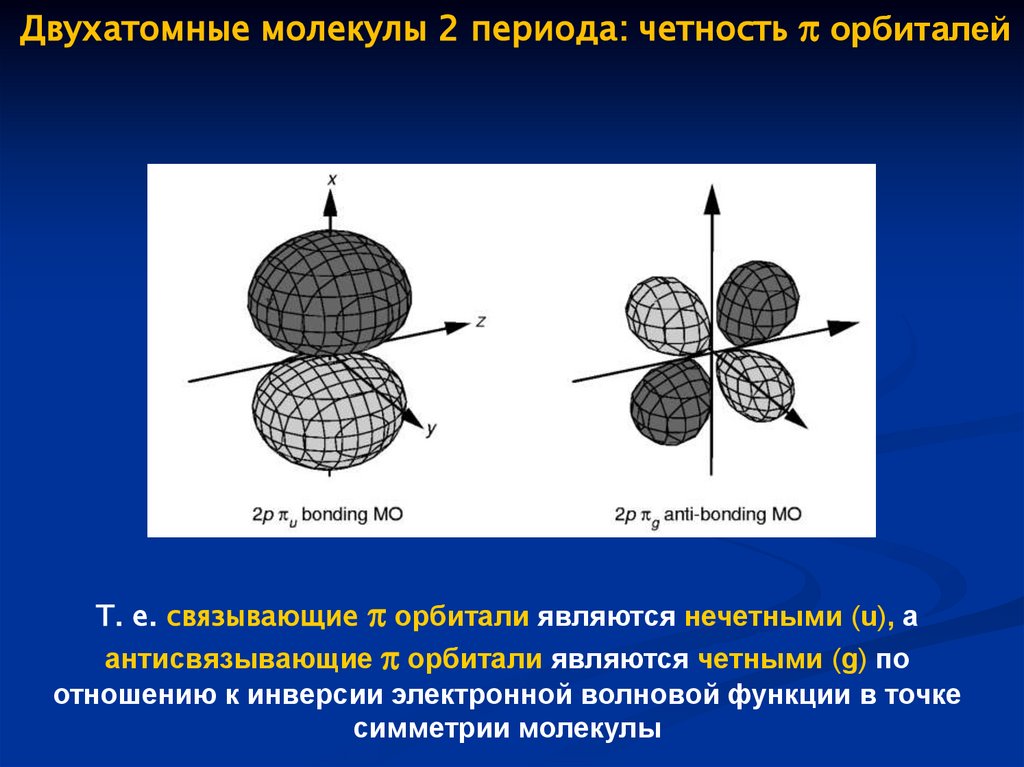
66.

Двухатомные молекулы 2 периода: четность орбиталей
Т. е. связывающие орбитали являются нечетными (u), а
антисвязывающие орбитали являются четными (g) по
отношению к инверсии электронной волновой функции в точке
симметрии молекулы

67.

Принципы построения многоэлектронной
волновой функции молекулы
После определения одноэлектронных волновых функций и уровней
энергии молекулы с помощью метода Хартри-Фока, или вариационного
метода, соответствующие орбитали заполняются электронами,
руководствуясь следующими принципами:
• Электроны должны заполнять различные орбитали приблизительно
в порядке возрастания их энергии
• Не более двух электронов могут заполнять одну невырожденную орбиталь
• Если одной электронной конфигурации молекулы соответствуют
несколько молекулярных термов, меньшей энергией будет обладать
терм с большим количеством неспаренных электронов (правило Гунда)

68.

Симметрия многоэлектронной волновой функции
Если пренебречь симметрией многоэлектронной волновой функции молекулы,
обусловленной принципом Паули, то она в рассматриваемом приближении
может быть записана в виде произведения одноэлектронных волновых
функций, рассчитанных по методу Хартри-Фока:
(r1 , r2 , rN ) 1 (r1 ) 2 (r2 ) N (rN )
Однако, принцип Паули требует, чтобы многоэлектронная волновая функция
была антисимметрична относительно перестановки координат любых двух
электронов. «Правильную» симметрию волновой функции можно обеспечить,
представив многоэлектронную волновую функцию в виде детерминанта:
1
(r1 , r2 , rN )
N!
1 (r1 )
1 (r2 )
2 (r1 ) N (r1 )
2 (r2 ) N (r2 )
1 (rN ) 2 (rN ) N (rN )

69.

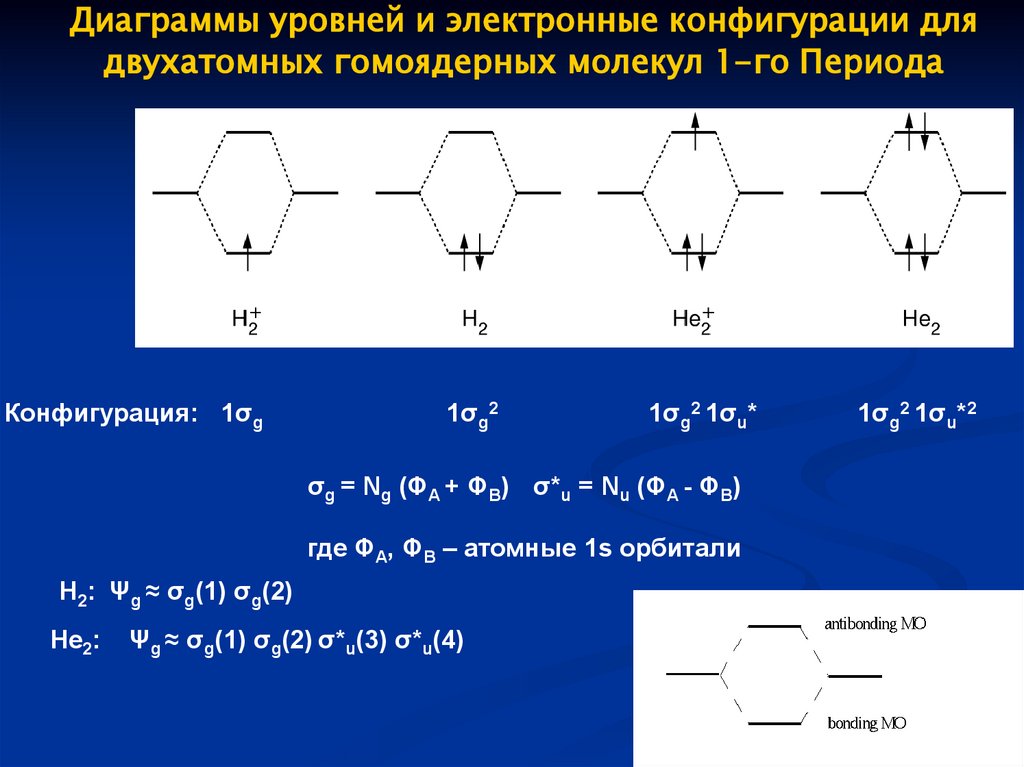
Диаграммы уровней и электронные конфигурации для
двухатомных гомоядерных молекул 1-го Периода
Конфигурация: 1σg
1σg2
1σg2 1σu*
σg = Ng (ΦA + ΦB) σ*u = Nu (ΦA - ΦB)
где ΦA, ΦB – атомные 1s орбитали
H2: Ψg ≈ σg(1) σg(2)
He2:
Ψg ≈ σg(1) σg(2) σ*u(3) σ*u(4)
1σg2 1σu*2

70.

Порядок химической связи
Количественной характеристикой силы связи в двухатомной молекуле
Является порядок химической связи, b:
b = ½(n - n*)
Где n – количество электронов на связывающих орбиталях, а n* количество электронов на разрыхляющих (антисвязывающих)
орбиталях.
примеры:
• H2
b = 1, соответствует единично связи H -- H,
• He2 b = 0, соответствует отсутствию связи.

71.

Электронная структура двухатомных
гомоядерных молекул 2-го периода Таблицы
Менделеева

72.

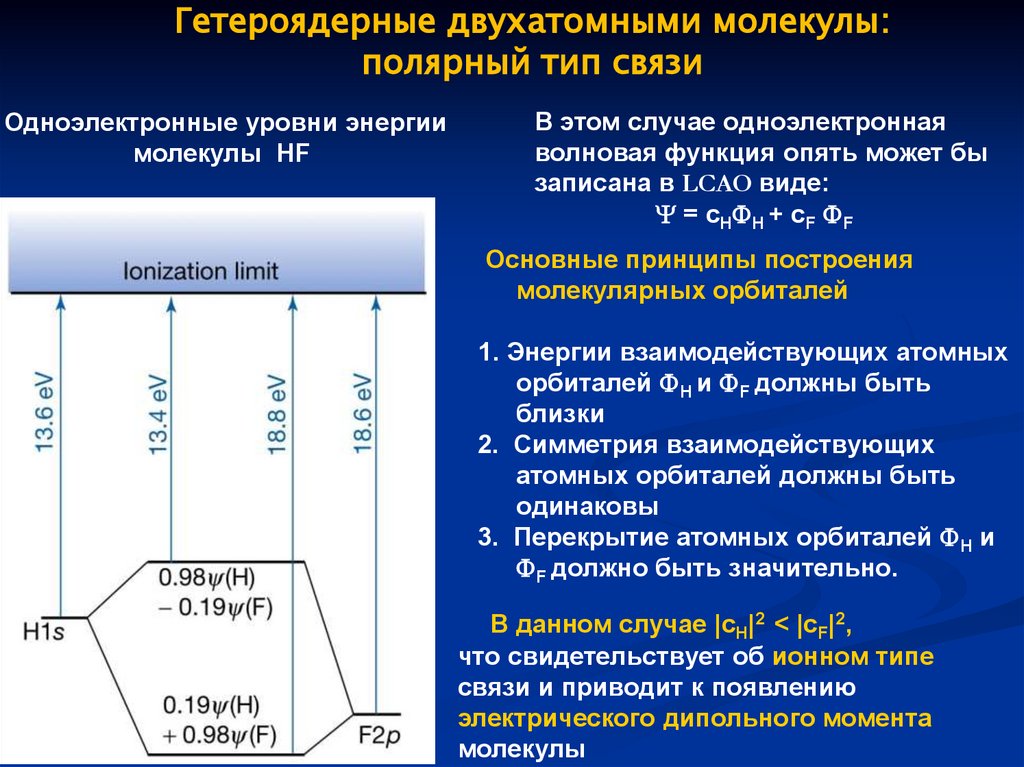
Гетероядерные двухатомными молекулы:
полярный тип связи
Одноэлектронные уровни энергии
молекулы HF
В этом случае одноэлектронная
волновая функция опять может бы
записана в LCAO виде:
= cH H + cF F
Основные принципы построения
молекулярных орбиталей
1. Энергии взаимодействующих атомных
орбиталей H и F должны быть
близки
2. Симметрия взаимодействующих
атомных орбиталей должны быть
одинаковы
3. Перекрытие атомных орбиталей H и
F должно быть значительно.
В данном случае |cH|2 < |cF|2,
что свидетельствует об ионном типе
связи и приводит к появлению
электрического дипольного момента
молекулы

73.

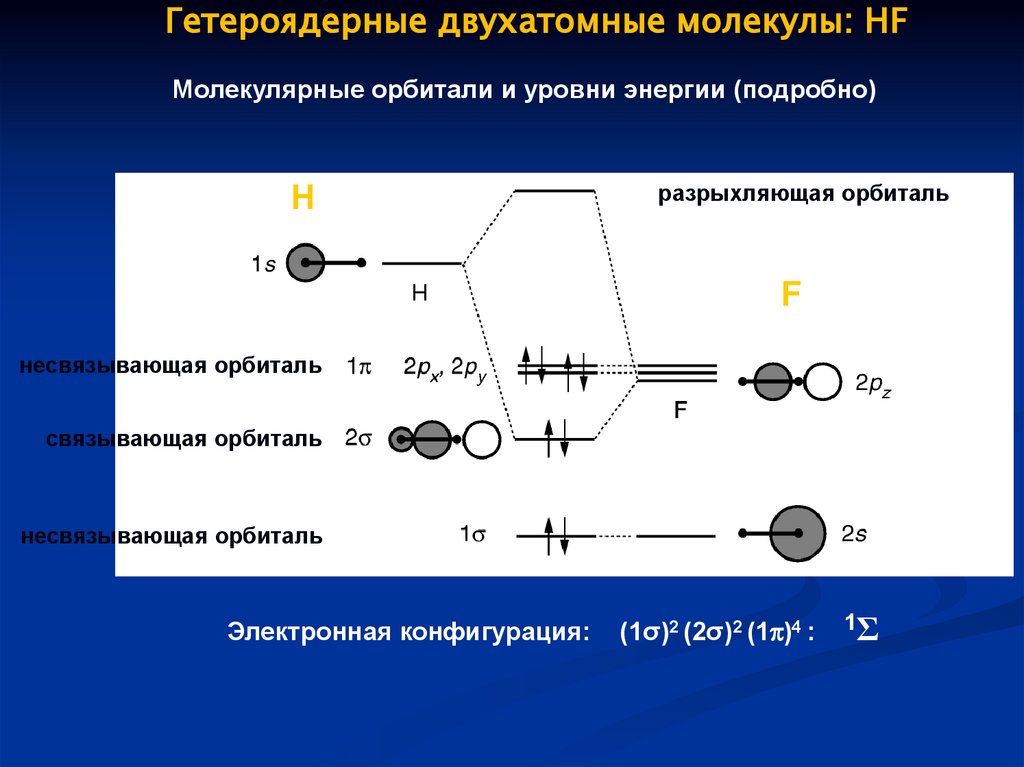
Гетероядерные двухатомные молекулы: HF
Молекулярные орбитали и уровни энергии (подробно)
H
разрыхляющая орбиталь
F
несвязывающая орбиталь
связывающая орбиталь
несвязывающая орбиталь
Электронная конфигурация:
(1σ)2 (2σ)2 (1 )4 :
1Σ

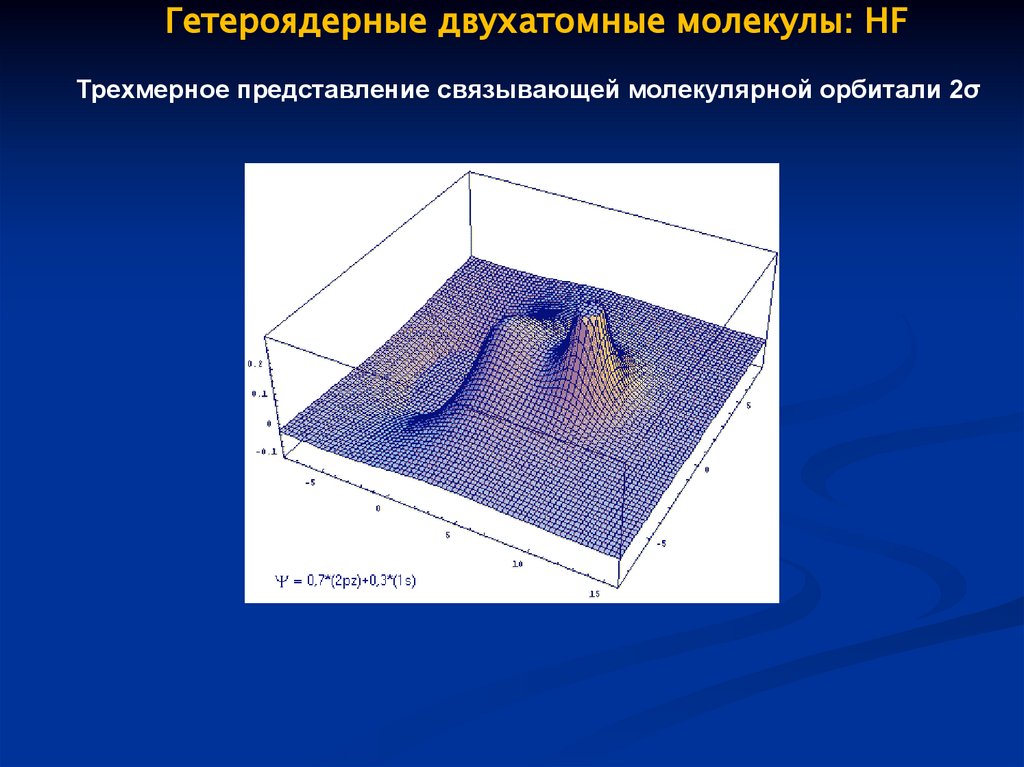
74.

Гетероядерные двухатомные молекулы: HF
Трехмерное представление связывающей молекулярной орбитали 2σ

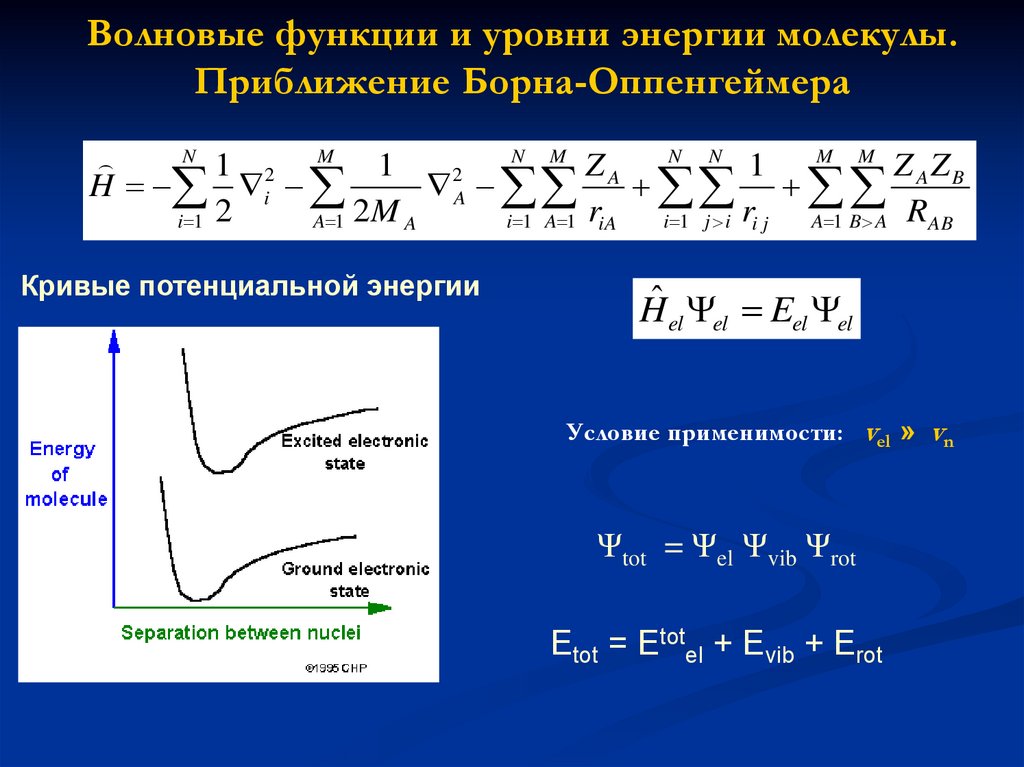
75.

Волновые функции и уровни энергии молекулы.
Приближение Борна-Оппенгеймера
N
N M
N N
M M
1 2 M 1
Z
1
Z Z
H i
2A A A B
i 1 2
A 1 2 M A
i 1 A 1 riA
i 1 j i ri j
A 1 B A R AB
Кривые потенциальной энергии
Hˆ el el Eel el
Условие применимости: vel » vn
Ψtot = Ψel Ψvib Ψrot
Etot = Etotel + Evib + Erot

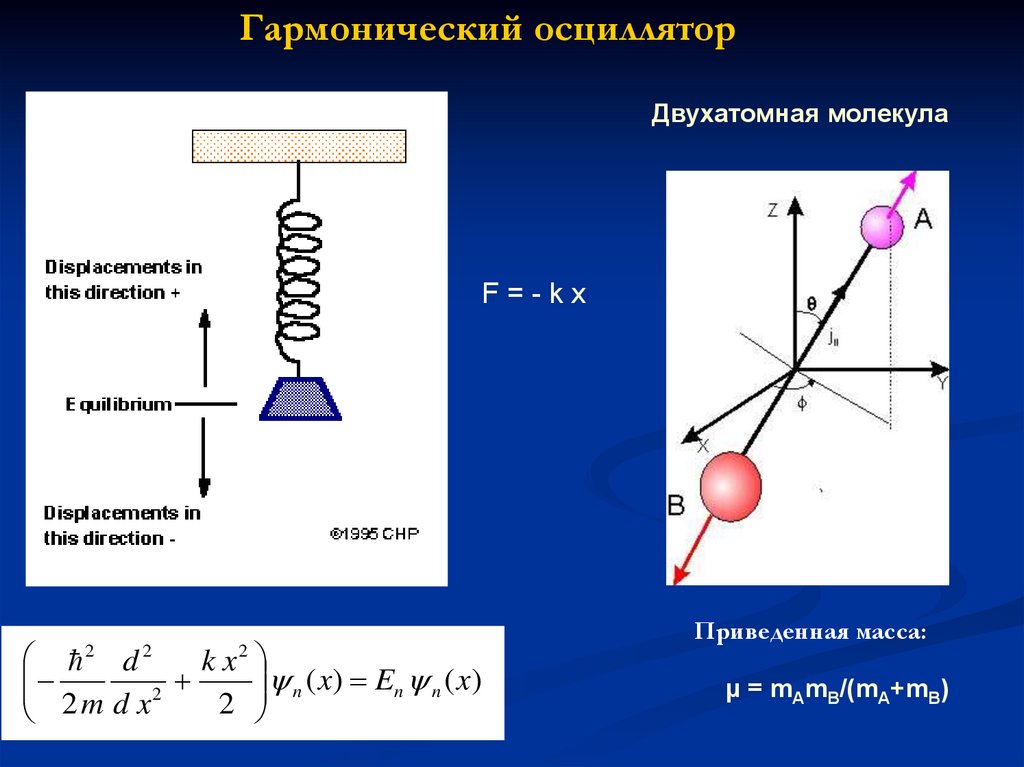
76.

Гармонический осциллятор
Двухатомная молекула
F=-kx
d
kx
n ( x) En n ( x)
2
2
2m d x
2
2
2
Приведенная масса:
μ = mAmB/(mA+mB)

77.

Уровни энергии гармонического осциллятора
Ev = (v + ½) ħ ω = (v + ½) h ,
v = 0, 1, 2, …
ω 2
m
m
µ
m m
1
2
A
B
A
B
k
µ
k
µ

78.

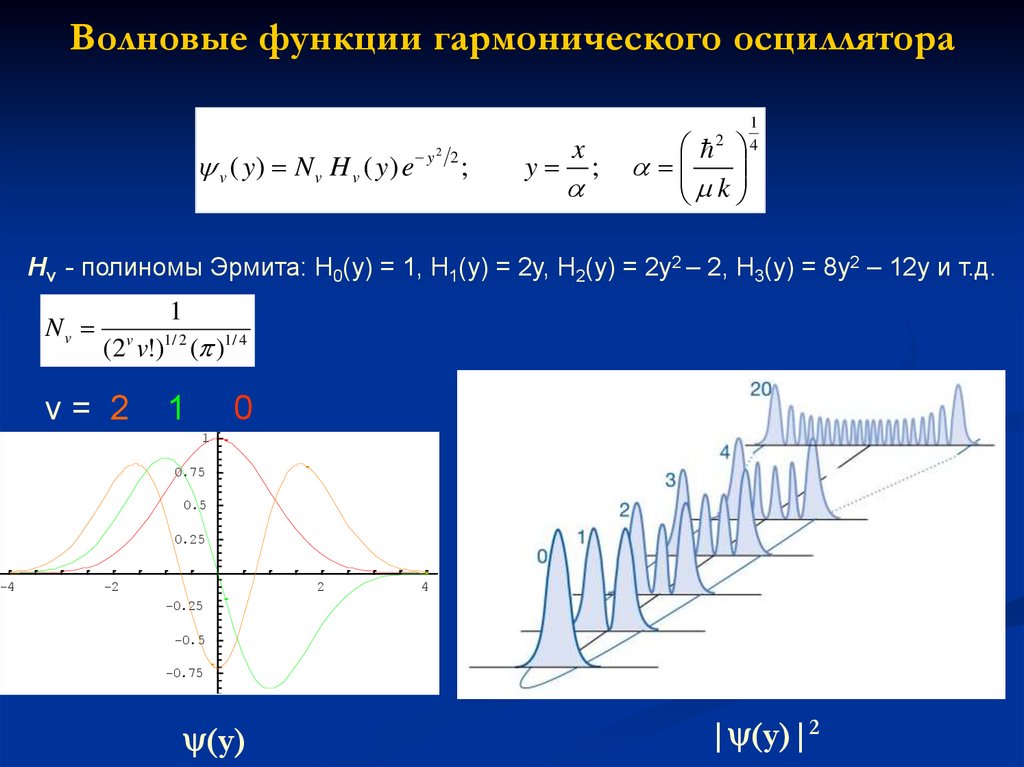
Волновые функции гармонического осциллятора
v ( y) N v H v ( y) e
y2 2
;
y
x
k
2
;
1
4
Hv - полиномы Эрмита: H0(y) = 1, H1(y) = 2y, H2(y) = 2y2 – 2, H3(y) = 8y2 – 12y и т.д.
Nv
1
(2v v!)1/ 2 ( )1/ 4
v= 2
1
0
1
0.75
0.5
0.25
-4
-2
2
4
-0.25
-0.5
-0.75
(y)
| (y)|2

79.

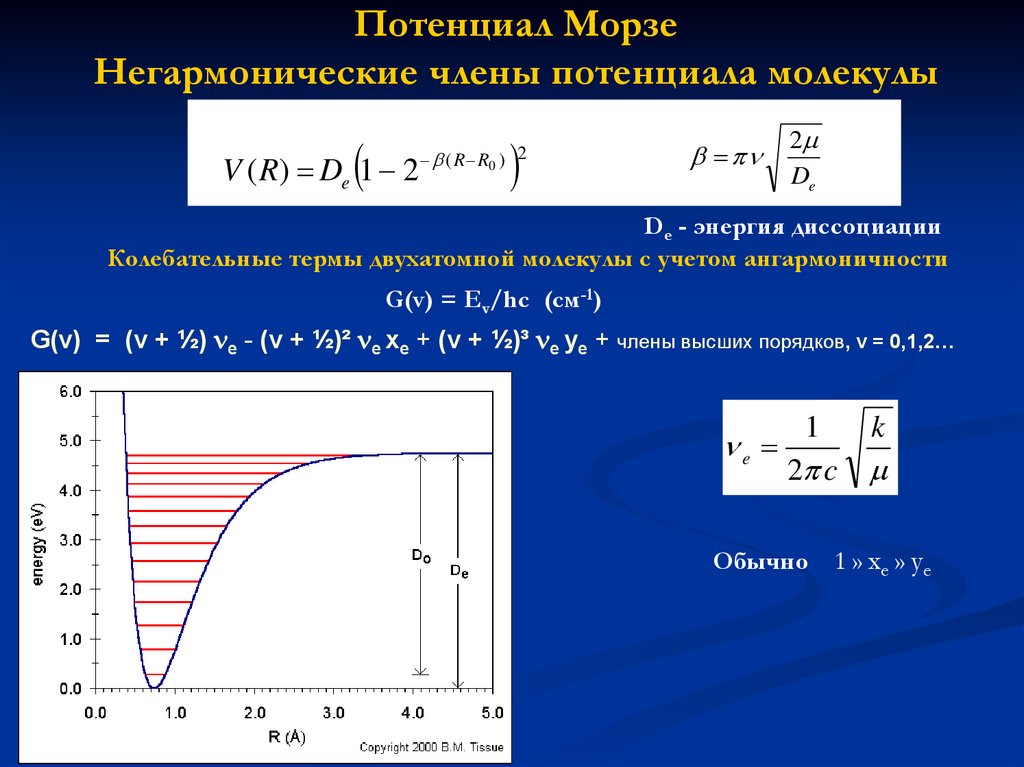
Потенциал Морзе
Негармонические члены потенциала молекулы
V ( R) De 1 2
( R R0 ) 2
2
De
De - энергия диссоциации
Колебательные термы двухатомной молекулы c учетом ангармоничности
G(v) = Ev/hc (cм-1)
G(v) = (v + ½) e - (v + ½)² e xe + (v + ½)³ e ye + члены высших порядков, v = 0,1,2…
e
1
k
2 c
Обычно 1 » xe » ye

80.

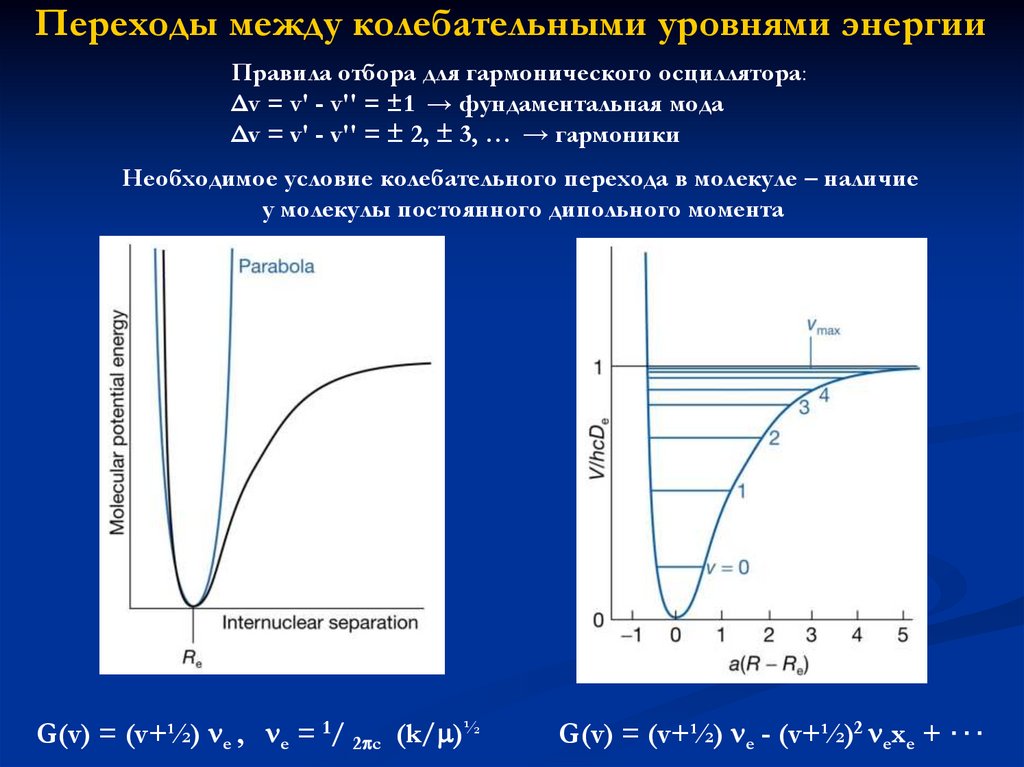
Переходы между колебательными уровнями энергии
Правила отбора для гармонического осциллятора:
Δv = v' - v'' = ±1 → фундаментальная мода
Δv = v' - v'' = ± 2, ± 3, … → гармоники
Необходимое условие колебательного перехода в молекуле – наличие
у молекулы постоянного дипольного момента
G(v) = (v+½) e , e = 1/ 2 c (k/ )½
G(v) = (v+½) e - (v+½)2 exe + ⋅⋅⋅

81.

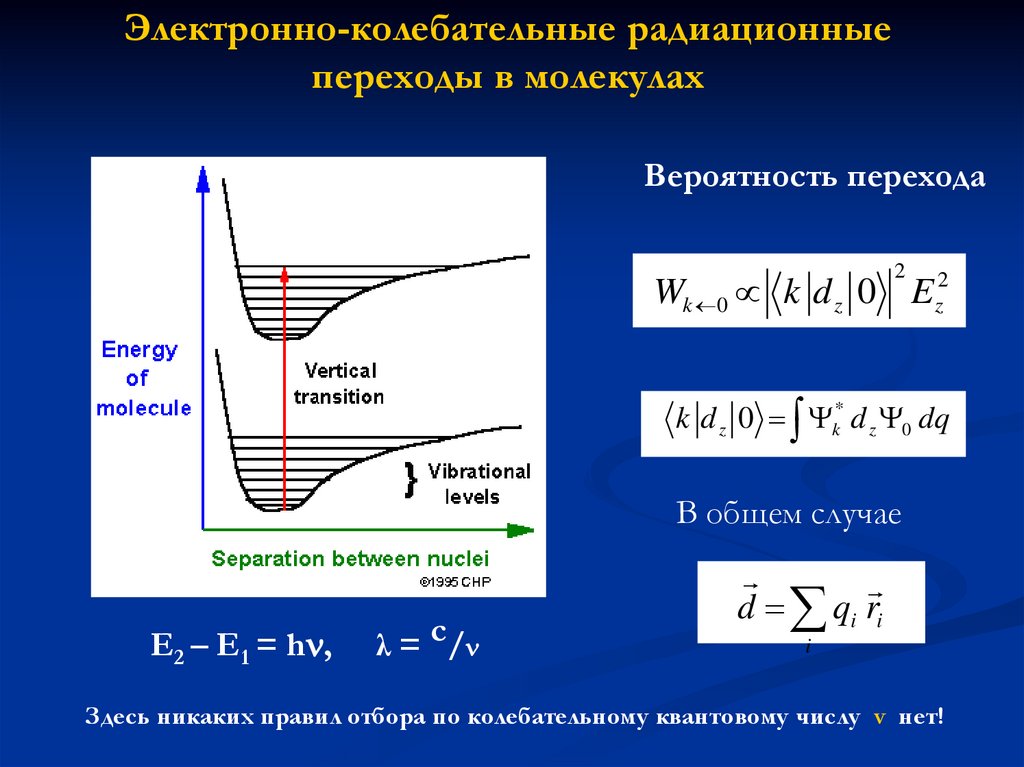
Электронно-колебательные радиационные
переходы в молекулах
Вероятность перехода
2
Wk 0 k d z 0 Ez2
k d z 0 k* d z 0 dq
В общем случае
E2 – E1 = h ,
λ = c/
d qi ri
i
Здесь никаких правил отбора по колебательному квантовому числу v нет!

82.

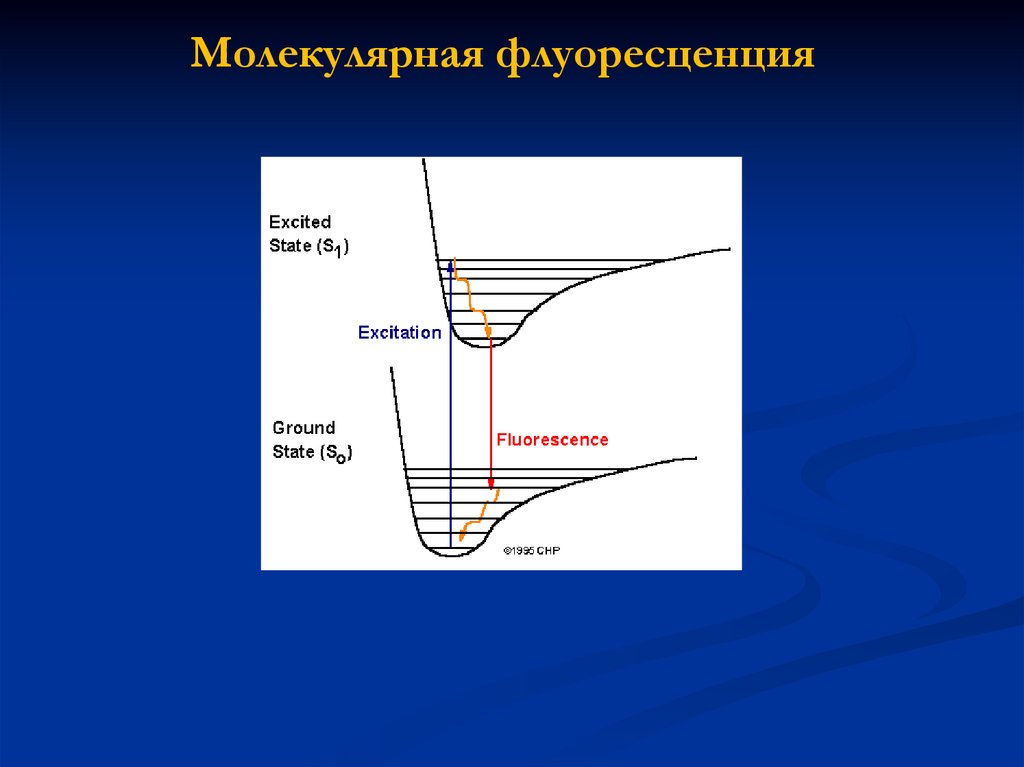
Молекулярная флуоресценция

83.

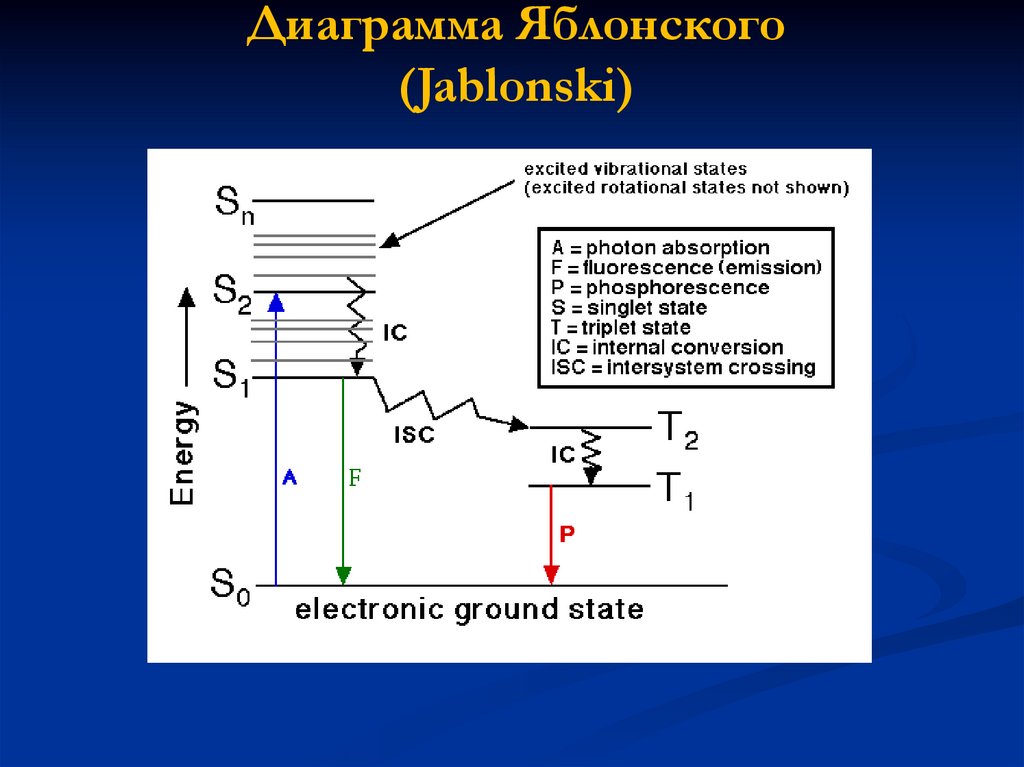
Диаграмма Яблонского
(Jablonski)

84.

Вращательные спектры в молекулах
1. Линейный ротатор
момент инерции
I 2
EK
I M 1r12 M 2 r22 r 2
2
L I
L2
EK
2I
Классическая механика:
ˆ2
L2
L
EK
Hˆ
2I
2I
где
M 1M 2
M1 M 2
Квантовая механика:
2
1
1
ˆ ,
L
sin
2
2
sin
sin
2
2
Hˆ YJM ( , ) EJ YJM ( , )
Волновые функции: YJM ( , )
2
Уровни энергии: E J
J ( J 1)
2I

85.

2. Объект произвольной формы
Классическая механика
Тензор инерции
В системе центра масс
J x I xx
J m(i ) [r (i ) v (i ) ] v (i ) r (i ) J y I yx
i
J I
z zx
I xy
I yy
I zy
I xz x
I yz y
I zz z
I kk m(i ) [r (i ) rk(i ) rk(i ) ]
2
i
I lk I kl m(i ) rl(i ) rk(i )
i
В системе главных осей молекулы A, B, C тензор инерции диагонален: Ilk = 0, если l ≠ k
J A I AA A , J B I BB B , J C I CC C
J C2
1
J A2
J B2
Ek J
2
2I A 2I B 2IC
(i )
I A m(i ) [rB(i ) rC(i ) ] m(i ) rBC
2
2
i
JA, JB, JC - проекции углового момента на главные оси
i
2

86.

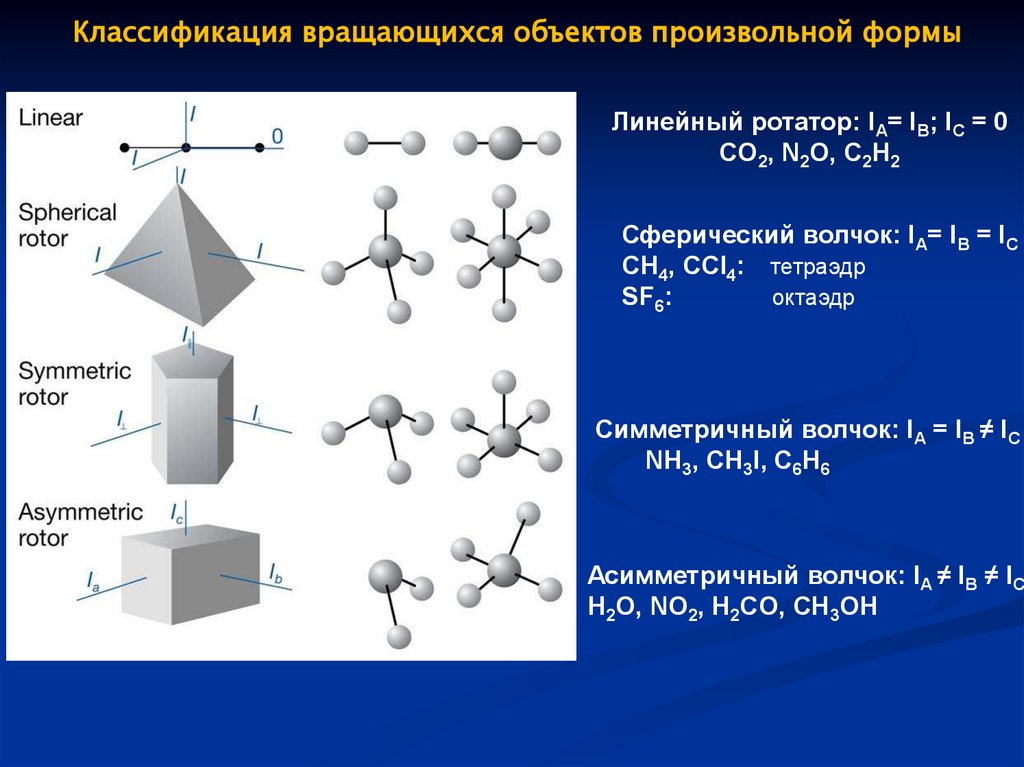
Классификация вращающихся объектов произвольной формы
Линейный ротатор: IA= IB; IC = 0
CO2, N2O, C2H2
Сферический волчок: IA= IB = IC
CH4, CCl4: тетраэдр
SF6:
октаэдр
Симметричный волчок: IA = IB ≠ IC
NH3, CH3I, C6H6
Асимметричный волчок: IA ≠ IB ≠ IC
H2O, NO2, H2CO, CH3OH

87.

Сферический волчок: IA = IB = IC = I
J A2 J B2 J C2 J 2
E
2I
2I
Переход к квантовой механике:
J 2 2 J ( J 1)
Вращательная постоянная
2
EJ
J ( J 1)
2I
B
(cm 1 )
4 c I
EJ h c B J ( J 1)
Вращательный терм:
F ( J ) B J ( J 1)
cm-1

88.

Симметричный волчок: IA = IB = I , IC = I‖, I I‖
I > I‖ → вытянутый волчок, I < I‖ → сплюснутый волчок
J A2 J B2 J C2
J2
1
2 1
E
JC
2I
2 I || 2 I
2 I || 2 I
где J2 = JA2 + JB2 + JC2 – квадрат полного момента вращения
Переход к квантовой механике:
2
J
1
2 1
ˆ
H
J ||
2I
2 I || 2 I
1
2
1
Уровни энергии: E JK
J ( J 1) 2 K 2
2I 2I
2I
||
Волновые функции:
*
J
JKM
DMK
( , , )
DMJ 0 ( , , )
Вращательный терм может быть представлен в виде:
FJK B J ( J 1) ( A B) K 2
где A и B – две вращательные константы:
A
4 cI ||
B
4 cI
4 *
YJM ( , )
2J 1

89.

Аргументы D-функции Вигнера - углы Эйлера
J
MK
D
( , , )

90.

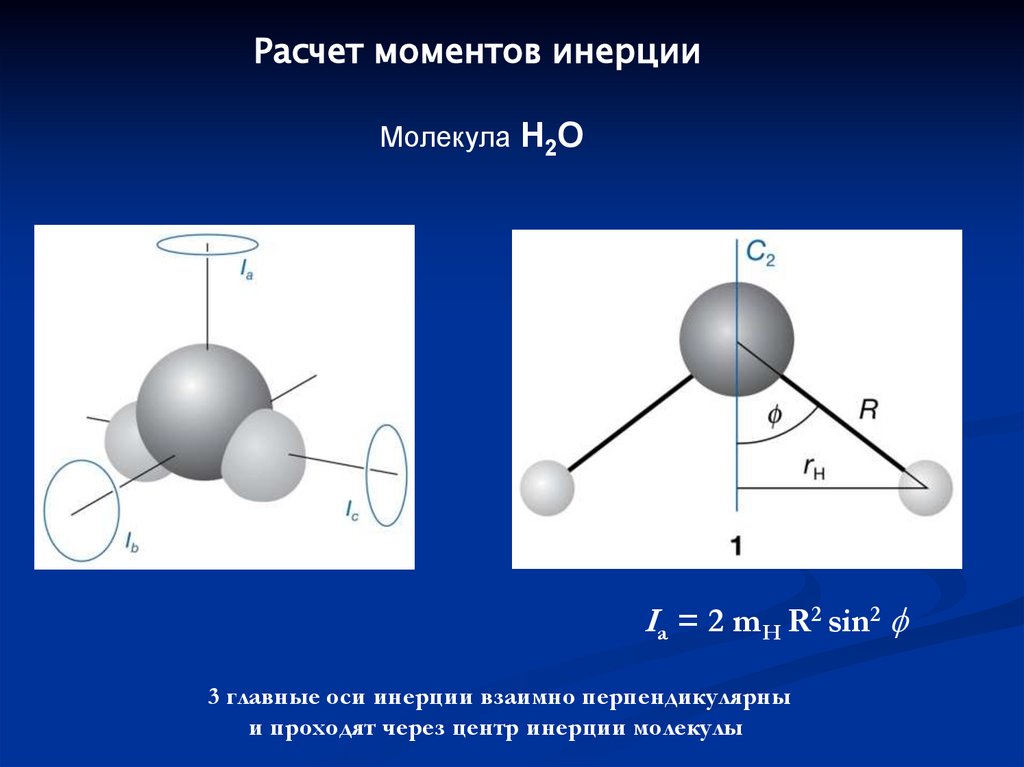
Расчет моментов инерции
Молекула H2O
Ia = 2 mH R2 sin2
3 главные оси инерции взаимно перпендикулярны
и проходят через центр инерции молекулы

91.

Симметричный волчок: роль квантовых чисел K и MJ
F(J) = BJ(J+1) + (A – B)K2
Уровни энергии
(вытянутый волчек)
Роль квантового числа K
Роль квантового числа MJ

92.

Симметричный волчок: частные случаи
|K| ≈ J
FJ, K = B⋅ J + A⋅J2 ≈ A⋅ J2
|K| = 0
FJ = B⋅ J (J+1)
Это случай большинства двухатомных молекул
Нежесткий волчок
FJ ≈ B⋅ J (J+1) - D⋅J2(J+1)2 + ⋅⋅⋅
где D – константа центоробежного возмущения, обычно D ≪ B.

93.

Асимметричный волчок: IA ≠ IB ≠ IC
J C2
J A2
J B2
ˆ
H
AJ A2 BJ B2 CJ C2
2I A 2I B 2I C
Hˆ JMk ( , , ) EJ JMk ( , , )
Волновые функции:
JMk ( , , ) A D
k
K
J *
MK
( , , )
K
Уравнение Шредингера:
Секулярное уравнение:
k
k
A
H
E
A
K K 'K
K K 'K
K
H K 'K E K 'K 0

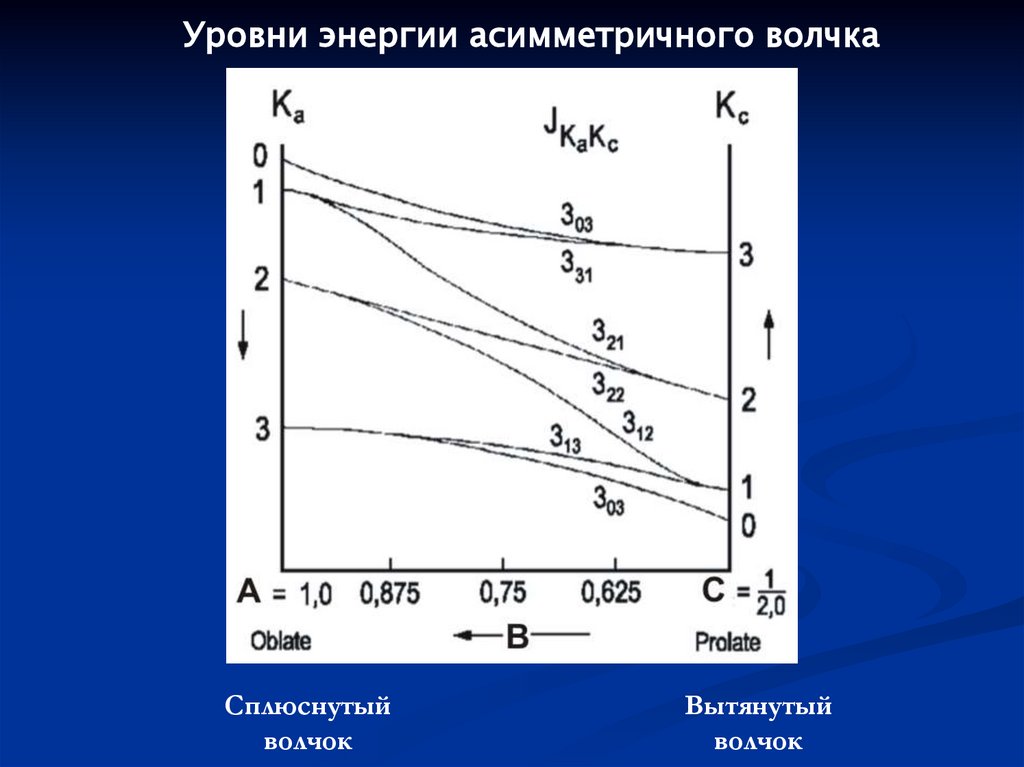
94.

Уровни энергии асимметричного волчка
Сплюснутый
волчок
Вытянутый
волчок

95.

Чисто вращательный спектр в молекулах
Условие существования вращательных переходов:
Электрический дипольный момент молекулы должен быть отличен от нуля!
→ В частности, в гомоядерных двухатомных молекулах и молекулах типа
сферического волчка вращательные переходы запрещены
Общие правила отбора:
ΔJ =± 1 ΔMJ = 0, ±1
ΔJ = 1 absorption
ΔJ = - 1 emission
Дополнительное правило отбора для
молекул типа симметричного волчка:
ΔK = 0
Частоты переходов:
FJ = B⋅(J+1)(J+2) – B⋅J(J+1) = 2B(J+1)
ΔFJ = 2B
Обычно B ~ 0.1 – 10 cm-1 и соответствующие частоты переходов лежат в
микроволновой области спектра

96.

Интенсивности во вращательных спектрах
I C g J ( N J N J ) v' , J ' M J ' DZ v, J , M J
N J N0 e
2
EJ
kT
где gJ – кратность вырождения
соответствующего вращательного
уровня энергии |v, J, MJ >
EJ = h c B J(J+1)

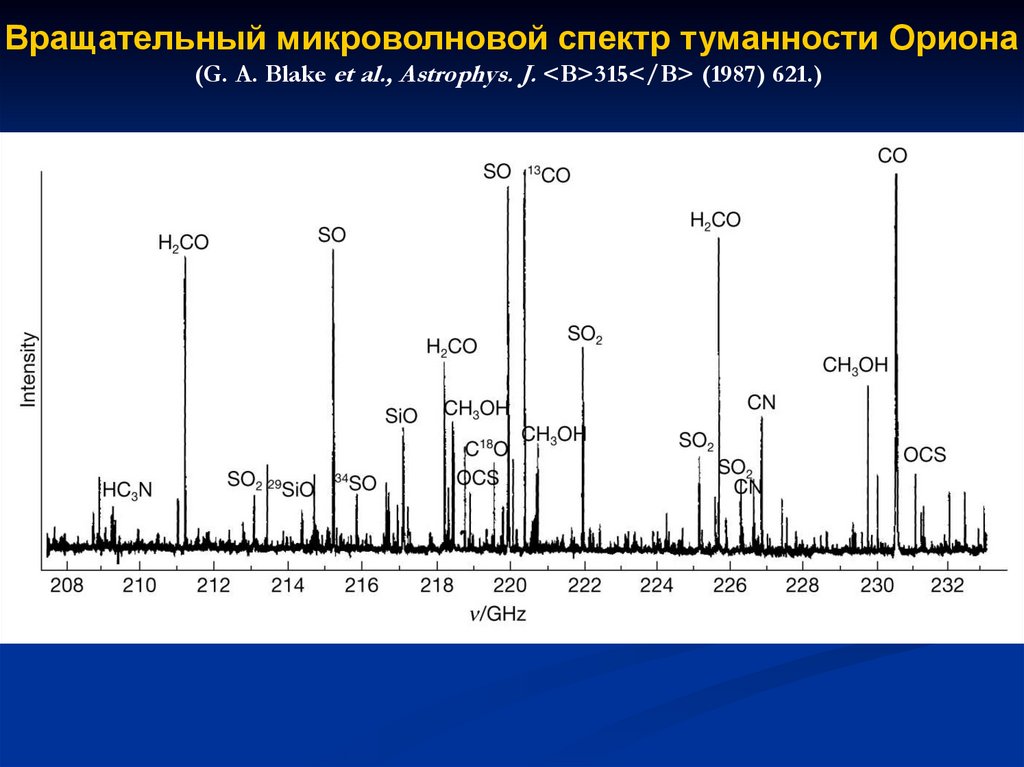
97.

Вращательный микроволновой спектр туманности Ориона
(G. A. Blake et al., Astrophys. J. <B>315</B> (1987) 621.)

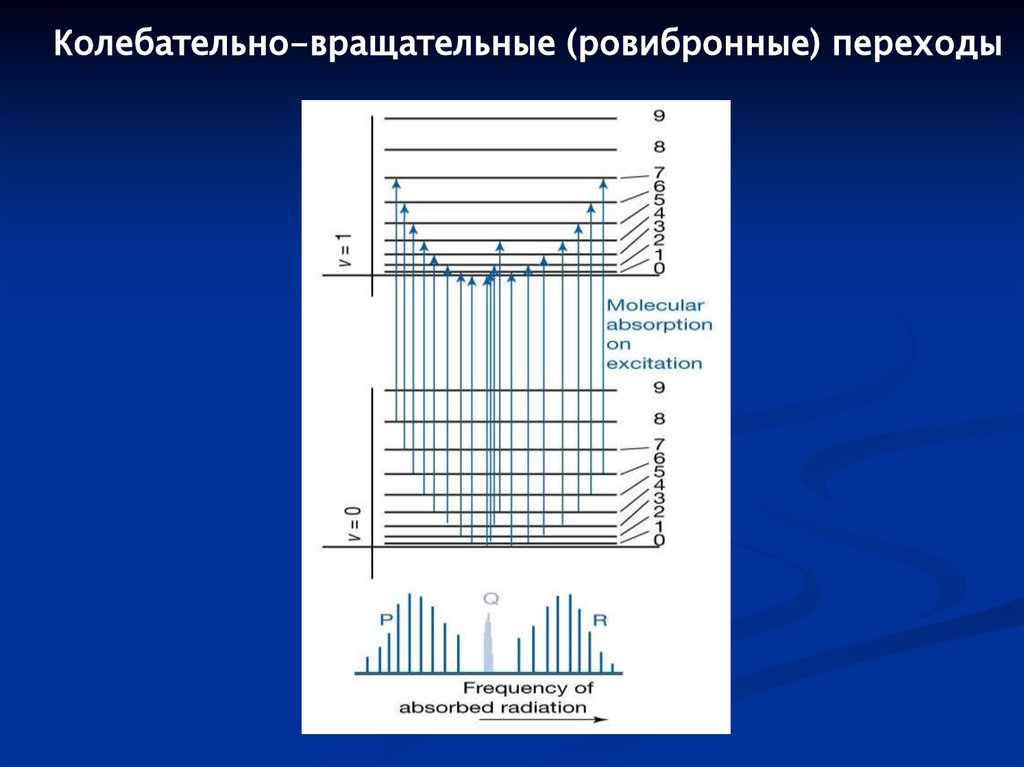
98.

Колебательно-вращательные (ровибронные) переходы

99.

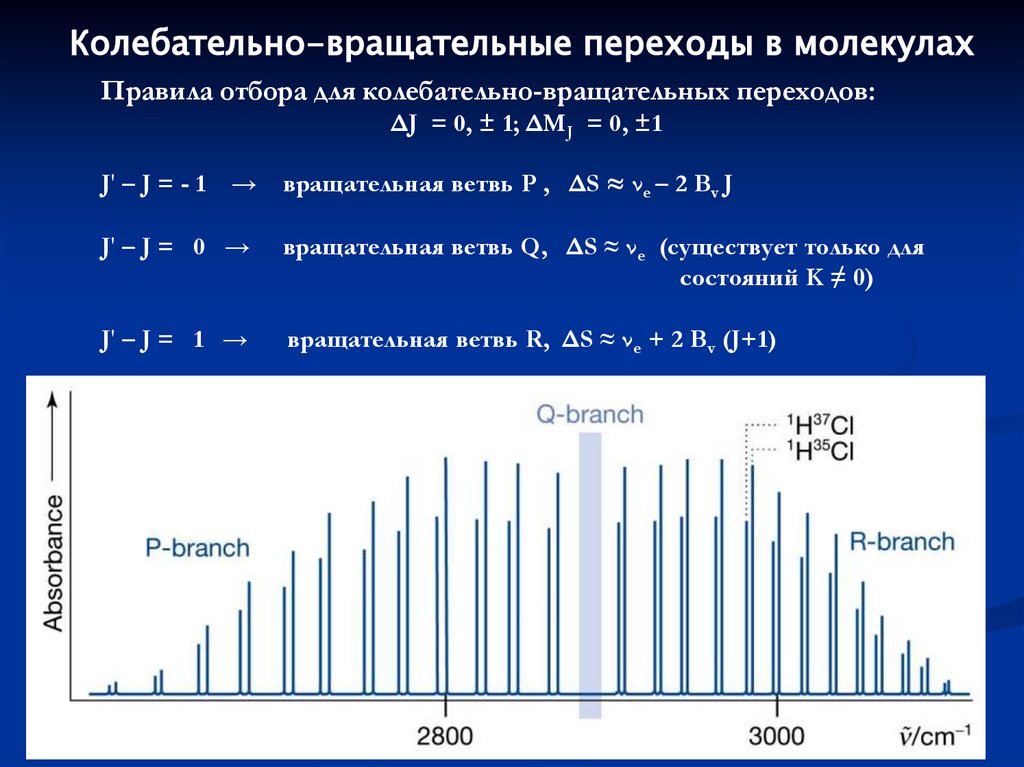
Колебательно-вращательные переходы в молекулах
Правила отбора для колебательно-вращательных переходов:
ΔJ = 0, ± 1; ΔMJ = 0, ±1
J' – J = - 1
→ вращательная ветвь P , ΔS ≈ νe – 2 Bv J
J' – J = 0 →
вращательная ветвь Q, ΔS ≈ νe (существует только для
состояний K ≠ 0)
J' – J = 1 →
вращательная ветвь R, ΔS ≈ νe + 2 Bv (J+1)

100.

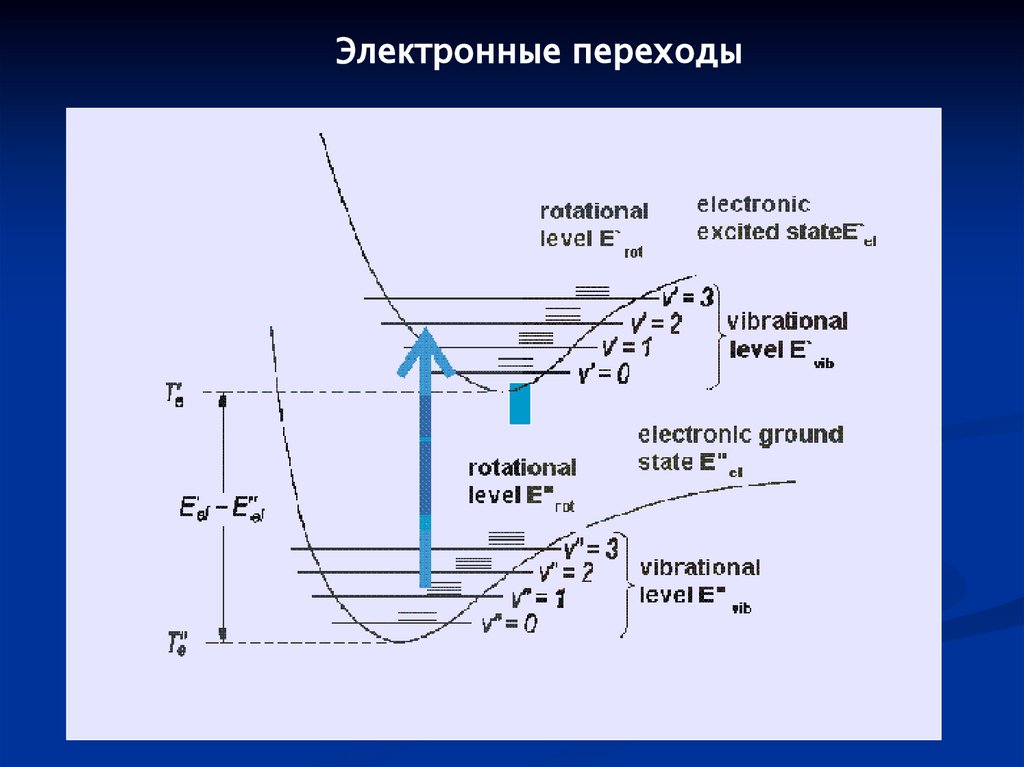
Электронные переходы

101.

Спектры электронных переходов в молекулах
E = Eel + Evib + Erot
Молекулярный терм:
Ee,v,J = Te + e (v+½) +Bv J(J+1),
где Te – минимум на потенциальной кривой
Волновая функция: Ψ = Ψnel Ψvvib ΨJrot
Частоты переходов:
Δ = Te' – Te''+ e' (v'+½) – e'' (v''+½) +Bv' J'(J'+1) – Bv'' J''(J''+1)
= el + vib + rot
Обычно: el » vib » rot

102.

Квантовые числа, характеризующие электронные
состояния двухатомных молекул
1.
2.
3.
4.
5.
Λ проекция полного электронного орбитального момента L на ось молекулы
S полный электронный спин
Σ проекция полного спина S на ось молекулы
Ω = Λ + Σ проекция полного момента J на ось молекулы
σ = ±1, симметрия при отражении электронной волновой функции
в плоскости, проходящей через ось молекулы (только для Λ = 0 состояний)
6. g, u симметрия при инверсии электронной волновой функции в центре молекулы
(только для гомоядерных молекул)
Обычно электронные термы обозначаются след. образом: 2S+1ΛΩ , или 2S+1ΛΩσ, или 2S+1Λg,u
Обозначения:
Термы с Λ=0,1,2 обозначаются как: Σ, Π, Δ
Термы с S=0 называются синглеты
Термы с S=1 называются триплеты

103.

Правила отбора для электронных переходов
в двухатомных молекулах
Разрешенные
переходы
Примеры
ΔΛ = 0, ±1
Σ ↔ Σ, Π ↔ Π,
Σ ↔ Π, Δ ↔ Π
ΔS = 0
1Σ ↔ 1Σ, 3Π ↔ 3Π,
3Σ ↔ 3Π, 1Δ ↔ 1Π
+↔+
–↔–
Σ+ ↔ Σ +
Σ- ↔ Σ -
g↔u
Σg+ ↔ Σu+, Σg ↔ Πu

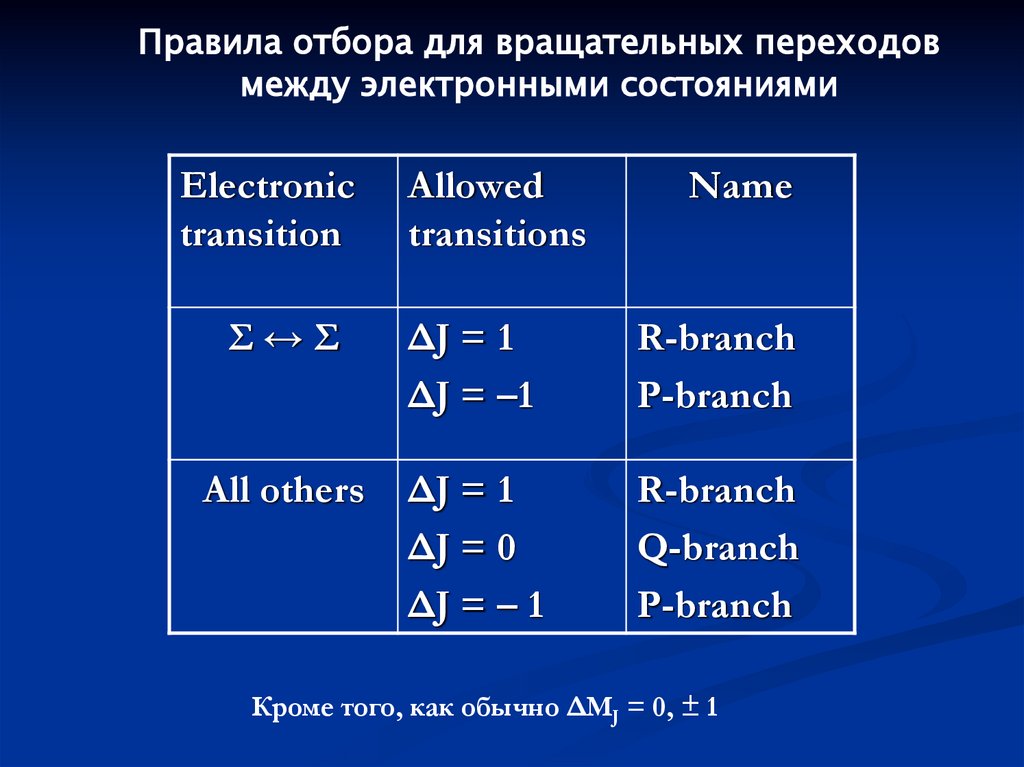
104.

Правила отбора для вращательных переходов
между электронными состояниями
Electronic
transition
Allowed
transitions
Name
Σ↔Σ
ΔJ = 1
ΔJ = –1
R-branch
P-branch
All others
ΔJ = 1
ΔJ = 0
ΔJ = – 1
R-branch
Q-branch
P-branch
Кроме того, как обычно ΔMJ = 0, ± 1

105.

Принцип Франка-Кондона (Frank-Condon):
Оптические переходы в молекулах преимущественно
происходят без изменения межъядерного расстояния
Обычно не существует никаких правил
отбора для колебательного квантового
числа v при электронных переходах:
v ' - v = любое целое число
Ψ = Ψe Ψv Ψrot
W ~ |<Ψf|DZ|Ψi>|2 ≈
≈ |<Ψv'|Ψv>|2 |<Ψe'ΨJ'|DZ|Ψe'ΨJ>|2
Интеграл перекрытия (фактор Франка-Кондона)

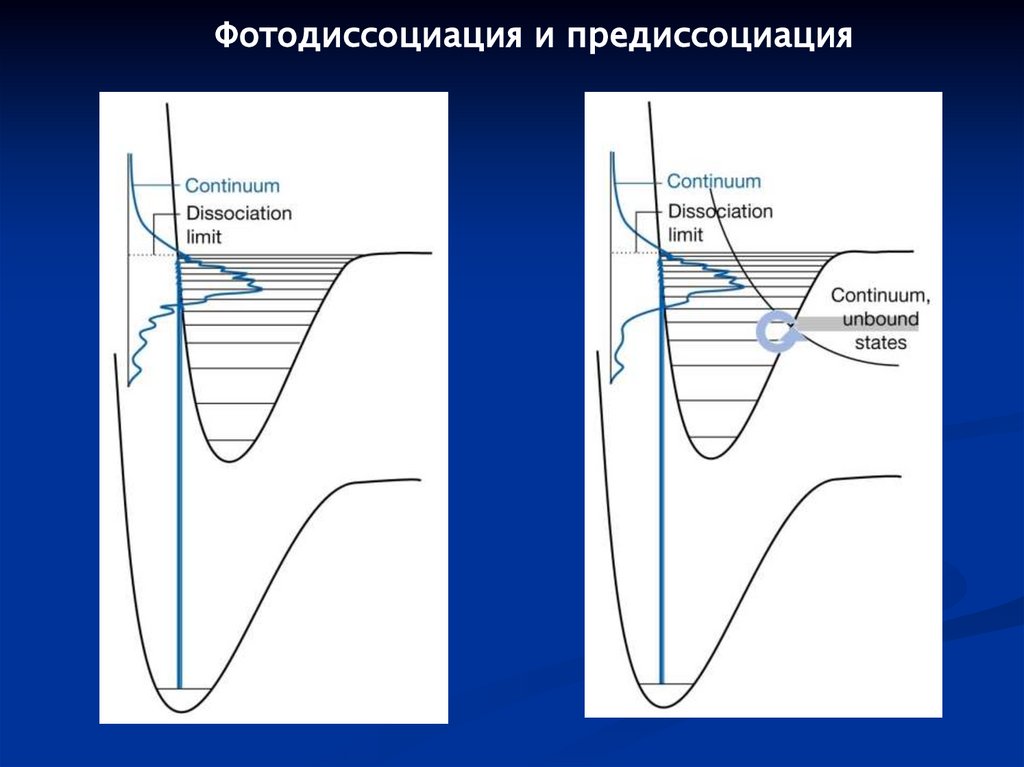
106.

Фотодиссоциация и предиссоциация

107.

Примеры фотодиссоциации
• Фотодиссоциация молекул озона УФ излучением
с длиной волны = 200 – 300 нм
A+B
O3 h O2 (1 g ) O(1D2 )
• Фотодиссоциация молекул кислорода ВУФ
излучением с длиной волны ≤ 175 нм
O2 h O(3Pj ) O(1D2 )
AB*
• Образование фотохимического смога:
фотодиссоциация NO и NO2 излучением с
длиной волны > 290 нм
NO2 h NO O( 3PJ )
• Разрушение стратосферного озона излучением
с длиной волны < 230 нм
AB
CCl2 F2 h CClF2 Cl
Cl O3 ClO O2

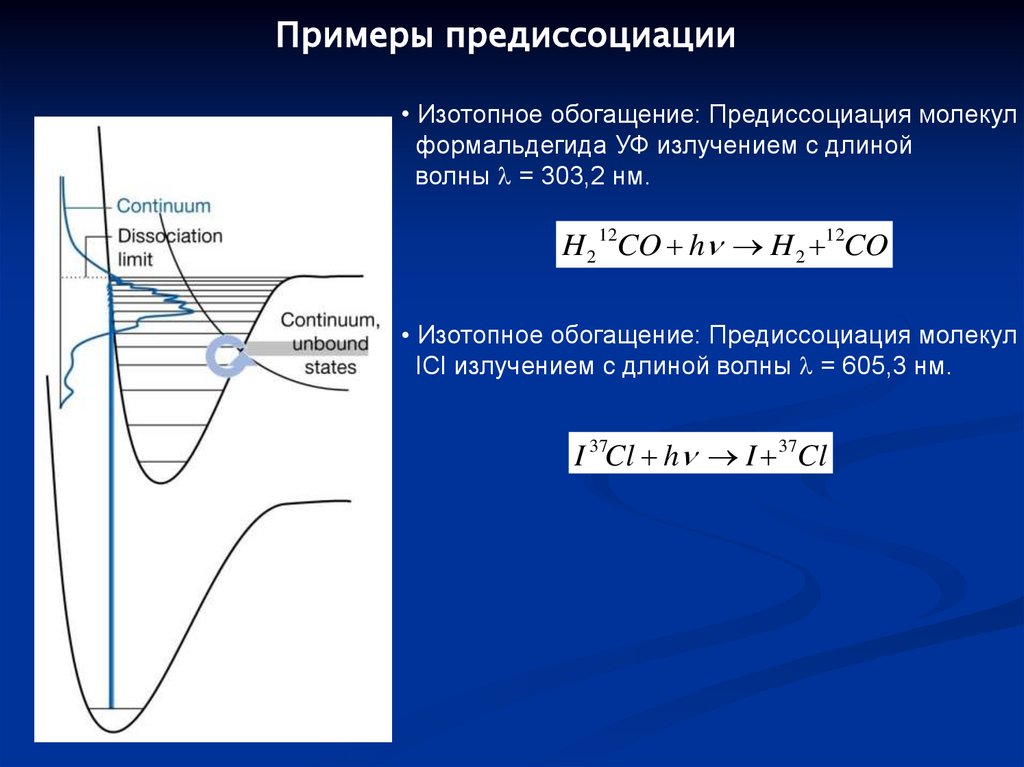
108.

Примеры предиссоциации
• Изотопное обогащение: Предиссоциация молекул
формальдегида УФ излучением с длиной
волны = 303,2 нм.
H 2 12CO h H 2 12CO
• Изотопное обогащение: Предиссоциация молекул
ICl излучением с длиной волны = 605,3 нм.
I 37Cl h I 37Cl

109.

Многофотонные переходы
Рассеяние фотона на молекуле:
hνi + M(Ei) → hνs + M(Es)
Если νi = νs , то это релеевское рассеяние (Rayleigh Scattering)
Если νi > νs , то это стоксовское рассеяние (Stokes Scattering)
Если νi < νs , то это антистоксовское рассеяние (anti-Stokes
Scattering)
В общем случае переход под действием каждого из фотонов не является
резонансным, Ev – Ei ≠ hνi , Ev – Ef ≠ hνs а соответствующее верхнее
состояние называется виртуальным.

110.

Комбинационное рассеяние в молекулах:
рамановское рассеяние
Необходимым условием существования Рамановских переходов является наличие в молекуле
анизотропной поляризуемости. Это значит, что под действием мощного электрического
поля лазерного излучения Е молекула приобретает наведенный электрический
дипольный момент:
din = α E
Большинство молекул, как гетероядерные, так и гомоядерные, обладают анизотропной
поляризуемостью и обладают Рамановской активностью. В то же время атомы, как
изотропные частицы, Рамановской активностью не обладают. Правила отбора для чисто
вращательных переходов в молекулах следующие:
Линейные ротаторы: Δ J = 0, ± 2.
Симметричные волчки: Δ J = 0, ± 1, ± 2 ; Δ K =0.
Шаровые волчки: не активны
Кроме того, переходы Δ J = 0 не приводят к изменению частоты рассеянного излучения и
Соответственно они дают вклад только в релеевское рассеяние.
Для колебательно-вращательных рамановских переходов правила отбора по J те-же.
Переходы между состояниями с Δυ = 1 – стоксовские, а переходы между состояниями с
Δυ = -1 – антистоксовские. Переходы с ΔJ = 0 называются Q ветвью, переходы с ΔJ = -2
называются О ветвью, а переходы с ΔJ = 2 называются S ветвью.

111. C. V. Raman, Л. И. Мандельштам, Г. С. Ландсберг

Chandrasekhara Venkata Raman
* 7 Nov. 1888 in Trichinopoly (India)
+ 21 Nov. 1970 Karnataka (India)
1930 Nobel price for Physics
Леонид Исаакович Мандельштам
* 22 Апр. 1879, Могилев
+ 27 Нояб. 1944, Москва
Григорий Самуилович Ландсберг
* 10 Янв. 1890, Вологда
+ 2 Февр. 1957, Москва

112.

Комбинационное рассеяние и двухфотонное поглощение
с точки зрения квантовой механики
Вероятность комбинационного рассеяния:
WR C2
i
f d2 i
2
i d1 g
i / 2 i / 2
ig
1
i
ig
2
i
Где константа С2 пропорциональна квадрату интенсивности
электромагнитного излучения.
Родственный эффект – двухфотонное
поглощение в атомах, молекулах, и
конденсированных средах.
REMPI 2+1
Обычно вероятность двухфотонного
поглощения на несколько порядков
меньше вероятности однофотонного
поглощения, поэтому для достижения
необходимой плотности
электромагнитного излучения луч
лазера обычно фокусируют.

113.

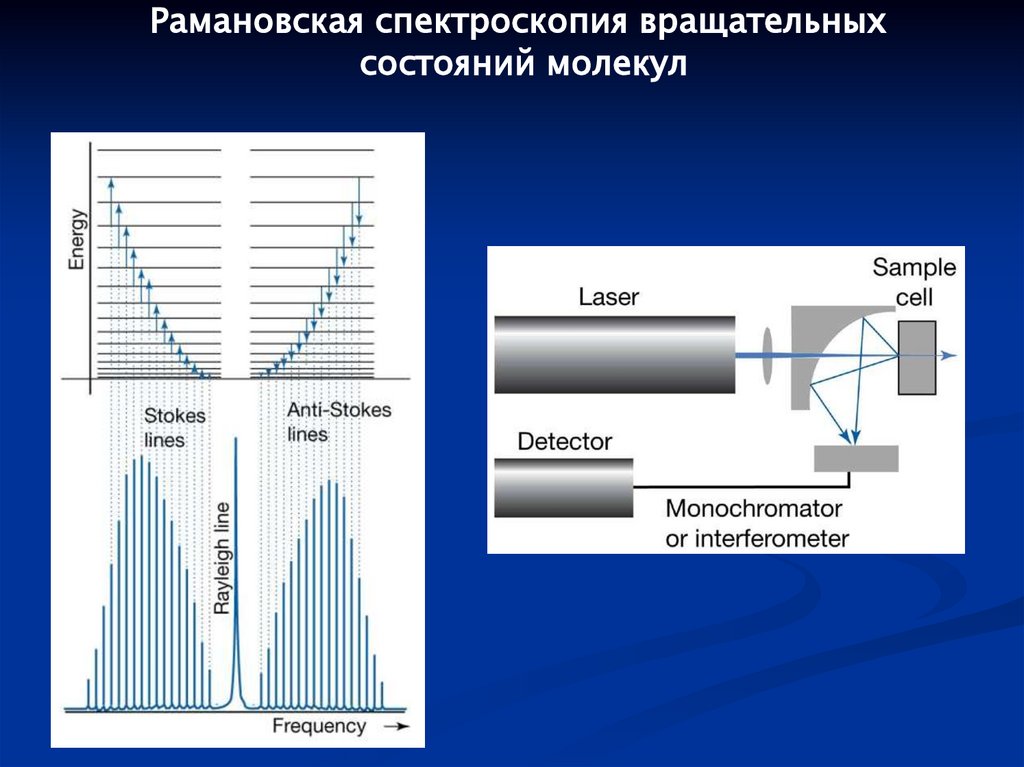
Рамановская спектроскопия вращательных
состояний молекул

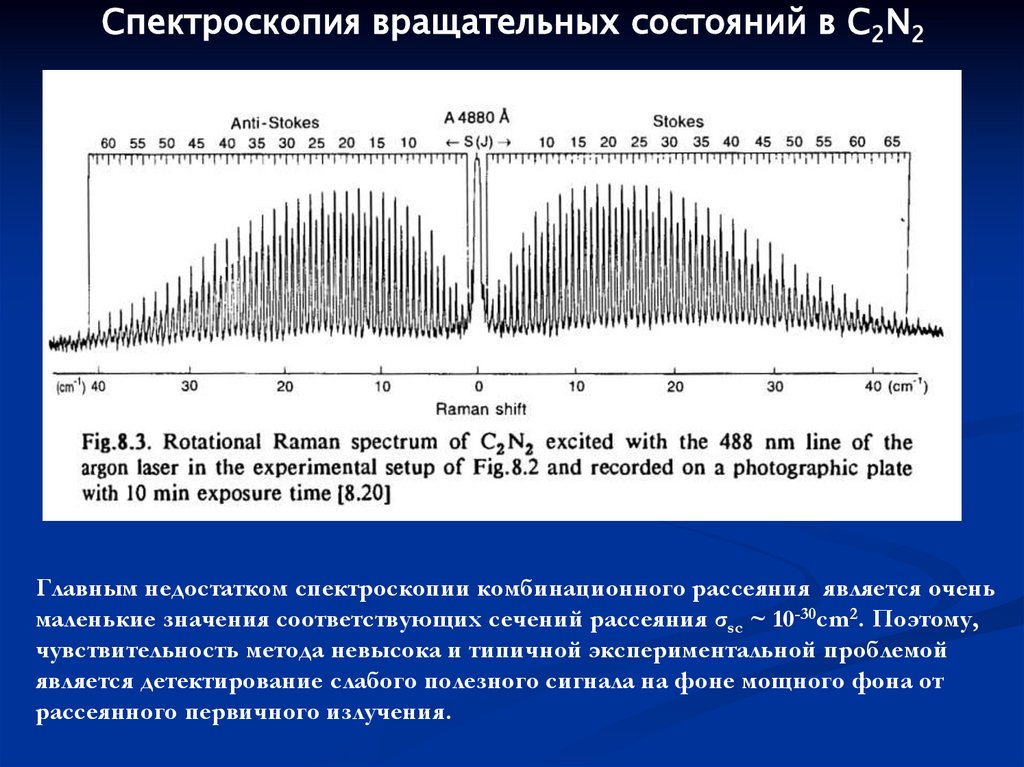
114.

Спектроскопия вращательных состояний в C2N2
Главным недостатком спектроскопии комбинационного рассеяния является очень
маленькие значения соответствующих сечений рассеяния σsc ~ 10-30cm2. Поэтому,
чувствительность метода невысока и типичной экспериментальной проблемой
является детектирование слабого полезного сигнала на фоне мощного фона от
рассеянного первичного излучения.

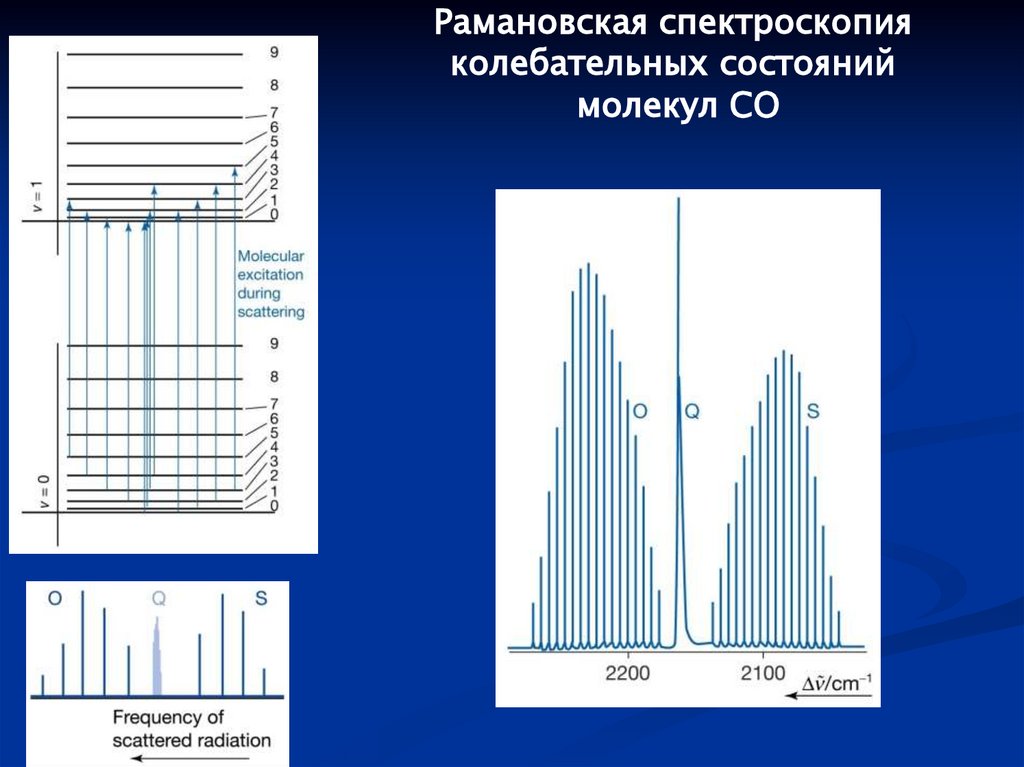
115.

Рамановская спектроскопия
колебательных состояний
молекул CO