Элементы статистической физики. (Лекция 8)

1.

Кафедра физики
ЛЕКЦИЯ 8
Элементы статистической физики
ПЛАН ЛЕКЦИИ
1. Функция распределения.
2. Распределение проекции скорости.
3. Распределение модуля скорости.
1

2.

Кафедра физики
Некоторые сведения из лекции 6 «основы молекулярнокинетической теории газов»:
газов»
Два метода описания свойств макросистем:
Термодинамика - устанавливает Статистическая
связи
между
непосредственно
измеряемыми в макроскопических
опытах величинами (объемом,
температурой, давлением и т.д.).
физика
-основана
на
модельных
представлениях о строении
макротел и математической
статистике.
Общая физика. "Основы молекулярно-кинетической теории газов"
2

3.

Δ
x
0
Δ
W
0
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ
ФИЗИКИ
Кафедра физики
Функция распределения
Пусть
X
- случайная величина,
x; x Δx - некоторый интервал значений этой величины.
Попадание значения X в этот интервал – событие случайное.
ΔW - вероятность этого события, зависит от ширины
интервала x.
Общая физика. «Элементы статистической физики»
3

4.

Δ
xΔ
Δ
W
x
fΔ
W
W
Δ
x
;
x
Δ
x
fx Δ
Кафедра физики
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ
Функция распределения
При малых
друг другу:
величины
и
пропорциональны
От чего зависит
? От того, в каком месте оси
ОХ располагается интервал
.
Следовательно, коэффициент пропорциональности
f есть функция от х:
Общая физика. «Элементы статистической физики»
4

5.

Δ
W
f
x
Δ
fxf x Δ
W
x
Кафедра физики
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ
Функция распределения
- функция распределения.
Функция распределения есть величина, численно равная
вероятности того, что значение случайной величины X
попадет
в
единичный
интервал,
расположенный в
окрестностях точки x.
Функция распределения
вероятности.
еще
Общая физика. «Элементы статистической физики»
называется
плотностью
5

6.

Кафедра физики
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ
Вероятность микросостояния.
Все микропараметры системы - величины случайные.
Максимальная информация о макросостоянии системы содержится в
функциях распределения всех её микропараметров.
Рассмотрим конкретную систему и конкретное её макросостояние:
системой будет идеальный газ;
состояние системы – равновесное.
Состояние этой системы полностью определяют координаты и
скорости всех её молекул. Поэтому надо найти функции
распределения координат и скоростей.
Рассмотрим чистый одноатомный идеальный газ.
Общая физика. «Элементы статистической физики»
6

7.

Кафедра физики
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ
Вероятность микросостояния.
Чистым газом называется газ, состоящий из одинаковых молекул.
Иными словами, он представляет собой химически чистое вещество.
Молекула
чистого
степенями свободы.
газа
обладает
тремя
Микросостояние молекулы с тремя степенями свободы – это набор
трёх координат (x, y, z) и трёх проекций скорости (vx, vy, vz). Задача
состоит в поиске шести функций распределения.
Рассмотрим две задачи:
Функции распределения скоростей (vx, vy, vz).
Функции распределения координат.
Общая физика. «Элементы статистической физики»
7

8.

Кафедра физики
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ
Распределение
Максвелла)
проекции
скорости
(распределение
Распределение скоростей молекул в равновесном идеальном газе
называется распределением Максвелла.
В основе распределений - два постулата Максвелла:
1. Постулат независимости
Три декартовые компоненты скорости молекулы vx, vy и vz являются
независимыми случайными величинами и имеют одну и ту же
функцию распределения.
2. Постулат нормальности
Распределение проекции скорости молекулы является нормальным
(самый распространённый вид распределения):
2
k – постоянная Больцмана
mv x
m
f(v x )
exp
2 kT
2kT
Общая физика. «Элементы статистической физики»
8

9.

Кафедра физики
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ
Распределение Максвелла
f vx
T1 < T2 < T3
Площадь под каждой из кривых одна
и та же, и равна 1. Это следует из
условия нормировки
T1
T2
f ( x )dx 1
T3
0
Общая физика. «Элементы статистической физики»
vx
9

10.

Кафедра физики
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ
Распределение Максвелла
Распределение модуля скорости
Зная функции распределения проекций скорости vx, vy, vz, можно
найти функцию распределения любого микропараметра, который
зависит от vx, vy, vz, – например модуля скорости v, связанного с vx,
vy, vz выражением:
v v x2 v 2y v z2
3
Конечный результат:
2
2
m
mv
2
f ( v ) 4
v exp
2 kT
2 kT
Эту формулу чаще всего и называют распределением Максвелла.
Общая физика. «Элементы статистической физики»
10

11.

Кафедра физики
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ
Распределение Максвелла
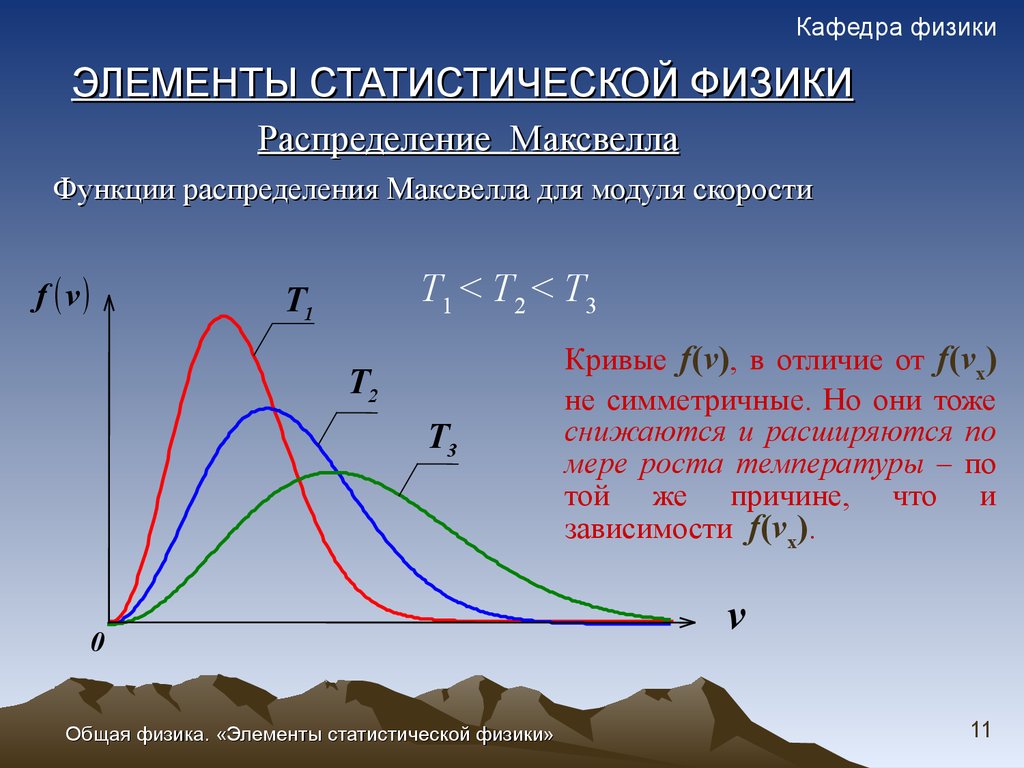
Функции распределения Максвелла для модуля скорости
f v
T1 < T2 < T3
T1
T2
T3
0
Общая физика. «Элементы статистической физики»
Кривые f(v), в отличие от f(vx)
не симметричные. Но они тоже
снижаются и расширяются по
мере роста температуры – по
той же причине, что и
зависимости f(vx).
v
11

12.

Кафедра физики
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ
f v
T1
Распределение Максвелла
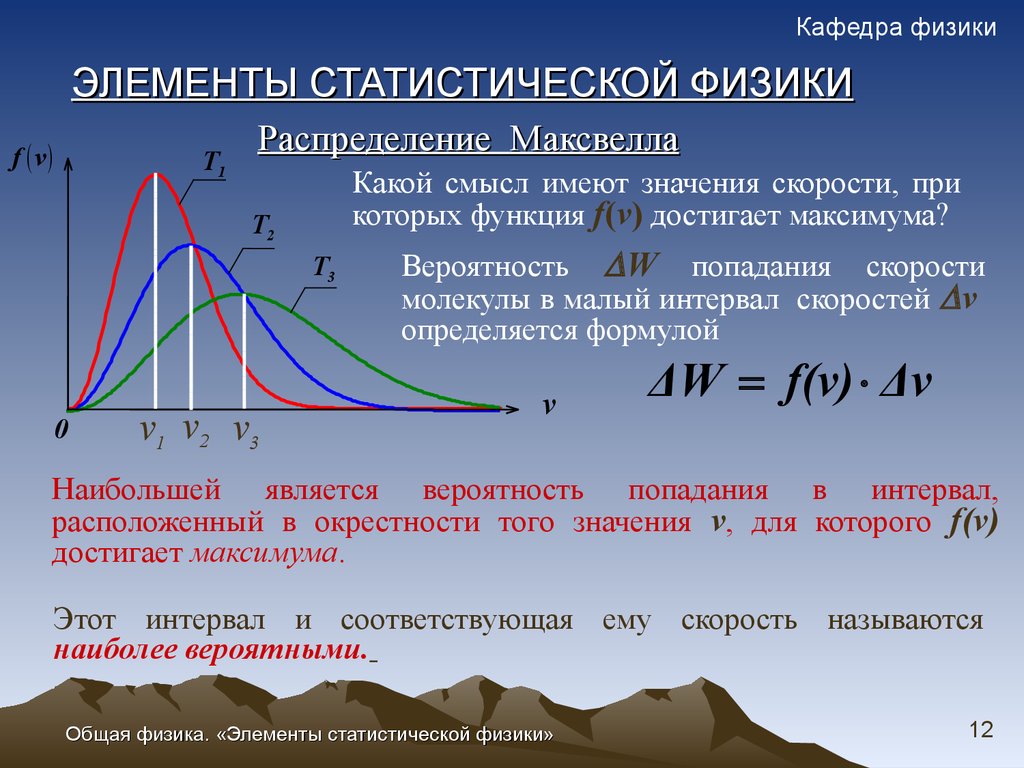
Какой смысл имеют значения скорости, при
которых функция f(v) достигает максимума?
T2
T3
0
v1 v2 v3
Вероятность W попадания скорости
молекулы в малый интервал скоростей v
определяется формулой
v
ΔW f(v) Δv
Наибольшей является вероятность попадания в интервал,
расположенный в окрестности того значения v, для которого f(v)
достигает максимума.
Этот интервал и соответствующая ему скорость называются
наиболее вероятными.
Общая физика. «Элементы статистической физики»
12

13.

Кафедра физики
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ
Распределение Максвелла
f v
T1
T2
Вычислим наиболее вероятную скорость vв,
используя правило нахождения экстремума
функции:
T3
0
v1 v2 v3
vв растёт с ростом температуры.
Наиболее вероятный интервал
скоростей v перемещается в
область более быстрых молекул.
Общая физика. «Элементы статистической физики»
df(v)
0
dv v vв
v Применение этого правила
приводит к следующему
результату:
2kT
vв
m
vв
2RT
μ
13

14.

Кафедра физики
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ
Распределение Максвелла
Кроме наиболее вероятной скорости в расчетных задачах часто
используют среднюю арифметическую и среднюю квадратичную
скорости:
8 kT
8 RT
v
m ,
3kT
3 RT
v ср .кв .
m
- средняя (средняя
арифметическая) скорость
- средняя квадратичная скорость
Общая физика. "Элементы статистической физики"
14

15.

Кафедра физики
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ
Распределение Максвелла
Сопоставление этих скоростей дает следующий результат:
vв : v : vср .кв . 2 : 8 : 3 = 1 : 1,13 : 1,22
f v
0
vв v v ср .кв .
Общая физика. "Элементы статистической физики"
v
15

16.

vu
m
в2kT
v
Кафедра физики
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ
Распределение Максвелла
Распределение относительной скорости
Перейдем от v к относительной скорости
u, которая определяется формулой:
Как и абсолютная скорость v, относительная u – случайная величина.
Функция распределения относительной скорости:
4 2
2
f(u)
u exp u
π
Общая физика. «Элементы статистической физики»
16

17.

Кафедра физики
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ
ЗАДАЧА 2. Распределение Больцмана
Найдем функции распределения координат.
Одномерная задача.
Функция распределения координаты x – это такая функция f(x),
умножение которой на ширину dx бесконечно малого интервала (x,
x+dx) даёт вероятность dW(x) того, что координата молекулы x
попадёт в этот интервал.
dW ( x ) f ( x )dx
Это вероятность попадания хаотически блуждающей в
пространстве молекулы в фиксированную область пространства
между двумя параллельными плоскостями, расположенными на
расстоянии dx друг от друга. Это бесконечно малая область.
Общая физика. "Элементы статистической физики"
17

18.

Кафедра физики
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ
Распределение Больцмана
Трехмерная задача. Методика решения.
Рассматривается бесконечно малая область пространства в виде
параллелепипеда (элементарный объём). Определяется вероятность
dW(x, y, z) попадания молекулы в фиксированный элементарный
объём, расположенный в окрестности точки с координатами (x, y, z).
y
Размеры элементарного объема
- dx, dy, dz ,
объём - dV = dx dy dz
dy
dz
z
dx
x
Общая физика. "Элементы статистической физики"
18

19.

Кафедра физики
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ
Распределение Больцмана
Решение задачи (без вывода):
Вероятность попадания молекулы в фиксированный элементарный
объём, расположенный в окрестности точки с координатами (x, y, z):
Wп ( x , y , z )
dW ( x , y , z ) B exp
dV
kT
Wп ( x , y , z )
- потенциальная энергия
Зная эту вероятность, можно определить среднее число молекул
<dN(x, y, z)> в элементарном объёме, находящемся в окрестности
точки с координатами (x, y, z).
Wп ( x , y , z )
dN x, y, z N B exp
dV
kT
N – полное число молекул в газе.
Общая физика. "Элементы статистической физики"
19

20.

Кафедра физики
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ
Распределение Больцмана
Wп ( x , y , z )
dN x, y, z N B exp
dV
kT
Отношение <N(x, y, z)>/dV – это концентрация молекул n
W ( x , y , z )
n( x , y , z ) NB exp п
kT
Пусть при n( x0 , y0 , z0 ) Wп (x, y, z) =0. Тогда n( x0 , y0 , z0 )= NB
Wп ( x , y , z )
n( x , y , z ) n( x0 , y0 , z0 ) exp
kT
W ( x , y , z )
n( x , y , z ) n0 exp п
kT
Общая физика. "Элементы статистической физики"
Это распределение
Больцмана.
20

21.

Кафедра физики
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ
Распределение Больцмана. Барометрическая формула
Построим модель атмосферы:
1. Температура воздуха с ростом высоты не меняется.
2. Воздух – это чистый идеальный газ.
3. Атмосфера – равновесная система.
p = nkT
W ( h )
mgh
n( h ) n0 exp п
n
exp
0
kT
kT
n0 – концентрация молекул на уровне Земли.
mgh
p (h) p0 exp
kT
Это барометрическая
формула.
p0 – давление у поверхности Земли.
Общая физика. "Элементы статистической физики"
21