Similar presentations:
Понятие корреляции. Прогнозирование на основании уравнения регрессии. Прогнозирование на основе кривой выживаемости
1. Лекция Методы прогнозирования д.б.н. Койчубеков Б.К.
2. План лекции
Понятие корреляцииПрогнозирование на основании
уравнения регрессии
Прогнозирование на основе кривой
выживаемости
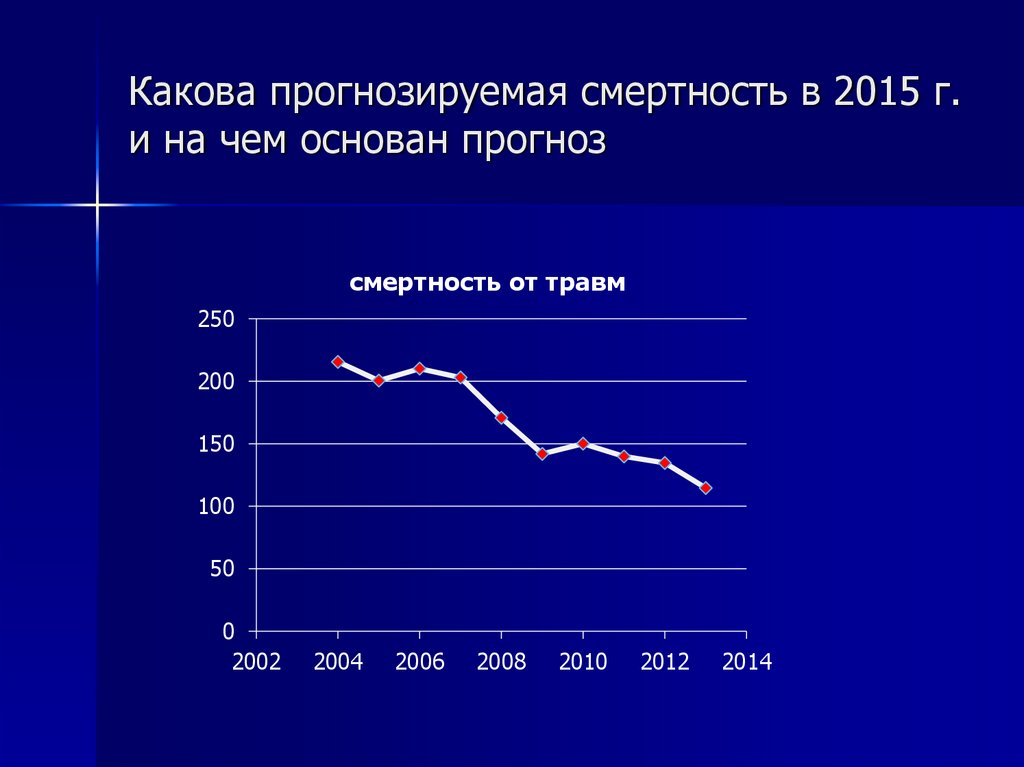
3. Какова прогнозируемая смертность в 2015 г. и на чем основан прогноз
смертность от травм250
200
150
100
50
0
2002
2004
2006
2008
2010
2012
2014
4.
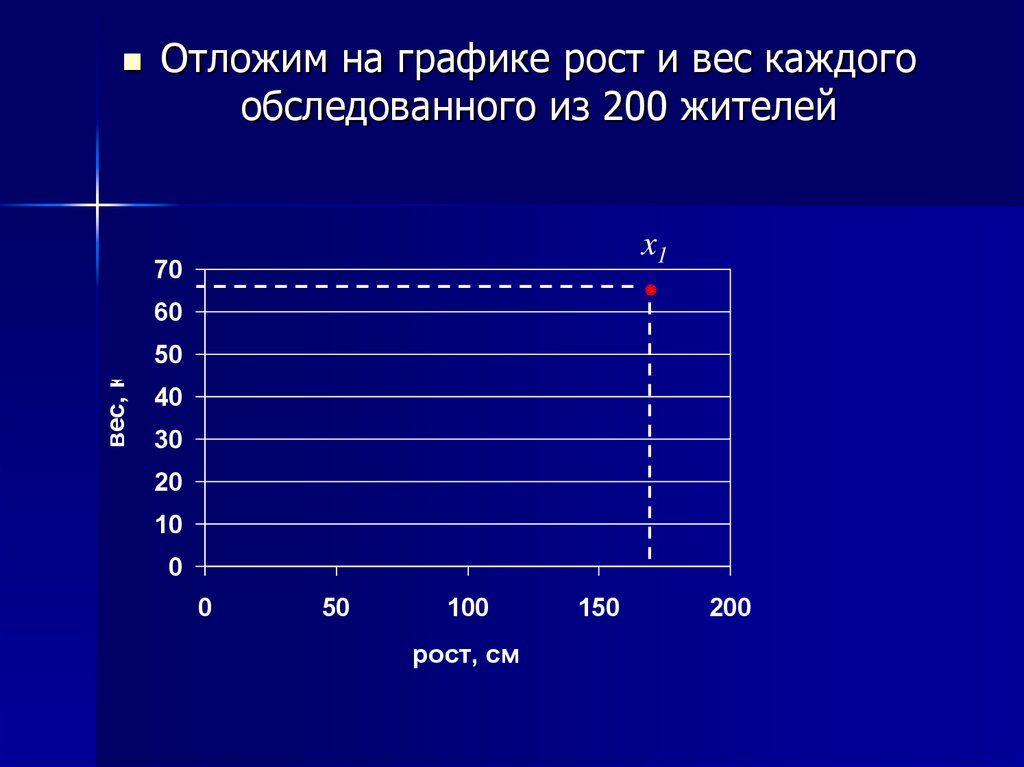
Отложим на графике рост и вес каждогообследованного из 200 жителей
x1
70
вес, кг
60
50
40
30
20
10
0
0
50
100
рост, см
150
200
5.
вес, кг95
90
85
80
75
70
65
60
55
50
160
170
180
рост, см
190
6.
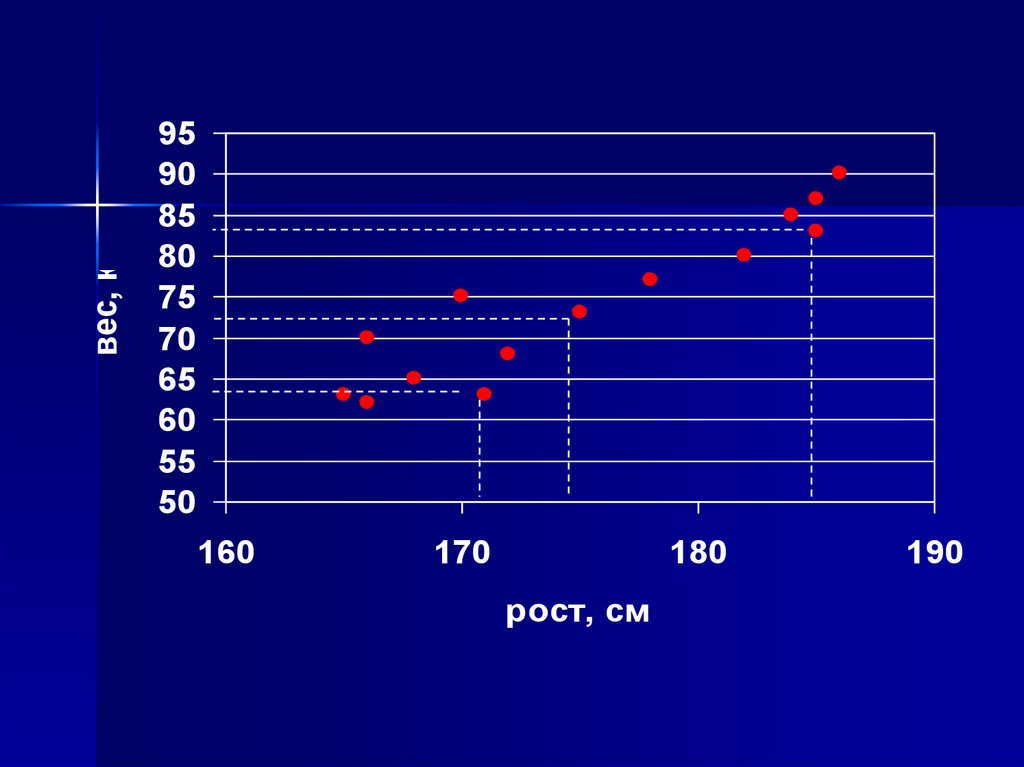
Из графика видно, что между ростом ивесом есть определенная взаимосвязь –
чем выше рост, тем больше вес. Эта связь
линейная.
7.
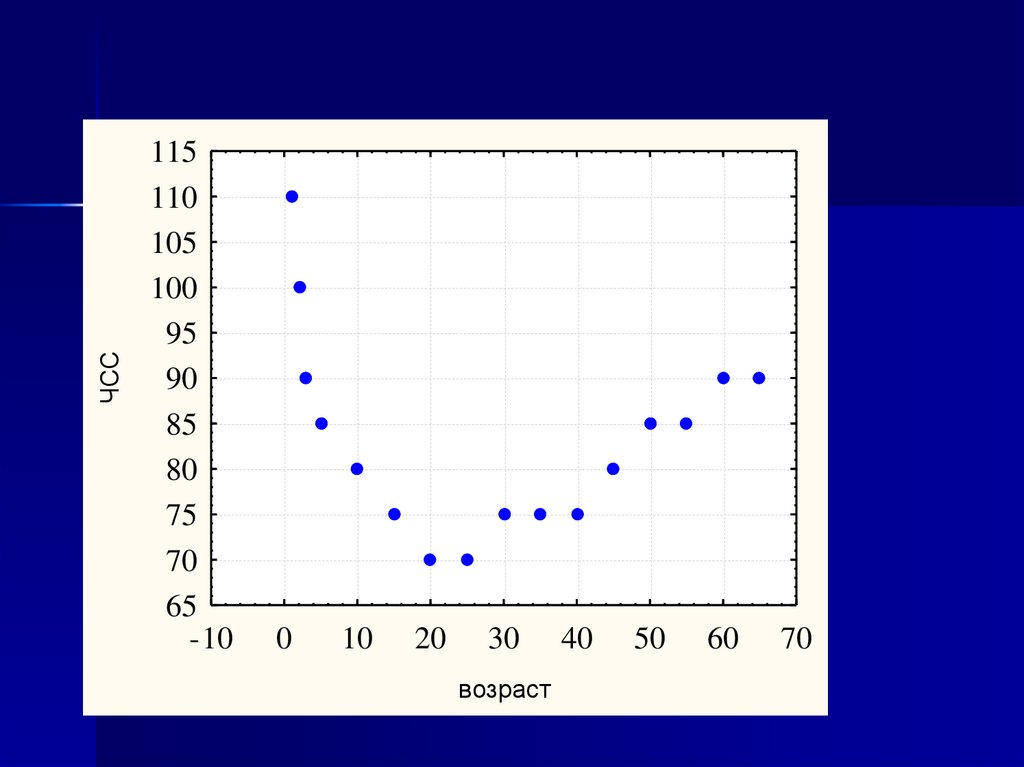
ЧСС115
110
105
100
95
90
85
80
75
70
65
-10
0
10
20
30
возраст
40
50
60
70
8.
Степень выраженности связи междувариационными рядами отражает
понятие корреляциию
Связь может быть слабой, средней,
сильной. Связь может и отсутствовать.
Количественно взаимосвязь между
случайными величинами определяет
коэффициент корреляции - r
9.
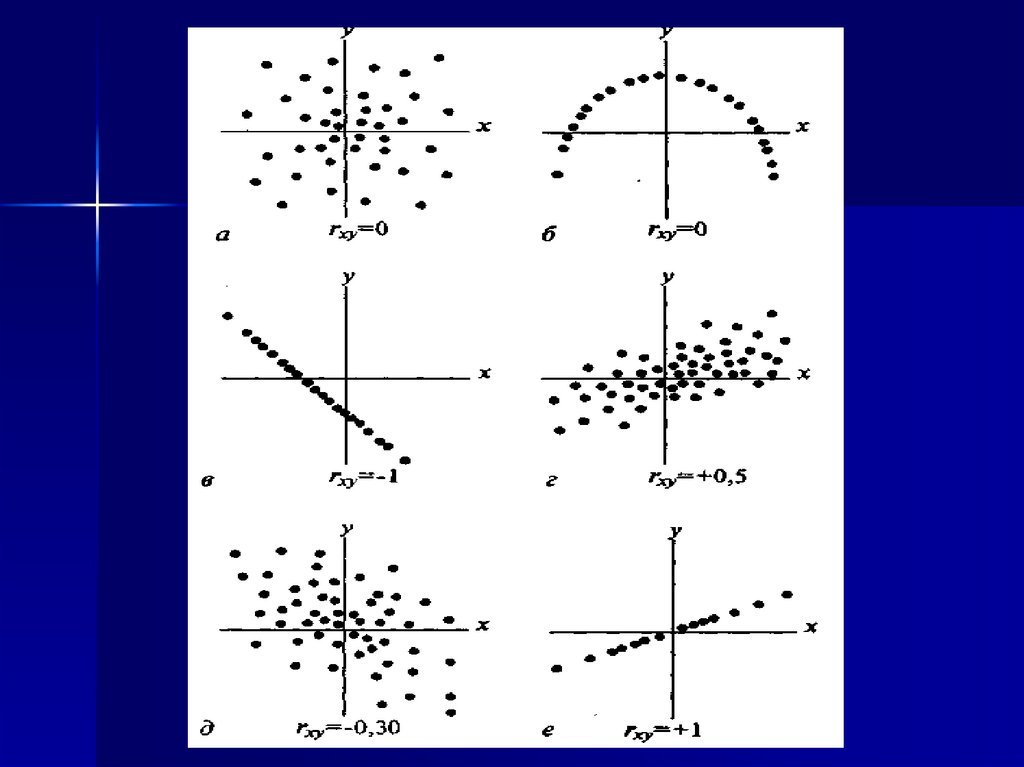
Коэффициент корреляции лежит в пределах-1 ≤ r ≤ 1.
Если r < 0, то это означает, что с увеличением
величины Х1 соответствующие им значения X2
второго вариационного ряда в среднем также
уменьшаются.
Если r> 0, то с увеличением значений одной
величины другая также в среднем возрастает.
Если r =0, то это означает, что случайные
величины Х1 и X2 абсолютно независимы.
При r = 1 между параметрами существует прямо
пропорциональная функциональная зависимость
(в медико-биологических исследованиях крайне
редкий случай).
10.
Обратная корреляция-1
Сильная
обратная
-0,7
Прямая корреляция
-0,5
Средняя
обратная
0,5
0
Слабая
обратная
Слабая
прямая
0,7
Средняя
прямая
1
Сильная
прямая
11.
12. Коэффициент корреляции Пирсона
Для двух случайных величин Х1 и Х2(n -объем каждой выборки),
если они нормально распределены, их
линейную взаимосвязь можно вычислить
n
r
(x
i 1
1i
X 1 ) ( x2 i X 2 )
n
n
i 1
i 1
2
2
(
x
X
)
(
x
X
)
1i 1 2i 2
13. Проверка на статистическую значимость
Н(0): r=0Проверяется гипотеза по критерию Стъюдента:
tкрит по таблице для заданного уровня значимости α и
числа степеней свободы f=n-2
Если │ tвыч│≥ tкрит
то принимается Н(1) и делается
вывод, что между величинами существует значимая
корреляция.
Если
│ tвыч│< tкрит то принимается Н(0) и делается
вывод о независимости исследуемых величин
(коэффициент корреляции незначим).
14.
Есливыборка мала
Или распределение выборки не соответствует
нормальному
Или имеем дело с качественными ординальными
величинами, то используется коэффициент
корреляции рангов К. Спирмена
n
rs 1
6 d
i 1
2
2
i
n ( n 1)
15. Проверка на статистическую значимость
Для проверки гипотезы о значимостикоэффициента корреляции Спирмена
можно воспользоваться таблицей
критических значений .
Если вычисленный коэффициент
корреляции превышает табличное
значение, то связь между величинами
признается достоверной.
16.
где di — разность между рангамисопряженных признаков, n — число
парных членов ряда.
При полной связи ранги признаков
совпадут и разность между ними будет
равна 0, соответственно коэффициент
корреляции будет равен 1. Если же
признаки варьируются независимо,
коэффициент корреляции получится
равным 0
17. Регрессионный анализ
18. Механическая модель сердца
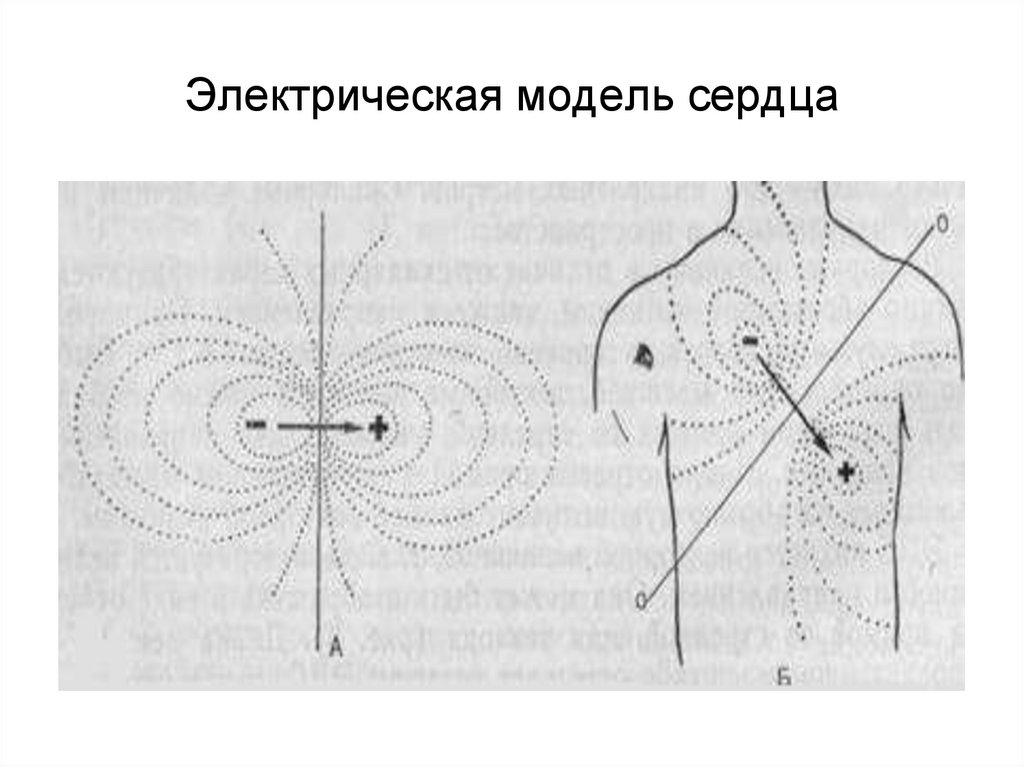
19. Электрическая модель сердца
20. Математическая модель сердца
• СО=z*Q*DР*S*T*1333/((T-S)*CЭ, где:• z - фактор поправки (отношение длины артериального русла ко
всему сосудистому руслу), который лежит в пределах от 0,48 до
0,607 (для человека г в большинстве случаев около 0,6 и
потому обычно берут эту величину);
• DР — истинная пульсовая амплитуда,
• S - время изгнания;
• Т — время полной сердечной инволюции
• (Т — S) — время диастолического периода в секундах;
• СЭ — скорость распространения пульсовой волны по артериям
эластического типа;
• Q — площадь поперечного сечения аорты.
21.
Вернемся к нашему графику зависимости весаот роста.
Как мы уже указали есть определенная
взаимосвязь между этими величинами,
которая оценивается коэффициентом
корреляции.
22.
вес, кг95
90
85
80
75
70
65
60
55
50
160
165
170
175
рост, см
180
185
190
23.
• Из графика видно, что при увеличении роставес также увеличивается, хотя и не во всех
случаях.
• Попытаемся вывести некоторую функцию,
связывающую эти величины
y f (x)
y
x
- зависимая величина (вес)
- независимая величина (рост)
24.
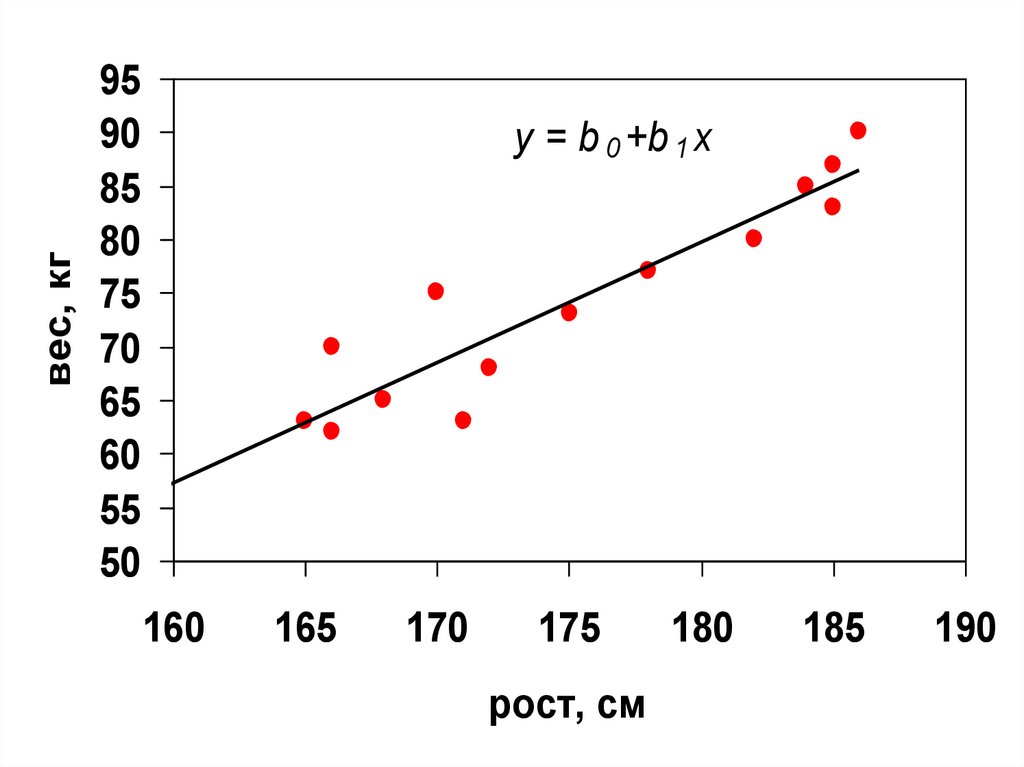
• Наиболее простой является линейнаяфункция, которая имеет вид
y b0 b1 x
и называется уравнением регрессии
• b0 и b1 - постоянные коэффициенты
b1 – коэффициент регрессии
• Иногда запись имеет вид
y a bx
25.
вес, кг95
90
85
80
75
70
65
60
55
50
y = b 0 +b 1 x
160
165
170
175
рост, см
180
185
190
26.
• Это функция показывает как в среднемменяется величина у при изменении
величины x
• Т.е. по этой функции зная величину х
можно вычислить (предсказать)
величину у
27.
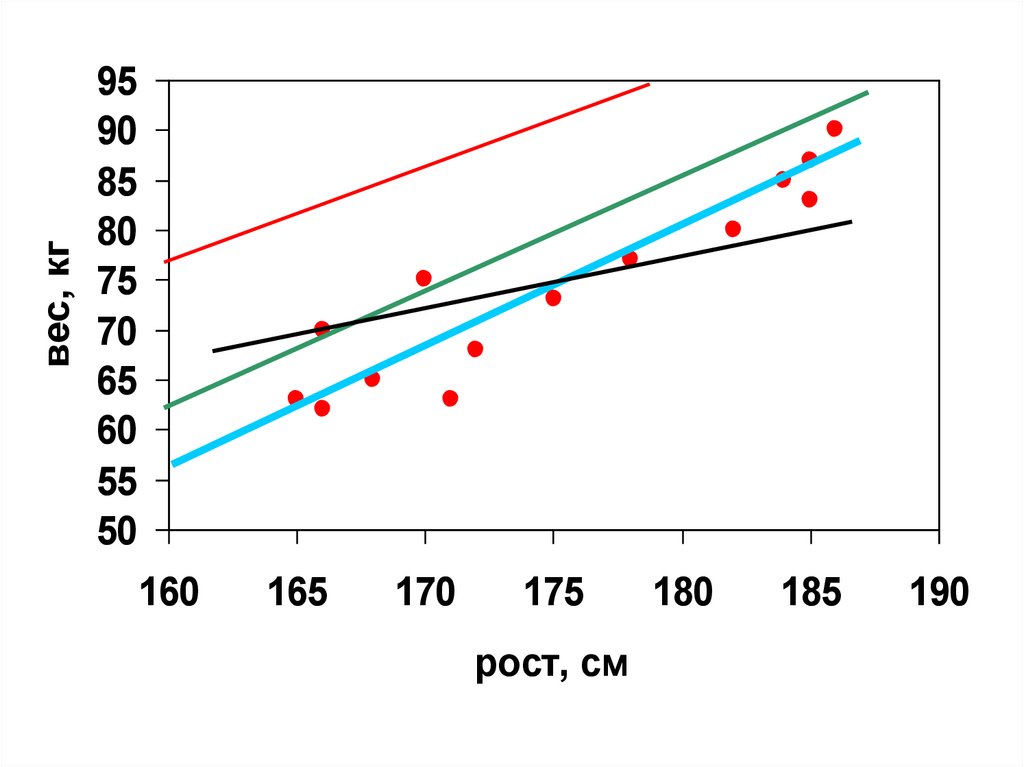
• Через точки на графике можно провестисколь угодно много прямых
28.
вес, кг95
90
85
80
75
70
65
60
55
50
160
165
170
175
рост, см
180
185
190
29.
• Каждая прямая отличается от другихзначениями коэффициентов b0 и b1
• Для выбора наиболее оптимального
служит метод наименьших квадратов,
который позволяет выбрать такие
коэффициенты b0 и b1 , что прямая
регрессии наилучшим образом
отражает взаимосвязь между
изучаемыми величинами
30.
90вес, кг
80
70
60
50
150
160
170
180
рост, см
190
200
31.
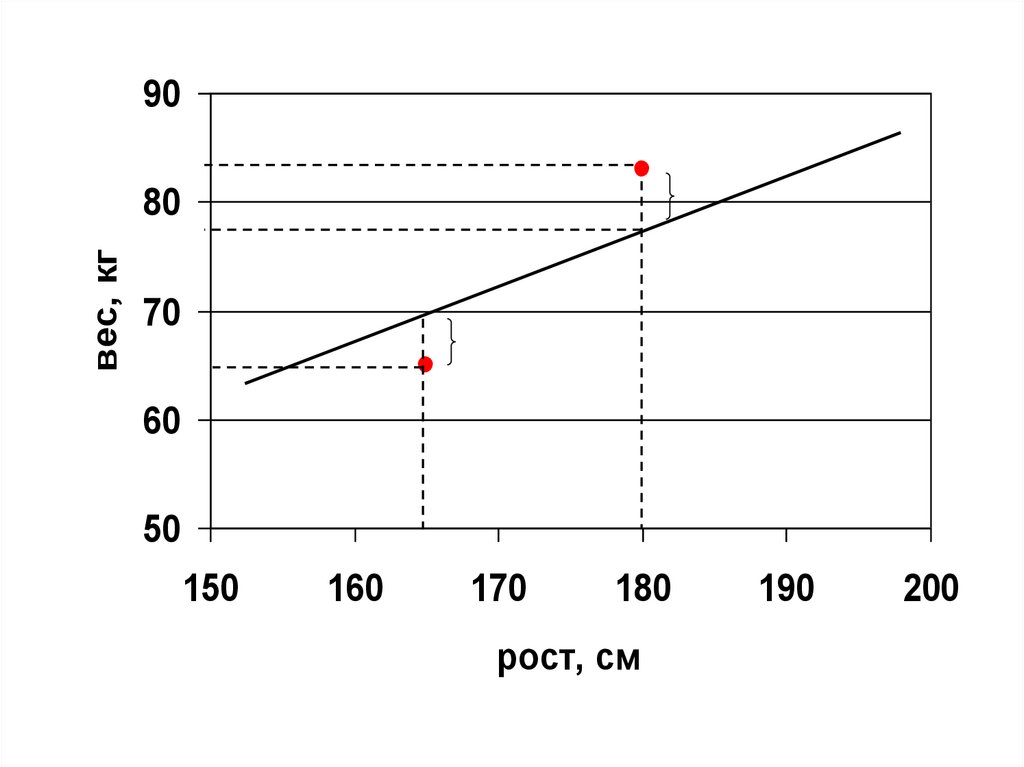
• Из графика видно, что реальныеданные и данные, полученные по
уравнению отличаются на некоторую
величину (т.е. существует отклонение)
• Необходимо выбрать такую линию,
чтобы сумма всех отклонений была
минимальной
32.
• Полученная функция являетсяматематической моделью взаимосвязи двух
случайных величин
• Т.к. мы рассмотрели зависимость только от
одной независимой переменной
и эта
зависимость носит линейный характер, то
такая модель носит название простой
линейной регрессии
x
33.
• Как оценить полученную модель, т.е.насколько хорошо модель отражает
взаимосвязь между исследуемыми
величинами.
• Можно использовать коэффициент
детерминации R2
Он показывает сколько процентов
исходных (выборочных) данных
вписывается в полученную модель
34.
• Если независимых переменных многоx1 , x2 ,.....xn
• То возможно построение уравнение
множественной линейной регрессии
y b0 b1 x1 b2 x2 ... bn xn
• Например, вес зависит также от места
проживания, типа питания, социального
положения, наследственных факторов,
хронических заболеваний и т.д.
35.
• Возможны также нелинейные моделиy b0 b x b2 x2
2
1 1
36.
• Математические модели можноиспользовать для прогнозирования


























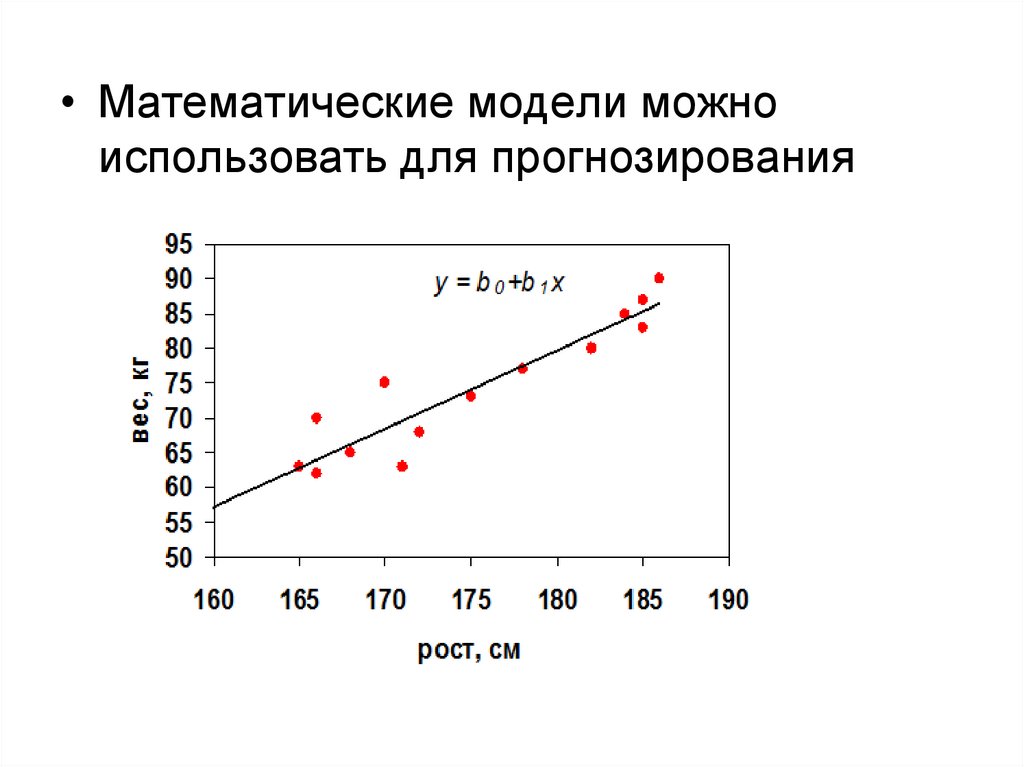
 mathematics
mathematics








