Курс Эконометрика

1. Курс Эконометрика

Хасанова
Светлана Фанилевна
LOGO
www.themegallery.com

2. Темы занятий

Парная регрессия
Множественная регрессия
Временные ряды
Системы одновременных уравнений
Проверка статистических гипотез

3. Парная линейная регрессия

• Основная цель – построить уравнение
(модель) вида:
Y = a + b*X
описывающее зависимость между
зависимой переменной (результатом - Y) и
независимой переменной (фактором – X).
a и b – называются параметрами модели.
Примеры зависимостей:
•Выручки предприятия от расходов на рекламу;
•Цены на нефть от курса доллара,
•Количества баллов по эконометрике от
количества часов, потраченных на её изучение
и т.д.

4. Пример построения парной линейной регрессии

xyi
Пример построения парной
линейной регрессии
Для 13 клиентов спортивного отдела магазина зафиксирована
сумма покупки (в у.е.) и время разговора с продавцом (мин):
Y
40
50
60
80
100 110 120 130 150 160 180 200 310
X
14
14
17
19
17
20
24
22
25
24
18
20
26
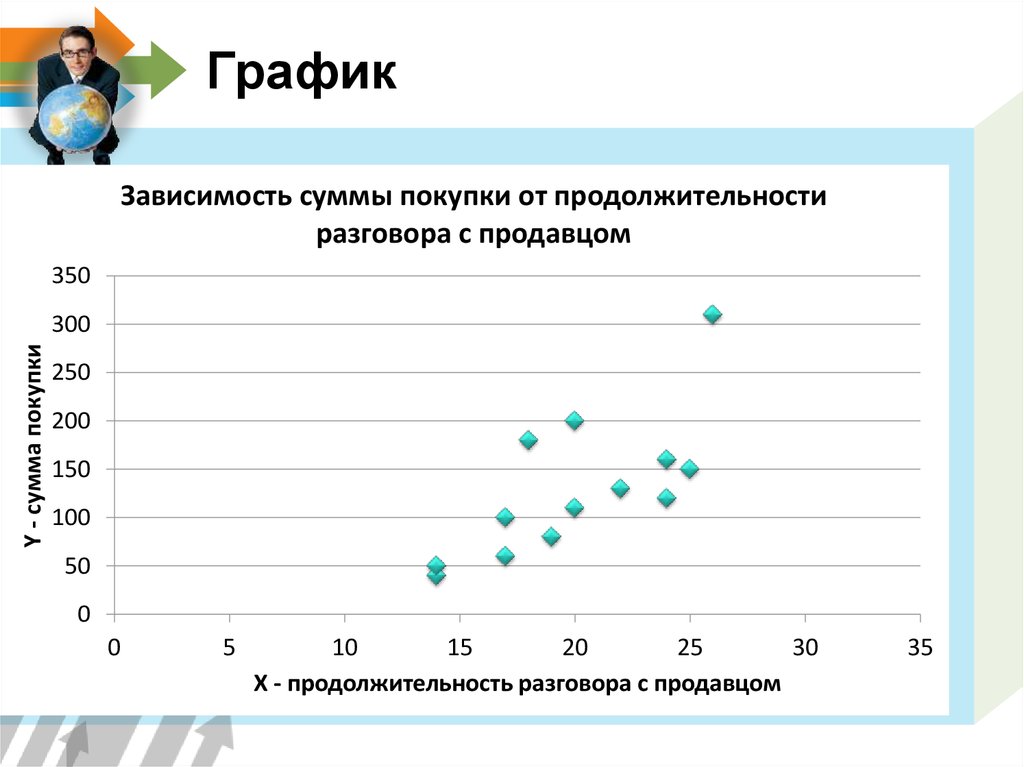
Построим график с осями Y – сумма покупки и Х – время разговора
Каждая точка графика соответствует
конкретному клиенту – всего 13 точек.

5. График

Зависимость суммы покупки от продолжительности
разговора с продавцом
350
Y - сумма покупки
300
250
200
150
100
50
0
0
5
10
15
20
25
30
Х - продолжительность разговора с продавцом
35

6. График линейной зависимости

Y = a + b*X
Зависимость суммы покупки от продолжительности
разговора с продавцом
350
Y - сумма покупки
300
e13
250
200
e12
150
100
50
0
0
5
10
15
20
25
30
Х - продолжительность разговора с продавцом
е ( y y
2
i
i
предсказ
) min
2
35

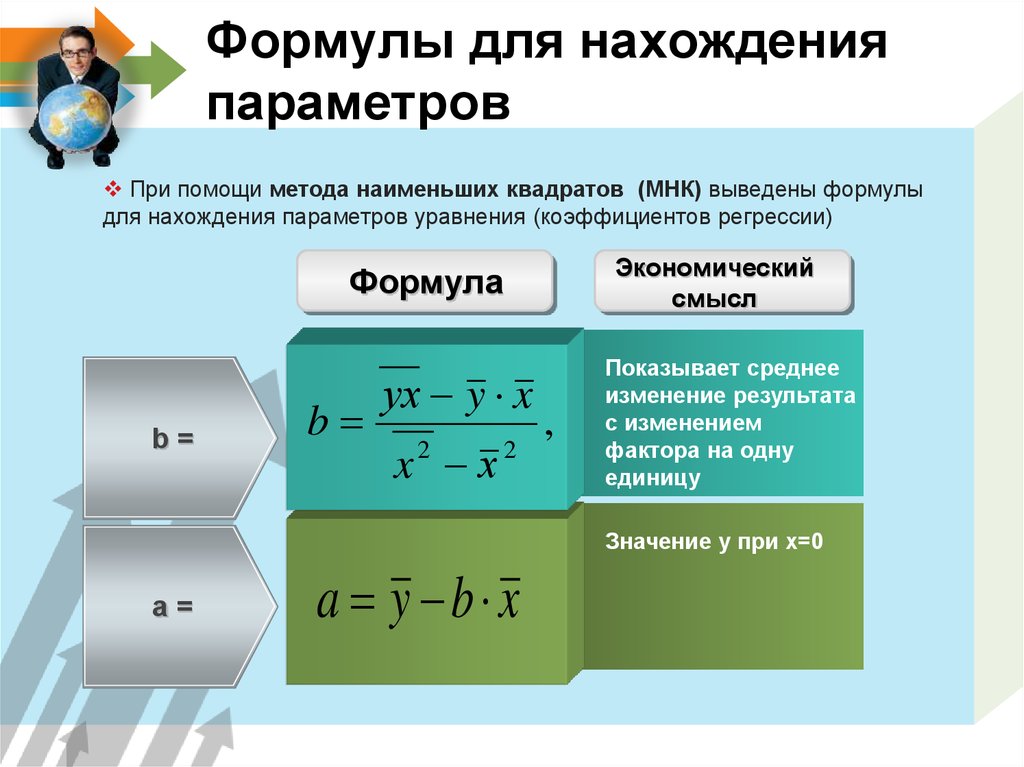
7. Формулы для нахождения параметров

При помощи метода наименьших квадратов (МНК) выведены формулы
для нахождения параметров уравнения (коэффициентов регрессии)
Экономический
смысл
Формула
b=
b
ух y x
x2 х 2
,
Показывает среднее
изменение результата
с изменением
фактора на одну
единицу
Значение y при x=0
a=
a y b x

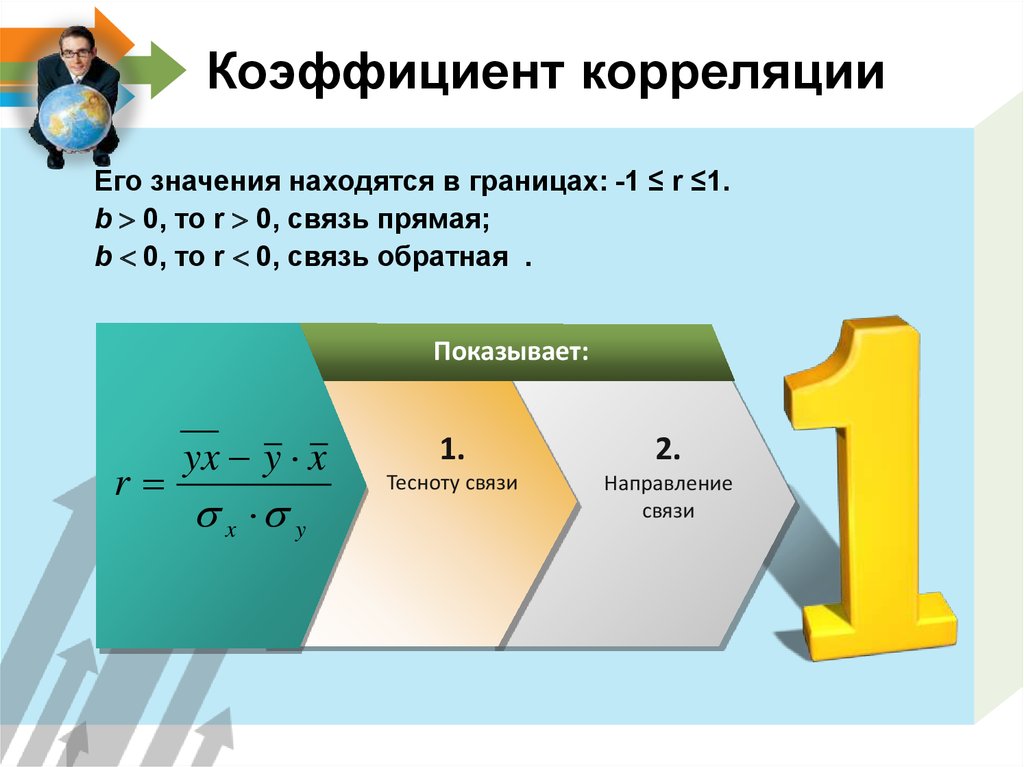
8. Коэффициент корреляции

Его значения находятся в границах: -1 ≤ r ≤1.
b 0, то r 0, связь прямая;
b 0, то r 0, связь обратная .
Показывает:
yx y x
r
x y
1.
2.
Тесноту связи
Направление
связи

9. Шкала Чеддока для интерпретации коэффициента корреляции

0,9 – 0,999 Связь весьма высокая
0,7 – 0,9 Связь высокая
0,5 – 0,7 Связь заметная
0,3 – 0,5 Связь умеренная
0,1 – 0,3 Связь слабая
0
│0,3│
│0,5│
│0,7│
│0,9│
│1│

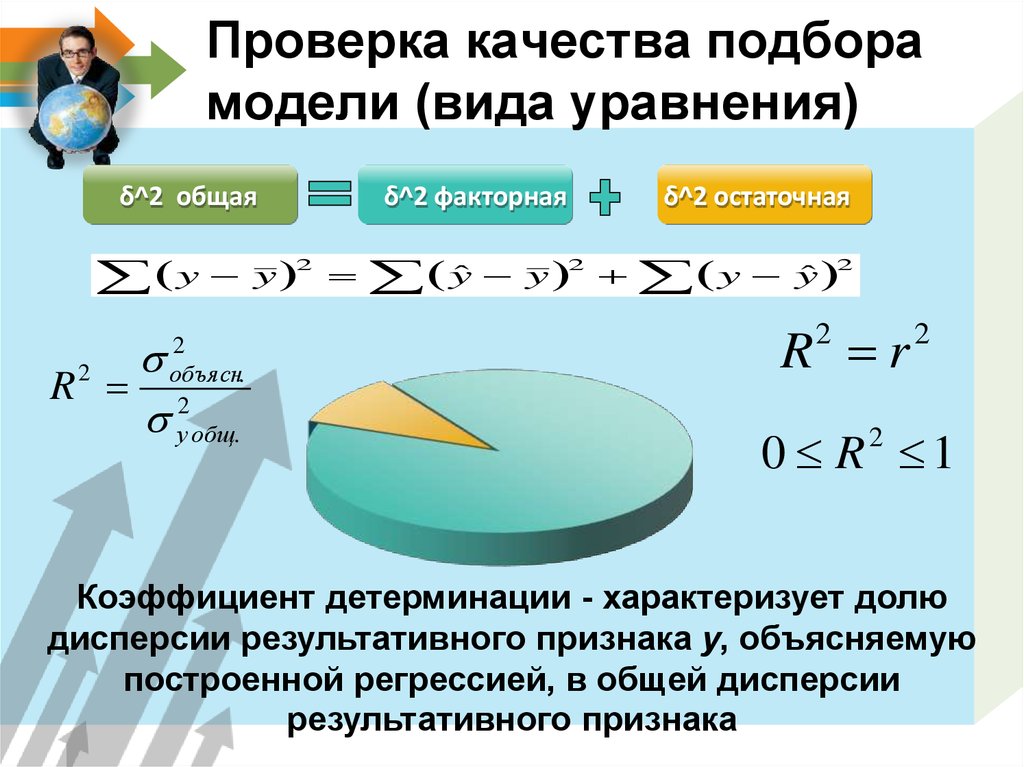
10. Проверка качества подбора модели (вида уравнения)

δ^2 общая
y
R
2
δ^2 факторная
y
2
объясн.
2
у общ.
2
yˆ
δ^2 остаточная
y
2
y
ˆ
y
2
R r
2
2
0 R 1
2
Коэффициент детерминации - характеризует долю
дисперсии результативного признака y, объясняемую
построенной регрессией, в общей дисперсии
результативного признака

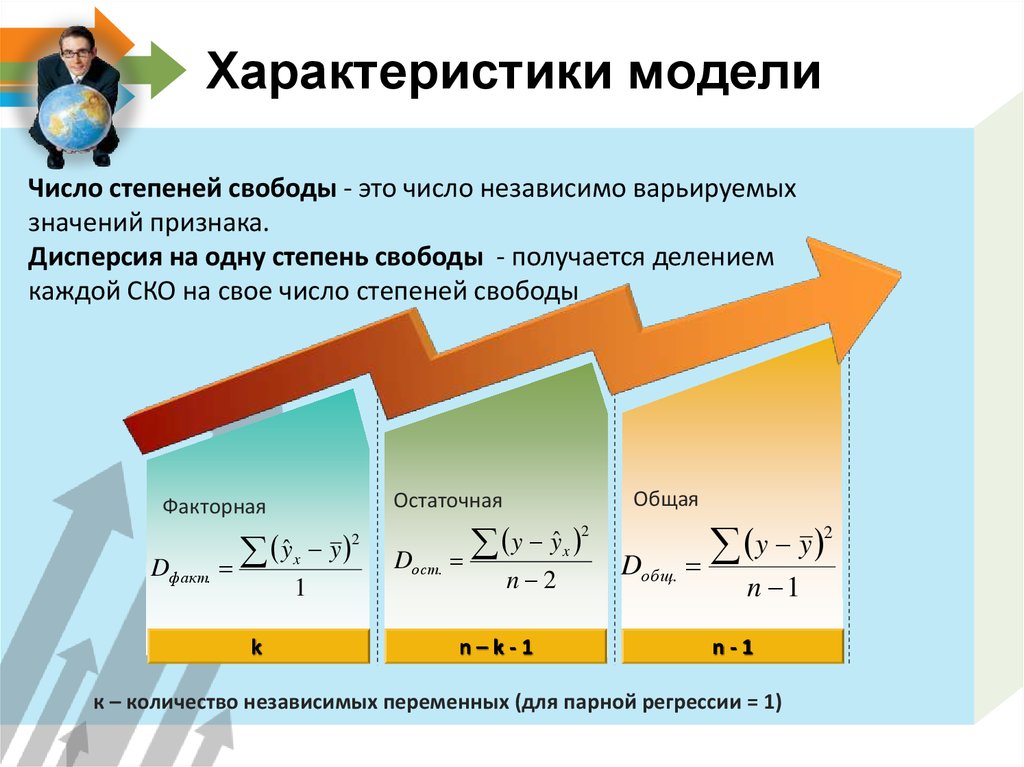
11. Характеристики модели

Число степеней свободы - это число независимо варьируемых
значений признака.
Дисперсия на одну степень свободы - получается делением
каждой СКО на свое число степеней свободы
Dфакт.
yˆ x y 2
1
k
Общая
Остаточная
Факторная
y yˆ x 2
Dост.
n 2
n–k-1
Dобщ.
2
y
y
n 1
n-1
к – количество независимых переменных (для парной регрессии = 1)

12. Проверка статистической значимости модели

H 0 : Dфакт. Dост.
Fнабл
Dфакт .
Fраспобр(α;1;n-2)
Dост.
Fнабл. Fтабл.
Модель
статистически не
значима
если:
Fнабл. Fтабл.
Модель
статистически
значима
Если справедлива
Н0, то дисперсии
не отличаются
друг от друга. Для
Н0 необходимо
опровержение,
чтобы факторная
дисперсия
превышала
остаточную в
несколько раз.

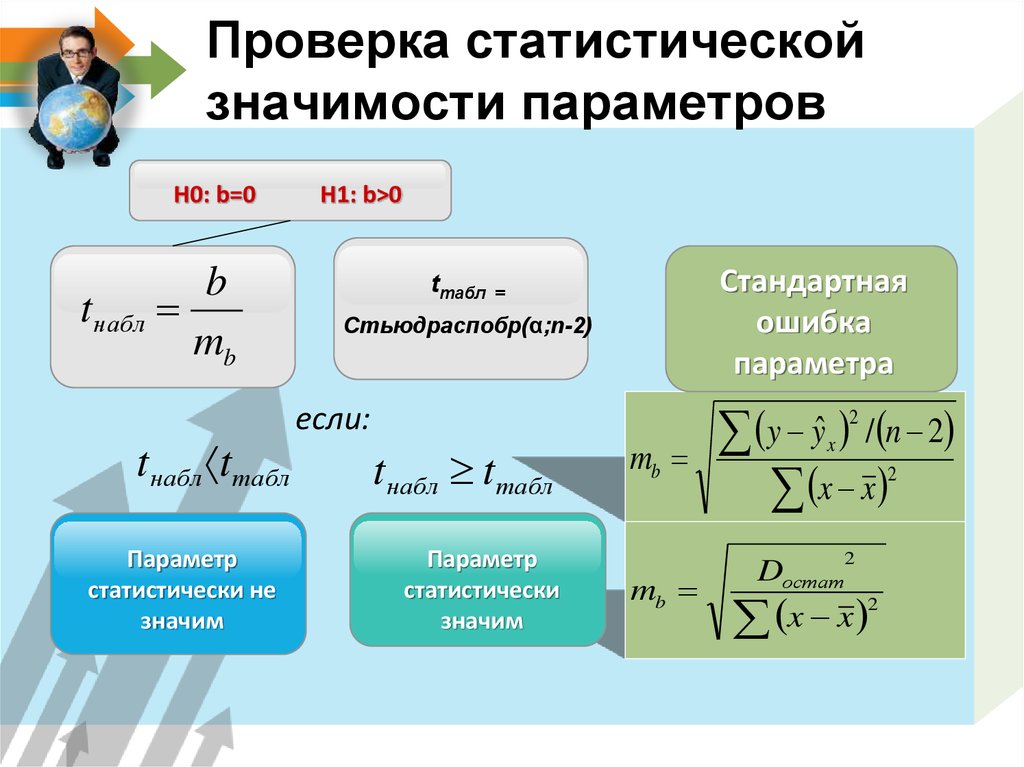
13. Проверка статистической значимости параметров

Н0: b=0
b
t набл
mb
tнабл tтабл
Параметр
статистически не
значим
H1: b>0
tтабл
Стандартная
ошибка
параметра
=
Стьюдраспобр(α;n-2)
если:
tнабл tтабл
Параметр
статистически
значим
mb
2
ˆ
y
y
x / n 2
2
x
x
2
mb
Dостат
2
x
x

14. Доверительный интервал для параметра

• параметр b с надежностью α лежит в
интервале:
b0 mb tтабл ( ; n 2) b b0 mb tтабл ( ; n 2)
• надежность (α) = 1 – вероятность (β)

15. Анализ данных

Регрессионная статистика
Множественный R
0,719494
R-квадрат
0,517671
Нормированный R-квадрат
0,473823
Стандартная ошибка
53,13959
Наблюдения
Объясненная
доля
Вероятность,
с которой
модель не
значима
13
Дисперсионный анализ
df
Регрессия
Остаток
Итого
SS
1
11
12
33338,02
31061,98
64400
MS
33338,02
2823,816
F
11,80602
Значимость F
0,005564
Вероятность, с которой не значим параметр
Y = -133,5 + 13,5*b
Y-пересечение
X
Стандартная
Коэффициенты
ошибка
-133,542
13,17708
78,10357
3,83502
t-статистика
-1,7098
3,435988
P-Значение
0,115324
0,005564
Нижние 95%
-305,446
4,736262
Верхние
95%
38,36313
21,6179

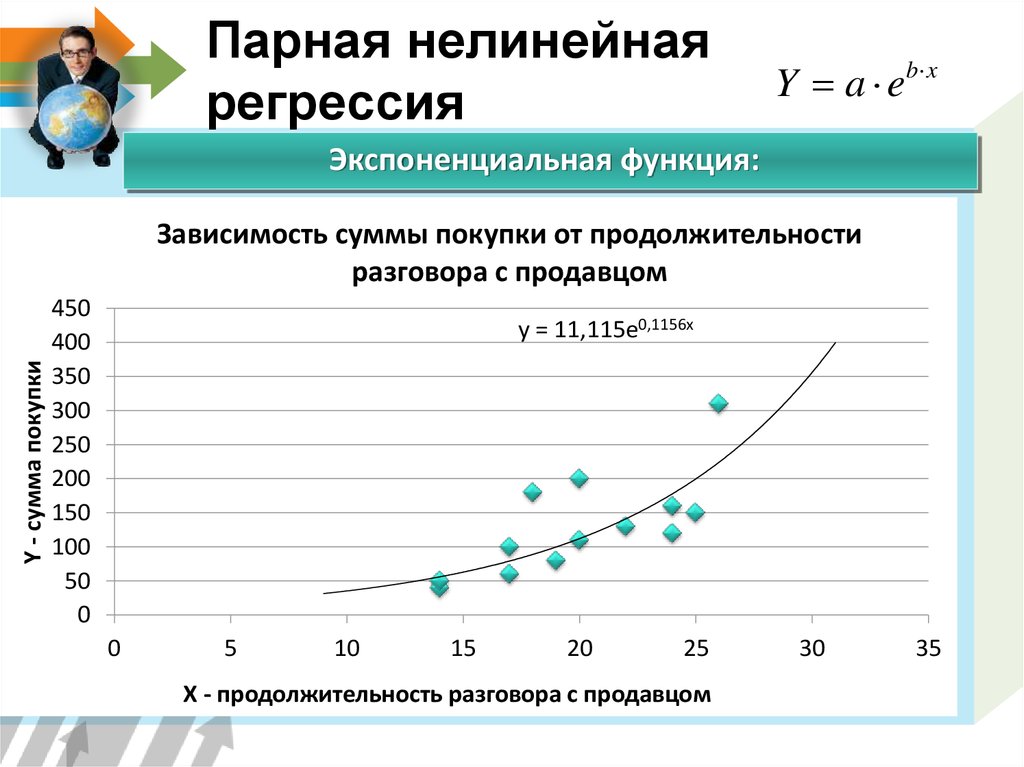
16. Парная нелинейная регрессия

Y a e
b x
Экспоненциальная функция:
Y - сумма покупки
Зависимость суммы покупки от продолжительности
разговора с продавцом
450
400
350
300
250
200
150
100
50
0
y = 11,115e0,1156x
0
5
10
15
20
25
Х - продолжительность разговора с продавцом
30
35

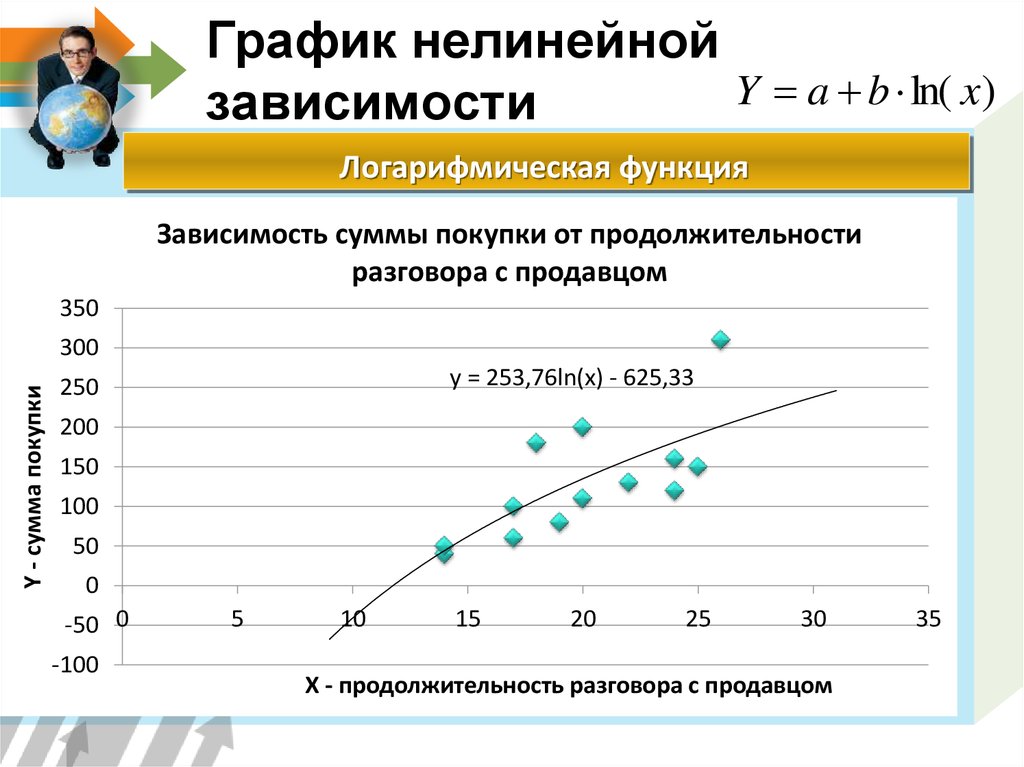
17. График нелинейной зависимости

График нелинейной
Y a b ln( x)
зависимости
Логарифмическая функция
Зависимость суммы покупки от продолжительности
разговора с продавцом
350
Y - сумма покупки
300
y = 253,76ln(x) - 625,33
250
200
150
100
50
0
-50 0
-100
5
10
15
20
25
30
Х - продолжительность разговора с продавцом
35

18. График нелинейной зависимости

Y a xb
Describe a Степенная
vision of company
or strategic contents.
функция
Зависимость суммы покупки от продолжительности
разговора с продавцом
Y - сумма покупки
350
y = 0,1246x2,2852
300
250
200
150
100
50
0
0
5
10
15
20
25
Х - продолжительность разговора с продавцом
30
35

19. Эластичность

• Эластичность определяется по формуле:
'
y
Эb
y
• Для парной регрессии:
• Для степенной:
b
Y a x
эb b
b
эb
a b x

20. Уравнение множественной регрессии

Линейная модель:
y a b1 x1 b2 x2 ... b p x p e
– На любой экономический показатель чаще всего
оказывает влияние не один, а несколько
факторов.
– Например, спрос на некоторое благо
определяется не только ценой данного блага, но
и ценами на замещающие и дополняющие
блага, доходом потребителей и многими
другими факторами.

21. Уравнение множественной регрессии в стандартизированном масштабе

• Уравнение регрессии в стандартизованном масштабе
имеет вид:
t y 1t x1 2t x2 pt x p
• стандартизированные параметры:
ty
y y
; tx j
y
• Система уравнений:
2 rx 2 x1
1
r
1 x1 x 2 2
1rx1 x p
xj xj
xj
,
j 1, n
3rx3 x1
p rx p x1
ryx1
2 rx 2 x p
3rx3 x p
p
ryx p
3rx3 x 2
p rx p x 2
ryx2

22. Проверка качества уравнения множественной регрессии

• Коэффициент детерминации:
R2 1
ei2
2
y
y
i
• Скорректированный к-т детерминации:
n 1
p
2
R 1 1 R
R
1 R2
n p 1
n p 1
2
2

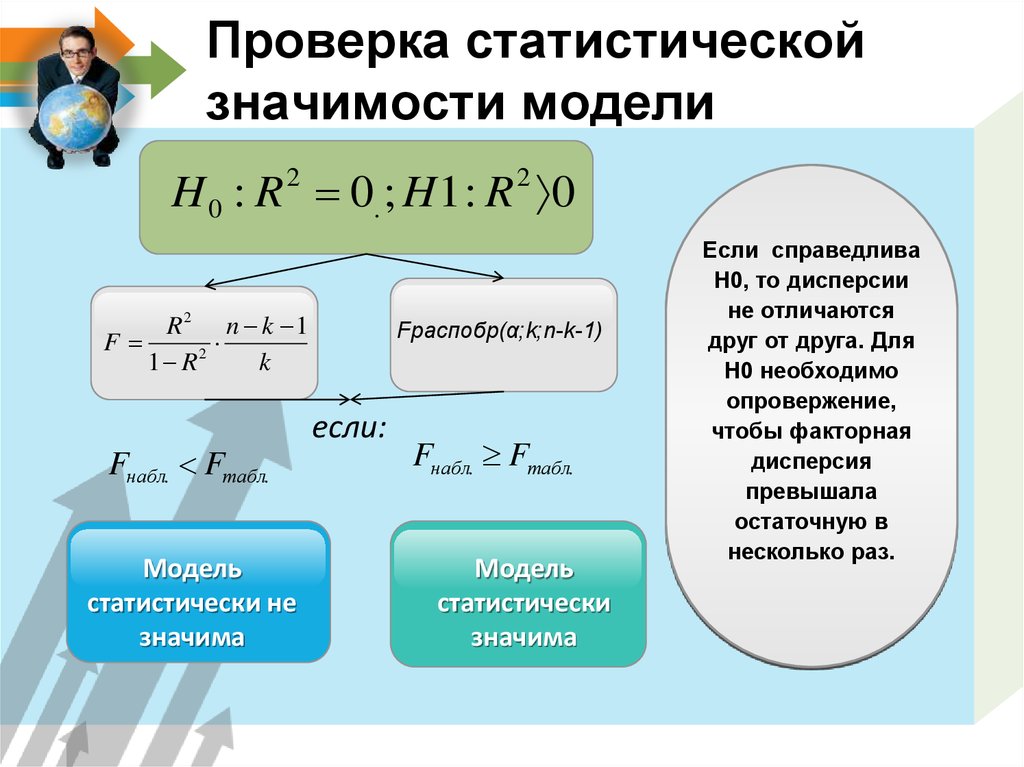
23. Проверка статистической значимости модели

H 0 : R 0. ; H 1 : R 0
2
2
R2 n k 1
F
2
1 R
k
Fнабл. Fтабл.
Модель
статистически не
значима
Fраспобр(α;k;n-k-1)
если:
Fнабл. Fтабл.
Модель
статистически
значима
Если справедлива
Н0, то дисперсии
не отличаются
друг от друга. Для
Н0 необходимо
опровержение,
чтобы факторная
дисперсия
превышала
остаточную в
несколько раз.

24.

До свидания!
LOGO
www.themegallery.com