Similar presentations:
Центральные проблемы эконометрики
1.
Дисциплина: ЭконометрикаПреподаватель: Кучерова Светлана Викторовна,
доцент кафедры математики и моделирования (ауд.1602)
Литература:
Елисеева И.И. Эконометрика: учебник. - М.: Финансы и статистика, 2002.
Елисеева И.И. С.В. Курышева, Н.М. Гордеенко и др. Практикум по
эконометрике: учеб. пособие. - М.: Финансы и статистика, 2001.
Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов. – М.: ЮНИТИДАНА, 2002.
Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный
курс: учебник. – М.: Дело, 2000.
1
2.
• Опр. эконометрика — это наука,которая дает количественное
выражение взаимосвязей
экономических явлений и
процессов.
2
3.
Центральные проблемыэконометрики
построение эконометрической модели
определение возможностей ее использования
для описания, анализа и прогнозирования
реальных экономических процессов.
3
4.
• Эконометрическое исследование включает решениеследующих проблем:
• качественный анализ связей экономических переменных —
выделение зависимых (у) и независимых переменных (х);
• подбор данных;
• спецификация формы связи между у и х,
• оценка параметров модели;
• введение фиктивных переменных;
• выявление тренда, циклической и случайной компонент; и
др.
4
5. этапы эконометрического исследования:
обработкарезультатов
оценка
параметров
спецификация модели
получение данных,
анализ их качества
постановка проблемы
5
6.
проблема точности связана с:• определением понятия экономической
величины;
• разработкой правил и методов измерений
• выявлением условий сравнимости
экономических величин (показателей);
• разработкой принципов конструирования
измерителей и измерений;
• основанием выбора типа шкал при
конструировании измерителя;
6
7.
• Регрессия в эконометрическихисследованиях.
7
8. Простая регрессия представляет собой регрессию между двумя переменными — у и х, т. е. модель вида:
y fˆ ( x),где:
у – зависимая переменная (результативный признак);
х – независимая, или объясняющая, переменная
(признак-фактор).
8
9.
Множественная регрессия представляетсобой регрессию результативного признака с
двумя и большим числом факторов, т. е.
модель вида:
y f ( x1, x2 ,...xk )
9
10. ПРИМЕР.
Так, если зависимость спроса у от цены х характеризуется,например, уравнением:
yˆ x 5000 2 x
10
11. В парной регрессии выбор вида математической функции
yˆ x f ( x)может быть осуществлен тремя методами:
• графическим;
• аналитическим, т. е. исходя из теории изучаемой
взаимосвязи;
• экспериментальным.
11
12.
регрессиялинейная
нелинейная
нелинейная по
объясняющим
переменным
нелинейная по
оцениваемым
параметрам
12
13. Основные типы кривых, используемые при количественной оценке связей между двумя переменными
a ) y x a b x;линейная
y
регрессия
0
a
х
y
б ) yx a b x c x2
полином второй степени
0
б
х
13
14.
yв ) y x a b / x;
равносторонняя гипербола
0
в
х
y
г ) y x a b x c x 2 d x3
полином третьей степени
0
г
х
14
15.
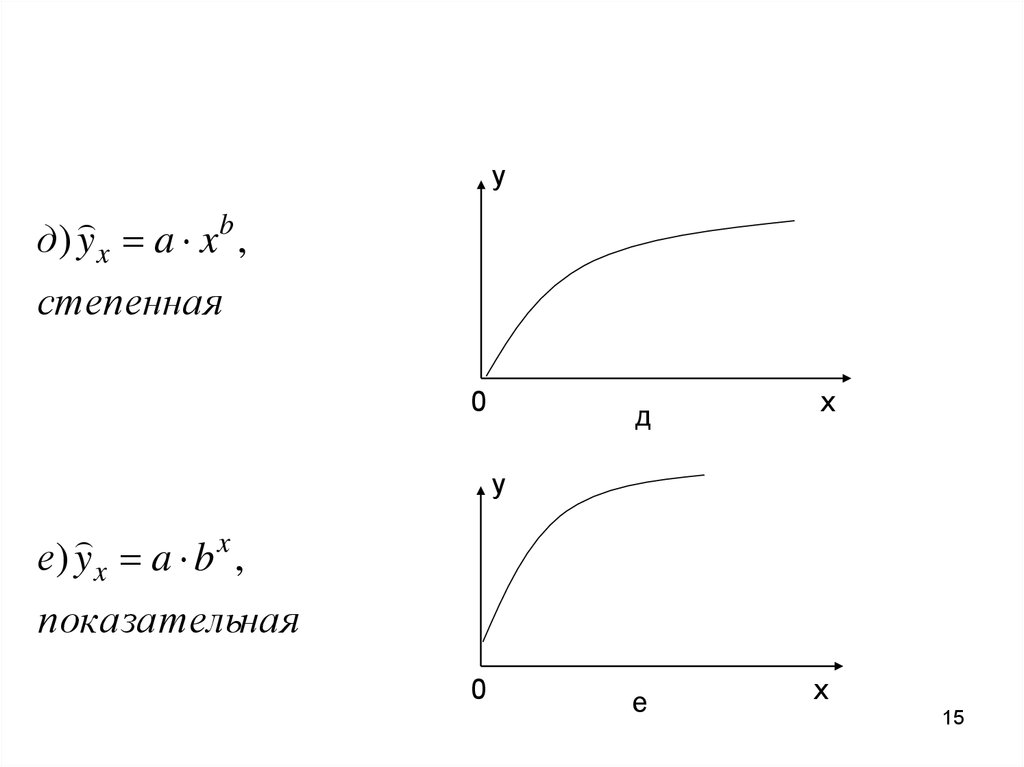
yд) y x a x b ,
степенная
0
д
х
е
х
y
x
е) y x a b ,
показательная
0
15
16. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).
МНК позволяет получить такие оценки параметров а и b,при которых сумма квадратов отклонений фактических
значений результативного признака (уi ) от расчетных yˆ x
(теоретических) минимальна:
y yˆ
2
i
xi
min
i
16
17.
• Геометрический смысл МНК: из всего множества линийлиния регрессии на графике выбирается так, чтобы сумма
квадратов расстояний по вертикали между точками и этой
линией была бы минимальной
у
0
х
17
18.
Обозначим i yi y xi ,n
S i min
2
i 1
S
i
yi y xi
y a b x
2
2
i
18
19.
nn
dS
da 2 yi 2 n a 2 b xi 0;
i 1
i 1
(1)
n
n
n
dS
2 y x 2 a x 2 b x 2 0.
i i
i
i
i 1
i 1
i 1
db
19
20. для оценки параметров а и b получим следующую систему нормальных уравнений
n a b xi yii 1
i 1
n
n
n
a x b x 2 x y
i
i
i
i
i 1
i 1
i 1
n
n
20
21.
Формулы расчета параметров a и b:a y b x
b
yx y x
x x
2
2
b - коэффициент регрессии. Его величина показывает
среднее изменение результата с изменением фактора на одну
единицу.
x2 x 2 x 2
21
22.
Линейный коэффициент корреляции является показателемтесноты связи:
σ x yx y x
rxy b
σy
σ xσ y
Линейный коэффициент корреляции должен находится в
границах:
1 rxy 1
22
23.
Для характеристики силы связи можно использовать шкалу Чеддока.Показатель
тесноты
0,1 – 0,3
0,3 – 0,5
0,5 – 0,7
0,7 – 0,9
0,9 – 0,99
связи
Характерист
ика
Весьма
Слабая
Умеренная
Заметная
Высокая
высокая
силы связи
23
24.
2yx
• Коэффициент детерминации
r
характеризует долю дисперсии результативного
признака :
• Величина 1- r 2 характеризует долю дисперсии
у, вызванную влиянием остальных не учтенных
в модели факторов.
24
25.
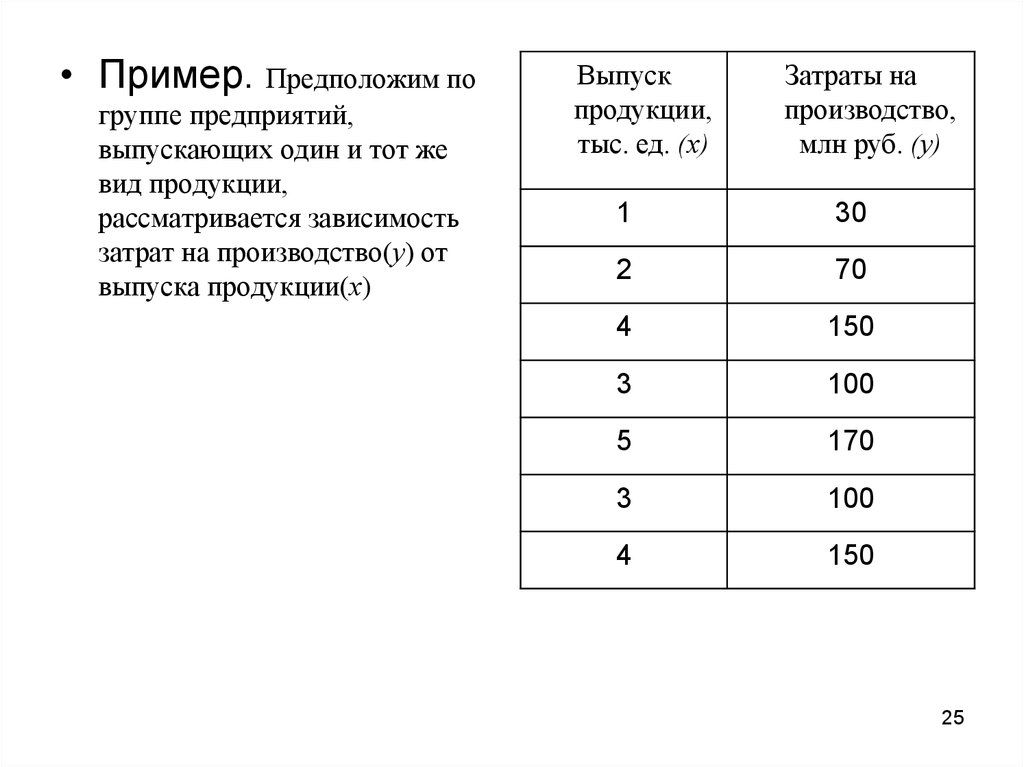
• Пример. Предположим погруппе предприятий,
выпускающих один и тот же
вид продукции,
рассматривается зависимость
затрат на производство(у) от
выпуска продукции(х)
Выпуск
продукции,
тыс. ед. (х)
Затраты на
производство,
млн руб. (у)
1
30
2
70
4
150
3
100
5
170
3
100
4
150
25
26.
• Система нормальных уравнений будетиметь вид
7a 22b 770
22a 80b 2820
• а = -5,798, b= 36,8443,
• r 2 = 0,982.
уравнение регрессии:
y x 5,79 36,84 x
26
27.
• Вывод:чем больше доля объясненной вариации, тем
соответственно меньше роль прочих
факторов, и линейная модель хорошо
аппроксимирует исходные данные и ею
можно воспользоваться для прогноза значений
результативного признака.
27
28.
Оценка существенности уравнениялинейной регрессии.
29.
• F критерий Фишера - оценивает качествоуравнения регрессии - состоит в проверке
гипотезы Н0 (о том, что коэффициент
регрессии равен нулю, т.е. b = 0, т.е. фактор
х не оказывает влияния на результат у ).
29
30.
• Расчету F-критерия предшествует анализдисперсии.
• Центральное место в нем занимает
разложение общей суммы квадратов
отклонений на две части «объясненную» и
«необъясненную» .
( y y)
• Общая
2
( yˆ
x
y)
2
факторная
(регрессионная)
( y yˆ )
2
x
остаточная
(необъясненная)
30
31.
• Любая сумма квадратов отклонений связана счислом степеней свободы – df (degrees of
freedom), т.е. с числом свободы независимого
варьирования признака.
31
32.
• Число степеней свободы остаточнойсуммы квадратов при линейной парной
регрессии составляет n - 2 ,
• общей суммы квадратов – n -1 ,
• для факторной суммы квадратов – 1,
Имеем равенство:
n – 1 = 1+ (n – 2).
32
33.
• дисперсии на одну степень свободыDобщ
( y y)
Dфакт
Dост
2
n 1
2
ˆ
(
y
y
)
x
1
2
ˆ
(
y
y
)
x
n 2
33
34.
FDфакт
Dост
34
35.
( yˆx
y)
( y yˆ )
х
2
2
r σ n
2
2
y
(1 r ) σ n
2
2
y
2
Fфакт
r
n
2
2
1 r
• n - число наблюдений
35
36.
• Значение F-критерия признаетсядостоверным, если оно больше табличного.
В этом случае гипотеза H0 отклоняется.
36
37.
•Если Fтабл< Fфакт, то Но – гипотезао случайной природе оцениваемых характеристик
отклоняется и признается их статистическая значимость
и надежность.
•Если Fтабл > Fфакт, то гипотеза Но
не отклоняется и признается статистическая незначимость
и ненадежность уравнения регрессии.
37
38.
• Таблица значений F-критерияФишера при уровне значимости
α =0,05
1
2
3
4
5
6
8
12
24
∞
1
161,45
199,50
215,72
224,57
230,17
233,97
238,89
243,91
249,04
254,32
2
18,51
19,00
19,16
19,25
19,30
19,33
19,37
19,41
19,45
19,50
3
10,13
9,55
9,28
9,12
9,01
8,94
8,84
8,74
8,64
8,53
4
7,71
6,94
6,59
6,39
6,26
6,16
6,04
5,91
5,77
5,63
5
6,61
5,79
5,41
5,19
5,05
4,95
4,82
4,68
4,53
4,36
6
5,99
5,14
4,76
4,53
4,39
4,28
4,15
4,00
3,84
3,67
7
5,59
4,74
4,35
4,12
3,97
3,87
3,73
3,57
3,41
3,23
8
5,32
4,46
4,07
3,84
3,69
3,58
3,44
3,28
3,12
2,93
k1
k2
38
39. ПРИМЕР
• Дисперсионный анализ результатоврегрессии
Вариация
результата
y
Общая
Факторная
Остаточная
Число
степеней
свободы
Сумма
квадратов
отклонений
Дисперсия
на одну
степень
свободы,D
df n 1 8
6,316
-
-
-
5,116
?
?
?
1,200
?
-
-
k1
1
k2 ?
Fфакт
Fтабл
39































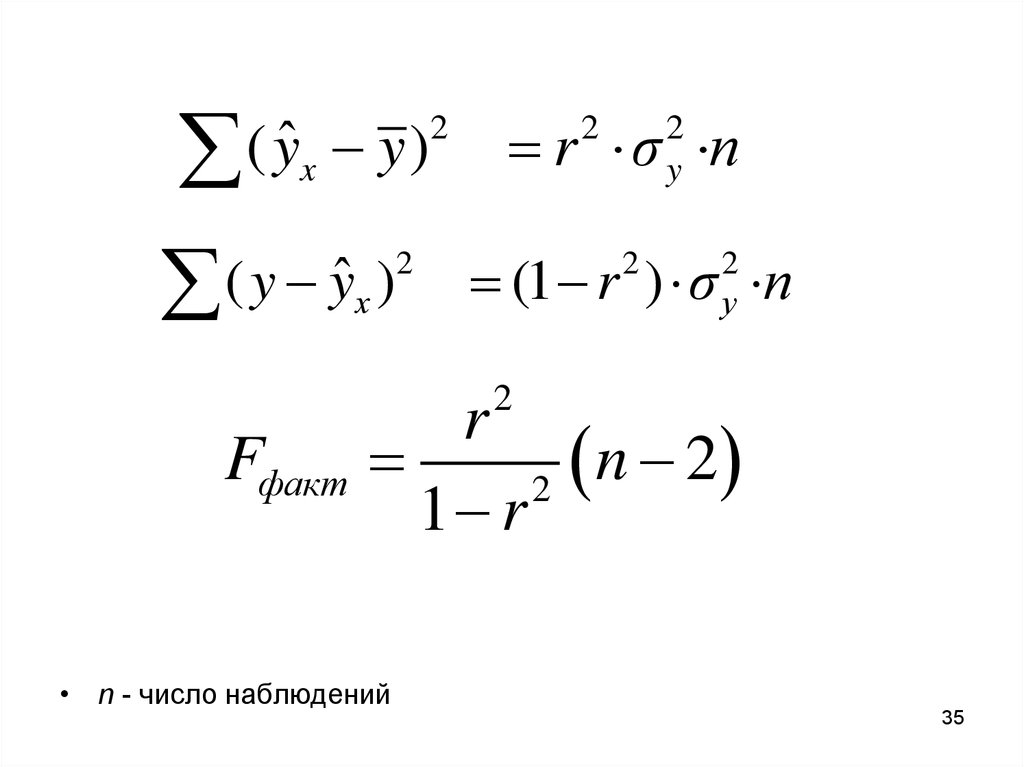




 mathematics
mathematics








