Построение и выбор аналитических моделей

1. ВЫБОР МОДЕЛИ

Лекция 9
Построение и выбор аналитических
моделей

2. ЧАСТЬ 1

Поиск аналитических
зависимостей
методом
наименьших
квадратов

3. Назначение и идея метода

Назначение метода:
Поиск аналитической зависимости z = f(x) по данным
эксперимента.
Идея метода
Полагаем известными:
а) предполагаемый вид исходной зависимости z = f(x);
б) таблицу, определяющую экспериментально полученную
зависимость уi (xi), где i - номер эксперимента
Идея состоит в поиске коэффициентов функции z=f(x)
которые бы минимизировали функцию S вида:
 
2
n
S
(y
i 1
i
z ( xi ) )
(1.1)

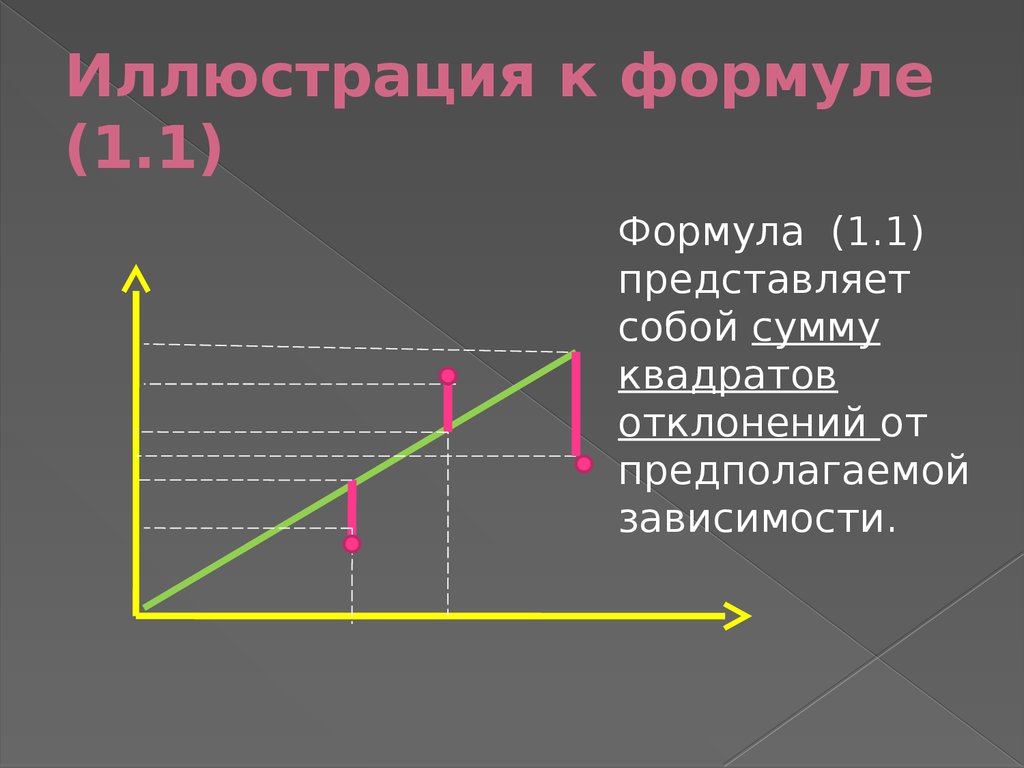
4. Иллюстрация к формуле (1.1)

Формула (1.1)
представляет
собой сумму
квадратов
отклонений от
предполагаемой
зависимости.

5. ПРИМЕР 1

Поиск коэффициентов полинома.
Пусть z(x) =c1 + c2x + c3x2 . Тогда
точке минимума функции S
соответствуют условия:
S
S
S
0;
0. (1.2
0;
c1
c3
c2

6. Полученная на основании (1.2) система уравнений

n
n
n
2
nC1 C2 xi C3 xi yi
i 1
i 1
i 1
n
n
n
2
3
C1 xi C2 xi C3 xi xi y (1.3)
i 1
i 1
i 1
n
n
n
n
2
3
3
2
C1 xi C2 xi C3 xi xi yi
i 1
i 1
i 1
i 1

7. ПОСЛЕДНИЙ ШАГ

Система (1.3) решается
относительно С1, С2, С3, что
позволяет определить вид
функции:
3
Z ( x)
c x
i 1
i
i 1

8. ЧАСТЬ 2

Решение
системы
линейных
уравнений
методом Гаусса

9. Форма представления исходных данных

Метод основан на
последовательном исключении
неизвестных. Пусть дана система
уравнений:
a11 x1
a21x1
...
a x
n1 1
a12 x2 ... a1n xn
a22 x2 ... a2 n xn
... ... ... ... ... ... ... ...
an 2 x2 ... ann xn
f1
f2
(1.4)
fn

10. Исключение x1 из (n-1) уравнений

Для этого i-ое уравнение делится на ai1,
а затем 1-ое уравнение вычитается из
всех остальных. При этом система (1.4)
принимает следующий вид:
x1
1
b12
x2 ...
1
b22 x2 ...
...
... ...
bn12 x2 ...
b11n xn
1
b2 n xn
...
...
1
bnn
xn
См. следующий слайд.
... ...
F11
1
F2
(1.5)
Fn1

11. Компоненты системы (1.5)

b
1
ij
aij
aii
a1 j
a11
fi
f1
F
ai1 a11
1
ii
i 1, n; j 1, n

12. Исключение xi в (n-i) уравнениях

Для этого в (1.5) повторяется
применительно к x2 предыдущая
процедура. Повторяя ее
последовательно для x3, x4, …, xn,
получим:1
1
x1 b12 x2 ... b11n xn
F1
2
2
x
...
b
x
F
2
2n n
2
... ... ... ... ...
(1.6)
n
xn
Fn

13. Решение системы (1.6)

Переменные системы
(1.6) вычисляются
последовательно,
начиная с xn. Т.о.
размерность матрицы
на каждой итерации
уменьшается на 1.

14. Пример 2

Поиск коэффициентов
аналитической модели,
описываемой экспонентой:
у ( x) C1e .
c2 x
(1.7)

15. Преобразование уравнения (1.7)

Логарифмируя, получим
полином:
T ln у ( x) ln C1 C2 x

16. Сведение задачи к известному виду

Таким образом, задачу вновь
удалось свести к поиску
коэффициентов полинома. Функция
S имеет вид:
2
S (ln yi Ti ) ln yi ln C1 C2 xi .
i 1
i 1
n
2
n

17. Приравнивая нулю производные, получим систему (1.8):

n ln C1 C2 xi ln yi
i 1
i 1
(1.8)
n
n
n
[ln C1 ] xi C2 xi2 xi ln yi
i 1
i 1
i 1
n
n

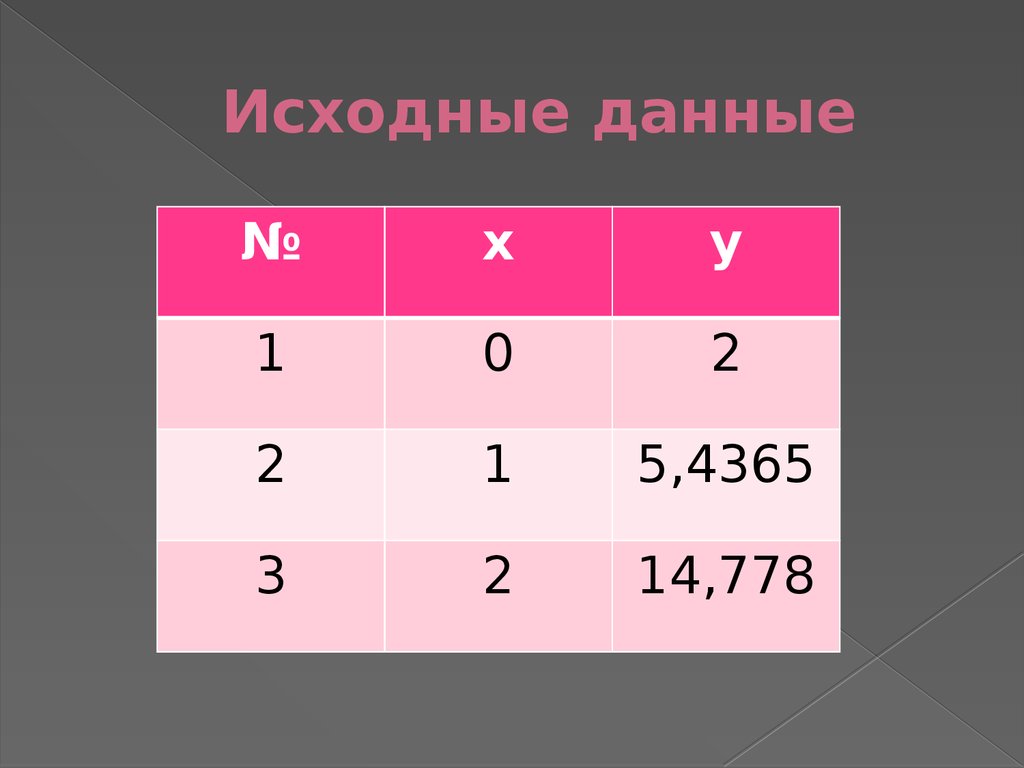
18. Исходные данные

№
х
у
1
0
2
2
1
5,4365
3
2
14,778

19. Вид системы (1.8)

3С 3C2 5,0793;
(1.9)
'
3C1 5C2 7,0793,
'
где С1 ln( C1 ).
'
1

20. Решение системы (1.9)

C1 2;
C2 1;
y 2e .
x

21. САМОСТОЯТЕЛЬНО

Поиск коэффициентов
аналитической модели,
описываемой уравнением вида:
у ( x) C1 х . (2.0)
c2
Исходные данные представлены в
таблице на следующем слайде.

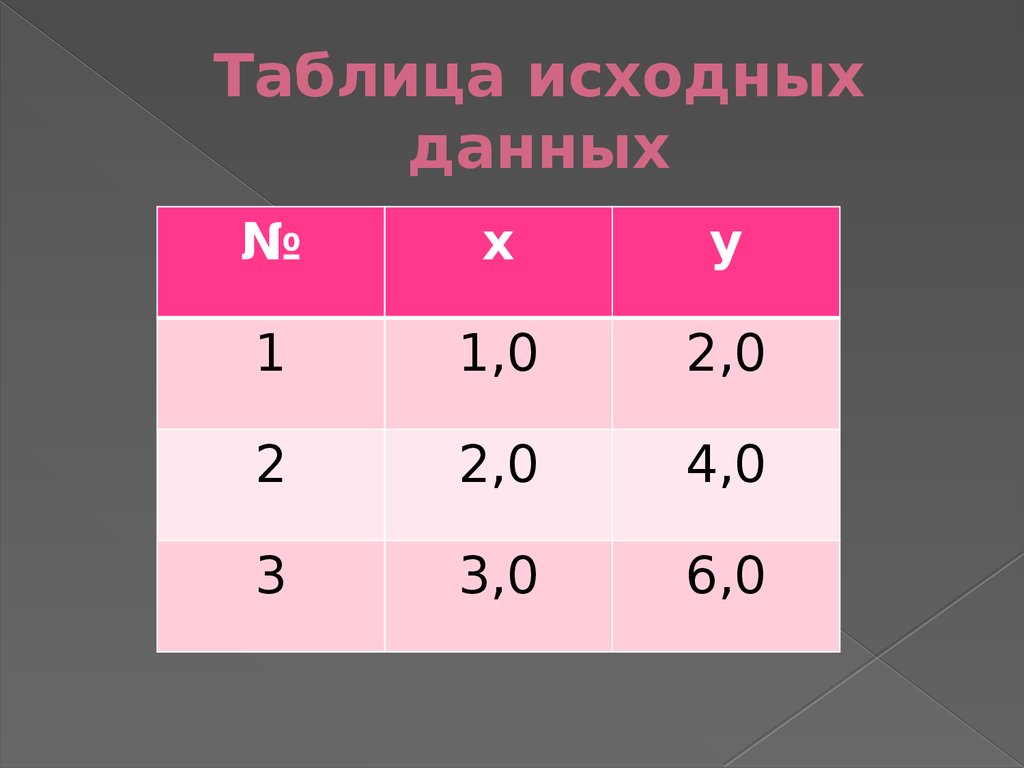
22. Таблица исходных данных

№
х
у
1
1,0
2,0
2
2,0
4,0
3
3,0
6,0

23. ЧАСТЬ 3

Выбор модели

24. Критерии качества аналитических моделей

Максимальное по абсолютной величине отклонение
от экспериментальных данных.
Квадратичное отклонение - квадратный корень из
суммы квадратов такого рода отклонений.
Среднее квадратичное отклонение - квадратный
корнем из суммы квадратов такого рода отклонений
деленный на число экспериментальных данных.
Сумма абсолютных величин отклонений от
экспериментальных данных.
Среднее абсолютное отклонение- сумма
абсолютных величин отклонений от
экспериментальных данных, деленная на число
экспериментальных данных.

25. САМОСТОЯТЕЛЬНО

Привести критерии
качества
аналитических
моделей,
отсутствующие на
предыдущем слайде.

26. Графическая интерпретация

Каждой аналитической модели у(x)
можно поставить в соответствие
некоторую точку в многомерном
пространстве, оси которого
соответствуют выбранным критериям
качества K , а конкретные значения
на этих осях отражают значения
соответствующих критериев. (см.
рис. на следующем слайде).

27. Сравнение интегрального критерия с эталоном

1
2
3
Сравнение
интегрального
критерия с эталоном
Поскольку
наилучшим
значением для
перечисленных
выше критериев
является нулевое,
качество модели
z(x) можно
оценить
расстоянием от
соответствующей
точки А до начала
координат О
К2
К3
А
0
Если имеется
несколько
моделей
такого рода,
то выбирается
та из них,
которой
соответствует
наиболее
близкая к
К1 началу
координат
точка.

28. САМОСТОЯТЕЛЬНО

Выбрать наилучшую из двух
моделей:
C2
y1 C1 ;
x
y2 C1 exp( C2 x ),
если критериями являются
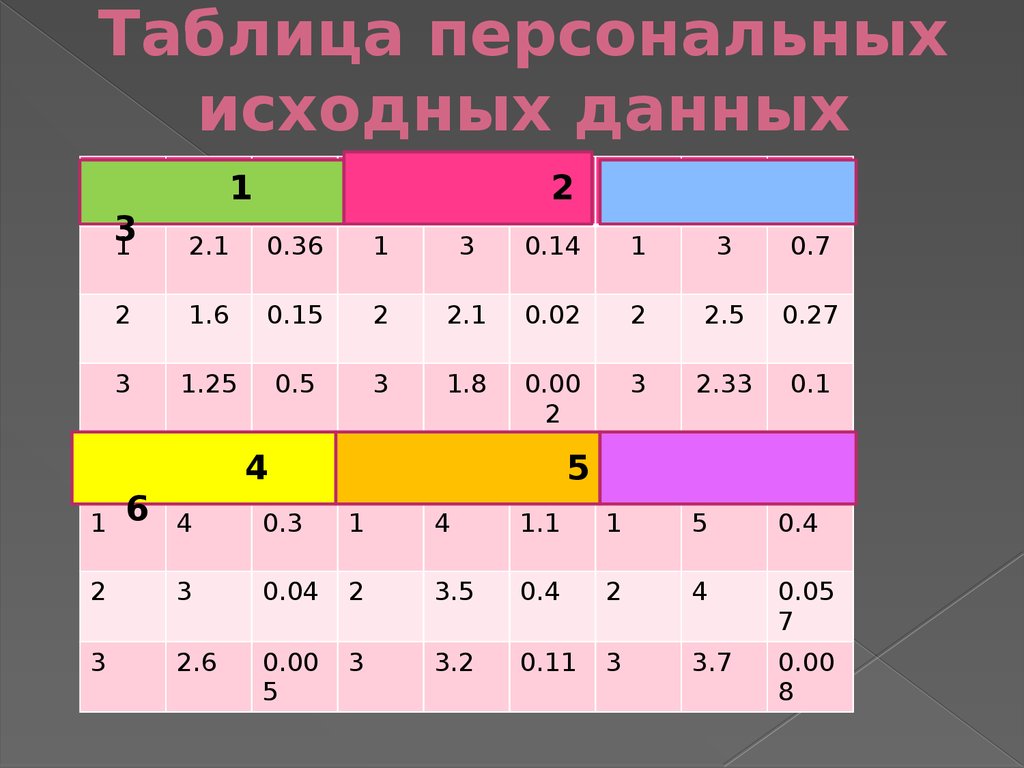
максимальное отклонение и
среднеквадратичное отклонение,
применительно к таблицам,
приведенным на следующих

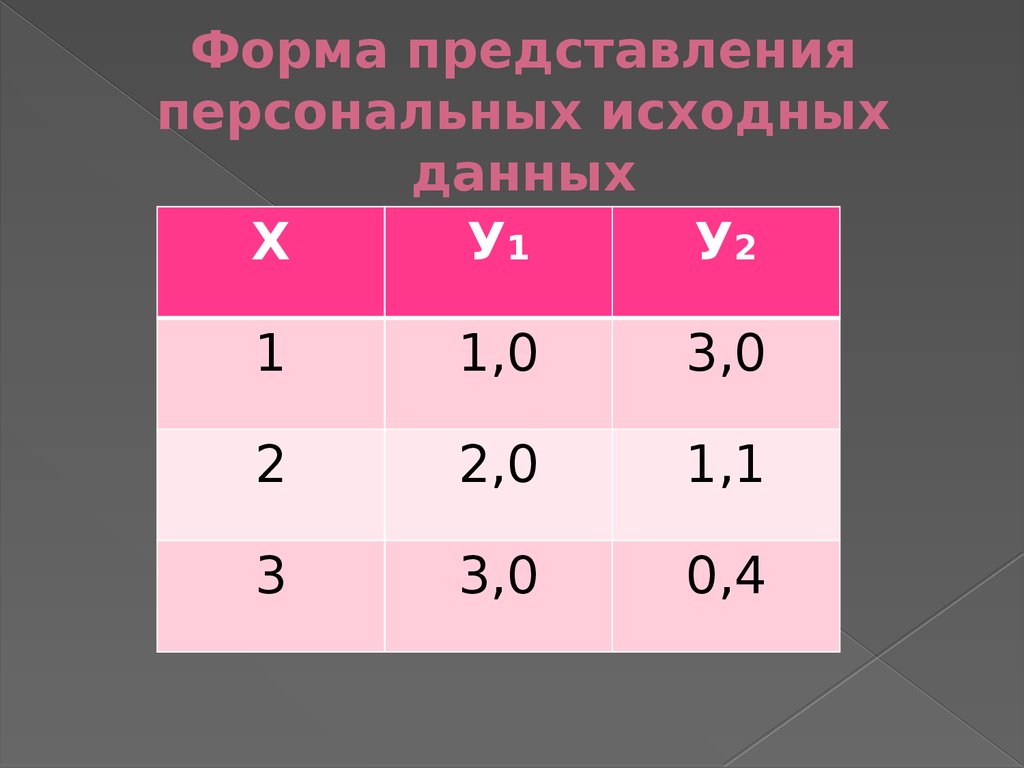
29. Форма представления персональных исходных данных

Х
У1
У2
1
1,0
3,0
2
2,0
1,1
3
3,0
0,4

30. Таблица персональных исходных данных

1
2
3
1
2.1
0.36
1
3
0.14
1
3
0.7
2
1.6
0.15
2
2.1
0.02
2
2.5
0.27
3
1.25
0.5
3
1.8
0.00
2
3
2.33
0.1
4
1
6
5
4
0.3
1
4
1.1
1
5
0.4
2
3
0.04
2
3.5
0.4
2
4
0.05
7
3
2.6
0.00
5
3
3.2
0.11
3
3.7
0.00
8

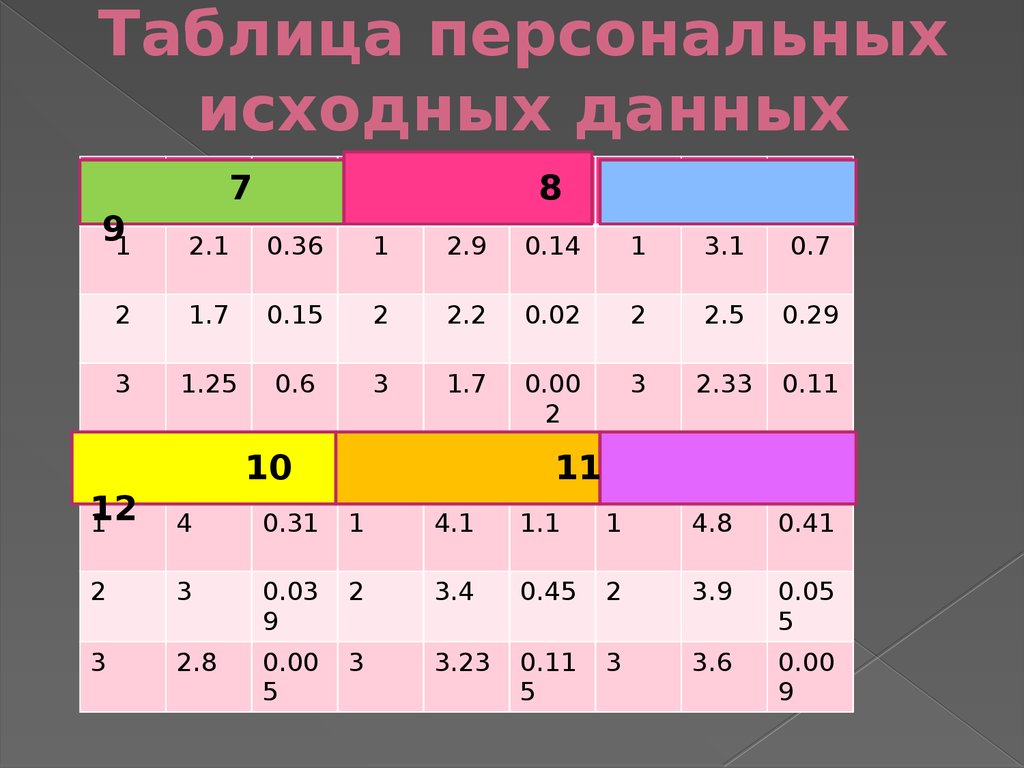
31. Таблица персональных исходных данных

7
8
91
2.1
0.36
1
2.9
0.14
1
3.1
0.7
2
1.7
0.15
2
2.2
0.02
2
2.5
0.29
3
1.25
0.6
3
1.7
0.00
2
3
2.33
0.11
10
11
12
1
4
0.31
1
4.1
1.1
1
4.8
0.41
2
3
0.03
9
2
3.4
0.45
2
3.9
0.05
5
3
2.8
0.00
5
3
3.23
0.11
5
3
3.6
0.00
9

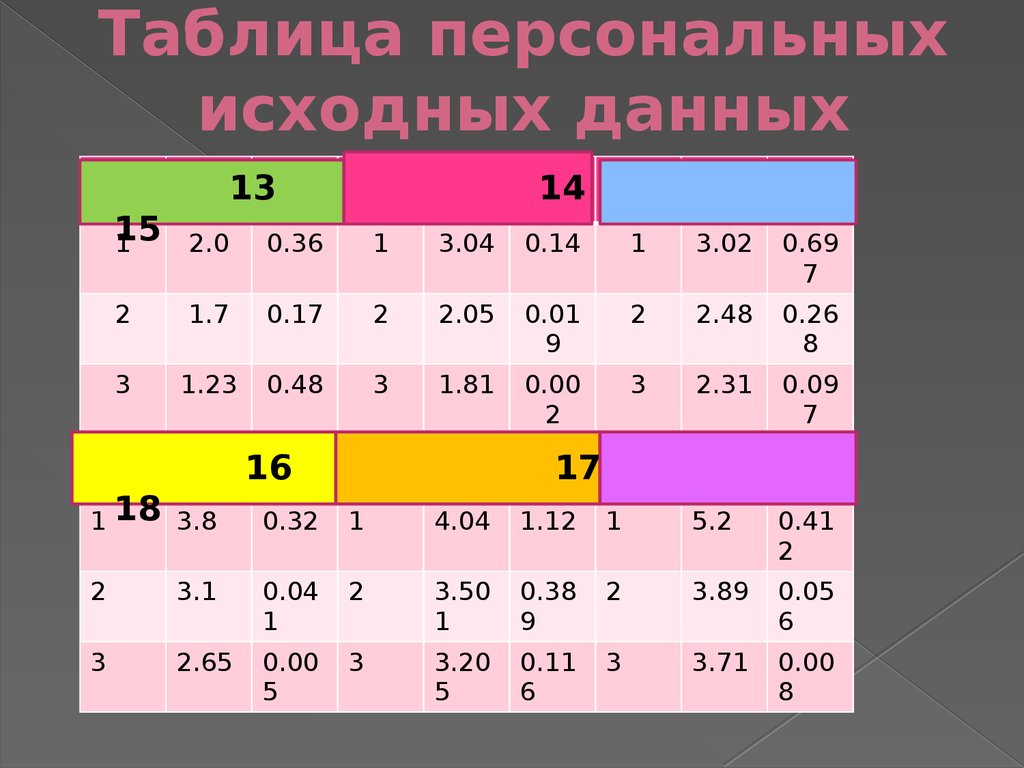
32. Таблица персональных исходных данных

13
14
15
1
2.0
0.36
1
3.04
0.14
1
3.02
0.69
7
2
1.7
0.17
2
2.05
0.01
9
2
2.48
0.26
8
3
1.23
0.48
3
1.81
0.00
2
3
2.31
0.09
7
16
1 18 3.8
17
0.32
1
4.04
1.12
1
5.2
0.41
2
2
3.1
0.04
1
2
3.50
1
0.38
9
2
3.89
0.05
6
3
2.65
0.00
5
3
3.20
5
0.11
6
3
3.71
0.00
8

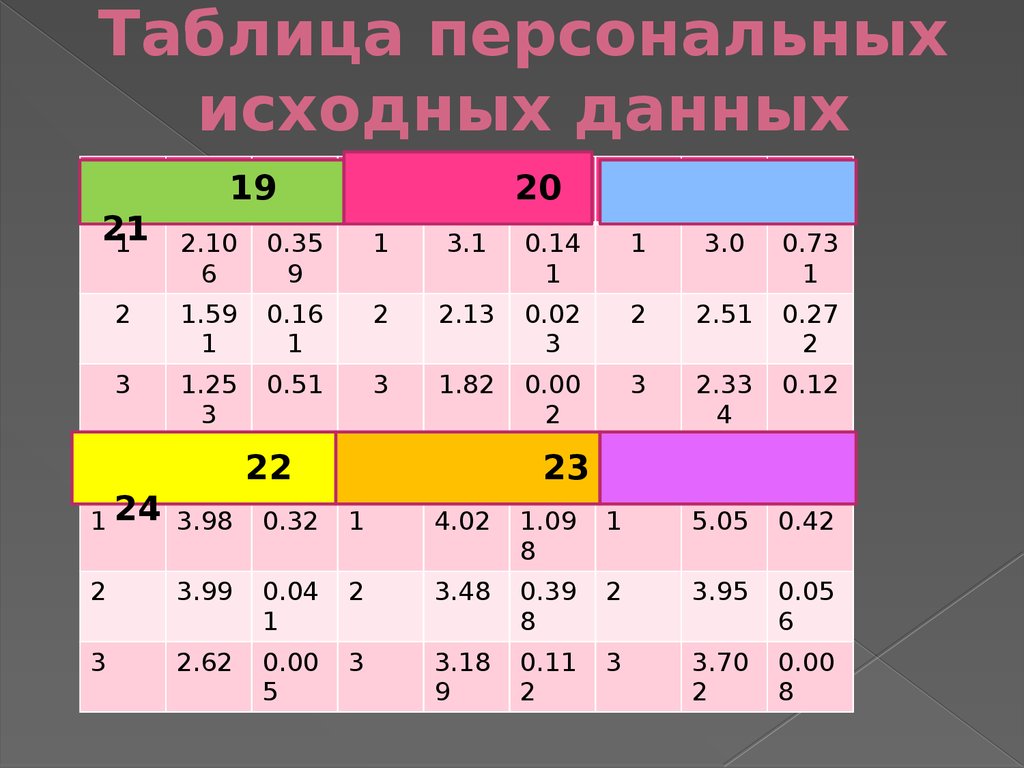
33. Таблица персональных исходных данных

19
21
1
20
2.10
6
0.35
9
1
3.1
0.14
1
1
3.0
0.73
1
2
1.59
1
0.16
1
2
2.13
0.02
3
2
2.51
0.27
2
3
1.25
3
0.51
3
1.82
0.00
2
3
2.33
4
0.12
22
1 24 3.98
23
0.32
1
4.02
1.09
8
1
5.05
0.42
2
3.99
0.04
1
2
3.48
0.39
8
2
3.95
0.05
6
3
2.62
0.00
5
3
3.18
9
0.11
2
3
3.70
2
0.00
8