Формирование гипотезы вариационного ряда для статистической модели. Анализ статистической модели

1.

Тема: 1.«Формирование гипотезы вариационного
ряда для статистической модели»
2. Анализ статистической модели.
автор: к.т.н., доц. Тимошек Игорь Николаевич

2. знакомство с некоторыми элементами аналитической алгебры и геометрии: исследование взаимосвязи между свойствами расчетного шага

Цель:
знакомство с некоторыми
элементами аналитической алгебры
и геометрии: исследование
взаимосвязи между свойствами
расчетного шага значений
вариационного ряда входных
факторов и характеристикой
нелинейности функции при
формировании гипотезы расчетных
процедур для будущей
статистической модели

3. Основные положения:

1.Форма проведения исследования
• Таблично-графическое представление информации
2.Решение поставленной цели достигается анализом:
• выявленных причинно-следственных связей между
«поведением» функции и свойствами аргумента;
• соблюдения ряда формальных условий применения
математических методов
3.Критерии анализа:
• типичные (наиболее распространенные) графики
функций
• относительный шаг изменения аргумента

4. Формулируем условия задачи

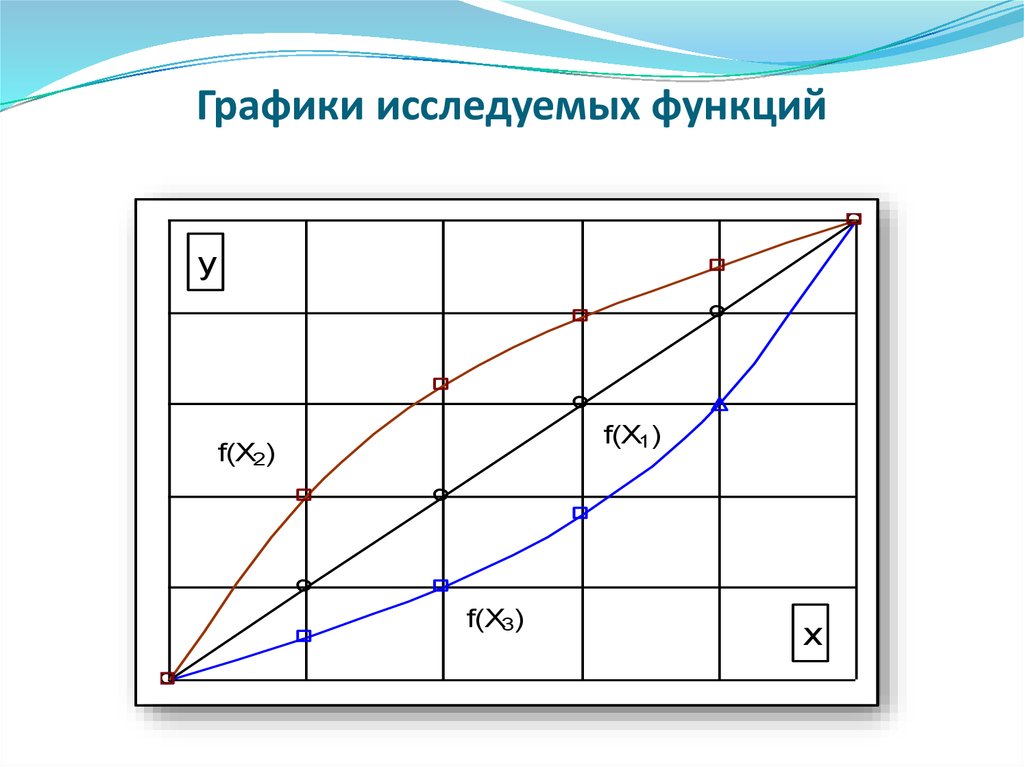
1. Для анализа указанной взаимосвязи рассмотрим
три монотонно возрастающие функции:
f(x1) – линейная функция;
f(x2), f(x3) – нелинейные выпуклая и вогнутая
соответственно (см. рисунок 6 а).;
2. Для упрощения расчетов допускается, что
значения каждой из функции равны при различных
значениях аргументов, в пределах от 0 до 5 и для
них найдется единое решение.
Так, к примеру, для аргументов при x1=1, x2=0,45, x3=2,
их функции равны у = f(x1) = f(x2) = f(x3)=1.

5. Графики исследуемых функций

у
f(Х1)
f(Х2)
f(Х3)
х

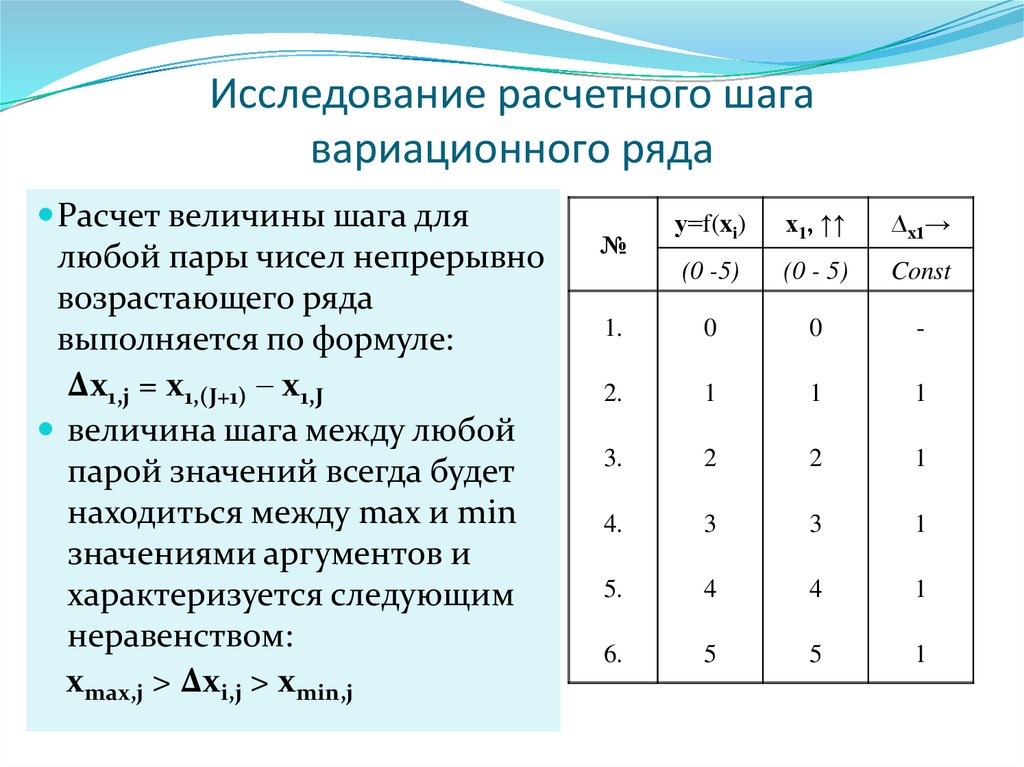
6. Исследование расчетного шага вариационного ряда

Расчет величины шага для
любой пары чисел непрерывно
возрастающего ряда
выполняется по формуле:
∆х1,j = x1,(J+1) x1,J
величина шага между любой
парой значений всегда будет
находиться между max и min
значениями аргументов и
характеризуется следующим
неравенством:
хmax,j > ∆хi,j > хmin,j
у=f(xi)
х1, ↑↑
∆х1→
(0 -5)
(0 - 5)
Const
1.
0
0
-
2.
1
1
1
3.
2
2
1
4.
3
3
1
5.
4
4
1
6.
5
5
1
№

7. Исследование расчетного шага вариационного ряда

Первая функция f(x1) выступает в роли эталонной;
она линейна и поэтому для значений указанных в
графе 3 (табл.) имеет одинаковую разницу (расчетный
шаг) между всеми парами чисел, расположенными
рядом, рассчитанную по формуле и равную единице.
∆х1,1 = ∆х1,2 = ∆х1,3= ∆х1,4 = ∆х1,5=1.
Для любых пар значений функции f(x1) для
исследуемого рада от 0 до 5 расчетный шаг имеет
постоянное значение, равный среднему значению шага
при i-том количестве опытов:
x x
xi
i max
i min
i 1
его отображение представлено на рисунке (∆х1).

8. Графики исследуемых функций

∆X
∆Х3
∆Х2
∆Х1
у

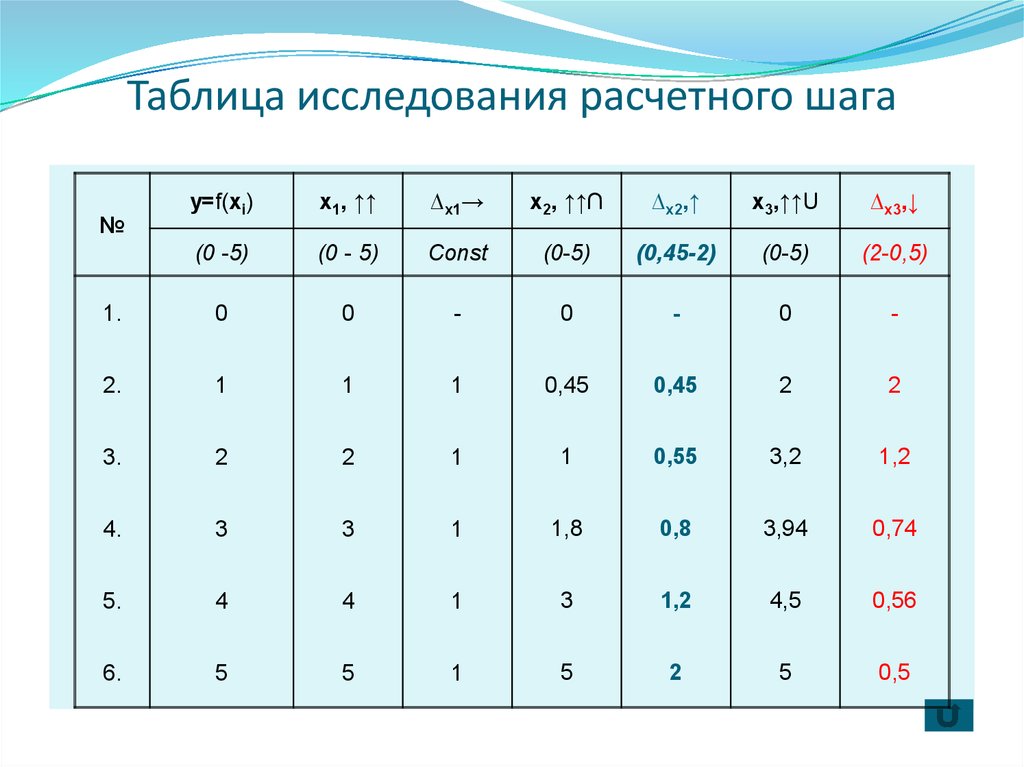
9. Исследование расчетного шага вариационного ряда

Для нелинейной возрастающей выпуклой функции
f(x2), величины расчетного шага для исследуемого
подмножества области определения от 0 до 5,
рассчитанные по формуле имеют тенденцию к
возрастанию (к тому же нелинейную).
Для нелинейной возрастающей вогнутой функции f(x3),
наблюдается тенденция к убыванию значений в
зависимости от возрастания функции.
Это наглядно демонстрируется данными таблицы
(графа 6) и графическим отображением ∆х2 и ∆х3 на
рисунке.

10. Таблица исследования расчетного шага

у=f(xi)
х1, ↑↑
∆х1→
х2, ↑↑∩
∆х2,↑
х3,↑↑U
∆х3,↓
(0 -5)
(0 - 5)
Const
(0-5)
(0,45-2)
(0-5)
(2-0,5)
1.
0
0
-
0
-
0
-
2.
1
1
1
0,45
0,45
2
2
3.
2
2
1
1
0,55
3,2
1,2
4.
3
3
1
1,8
0,8
3,94
0,74
5.
4
4
1
3
1,2
4,5
0,56
6.
5
5
1
5
2
5
0,5
№

11. Исследование расчетного шага

В результате исследований можно сделать вывод:
если простая нелинейная монотонная (или
дискретная) возрастающая функция имеет выпуклый
вид на отрезке изменения величин исследуемой
области, то расчетный шаг может принимать величины
от минимальных к максимальным значениям, и
является одной из характеристик исследуемой
функции.
если же возрастающая нелинейная функция имеет
вогнутый вид (что отражаться символами «U↑»), то шаг
между значениями аргументов в начале ряда может
иметь наоборот большую величину и уменьшаться к
концу исследуемой области до минимальной величины.

12. Формирование гипотезы вариационного ряда

Для формирования гипотезы вариационного ряда
детерминированных значений выходного фактора
студент может воспользоваться excel-программой,
разработанной автором (она находится в
компьютерном классе Г210).
Программа обеспечивает ввод, обработку,
корректировку и представление необходимой
информации о входном и выходных факторах для
использования в дальнейшем процессе проектирования
статистической модели.

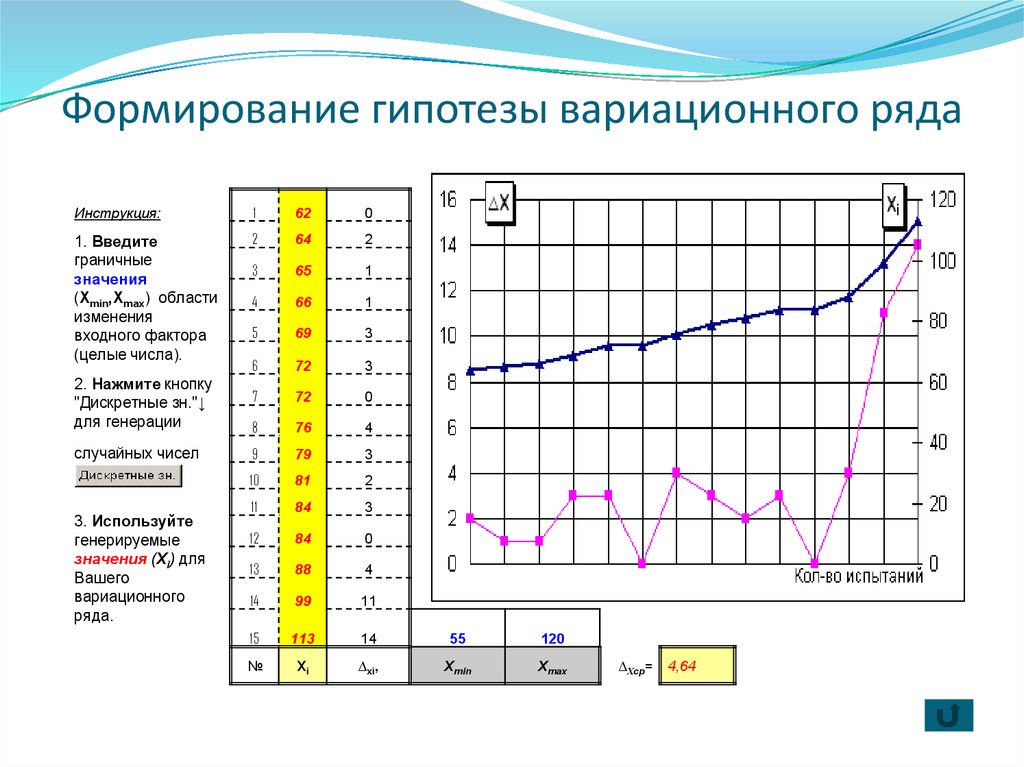
13. Формирование гипотезы вариационного ряда

1. Пользователь вводит минимальное (x1min) и
максимальное (x1max) целочисленные значения из
области для данного фактора в поля, отмеченные
синим цветом (см. пункт 1 Инструкции на рисунке).
2. Далее (согласно пункту 2) нажатием кнопки
«Дискретные зн.» программой выполняется генерация
15 случайных чисел для указанной области.
3. В результате, в желтой части таблицы выводятся
отсортированные значения возрастающего
вариационного ряда и их графический вид.
4. Выполняется расчет средней величины шага, а также
текущего шага для парных значений расчетного ряда.

14. Формирование гипотезы вариационного ряда

Инструкция:
1
62
0
1. Введите
граничные
значения
(Хmin,Хmax) области
изменения
входного фактора
(целые числа).
2
64
2
3
65
1
4
66
1
5
69
3
6
72
3
2. Нажмите кнопку
"Дискретные зн."↓
для генерации
7
72
0
8
76
4
случайных чисел
9
79
3
10
81
2
11
84
3
12
84
0
13
88
4
14
99
11
15
113
14
55
120
№
Хi
∆хi,
Хmin
Хmax
3. Используйте
генерируемые
значения (Хi) для
Вашего
вариационного
ряда.
∆Хср=
4,64

15. ПРИМЕР формирования гипотезы вариационного ряда

1. Для входного фактора модели (X1i), вносятся
натуральные значения x1min= 55 и x1max= 120 (см. рисунок)
2. Нажимается кнопка «Дискретные зн.», а результат 15-и
значений вариационного ряда выводится в табличной
форме в центральной (желтой) части таблицы.
3. Рядом со значениями входного фактора располагаются
величины шага = 2, = 1 и т.д., ср. значение ∆Хср=4,64.
4. Справа от табличного ряда располагается графическое
изображение полученного результата.
ломаной линией темно-синего цвета (с «Δ» в местах пересечения с
основной сеткой) обозначается график анализируемого входного
фактора (X1i),
ломаной линией сиреневого цвета (с «□» в местах пересечения с
сеткой) обозначается график данных расчетного шага (∆Хi).

16. Исходные данные для расчета статистической модели

1. Полученные исследователем при помощи excel-
программы данные, вносятся в табличную формушаблон по определенным правилам и согласно
установленным признакам для каждого из факторов:
значимость для процесса исследования (новый ранг);
характер взаимосвязи (↑↑, ↑↓).
№
Yi, ↑,
X1i, ↑↓,
X2i, ↑↑,
X3i, ↑↓,
X4i, ↑↓,
…
XMi, ↑↑,
п/п
(ymin - ymax)
(x1max -x1min)
(x2min-x2max)
(x3max -x3min)
(x4max-x4min)
…
(xMmin-xMmax)
1
2
3
4
5
6
…
…
1.
ymin
...
...
ymax
x1max
...
...
x1min
x2min
...
...
x2max
x3max
...
...
x3min
x4max
...
...
x4min
...
...
...
...
xMmin
...
...
xMmax
...
16.

17. Исходные данные для расчета статистической модели

2. После заполнения таблицы необходимо выполнить
анализ данных на предмет их соотносимо-значимости:
соотношение величины выходного фактора к величине
входного должно быть примерно равно - 10:1;
соотношение между величинами входных факторов
должно примерно соответствовать - 1:1.
Выполнение указанных условий обеспечит удобство
представления информации, а так же повысит
возможность качества проведения анализа результатов
моделирования.
Если условия не выполняются, то необходимо
выполнить модификацию исходных данных.

18. Модификация исходных данных

Модификация данных может осуществляется двумя
способами:
1. Применяя умножение на степенные коэффициенты 10n - (простой, но не в полной мере корректный).
2. Используя графическое отображение данных на осях
с различными шкалами – (наиболее корректный).
Xmin … X1… X2… X3… X4..…X5…… X6…… X7…… X8…… X9…… X10…… X11… X12,X13… X14… X15….Xmax
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

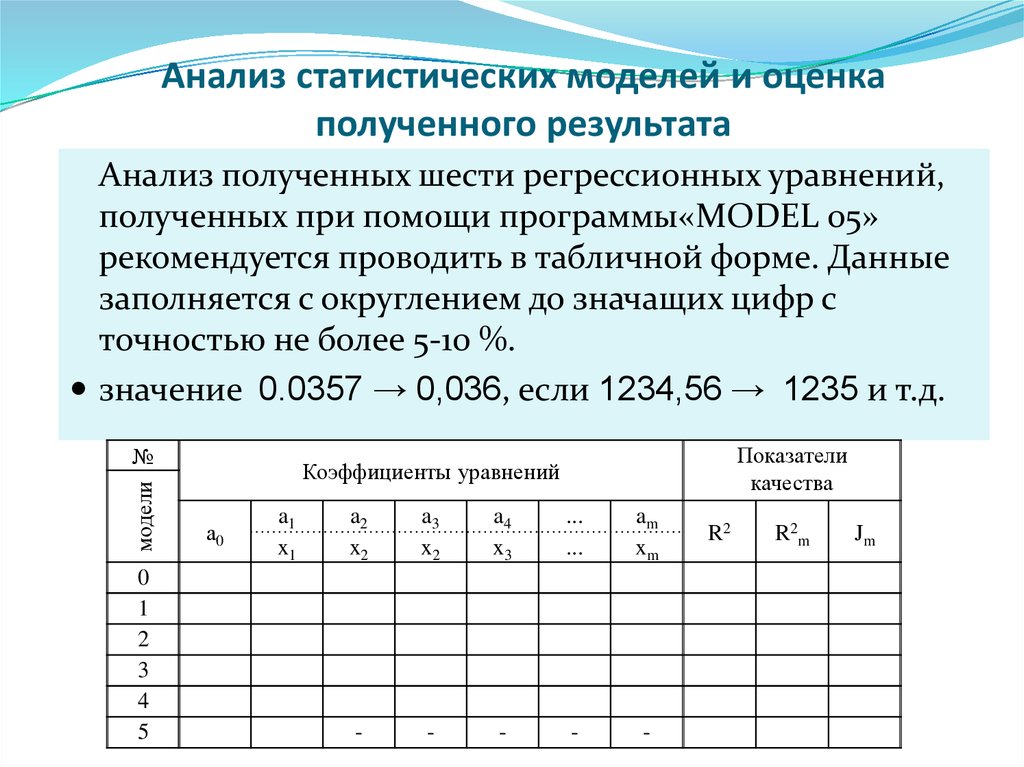
19. Анализ статистических моделей и оценка полученного результата

Анализ полученных шести регрессионных уравнений,
полученных при помощи программы«MODEL 05»
рекомендуется проводить в табличной форме. Данные
заполняется с округлением до значащих цифр с
точностью не более 5-10 %.
значение 0.0357 → 0,036, если 1234,56 → 1235 и т.д.
модели
№
0
1
2
3
4
5
Показатели
качества
Коэффициенты уравнений
а0
a1
x1
a2
x2
a3
x2
a4
x3
...
...
am
xm
-
-
-
-
-
R2
R2 m
Jm

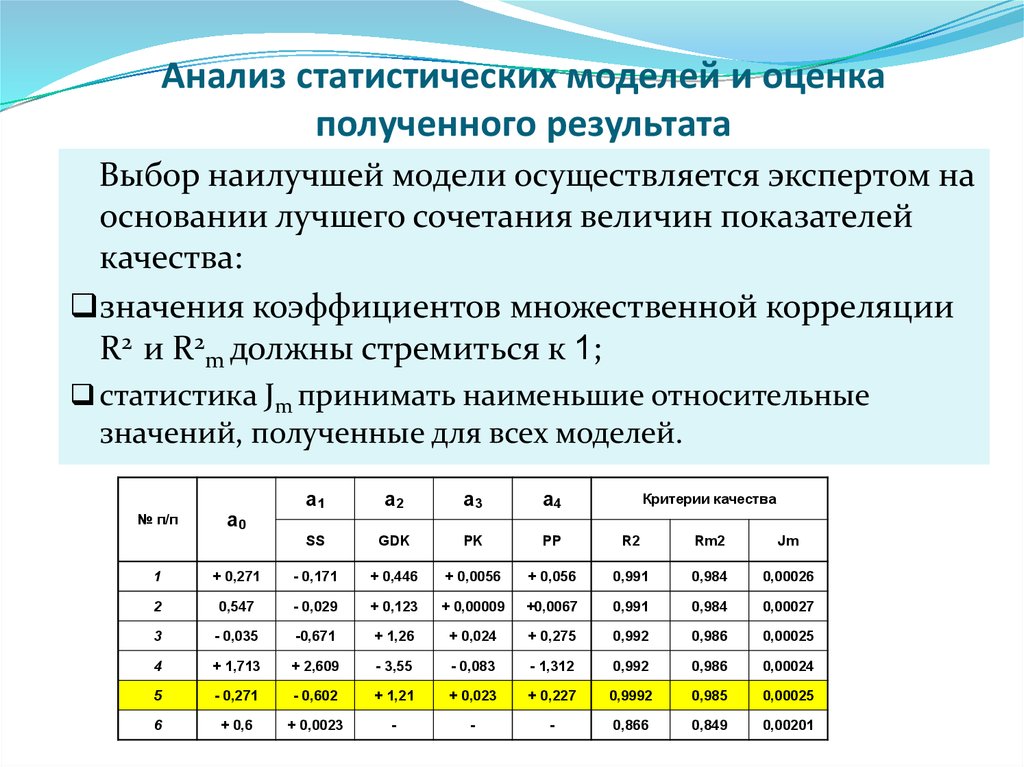
20. Анализ статистических моделей и оценка полученного результата

Выбор наилучшей модели осуществляется экспертом на
основании лучшего сочетания величин показателей
качества:
значения коэффициентов множественной корреляции
R2 и R2m должны стремиться к 1;
статистика Jm принимать наименьшие относительные
значений, полученные для всех моделей.
№ п/п
а0
а1
а2
а3
а4
SS
GDK
PK
PP
R2
Rm2
Jm
Критерии качества
1
+ 0,271
- 0,171
+ 0,446
+ 0,0056
+ 0,056
0,991
0,984
0,00026
2
0,547
- 0,029
+ 0,123
+ 0,00009
+0,0067
0,991
0,984
0,00027
3
- 0,035
-0,671
+ 1,26
+ 0,024
+ 0,275
0,992
0,986
0,00025
4
+ 1,713
+ 2,609
- 3,55
- 0,083
- 1,312
0,992
0,986
0,00024
5
- 0,271
- 0,602
+ 1,21
+ 0,023
+ 0,227
0,9992
0,985
0,00025
6
+ 0,6
+ 0,0023
-
-
-
0,866
0,849
0,00201

21. Анализ статистических моделей и оценка полученного результата

Выбранная лучшая модель из расчетных шести
регрессионных уравнений вида;
0 a0 a1 x1 a2 x2 ... an xn
1
1
1
3 a0 a1 a2 ... an
x1
x2
xn
1 a0 a1 ( x1 ) 2 a2 ( x2 ) 2 ... an ( xn ) 2
2 a0 a1Log ( x1 ) a2 Log ( x2 ) ... an Log ( xn )
4 a0 a1 x1 a2 x2 ... an xn
5 a0 a1 x1 x2 ... xn
выписывается из табличной формы в виде уравнения
Z= 39,76+0,363R2-0,025M2 +0,087PG2 -0,344PD2 +1.637PM2

22. Анализ статистических моделей и оценка полученного результата

Выбранное регрессионное уравнение подвергается
элементарной проверке на адекватность соответствия
исходным данным. Для этого:
вместо переменных входных факторов в уравнении
регрессии необходимо подставить данные одного из 16
опытов из таблицы «Исходные данные …»:
вычислить уравнение и определить величину
выходного фактора (Y).
рассчитать относительную погрешность по формуле:
y
y
y
м од
дан
i
i
м од
i
100%
мод
дан
i
i
y ,y
-значения выходного фактора, (мод)рассчитанное при помощи модели и
(дан) - взятое из таблицы исходных
данных для i-ого опыта

23. Заключение к выполненной работе

1. Итоговое заключение в целом по работе
формулируется на основании полученных результатов
в каждом из разделов работы и обязательно должно
отражать степень выполнение поставленных задач на
пути достижения сформулированной цели:
в нем кратко излагаются как достигнутые основные
результаты работы, так и нерешенные вопросы.
заключение не должно содержать ни чего того, что не
касается выполняемых исследований и, а также не
должны представляться результаты, полученные
другими исследователями;

24. Заключение должно содержать:

краткую характеристику актуальности выбранной тематики и степени ее
изученности, а также личную мотивацию на ее выполнение;
описание системы сбора (выбора) данных для проектирования модели;
краткое описание вида и структуры полученной модели допущений, а
также других особенностей, применяемых при проектировании;
сравнительную характеристику значимости наиболее важных входных
факторов модели на исследуемый результат, с учетом информации
соответствия итогам экспертной характеристики;
сформулированные предположения о практическом использовании
проведенного исследования и полученной аналитической модели;
перспективу продолжения работы по выбранной тематике;
влияние на подготовку кадров и повышение квалификации
оперативного персонала;
влияние разработанного элемента малозатратной технологии на
реализацию общей технологии перевозочного процесса.

25. ПРИМЕР :

Проблема рационального нормирования расхода топлива для с учетом
местных особенностей и условий организации движения поездов является
одной из перспективных составляющих Программы развития железных
дорог на среднесрочную перспективу.
Процесс выбора структуры модели, расчета коэффициентов уравнения и
критериев качества осуществляется с помощью программы “MODEL”,
поэтапным анализом полученного результата, усложнением модели и
перебором различных вариантов входных переменных.
В основе сбора статистических данных лежит анализ маршрутов
машинистов и скоростимерных лент на участке М. Горький - Морозовская.
В результате проведенных расчетов и анализа получаемых различных
структур модели, получена модель для целей прогнозирования месячного
удельного расхода топлива депо с лучшими показателями качества:
P = - 11602 + 110,6∙Q + 630,2∙Vуч + 186,9∙Nтр + 464,5∙Nост + 71,3∙Nсв

26. ПРИМЕР :

Анализ полученной модели позволяет сделать вывод, что наиболее
влияющими факторами эксплуатационных затрат на организацию
движения поездов на участке М. Горький – Морозовская являются
участковая скорость и количество остановок поездов из-за запрещающих
показаний светофоров как на перегонах, так и при приеме на станции.
Структура модели степень влияния входных факторов полностью
совпадает предшествующей гипотезе и экспертной характеристике.
Относительная погрешность расчетов по модели, составляющая не более
3,5 % для различных значений из вариативной области;
она может быть использована в эксплуатационной работе депо станции
М.Горький для нормирования потребления электрической энергии на тягу
поездов в нечетном направлении.
Для внедрения полученной модели в производственный процесс
необходимо проведение обучающих семинаров для теплотехника депо и
машинистов электровозов.
Ее внедрение не повлияет на изменение общей технологии перевозочной
работы, а только дополнит процесс нормирования электроэнергии.

27.

Пожелания и предложения можно высказывать:
лично - аудитория А 204;
или письменно - [email protected]