Similar presentations:
Этапы расчета прогнозных значений с помощью корреляционно-регрессионного анализа (многофакторная модель)
1. этапы расчета прогнозных значений с помощью корреляционно-регрессионного анализа (многофакторная модель)
ЭТАПЫ РАСЧЕТА ПРОГНОЗНЫХ ЗНАЧЕНИЙС ПОМОЩЬЮ КОРРЕЛЯЦИОННОРЕГРЕССИОННОГО АНАЛИЗА
(МНОГОФАКТОРНАЯ МОДЕЛЬ)
2. Исходные данные
Наоснове
статистических
данных,
представленных в таблице, выявить
причинно-следственные
зависимости
между
показателями,
количественно
оценить тесноту связи и рассчитать
прогнозные значения на последующие
два месяца.
3. Исходные данные
Датаянв.08
фев.08
мар.08
апр.08
май.08
июн.08
июл.08
авг.08
сен.08
окт.08
ноя.08
дек.08
янв.09
фев.09
мар.09
апр.09
май.09
июн.09
июл.09
авг.09
сен.09
окт.09
ноя.09
дек.09
Y
16 160
23 240
17 200,52
30 642,61
27 072,20
20 852,37
34 611,48
38 620
17 340
35 576,32
7 346,14
8 490
7 063,24
16 728,02
13 673,71
9 813,96
9 104
33 835,22
32 343,30
21 470
8 008,51
8 415,75
9 553,95
12 392,22
X1
51 956,60
58 174,30
56 474,68
59 717,99
54 231,12
50 579
65 163
53 281
51 245
39 921,50
36 355,70
34 500
36 780
34 500
36 441
39 921,50
45 183
36 897
41 534,70
32 890
35 670,60
31 230
33 450,80
34 500
X2
1 521 102,60
2 075 307,30
3 111 711,45
3 815 843,21
3 453 306,93
3 060 939,64
5 844 803,26
7 407 108,39
2 247 556,27
5 390 191,03
520 377,04
1 152 246,20
34 323,84
1 223 140,80
695 371,17
749 840,74
581 770,68
2 921 998,60
3 149 584,34
1 692 286,38
321 347,22
1 019 497,36
475 896,36
567 222,46
X3
19
19
19
18
18
20
21
21
21
21
21
21
21
18
18
18
17
14
14
14
14
14
14
14
4. Последовательность этапов
После сбора информации и анализаисходных
данных,
первоначально
необходимо
произвести
корреляционный
анализ,
путем
построения матрицы коэффициентов
парной
корреляции,
отражающей
тесноту связи между показателями.
5. Последовательность этапов
!!! Одним из условий регрессионной модели являетсяпредположение
о
функциональной
независимости
объясняющих переменных. Высокая корреляция между
входными переменными модели (Х) множественной
линейной
регрессии
называется
мультиколлинеарностью.
Мультиколлинеарность вызывает неустойчивость работы
модели, когда коэффициенты регрессии сильно меняются
даже при незначительном изменении исходных данных.
Считают явление мультиколлинеарности в исходных
данных
установленным,
если
коэффициент
парной
корреляции между двумя переменными больше 0,8. Для
борьбы с данным явлением используются различные
методы, такие как исключение сильно коррелированных
переменных, комбинирование переменных и др.
6. Последовательность этапов
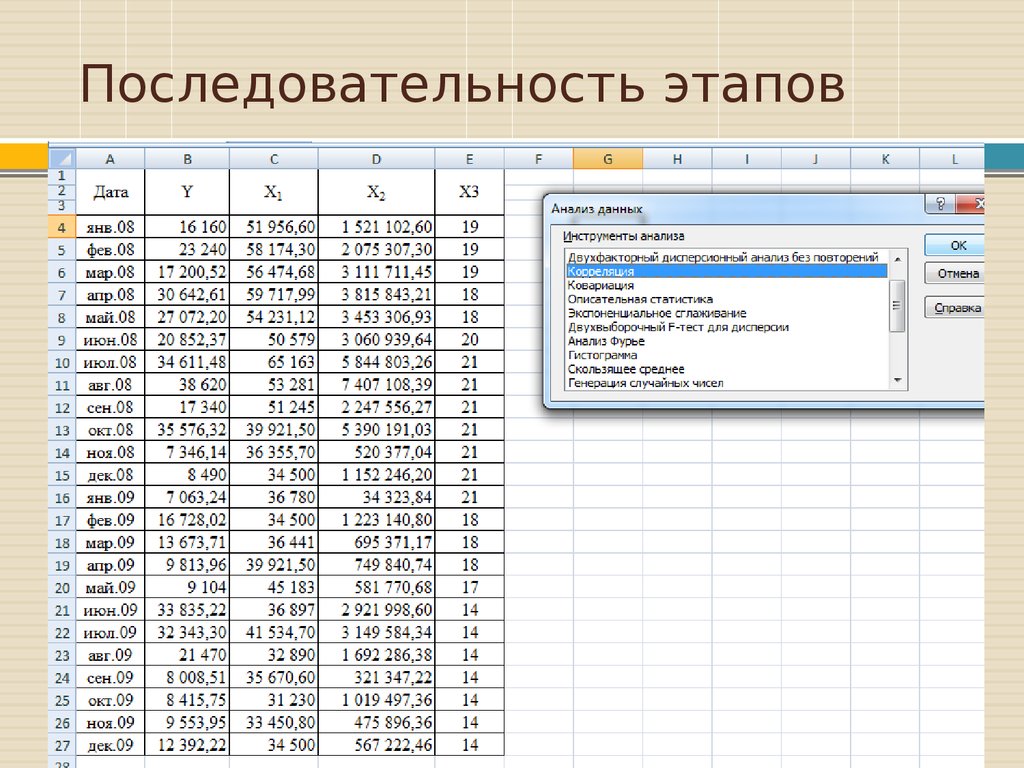
Для проведения корреляционногоанализа можно воспользоваться
пакетом анализа MS Excel, выбрав
вкладку «Данные» => «Анализ
данных» => «Корреляция».
7. Последовательность этапов
8. Последовательность этапов
Диалоговое окно «Корреляция»:9. Последовательность этапов
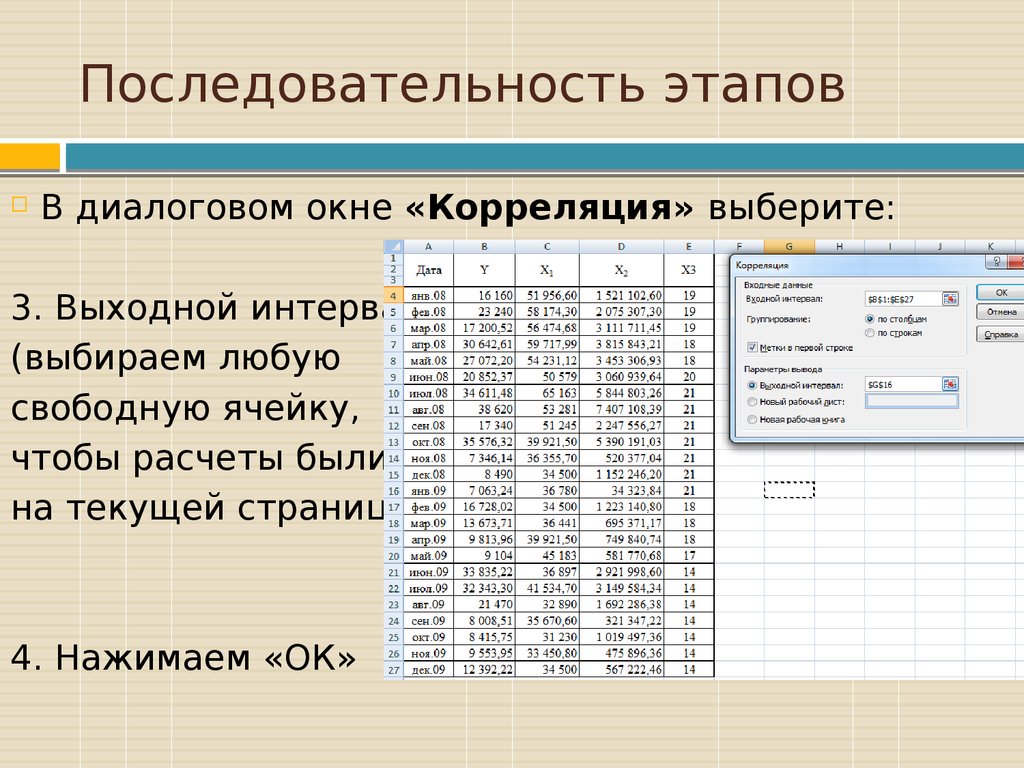
В диалоговом окне «Корреляция»выберите:
1. Входной интервал:
все исходные данные,
включая У и все
* Для наглядности
и
факторы
Х
удобства выделять
данные необходимо с
названием столбца,
для этого в
диалоговом окне
необходимо
поставить
10. Последовательность этапов
В диалоговом окне «Корреляция» выберите:3. Выходной интервал
(выбираем любую
свободную ячейку,
чтобы расчеты были
на текущей странице)
4. Нажимаем «ОК»
11. Последовательность этапов
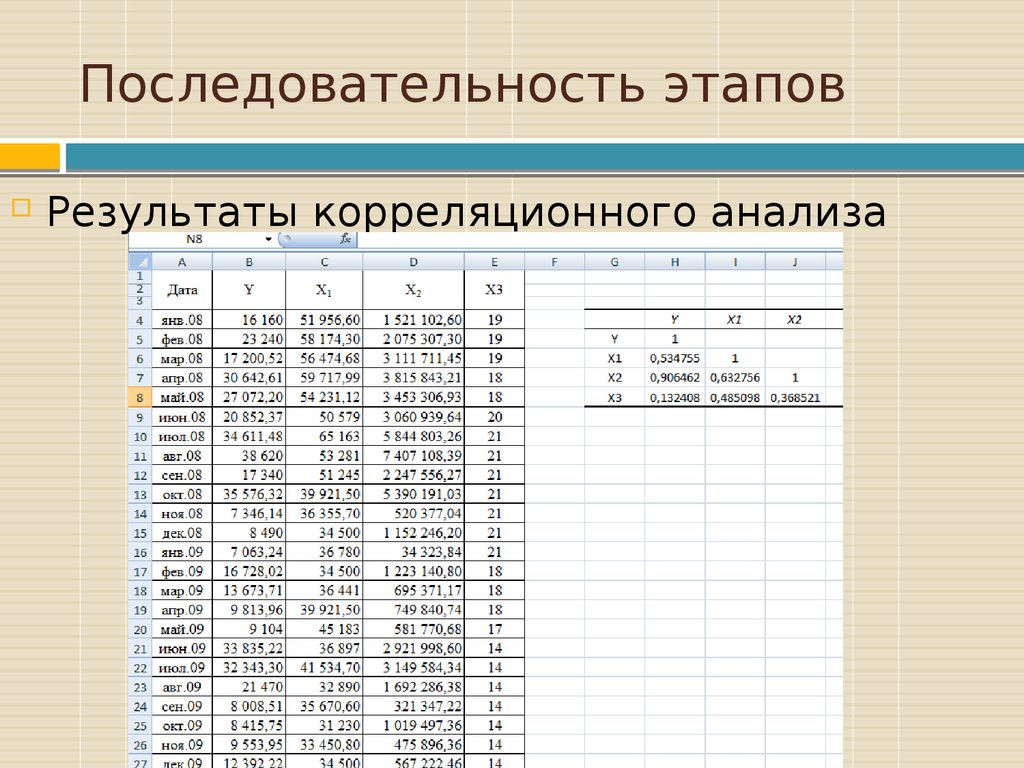
Результаты корреляционного анализа12. Последовательность этапов
На основе анализа матрицы оценоккоэффициентов парной корреляции
можно сделать вывод о том, что в
рассматриваемом примере явления
мультиколлинеарности
не
наблюдается, что свидетельствует об
отсутствии
функциональной
зависимости между переменными.
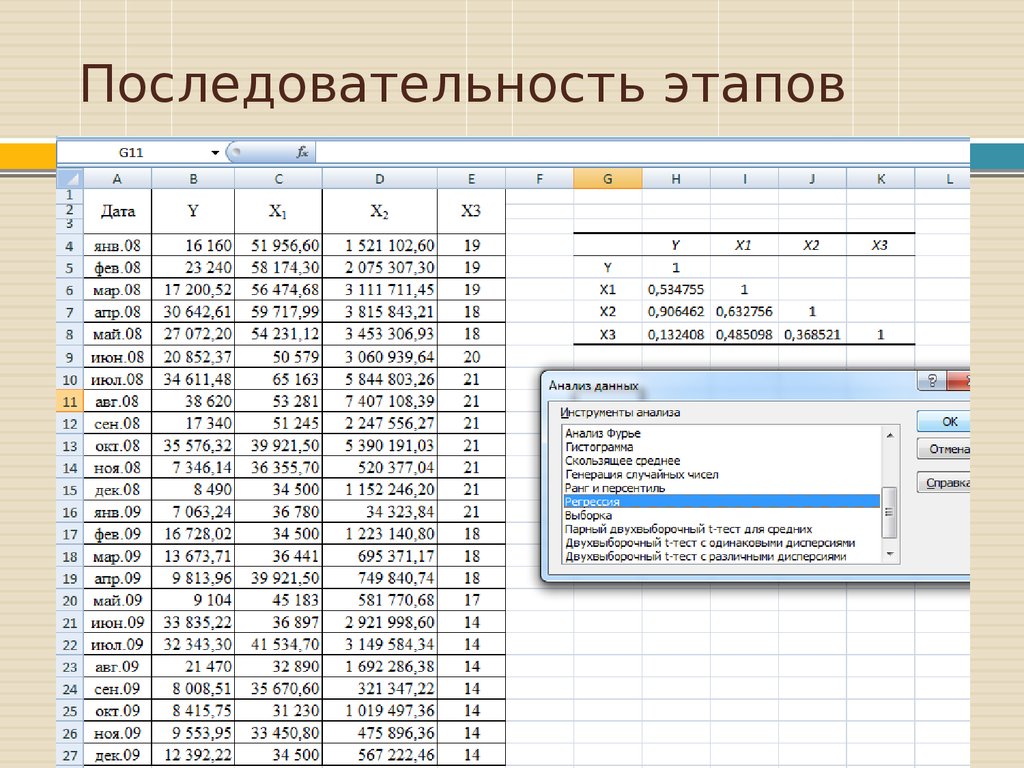
13. Последовательность этапов
Далее необходимо провестирегрессионный анализ, для этого
можно воспользоваться пакетом
анализа MS Excel, выбрав вкладку
«Данные» => «Анализ данных» =>
«Регрессия».
14. Последовательность этапов
15. Последовательность этапов
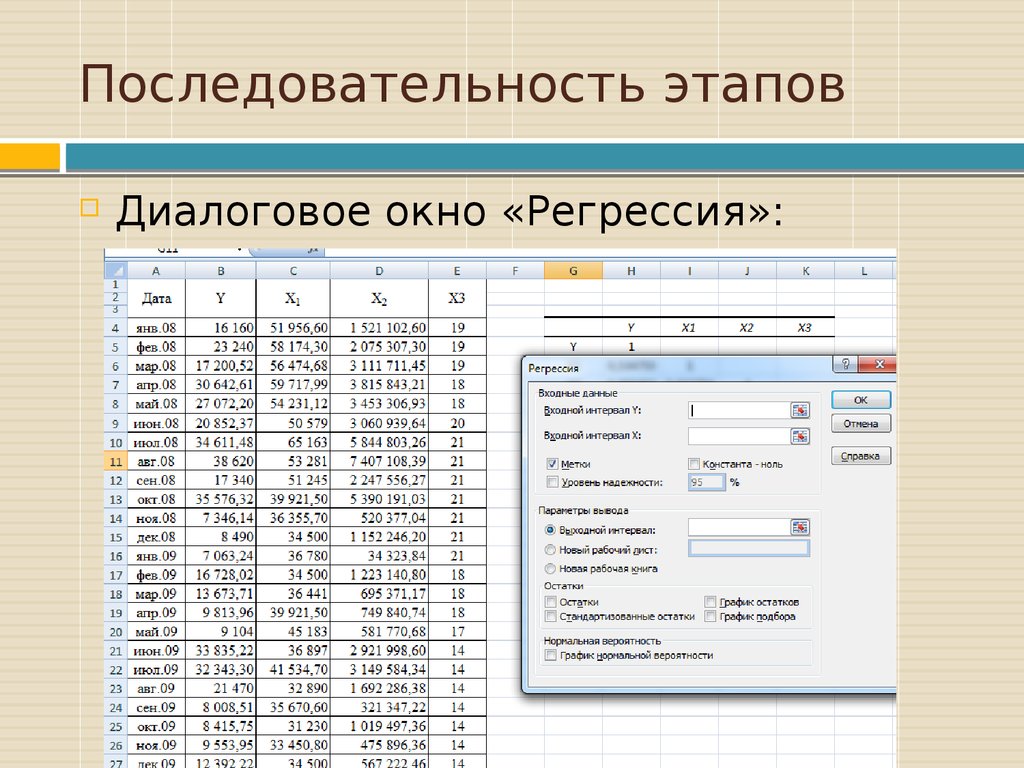
Диалоговое окно «Регрессия»:16. Последовательность этапов
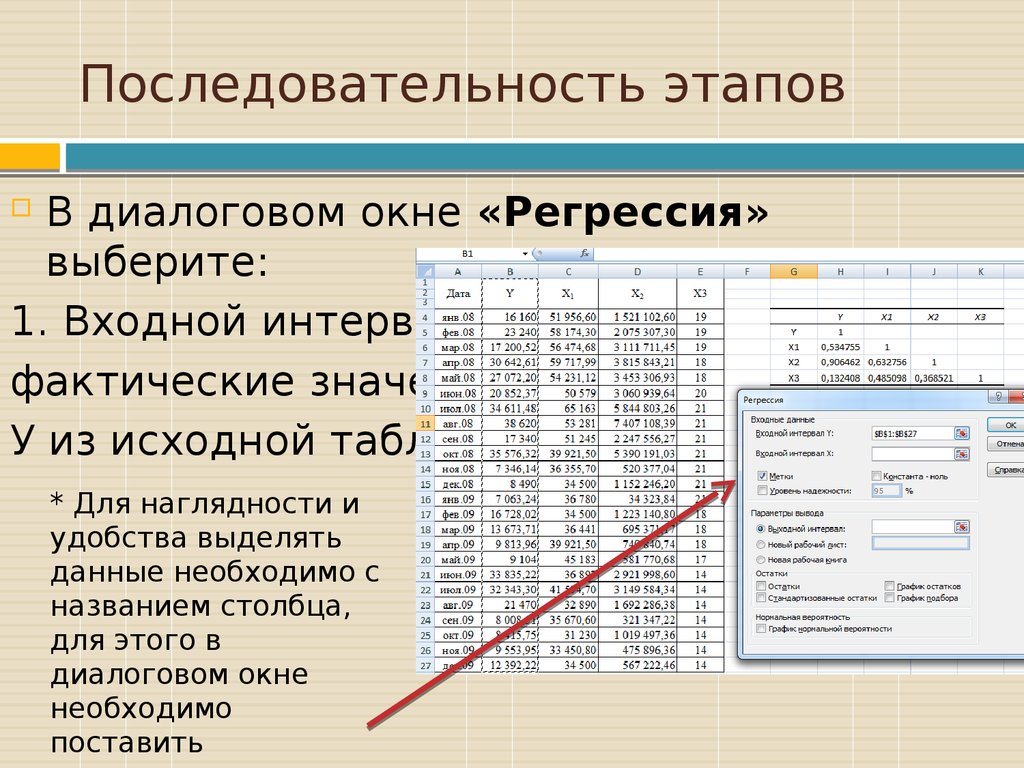
В диалоговом окне «Регрессия»выберите:
1. Входной интервал У:
фактические значения
У из исходной таблицы
* Для наглядности и
удобства выделять
данные необходимо с
названием столбца,
для этого в
диалоговом окне
необходимо
поставить
17. Последовательность этапов
В диалоговом окне «Регрессия»выберите:
2. Входной интервал Х:
значения всех факторов Х
из исходной таблицы
18. Последовательность этапов
В диалоговом окне «Регрессия» выберите:3. Выходной интервал
(выбираем любую
свободную ячейку,
чтобы расчеты были
представлены
на текущей странице)
4. Нажимаем «ОК»
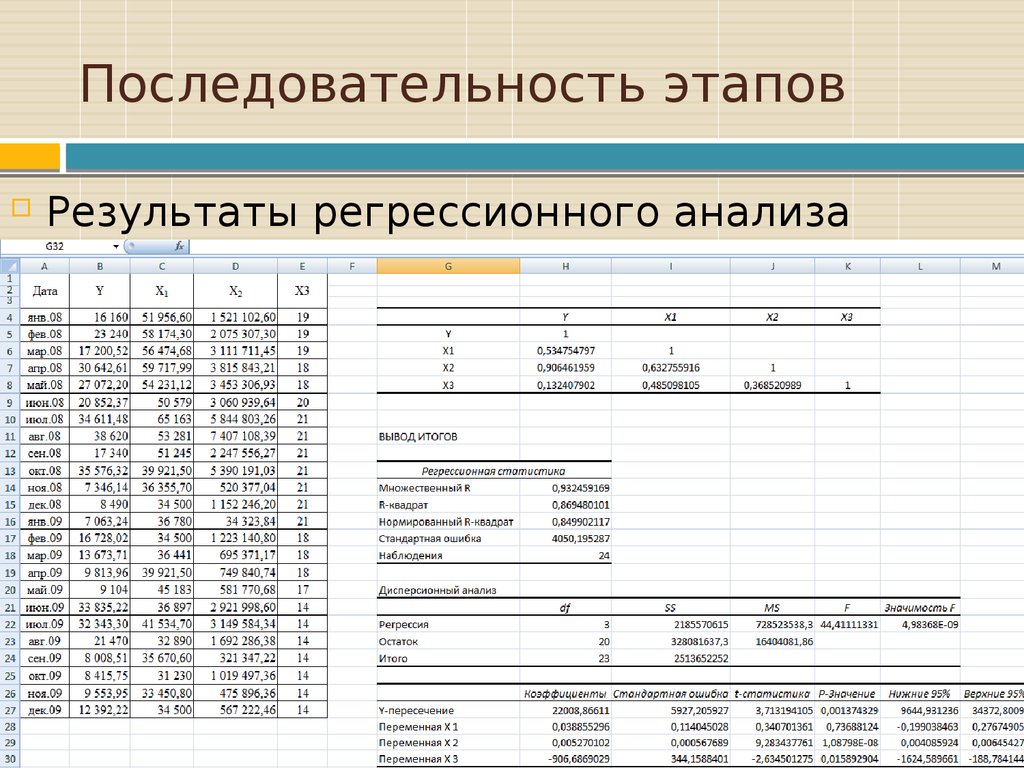
19. Последовательность этапов
Результаты регрессионного анализа20. Последовательность этапов
Главная цель регрессионного анализа – этовыявление существенных факторов (Х),
влияющих на исследуемый показатель (У).
Для
того,
чтобы
определить,
какие
факторы
являются
существенными,
необходимо сравнить полученные значения
«t-статистика»,
которые
дают
более
точную оценку значимости коэффициентов,
с рассчитанным t-критерием Стьюдента.
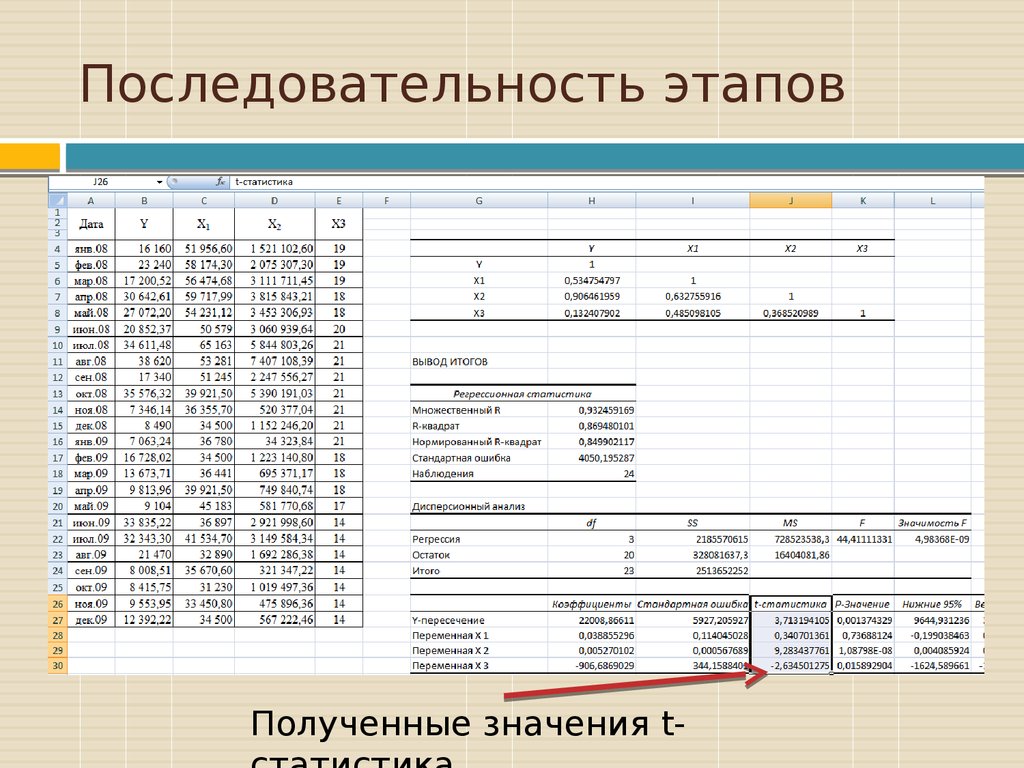
21. Последовательность этапов
Полученные значения t-22. Последовательность этапов
Для того чтобы рассчитать t-критерийСтьюдента, необходимо воспользоваться в
MS Excel функцией «СТЬЮДРАСПОБР».
23. Последовательность этапов
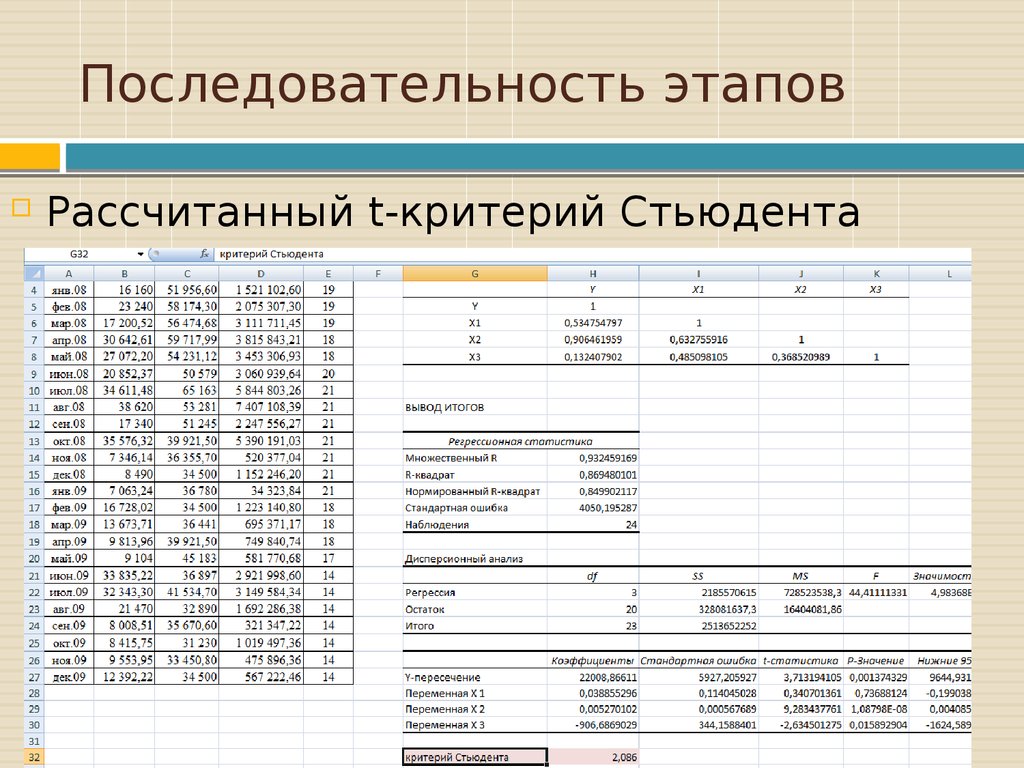
Рассчитанный t-критерий Стьюдента24. Последовательность этапов
Если |tстат. | < tкр. Ст. значит,рассматриваемый фактор не является
статистически значимыми (то есть
является несущественным).
Если | tстат. |> tкр. Ст. значит, коэффициент
является статистически значимыми (то
есть является несущественным).
25. Последовательность этапов
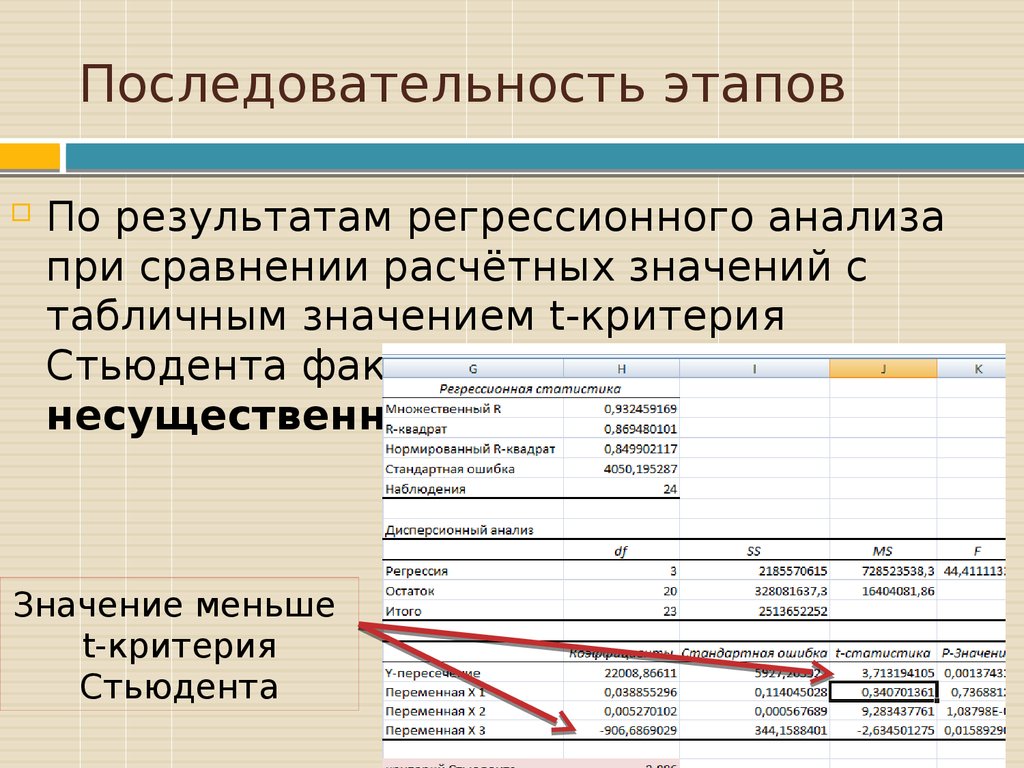
По результатам регрессионного анализапри сравнении расчётных значений с
табличным значением t-критерия
Стьюдента фактор Х1 является
несущественным.
Значение меньше
t-критерия
Стьюдента
26. Последовательность этапов
Таккак
фактор
Х1
является
несущественным,
следовательно,
его
необходимо исключить из анализа и
провести
регрессионный
анализ
с
оставшимися факторами ЗАНОВО!!!
27. Последовательность этапов
Результатызаново
регрессионного анализа
проведенного
28. Последовательность этапов
Далее заново определяем какие факторыявляются существенными, путем сравнения
полученных значений «t-статистика» с
рассчитанным t-критерием Стьюдента.
29. Последовательность этапов
Заново пересчитываем t-критерийСтьюдента, воспользовавшись в MS Excel
функцией «СТЬЮДРАСПОБР».
30. Последовательность этапов
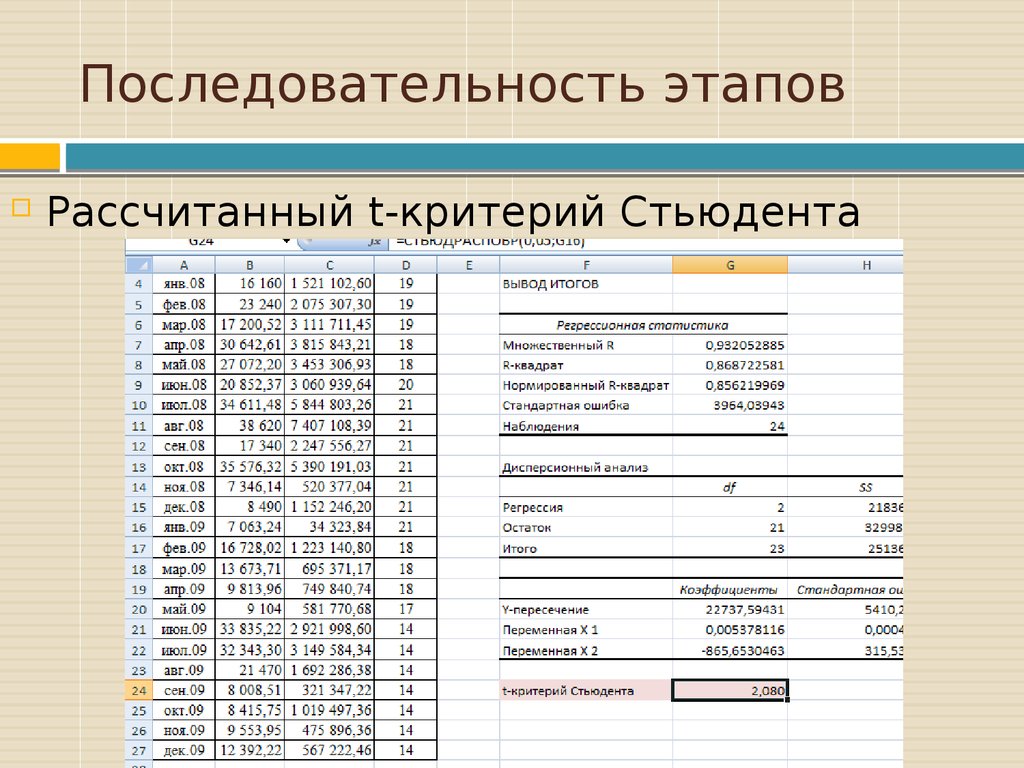
Рассчитанный t-критерий Стьюдента31. Последовательность этапов
По результатам повторногорегрессионного анализа при сравнении
расчётных значений с табличным
значением t-критерия Стьюдента все
факторы является существенным.
32. Последовательность этапов
Также результатом регрессионногоанализа являются рассчитанные
коэффициенты уравнения регрессии.
Коэффициенты
уравнения регрессии
33. Последовательность этапов
Таким образом, уравнение регрессииимеет следующий вид:
У = 22737,59 + 0,005 * Х2 – 865,653 *
Х3
Прогнозные значения Y определяются
путём последовательной подстановки
в эту модель значений факторов Х2 и
Х3, взятых для каждого момента
времени t.
34. Последовательность этапов
Дляпрогнозирования
значений
факторов
Х2
и
Х3
необходимо
использовать
метод
прогнозной
экстраполяции.
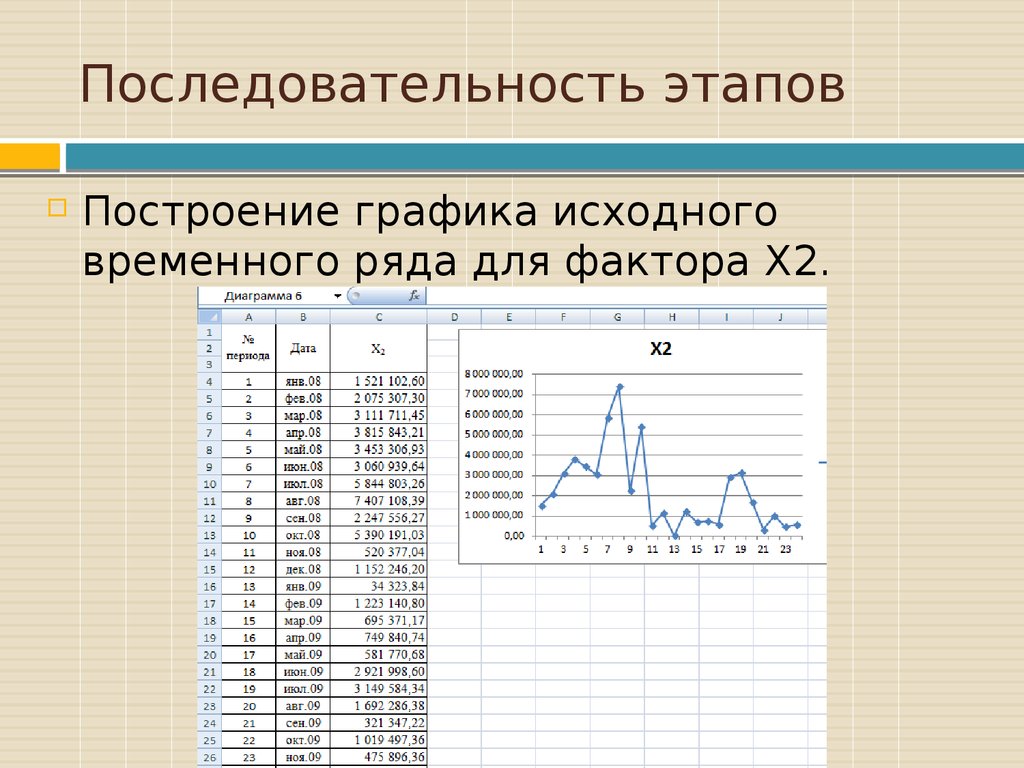
35. Последовательность этапов
Построение графика исходноговременного ряда для фактора Х2.
36. Последовательность этапов
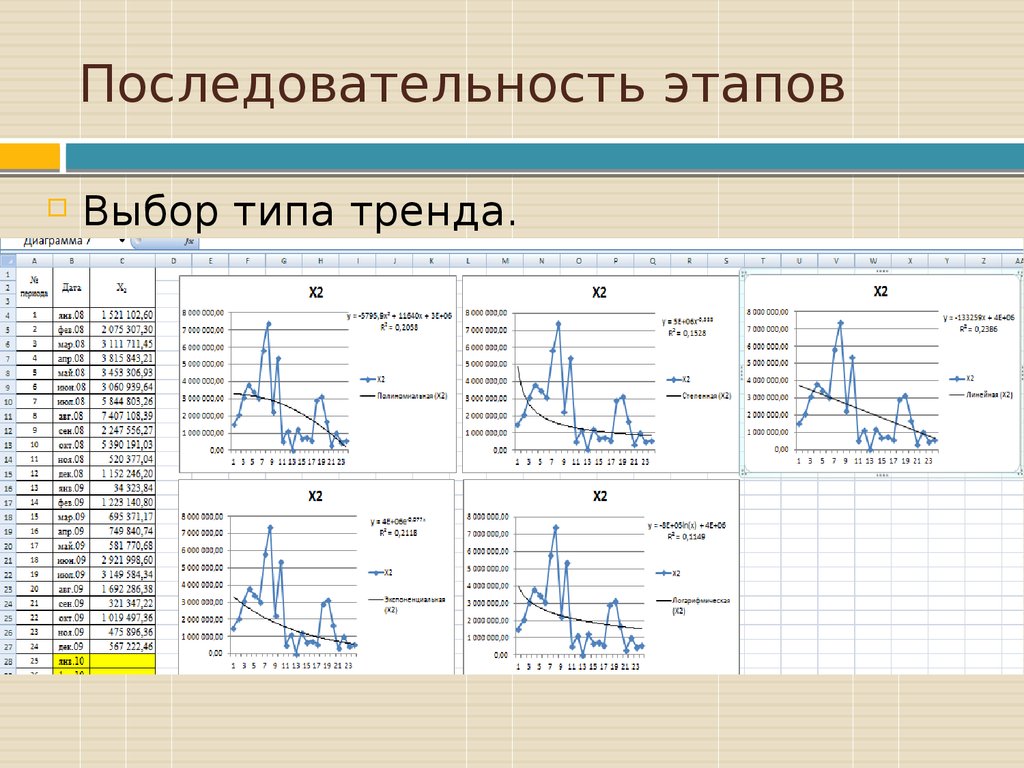
Выбор типа тренда.37. Последовательность этапов
Болееточные
значения
прогнозируемой переменной можно
получить,
если
воспользоваться
Линейным уравнением линии тренда
(так как R^2 принимает максимальное
значение по сравнению с другими).
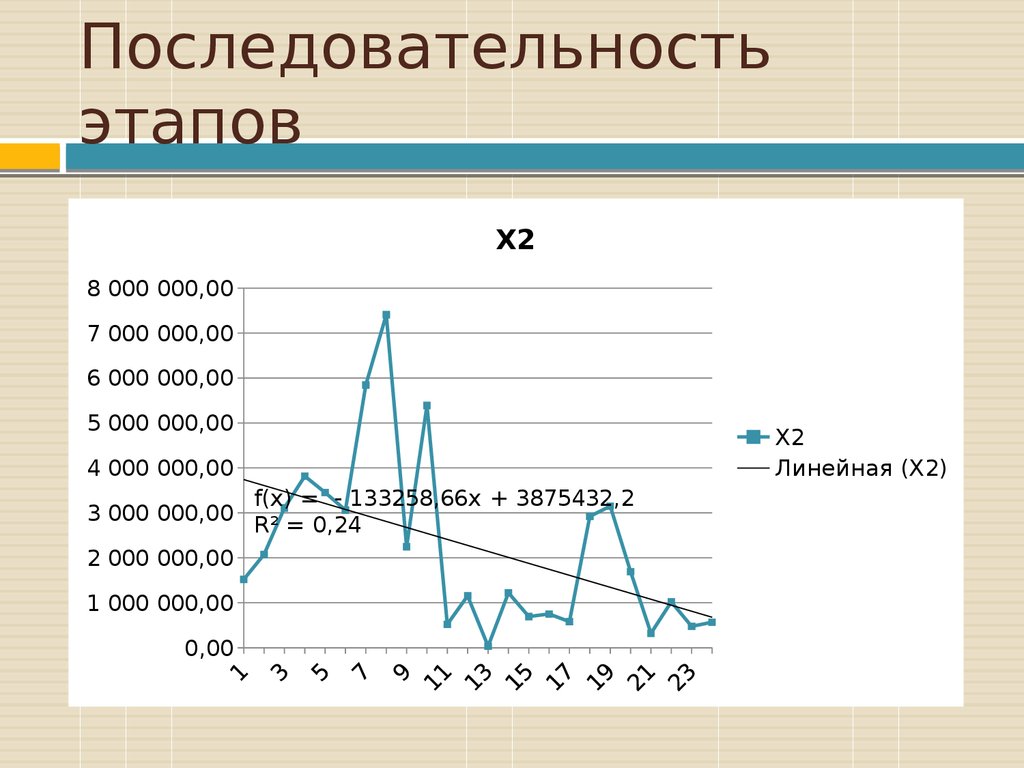
38. Последовательность этапов
Х28 000 000,00
7 000 000,00
6 000 000,00
5 000 000,00
Х2
Линейная (Х2)
4 000 000,00
3 000 000,00
2 000 000,00
1 000 000,00
0,00
f(x) = - 133258,66x + 3875432,2
R² = 0,24
39. Последовательность этапов
Рассчитаем прогнозные значенияфактора Х2
40. Последовательность этапов
Прогнозные значения фактора Х241. Последовательность этапов
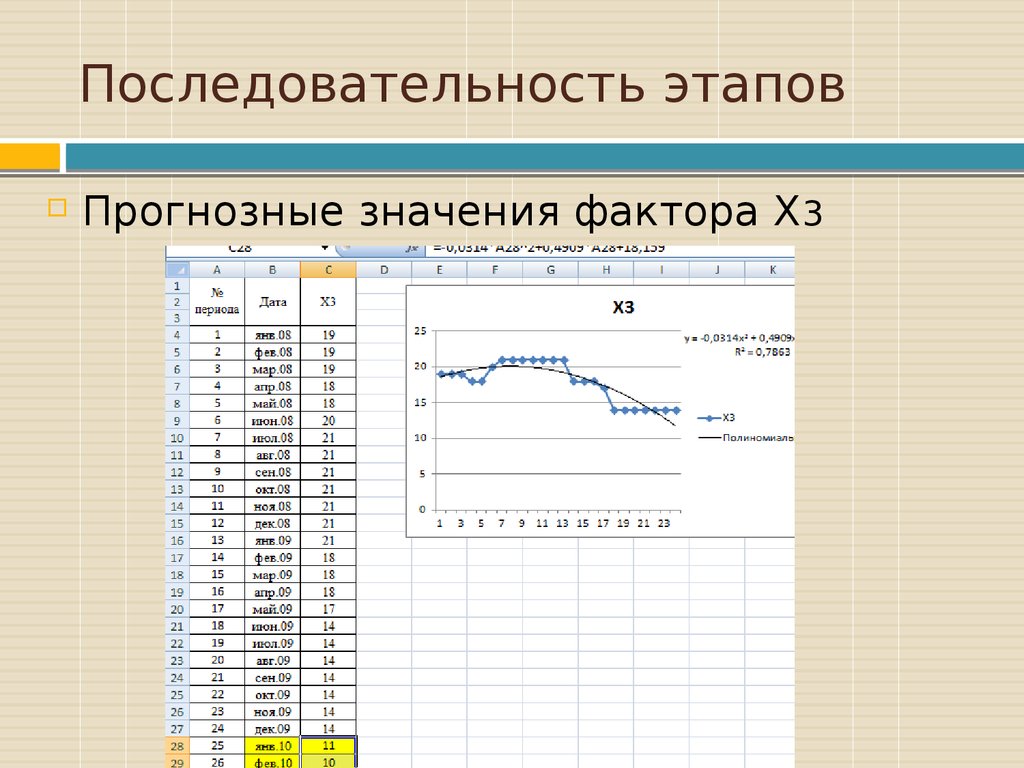
Построение графика исходноговременного ряда для фактора Х3.
42. Последовательность этапов
Выбор типа тренда.43. Последовательность этапов
Болееточные
значения
прогнозируемой переменной можно
получить,
если
воспользоваться
Полиномиальным уравнением линии
тренда (так как R^2 принимает
максимальное значение по сравнению
с другими).
44. Последовательность этапов
X325
20
15
10
5
0
f(x) = - 0,03x^2 + 0,49x + 18,16
R² = 0,79
X3
Полиномиальная (X3)
45. Последовательность этапов
Рассчитаем прогнозные значенияфактора Х3
46. Последовательность этапов
Прогнозные значения фактора Х347. Последовательность этапов
Послеопределения
прогнозных
значений факторов Х2 и Х3, рассчитаем
прогнозные
значения
исследуемой
характеристики У, путем подставления
в уравнение регрессии, полученных
значений.
48. Последовательность этапов
Коэффициенты
уравнения
регрессии
Прогнозные
значения
факторов Х2
и Х3
49. Последовательность этапов
Коэффициенты
уравнения
регрессии
Прогнозные
значения
факторов Х2
и Х3
50. Последовательность этапов
Таким образом,прогнозные
значения
исследуемой
характеристики
У на
последующие
два месяца
равны
16 978,32 и
17 222,95.



































 mathematics
mathematics








