Корреляционно-регрессионная модель

1.

Корреляционнорегрессионные
модели

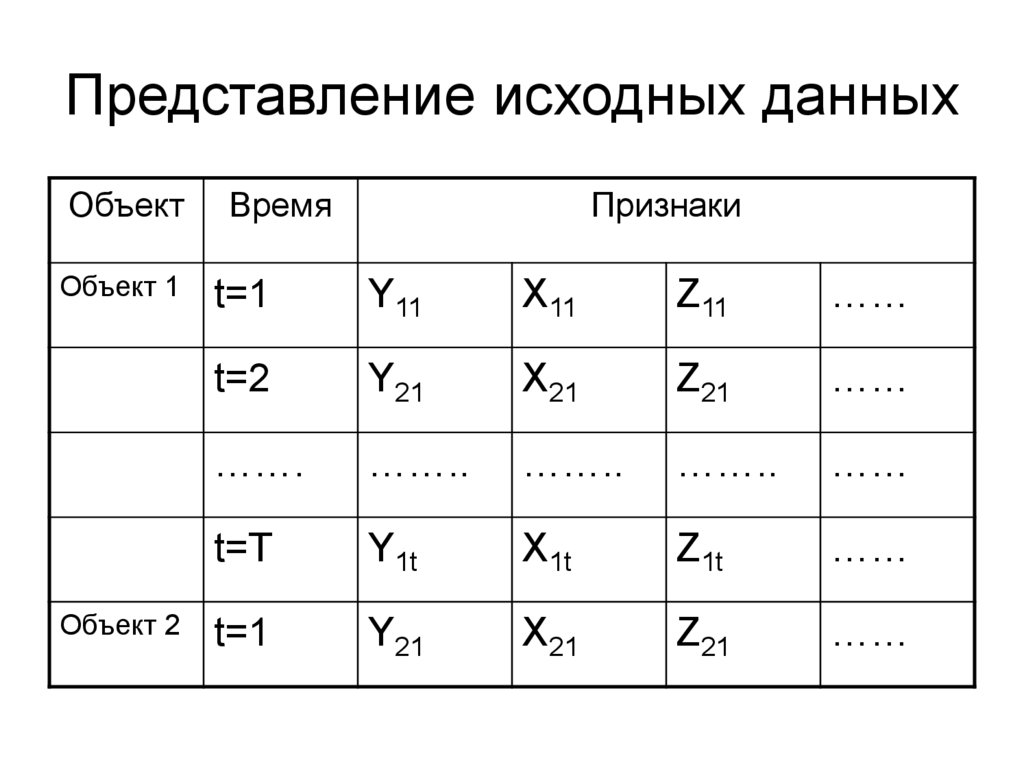
2. Представление исходных данных

Yt1, Yt2, Yt3………………Ytn

3. Представление исходных данных

У1
У2
…
Уn
Х11 Х12 …………X1k
Х21 Х22 …………X2k
………… ………
Xn1 Xn2 …………Xnk
n>k~3

4. Представление исходных данных

Объект
Объект 1
Объект 2
Время
Признаки
t=1
Y11
X11
Z11
……
t=2
Y21
X21
Z21
……
…….
……..
……..
……..
……
t=T
Y1t
X1t
Z1t
……
t=1
Y21
X21
Z21
……

5. Построение корреляционно-регрессионной модели

Построение корреляционнорегрессионной модели
У=в0+в1*х1+в2*х2 + … BkXk +ε

6. Оценка параметров модели

• Оценка параметра называется несмещенной,
если ее математическое ожидание равно
оцениваемому параметру
• Оценка параметра называется
состоятельной, если она сходится по
вероятности к оцениваемому параметру при
возрастании количества наблюдений
• Оценка параметра называется
эффективной, если она имеет наименьшую
дисперсию среди возможных несмещенных
оценок параметра, вычисленных по выборкам
одного и того же объема n

7. Требования к исходным данным

• Объясняющие переменные х1, х2…..хк
рассматриваются как неслучайные
величины
• Величины х1, х2…..хк не связаны между
собой линейной функциональной
зависимостью

8. Требования к регрессионным остаткам

• Регрессионные остатки εi есть
взаимонезависимые случайные
величины с нулевым математическим
ожиданием
• Регрессионные остатки εi имеют
постоянную остаточную дисперсию
• Вектор регресионных остатков
подчиняется n-мерному нормальному
закону распределения вероятностей

9. Исходная информация

• В=(ХтХ)-1ХтУ
У1
У2
…
Уn
1 Х11 Х12
1 Х21 Х22
…………
1 Xn1 Xn2

10. Используемые функции

• Хт транспонированная матрица.
• Копировать, специальная вставка, выбрать
окошко «транспонировать», ввод
• МУМНОЖ
• МОБР
• Shift + Alt + Enter

11. Оценка значимости уравнения в целом

• Fрасч =
Qr /( k 1)
Qост /( n k 1)

12. Сравнение расчетного и табличного значения

Fтабл =FРАСПОБР
Вероятность = вероятности ошибки
V1 = K+1
V2 = n-k-1
Fрасч > Fтабл Уравнение значимо

13. Оценка значимости регрессоров

• Tbj = bj/sbj
• Ковариационная матрица по bj
S*(XтХ)-1
S2 = Qост/(n-k-1)
По диагонали этой матрицы находим Sbj в квадрате

14. Определение значимости регрессоров

• tтабл = СТЬЮДРАСПОБР
• Вероятность ошибки
• V1=n-k-1
• tрасч > tтабл по абсолютной величине,
то регрессор значим

15. Множественный коэффициент детерминации

n
Ry 1
2
( y y
i 1
n
i
мод
( y y
i 1
i
)
2
ср
)
2

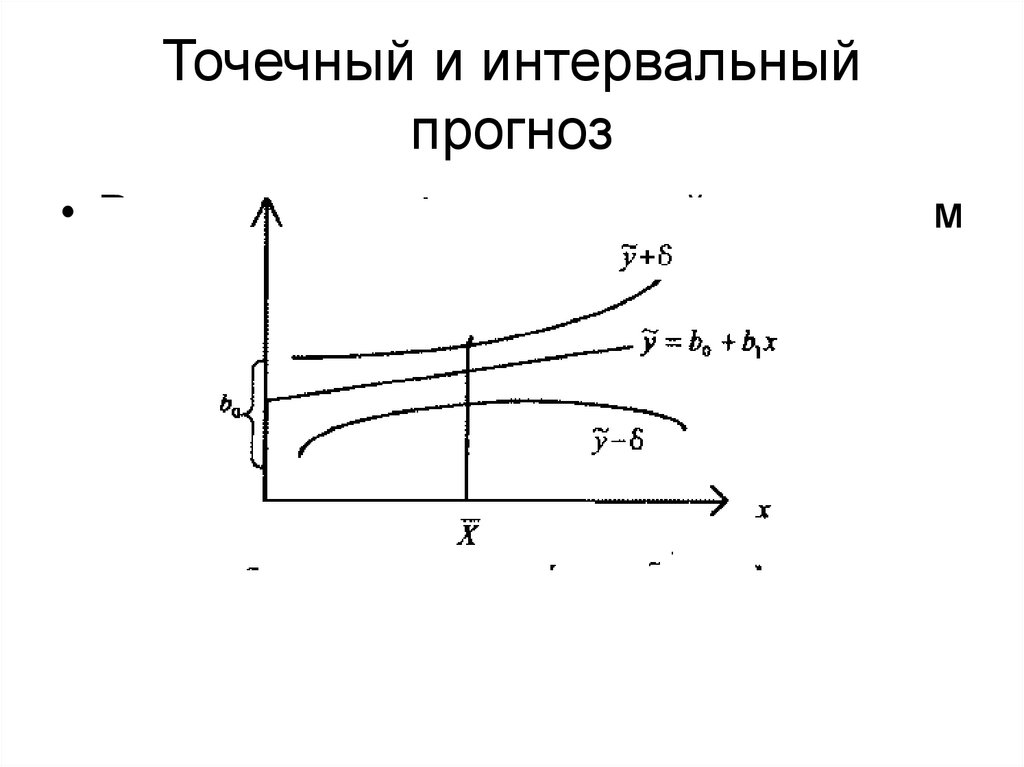
16. Точечный и интервальный прогноз

• Расчет прогнозных значений по лекциям

17. Расчет интервального прогноза для простейшей модели

( xn 1 xср )
1
n
1
n
2
(
x
x
)
i ср
2
• Yn+1∈Yn+1 ±tтS
i 1

18. Расчет интервального прогноза для множественной модели

• Yn+1∈ Yn+1±tтS
1
( X ) ( X X ) Х 1
0 Т
Т
0