Similar presentations:
Режимы движения жидкости. Лекция 3
1.
2.
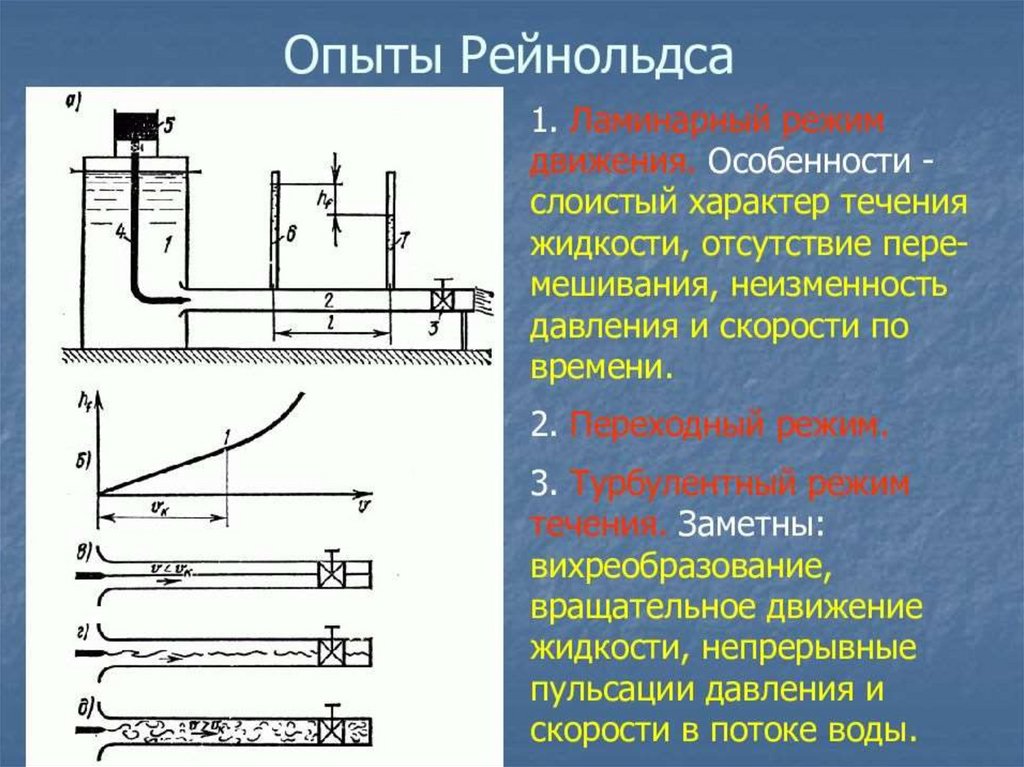
При наблюдении за движением жидкости втрубах и каналах, можно
заметить, что в одном случае жидкость
сохраняет определенный строй
своих частиц, а в других –
перемещаются бессистемно.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
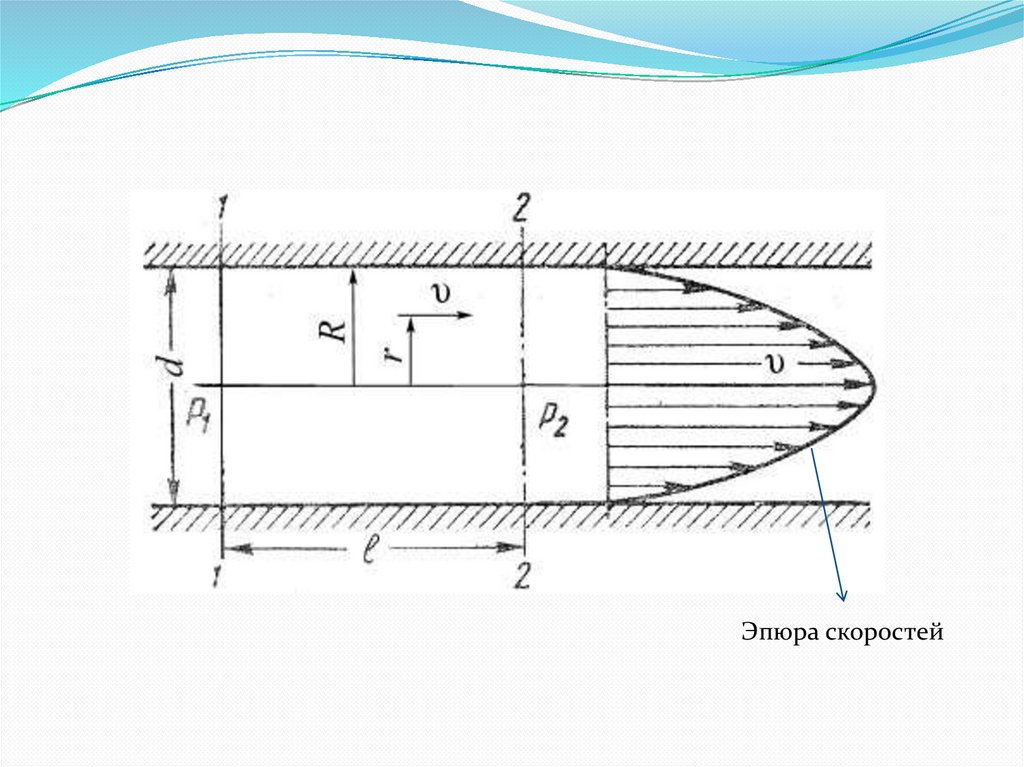
Как показывают исследования, при ламинарномтечении жидкости в круглой трубе максимальная
скорость находится на оси трубы. У стенок трубы
скорость равна нулю, т.к. частицы жидкости покрывают
внутреннюю поверхность трубопровода тонким
неподвижным слоем. От стенок трубы к ее оси
скорости нарастаю плавно. График распределения
скоростей по поперечному сечению потока
представляет собой параболоид вращения, а сечение
параболоида осевой плоскостью – квадратичную
параболу
14.
Эпюра скоростей15.
16.
17.
18.
Для турбулентного течения характерноперемешивание жидкости, пульсации скоростей и
давлений. Если с помощью особо чувствительного
прибора-самописца измерять пульсации,
например, скорости по времени в фиксированной
точке потока, то получим картину, подобную
показанной на рис.4.4. Скорость беспорядочно
колеблется около некоторого осредненного по
времен значения υоср, которое данном случае
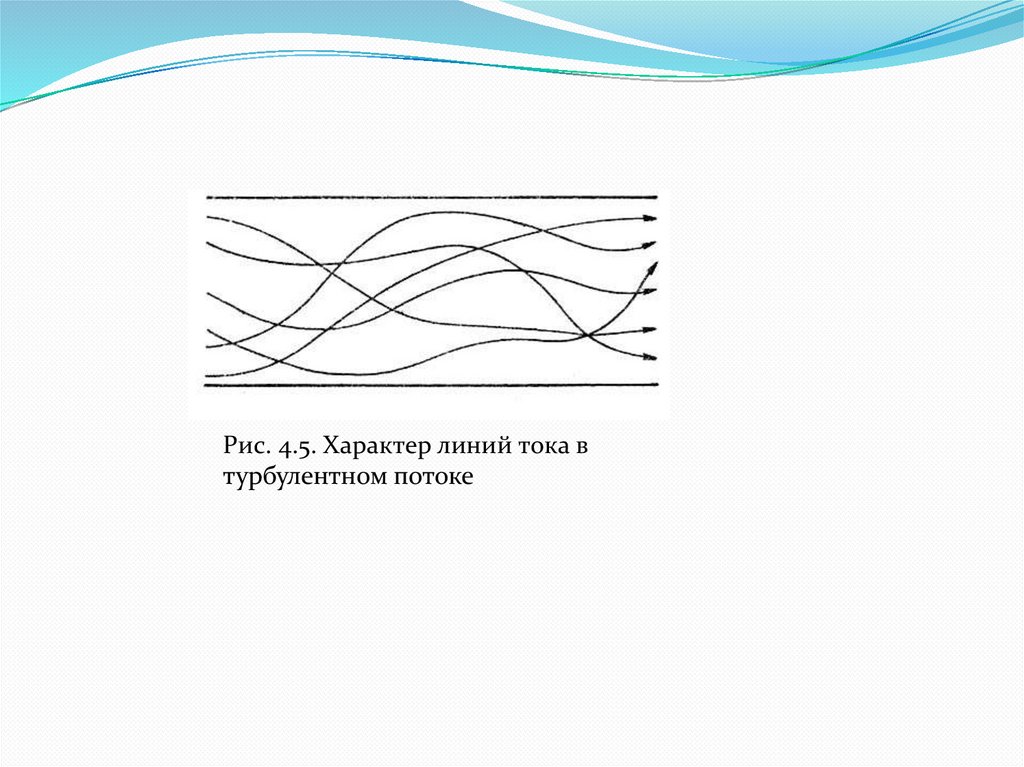
остается постоянным. Характер линий тока в трубе
в данный момент времени отличается большим
разнообразием (рис.4.5). Рис. 4.4. Пульсация
скорости в турбулентном потоке
19.
Рис. 4.4. Пульсация скорости втурбулентном потоке
20.
Рис. 4.5. Характер линий тока втурбулентном потоке
21.
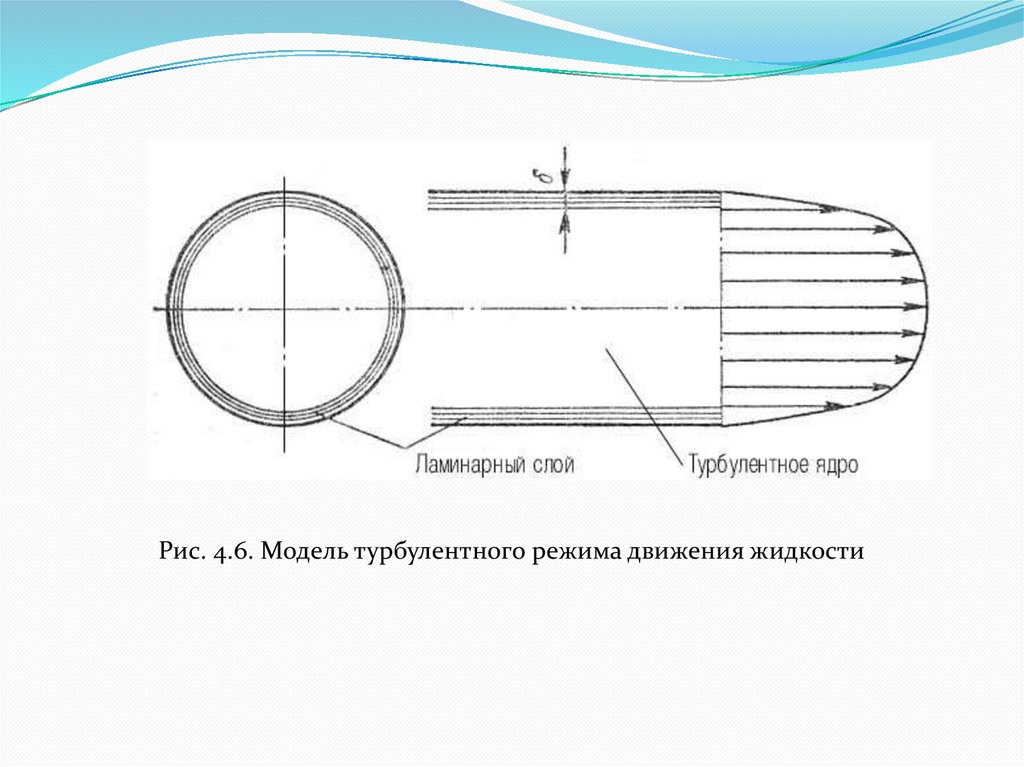
При турбулентном режиме движения жидкости втрубах эпюра распределения скоростей имеет вид,
показанный на рис. 4.6. В тонком пристенном слое
толщиной δ жидкость течет в ламинарном
режиме, а остальные слои текут в турбулентном
режиме, и называются турбулентным ядром.
Таким образом, строго говоря, турбулентного
движения в чистом виде не существует. Оно
сопровождается ламинарным движением у
стенок, хотя слой δ с ламинарным режимом
весьма мал по сравнению с турбулентным ядром.
22.
Рис. 4.6. Модель турбулентного режима движения жидкости23.
Основной расчетной формулой для потерь напора притурбулентном течении жидкости в круглых трубах
является уже приводившаяся выше эмпирическая
формула , называемая формулой Вейсбаха-Дарси и
имеющая следующий вид:
Различие заключается лишь в значениях
коэффициента гидравлического трения λ. Этот
коэффициент зависит от числа Рейнольдса
Re и от безразмерного геометрического фактора –
относительной Шероховатости ∆/d (или ∆/r0, где r0 –
радиус трубы).
24.
25.
26.
Задача 1.Задача 2.
Q=1000 л/мин.
D=100 мм.
L= 5 км.
∆= 0.2 мм.
ν = 0,013 см^2/ c.
γ= 8000 Н/м^3
Pl-?
Hl-?
Q=2000 л/мин.
D=200 мм.
L= 20 м.
∆= 0.2 мм.
ν = 0,01 см^2/ c.
γ= 8000 Н/м^3
Pl-?
Hl-?
27.
Местные потери. Формула Вейсбаха2
V
hм
2g
Потери напора
pм ghм
V
2
Потери давления
2
(кси) (иногда ζ (дзета)) -
коэффициент местного
сопротивления, зависит от его
вида, размера и конструктивного
выполнения.
hм
2
V / 2g
V – средняя скорость потока перед препятствием.
Иначе - обязательно оговаривается.
28.
Определение коэффициентов местныхсопротивлений
2
V
hм
2g
Формула Вейсбаха
Коэффициент в основном берется из справочной
литературы, кроме случаев:
• внезапное расширение потока;
• внезапное сужение;
• диффузор и конфузор (плавное расширение/сужение);
• резкий и плавный поворот русла (колено/отвод).
Во всех случаях - только для турбулентного режима
течения.
29.
Коэффициент сопротивления привнезапном расширении потока
Потеря напора
(энергии) при
внезапном
расширении русла
расходуется на
вихреобразование,
связанное с отрывом
потока от стенок, т.е.
на поддержание
вращательного
непрерывного
движения жидких масс.
30.
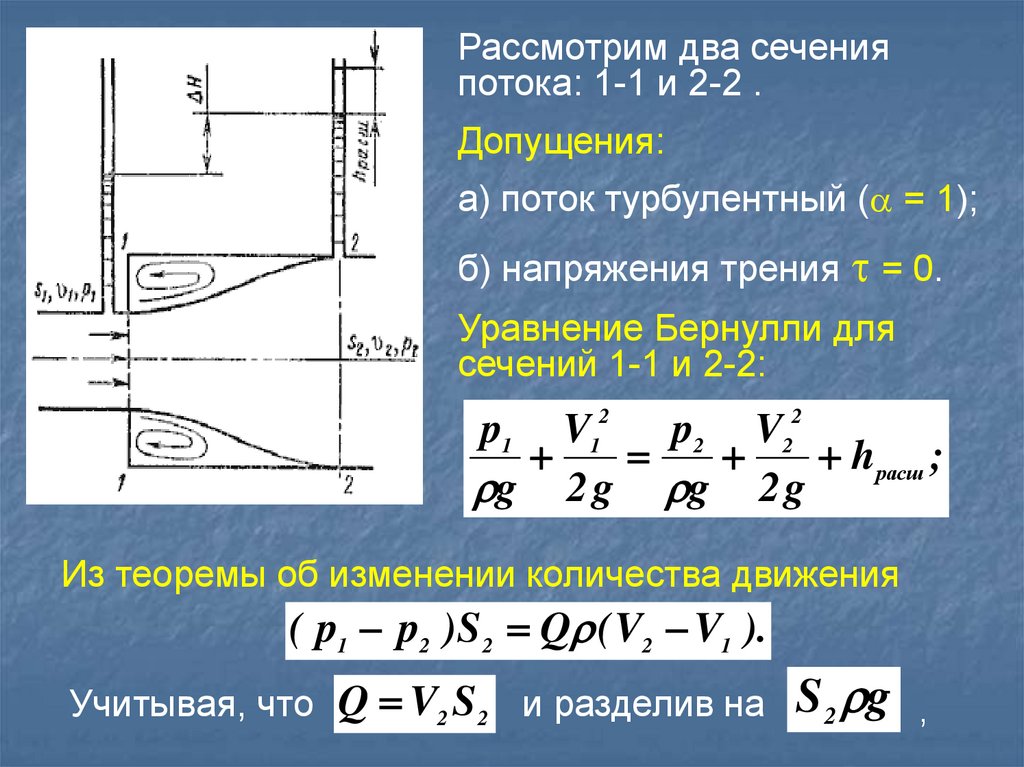
Рассмотрим два сеченияпотока: 1-1 и 2-2 .
Допущения:
а) поток турбулентный ( = 1);
б) напряжения трения = 0.
Уравнение Бернулли для
сечений 1-1 и 2-2:
p1 V12 p2 V22
hрасш ;
g 2 g g 2 g
Из теоремы об изменении количества движения
( p1 p2 )S 2 Q ( V2 V1 ).
Учитывая, что Q V2 S 2 и разделив на
S 2 g
,
31.
получаем:p1 p2 V2
V22 V22 2V1V2 V12 V12
( V2 V1 )
g
g
2g 2g
2g
2g 2g
или
p1 V12 p2 V22 ( V1 V2 )2 , то есть
g 2 g g 2 g
2g
( V1 V2 )
V
hрасш
расш
2g
2g
2
2
1
- теорема Борда
(1766)
Теорема Борда - потеря напора при внезапном
расширении русла равна скоростному напору,
определенному по разности скоростей
32.
Из уравнения неразрывности V1 S1 V2 S 22
hрасш
S1 V
V
1
расш
S2 2 g
2g
2
1
2
1
и расш
и
S1
1
S2
Частный случай:
при
S2
2
1
(расширение из трубы в бассейн)
V
hрасш ; и расш 1
2g
- полная потеря напора
2
33.
Коэффициент сопротивления приплавном расширении русла (диффузор)
Течение в диффузоре
сопровождается
уменьшением скорости и
увеличением давления,
т.е. преобразованием
кинетической энергии
жидкости в энергию
давления.
В диффузоре, как и при внезапном расширении русла,
происходит отрыв основного потока от стенки и
вихреобразование. Интенсивность этих явлений
возрастает с увеличением угла расширения диффузора α.
34.
Кроме того, в диффузоре имеются и обычные потери натрение, подобные тем, которые возникают в трубах
постоянного сечения.
Полную потерю напора в диффузоре рассматривают как
сумму двух слагаемых:
hдиф hтр hрасш
hтр и hрасш - потери напора на трение и расширение
(вихреобразование).
Без вывода:
2
т
1
V
1
hтр
1 2
8 sin( / 2 )
n 2g
2
hрасш
2
S1
V1
1 S
k 2g
2
где n = S2/S1 = ( r2/r1 ) 2 степень расширения
диффузора;
k - коэффициент
смягчения (отн. уступа).
При = 5…20° k = sin .
35.
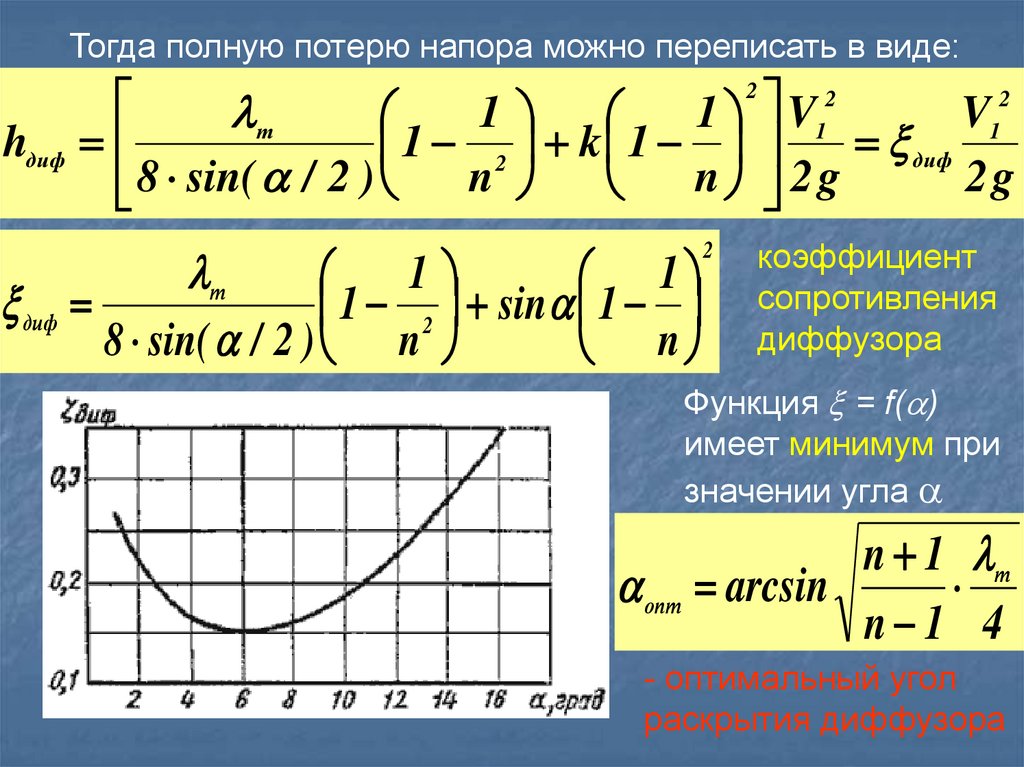
Тогда полную потерю напора можно переписать в виде:hдиф
т
1
1
1 2 k 1
n
n
8 sin( / 2 )
т
1
1
диф
1 2 sin 1
8 sin( / 2 ) n
n
2
2
2
V12
V1
диф
2g
2g
коэффициент
сопротивления
диффузора
Функция = f( )
имеет минимум при
значении угла
n 1 т
опт arcsin
n 1 4
- оптимальный угол
раскрытия диффузора
36.
Коэффициент сопротивления привнезапном и плавном сужении русла
Внезапное сужение
Конфузор
Потеря напора обусловлена трением потока при
входе в более узкую трубу и потерями на
вихреобразование, которые образуются в кольцевом
пространстве вокруг суженой части потока
37.
Полная потеря напора определится по формуле:2
2
Коэффициент сопротивления
сужения суж определяется по
полуэмпирической формуле
И.Е. Идельчика:
hсуж
V
суж
2g
суж
S2
1
0 ,5 1 0 ,5 1
S1
n
где
n = S1/S2
При выходе трубы из резервуара больших
размеров (когда можно считать, что S2/S1 = 0), а
также при отсутствии закругления входного угла,
коэффициент сопротивления суж = 0,5.
38.
Течение жидкости в конфузоре сопровождаетсяувеличением скорости и падением давления. В
конфузоре имеются лишь потери на трение
hконф
2
т
1
V
2
1 2
8 sin( / 2 )
n 2g
где коэффициент сопротивления конфузора
определяется по формуле
т
1
конф
1 2
8 sin( / 2 ) n
где n = S1/S2 - степень
сужения
Внимание! При сужении русла потери напора
относятся к скорости за препятствием V2 !
39.
Внезапный и плавный поворот потокаКолено
Отвод
d ≈ 40 мм
hкол
V2
кол
2g
Плавность поворота значительно уменьшает
интенсивность вихреобразования, т.е. сопротивление
отвода по сравнению с коленом.
40.
Коэффициент сопротивления отвода отв зависитот отношения R / d, угла δ, и формы поперечного
сечения трубы. Для отводов круглого сечения с
углом δ= 90° и R/d > 1 при турбулентном течении
можно воспользоваться эмпирической формулой:
1
отв
1 ,19 d
0 ,051
R
Для углов δ 70°
коэффициент сопротивления
отв 0 ,9
1
отв
sin
При δ > 100°
1
отв 0 ,7 0 ,35 отв
90
41.
Справочные коэффициенты местных потерьВид местного сопротивления
Коэфф.
Вход в трубу без закругления
входных кромок
То же, но при хорошо закругленных
кромках
Выход из трубы в сосуд больших
размеров
Резкий поворот без закругления при
угле поворота 900
Колено (плавное закругление) при
радиусе закругления (5-7)d
0,5
0,1
1
1,32
0,5–0,3
Кран
5-10
Вход во всасывающую коробку
насоса с обратным клапаном
5-10
42.
Зависимость коэффициента местныхпотерь от Re
• Если на трубопроводе
1-е критическое число Рейнольдса
имеется несколько местных
сопротивлений и
расстояние между ними
больше (40-60)d, то потери
в них суммируются,
считается, что взаимное
влияние местных
сопротивлений отсутствует
.
• При меньшем расстоянии
соседние местные
Reкр=1260...1580
сопротивления считаются
одним сопротивлением;
• При турбулентном режиме
коэффициент для него
коэффициенты местного
определяется опытным
сопротивления не зависят
путем.
от числа Рейнольдса.




































 physics
physics








