Similar presentations:
Потери давления при движении жидкости
1.
Потери давления придвижении жидкости
2.
Режимы движения жидкости и газаМногочисленными экспериментальными исследованиями установлено, что в природе существует два
режима движения жидкости и газа: ламинарный режим движения; турбулентный режим движения.
Ламинарный режим характеризуется параллельным движением слоев жидкости без перемешивания последних.
3.
Многочисленными экспериментальными исследованиями установлено, что в природе существует дварежима движения жидкости и газа: ламинарный режим движения; турбулентный режим движения.
При турбулентном режиме движения жидкости наблюдается интенсивное хаотическое перемешивание жидких
частиц.
4.
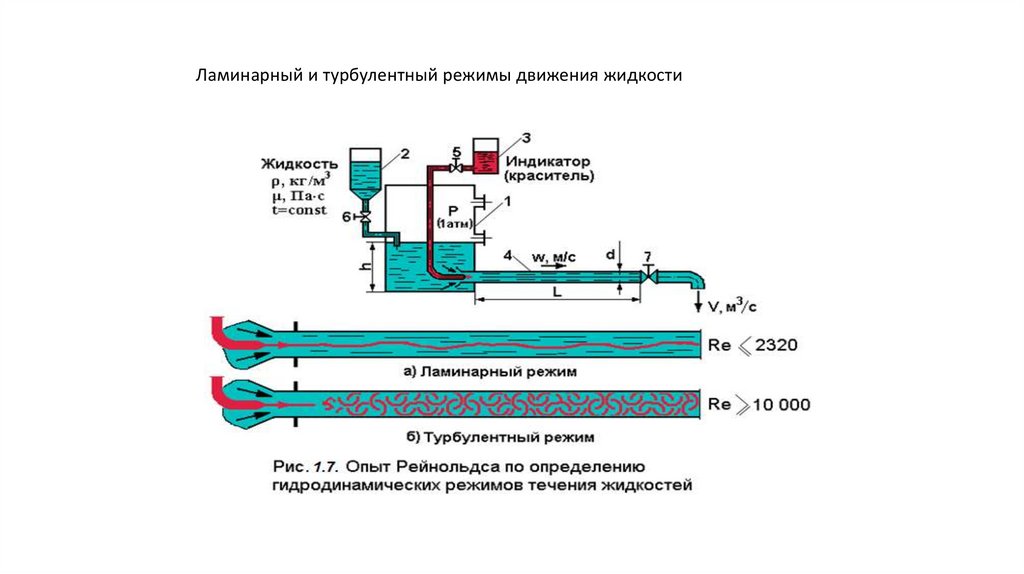
Ламинарный и турбулентный режимы движения жидкости5.
Гидравлические сопротивленияПотери давления возникают при трении о стенки трубы и в местных сопротивлениях
Движение жидкости может быть: ламинарным и турбулентным.
Критическая скорость:
Критерий Рейнольдса
Vкр
Reкр
d
k
Vкр d
Re <2300 – ламинарное движение,
2300 < Re < 4000 – переходная зона или критическая
Re > 4000 – турбулентное движение
6.
Потери напора при ламинарном течении жидкостиV
P1 P2 2 2
R r
4 l
P1 P2 2
P1 P2 2
Vmax
R 0
R
4 l
4 l
Максимальная скорость дает высоту параболоида h Vmax
Объем параболоида высотой h и площадью ρR2 равен
1
P P
P P
Q R 2 1 2 R 2 1 2 R 4
2
4 l
8 l
P1 P2 2
R
4 l
V R
2 h
2
7.
Если вместо R подставить диаметр трубы d, то формула:P1 P2 4
Q
d
128 l
Расход в трубе можно выразить через среднюю скорость:
P1 P2 4
d 2
Q
d Vср
128 l
4
P1 P2 2
Vср
d
32 l
Потеря давления в трубопроводе будет равна
32 l
P1 P2 2 Vср
d
Если разделить обе части равенства на объемный вес жидкости γ = ρg,
то получим
32 l
V
2 ср
gd
P1
P2
8.
Так как левая часть полученного равенства равна потерям напора hпот втрубе постоянного диаметра, то окончательно это равенство примет вид:
32 l
hпот
V
2 ср
gd
Универсальная формула Дарси-Вейсбаха:
l V2
hпот
d 2g
где λ – коэффициент гидравлического трения, который для ламинарного
потока вычисляется по выражению:
64
Re
9.
Потери давления при турбулентном режимеХарактер линий тока в турбулентном потоке
Модель турбулентного режима движения жидкости
10.
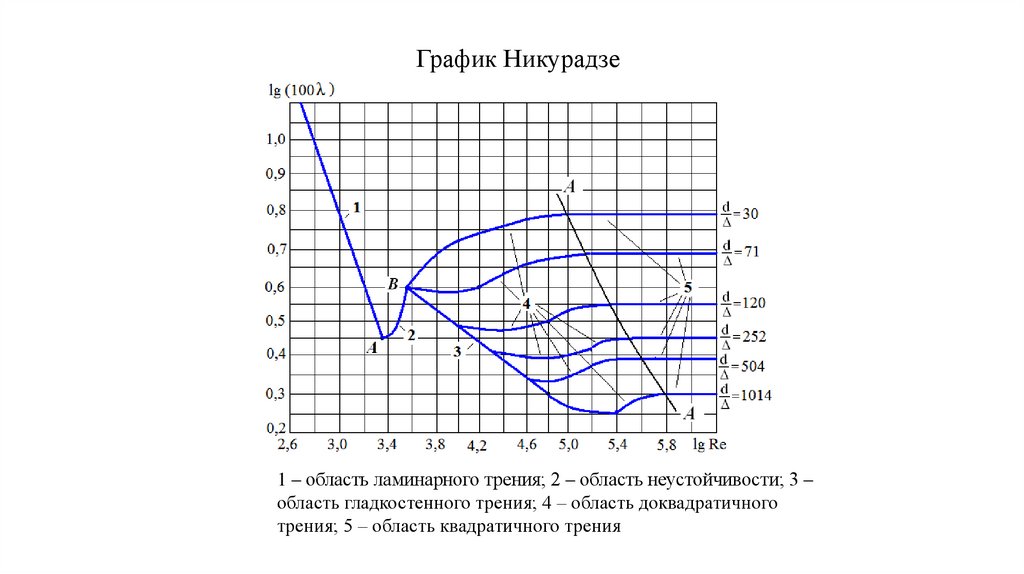
График Никурадзе1 – область ламинарного трения; 2 – область неустойчивости; 3 –
область гладкостенного трения; 4 – область доквадратичного
трения; 5 – область квадратичного трения
11.
Различают 5 зон гидравлического сопротивленияПрямая I соответствует ламинарному режиму движения жидкости.
Первая зона – зона вязкого сопротивления
64
Re
Первая область – область малых Re и Δ/r0, где коэффициент λ не зависит
от шероховатости, а определяется лишь числом Re
Вторая – переходная зона.
Если число Рейнольдса лежит в диапазоне 4000 < Re < 10 (d/кэ), то
Третья зона – гладкостенного сопротивления
0,3164
4
Re
- Формула Блазиуса
Четвертая зона – зона доквадратичного сопротивления
К
0,11
d
Red 500
0, 25
d
КЭ
- Формула Шифринсона
Пятая зона – квадратичного сопротивления
2
l V2
К l V
hl
0,11
KT V 2
d 2g
d d 2g
12.
Местные гидравлические сопротивления1. Постепенное расширение потока
2
S1 V12
h расш 1
S2 2 g
Это выражение является следствием теоремы Борда, которая гласит, что
потеря напора при внезапном расширении русла равна скоростному напору,
определенному по разности скоростей:
V1 V2
2
h расш
2g
Тогда,
V12
h расш
2g
13.
2. Внезапное расширениеhдиф hтр hраш
1 V12
hтр
1 2
8 sin / 2 n 2 g
n = S2/S1 = (r2/r1)2 – степень расширения диффузора
S1 V12
2
2
h расш 1 k
1
1
V12
V1
S 2 2 g hдиф 8 sin / 2 1 n 2 k 1 n 2 g диф 2 g
Коэффициент сопротивления диффузора:
1
1
диф
1
sin
1
2
8 sin / 2 n
n
2
14.
3. Внезапное сужениеВнезапное сужение трубы
Конфузор
V22
Полная потеря напора определится по формуле: hсуж суж
2g
Коэффициент сопротивления сужения определяется по полуэмпирической
формуле И.Е. Идельчика
S2
1
суж 0,5 1 0,5 1
S1
n
в которой n = S1/S2 – степень сужения
15.
4. Постепенное сужение- сопло
1 V22
hконф
1 2
8 sin / 2 n 2 g
5. Внезапный поворот трубы
1
конф
1 2
8 sin / 2 n
0,19d
R
sin
отв 0,9 отв
0,051
отв
Для углов δ ≤ 70 коэффициент сопротивления
0
,
35
отв
а при δ ≥ 100
90
V2
Потеря напора в колене определится как hотв отв 2 g
отв 0,7
16.
17.
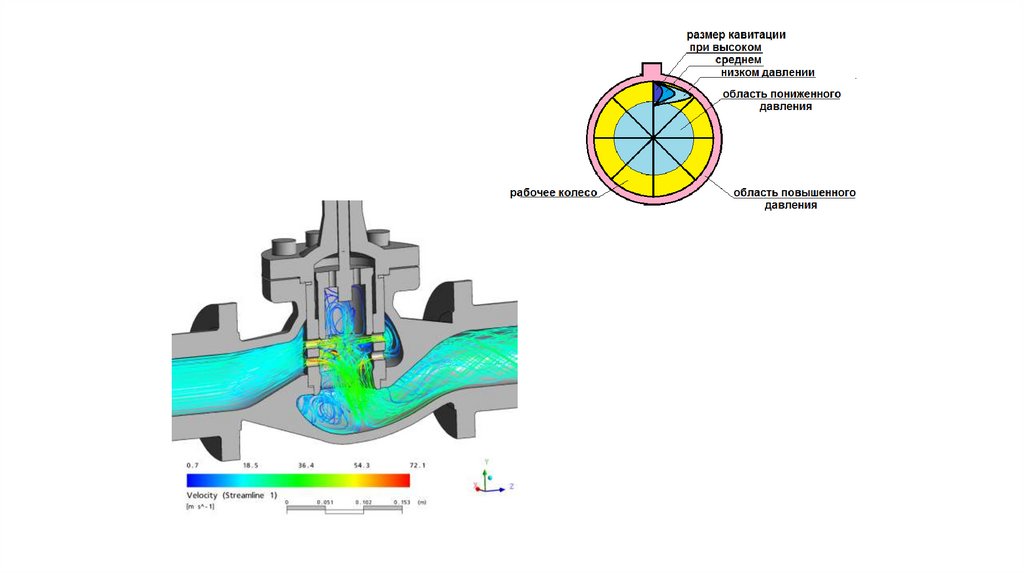
Явление кавитацииВода под давлением движется от сечения 1-1 через сечение 2-2 к
сечению 3-3. Как видно из рисунка, сечение 2-2 имеет меньший диаметр.
Скорость течения жидкости в трубе можно изменять, например,
установленным после сечения 3-3 краном















 physics
physics








