Гидродинамика. Поток жидкости и его основные понятия

1. ГИДРОДИНАМИКА

2. Поток жидкости и его основные понятия

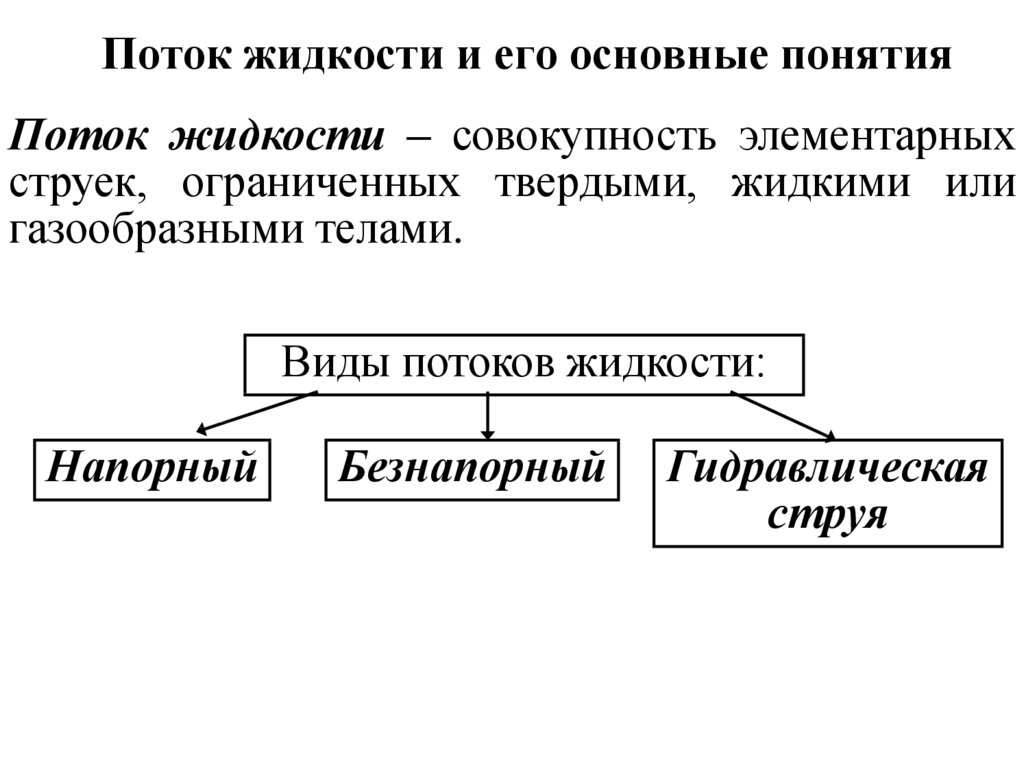
Поток жидкости – совокупность элементарных
струек, ограниченных твердыми, жидкими или
газообразными телами.
Виды потоков жидкости:
Напорный
Безнапорный
Гидравлическая
струя

3.

Параметры потока жидкости:
1. Живое сечение S, м2 поперечное сечение,
нормальное к направлению движения потока.
2. Смоченный периметр , м длина контура
живого сечения потока по твердым стенкам,
ограничивающим поток.
3. Гидравлический радиус Rг, м
Rг S /
4. Эквивалентный диаметр , м
d экв 4 Rг 4S /
d экв 4S /
2
4 d тр
4 d тр
d тр

4.

5. Расход количество жидкости, протекающей
за единицу времени через живое сечение потока.
объемный, м3/с
Q V /t
R
Qm m / t
массовый, кг/с
u1
u2
весовой, Н/с
QG G / t
umax
6. Средняя скорость усредненная величина,
выбранная таким образом, что расход жидкости,
вычисленный по ней, равен действительному
Q
расходу жидкости.
S

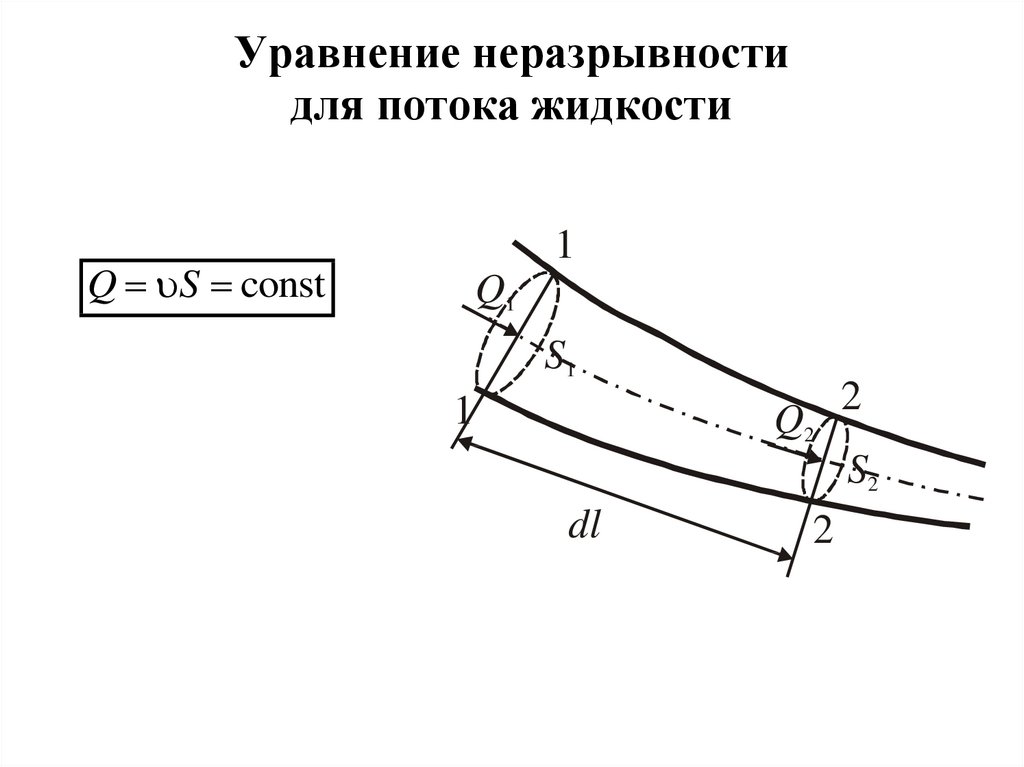
5. Уравнение неразрывности для потока жидкости

1
Q S const
Q1
S1
1
Q2
2
S2
dl
2

6. Уравнение Бернулли для потока идеальной жидкости

Идеальная жидкость
1. абсолютна несжимаема
2. абсолютна текуча
(отсутствие сил внутреннего трения)
0

7.

H const
Физический смысл уравнения Бернулли:
величина гидродинамического напора
постоянна для всех живых сечений потока
идеальной жидкости.

8. Геометрический и энергетический смысл уравнения Бернулли для идеальной жидкости

p1 u12
p2 u22
z1
z2
H const
g 2 g
g 2 g
z − геометрический напор,
p
− пьзометрический напор,
g
u2
− скоростной напор.
2
2
u
2g
Q 1
2g S 2g

9.

mp mu 2
mgz
mgH const
2
mgz – потенциальная энергия положения частицы;
mp / – потенциальная энергия давления частицы;
mu 2 / 2 – кинетическая энергия частицы;
mgH – полная механическая энергия частицы.
Закон сохранения энергии в идеальной жидкости:
в процессе движения идеальной жидкости одна
форма энергии может преобразовываться в
другую, однако полная механическая энергия
жидкости остается постоянной.

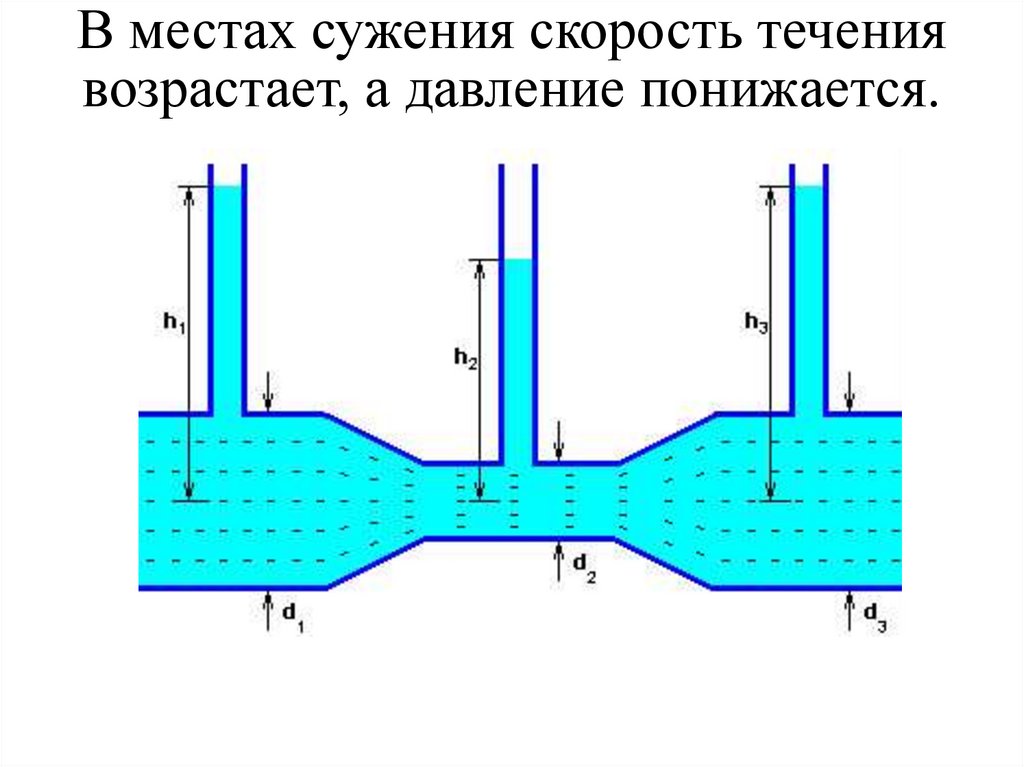
10.

В местах сужения скорость течения
возрастает, а давление понижается.

11. Уравнение Бернулли для установившегося потока реальной жидкости

Мощность потока – полная энергия, которую
поток проносит через живое сечение в единицу
времени:
N H gQ HQ
G
N
p 2
H
z
gQ
g 2 g
где
3
u
dS
S
S
3
– коэффициент Кориолиса.

12.

p1 1 12
p2 2 2 2
z1
z2
hп1 2 ,
g
2g
g
2g
Уравнение Бернулли для реальной жидкости в
сравнении с уравнением Бернулли для
идеальной
жидкости
имеет
следующие
отличия:
1. скоростной напор определяется через среднюю
по сечению потока скорость;
2. неравномерность распределения скорости по
живому
сечению
потока
учитывается
коэффициентом Кориолиса;
3. учитываются существующие потери напора.

13. Физический смысл коэффициента Кориолиса

3
u
dS
äåéñò
E
S 3 êèíóñë
S
Eêèí
.
.
При
При
u const
u const
1
1

14. Общие сведения о гидравлических потерях

1. По длине (формула Дарси – Вейсбаха):
l 2
hдл
,
d 2g
l 2
pдл
,
d 2
2. Местные (формула Вейсбаха):
2
hм
,
2g
2
pм
,
2
hп1 2 hдлi hмi

15. Местные гидравлические сопротивления

6
8
1
2
3
4
9
5
7
1 - вход жидкости в трубу, 2 и 3 - внезапное
расширение и сужение потока, 4 и 5 - постепенное
расширение и сужение потока,6 - кран, 7 и 8 резкий и плавный поворот, 9 - выход из трубы.

16. Практическое применение уравнения Бернулли

h
p1 1 12
p2 2 22
z1
z2
hп1 2 .
g
2g
g
2g
z1 z2 , Q 1S1 2 S2
Q
S2 2 p /
2 1 S2 / S1
2
p p1 p2 2 g h,
S2 2 p / S2 2 g h
2 1 S2 / S1
2
0,5

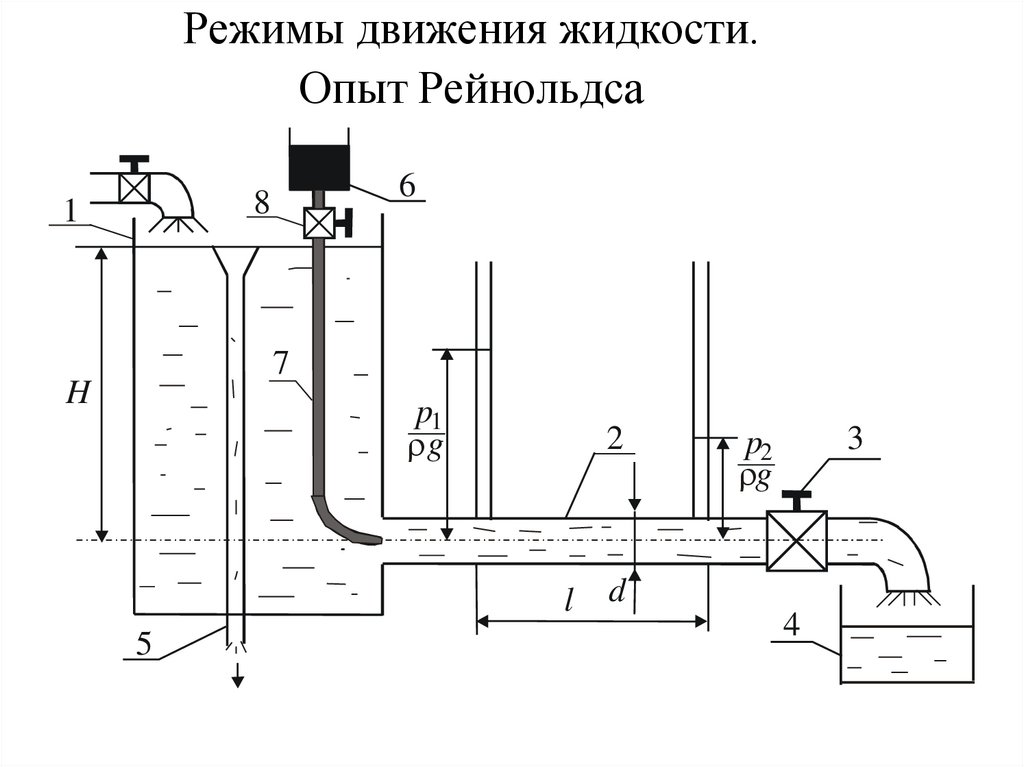
17. Режимы движения жидкости. Опыт Рейнольдса

6
8
1
7
H
p1
g
2
l
5
3
p2
g
d
4

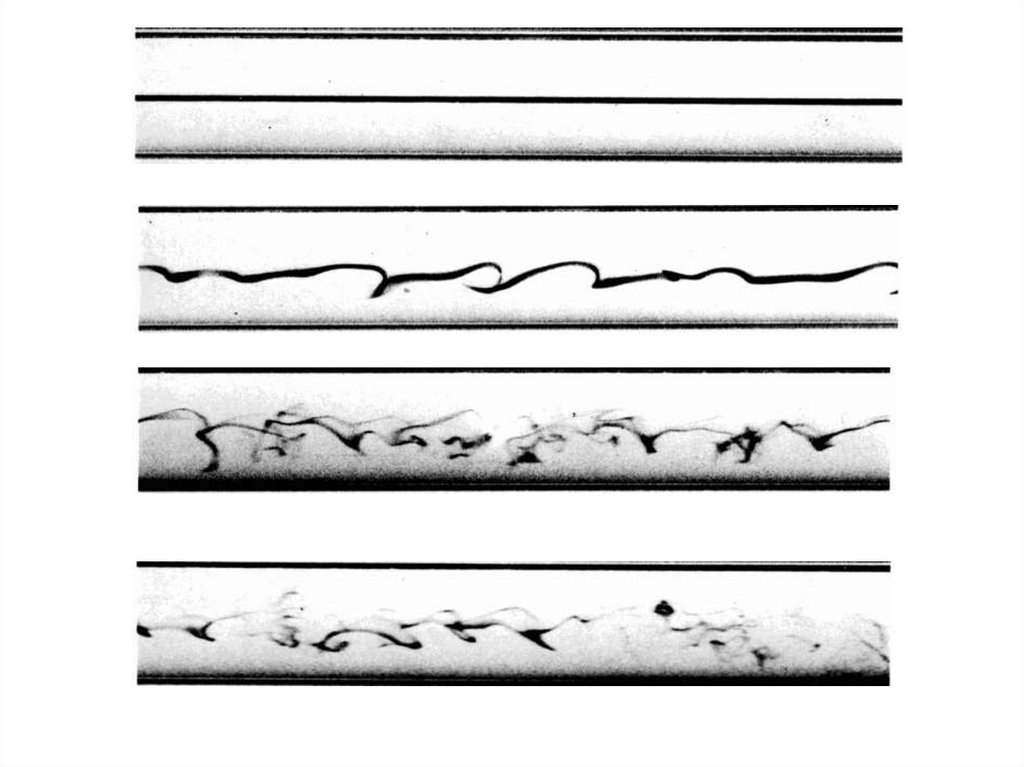
18.

19.

Ламинарный режим – слоистое движение.
Турбулентный режим – хаотичное движение.
õàð dýêâ
Re
С
lnhдл
2
число Рейнольдса
Reкp 2320
B
1
hдл a n
n tg 1 1
n tg 2 1,75 2
А
ln

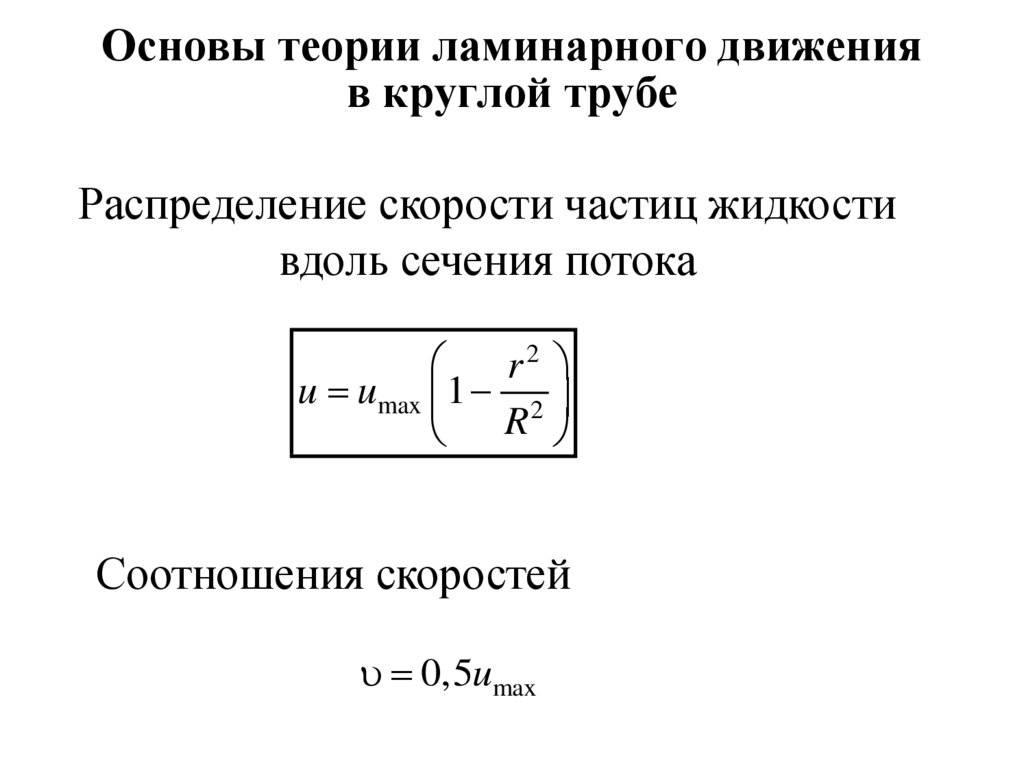
20. Основы теории ламинарного движения в круглой трубе

Распределение скорости частиц жидкости
вдоль сечения потока
r2
u umax 1 2
R
Соотношения скоростей
0,5umax

21. Потери напора в ламинарном потоке жидкости

формула Пуазеля – Гагена
128 lQ 32 l
häë
4
gd
gd 2
l 2
hдл
d 2g
л 64 / Re

22. Коэффициент Кориолиса для ламинарного потока

3
u
dS
S
S
3
2
S
3
1 r / R dS
2 3
S
3
2
R
2r
2 3
8 2 1 r / R dr
0 R

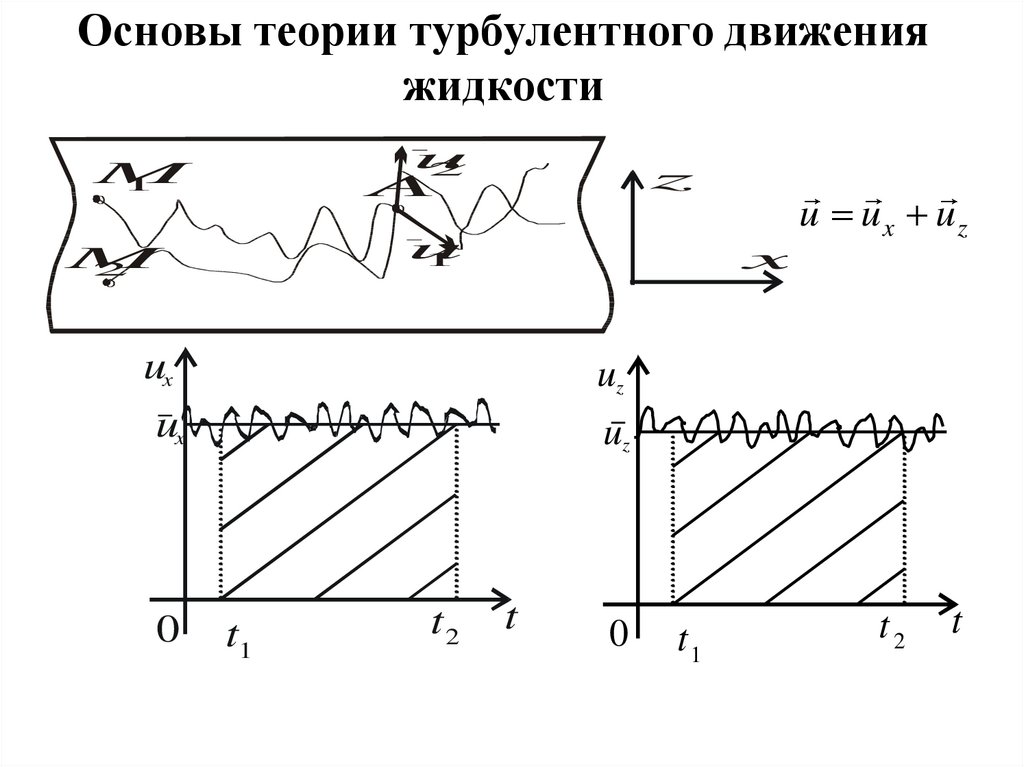
23. Основы теории турбулентного движения жидкости

u
2
A
M
1
z
u
1
M
2
x
ux
uz
ux
0
u ux uz
uz
t1
t2
t
0
t1
t2
t

24. Структура турбулентного потока

25. Распределение скоростей по сечению турбулентного потока

1
d
2
Формулы Альтшуля
r
u umax 1
R
0,9
,
1 2,65 ,
,
1 113
umax
1
1 1,35
0,77 0,88

26. Шероховатость поверхностей стенок и потери напора в турбулентном режиме

э
э / d
( э )
- гидравлически гладкие трубы
( э ) - гидравлически шероховатые трубы
( э )
- гидравлически переходные трубы

27.

I зона – ламинарный режим
Re 2320,
hдл f ,
1
64
Re
II зона – турбулентный режим
Re 2320,
hдл f 2 ;
68
0,11
Re
0,25
– формула Альштуля.