Similar presentations:
Наглядное решение задач по начертательной геометрии из рабочей тетради
1. НАГЛЯДНОЕ РЕШЕНИЕ ЗАДАЧ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ ИЗ РАБОЧЕЙ ТЕТРАДИ
2. Практикум № 1. Точка, прямая, плоскость на комплексном чертеже.
Задача 1Задача 2
Задача 3
Задача 4
Задача 5
Задача 6
Задача 7
Задача 8
Задача 9
Задача 10
Задача 11
3. Практикум № 2. Взаимное расположение геометрических элементов. Основные позиционные задачи.
Задача 12Задача 13
Задача 14
Задача 15
Задача 16
Задача 17
Задача 18
Задача 19
Задача 20
Задача 21
Задача 22
Задача 23
Задача 24
Задача 25
4. Практикум № 3. Перепендикулярность прямых и плоскостей. Метрические задачи.
Задача 26Задача 27
Задача 28
Задача 29
Задача 30
5. Практикум № 4. Способы преобразования комплексного чертежа.
Задача 32Задача 33
Задача 34
Задача 35
Задача 36
Задача 37
Задача 38
6. Практикум № 5. Поверхности, их образование и задание на чертеже.
Задача 39Задача 40
Задача 41
Задача 42
7. Практикум № 6. Позиционные задачи. Развертка поверхностей.
Задача 43Задача 44
Задача 45
Задача 46
Задача 47
8. Практикум № 7. Позиционные задачи. Пересечение поверхностей плоскостью и прямой линией.
Задача 48Задача 49
Задача 50
Задача 51
Задача 52
Задача 53
Задача 54
Задача 55
Задача 56
Задача 57
Задача 58
9. Практикум № 8. Взаимное пересечение поверхностей.
Задача 59Задача 60
Задача 61
Задача 62
Задача 63
Задача 64
10. Практикум № 9. Особые случаи пересечения поверхностей.
Задача 65Задача 66
Задача 67
Задача 68
11.
ZП2
C
C2
-Y
A1
B
Ax
B
X
2
B Dx D2
A2
0
1
Cx
x
A
C
П
B
1
1
D D
1
Y
-Z
A(73, наглядное
-38,и-18)
– 3-ий
Измерим
Имея
запишем
изображение
координаты
точек,
точек
измерить
по осямиX,запис
Yи
октант
построить
комплексный чертеж.
В(54, 24, 8) – 1-ый
октант
12.
C3 C2A1
y
C1
B2
X
Ax
Z(Y)
C
Bx
D3 D
Dx D 2
Ay
A2
B3
By
Cx
A
B1
3
D1
Y(Z)
Теперь
отложим
координаты
точкиточками
Аотложим
по
Построим
точу
А,
для
этого
Так
Далее
же мы
найдем
поступим
точки
сА3
остальными
и Аy сначала
осям Y и Z и по
назовем
координату
оси Х их
и
A1 и A2 соответственно
Назовем
ее Ax
Yy
13.
ZП2
Z
B2
B B2
B3
A3
A2
П3
A
E3
E2
C2
X
B1
A1
0 D3 C3
D1 D2 Y
X
E1
E
Ax
C2
A1
D 0
E1
B1
C C1
П1
C1
Y
Y
Построим
третьи
проекции
точек
на
По
Построим
двум
точек
точек,
третьи
не забывая
проекци
п
Для
построения
наглядного
изображения
запишем
А(46,
16,проекциям
41)наглядное
В(33,
0,изображение
55) построить
С(22,
20,
0)
D(8,
0,
0) коо
E(
примере задания
1
изображение
искажения
поиоси
записать
Y
координаты точек
14.
Z(Y)B1
X
A2
A3
D3
B2 D2
B3
C2
D1
A1 C1
Y
C3
Y(X)
Построить
комплексный
чертеж
точки
А
15) и В
(6
Так
как точка
С симметрична
точке
А относительно
П1
Построим
комплексный
чертеж
точек
А (30,
и В 25,
согласно
за
проекции
точки
симметричной
точкеу А
относительно
точки С (30,
25, С,
-15),
соответственно
точки
D,симметр
симметричной
В относительно
относительноточке
П2 координаты
будут П2.
D(60, 15, -10)
15.
ZП2
П3
A2
A3
0
X
A1
Укажем плоскости на чертеже
П1
Построить проекции точки А,
Используя
пространственное
отстоящей
от плоскости П1
Y
воображение
на
расстоянииприходим
30 мм, отк выводу,
что
точка А
координаты
плоскости
П2имеет
на расстоянии
20 мм
А(0,
20, 30) в плоскости П3 .
и лежащей
Записать координаты этой точки.
Y
16.
A A2Построить проекции
Z точки В, симметричной точке А относительно плоскости П1
0
X
A1 B1
III
B B2
Y
Y
17.
Построить комплексный чертеж прямой АВ по координатамдвух ее точек А (40, 20, 10), В (0, 25, 30).Построить
наглядное изображение.
Z
Z
B2
B3
B
A2
A3
0
X
X
A
0
A1
A1
B1
Y
B1
Y
18.
Построить комплексный чертеж треугольника АВС покоординатам его вершин А (0, 20, 10), В (45, 30, 10).
Построить наглядное изображение треугольника АВС.
Z
Z
C2
C
A2
0
B2
X
C1
X
0 A
B
B1
C1
A1
A1
B1
Y
Y
19.
Построить следы прямой a и указать октанты, черезКоторые она проходит.
Z
F2 F
VI
a1
II
H2
Y
X
IV
F1
I
a1
H H1
Прямая проходит через 4, 1
, 2 , 6-ой
октанты.
Y
20.
Построить следы прямой b и указатьоктаны, через которые она проходит.
Z
b2
II
III
X
H H1
F F2
H2
F1
V
I
0
b1
Прямая проходит через 3, 2,
1 , 5-ой
октанты.
Y
Y
21. 10. Построить фронтальный след плоскости ABC. Выделить цветным карандашом след, находящийся в 1-ом октанте и обозначить точку
пересеченияс осью X
B2
C2
P2
A2
f0≡f02
Sx
K1
f01
P1
K2
A1
C1
B1
22. 11. Построить горизонтальный след плоскости Σ (a ∩ b).
a2C2
b2
x
h02
K2
S2
a1
b1
K1≡K
C1
h0≡h01
S1≡S
23. 12. Определить координаты точки приземления B парашютиста, если скорость снижения – вектор AB, скорость относа его ветром –
вектор AC.A2
Z
C2
B2
D2≡Dx
X
O
Y
D1≡D
Dy
C1
Y
A1≡B1
D (44, 15, 0)
24.
a2C2
M2 K
2
b2
D2
X
K1
D1
b1
M1
C1
a1
Найдем
Определить
проекцию
положение
точки
С
(a b)
относитель
Соединив
точки
С1
и К2
М1плоскости
спрямой
прямой
b1 пол
Соединим
точки
С2
и
ина
напересечении
полученной
найдем
проекций.
на
прямой
a1
недостающие
проекции точек С и М из
найдем
ееНайти
проекцию
на b2
принадлежности плоскости
25.
f0f 20
f2
E2
K2
12
Sx
11
h2
h2
22
K1
f 10
0
E1
f1
21
h1
h 0 h1
0
Согласно
условию
проведем
через
К горизонталь,
Определить
Найдем проекции
недостающие
точек
КиЕ
проекции
на h1 точку
и f2точек
соответственно.
К и Е из условч
плоскости (h0 f0). Через точку К провести горизонталь,
точку Е – фронталь.
26.
f012
B2
h2
C2
h2’
22
Sx
f 20
D2
11
21
C1
h20
f 10
B1
h1
D1
h0
h1’
h10
Найдем
Достроить
Проведем
Соединим
проекцию
горизонталь
получившиеся
горизонтальную
точкичерез
С.
точки.
Проведем
проекцию
точку D2
горизонталь
итреугольника
найдем еечерез
прое
B
Треугольник
проекцию
точки
BCDВпринадлежит
на h1
(h0 f0).
27. 20. Определить взаимное положение прямой l и плоскости Г(a ∩ b).
a2l2
12
K2
22
b2
a1
11
K1
l1
21
b1
28. 21. Определить взаимное положение прямой l и плоскости Г(f0 ∩ h0).
l212
f0 ≡
f20
K2
11
Sx
22
K1
l1
h0 ≡ h10
21
h20 ≡
29. Определить взаимное положени плоскостей DABC и DDEF, видимость
B2E2
A2
Задача 23
F2
C2
C1
D2
F1
E1
B1
A1
D1
30.
B2E2
A2
Задача 23
F2
C2
C1
D2
F1
E1
B1
A1
D1
•Даны две плоскости произвольного положения.
•Надо определить, как эти плоскости расположены друг относительно друга, т.е. найти
линию их пересечения.
31.
B2E2
A2
Задача 23
F2
C2
C1
D2
F1
E1
B1
A1
D1
•Можно сказать, что плоскость DEFD задана двумя пересекающимися прямыми EF и ED.
•Поэтому, найдя точки пересечения прямых EF и ED с плоскостью DABC, мы найдём
линию пересечения этих треугольников.
32.
B2E2
Задача 23
n2
A2
F2
C2
C1
D2
F1
E1
B1
A1
D1
Для того чтобы найти точку пересечения EF с DABC, надо взять прямую n, лежащую
в плоскости DABC, проекция n2 которой совпадает с E2F2.
33.
B2E2
n2
Задача 23
12
22
A2
F2
C2
D2
C1
F1
E1
21
A1
11
n1
Затем спроецируем n2 в π1.
D1
B1
34.
B2E2
n2
Задача 23
12
22
A2
32
F2
C2
D2
C1
31
F1
E1
21
A1
11
n1
B1
D1
Точка пересечения n1 и E1F1 (точка 3) будет искомой точкой пересечения EF c
плоскостью ABC π1.
Спроецируем её в π2.
35.
l2B2
E2
n2
Задача 23
12
22
A2
42
62
32
F2
52
C2
C1
E1
D2
31
51
61
21
B1
41
A1
l1
11
n1
D1
Точно так же ищем точку пересечения ED с плоскостью ABC.
F1
36.
l2B2
E2
n2
Задача 23
12
22
A2
42
62
32
F2
52
C2
C1
E1
D2
31
51
61
21
F1
B1
41
A1
l1
11
n1
D1
Соединив эти точки, получим линию пересечения плоскостей треугольников.
Но т.к. это конкретные треугольники, то линия пересечения будет заканчиваться на
границе треугольников.
37.
B2E2
32
A2
Задача 23
42
12 22
52 62
72
F2
82
C2
C1
D2
F1
E1
B1
A1
D1
•Следующий этап - определение видимости. Для этого надо воспользоваться
конкурирующими точками. В данном случае это пары точек 1 и 2, 3 и 4, 5 и 6, 7 и 8.
38.
B2E2
32
A2
Задача 23
42
12 22
52 62
72
F2
82
C2
C1
D2
F1
E1
21
A1
11
B1
D1
•Рассмотрим пару точек 1 и 2. Точка 1 лежит на АВ, а 2 - на EF. Т.к. эти точки
конкурируют в π2, то видимость будет определяться по координате y в π1. Т.к. y11 > y21, то
в π2 будет видна точка 1, а значит и прямая АВ, на которой лежит эта точка.
39.
B2E2
32
A2
Задача 23
42
12 22
52 62
72
F2
82
C2
C1
D2
F1
E1
B1
A1
D1
•Аналогично видимость определяется и для других пар конкурирующих точек.
40.
B2E2
A2
Задача 23
F2
C2
C1
E1 3 1 4 1
11
D2
F1
51 61
21
A1
71
111
121
81
B1
91 101
D1
•Теперь определим видимость в π1.
• Для этого надо воспользоваться конкурирующими точками. В данном случае это пары
точек 1 и 2, 3 и 4, 5 и 6, 7 и 8, 9 и 10, 11 и 12.
41.
B2E2
Задача 23
22
A2
F2
12
C2
C1
E1 3 1 4 1
11
A1
D2
F1
51 61
21
71
111
121
81
B1
91 101
D1
•Рассмотрим пару точек 1 и 2. Точка 1 лежит на АС, а 2 - на ED. Т.к. эти точки
конкурируют в π1, то видимость будет определяться по координате z в π2. Т.к. z22 > z12, то
в π1 будет видна точка 2, а значит и прямая ED, на которой лежит эта точка.
42.
B2E2
A2
Задача 23
F2
C2
D2
C1
51 61
E1 3 1 4 1
11
A1
F1
21
71
111
121
81
B1
91 101
D1
•Аналогично видимость определяется и для других пар конкурирующих точек.
Конец
43. Определить взаимное положение плоскостей DABC и DDEF
Определить взаимное положение плоскостейЗадача 24
DABC и DDEF E
B
2
2
F2
A2
C2
D2
E1
C1
F1
A1
B1
D1
44.
Задача 24B2
E2
F2
A2
C2
D2
E1
C1
F1
A1
B1
D1
•В данном случае плоскости заданы треугольниками. Это плоскости
общего положения.
•Если найти хотя бы две общие точки этих плоскостей, то можно будет
найти и линию их пересечения.
45.
Задача 24B2
E2
F2
A2
C2
D2
E1
C1
F1
A1
21
f1 1
1
B1
f`1
31
41
D1
Для того чтобы найти точку пересечения плоскостей DABC и DDEF,
надо построить пару фронталей f и f`, лежащих соответственно в
плоскости DABC и DDEF.
46.
Задача 24B2
f2
М2
E2
22
12
F2
A2
C2
32
f`2
42
D2
E1
C1
F1
A1
M1
21
f1 1
1
B1
Спроецируем фронтали в π2.
Точка их пересечения и даст искомую точку.
f`1
D1
31
41
47.
Задача 24B2
f2
М2
E2
72
22
12
A2
f``2
C2
32
f`2
42
D2
E1
C1
f``1
51
A1
M1
f```1
61
21
f1 1
1
B1
f```2
F2
N2
62
52
82
N1
F1
81
71
f`1
31
D1
С помощью другой пары фронталей f`` и f``` аналогично находим
вторую точку пересечения плоскостей DABC и DDEF.
41
48.
Задача 24B2
f2
М2
E2
72
22
12
A2
f``2
C2
32
f`2
42
D2
E1
C1
f``1
51
A1
M1
f```1
61
N1
21
f1 1
1
F1
81
71
f`1
31
41
D1
B1
Соединив эти точки, получим линию пересечения плоскостей DABC и
DDEF.
Конец
f```2
F2
N2
62
52
82
49.
№26 Из точек А, В, С опустить перпендикуляры на соответствующие им на эпюрах прямые уровня.50.
№261.Проведем из горизонтальной проекции т.А горизонтальную проекцию
перпендикуляра к горизонтальной проекции прямой h
2.Проведем из фронтальной проекции т.В фронтальную проекцию
перпендикуляра к фронтальной проекции прямой f
3.Для 3-й прямой найдем её проекцию в плоскости П3.
51.
№261.Найдем фронтальную проекцию основания перпендикуляра.
2.Найдем горизонтальную проекцию основания перпендикуляра
3.Найдём 13 и 23.
52.
№261.Соединяем получившиеся точки с точками А2 и В2.
2.Найдем проекцию т.С в плоскости П3, и из С3 опустим перпедикуляр на прямую 13 23.
53.
№263.Найдем фронтальную и горизонтальную проекции т.3
54.
№267.Соединяем получившиеся точки с точками С1 и С2,получаем
изображение перпендикуляра в плоскостях П1 и П2.
55.
№27 Провести перпендикуляр к плоскости из т.D принадлежащей АВС.56.
№271.Проведем прямую через А1 и D1 . Точку пересечения с В1С1
обозначим 21 и найдем фронтальную проекцию этой прямой
57.
№272.Найдем фронтальную проекцию т.D
58.
№273.Проведем горизонтальную и фронтальную проекции горизонтали и фронтали.
59.
№274.Опустим перпендикуляр из D1 на горизонтальную проекцию
горизонтали, а из D2-на фронтальную проекцию фронтали.
60.
№275.Определяем видимость.
61.
№28Опустить перпендикуляр из т.А На плоскость заданной
следами,определить точку пересечения перпендикуляра
и этой плоскости.
62.
№281.Возьмём плоскость проходящую через точку А и
перпендикулярная плоскости f=f2 до пересечения с плоскостью
Sx.
63.
№282.Далее находим след этой прямой,опустив перпендикуляры из
точек пересечения плоскостей, затем соединяем их.
64.
№283.Опускаем перпендикуляр из точки А1 на h=h1,продолжая его до
пересечения с проекцией прямой А2 12.
65.
№284.Из получившейся точки опустить перпендикуляр на прямую
А212,получаем точку пересечения плоскости и перпендикуляра.
66.
№29 Через прямую АВ провести плоскость перпендикулярнуюплоскости F(a || b).
67.
№291.Проводим горизонталь в плоскости П2.
68.
№292.Опускаем перпендикуляры из точек пересечения горизонтальной проекции с прямыми a2 и b2.Нашли фронтальную проекцию
горизонтали.
69.
№293.Берём произвольную точку фронтальной проекции, находим
проекцию на прямой А1В1.
70.
№294.Опускаем перпендикуляр.
71.
№295.Из полученной точки опускаем перпендикуляр на прямую а2,
получаем плоскость перпендикулярную плоскости Ф(a b).
72.
№30Изобразить направление движения шара, скатывающегося
с наклонного щита ВDСЕ, и определить угол наклона
щита к горизонту.А-точка касания шара со щитом.
73.
№301.Опускаем перпендикуляры из точки касания шара.
74.
№302.Из точки 11 проводим перпендикуляр к плоскости П2.
75.
№303.Полученную точку соединяем с точкой касания шара.
76.
№304.Откладываем на стороне Е1D1 расстояние равное Z,т.к. Z- высота на которой находится шар.
77.
Определение натуральной величиныпрямых AS и BS и угла наклона между ними.
S2
B2
A2
X
Задача решается способом
замены плоскостей.
Для того, чтобы определить
натуральную величину
A1
прямых AS и BS необходимо
ввести дополнительную
плоскость проекции.
Переведем прямые AS и BS
из общего положения в прямые уровня.
B1 ≡ S1
78.
Чтобы прямые стали прямыми уровнявводим дополнительную плоскость
проекции П4 : X1 ║ A1B1S1
S2
B2
A2
X
B1 ≡ S1
A1
П1
X1
П4
79.
Из точек A1 и B1 проводим линии связиS2
B2
A2
X
B1 ≡ S1
A1
П1
X1
П4
80.
Спроецируем точки A,B,S,в плоскость П4
S2
hS
B2
hB
A2
X
B1 ≡ S1
A1
hB
П1
X1
B4
hS
A4
П4
S4
81.
Соединяем точки A4 с S4 и B4 с S4.Угол, между прямыми A4S4 и B4S4 – искомый.
S2
hS
B2
hB
A2
X
B1 ≡ S1
A1
hB
П1
П4
B4
hS
A4
α
S4
82. Определение расстояния от точки D до ΔABC и угла наклона ΔABC к П1.
D2B2
A2
C2
X
C1
D1
A1
B1
Задача решается способом
замены плоскостей.
Чтобы определить расстояние
от точки D до ΔABC необходимо
построить вырожденную проекцию
ΔABC на плоскость П4,
спроецировать туда же точку D.
Искомое расстояние определяется
длиной ┴ от точки D до A4B4C4.
83.
Нужно построить горизонталь hΔABC, чтобы в дальнейшем
построить дополнительную
плоскость проекции П4: X1 ┴ h1,
X1 ┴ П4
B2
D2
12
A2
h2 Строим фронтальную проекцию
горизонтали h2
C2
X
C1
D1
11
A1
B1
h1
Строим горизонтальную проекцию
горизонтали h1
84.
Вводим дополнительную плоскостьпроекции П4 : X1 ┴ h1, X1 ┴ П4
D2
B2
12
A2
h2
C2
X
C1
D1
11
B1
h1
П1 П
4
X1
85.
Из точек B 1,C1, D1 проводим линии связиD2
B2
12
A2
h2
C2
X
C1
D1
11
B1
h1
П1 П
4
X1
86.
Спроецируем точку Cв плоскость П4
D2
B2
12
A2
h2
C2
По аналогии с точкой С, спроецируем
в плоскость П4 точки A,B,D.
hC
X
C1
D1
11
hC
C4
D4
h1
A4
B1
П1 П
4
X1
B4
87.
D2Проводим прямую, соединяющую точки A4, B4 , C4
до пересечения с X1.
A4B4C4 – вырожденная проекция ΔABC
B2
12
A2
A4B4C4 ∩ X1 = α
h2
Из точки D4 опускаем
перпендикуляр на A4B4C4
и получаем точку K4
C2
X
C1
D1
11
α
C4
D4
h1
A4
K4
B1
П1 П
4
X1
B4
88.
Из точки D4 проводим линиюсвязи
D2
B2
12
A2
Из точки D1 проводим
прямую, параллельную оси
X1, т.к. прямая DK является
фронталью, ее проекция на
П4 проецируется без
искажения.
h2
K2
hK
C2
Спроецируем точку K1
в плоскость П2
X
C1
D1
11
K1
α
C4
D4
h1
A4
hK
B1
П1 П
4
X1
K4
B4
89.
DK – искомое расстояниеD2
B2
12
A2
h2
K2
C2
X
C1
D1
11
K1
α
C4
D4
h1
A4
K4
B1
П1 П
4
X1
B4
90.
Определение угла наклона между двумяпересекающимися прямыми AB и BC.
B2
Задача решается способом A2
замены плоскостей.
Плоскость ABC находится
X
в общем положении.
Чтобы определить угол
необходимо найти
натуральную величину AB и BC.
Для этого введем дополнительную
плоскость проекции П4,
т. е. переводим плоскость
ABC в плоскость уровня. A1
Проекция ABC получится
вырожденной.
Для того чтобы найти угол нужно
ввести дополнительную
плоскость П5.
C2
C1
B1
91.
B2h2
12
Нужно построить горизонталь,
чтобы в дальнейшем ввести
дополнительную плоскость проекции П4
Проводим фронтальную проекцию
горизонтали h2 через точку C2
C2
A2
Строим горизонтальную проекцию
горизонтали h1
X
C1
A1
h1
11
B1
92.
B2h2
Вводим дополнительную плоскость
проекции П4 : X1 ┴ h1, X1 ┴ П1.
12
C2
A2
X
C1
A1
h1
11
B1
П 1 П4
X1
93.
Из точек B 1,C1, A1 проводим линии связи.Спроецируем точку B
в плоскость П4
B2
h2
По аналогии с точкой B, спроецируем
в плоскость П4 точки A,C.
C2
12
A2
X
A4
C4
C1
A1
h1
11
B1
П 1 П4
X1
B4
94.
Соединяем точки A4, B4, и C4.A4B4C4 – вырожденная проекция.
B2
h2
Для того, чтобы найти угол нужно
ввести дополнительную плоскость
12
проекции П5 : X2 ║ A4B4C4
C2
A2
X
П5
A4
C4
C1
A1
h1
B1
П 1 П4
X1
B4
П4
X2
95.
A5B2
h2
α
B5
12
C2
A2
C5
X
Из точек B 4,C4, A4 проводим линии связи
C4
C1
Спроецируем точку B
в плоскость П5
A1
h1
11
По аналогии с точкой B, спроецируем
в плоскость П4 точки A,C.
B1
П5
A4
П 1 П4
X1
B4
П4
X2
96. Определение кратчайшего расстояния между траекториями полета двух самолетов.
a2X
b2
b1
a1
Задача решается способом замены плоскостей.
Кратчайшее расстояние между двумя
прямыми - это длина взаимного перпендикуляра.
Одна из прямых переводится в положение уровня.
Эта же прямая переводится на плоскость П5
в проецирующее положение.
Вторая прямая переводится на плоскость П4,
затем на П5 в общем положении по закону проекционной связи
На плоскости П5 определяется искомое расстояние.
97.
На прямых a и b произвольно отметим точкиСпроецируем эти точки в плоскость П1
Чтобы перевести прямую
в положение уровня нужно
ввести дополнительную плоскость
проекции П4 : X1 ║ a1
A2
a2
X
a1
A1
A′2
B′2
B2
B′1
B1
b2
b1
A′1
П1
П4
X1
98.
Через точки A1, A′1, B1, B′1 проведем линии связи.Спроецируем точку A′ в плоскость П4
По аналогии с точкой A′, спроецируем
в плоскость П4 точки A,B′,B
A′2
B′2
A2
b2
B2
a2
X
a1
B′1
A1
A4
b1
B1
A′1
П1
B4
h A′
B′4
h A′
A′4
П4
X1
99.
Соединим точки A4 и A′4; B4 и B′4Вводим дополнительную плоскость
проекции П5 : X2 ┴ A4A′4,
чтобы перевести прямую
в проецирующее положение.
A′2
B′2
A2
b2
B2
a2
X
a1
B′1
A1
A4
B1
A′1
П1
B4
B′4
П5
П4
X2
b1
П4
A′4
X1
100.
Из точек B4, B′4, A4 проводим линии связи.Прямая a становится проецирующей
линией относительно плоскости П5 ;
все ее точки (вся прямая) проецируются
на плоскость П5 в виде одной точки A5 ≡ A′5 ≡ 15
A′2
B′2
Спроецируем точки B и B′
A2
b2
B2
a2
X
B5
B′5
A5 ≡ A′5 ≡ 15
a1
B′1
A1
A4
B1
A′1
П1
B4
B′4
П5
П4
X2
b1
П4
A′4
X1
101.
Соединяем точки B5 и B′5Из точки 15 проводим перпендикуляр к прямой b
A′2
B′2
A2
b2
B2
a2
X
B5
25
B′5
A5 ≡ A′5 ≡ 15
a1
B′1
A1
A4
B1
A′1
П1
B4
B′4
П5
П4
X2
b1
П4
A′4
X1
102.
Из точки 25 проводим линию связидо пересечения с прямой b.
Из точки 25 опускаем перпендикуляр на прямую a.
Точки 15 и 25 спроецируем в П1, а затем в П2
B′2
A2
X
B5
25
B′5
A5 ≡ A′5 ≡ 15
b2
B2
21
a1
b1
B1
A1
11
A4
14
B′4
П5
П4
X2
22
12
a2
A′2
24
A′1
П1
B4
П4
A′4
X1
103.
РАБОТА №37На прямой l определить точку
М, удаленную от плоскости ∑
(h0 f0 ) на расстоянии 20 мм и
определить угол наклона ∑ к П1
далее
104.
12l2
32
РАБОТА №37
f0 = f2 0
М2
22
h20 = f10
x
11
21
М1
l1
31
24
14
20
мм
h0 = h10
П1
М4
П4
34
105.
РАБОТА №38Изобразить направление
напряженности магнитного поля в
точке С при движении по проводнику
электрического тока от А к В
далее
106.
П2РАБОТА №38
П4
C4
C2
B2
x А2
А1
B1
C2
А4 =B4
107. Задача № 39
ЗАДАНИЕ Построить проекции трехграннойпирамиды SABC с основанием ΔABC и высотой
SA=40 мм.
ДАНО
B2
C2
A2
x
C1
A1
B1
Меню
108.
№391) Строим фронтальную проекцию
горизонтали h2, плоскости ABC. Находим точку её
пересечения с ребром A2B2.
B2
h2
12
C2
A2
x
C1
A1
B1
Меню
109.
№392) Строим горизонтальную проекцию
горизонтали h1.
Находим точку 11,
пересечения h1 со стороной A1B1.
B2
h2
12
C22
A2
x
C1
A1
h1
B11
Меню
110.
3) Введем дополнительнуюплоскость
проекции П4,
перпендикулярную горизонтали h и
плоскости проекции П1.
№39
B2
h2
12
C22
A2
x
x1
C1
A1
h1
П4 П 1
B11
Меню
111.
B2№39
2
h2 на1П
4) Спроецируем ΔABC
4.
A2
C22
ZB
x
x1
C1
A1
A1
A4
B11
h1 C4
B4
ZB
П4 П1
Меню
112.
№395) Построим AS12
h2
перпендикуляр к
плоскости ΔABC. В
A2
проекции на П4
A4S4=40мм и
перпендикулярен x
x1
B4A4.
40м
A1
м
S
A1
4
A4
h1 C4
B2
C22
C1
B11
П4 П1
B4
Меню
113.
№396) Строим S1. Во12
h2
первых, S1S4
перпендикулярен x1.
A2
Во-вторых, S1A1
параллелен x1. x1
Значит S1 лежит наSx1
x1.
S
B2
C22
x
C1
AA11
4
A4
h1 C4
B11
П4 П1
B4
Меню
114.
S2№39
7) Строим S2.
Проведем
zs
соединительную
A2
линию из S1.
x1
Zs=S1S4.
zs
S1
B2
C2
x
C1
S
A1
4
A4
C4
B1
П4 П1
B4
Меню
115.
№398) Определяем
видимость ребер
пирамиды. По
правилу
конкурирующих
точек, ребро S2C2
невидимо, так как
y1>y2 , ребро A1C1
невидимо , так как
z3>z4.
32
S2
B2
12=22
A2
C2
42
x
S1
21
A1
31=
41 11
C1
B1
Меню
116.
№39Ответ.
B2
S2
C2
A2
x
S1
C1
A1
B1
Меню
117. Задача № 40.
ЗАДАНИЕПостроить
фронтальный очерк поверхности косой
плоскости, заданной направляющими d и
d’ и плоскостью параллелизма П2
d2
d’2
ДАНО
x
d1
d’1
Меню
118.
№401) Построим фронтальные проекции
фронталей f1, f’1, f”1.. Они параллельны, так как
плоскость проекции П2- является плоскостью
параллелизма.
d’2
d2
x
A1
f1 A’
1f’
B’1 1 f’’1
C’
B1
C
D1
1
1
D’
E
1
d1
E’
1
1
d’1
Меню
119.
№402)Строим фронтальные проекции
фронталей..
A’
2
d2 E
2
D2
E’
C
2
x
C
D1
2
B2 A2
A1
d1
1
f1 A’
1 f’
B’11 f’’1
C’
B1
1
1
D’
E
1
B’2
C’ d’2
2D’
E’
1
1
d’1
Меню
120.
№40ОТВЕТ..
d’2
d2
x
d1
d’1
Меню
121. Задача 41
122.
Задача 41Условия задачи:
Построить фронтальный очерк поверхности вращения заданной осью i и образующей q.
i2
q2
x
q1
i1
123.
Задача 41Возьмем проекции точек 12,22,42,52 на q2. По принадлежности найдем проекции точек на
П1
i2
12
22
42
52
q2
x
51
i1
41
11
21
q1
124.
Задача 41Проекцию точки 31 возьмем в точке пересечения перпендикуляра к q1 проведенного через
i1 и q1 . По принадлежности найдем 32.
i2
12
22
32
42
52
q2
x
51
i1
41
31
11
21
q1
125.
Задача 41Через проекции точек 11,21,31,41,51 на П1 проводим окружности
i2
12
22
32
42
52
q2
x
51
i1
41
31
11
21
q1
126.
Задача 41Через проекцию i1 проведем фронталь
i2
12
22
32
42
52
q2
x
51
i1
41
31
11
21
q1
127.
Задача 41На П2 проекции этих окружностей будут выглядеть отрезками параллельными П1. Поэтому
начертим прямые горизонтального уровня на которых будут лежать эти окружности.
i2
12
22
32
42
52
q2
x
51
i1
41
31
11
21
q1
128.
Задача 41Измеряем радиусы окружностей на П1 и отмечаем эти радиусы на проециях окружностей в
П2 (ставим засечки).
i2
12
22
32
42
52
q2
x
51
i1
41
31
11
21
q1
129.
Задача 41Аппроксимируем получившиеся засечки и ограничиваем плоскость.
i2
12
22
32
42
52
q2
x
51
i1
41
31
11
21
q1
130.
Задача 41Результат решения
Стираем линии построения. В результате получается поверхность вращения гиперболоид
i2
q2
x
q1
i1
Зад. 42 Главное меню
131. Задача 42
132.
Задача 42Условия задачи:
Построить фронтальный очерк поверхности вращения, заданной осью i,
образующей АВ и шагом Р.
i2
B2
Х
А2
А1
i1≡B1
133.
Задача 42Разделим расстояние Р на 8 частей – уровней.
i2
B2
Х
А2
А1
i1≡B1
134.
Задача 42Проекции точки В на П2 уже обозначены(здесь B2` положение на последнем
уровне.
B2’
i2
B2
Х
А2
А1
i1≡B1
135.
Задача 42Построим проекции очки А в П1 на каждом уровне. Для этого:
В П2 проведем через проекции точки В горизонтали на которых будут лежать проекции
точки А
B2’
i2
B2
Х
А2
А1
i1≡B1
136.
Задача 42В П1 разделим окружность на 8 частей и обозначим положения точки А на
каждом уровне цифрами.
B2’
i2
B2
Х
А2
3
2
4
i1≡B1
А1
5
1
6
8
7
137.
Задача 42Проводим вспомогательные линии из положений 2,4,6,8.
B2’
i2
B2
Х
А2
3
2
4
i1≡B1
А1
5
1
6
8
7
138.
Задача 42Отмечаем положение точки А на каждом уровне в плоскости П2. Здесь А2`
положение проекции на последнем уровне
B2’
А2’
i2
B2
Х
А2
3
2
4
i1≡B1
А1
5
1
6
8
7
139.
Задача 42Чертим проекции прямой АВ на П2 т.е. соединяем А2 и В2 на каждом из восьми
уровней.
B2’
А2’
i2
B2
Х
А2
3
2
4
i1≡B1
А1
5
1
6
8
7
140.
Задача 42Аппроксимируем проекции точек А2 – А2`
B2’
А2’
i2
B2
Х
А2
3
2
4
i1≡B1
А1
5
1
6
8
7
141.
Задача 42Соединяем точки В2 и В2’
B2’
А2’
i2
B2
Х
А2
3
2
4
i1≡B1
А1
5
1
6
8
7
142.
Задача 42Результат решения
Получилась такая поверхность вращения:
B2’
А2’
i2
B2
Х
А2
3
2
4
i1≡B1
А1
5
1
6
8
7
Зад. 43 Главное меню
143. Задача 43
144.
Задача 43Условия задачи:
Построить недостающие проекции точек, принадлежащих поверхности
трехгранной пирамиды.
S2
S3
12
22
X
A2
A1
B2
C2
S1
C1
41
31
B1
A3 ≡
C3
B3
145.
Задача 43Точка 1 лежит на ребре SA. Поэтому сначала по принадлежности находим
проекцию 11,
S2
S3
12
22
X
A2
A1
B2
11
C2
S1
C1
41
31
B1
A3 ≡
C3
B3
146.
Задача 43Затем проекцию 13 точки 1
S3
12
13
22
X
A2
A1
B2
11
C2
S1
C1
41
31
B1
A3 ≡
C3
B3
147.
Задача 43Точка 2 лежит в грани ABS. Чтобы найти недостающие проекции точки
проведем через неё в грани ABS линию MN параллельную АВ.
S2
S3
12
22
M2
X
A2
A1
11
13
N2
B2
C2
S1
C1
41
31
B1
A3 ≡
C3
B3
148.
Задача 43По принадлежности найдем M1
S2
S3
12
M2
X
A2
A1 M1 11
22
13
N2
B2
C2
S1
C1
41
31
B1
A3 ≡
C3
B3
149.
Задача 43Параллельно А1В1 проводим M1N1
S2
S3
12
M2
X
A2
A1 M1 11
22
13
N2
B2
C2
S1
C1
41
31
N1
B1
A3 ≡
C3
B3
150.
Задача 43На M1N1по принадлежности находим 21
S2
S3
12
M2
X
22
A2
13
N2
B2
C2
S1
A1 M1 11
C1
41
21
31
N1
B1
A3 ≡
C3
B3
151.
Задача 43Чтобы найти 23 проведем через проекцию точки 22 линию P2Q2║S2B2
S2
S3
P2
12
M2
X
22
A2
13
N2
B2
C2
Q2
S1
A1 M1 11
C1
41
21
31
N1
B1
A3 ≡
C3
B3
152.
Задача 43Найдем P3Q3 . Для этого: 1)по принадлежности найдем P3
S2
S3
P2
P3
12
M2
X
22
A2
13
N2
B2
C2
Q2
S1
A1 M1 11
C1
41
21
31
N1
B1
A3 ≡
C3
B3
153.
Задача 432)параллельно S3B3 прочертим P3Q3
S2
S3
P2
P3
12
M2
X
22
A2
13
N2
B2
C2
Q2
S1
A1 M1 11
C1
41
21
31
N1
B1
A3 ≡
C3
Q3
B3
154.
Задача 43Теперь по принадлежности находим проекцию 23 .
S2
S3
P2
P3
12
M2
X
22
A2
13
N2
B2
C2
Q2
S1
A1 M1 11
C1
41
21
31
N1
B1
23
A3 ≡
C3
Q3
B3
155.
Задача 43Точка 31 лежит на ребре SB. Чтобы найти 32 в грани SBC проведем через точку
3 линию параллельную ВС . Назовем её l .
S2
S3
P2
P3
12
M2
X
22
A2
13
N2
B2
C2
Q2
S1
A1 M1 11
C1
l1
41
21
31
N1
B1
23
A3 ≡
C3
Q3
B3
156.
Задача 43Найдем проекцию l2 этой линии на П2
S2
S3
P2
P3
l2
12
M2
X
22
A2
13
N2
B2
C2
Q2
S1
A1 M1 11
C1
l1
41
21
31
N1
B1
23
A3 ≡
C3
Q3
B3
157.
Задача 4332 будет лежать в точке пересечения l2 с S2B2
S2
S3
P2
P3
l2
32
12
M2
X
22
A2
13
N2
B2
C2
Q2
S1
A1 M1 11
C1
l1
41
21
31
N1
B1
23
A3 ≡
C3
Q3
B3
158.
Задача 43Проекцию 33 можно найти по принадлежности. Для этого проведем через 32
соединительную линию на П3
S2
S3
P2
P3
l2
32
12
M2
X
22
A2
13
N2
B2
C2
Q2
S1
A1 M1 11
C1
l1
41
21
31
N1
B1
23
A3 ≡
C3
Q3
B3
159.
Задача 43В точке пересечения с S3B3 ставим проекцию 33
S2
S3
P2
P3
l2
32
12
M2
X
33
22
A2
13
N2
B2
C2
Q2
S1
A1 M1 11
C1
l1
41
21
31
N1
B1
23
A3 ≡
C3
Q3
B3
160.
Задача 43Точка 4 лежит на ребре ВС. Поэтому, чтобы найти 42 проводим соединительную
линию в плоскость П2
S2
S3
P2
P3
l2
32
12
M2
X
33
22
A2
13
N2
B2
C2
Q2
S1
A1 M1 11
C1
l1
41
21
31
N1
B1
23
A3 ≡
C3
Q3
B3
161.
Задача 43На А2С2 ставим проекцию 42
S2
S3
P2
P3
l2
32
12
M2
X
33
22
A2
13
N2
B2
C2
42
Q2
S1
A1 M1 11
C1
l1
41
21
31
N1
B1
23
A3 ≡
C3
Q3
B3
162.
Задача 43Через 42 проводим линию 42F2 параллельную S2B2
S2
S3
P2
P3
l2
32
12
M2
X
22
A2
N2
B2
2
13
S1
C1
l1
41
21
31
N1
B1
23
C2
42
Q2
A1 M1 11
33
F
A3 ≡
C3
Q3
B3
163.
Задача 43По принадлежности находим проекцию F3 на П3 , и чертим через F3 линию
параллельно S3B3
S2
S3
P2
P3
l2
32
12
M2
X
22
A2
N2
B2
F
2
13
C1
l1
41
21
31
N1
B1
3
23
C2
S1
A1 M1 11
F
42
Q2
33
A3 ≡
C3
Q3
B3
164.
Задача 43Точка 4 лежит на ребре ВС. Поэтому проекция 43 в точке пересечения А3В3
и линии проходящей через F3║S3B3. Проекция будет невидимой потому
что на П3 В3С3 лежит за А3В3
S2
S3
P2
P3
l2
32
12
M2
X
22
A2
N2
B2
F
2
13
3
23
C2
S1
A1 M1 11
F
42
Q2
33
C1
A3 ≡ 43 Q3
C3
B3
l1
41
21
31
N1
B1
Зад. 44 Главное меню
165. Задача 44
166.
Задача 44Условия задачи:
Построить недостающие проекции точек, принадлежащих поверхности
сферы.
A2
C2
O2
O3
E2
P3
X
O1
B1
167.
Задача 44Точка А :
Т.к в П1 проекция А2 принадлежит окружности, то очевидно что в П1 проекция
А1 будет лежать на экваторе окружности, т.е. на штрихпунктирной линии :
A2
C2
O2
O3
E2
P3
X
O1
A1
B1
168.
Задача 44В П3 проекция А3 также будет лежать на штрихпунктирной линии:
A2
A3
C2
O2
O3
E2
P3
X
O1
A1
B1
169.
Задача 44Точка В :
Проекция точки В в П1 лежит на окружности. Значит в П2 Проекция В2 будет
лежать на экваторе (штрихпунктирной линии) :
A2
A3
C2
B2
O2
O3
E2
P3
X
O1
A1
B1
170.
Задача 44Чтобы найти В3 проведем через точку вспомогательную плоскость 1 . 1 будет
горизонтально проецирующая :
21
A2
A3
C2
B2
O2
O3
E2
P3
X
O1
A1
B1
171.
Задача 44Плоскость пересекает сферу по окружности. Начертим в П3 ту ее часть, на
которой будет лежать проекция В3 :
21
A2
A3
C2
B2
O2
O3
E2
P3
X
O1
A1
B1
172.
Задача 44В точке пересечения с экватором окружности ставим В3
21
A2
A3
C2
B2
O2
O3
E2
X
O1
A1
B1
B3
P3
173.
Задача 44Точка С :
Для нахождения С3 через точку С проведем вспомогательную секущую
горизонтально прецирующую плоскость 2 :
21
22
A2
A3
C2
B2
O2
O3
E2
X
O1
A1
B1
B3
P3
174.
Задача 44Плоскость будет пересекать сферу по окружности. Начерти часть ее в П3
21
22
A2
A3
C2
B2
O2
O3
E2
X
O1
A1
B1
B3
P3
175.
Задача 44Теперь по принадлежности найдем С3 :
21
22
A2
A3
C3
C2
B2
O2
O3
E2
X
O1
A1
B1
B3
P3
176.
Задача 44Для нахождения С1через точку С проведем D1 – секущую профильно
проецирующую плоскость:
21
22
A2
D21
A3
C3
C2
B2
O2
O3
E2
X
O1
A1
B1
B3
P3
177.
Задача 44На П1 рисуем окружность по которой D1 пересекает сферу
21
22
A2
D21
A3
C3
C2
B2
O2
O3
E2
X
O1
A1
B1
B3
P3
178.
Задача 44По принадлежности находим С1 :
21
22
A2
D21
A3
C3
C2
B2
O2
O3
E2
X
O1
A1
B1
C1
B3
P3
179.
Задача 44Точка
Е:
Т.к. в П2 проекция точки Е лежит на экваторе окружности (штрихпунктирной
линии) то в П1 проекция точки Е будет лежать в нижней части окружности:
21
22
A2
D21
A3
C3
C2
B2
O2
O3
E2
X
O1
A1
B1
C1
E1
B3
P3
180.
Задача 44Для нахождения Е3 воспользуемся вспомогательной плоскостью . Начертим 3
– горизонтально проецирующую
21
22
23
A2
D21
A3
C3
C2
B2
O2
O3
E2
X
O1
A1
B1
C1
E1
B3
P3
181.
Задача 44В П3 проведем ту часть окружности, по которой 3 пересекает сферу, где лежит
проекция Е3 .
21
22
23
A2
D21
A3
C3
C2
B2
O2
O3
E2
X
O1
A1
B1
C1
E1
B3
P3
182.
Задача 44По принадлежности находим Е3. проекция будет невидимой.
21
22
23
A2
D21
A3
C3
C2
B2
O2
O3
E2
X
O1
A1
B1
C1
E1
E
B3
P3
3
183.
Задача 44Точка Р:
Чтобы построить проекцию Р2 , проведем вспомогательную горизонтально
проецирующую плоскость плоскость 4
21
22
23
34
A2
D21
A3
C3
C2
B2
O2
O3
E2
X
O1
A1
B1
C1
E1
E
B3
P3
3
184.
Задача 44Плоскость пересекает сферу по окружности. Начертим ту ее часть, где будет
лежать проекция Р2
21
22
23
34
A2
D21
A3
C3
C2
B2
O2
O3
E2
X
O1
A1
B1
C1
E1
E
B3
P3
3
185.
Задача 44По принадлежности находим проекцию точки Р2
21
22
23
34
A2
D21
A3
C3
C2
B2
P2
O2
O3
E2
X
O1
A1
B1
C1
E1
E
B3
P3
3
186.
Задача 44Чтобы найти Р1 проведем ещё одну вспомогательную плоскость D2 –
профильно проецирующую
21
22
23
34
A2
D21
A3
C3
C2
B2
P2
D22
O2
O3
E2
X
O1
A1
B1
C1
E1
E
B3
P3
3
187.
Задача 44D2 пересекает сферу по окружности. В П1 начертим ту её часть, где лежит
проекция Р1
21
22
23
34
A2
D21
A3
C3
C2
B2
P2
D22
O2
O3
E2
X
O1
A1
B1
C1
E1
E
B3
P3
3
188.
Задача 44Теперь по принадлежности находим Р1
22
21
23
34
A2
D21
A3
C3
C2
B2
P2
D22
O2
O3
E2
X
O1
A1
B1
P1
C1
E1
E
B3
P3
3
189.
Задача 4422
21
23
34
A2
D21
A3
C3
C2
B2
P2
D22
O2
O3
E2
E
B3
P3
3
X
O1
A1
B1
P1
C1
E1
Зад. 45 Главное меню
190. Задача 45
191.
Задача 45Условия задачи:
Построить проекции точек, принадлежащих поверхности конуса.
S3
S
A
2
2
E
F
3
3
B
X
2
O
O
2
D
1
S1 ≡
O1
C
1
3
192.
Задача 45Точка А :
На П2 находится на левой крайней образующей . Поэтому на П1 и П3 проекции
точки будут лежать на штрихпунктирных линиях. По принадлежности находим
проекцию А1 :
S3
S
A
2
2
E
F
3
3
B
X
2
O
O
2
D
1
A
1
S1 ≡
O1
C
1
3
193.
Задача 45Затем проекцию А3 :
S3
A
S
A
2
3
2
E
F
3
3
B
X
2
O
O
2
D
1
A
1
S1 ≡
O1
C
1
3
194.
Задача 45Точка В :
Для нахождения проекции В1 через точку В проведем вспомогательную
плоскость горизонтального уровня.
S3
A
S
A
2
3
2
E
F
3
3
B
X
2
O
O
2
D
1
A
1
S1 ≡
O1
C
1
3
195.
Задача 45Эта плоскость пересекает конус по окружности. Радиус можно
измерить на П2 (он выделен зеленым цветом, используйте кнопку
видео). Начертим эту окружность на П1 :
S3
A
S
A
2
3
2
E
F
3
3
B
X
2
O
O
2
D
1
A
1
S1 ≡
O1
C
1
3
196.
Задача 45Теперь по принадлежности находим проекцию В1 лежащую на окружности.
Проекция будет лежать в нижней части окружности.
S3
A
S
A
2
3
2
E
F
3
l2
B
X
2
l31
B
O
3
O
2
D
1
A
1
B
1
S1 ≡
O1
C
1
3
197.
Задача 45Точка С :
На П1 проекция С1 лежит на штрихпунктирной линии. Значит и на П2 проекция
точки С будет лежать на штрихпунктирной линии.
S3
A
S
A
2
3
2
E
F
3
l2
B
X
2
l31
B
O
3
O
2
D
1
A
1
B
1
S1 ≡
O1
C
1
3
198.
Задача 45С помощью соединительных линий находим С2 :
S3
A
S
A
2
3
2
E
F
3
X
l2 C
B 2
l31
B
O
3
2
O
2
D
1
A
1
B
1
S1 ≡
O1
C
1
3
199.
Задача 45В П3 проекция С3 будет лежать на правой крайней образующей:
S3
A
S
A
2
3
2
E
F
3
X
l2 C
B 2
l31
O
3
2
B
O
2
D
1
A
1
B
1
S1 ≡
O1
C
1
3
C
3
200.
Задача 45Точка D лежит на нижнем основании конуса поэтому ее проекцию D2 можно
найти с помощью соединительных линий . Проекция D2 невидимая :
S3
A
S
A
2
3
2
E
F
3
l2 C
B 2
X
2
l31
B
O
D
2
2
O
D
3
1
A
1
B
1
S1 ≡
O1
C
1
3
C
3
201.
Задача 45Для нахождения проекции D3 на П2 проведем вспомогательную прямую q
параллельную правой крайней образующей:
S3
A
S
A
2
3
2
E
F
3
q
l2 C
B 2 2
X
2
l31
B
O
D
2
2
O
D
3
1
A
1
B
1
S1 ≡
O1
C
1
3
C
3
202.
Задача 45Найдем проекцию прямой q на П3 :
S3
A
S
A
2
3
2
E
q
q
l2 C
B 2 2
X
2
1
B
1
l31
B
1
O
D
2
2
O
D
3
1
A
F
3
S1 ≡
O1
C
1
3
C
3
203.
Задача 45Теперь в точке пересечения с основанием конуса ставим проекцию D3 –
невидимую :
S3
A
S
A
2
3
2
E
q
q
l2 C
B 2 2
X
2
1
B
1
l31
B
1
O
D
2
2
D O
D
3
1
A
F
3
S1 ≡
O1
C
1
3
3
C
3
204.
Задача 45Точка Е :
S3
A
S
A
2
3
2
E
q
q
l2 C
B 2 2
X
2
1
B
1
l31
B
1
O
D
2
2
D O
D
3
1
A
F
3
S1 ≡
O1
C
1
3
3
C
3
205.
Задача 45На П3 точка E лежит на левой крайней образующей, поэтому очевидной что на
П2 проекция точки E будет лежать на штрихпунктирной линии. По
принадлежности находим E2 :
S3
A
S
A
2
3
2
E
E
2
3
q
q
l2 C
B 2 2
X
2
1
B
1
l31
B
1
O
D
2
2
D O
D
3
1
A
F
S1 ≡
O1
C
1
3
3
C
3
206.
Задача 45А на П1 проекция точки E1 будет лежать на окружности. Радиусом этой
окружности будет зеленая прямая(используйте кнопку видео) :
A
A
3
2
E
E
2
3
q
q
l2 C
B 2 2
X
2
1
B
1
B
O
D
2
2
D O
D
3
E
A
l31
1
1
1
F
S1 ≡
O1
C
1
3
3
C
3
207.
Задача 45Точка F :
Чтобы найти проекцию F2, проведем в П3 через точку F прямую k ║ образующей
цилиндра совпадающей со штрихпунктирной линией.
S3
A
S
A
2
3
2
E
E
2
3
q
X
O
D
2
2
D O
D
3
E
A
1
B
1
S1 ≡
O1
C
1
l31
B
1
1
1
1
q
l2 C
B 2 2
2
k F
3
3
C
3
208.
Задача 45На П2 эта образующая показана жирной линией (она мигает):
S3
A
S
A
2
3
2
E
E
2
3
q
X
O
D
2
2
D O
D
3
E
A
1
B
1
S1 ≡
O1
C
1
l31
B
1
1
1
1
q
l2 C
B 2 2
2
k F
3
3
C
3
209.
Задача 45Исходя из этого находим проекцию k2 прямой.
S3
A
S
A
2
3
2
k
2
E
E
2
3
q
X
O
D
2
2
D O
D
3
E
A
1
B
1
S1 ≡
O1
C
1
l31
B
1
1
1
1
q
l2 C
B 2 2
2
k F
3
3
C
3
210.
Задача 45Теперь по принадлежности находим проекцию F2:
S3
A
S
A
2
3
2
k
F2
2
X
E
E
2
3
q
O
D
2
2
D O
D
3
E
A
1
B
1
S1 ≡
O1
C
1
l31
B
1
1
1
1
q
l2 C
B 2 2
2
k F
3
3
C
3
211.
Задача 45Аналогично тому как мы находили проекцию В1 точки В находим проекцию F1
S3
A
S
A
2
3
2
k
F2
2
E
2
3
q
k F
1
q
l2 C
B 2 2
2
X
E
l31
C
3
B
1
O
D
2
2
D O
D
3
3
3
1
E
1
A
F
1
1
B
1
S1 ≡
O1
C
1
Главное меню
212. Построить развертку наклонной призмы. На развертке определить положение точки M, принадлежащей видимой грани.
A'B'
2
C'
2
2
M
2
П
ПA
2
2
1
B
2
A'
C
2
1
C'
1
B'
1
A
1
C
1
B
1
Задача №46
Построить развертку
наклонной призмы. На
развертке определить
положение точки M,
принадлежащей видимой
грани.
213.
A'B'
2
C'
2
Дано: фронтальная и
горизонтальная проекции
наклонной
призмы, фронтальная проекция
точки M, принадлежащей грани
AA’B’B.
2
M
2
П
ПA
2
2
1
B
2
A'
C
2
1
C'
1
B'
1
A
1
C
1
B
1
214.
A'B'
2
C'
2
Построим диагональ A’1B1.
2
M
2
П
ПA
2
2
1
B
2
A'
C
2
1
C'
1
B'
1
I
A
1
C
1
B
1
215.
A'B'
2
C'
2
Построим диагональ B’1C1.
2
M
2
П
ПA
2
2
1
B
2
A'
C
2
1
C'
1
B'
1
I
II
A
1
C
1
B
1
216.
A'B'
2
C'
2
Построим диагональ C’1A1.
2
M
2
П
ПA
2
2
1
B
2
A'
C
2
1
C'
1
III
B'
1
I
II
A
1
C
1
B
1
217.
A'B'
2
C'
2
2
M
2
П
ПA
2
2
1
B
2
A'
C
2
1
C'
1
III
B'
1
I
II
A
1
C
1
B
1
Найдем натуральную
величину диагоналей и
ребер способом
прямоугольного
треугольника.
Построим 1-ый катет,
равный разности
координат концов
отрезков диагоналей и
ребер на фронтальной
плоскости проекций.
218.
A'B'
2
C'
2
2
M
2
П
ПA
2
2
1
B
2
A'
C
2
1
C'
1
III
B'
1
I
II
A
1
C
1
B
1
Найдем натуральную
величину ребер.
Построим 2-ой катет,
равный
горизонтальным
проекциям этих ребер.
219.
A'B'
2
C'
2
2
M
2
Н.В.
ребро
П
ПA
2
2
1
B
2
A'
C
2
1
C'
1
III
B'
1
I
II
A
1
C
1
B
1
Гипотенуза – искомая
натуральная величина
ребер.
220.
A'B'
2
C'
2
2
M
2
Н.В.
ребро
П
ПA
2
2
1
B
2
A'
I
C
2
1
C'
1
III
B'
1
I
II
A
1
C
1
B
1
Аналогично найдем
натуральную величину
диагонали A’B.
221.
A'B'
2
C'
2
2
M
2
Н.В.
ребро
П
ПA
2
2
1
B
2
A'
I
C
2
1
C'
1
III
B'
1
I
II
A
1
C
1
B
1
Гипотенуза – искомая
натуральная величина
диагонали A’B..
222.
A'B'
2
C'
2
2
M
2
Н.В.
ребро
П
ПA
2
2
1
B
2
A'
II
C
2
I
1
C'
1
III
B'
1
I
II
A
1
C
1
B
1
Аналогично найдем
натуральную величину
диагонали B’C.
223.
A'B'
2
C'
2
2
M
2
Н.В.
ребро
П
ПA
2
2
1
B
2
A'
II
C
2
I
1
C'
1
III
B'
1
I
II
A
1
C
1
B
1
Гипотенуза – искомая
натуральная величина
диагонали B’C.
224.
A'B'
2
C'
2
2
M
2
Н.В.
ребро
П
ПA
2
2
1
B
2
A'
II
C
2
III
I
1
C'
1
III
B'
1
I
II
A
1
C
1
B
1
Аналогично найдем
натуральную величину
диагонали C’A.
225.
B'A'
M
C'
2
2
2
2
Н.В.
ребро
П
ПA
2
2
1
A'
B
2
II
C
2
1
C'
1
III
B'
1
I
II
A
1
C
1
B
1
III
I
Гипотенуза – искомая
натуральная величина
диагонали C’A.
226.
B'A'
M
C'
2
2
2
2
Н.В.
ребро
П
ПA
2
2
1
A'
B
2
II
C
2
1
C'
1
III
B'
A'
1
I
II
A
1
C
1
B
1
Построим первый элемент развертки –
натуральную величину ребра AA’.
A
III
I
227.
B'A'
M
C'
2
2
2
2
Н.В.
ребро
П
ПA
2
2
1
A'
B
2
II
C
2
1
C'
1
III
B'
A'
1
I
II
A
1
C
1
B
1
Сделаем засечки радиусами A1B1 и A’B из
точек A и A’ соответственно. Точка
пересечения засечек – искомая точка B.
A
III
I
228.
B'A'
M
C'
2
2
2
2
Н.В.
ребро
П
ПA
2
2
1
A'
B
2
II
C
2
1
C'
1
III
B'
A'
1
I
II
A
1
C
1
B
1
Проводим ребро AB.
A
B
III
I
229.
B'A'
M
C'
2
2
2
2
Н.В.
ребро
П
ПA
2
2
1
A'
B
2
II
C
2
1
C'
1
III
B'
A'
1
I
II
A
1
C
1
B
1
Сделаем засечки радиусами AA’ и A’1B’1 из
точек B и A’ соответственно. Точка
пересечения засечек – искомая точка B’.
A
B
III
I
230.
B'A'
M
C'
2
2
2
2
Н.В.
ребро
П
ПA
2
2
1
A'
B
2
II
C
2
1
C'
1
III
B'
A'
1
I
B'
II
A
1
C
1
B
1
Проводим ребра BB’ и A’B’. 1-ая грань
призмы построена.
A
B
III
I
231.
B'A'
M
C'
2
2
2
2
Н.В.
ребро
П
ПA
2
2
1
A'
B
2
II
C
2
1
C'
1
III
B'
A'
1
I
B'
II
A
1
C
1
B
1
Сделаем засечки радиусами B’C и B1C1 из
точек B’ и B соответственно. Точка
пересечения засечек – искомая точка C.
A
B
III
I
232.
B'A'
M
C'
2
2
2
2
Н.В.
ребро
П
ПA
2
2
1
A'
B
2
II
C
2
1
C'
1
III
B'
A'
1
I
B'
II
A
1
C
1
B
1
Проводим ребро BC.
C
A
B
III
I
233.
B'A'
M
C'
2
2
2
2
Н.В.
ребро
П
ПA
2
2
1
A'
B
2
II
C
2
1
C'
1
III
B'
A'
1
I
B'
II
A
1
C
1
B
1
Сделаем засечки радиусами B’B и B’1C’1
из точек B’ и C соответственно. Точка
пересечения засечек – искомая точка C’.
C
A
B
III
I
234.
B'A'
M
C'
2
2
2
2
Н.В.
ребро
П
ПA
2
2
1
A'
B
2
II
C
2
1
C'
1
III
B'
C'
A'
1
I
B'
II
A
1
C
1
B
1
Проводим ребра CC’ и B’C’. 2-ая грань
призмы построена.
C
A
B
III
I
235.
B'A'
M
C'
2
2
2
2
Н.В.
ребро
П
ПA
2
2
1
A'
B
2
II
C
2
1
C'
1
III
B'
C'
A'
1
I
B'
II
A
1
C
1
B
1
Сделаем засечки радиусами C’A и C1A1 из
точек C’ и C соответственно. Точка
пересечения засечек – искомая точка A.
C
A
B
III
I
236.
B'A'
M
C'
2
2
2
2
Н.В.
ребро
П
ПA
2
2
1
A'
B
2
II
C
2
1
III
I
C'
1
III
B'
C'
A'
1
I
B'
II
A
1
C
1
B
1
Проводим ребро CA.
C
A
B
A
237.
B'A'
M
C'
2
2
2
2
Н.В.
ребро
П
ПA
2
2
1
A'
B
2
II
C
2
1
III
I
C'
1
III
B'
C'
A'
1
I
B'
II
A
1
C
1
B
1
Сделаем засечки радиусами C’C и C’1A’1
из точек A и C’ соответственно. Точка
пересечения засечек – искомая точка A’.
C
A
B
A
238.
B'A'
M
C'
2
2
2
2
Н.В.
ребро
П
ПA
2
2
1
A'
B
2
II
C
2
1
III
I
C'
1
III
B'
C'
A'
1
I
A'
B'
II
A
1
C
1
B
1
Проводим ребра AA’ и C’A’. 3-я грань
призмы построена.
C
A
B
A
239.
B'A'
M
C'
2
2
2
2
Н.В.
ребро
П
ПA
2
2
1
A'
B
2
II
C
2
1
III
I
C'
1
III
B'
C'
A'
1
I
A'
B'
II
A
1
C
1
B
1
Сделаем засечки радиусами A’1B’1 и C’1B’1
из точек A’ и C’ соответственно. Точка
пересечения засечек – искомая точка B’.
C
A
B
A
240.
B'A'
M
C'
2
2
2
2
Н.В.
ребро
П
ПA
2
2
1
A'
B
2
II
C
2
1
III
I
B'
C'
1
III
B'
C'
A'
1
I
A'
B'
II
A
1
C
1
B
1
Проводим ребра A’B’ и C’B’. 4-я грань
призмы построена.
C
A
B
A
241.
B'A'
M
C'
2
2
2
2
Н.В.
ребро
П
ПA
2
2
1
A'
B
2
II
C
2
1
III
I
B'
C'
1
III
B'
C'
A'
1
I
A'
B'
II
A
1
C
1
B
1
Сделаем засечки радиусами A’B’ и C’B’из
точек A и C соответственно. Точка
пересечения засечек – искомая точка B.
C
A
B
A
242.
B'A'
M
C'
2
2
2
2
Н.В.
ребро
П
ПA
2
2
1
A'
B
2
II
C
2
III
I
1
B'
C'
1
III
B'
C'
A'
A'
1
I
B'
II
A
1
C
1
B
1
Проводим ребра AB и CB. Развертка
призмы построена.
C
A
B
A
B
243.
B'A'
M
C'
2
2
2
2
Н.В.
ребро
П
ПA
2
2
1
A'
B
2
II
C
2
IIII
B'
1
C'
1
III
B'
C'
A'
A'
1
I
B'
II
A
1
C
1
B
1
Проводим горизонталь через
фронтальную проекцию точки M.
C
A
B
A
B
244.
B'A'
M
C'
2
2
2
M
2
Н.В.
ребро
П
ПA
2
2
1
A'
B
2
II
C
2
III
I
1
B'
C'
1
III
B'
C'
A'
A'
1
I
B'
II
A
1
C
1
B
1
Находим, в каком отношении эта
горизонталь делит натуральную величину
ребер.
C
A
B
A
B
245.
B'A'
M
C'
2
2
2
M
2
Н.В.
ребро
П
ПA
2
2
1
A'
B
2
II
C
2
III
I
1
B'
C'
1
III
B'
C'
A'
A'
1
I
B'
II
A
1
C
1
B
1
Находим по принадлежности
горизонтальные проекции точек
пересечения горизонтали с ребрами
призмы.
C
A
B
A
B
246.
A'B'
2
C'
2
2
M
M
2
Н.В.
ребро
П
ПA
2
2
1
B
2
A'
II
C
2
III
I
1
B'
C'
1
III
B'
C'
A'
A'
1
I
B'
II
A
1
C
1
B
1
Проводим проекцию горизонтали в
плоскости П1
C
A
B
A
B
247.
A'B'
2
C'
2
2
M
M
2
Н.В.
ребро
П
ПA
2
2
1
B
2
A'
II
C
2
III
I
1
B'
C'
1
M
1
III
B'
C'
A'
A'
1
I
B'
II
A
1
C
1
B
1
Находим по принадлежности
горизонтальную проекцию точки M.
C
A
B
A
B
248.
A'B'
2
C'
2
2
M
M
2
Н.В.
ребро
П
ПA
2
2
1
B
2
A'
II
C
2
III
I
1
B'
C'
1
M
1
III
B'
C'
A'
A'
1
I
II
B'
A
1
C
1
B
1
Сделаем засечки, радиусы которых равны
A
большему из отрезков, на которые
горизонталь делит натуральные
величины ребер. Засечки делаем из точек
A и B.
C
B
A
B
249.
A'B'
2
C'
2
2
M
M
2
Н.В.
ребро
П
ПA
2
2
1
B
2
A'
II
C
2
III
I
1
B'
C'
1
M
1
III
B'
C'
A'
A'
1
I
B'
II
A
1
C
1
B
1
Проводим отрезок горизонтали на
развертке.
C
A
B
A
B
250.
A'B'
2
C'
2
2
M
M
2
Н.В.
ребро
П
ПA
2
2
1
B
2
A'
II
C
2
III
I
1
B'
C'
1
M
1
III
B'
C'
A'
A'
1
I
B'
II
A
1
C
1
B
1
Сделаем засечку радиусом, равным
отрезку горизонтали между точкой M1 и
ребром B1B’1.
C
A
B
A
B
251.
A'B'
2
C'
2
2
M
M
2
Н.В.
ребро
П
ПA
2
2
1
B
2
A'
II
C
2
III
I
1
B'
C'
1
M
1
III
B'
C'
A'
A'
1
I
B'
II
M
A
1
C
1
B
1
Строим точку M на развертке.
C
A
B
A
B
252.
A'B'
2
C'
2
2
M
M
2
Н.В.
ребро
П
ПA
2
2
1
B
2
A'
II
C
2
III
I
1
B'
C'
1
M
1
III
B'
C'
A'
A'
1
I
B'
II
M
A
1
C
1
B
1
Задача решена.
C
A
B
A
B
253. Построить развертку эллиптического цилиндра с круговым основанием способом раскатки. На развертку нанести видимую точку М.
Задача № 47Построить развертку эллиптического цилиндра с
круговым основанием способом раскатки. На развертку
нанести видимую точку М.
О2
М2
О'
2
О'
1
О1
254.
О2М2
Дано: фронтальная и
горизонтальная проекции
эллиптического цилиндра с
круговым основанием,
фронтальная проекция видимой
точки M.
О1
О'
2
О'
1
255.
О2М2
Разделим фронтальную проекцию
основания цилиндра на 8 равных
частей.
О1
О'
2
О'
1
256.
7О2
М2
6
О'
2
5
4
О1
1
2
3
Будем раскатывать цилиндр по
часовой стрелке.
8
О'
1
257.
7О2
М2
6
О'
2
5
4
О1
1
2
3
Находим по принадлежности
горизонтальные проекции
пронумерованных точек.
8
О'1
258.
7О2
М2
6
5
4
Проведем через
пронумерованные точки линии,
перпендикулярные к
горизонтальным проекциям
образующих цилиндра.
О1
О'
2
8
1
2
3
18 2 1
5 6 4 3 7 О'
259.
О2М2
6
О'
2
5
4
На горизонтальной плоскости
проекций от точки 1 до линии 2
отложим хорду, стягивающую токи
1 и 2 на фронтальной плоскости
проекций.
О1
7 8
1
2
3
18 2 1
5 6 4 3 7 О'
2
260.
7О2
М2
6
5
4
Далее из полученной точки
откладываем такую же хорду так,
чтобы она пересекала линию 3.
О'
2
8
1
2
3
18 2 1
5 6 4 3 7 О'
3
О1
261.
О2М2
6
5
7
О'
2
4
Затем из вновь полученной точки
откладываем такую же хорду так,
чтобы она пересекала линию 4.
1
2
3
18 2 1
5 6 4 3 7 О'
4
О1
8
262.
О2М2
6
5
7
О'
2
4
Потом из вновь полученной точки
откладываем такую же хорду так,
чтобы она пересекала линию 5.
1
2
3
18 2 1
5 6 4 3 7 О'
5
О1
8
263.
7О2
М2
6
5
4
И так далее, до тех пор, пока не
построим 8 точек.
8
О'
2
1
2
3
18 2 1
5 6 4 3 7 О'
6
О1
264.
О2М2
6
7
8
О'
2
5
4
1
2
3
18 2 1
5 6 4 3 7 О'
7
О1
265.
О2М2
6
7
8
О'
2
5
4
1
2
3
18 2 1
5 6 4 3 7 О'
8
О1
266.
О2М2
6
7
8
О'
2
5
4
1
2
3
18 2 1
5 6 4 3 7 О'
1
О1
267.
О2М2
6
О1
8
О'
2
5
4
В итоге построено 8 точек
7
1
2
3
18 2 1
5 6 4 3 7 О'
268.
О2М2
6
О1
8
О'
2
5
4
Проведем через полученные
точки линию основания цилиндра.
7
1
2
3
5 6 4 3 7 О'
18 2 1
269.
О2М2
6
О1
8
О'
2
5
4
Через эти же точки проводим 8
взаимно параллельных
образующих цилиндра.
7
1
2
3
18 2 1
5 6 4 3 7 О'
270.
О2М2
6
О1
8
О'
2
5
4
Через конечные точки этих
образующих проводим линию 2-го
основания цилиндра.
7
1
2
3
182 1
5 6 4 3 7 О'
271.
О2М2
6
О1
8
О'
2
5
4
Перенесем на развертку
фронтальные проекции оснований
цилиндра без изменений.
7
1
2
3
18 2 1
5 6 4 3 7 О'
272.
О2М2
6
О1
8
О'
2
5
4
Развертка цилиндра способом
раскатки построена.
7
1
2
3
18 2 1
5 6 4 3 7 О'
273.
О2М2
6
О1
8
О'
2
5
4
Проводим образующую цилиндра
через точку M на фронтальной
плоскости проекций.
7
1
2
3
18 2 1
5 6 4 3 7 О'
274.
О2М2
6
О1
8
О'
2
5
4
Проводим эту же образующую в
горизонтальной плоскости
проекций.
7
1
2
3
18 2 1
5 6 4 3 7 О'
275.
О2М2
6
8
О'
2
5
4
Проводим эту образующую на
развертке без изменений.
7
1
2
3
18 2 1
5 6 4 3 7 О'
8
О1
276.
О2М2
6
8
О'
2
5
4
1
2
3
18 2 1
5 6 4 3 7 О'
Находим по
принадлежности
горизонтальную
проекцию точки M.
М1
О1
7
277.
О26
М2
8
О'
2
5
4
Находим точку M на
развертке. Для этого
через M1 проводим
прямую
перпендикулярную
образующей до
пересечения с этой
образующей на
развертке.
7
1
2
3
18 2 1
5 6 4 3 7 О'
М1
О1
М
278.
О2М2
О'
2
О'
1
Задача решена.
М1
О1
М
279.
Задача №49280.
Задача №49Условие задачи: построить линию пересечения сферы с плоскостью
02
2
03
281.
Задача №49Находим опорные точки (1,4) и точки смены видимости (2,3):
42
43
02
03
33
22 32
2
12
23
13
282.
Задача №49Находим промежуточные точки(5,6,7,8):
42
52
02
43
63
62
53
03
33
72
82
22
32
73
83
R
2
12
13
23
283.
Задача №49Строим линию пересечения сферы и плоскости :
42
52
02
43
63
62
53
03
33
72
2
12
82
22
32
73
83
13
23
284.
Задача №49Ответ:
42
52
02
43
63
62
53
03
33
72
12
82
22
32
73
83
13
23
285.
Задача №50286.
Задача №50Условие задачи: построить проекции и
натуральную величину сечения
пирамиды плоскостью
S2
B2
A2
C2
B1
A1
C1
S1
2
287.
Задача №50Находим точки пересечения ребер пирамиды AB(т.1), AC(т.2), SB(т.3), SC(т.4)
и плоскости :
S2
52
h2
42
32
12
22
C2
B2
A2
11
B1
31
A1
2
21
51
C1
41
S1
288.
Задача №50Находим проекцию сечения и определяем его видимость(если линии лежат
на видимых гранях, то они также видимы; если нет, то линии невидимы):
S2
2
52
h2
42
32
12
22
C2
B2
A2
11
B1
31
A1
21
51
C1
41
S1
289.
Задача №5045
П5
Находим проекции точек
пересечения на
плоскость П5 для нахождения
натуральной величины
сечения:
П2
S2
35
52
25
h2
42
15
32
12
22
C2
B2
A2
11
B1
31
A1
2
21
51
C1
41
S1
290.
Задача №5045
П5
Находим натуральную
величину сечения:
П2
S2
35
52
25
h2
42
15
32
12
22
C2
B2
A2
11
B1
31
A1
2
21
51
C1
41
S1
291.
Задача №5045
П5
Ответ:
П2
S2
35
52
25
h2
42
15
32
12
22
C2
B2
A2
11
B1
31
A1
2
21
51
C1
41
S1
292.
Задача №51293.
Задача №51Условие задачи: построить
линию пересечения поверхности
конуса с плоскостью
S2
S1
1
294.
Задача №51Находим опорные точки(1,2),
точки смены видимости(3) и
промежуточные точки(4):
S2
32
42
12
22
11
41
R
S1
31
21
1
295.
Задача №51Находим дополнительно промежуточные
S точки(5,6):
2
32
42
52
62
12
11
22
51
R
41
S1 R
31
61
21
1
296.
Задача №51Находим линию пересечения
конуса и плоскости :
S2
32
42
52
62
12
11
22
51
S1
41
31
61
21
1
297.
Задача №51Ответ:
S2
32
42
52
62
12
11
22
51
S1
41
31
61
21
1
298.
Задача №52299.
Задача №52Условие задачи: построить линию пересечения поверхности призмы с плоскостью (H0 f0)
A2'
A2
B2 '
C1 '
C1
h10
C2 '
C2
B2
A1'
h0
f0
A1
B1 '
B1
f2
300.
Задача №52И поверхность(призма) и плоскость - общего положения, поэтому выполняем преобразование
комплексного чертежа, т.е. строим проекции вершин призмы и след плоскости на П4:
A2'
f0
B2 '
f2
C2 '
12
A2
C2 11
B2
C1 '
A1'
C1
h0
h10
A1
B1 '
14
C4
C4 '
B1
A4
П1
П4
B4
A'4 B'4
301.
Задача №52Строим проекцию призмы на плоскость П4 и линию пересечения призмы
и плоскости :
0
f2
f
'
A2
B2 '
C2 '
12
A2
C2 11
B2
C1 '
A1'
C1
h0
h10
A1
B1 '
14
C4
C4 '
B1
П1
A4
П4
B4
A'4 B'4
302.
Задача №52Строим проекции точек пересечения призмы и плоскости на плоскости П1 и П2:
A2'
f0
B2 '
f2
C2 '
12
A2
C2 11
B2
C1 '
A1'
C1
h0
h10
A1
B1 '
14
C4
C4 '
B1
П1
A4
П4
B4
A'4 B'4
303.
Задача №52Строим линию пересечения призмы с плоскостью (ответ) :
A2'
f0
B2 '
f2
C2 '
12
A2
C2 11
B2
C1 '
A1'
C1
h0
h10
A1
B1 '
14
C4
C4 '
B1
П1
A4
П4
B4
A'4 B'4
304. Задача № 53
2Задание: построить
линию
пересечения
поверхности тора
плоскостью .
305. Решение задачи № 53
Поверхность тора проецирующего положения, тогданесколько проекций линии
пересечения тора с плоскостью на чертеже уже есть,
их нужно обозначить, а вторые проекции найти по принадлежности. Недостающие
проекции линии пересечения находим с помощью
проведения вспомогательных прямых (M,N,O).
12 22
M2
N2
2
32 42 52 62
72 82 92
102 112
O2
122 132
142
101
71
31
121
11
41
141
81
51
131
21
61
111
91
306. Задача № 54
Задание:a)
Построить точки пересечения линии L с заданными
поверхностями.
S2
б)
а2
S2
l2
В2
А2
O2
C2
х
x
А1
C1
S1
O 1 S1
l1
а1
В1
307. Задача № 54
в)г)
а2
о2
а2
x
а1
о1
а1
308. Для того чтобы определить точки пересечения прямой с поверхностью надо: · Через прямую провести произвольную вспомогательную
Решение задачи 54а:Для того чтобы определить
точки пересечения прямой с
поверхностью надо:
Через прямую провести
произвольную вспомогательную
плоскость ( ). В нашем случае
плоскостью явл-ся треугольник,
подобный основанию пирамиды.
Построить линии пересечения
плоскости с поверхностью.
И там где данные линии
пересекают прямую находятся
точки пересечения прямой с
поверхностью.
a)
l2 2
S2
12
22
А2
В2
C2
x
А1
C1
S1
11
l1
21
В1
309. Решение задачи 54б:
Для решения даннойзадачи требуется провести
образующую конуса,
которая пересекает прямую
a в точке К. получившаяся
точка К является точкой
пересечения прямой а с
заданной поверхностью
конуса.
б)
S2
а2
К2
O2
х
а1
O 1 S1
К1
310. Решение задачи 54в:
в)В данной задаче поверхностью
является цилиндр горизонтальнопроецирующего положения, значит
а
дополнительных плоскостей
проводить не надо. Но при
x
нахождении точек пересечения
нужно быть внимательным, так как
точка 2 на фронтальной плоскости
проекции будет невидимой.
22
12
2
а1
21
1
1
311. Решение задачи 54г:
г)Порядок решения этой задачи
такой же как и у з. 54а. Сперва
проводим вспомогательную
плоскость ( ). этой плоскостью
будет окружность. Затем строим
линии пересечения плоскости с
поверхностью. И там где данная
окружность пересекает прямую
находятся точки пересечения
прямой с заданной поверхностью.
а 2 2
12
о2
22
а1
о1
11
21
312. Задача № 55
Задание: построить точкиS2
B2
22
12
A2
О2
X
S1
О1
A1
11
21
B1
пересечения прямой АВ с поверхностью конуса.
Решение:чтобы определить
точки пересечения прямой с
поверхностью конуса нужно
через прямую провести вспомогательную произвольную
плоскость (через следы плоскости h0 и f0). Затем построить
линии пересечения поверхности конуса с этой плоскостью.
И там где эти линии пересекают прямую АВ, и есть точки
пересечения прямой АВ с поверхностью конуса. Обе точки
– видимые.
313. Задача № 56
Задание: построить точкиA2
12
22
B2
X
A1
11
21
B1
пересечения прямой АВ с поверхностью цилиндра. Опреде-лить
видимость.
Решение данной задачи анало-гично
решению предыдущей задачи: сперва
нужно через прямую провести вспомогательную произвольную плоскость (через следы плос-кости h0 и f0).
Затем построить линии пересечения
поверхности цилиндра с этой плоскостью. И там где эти линии пересекают прямую АВ, и есть точки пересечения прямой АВ с поверхностью
цилиндра. Обе точки – видимые.
314.
П2 П312
M2
13
O2
M3
K3
K2
22
15
M5
K5
O3
23
Построить точки пересечения
сферы с прямой l, применив
25
O5
способ замены плоскостей проекций
315.
Будет ли виден самолет (точка А),движущийся вНаправлении S, наблюдателю (точка
22’B),
Смотрящему в иллюминатор?
22
12’
32’
12
32
A2
42’
42
A1
31
11
32’
21 41
11’
21’ 42’
316.
Построить линиюпересечения
цилиндра и конуса.
22
32 32’
42
12 12’
11
31
21
41
31’
11’
317.
E2Достроить горизонтальную
проекцию пирамиды с
призматическим
отверстием
12 12’ 52’
52
Г2 62 42 42’
61
41
51
32
22 22’ 62’
11
21 61’
51’
41’
11’
31
21’
318.
Г2Z2
42
32 32’
42’
22 22’
12
Построить линию 52 52’
пересечения конуса
и призмы.
51
62
4 1 31
21
S1
31’ 21’
51’
41’
1 1 61
319.
Задача №62.Задание: построить линию пересечения цилиндра и сферы.
320.
О2Дано:
О1
321.
О2Дано:
Решение:
О1
322.
О2Дано:
Решение:
О1
Проведем вспомогательную плоскость
∆1
∆1
323.
О2Дано:
Решение:
О1
Обозначим точку
пересечения ∆1 с
цилиндром
∆1
21
324.
О2Дано:
Решение:
О1
Построим окружность,
образовавшуюся при
пересечении ∆1 сферы,
в п2(в пределах
цилиндра)
∆1
21
325.
О2Дано:
Решение:
22
О1
Спроецируем точку 21
на п2.
∆1
21
326.
О2Дано:
Решение:
22
О1
∆5
∆4
Проведем в п1
вспомогательные
плоскости ∆2, ∆3, ∆4 и
∆5 .
∆3
∆2
∆1
21
327.
О2Дано:
42
Решение:
32
62
22
52
72
12
О1
∆5
41
51
71
81
1
Проделаем аналогичные 1
операции, как в случае с ∆1.
∆4
31
61
21
∆3
∆2
∆1
328.
О2Дано:
32
42
Решение:
62
62
22
52
72
12
О1
∆5
41
51
71
Красная линия – линия 11
пересечения двух данных
поверхностей.
∆4
31
81
61
21
∆3
∆2
∆1
329. 63. Построить линию пересечения конуса и сферы.
S2O'2
O2
O‘1
Задача №63
S1=O1
330. 1. Строим вспомогательные секущие плоскости.
S2O'2
O2
Затем на фронтальной проекции
замеряем расстояния от оси цилиндра
до его образующих, и этим радиусом
проводим окружности на
горизонтальной проекции с центром в
т. О1.
Потом замеряем расстояние от оси
шара до окружности ( на фронт.
проекции) и строим окружности на
горизонтальной проекции.
Точки их пересечения и будут точками
пересечения двух поверхностей.
O‘1
Задача №63
S1=O1
331. Строим точки пересечения поверхностей.
S242
По аналогии строим остальные точки
пересечения плоскостей.
Точки расположенные на оси
поверхностей, будут точками смены
видимости.
O'2
=> 1 и 2 – точки смены видимости.
12=22
32
O2
11
31
S1=O1
O‘1
41
21
Задача №63
Точки 3 и 4 – опорные точки, т.к. лежат
на пересечении образующей конуса с
сферой.
332. Строим саму линию пересечения.
S212=22
σ2
O'2
O2
11
S1=O1
O‘1
21
Задача №63
333. 64. Построение линии пересечения конуса и цилиндра.
Задача №64334. На ПРОФИЛЬНОЙ проекции цилиндр занимает проецирующее положение, => на ПРОФИЛЬНОЙ проекции линия пересечения уже есть.
На ПРОФИЛЬНОЙ проекции цилиндр занимает проецирующееположение, => на ПРОФИЛЬНОЙ проекции линия пересечения уже
есть.
Задача №64
335. 1.Строим вспомогательные плоскости уровня.
S2S1
Задача №64
S3
336. 2.Строим линию пересечения, замеряем r, на фронтальной проекции и делаем засечки на соответствующих вспомогательных плоскостях,
горизонтальной проекции. Полученные точки будут принадлежать линиипересечения.
S3
S2
32
33=43
42
Σ3
Σ3
11
Задача №64
31
S1
41
21
В3
13=23
22
12
А3
Для плоскости Σ3, r является
отрезок АВ, то есть расстояние
от оси конуса, до его
образующей.
337. Строится искомая линия пересечения.
S3S2
32
33=43
42
А3
Σ3
72=82
52=62
53=63
71
51
11
Задача №64
21
61
S1
81
Σ3
31
41
73=83
13=23
22
12
В3
Точки, расположенные на оси
поверхностей будут точками смены
видимости => точки 5,6,7,8 –
точки смены видимости.
338. 65. Построить линию пересечения конуса и цилиндра.
S2Задача №65
S3
339. На ПРОФИЛЬНОЙ проекции цилиндр находится в проецирующем положении => на ПРОФИЛЬНОЙ проекции линия пересечения уже есть.
На ПРОФИЛЬНОЙ проекции цилиндр находится впроецирующем положении => на ПРОФИЛЬНОЙ проекции
линия пересечения уже есть.
S2
Задача №65
S3
340. Искомую линию пересечения находим согласно теореме Монжа: Если две поверхности второго порядка описаны около третьей
поверхности второгопорядка или вписаны в неё, то они пересекаются по двум кривым, плоскости
которых проходят через прямую, соединяющую точки пересечения линий
прикосновения.
=> строится вписанная сфера, и теперь теорема Монжа применима к этой задаче.
S2
Задача №65
S3










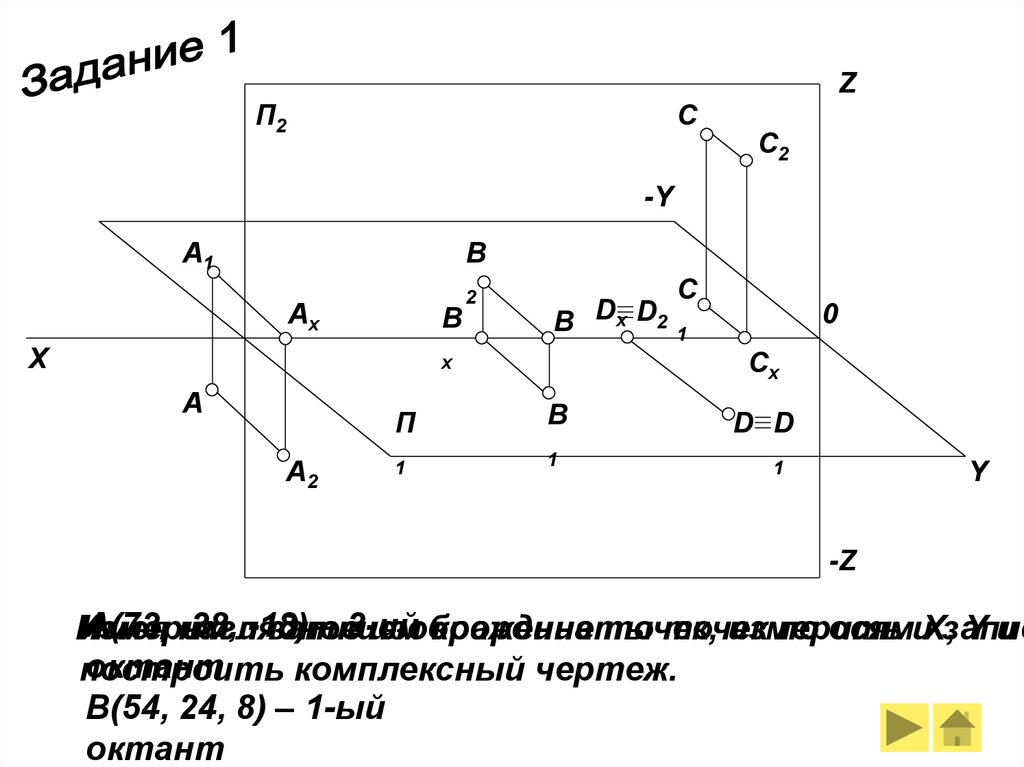
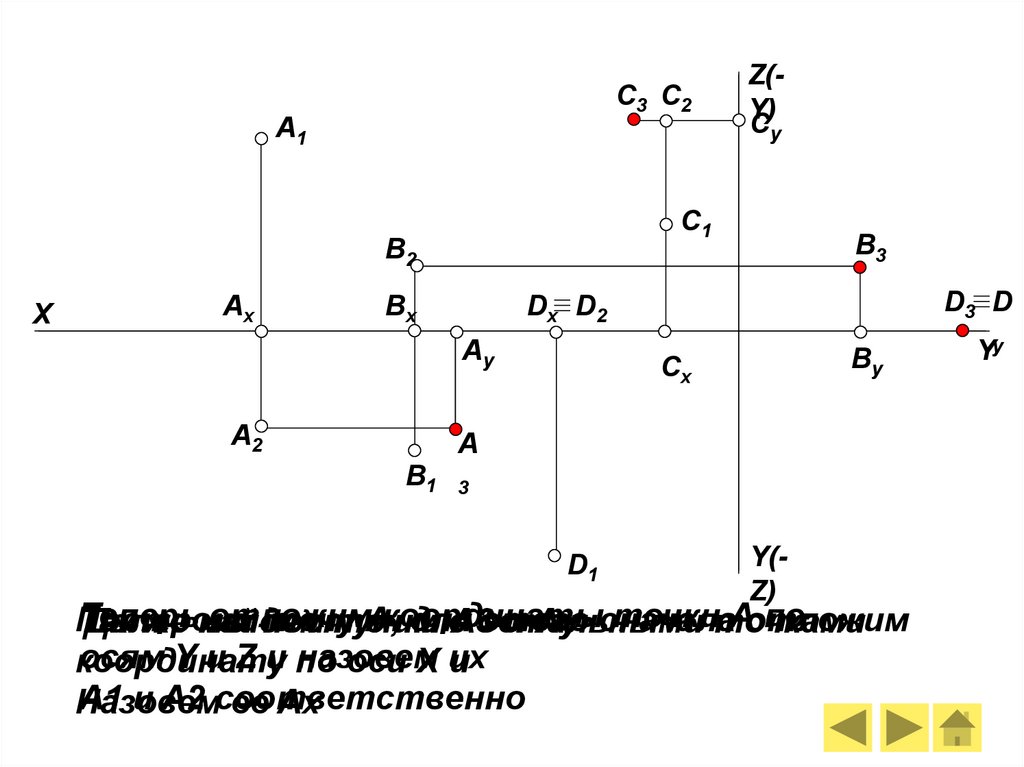
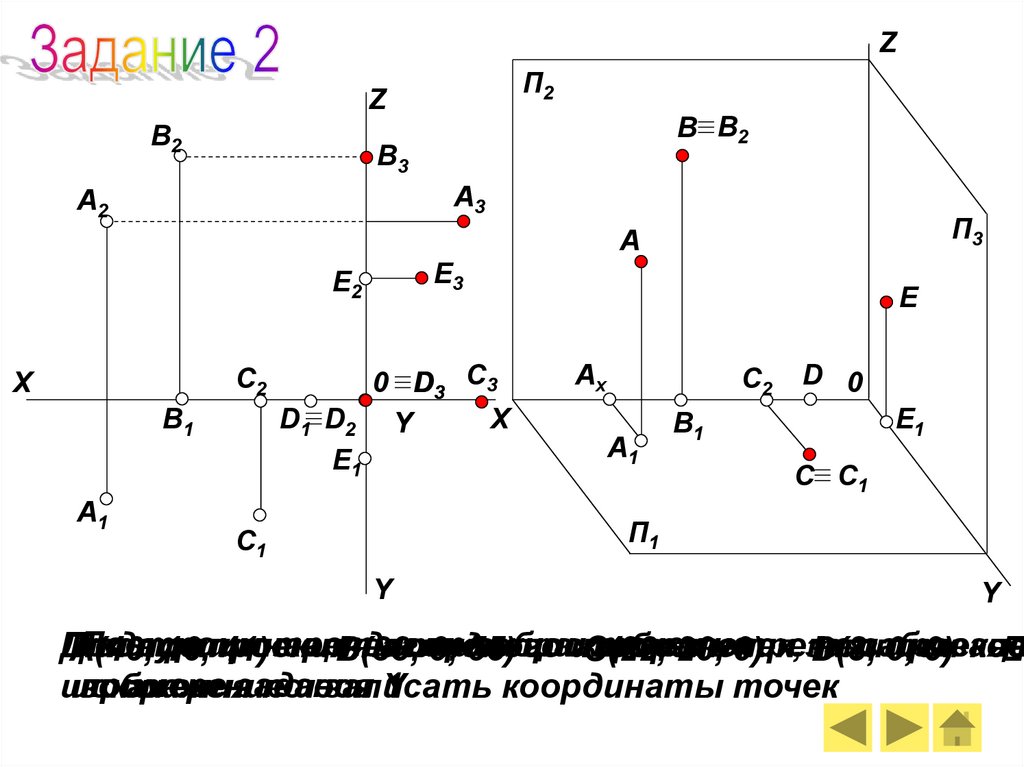
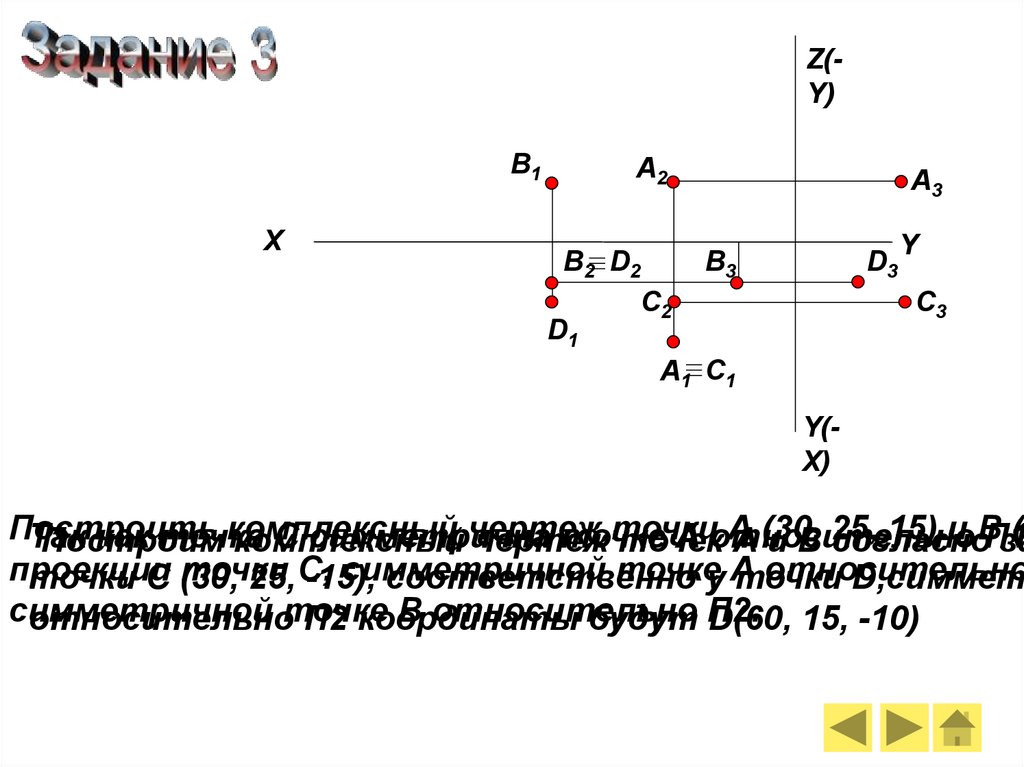
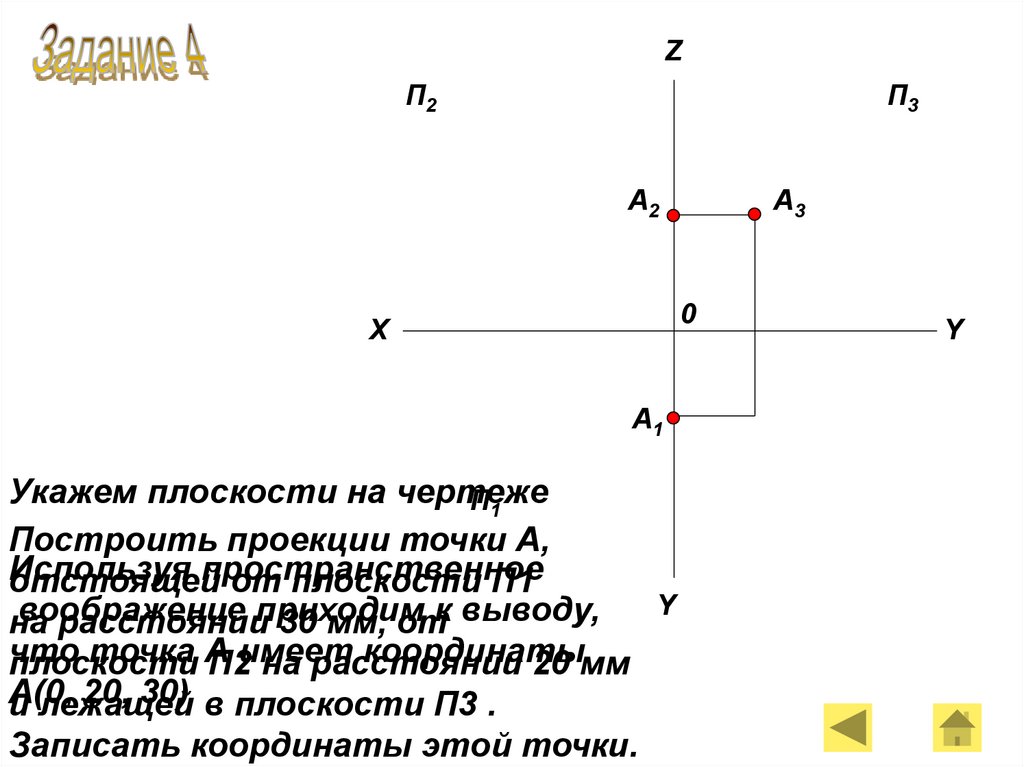
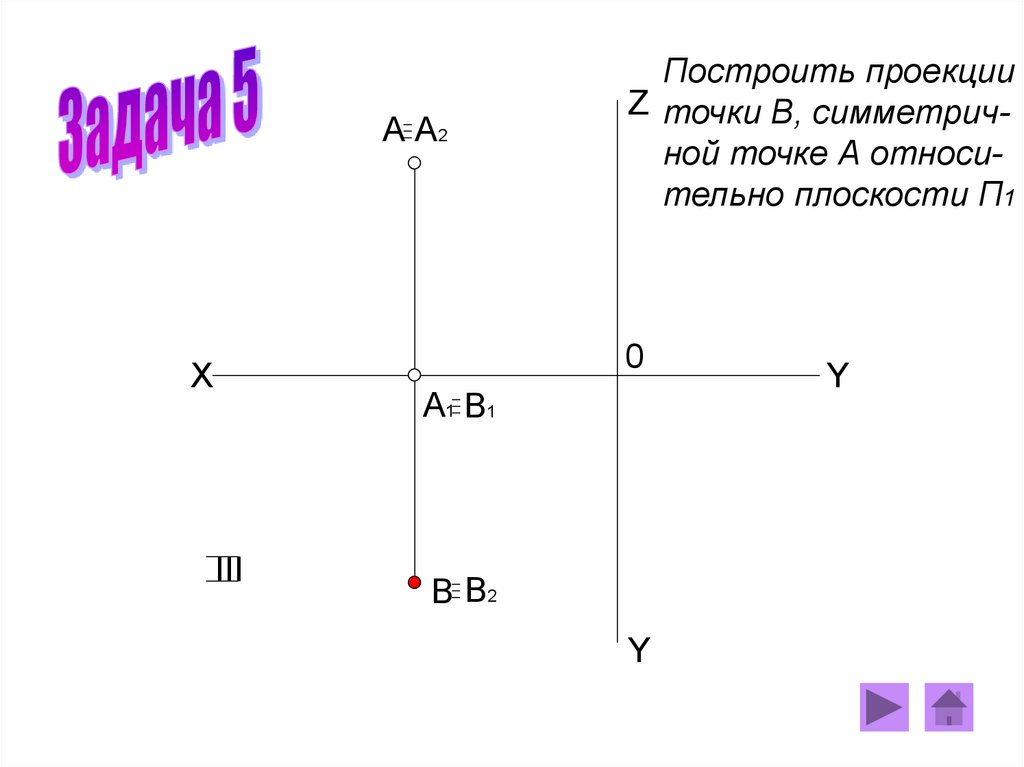
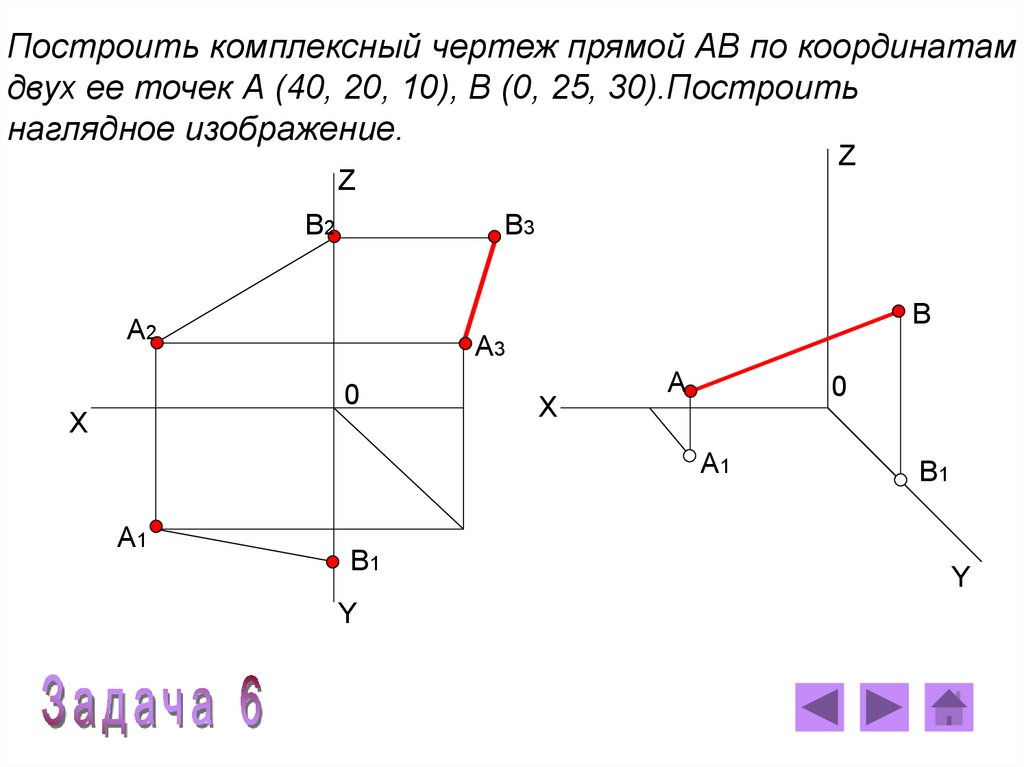
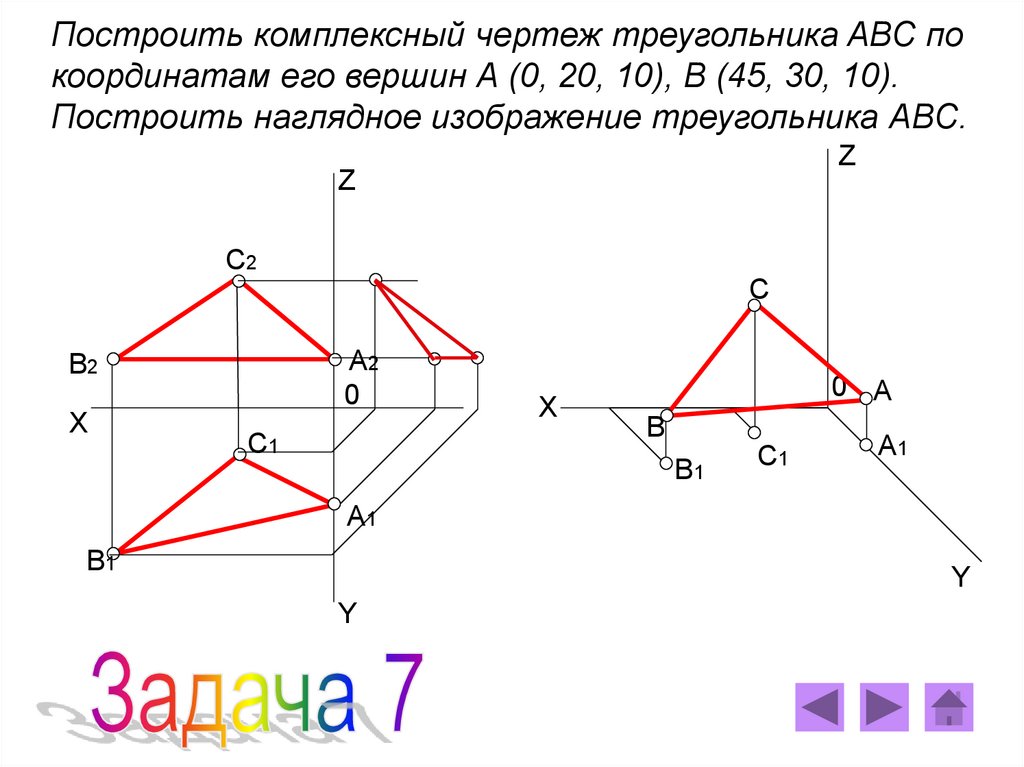
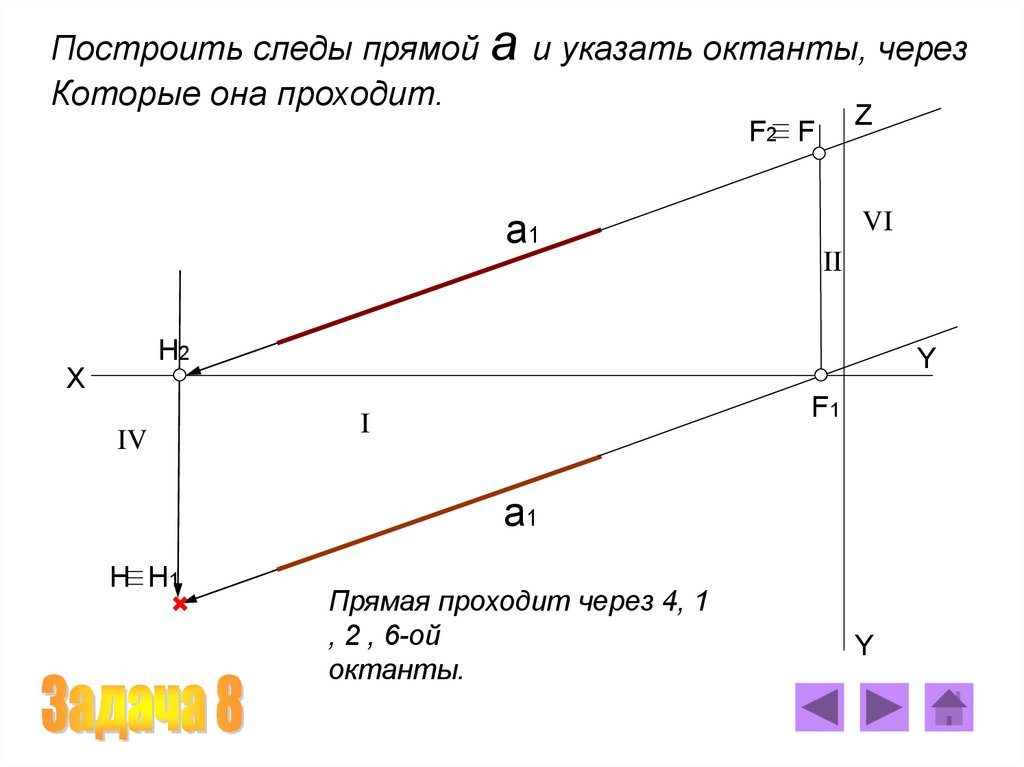
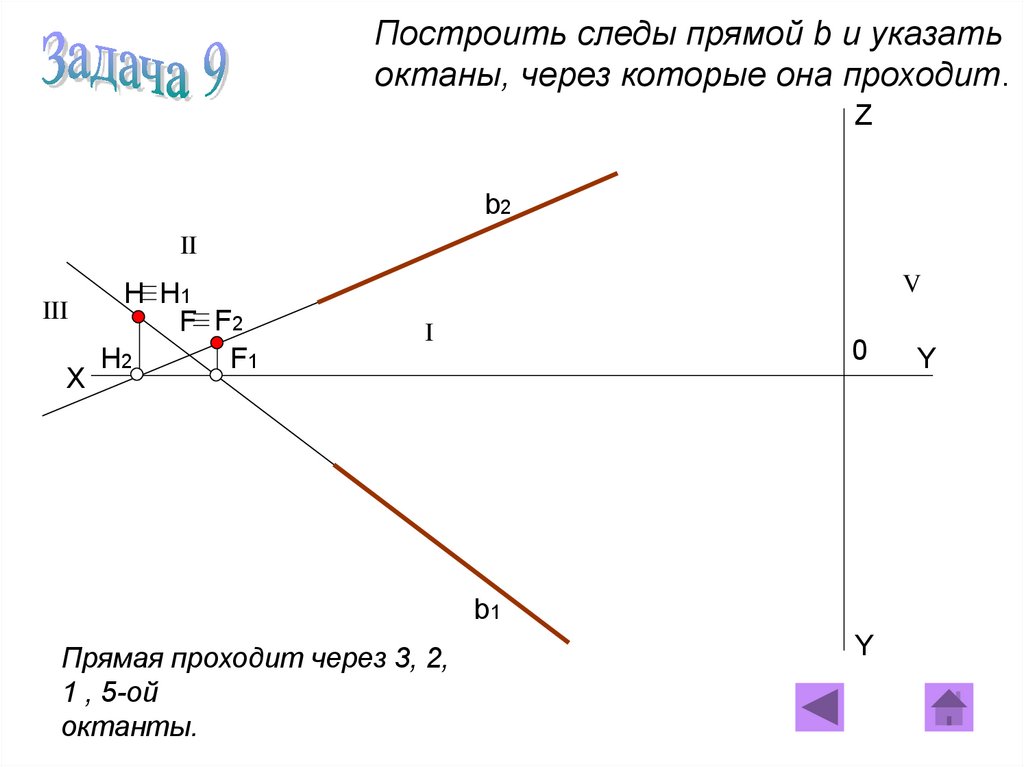
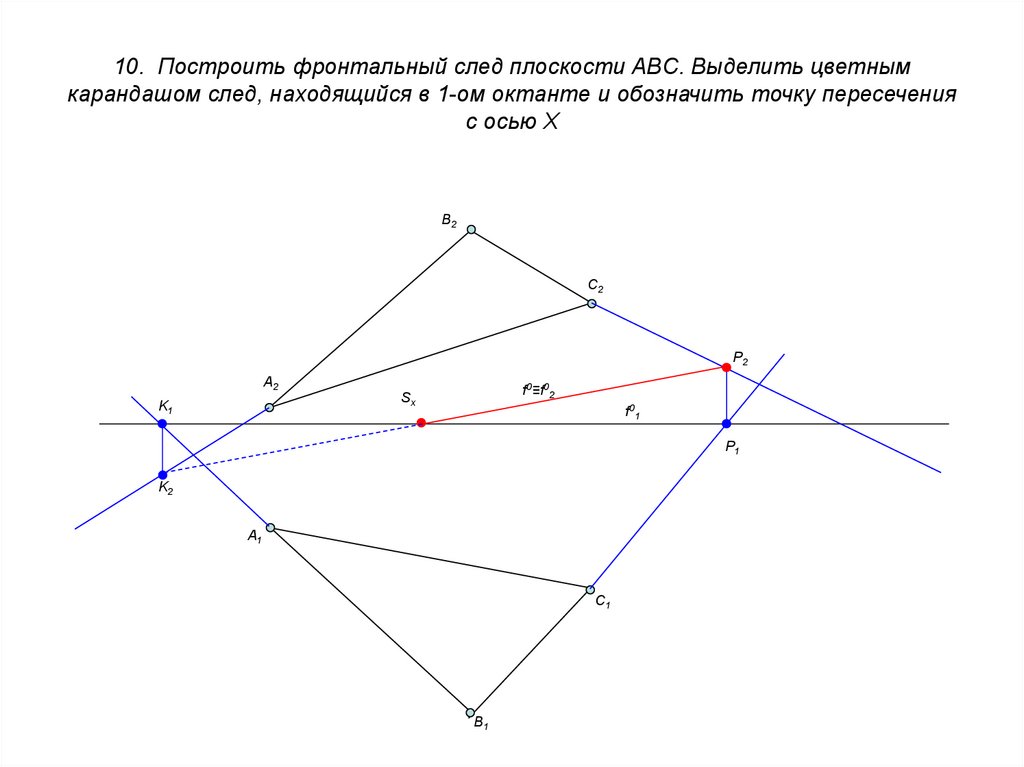
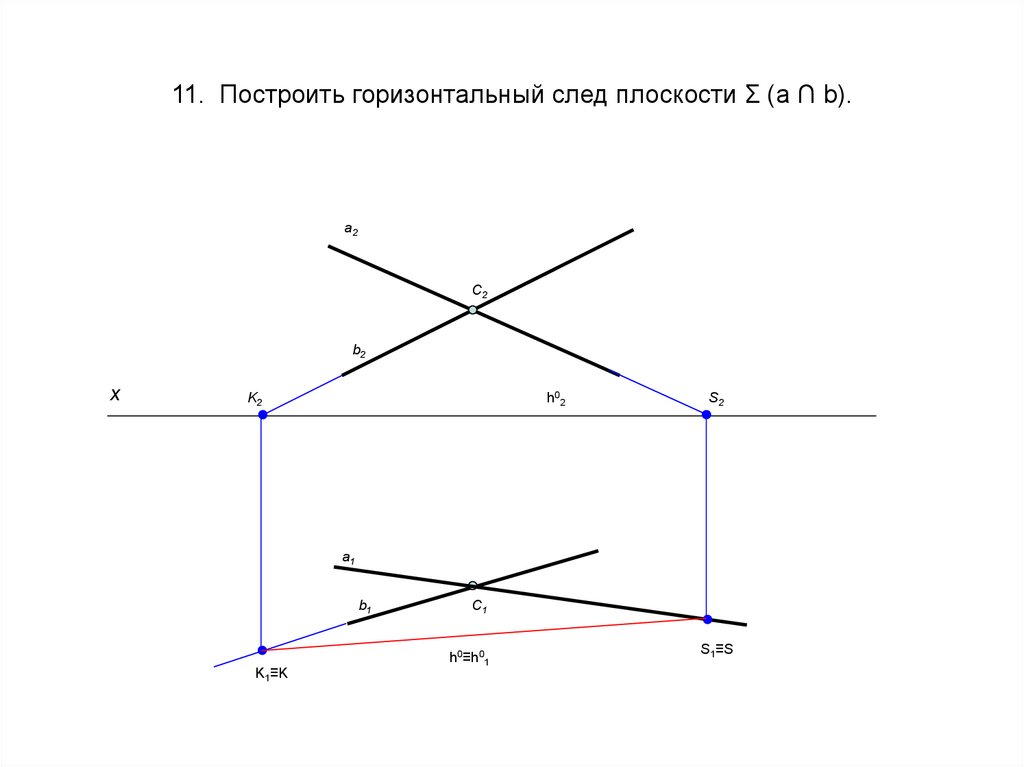
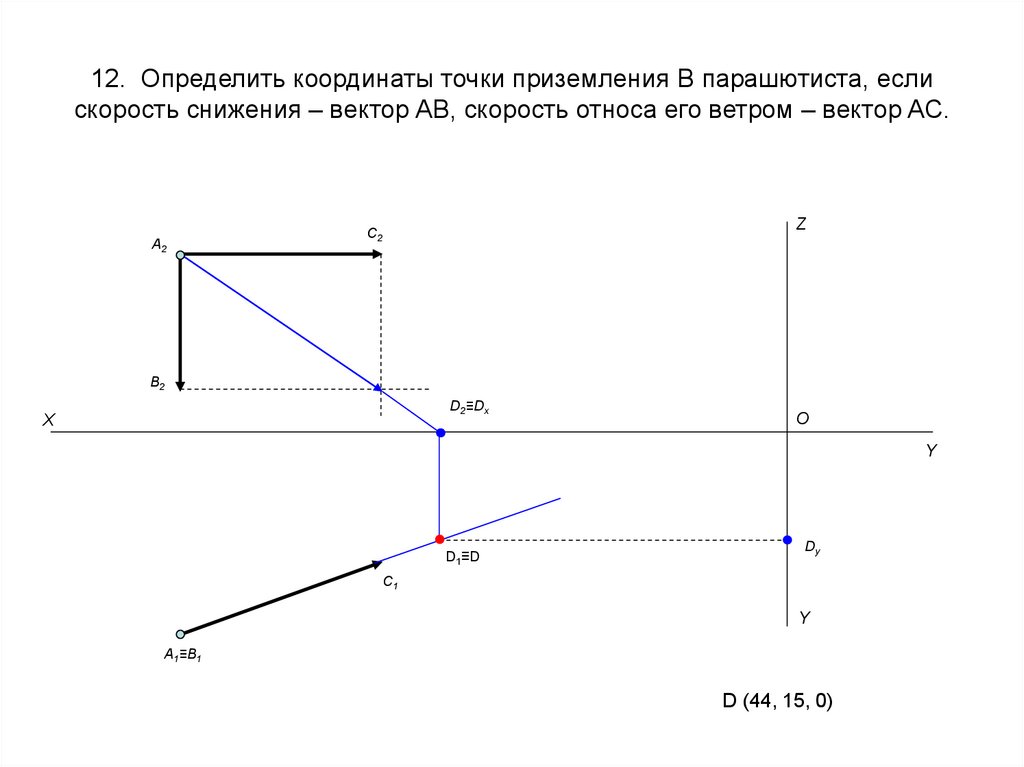
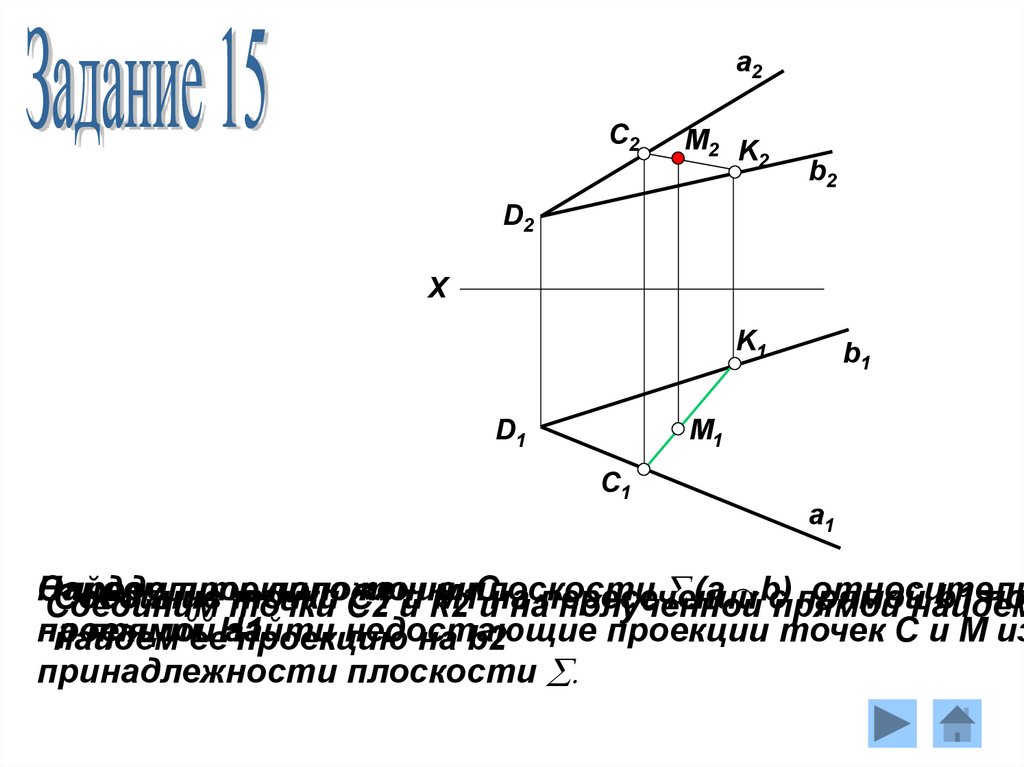
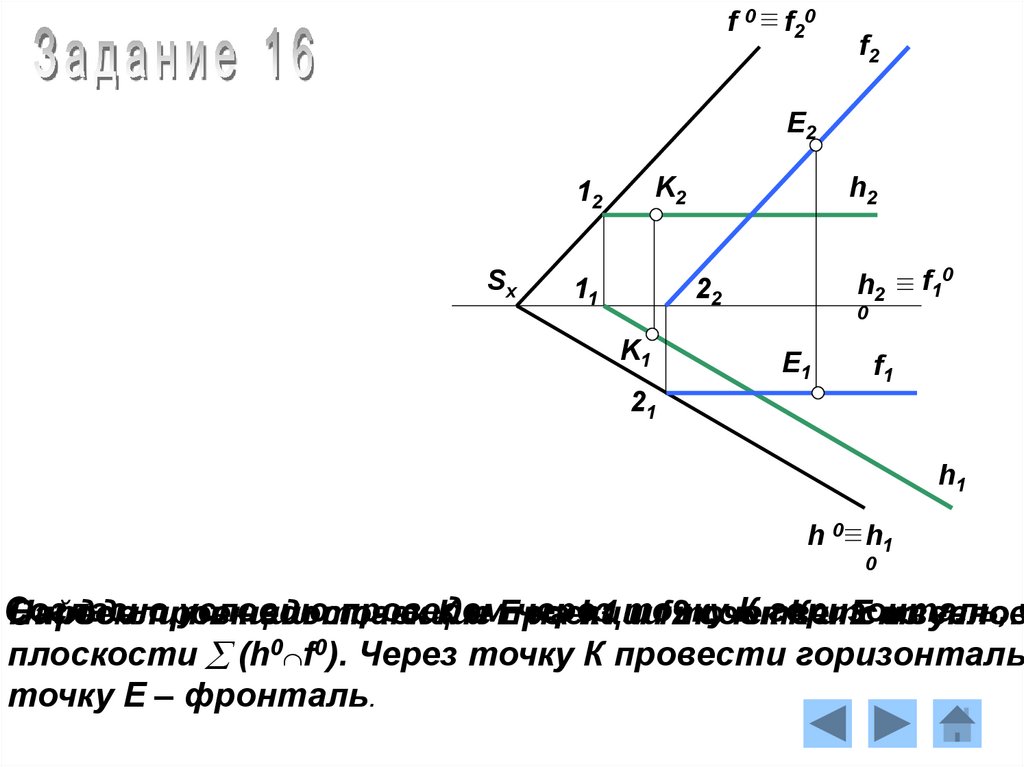
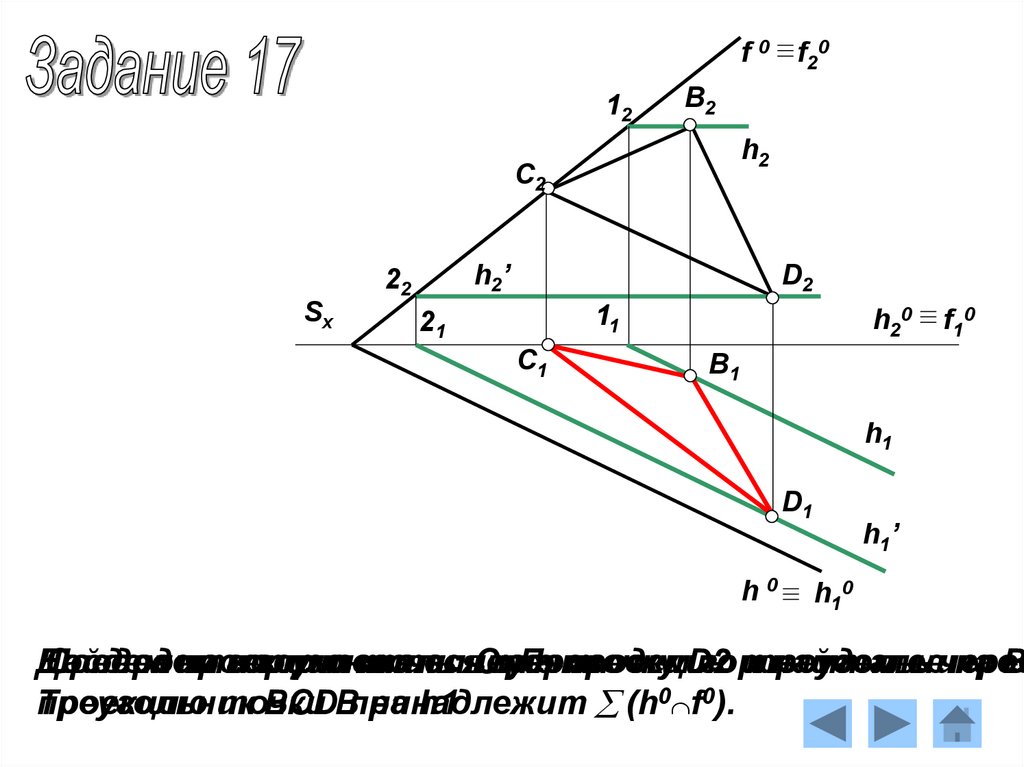
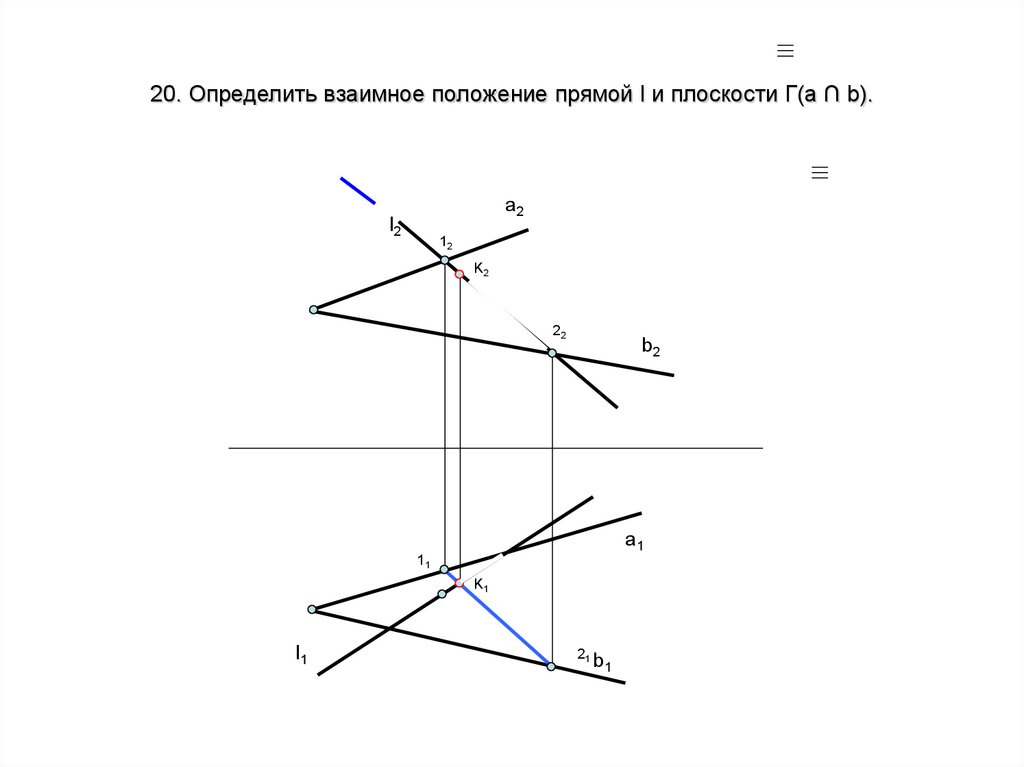
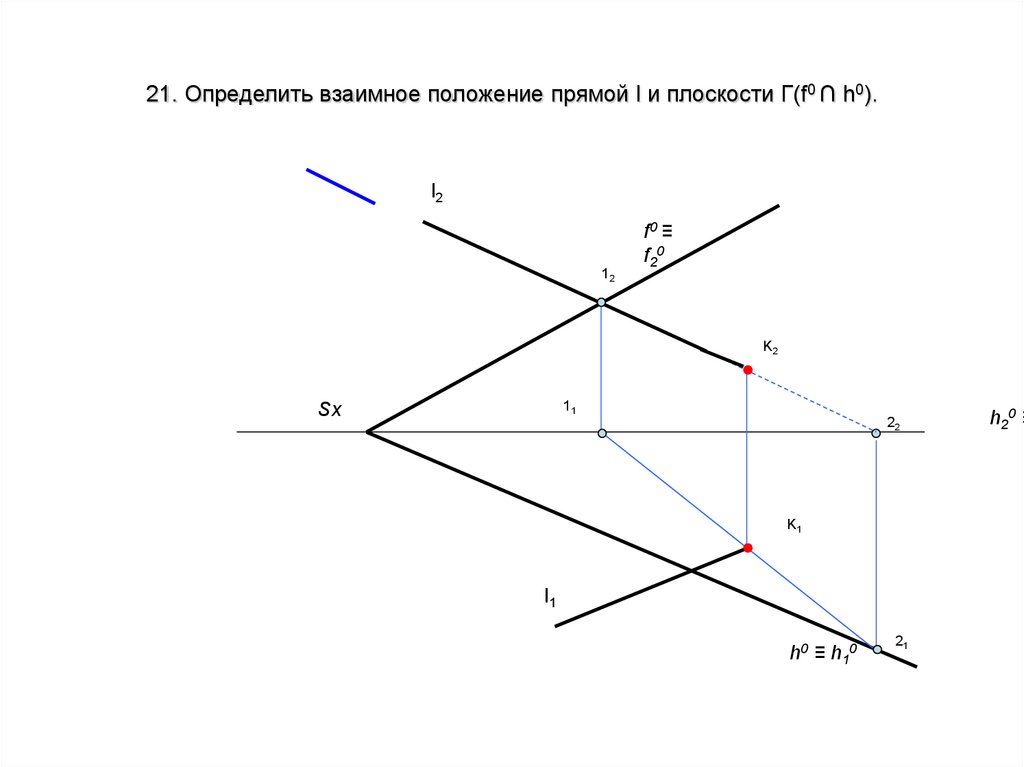
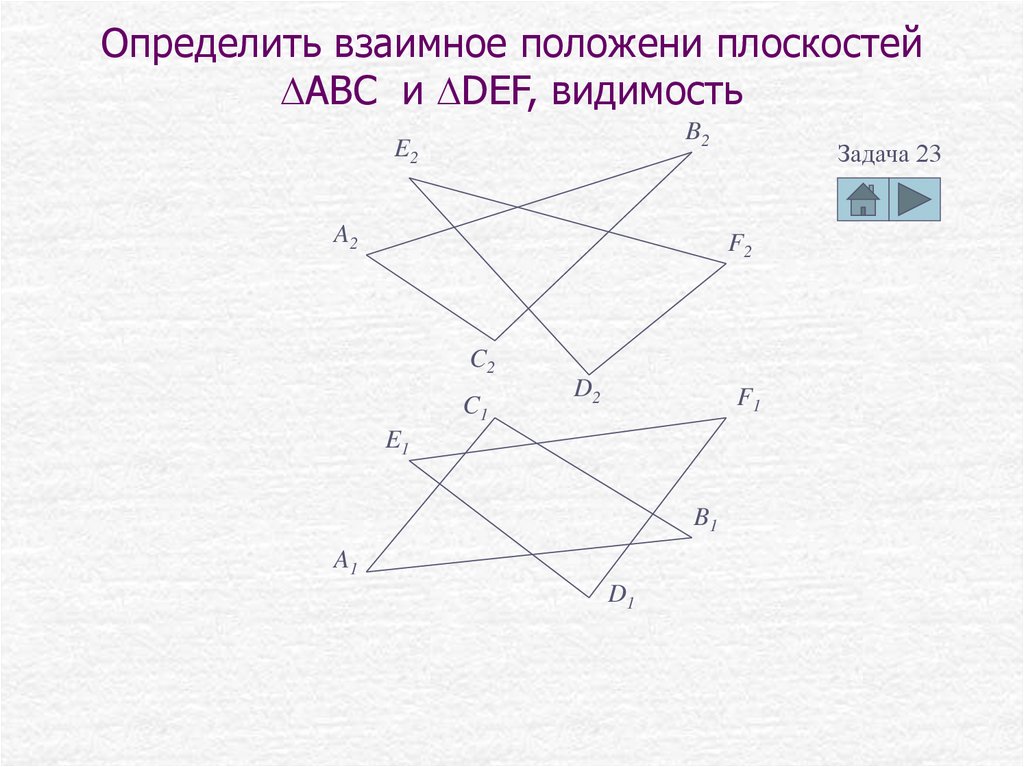
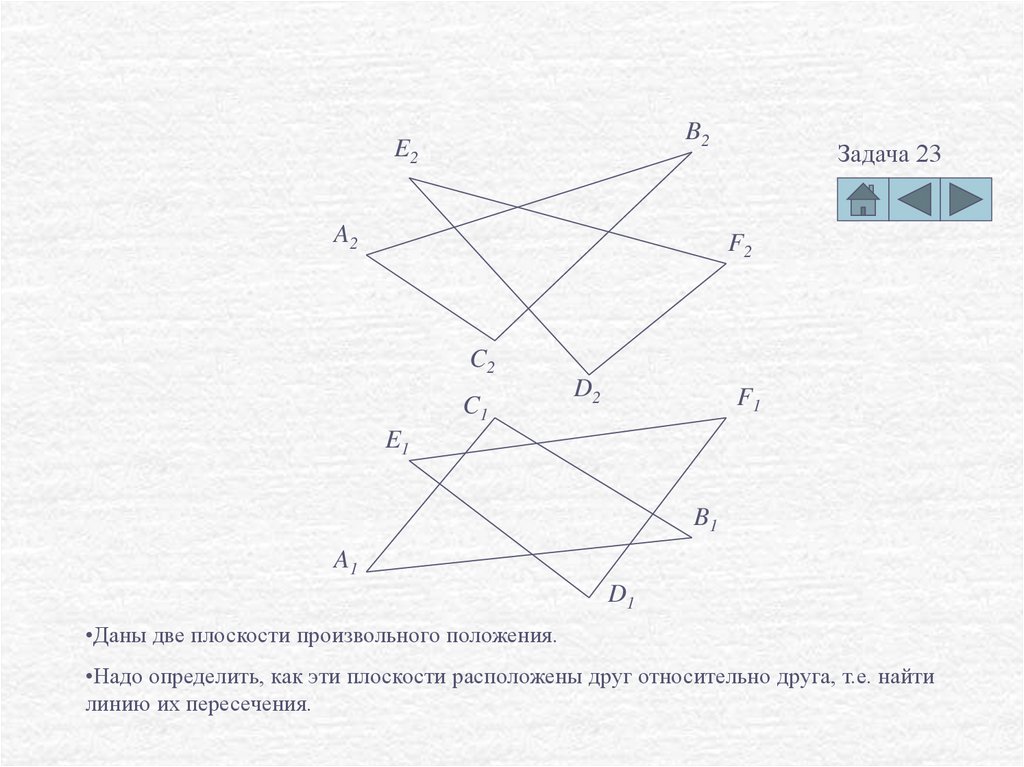
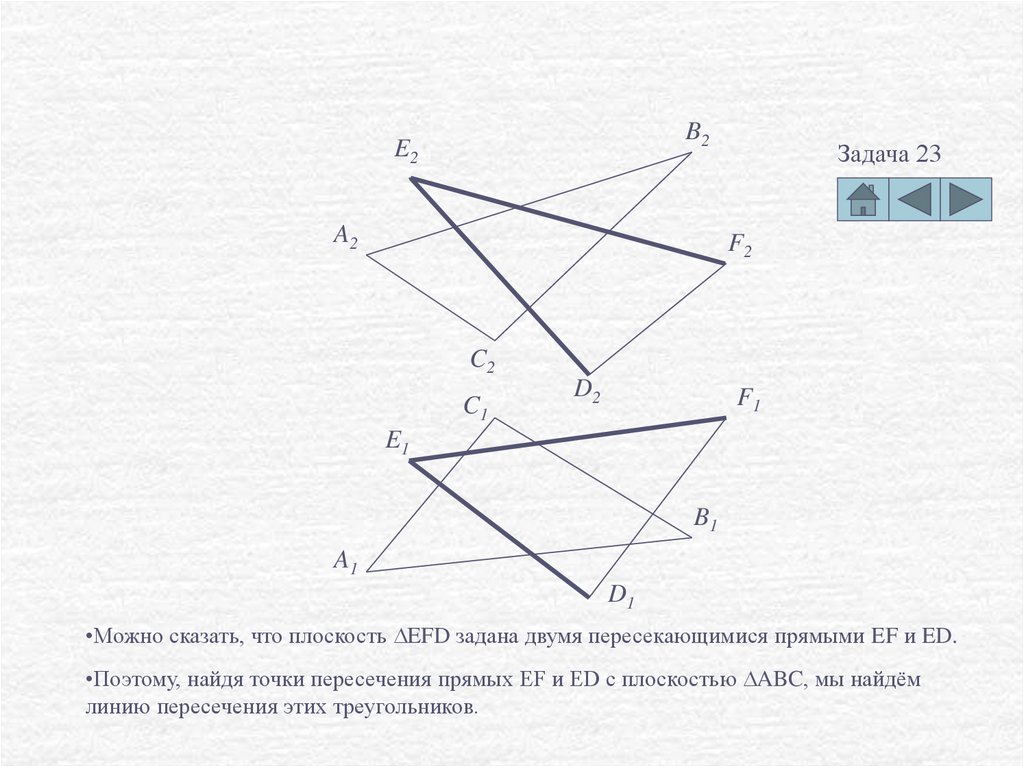
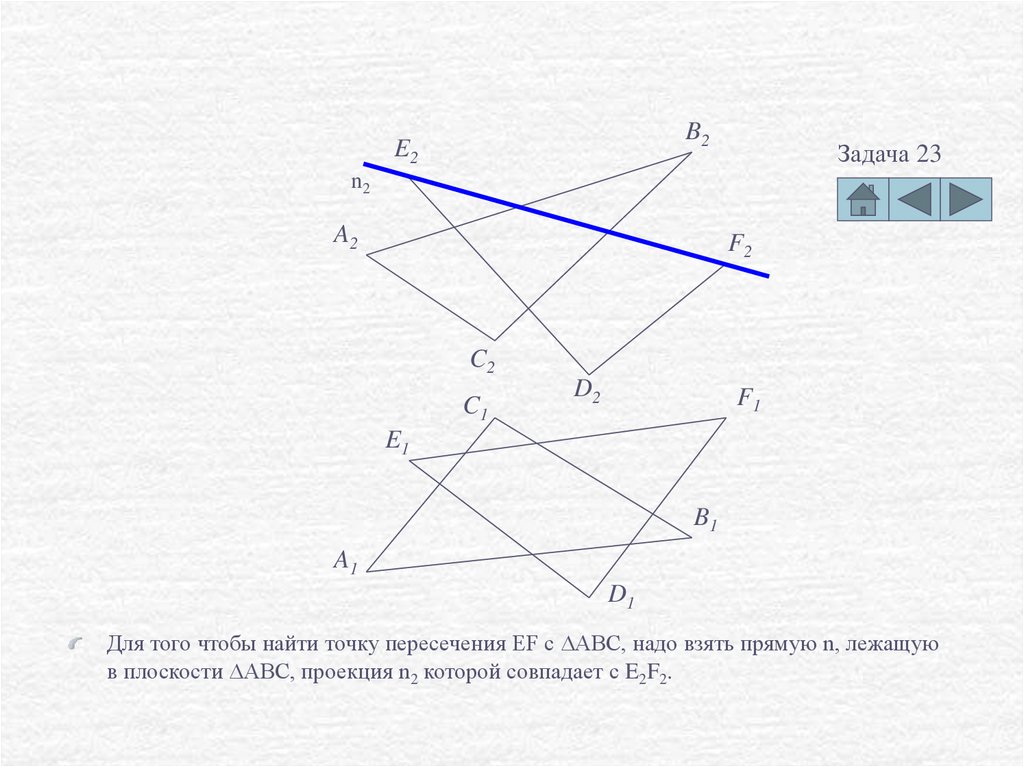
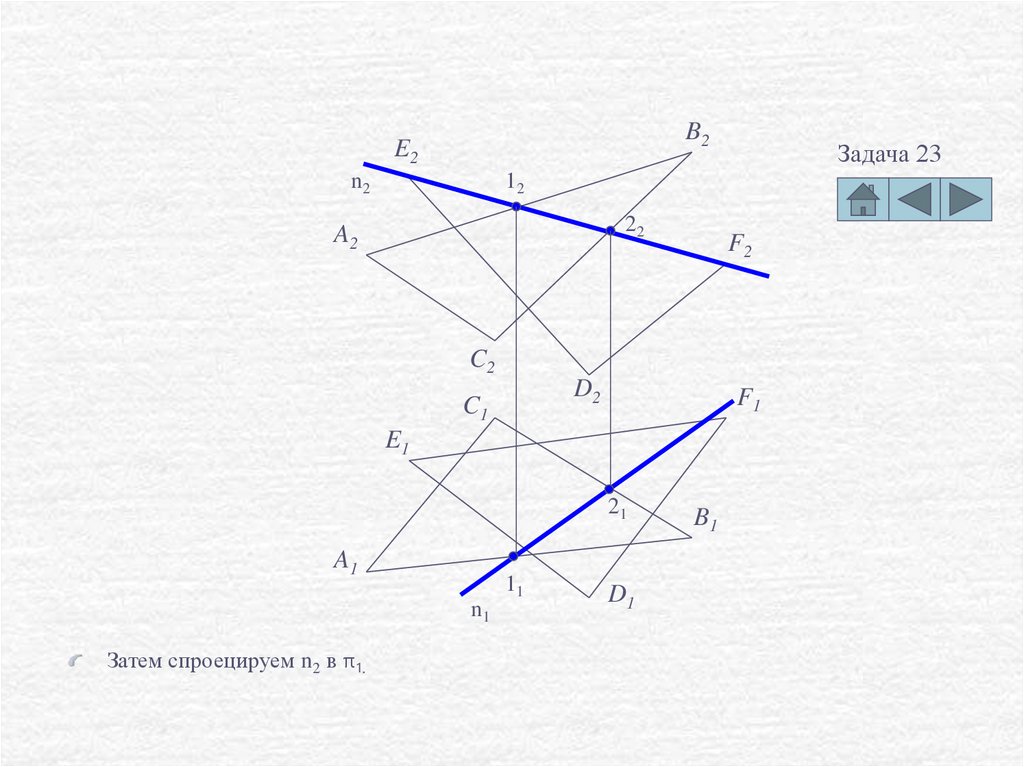
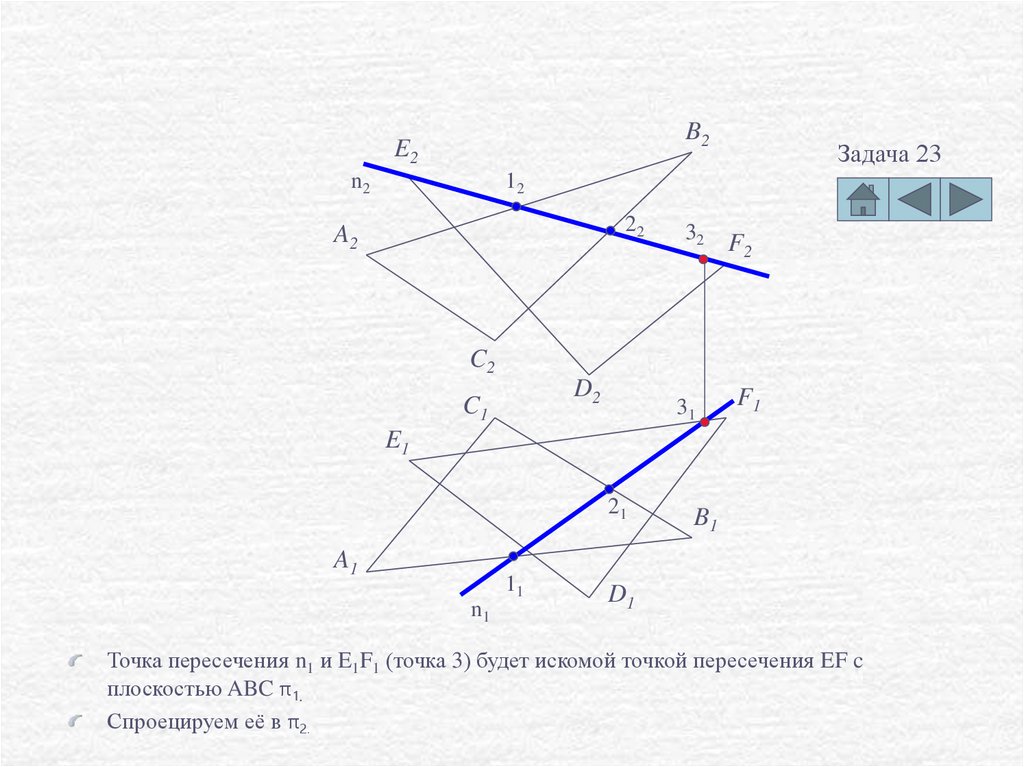
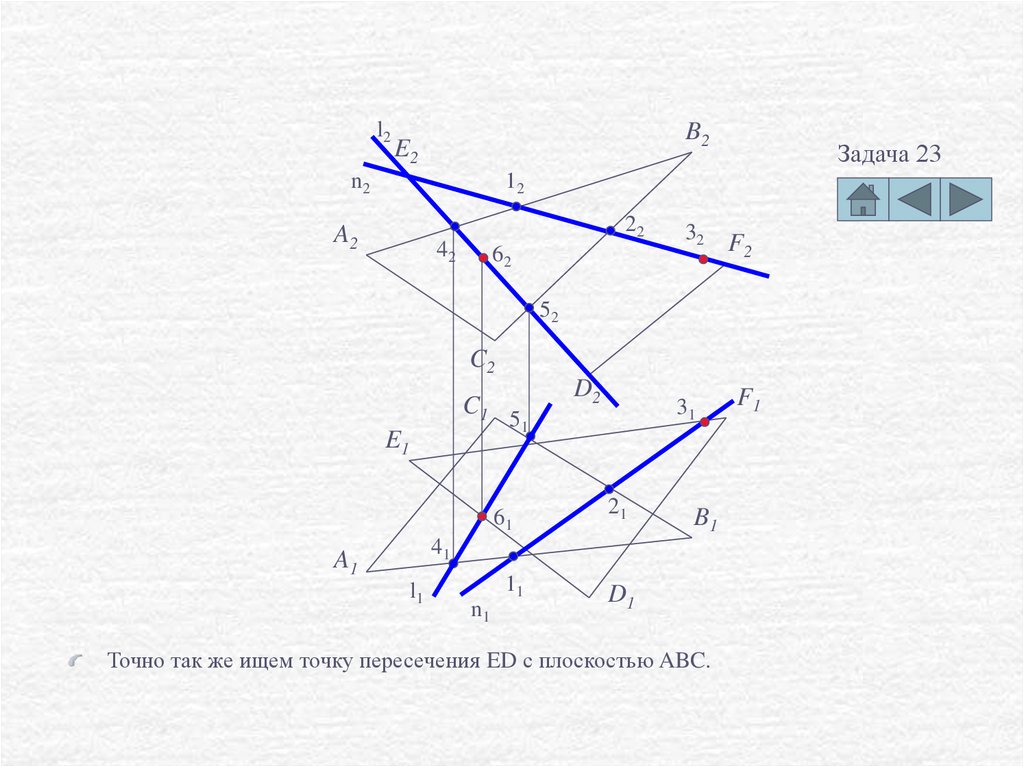
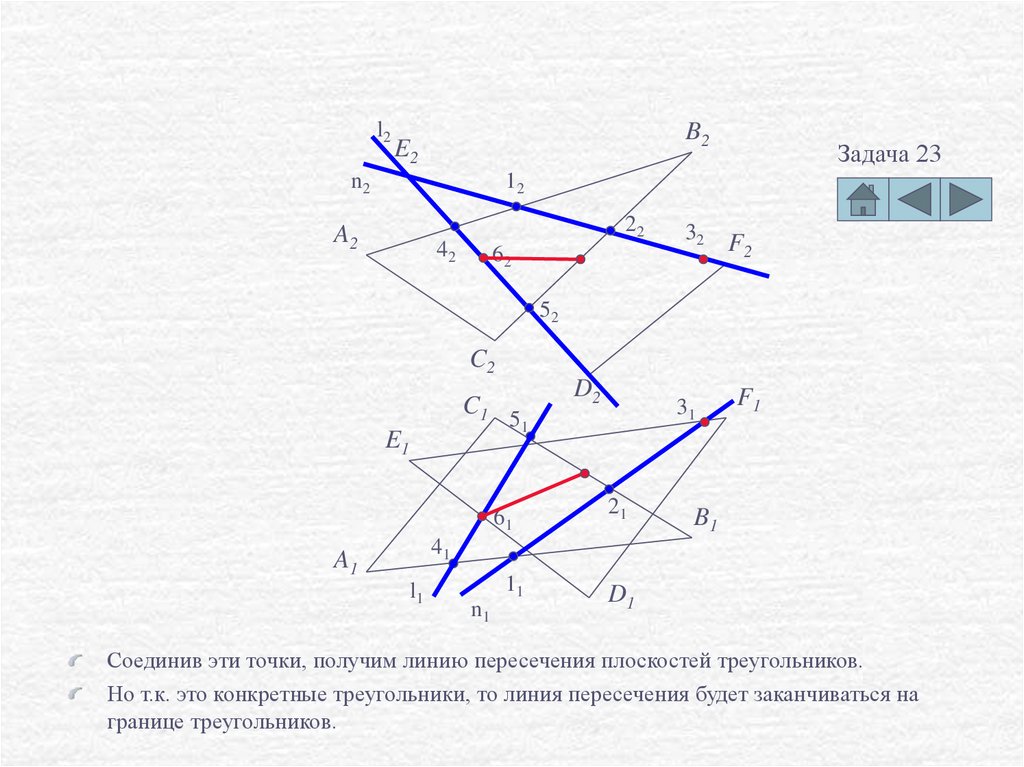
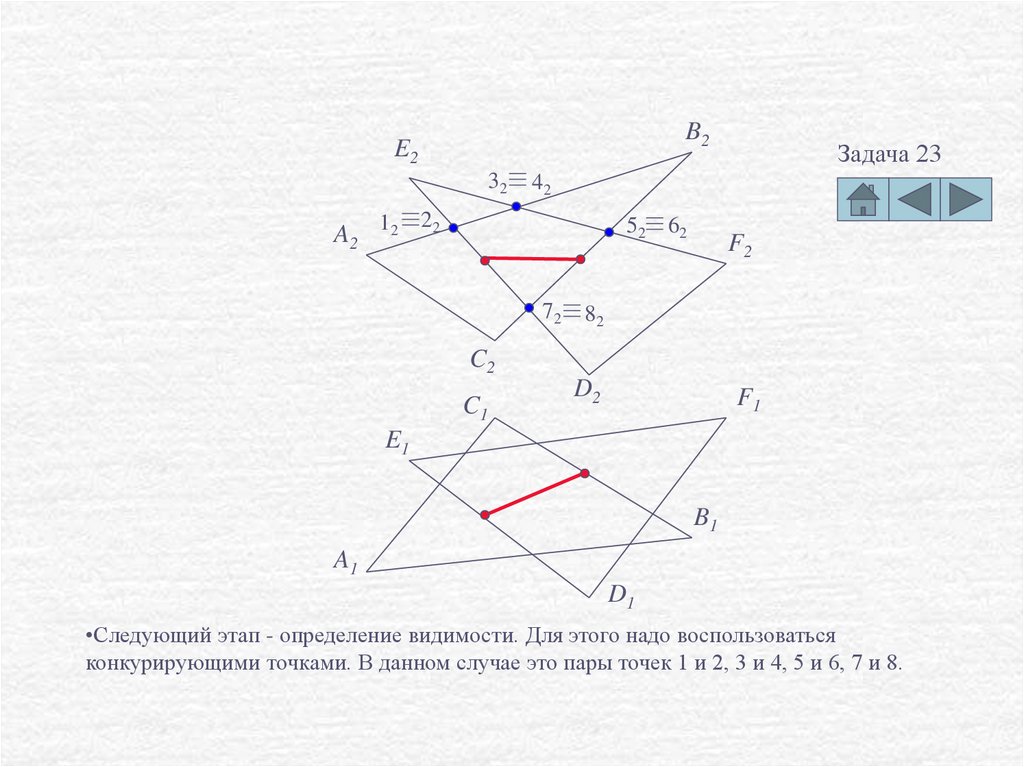
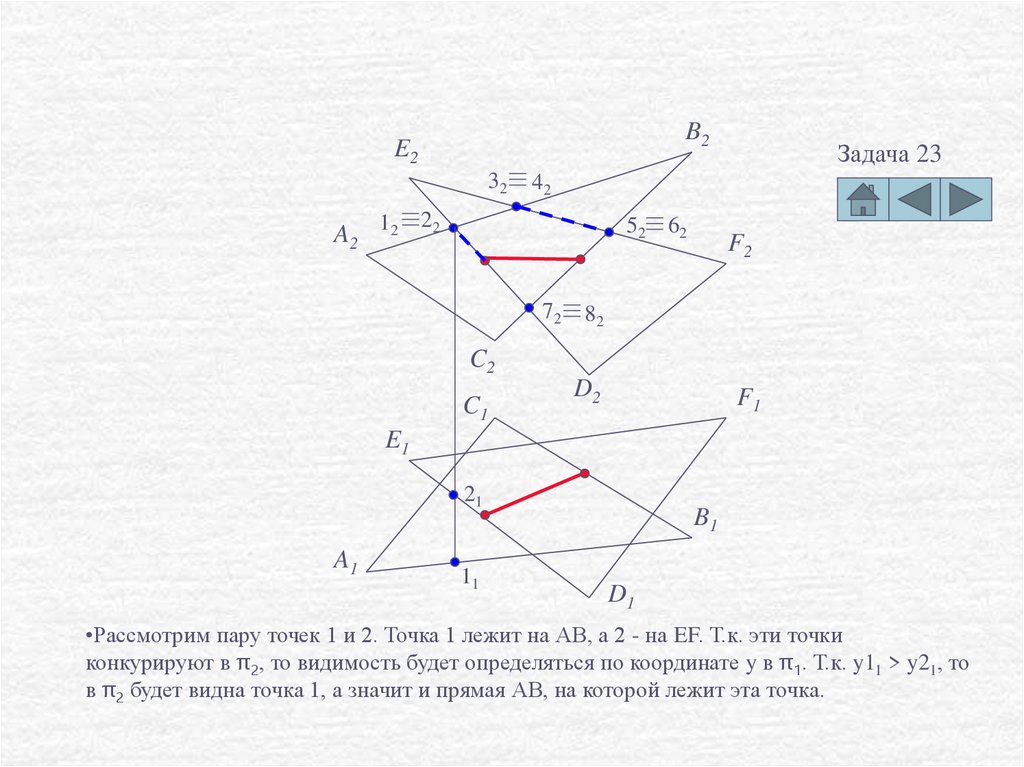
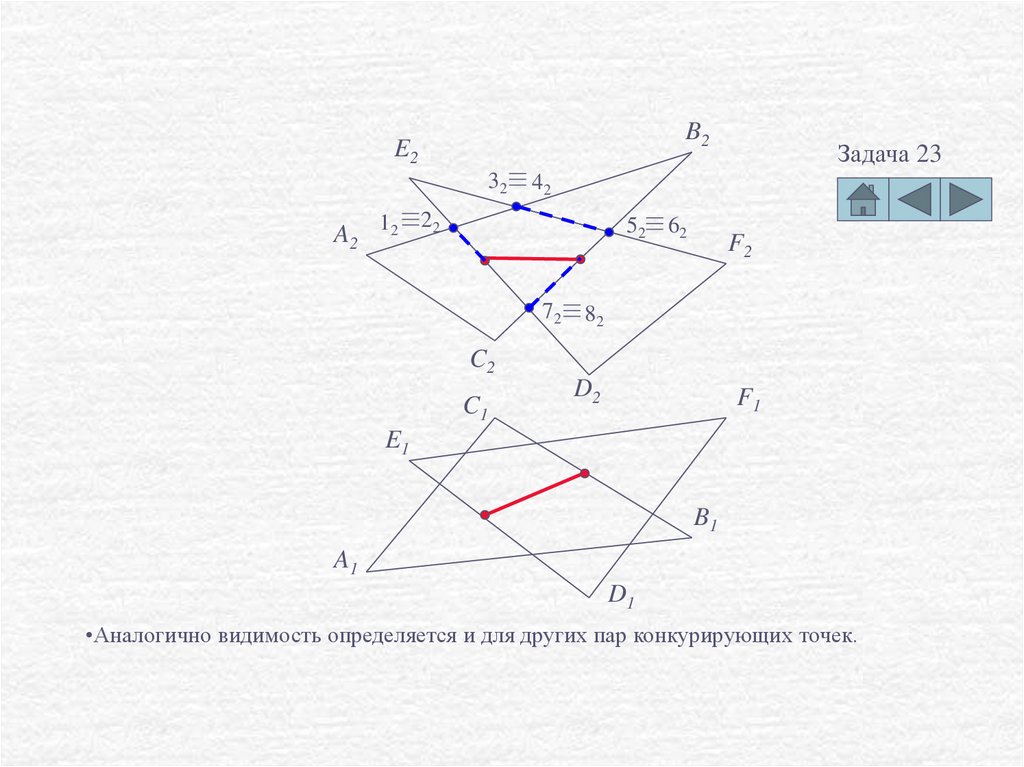
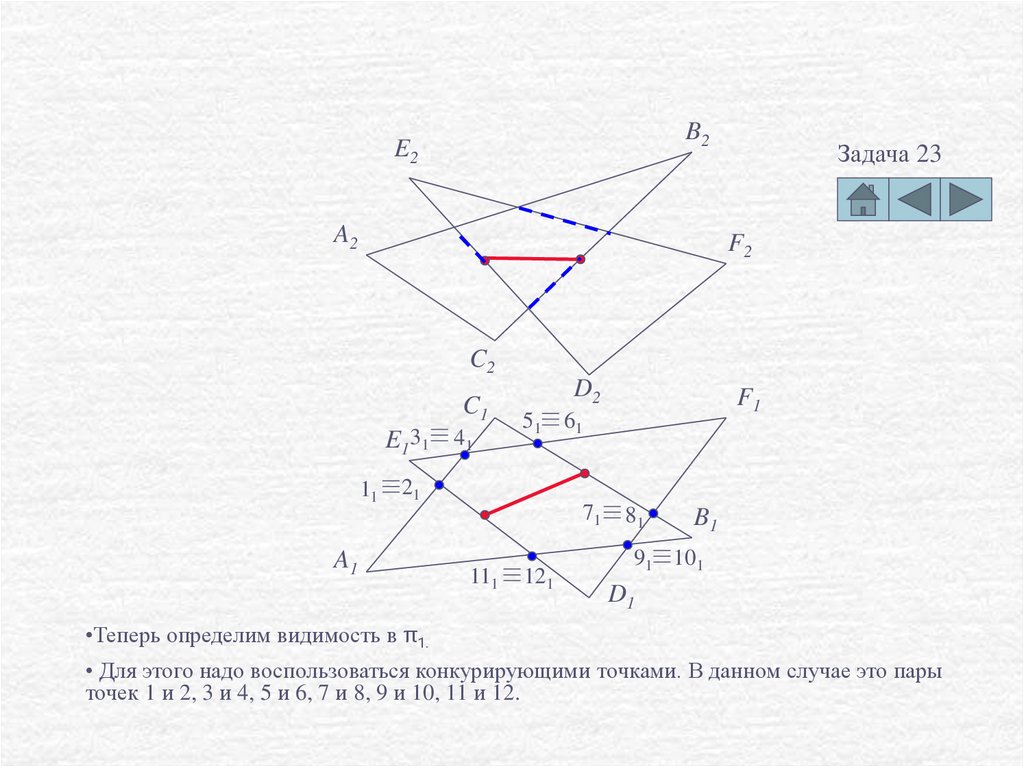
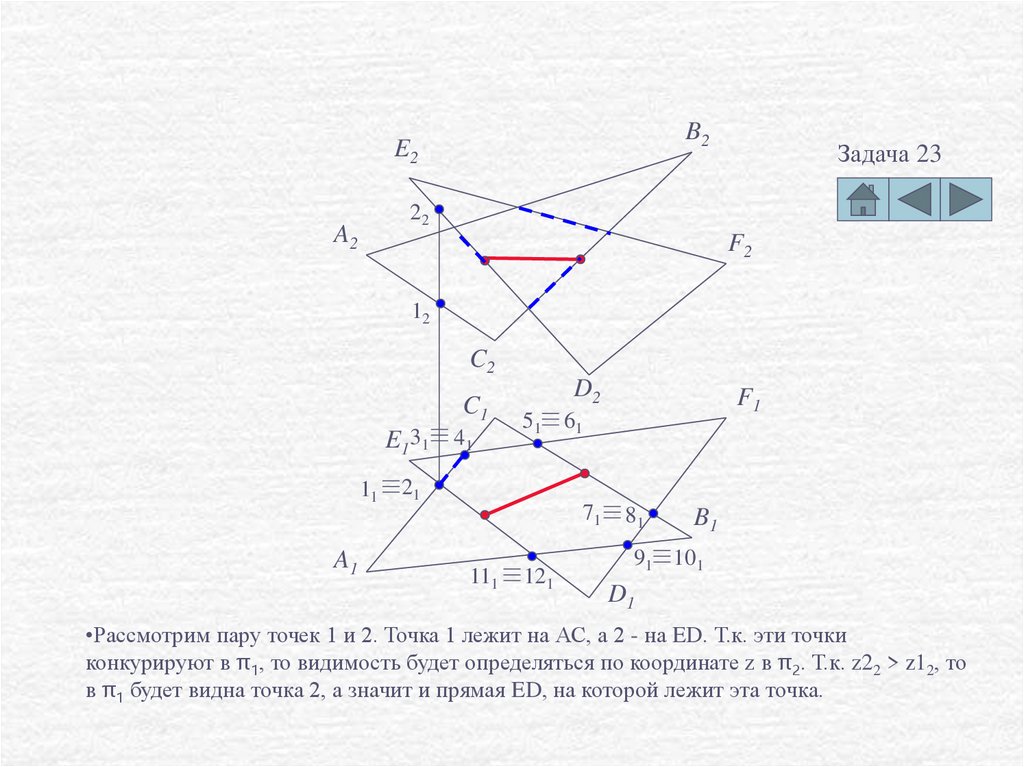
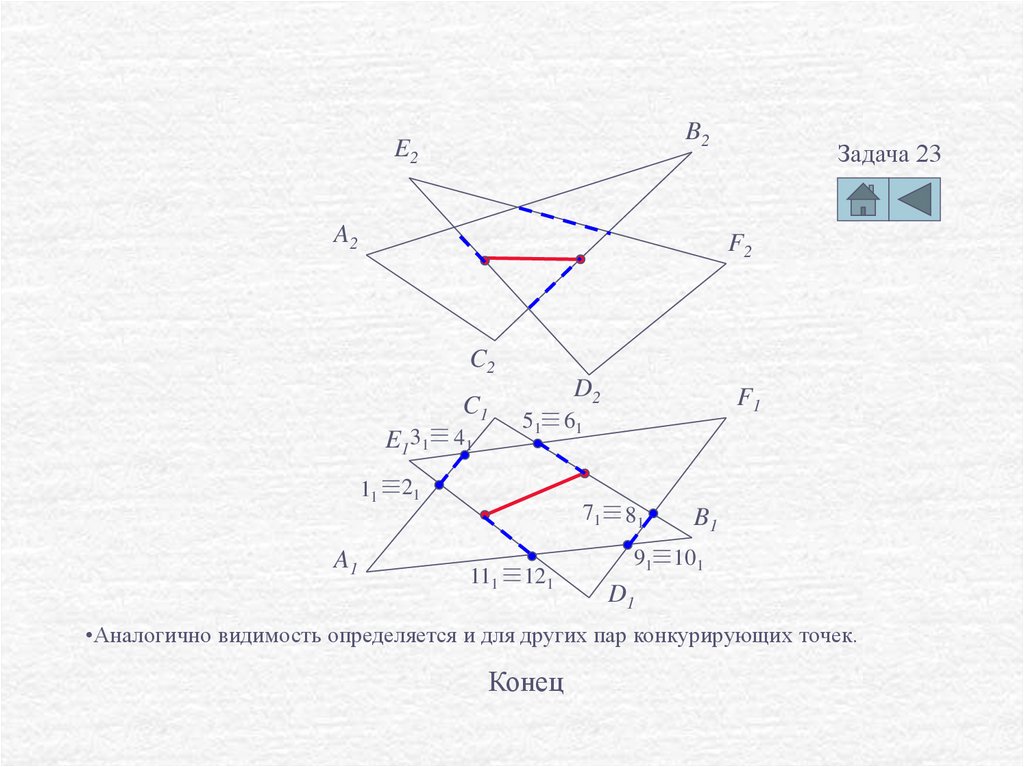
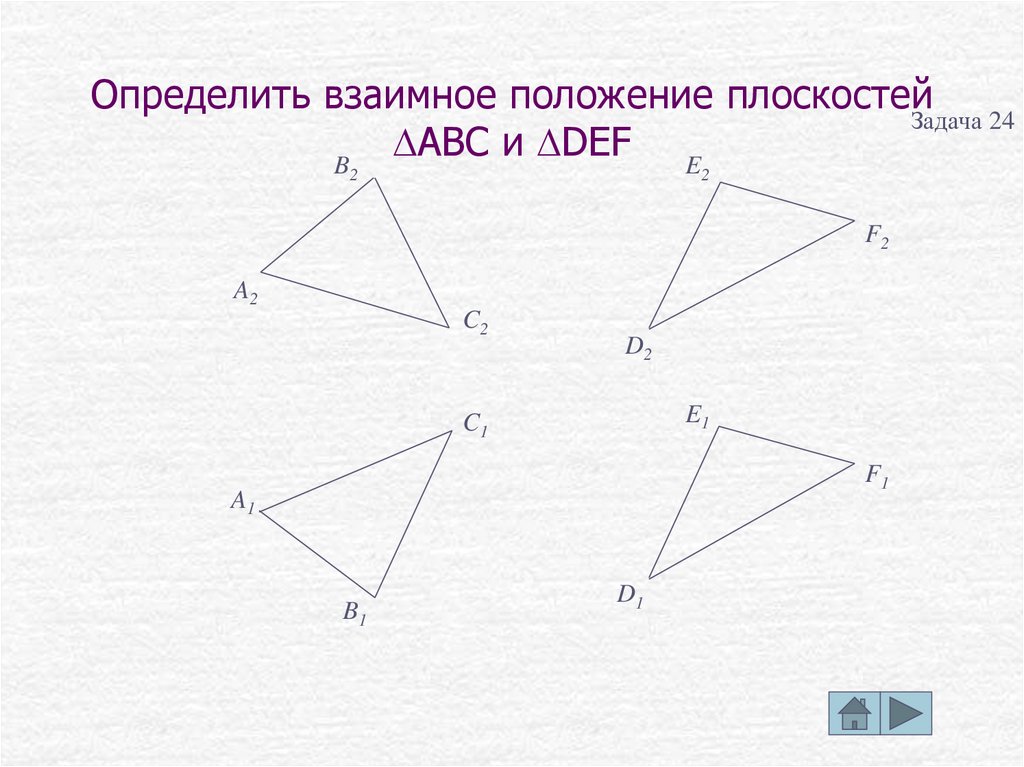
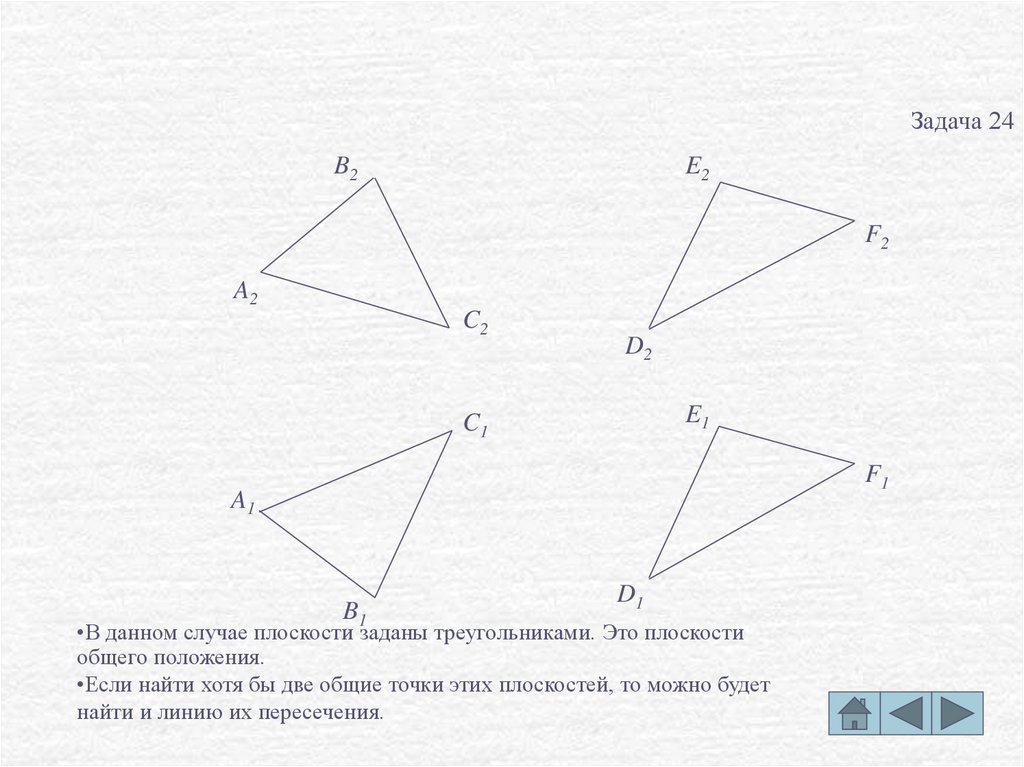
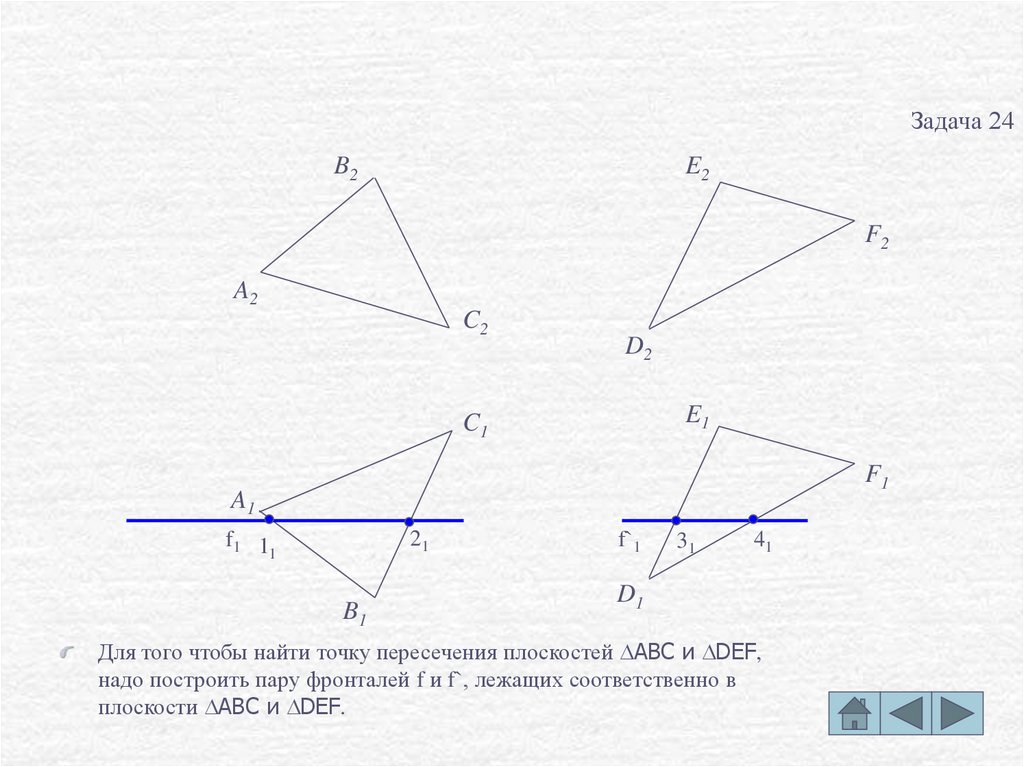
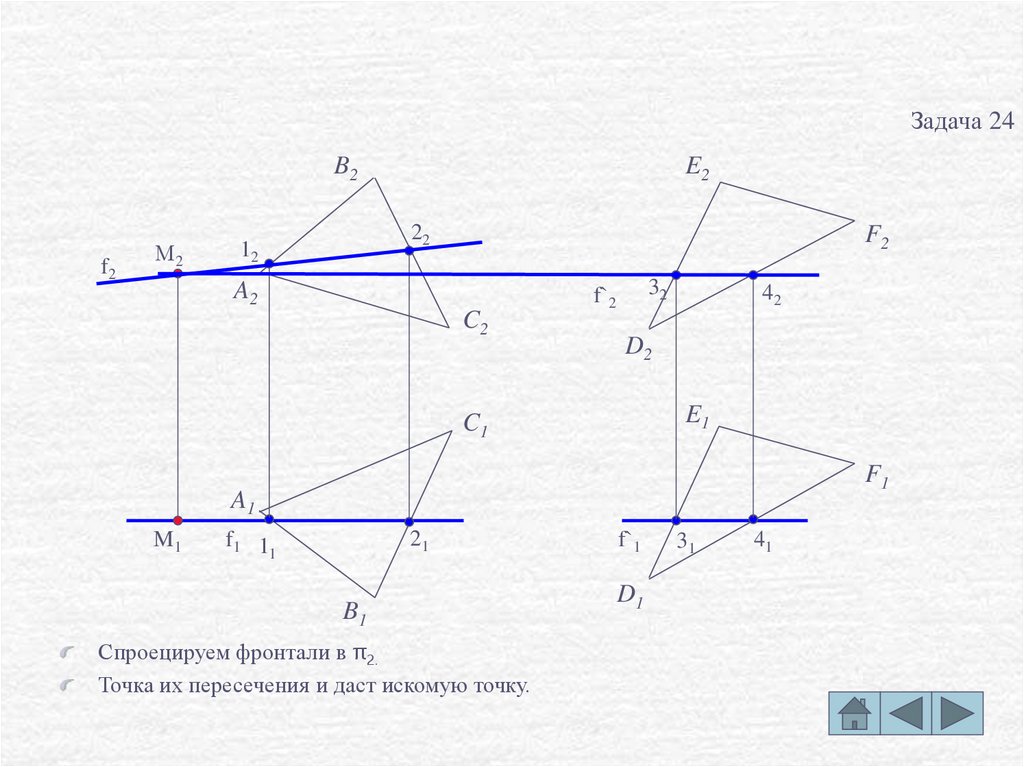
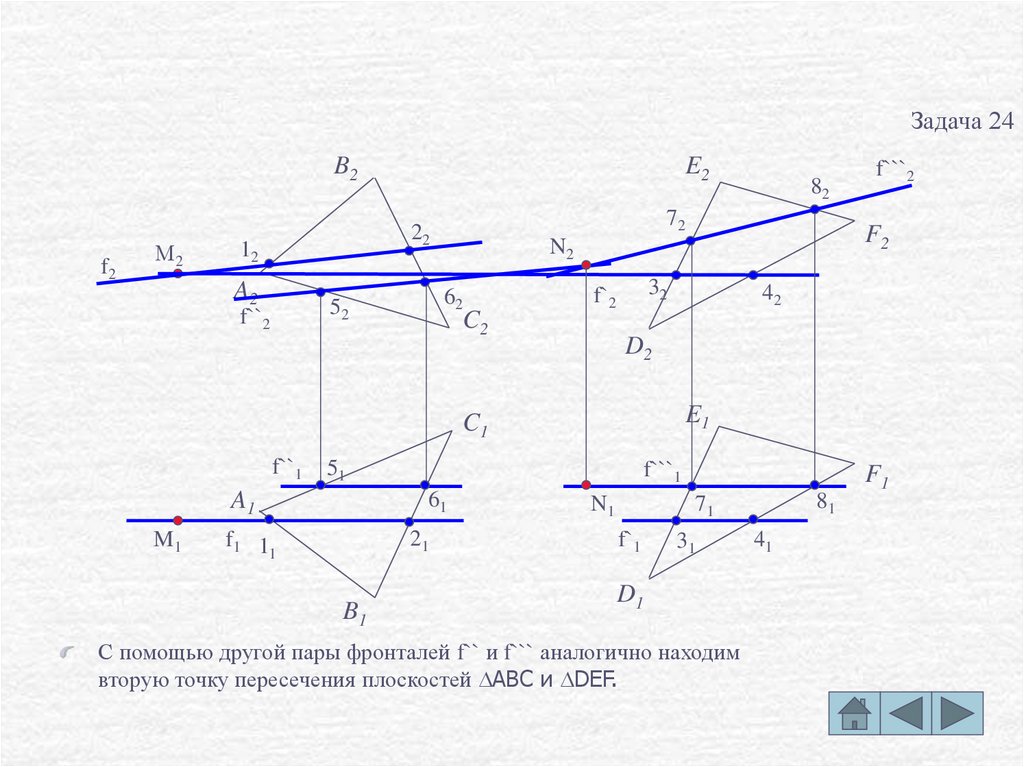







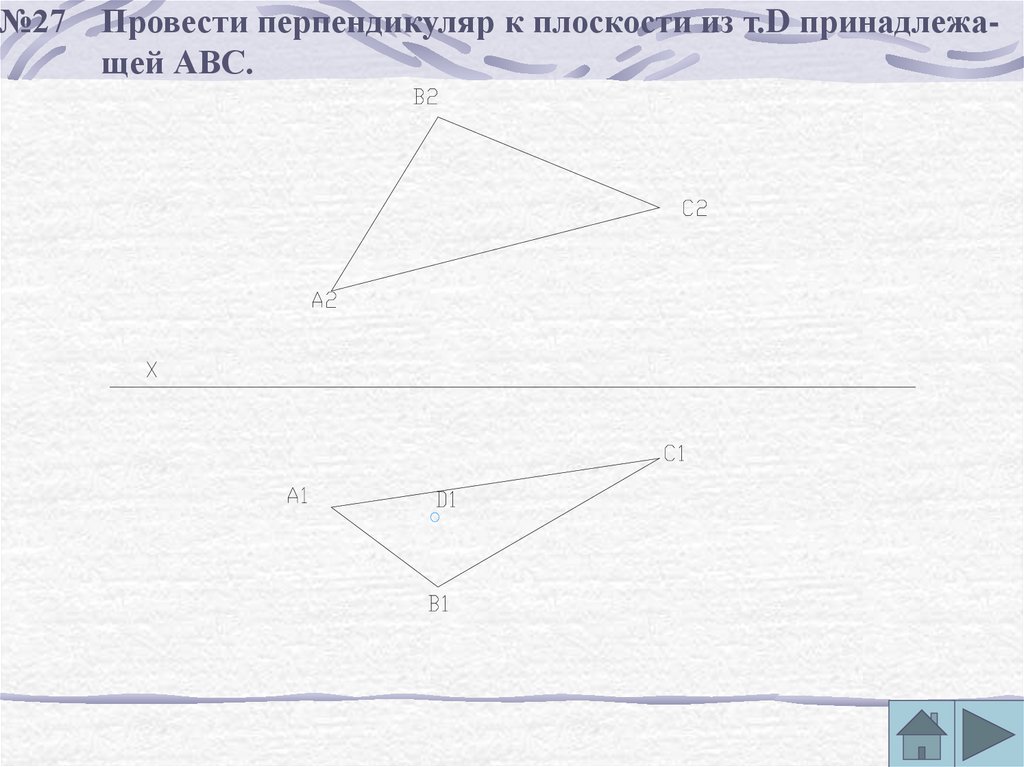
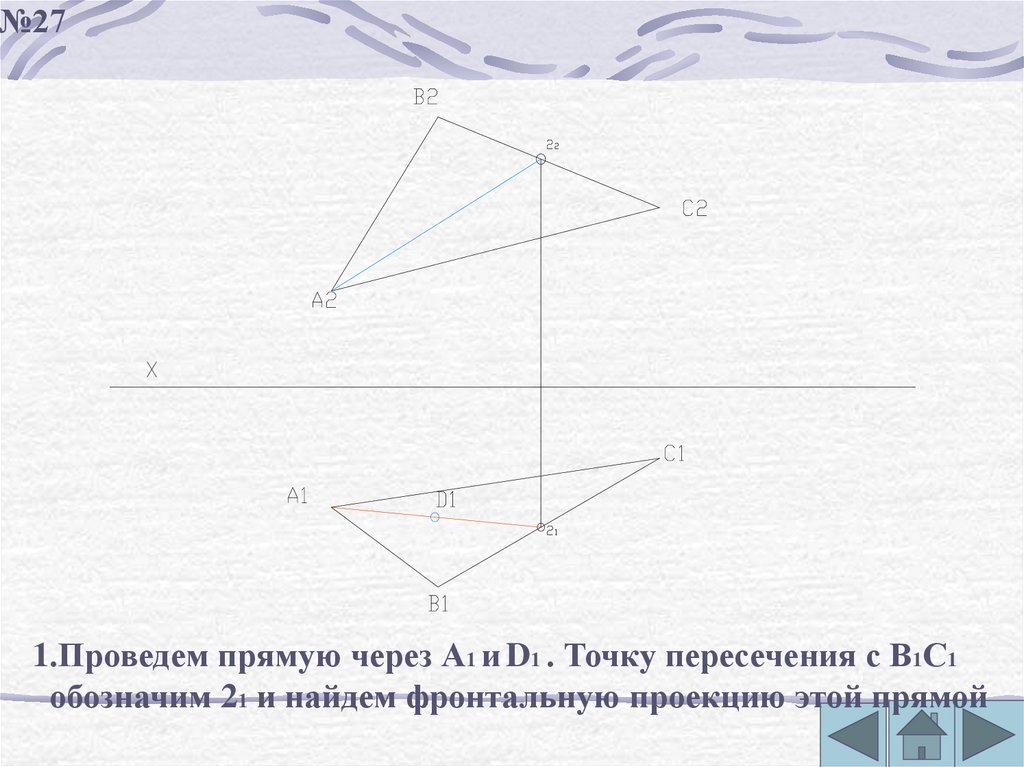
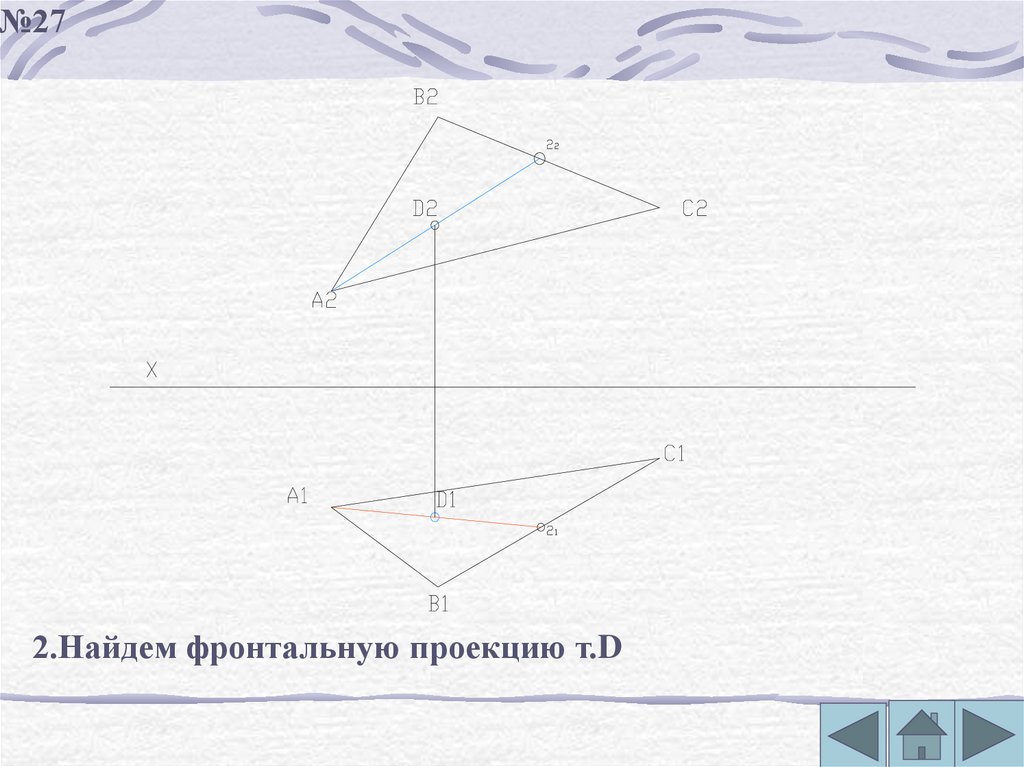

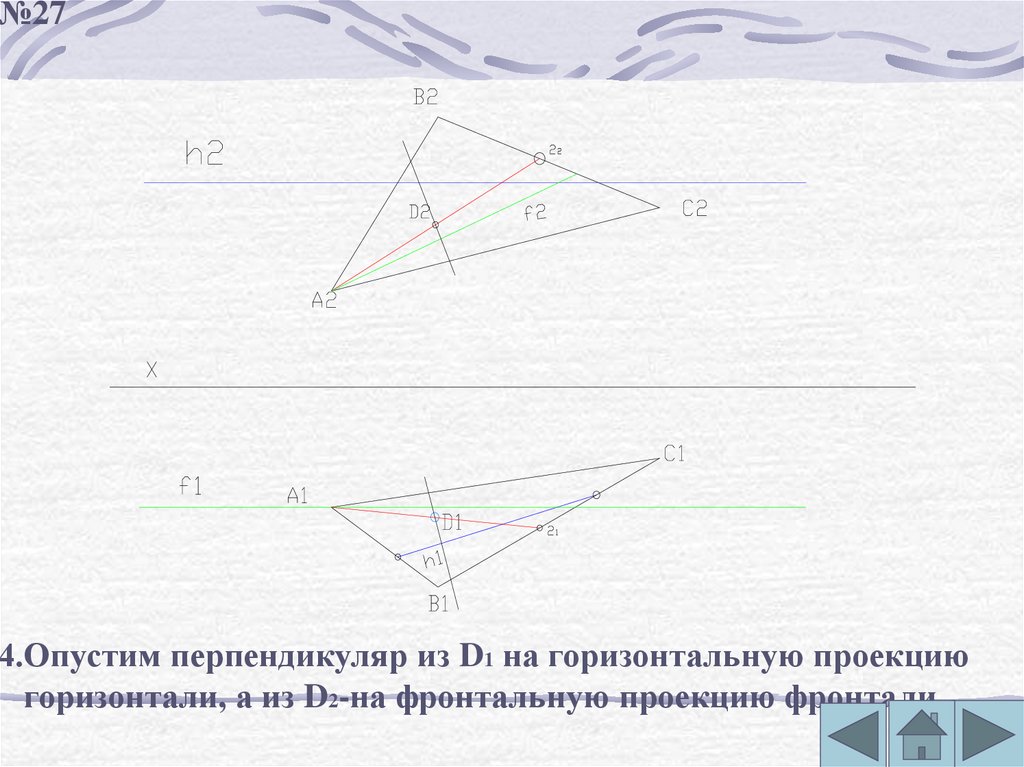
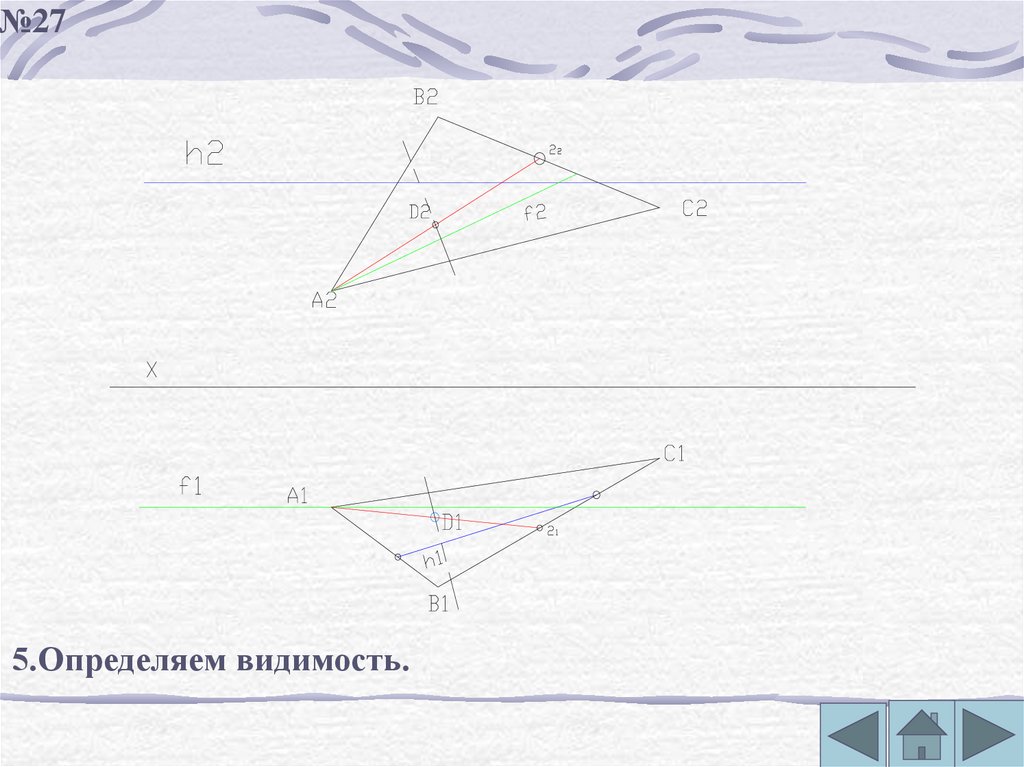









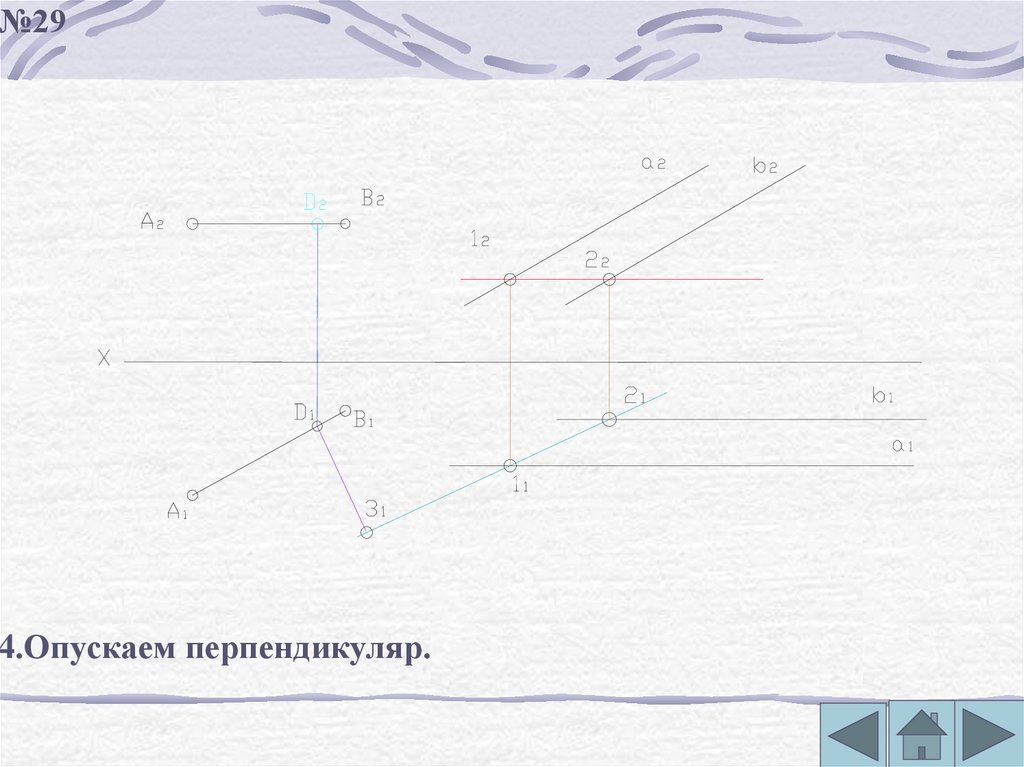

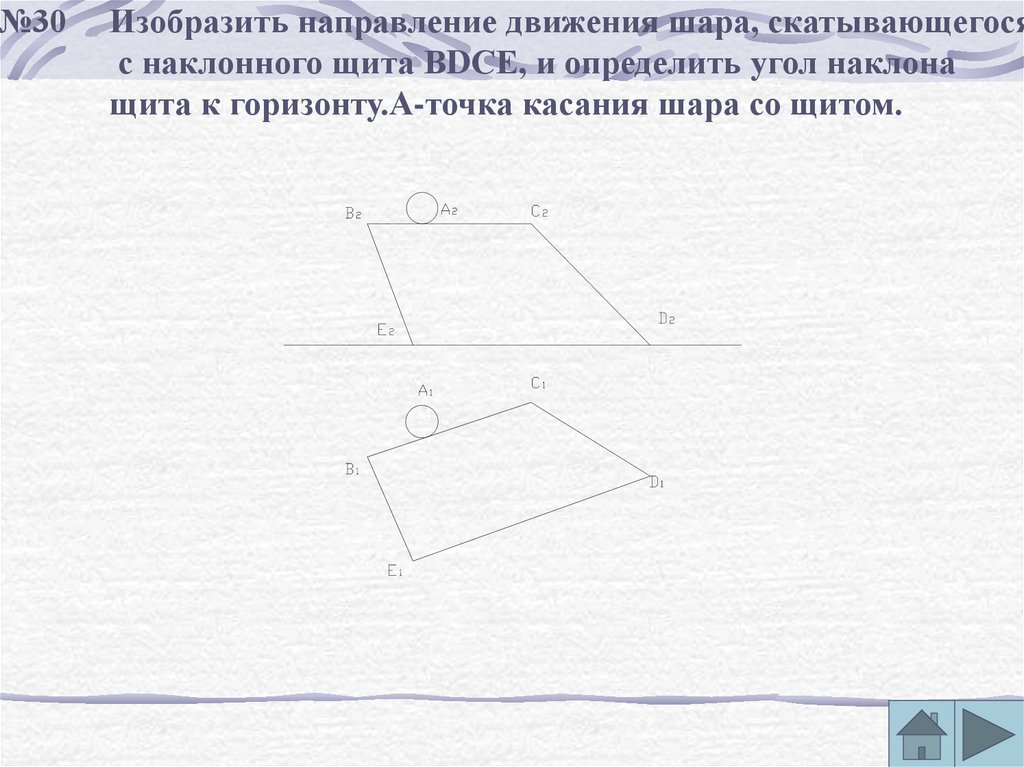
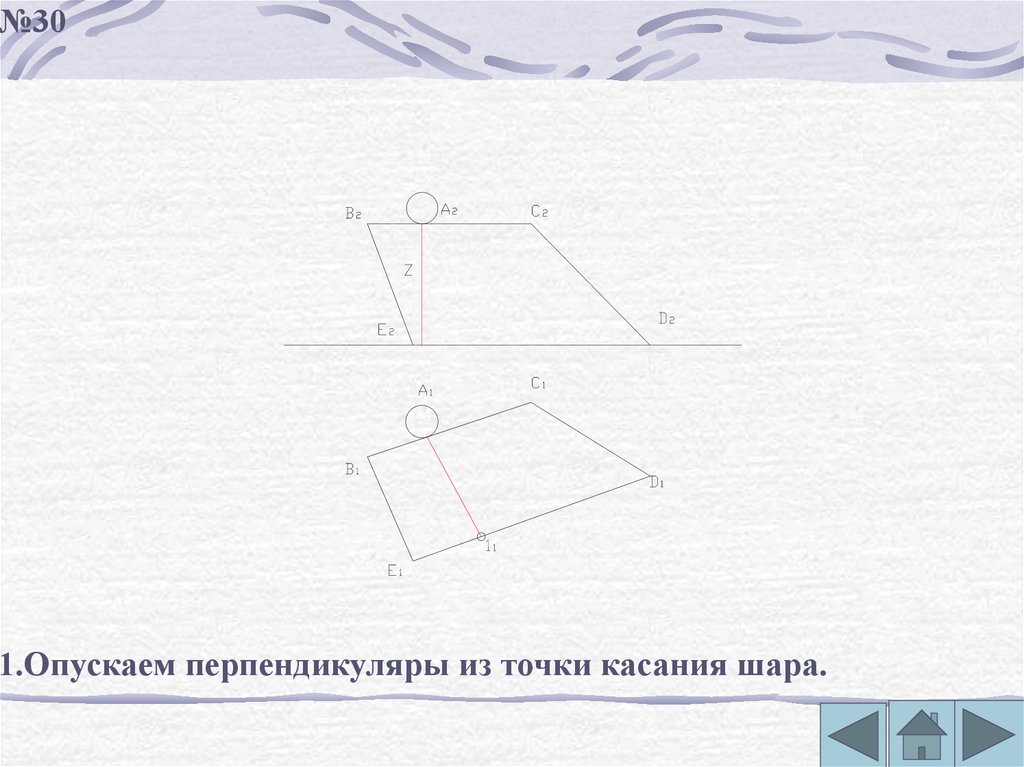
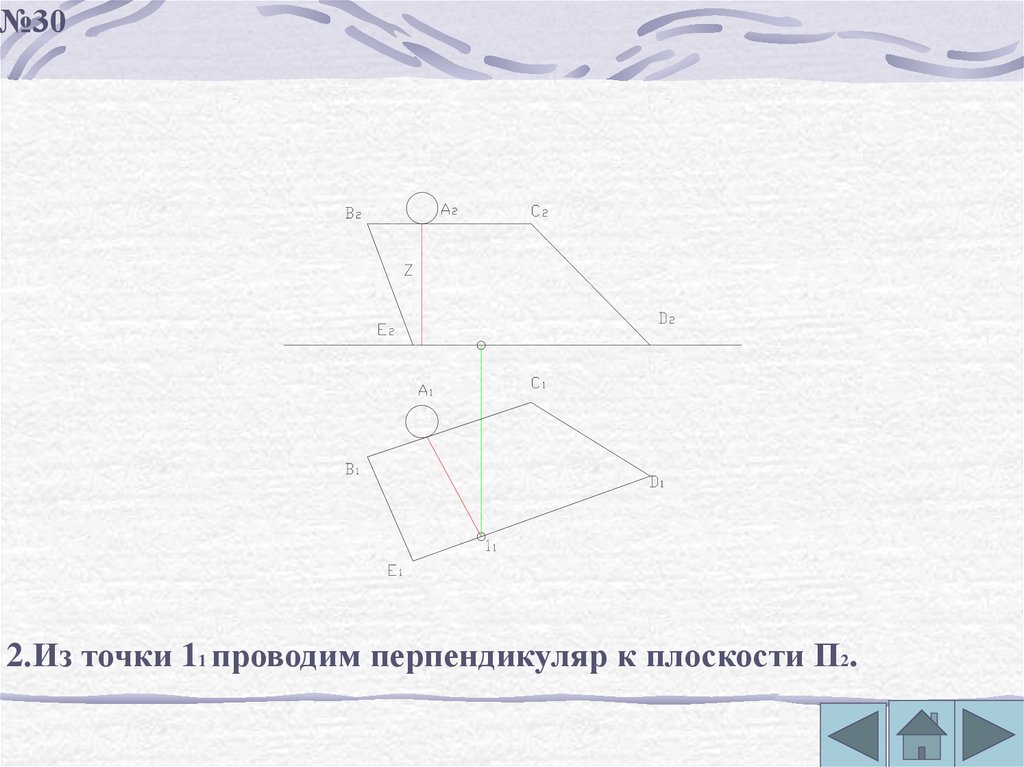
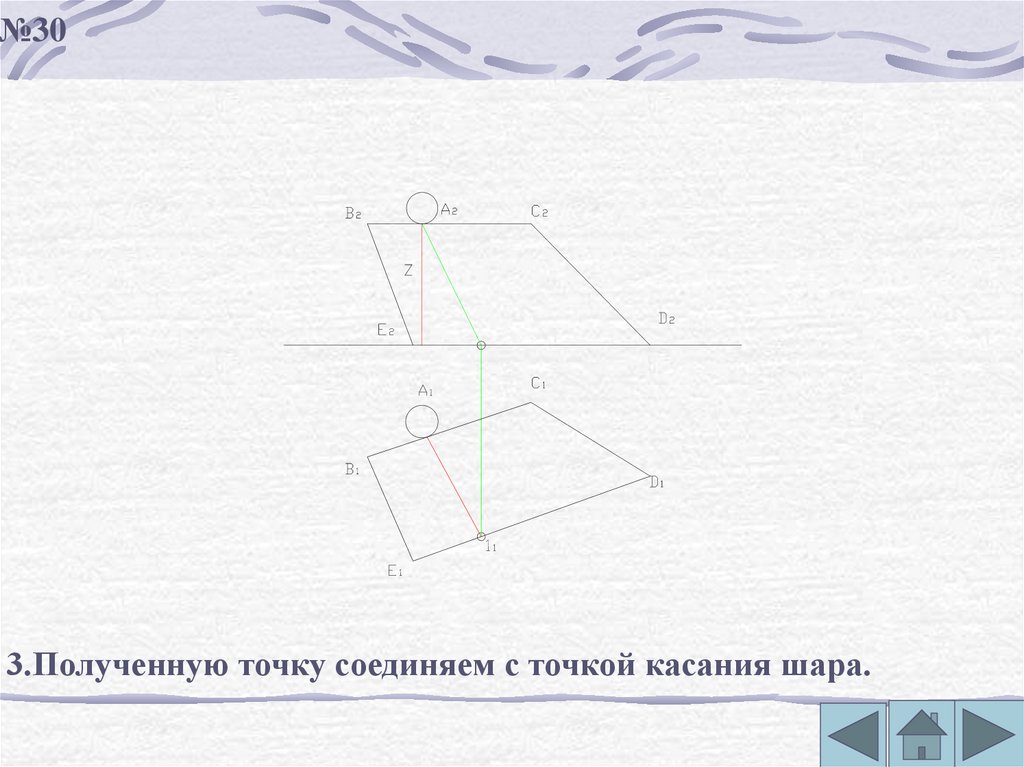
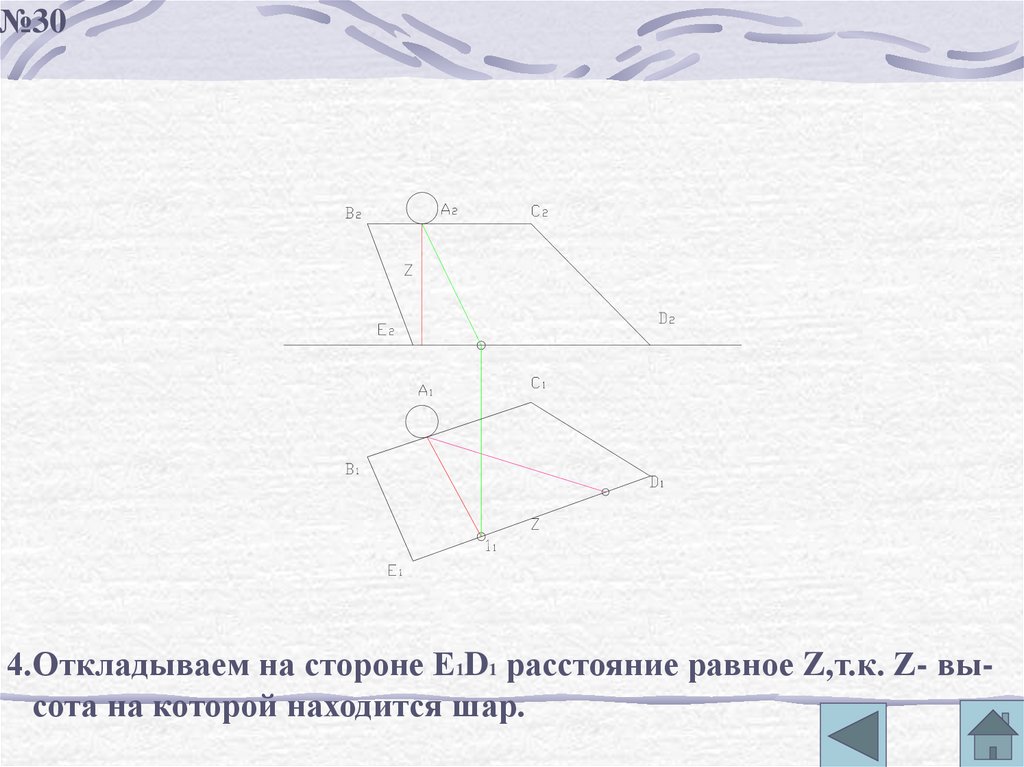
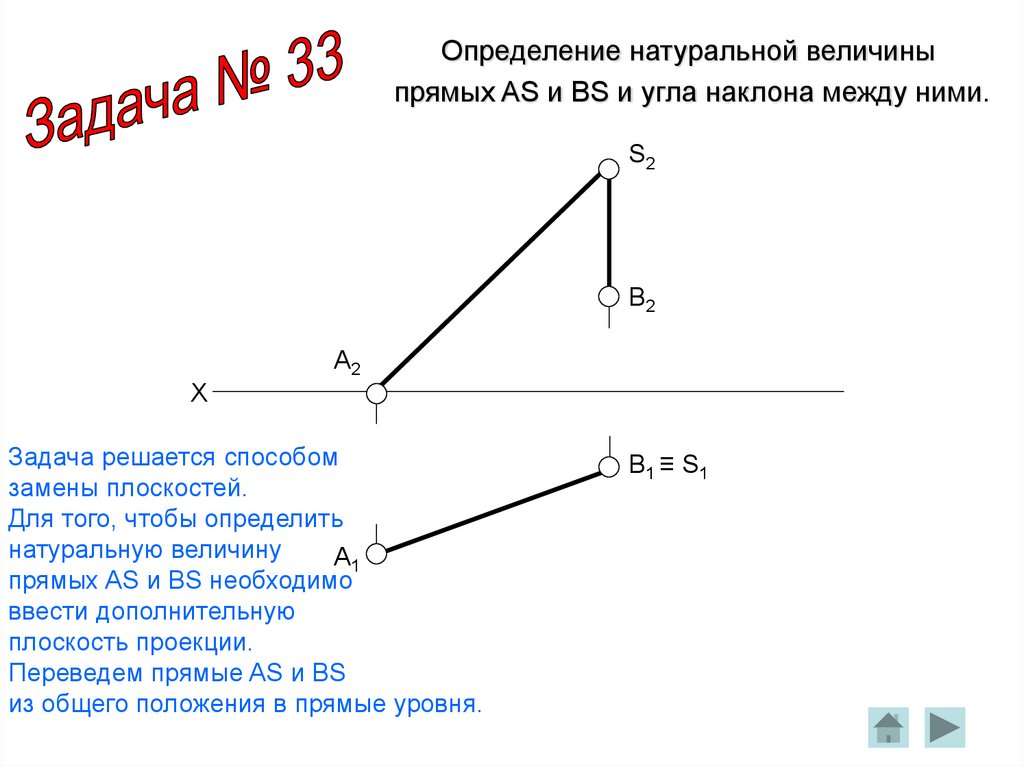

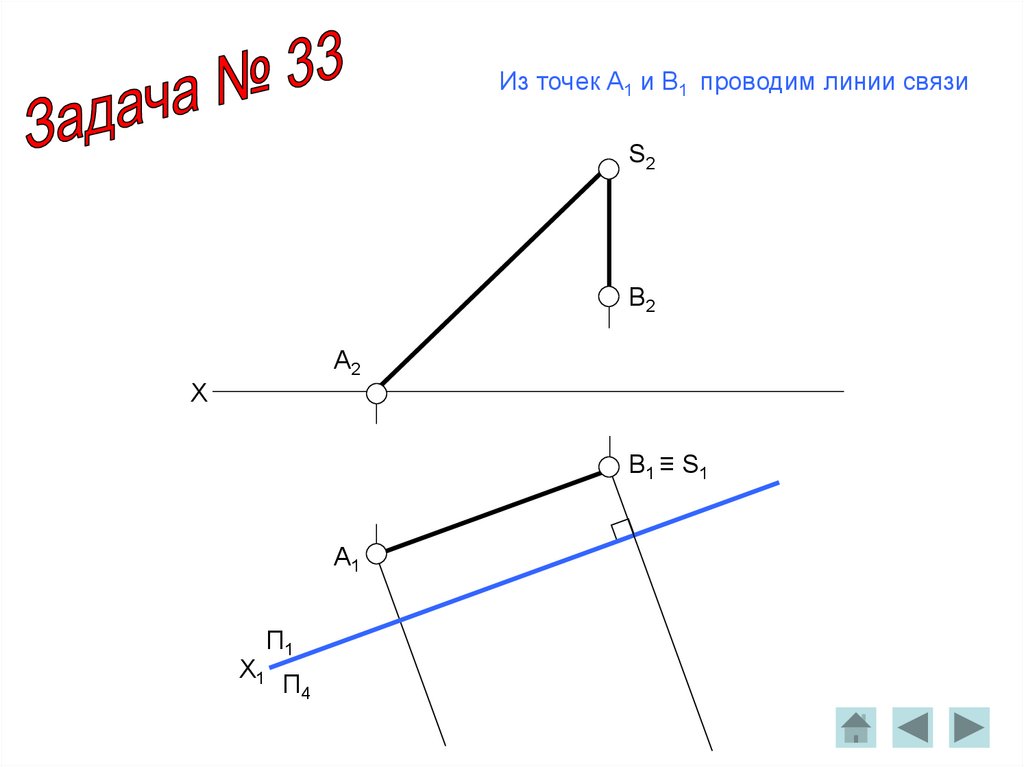
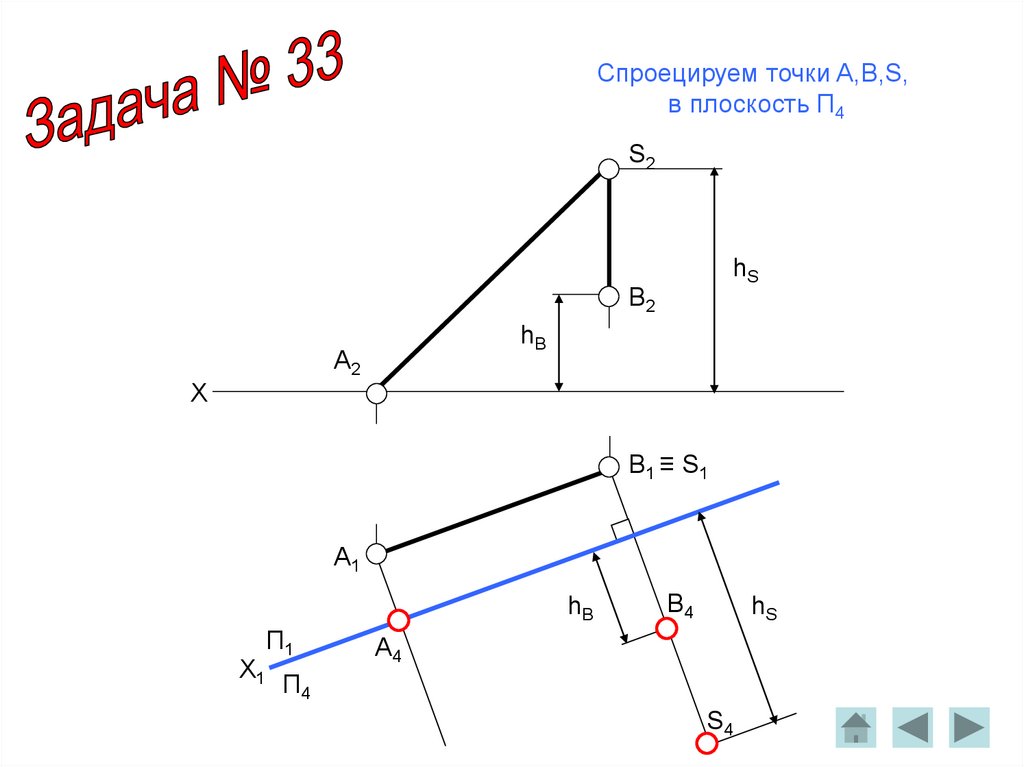
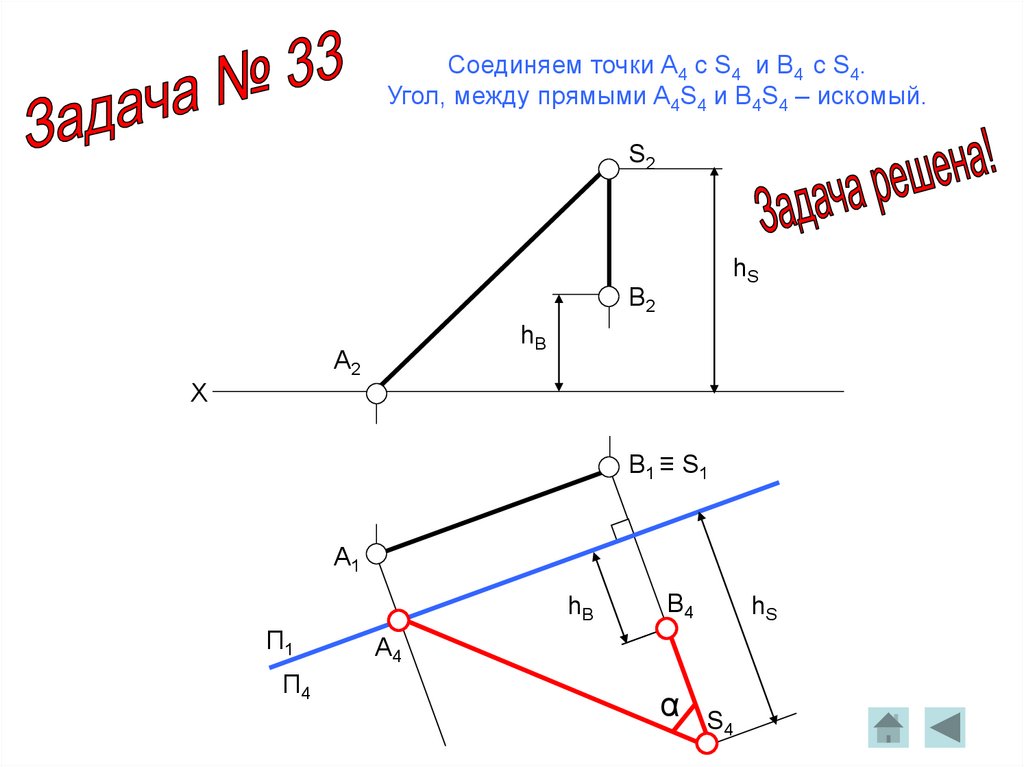
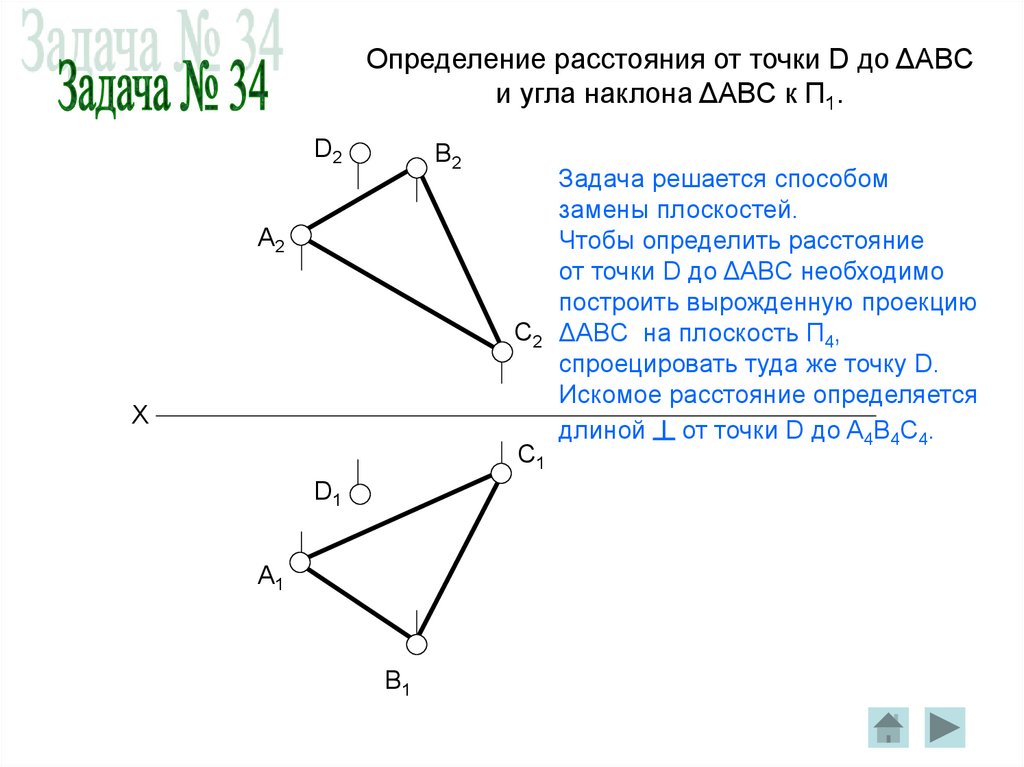
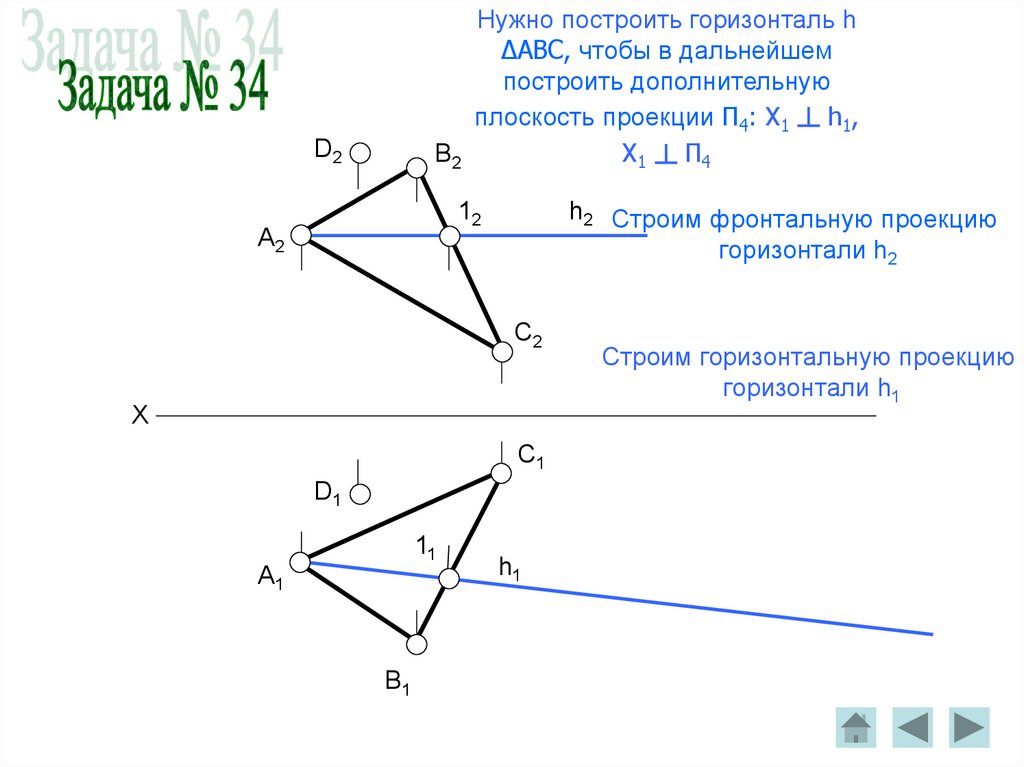
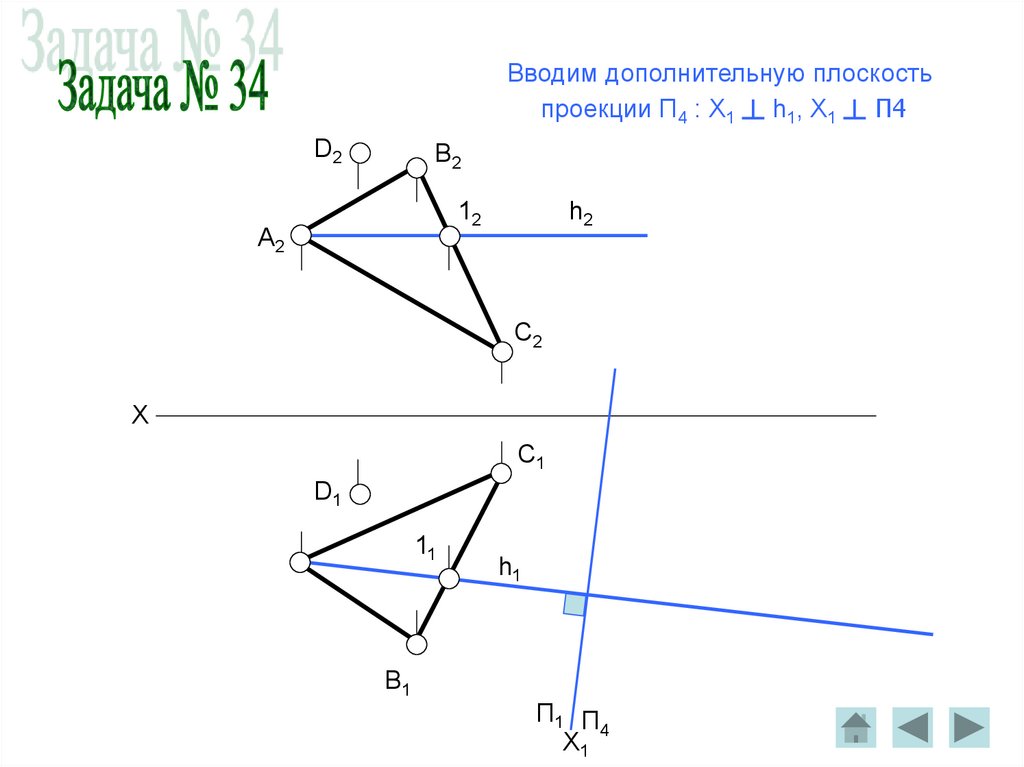
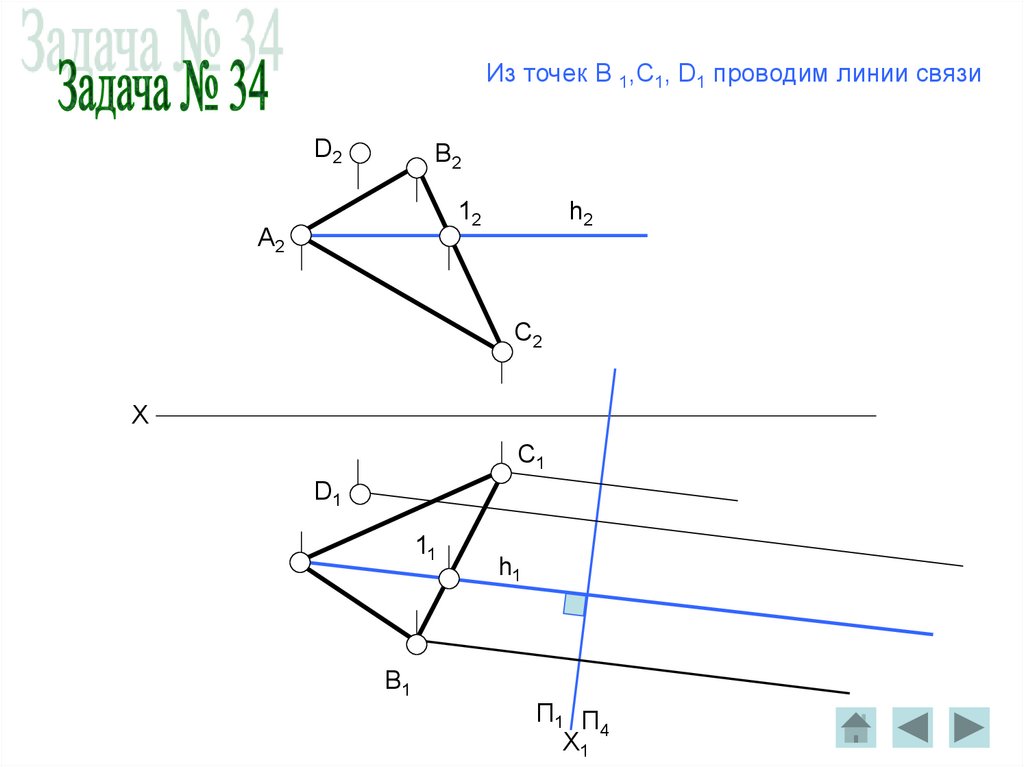
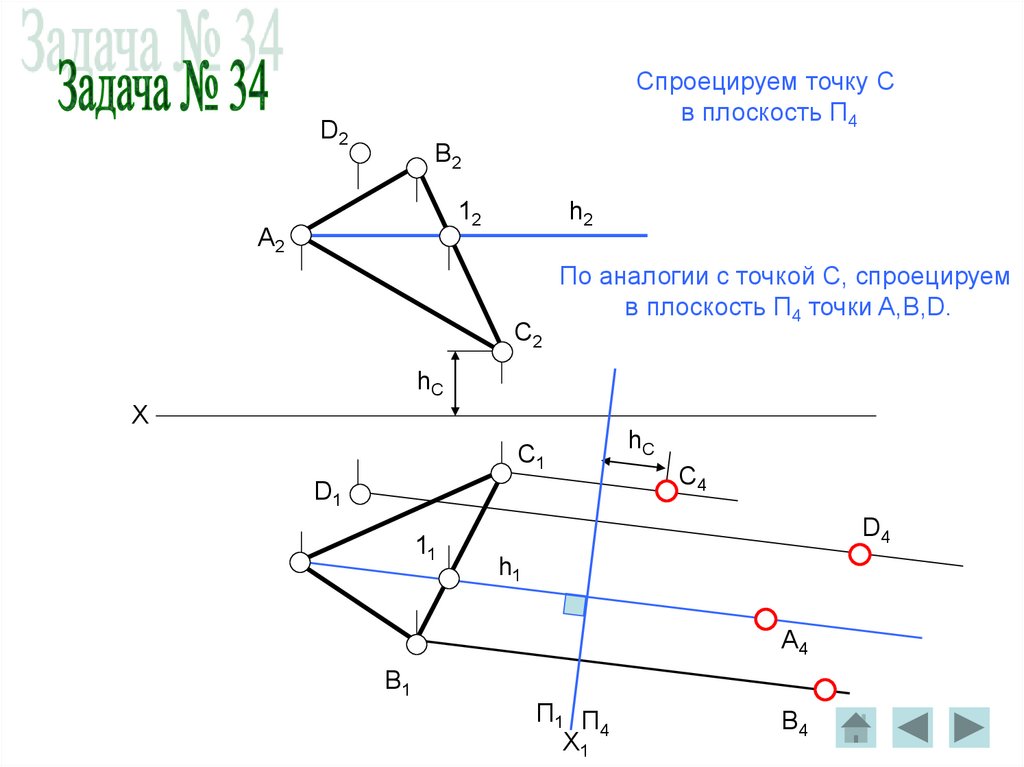
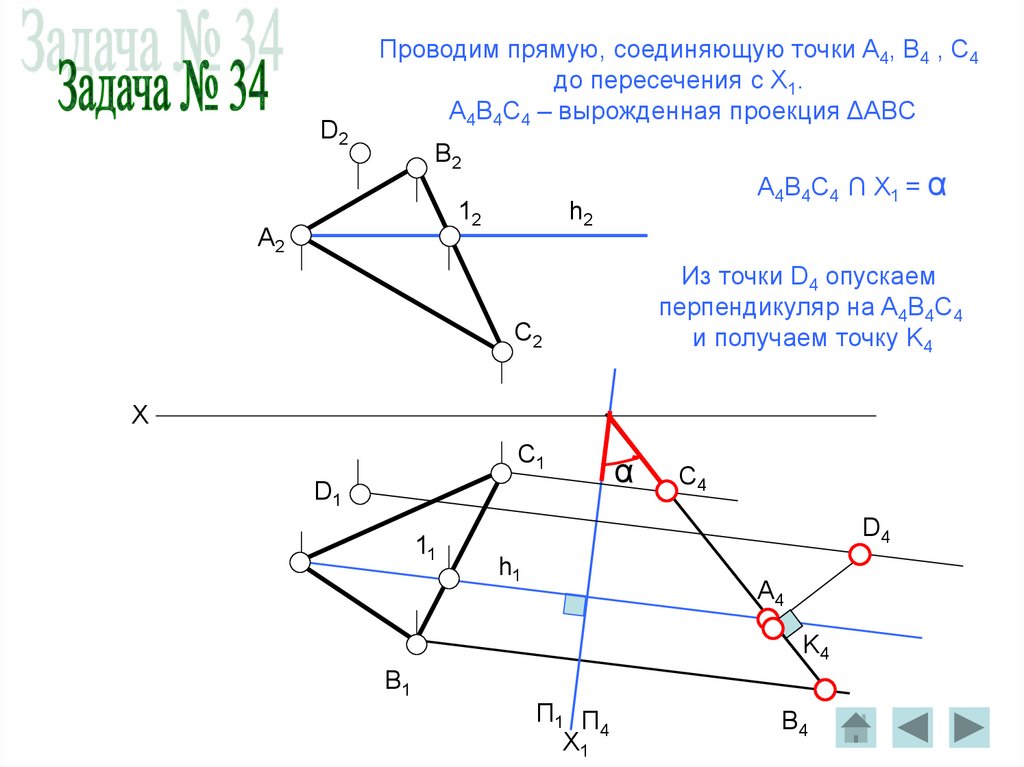
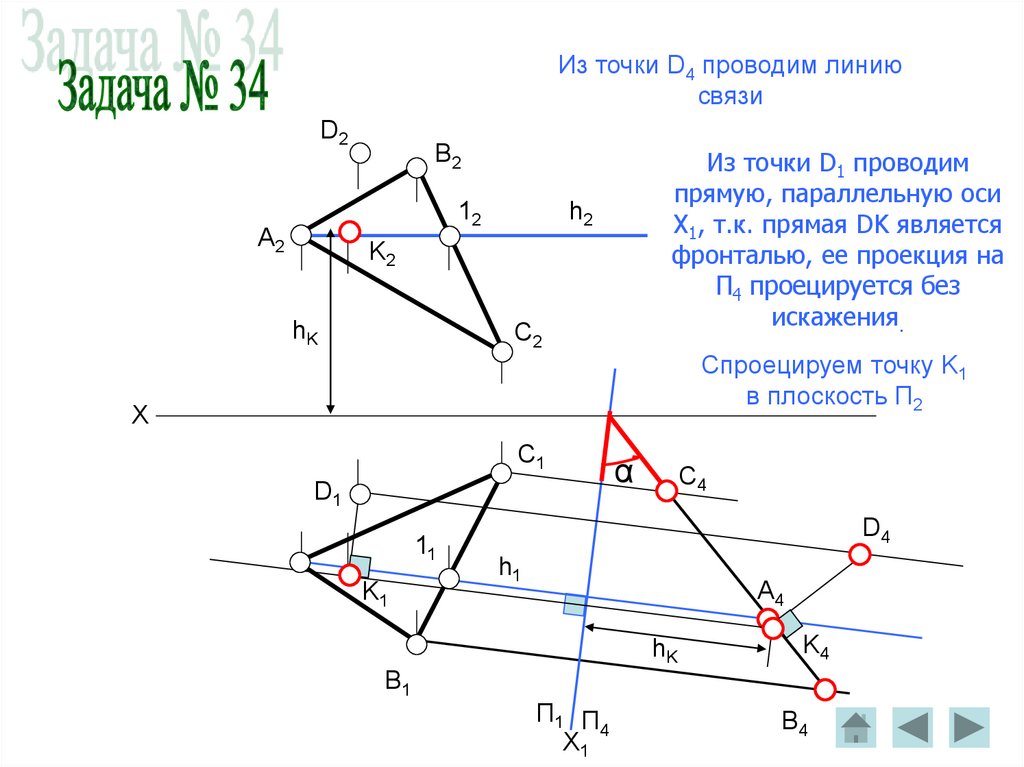
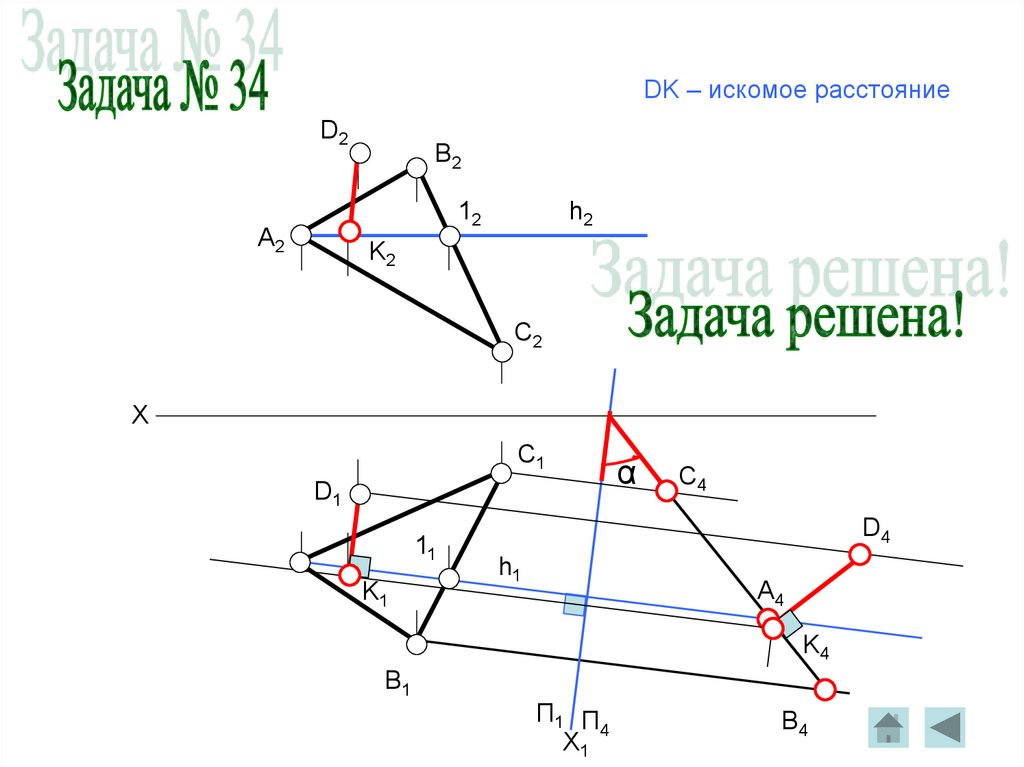
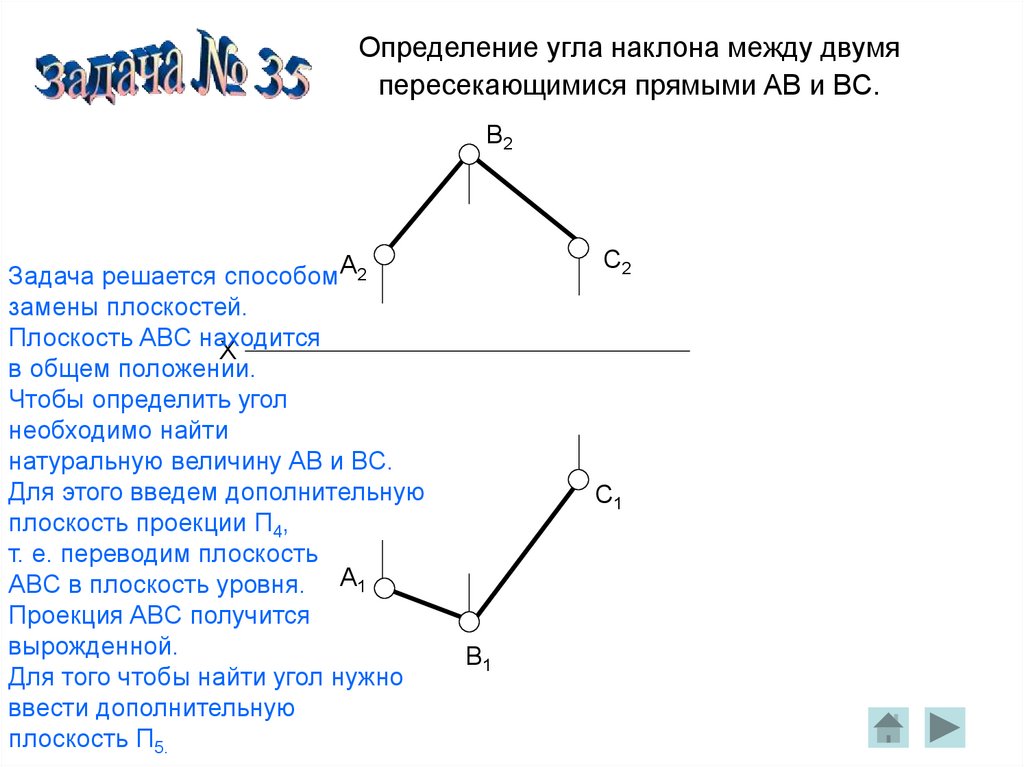
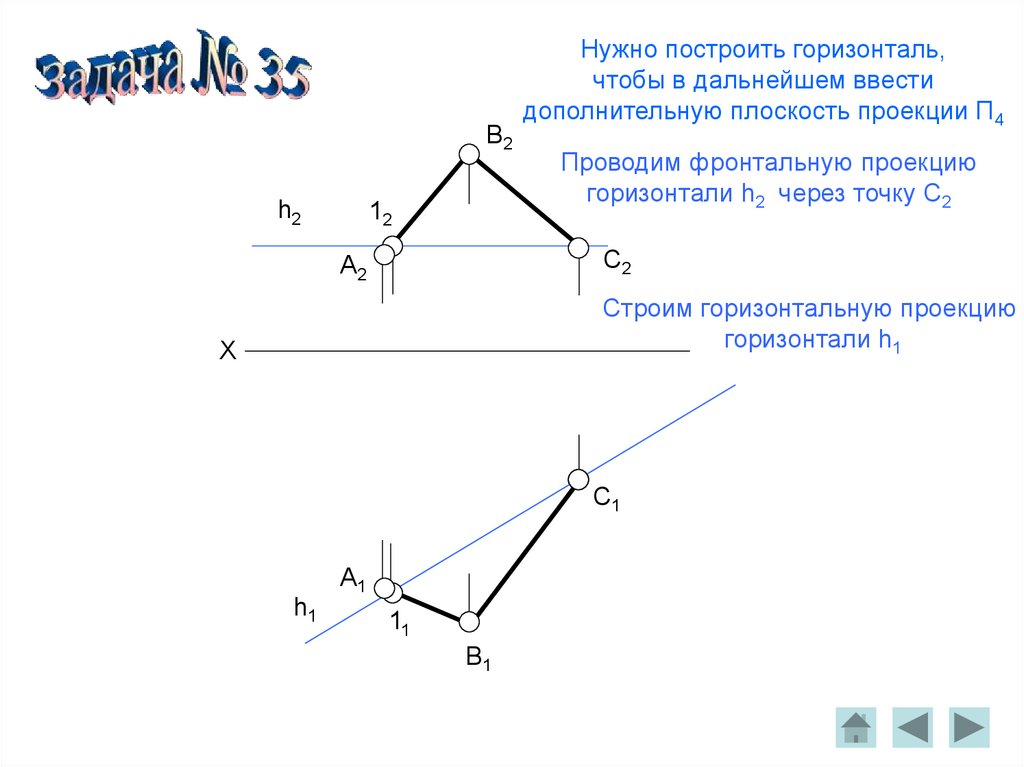
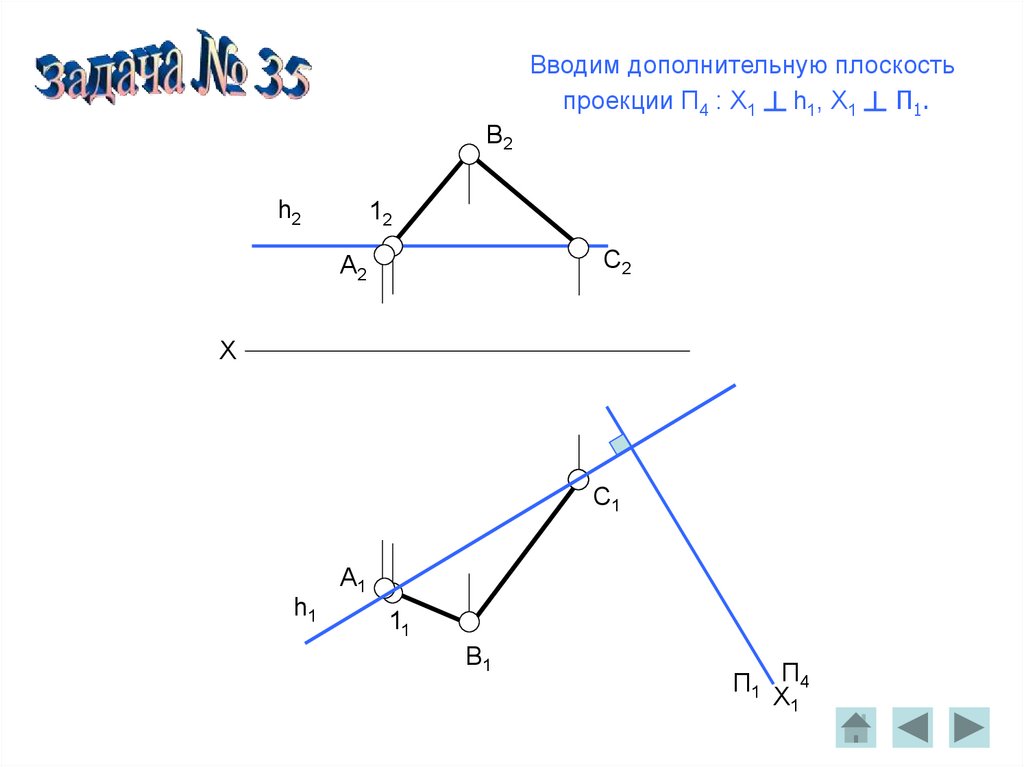
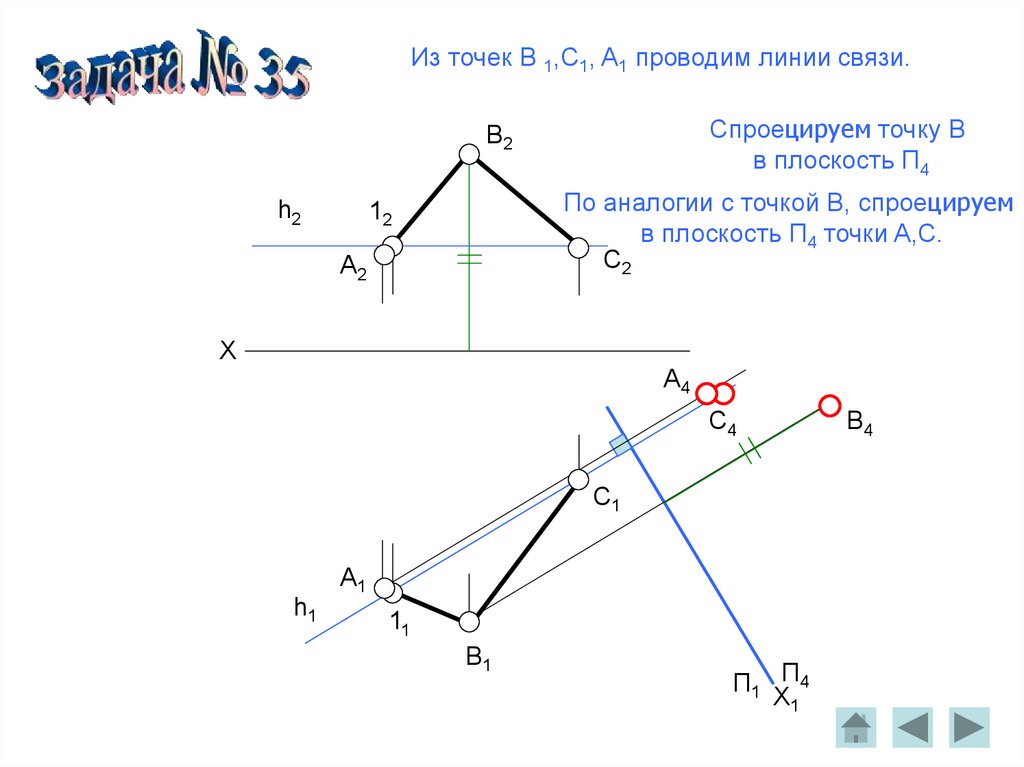
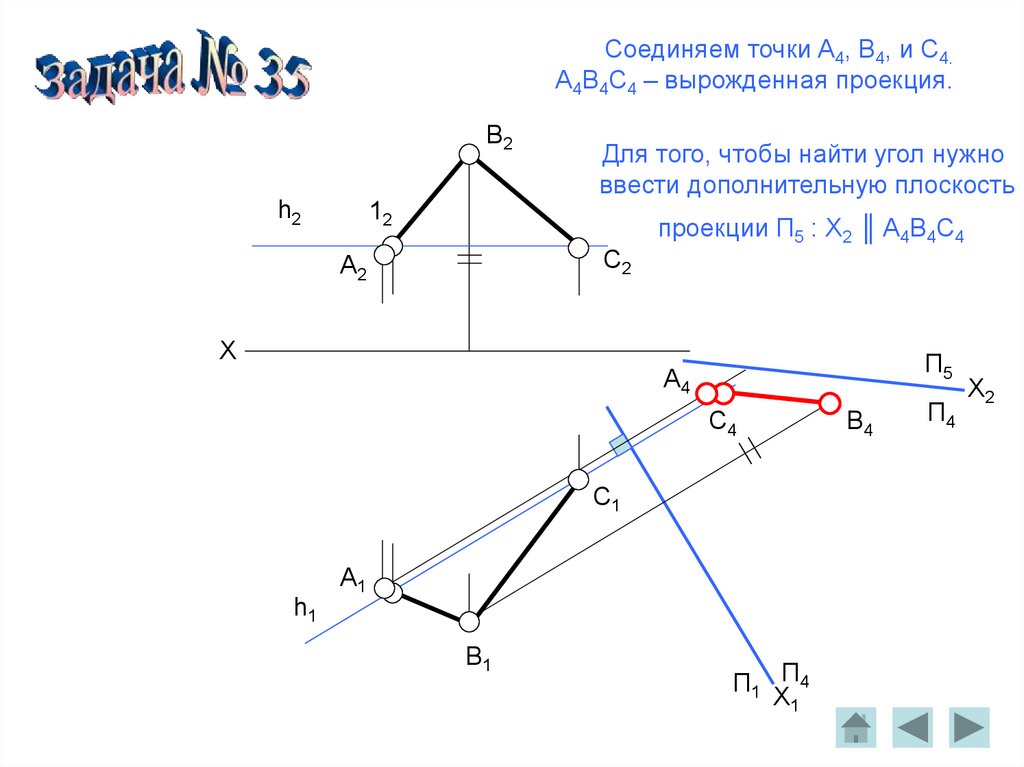
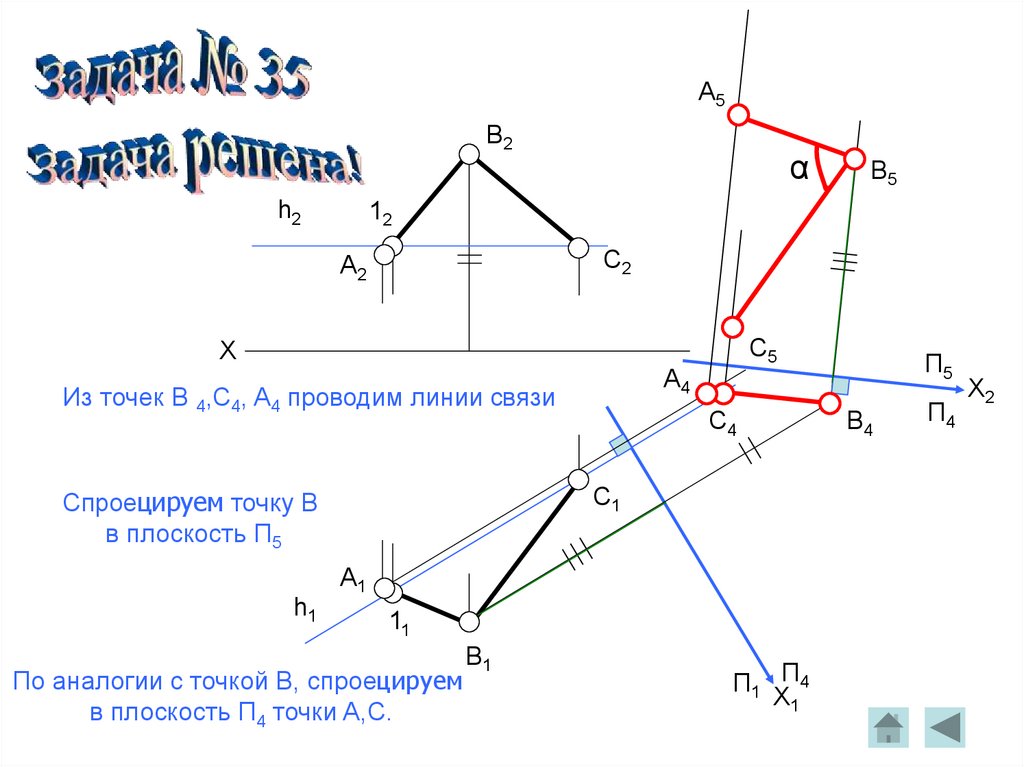
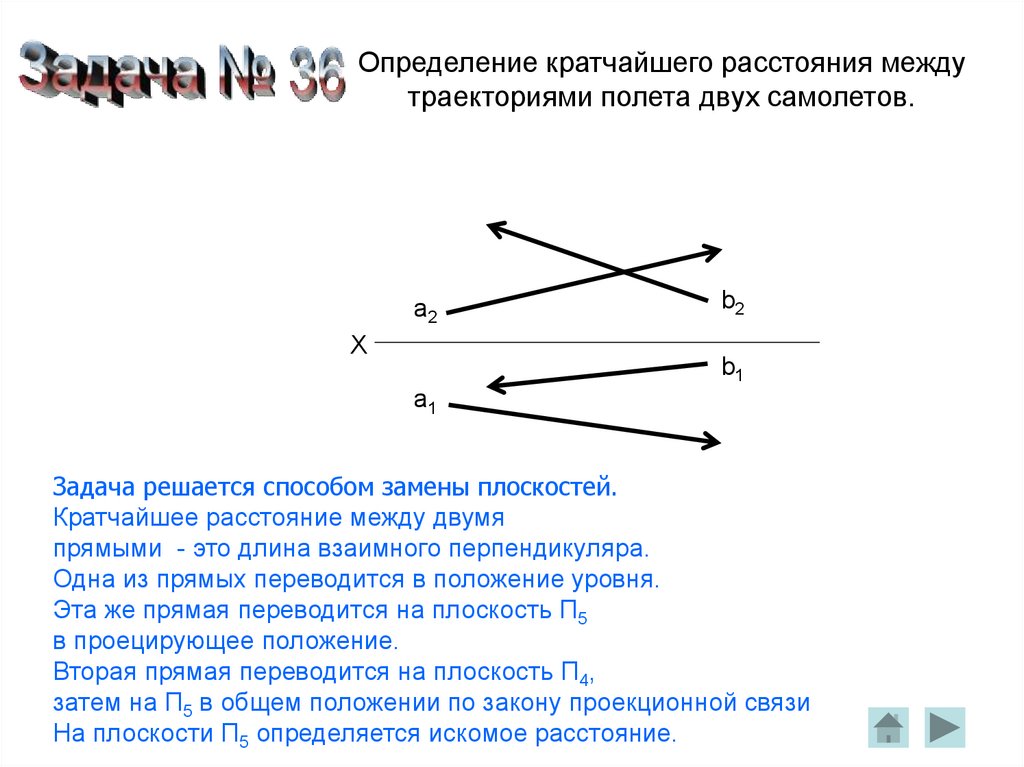
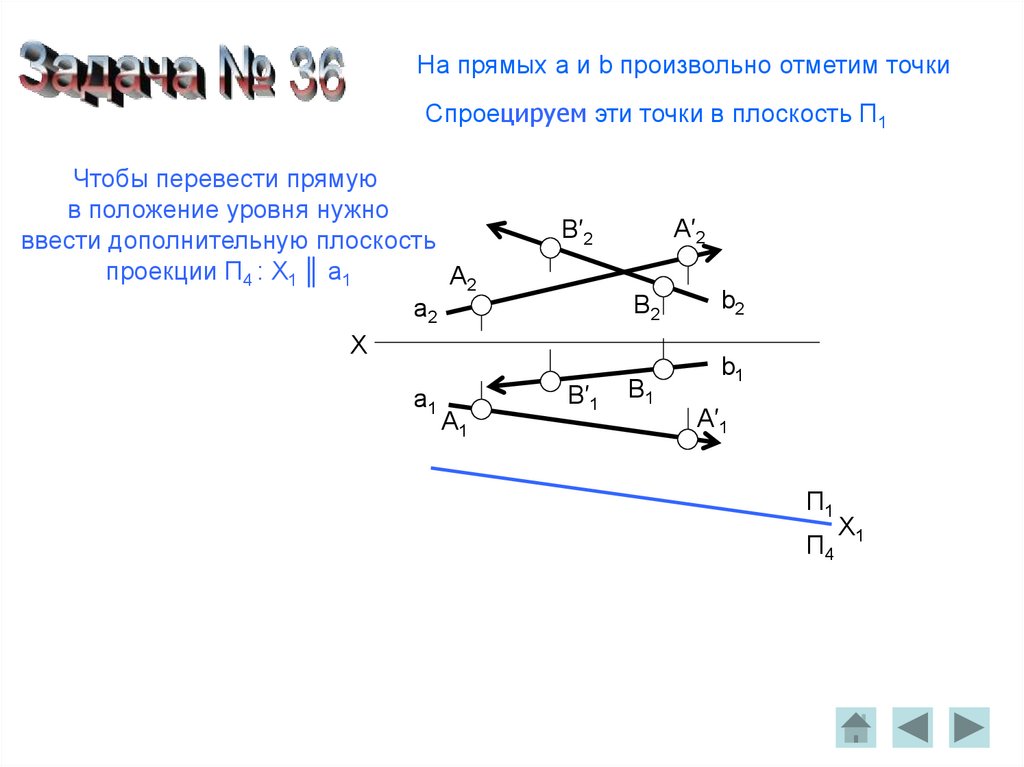
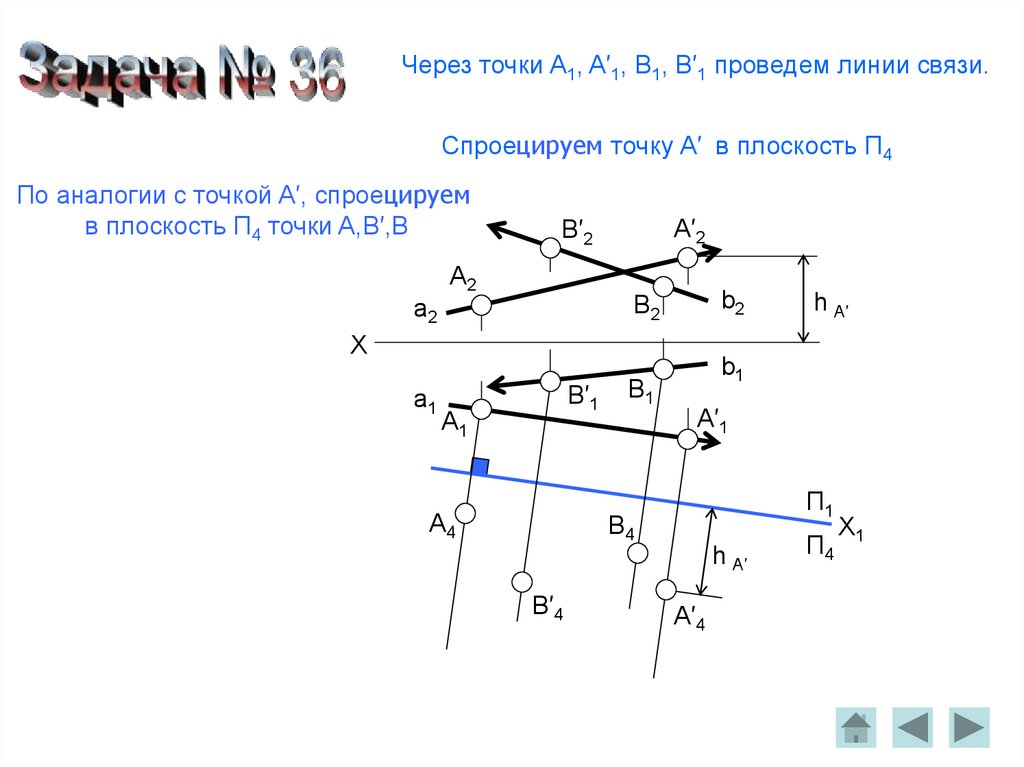
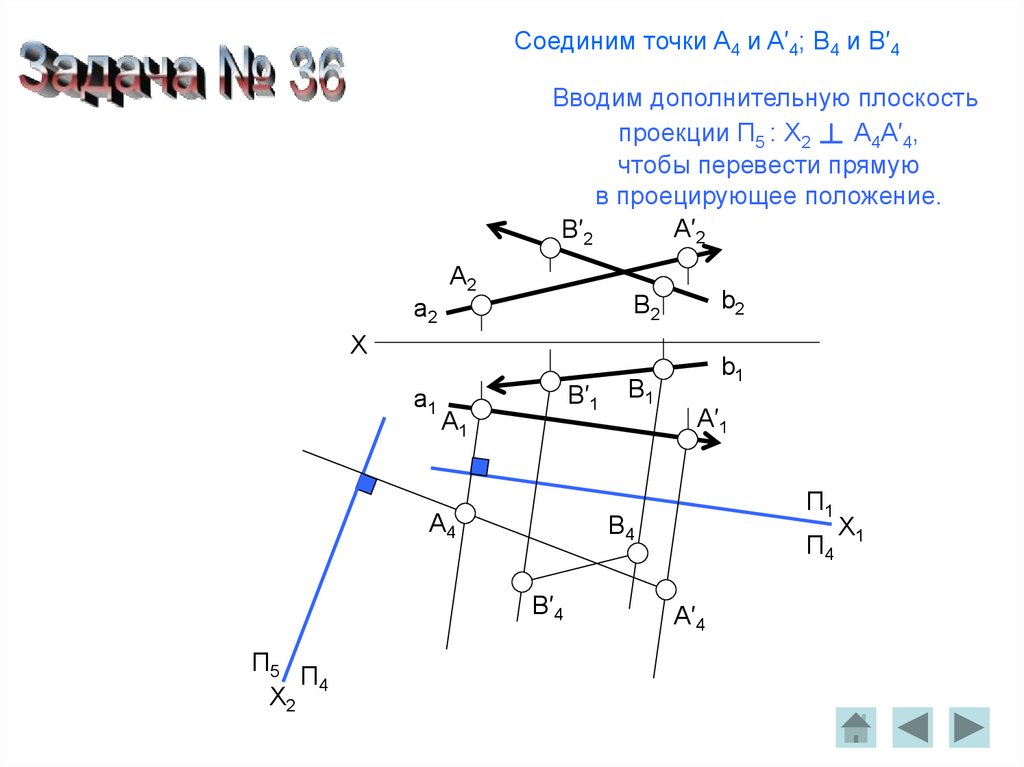
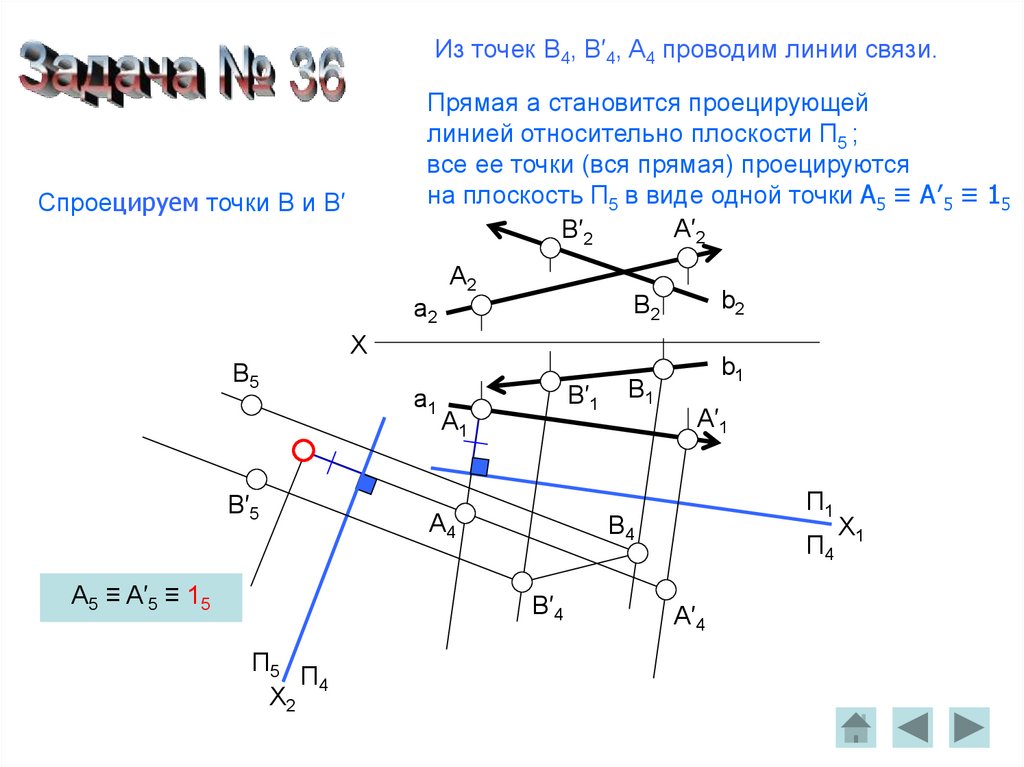
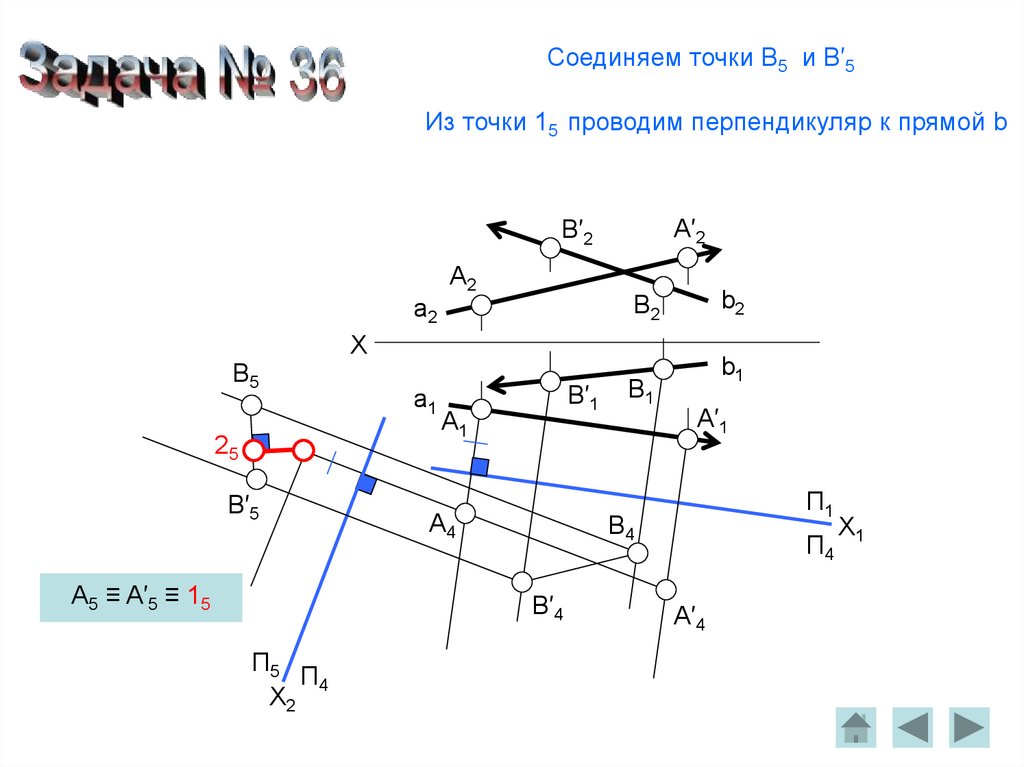
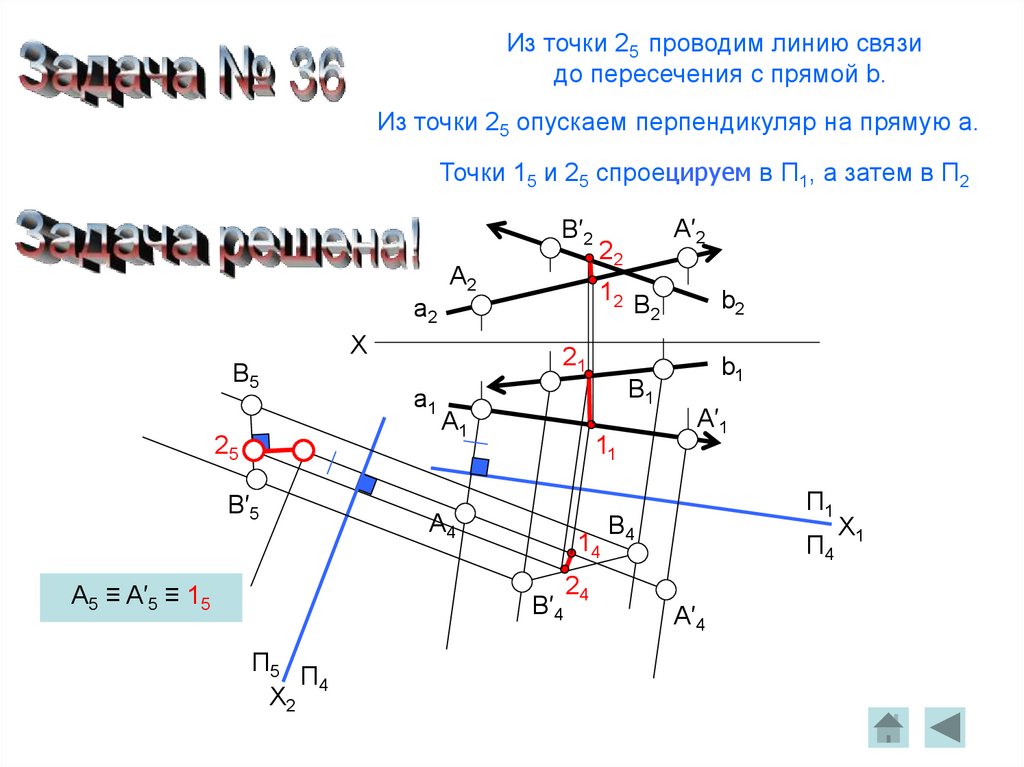

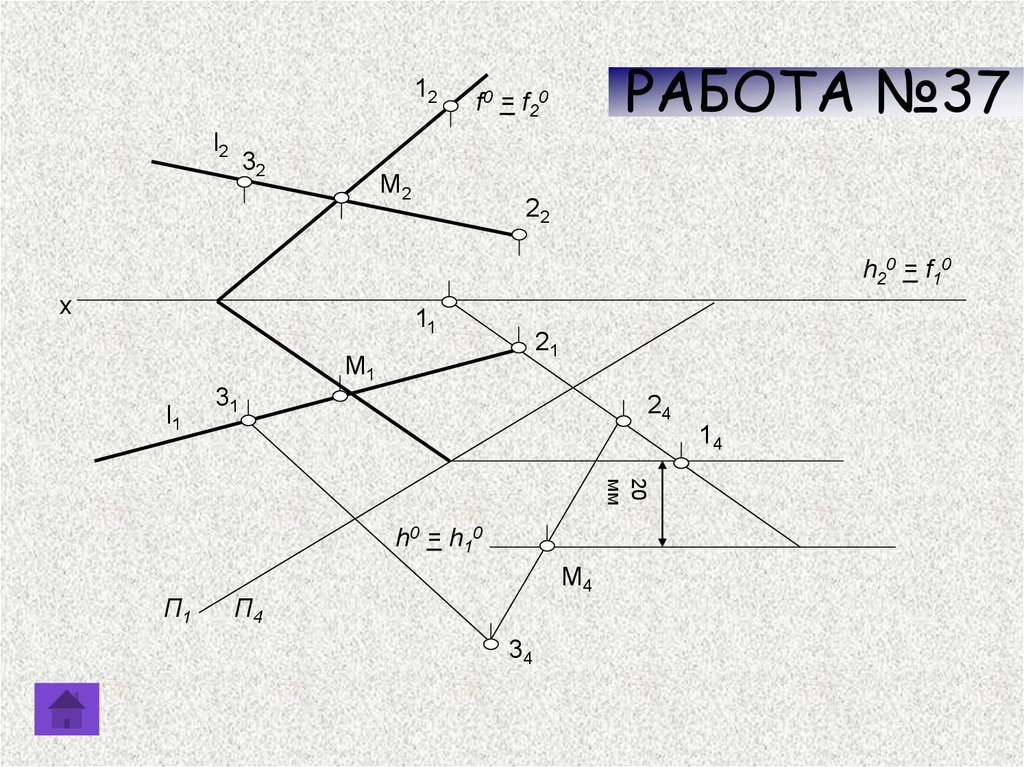

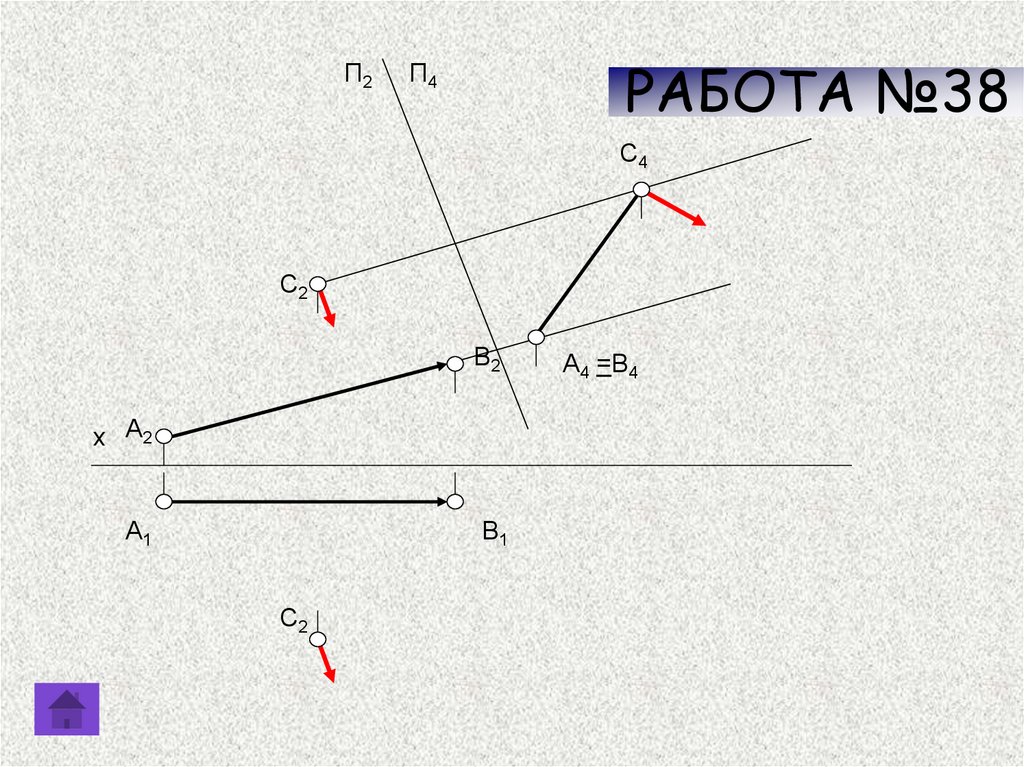
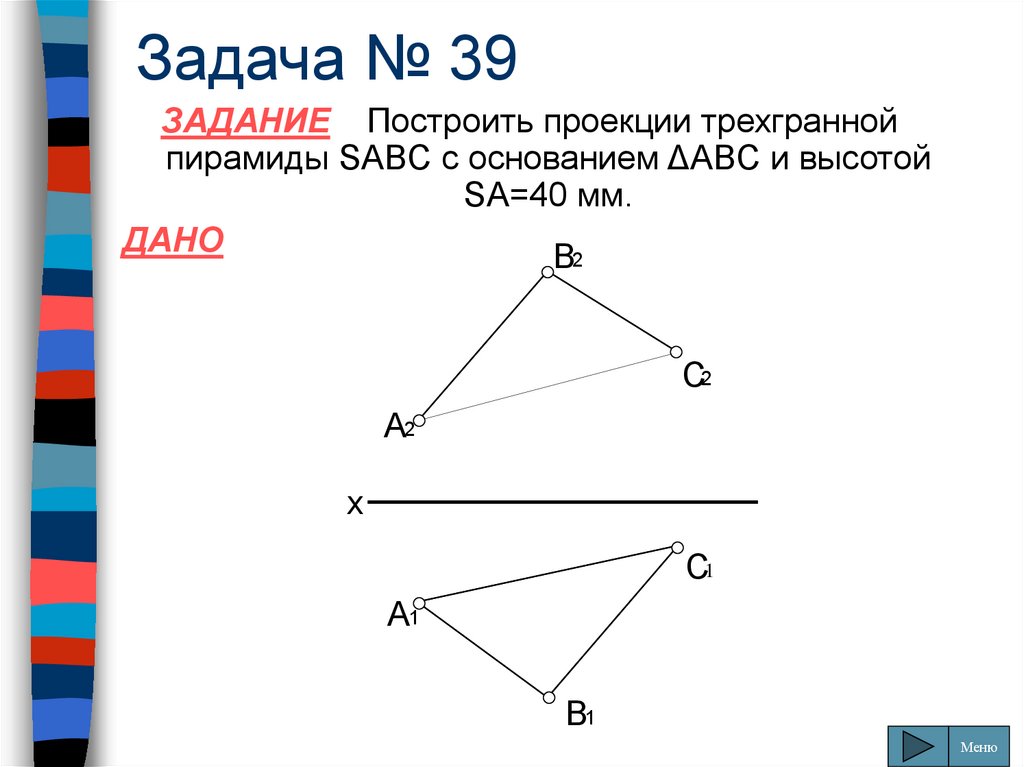
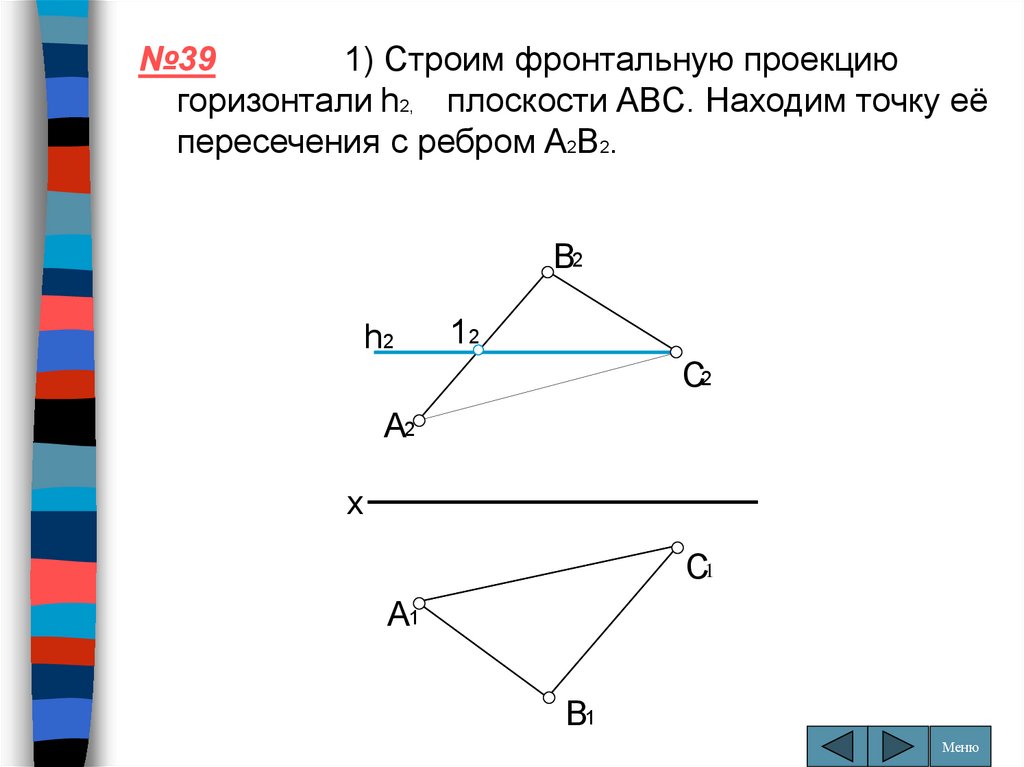
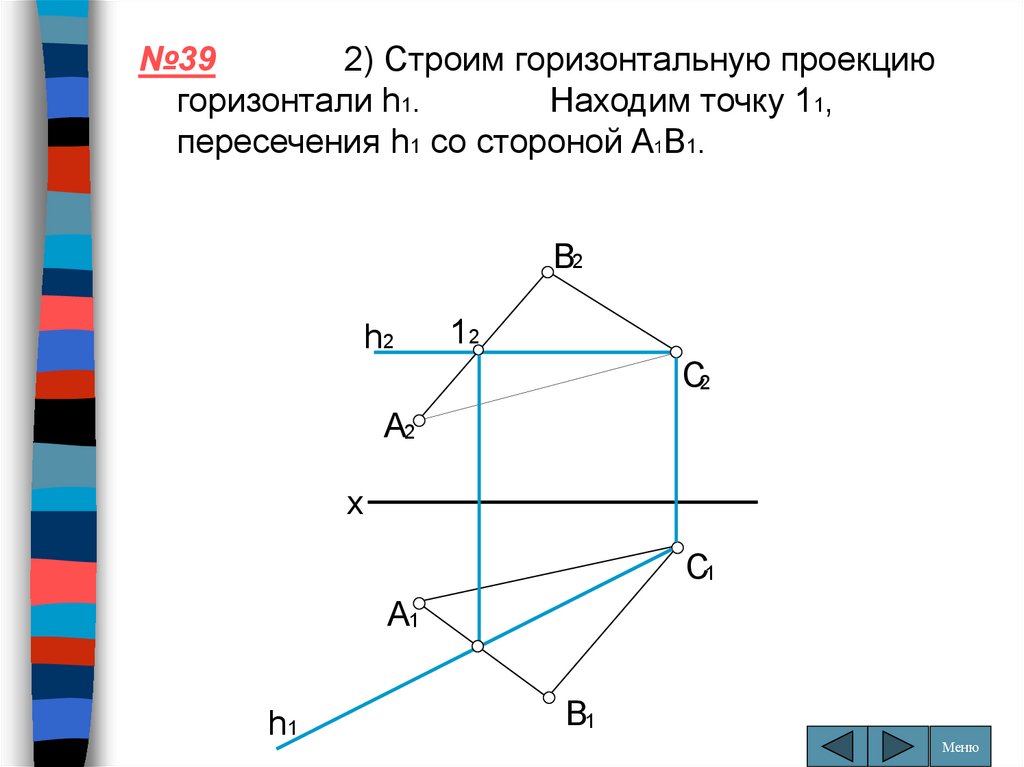
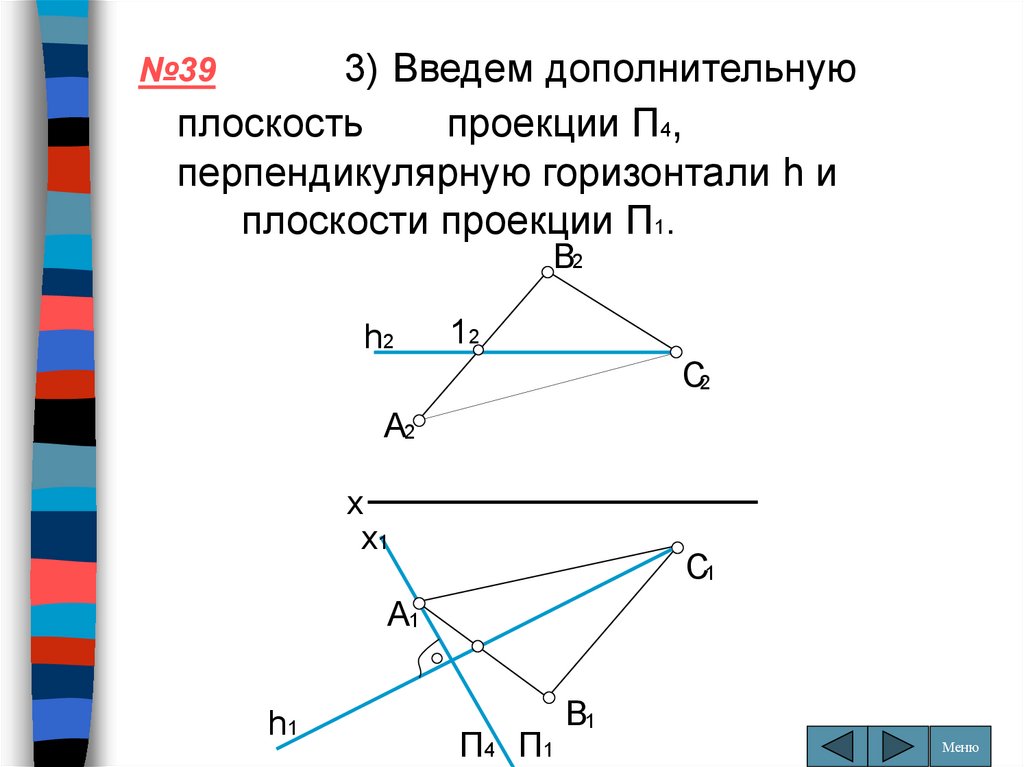
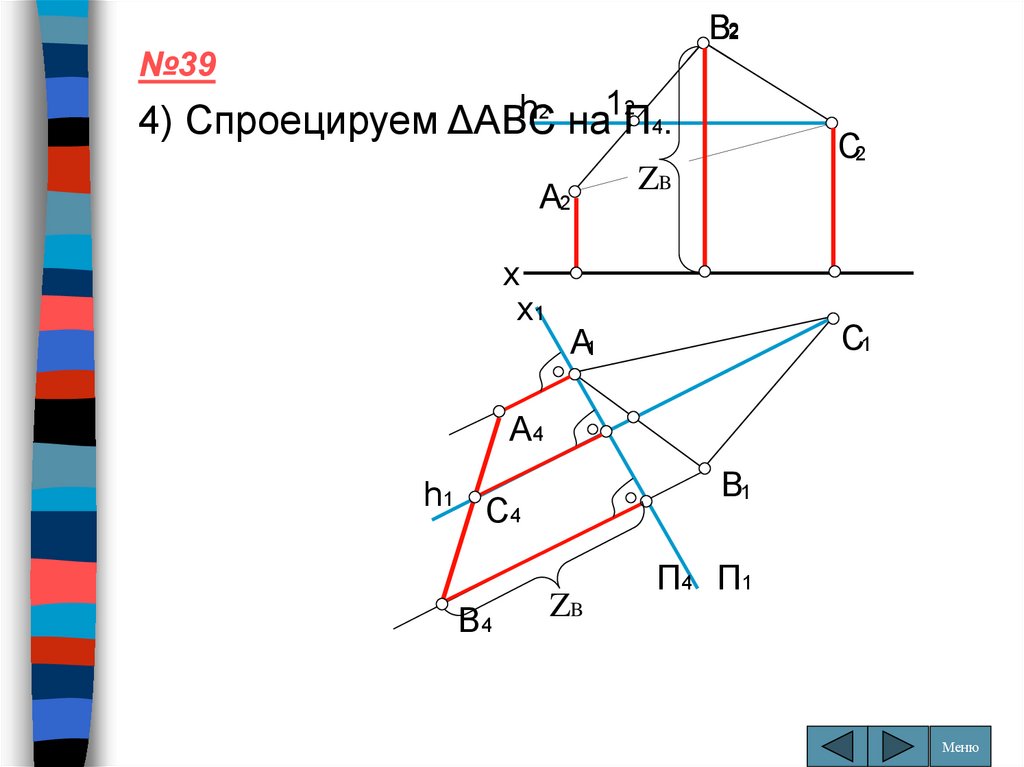
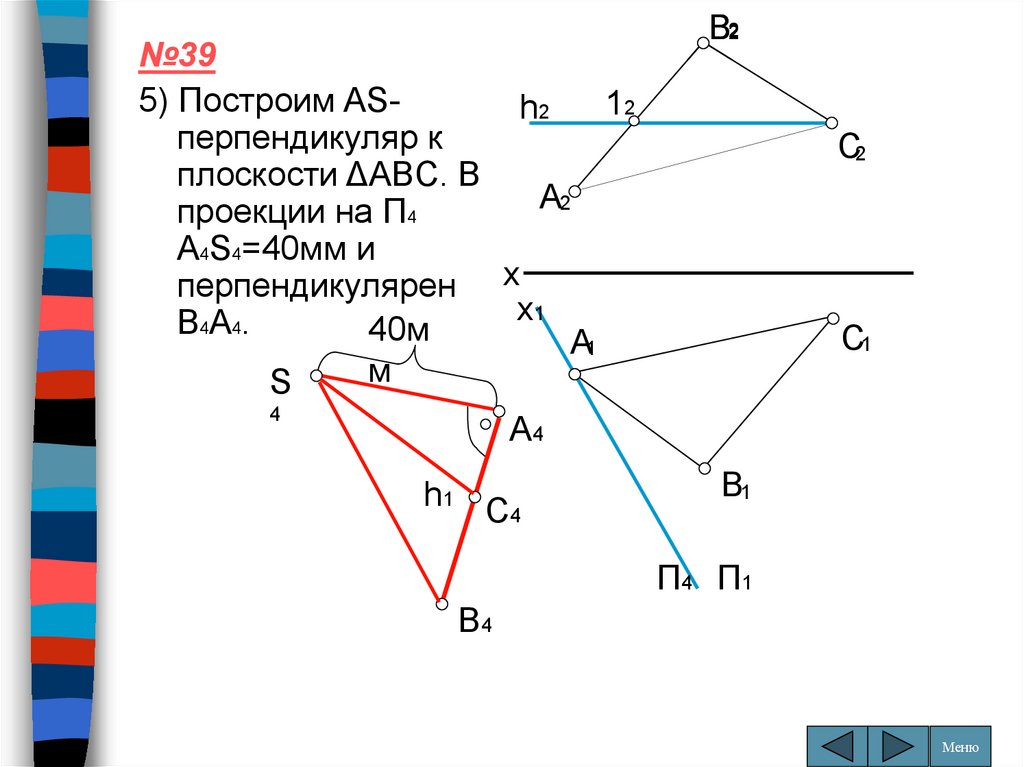
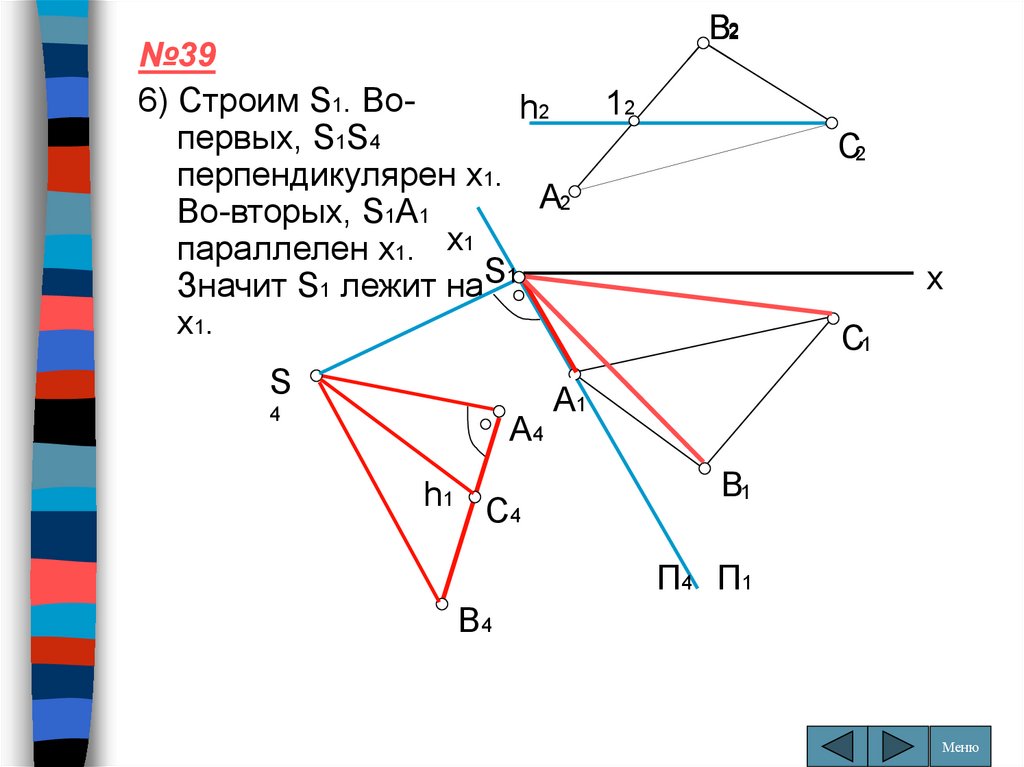
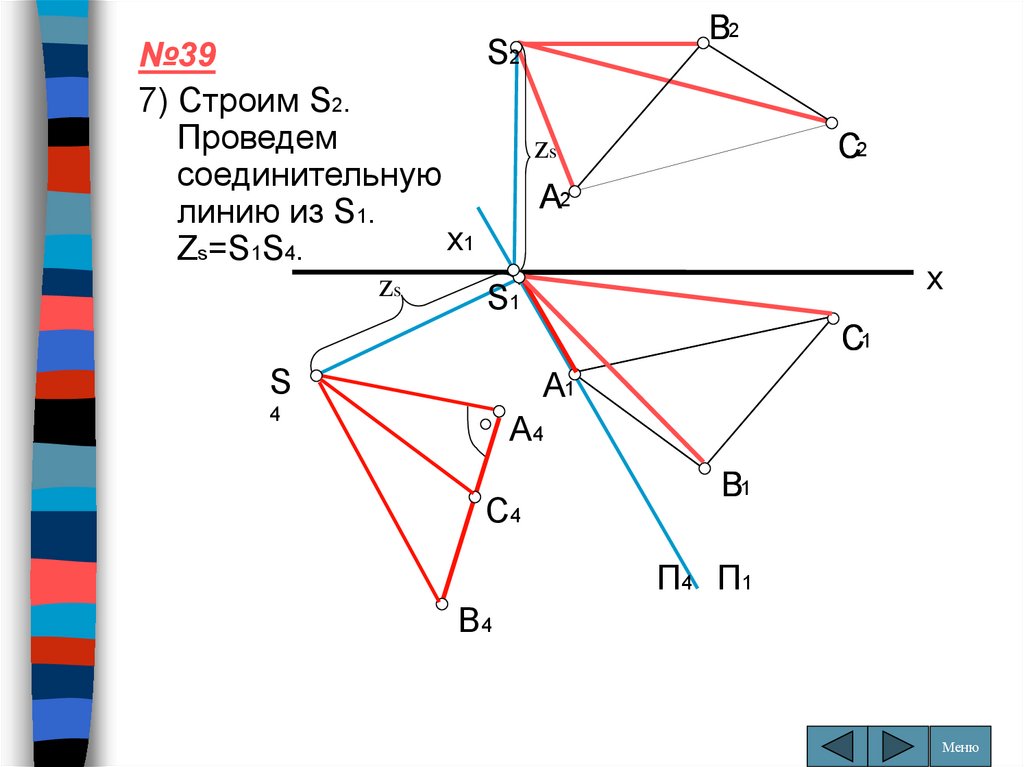
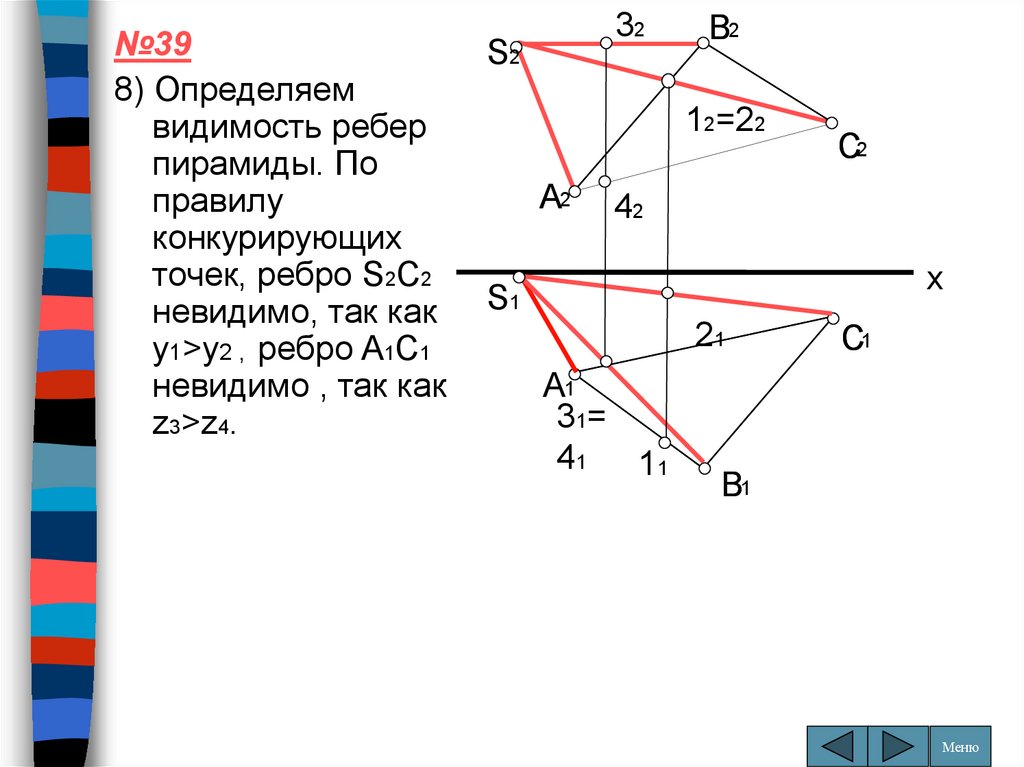
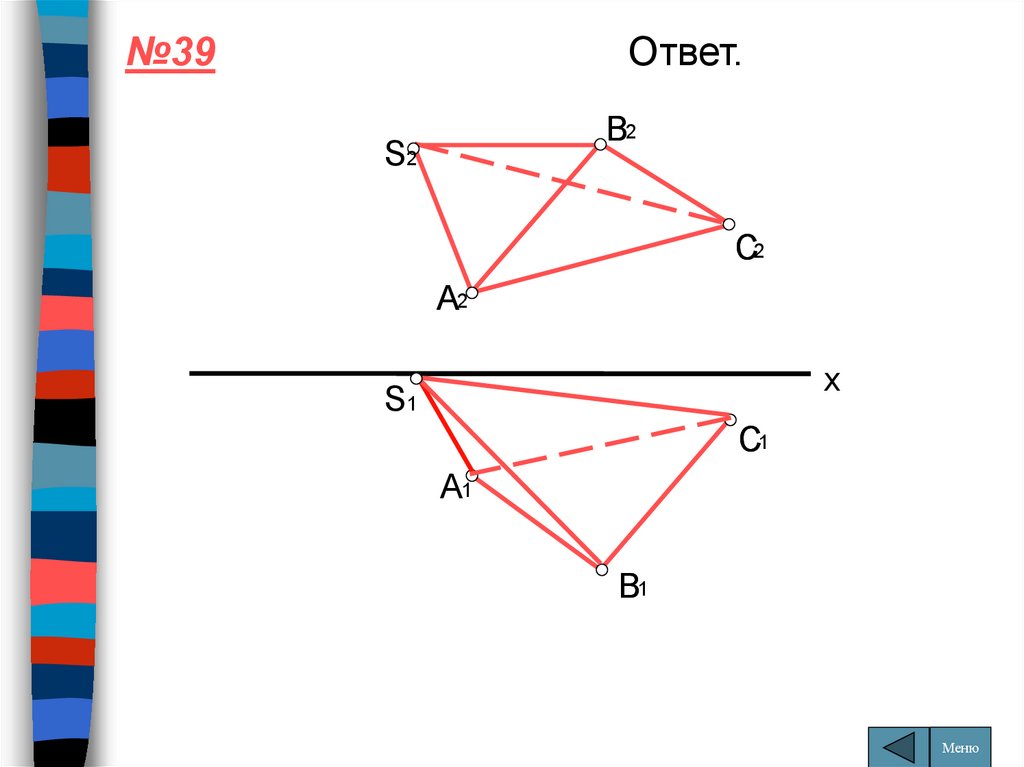
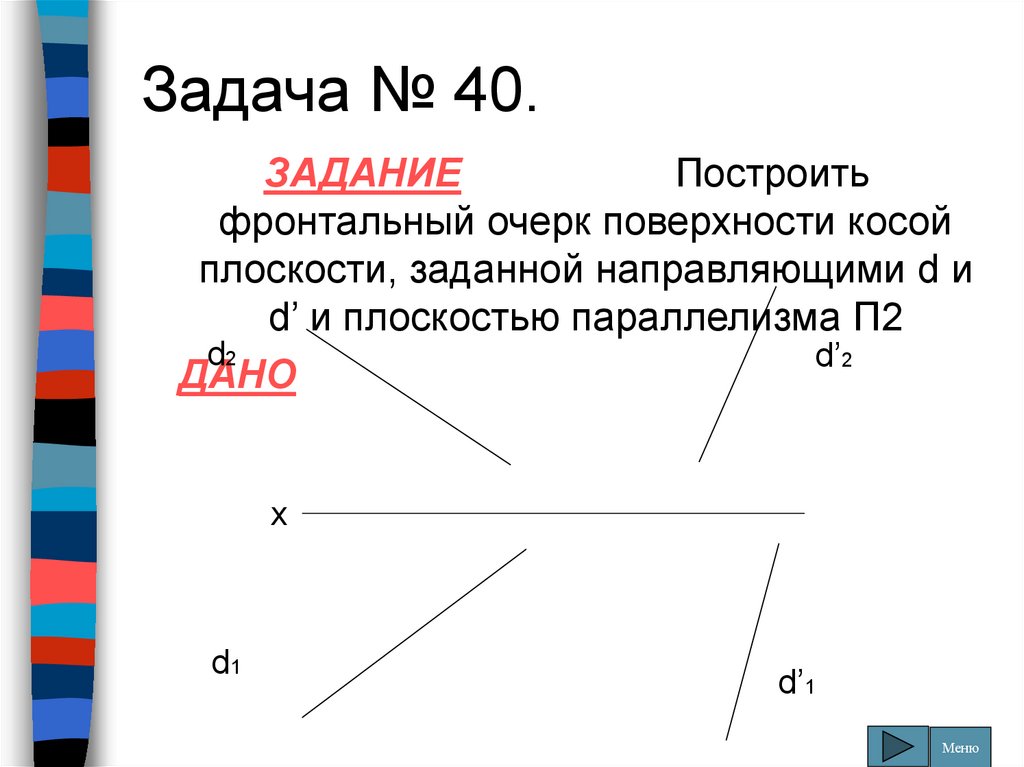
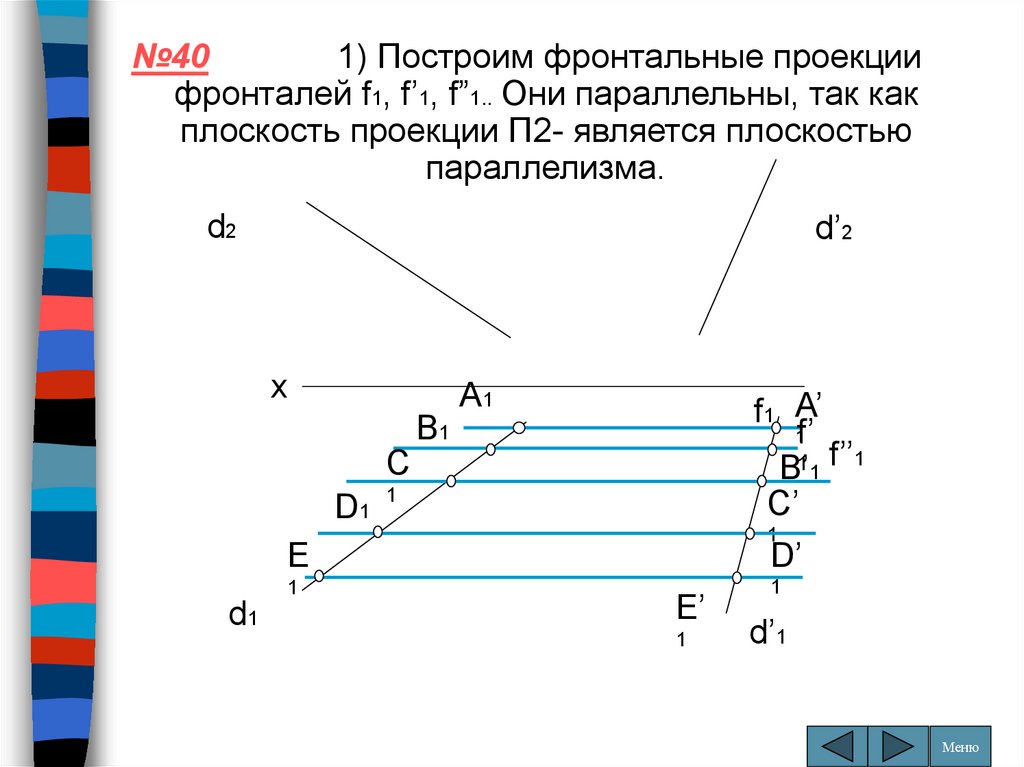
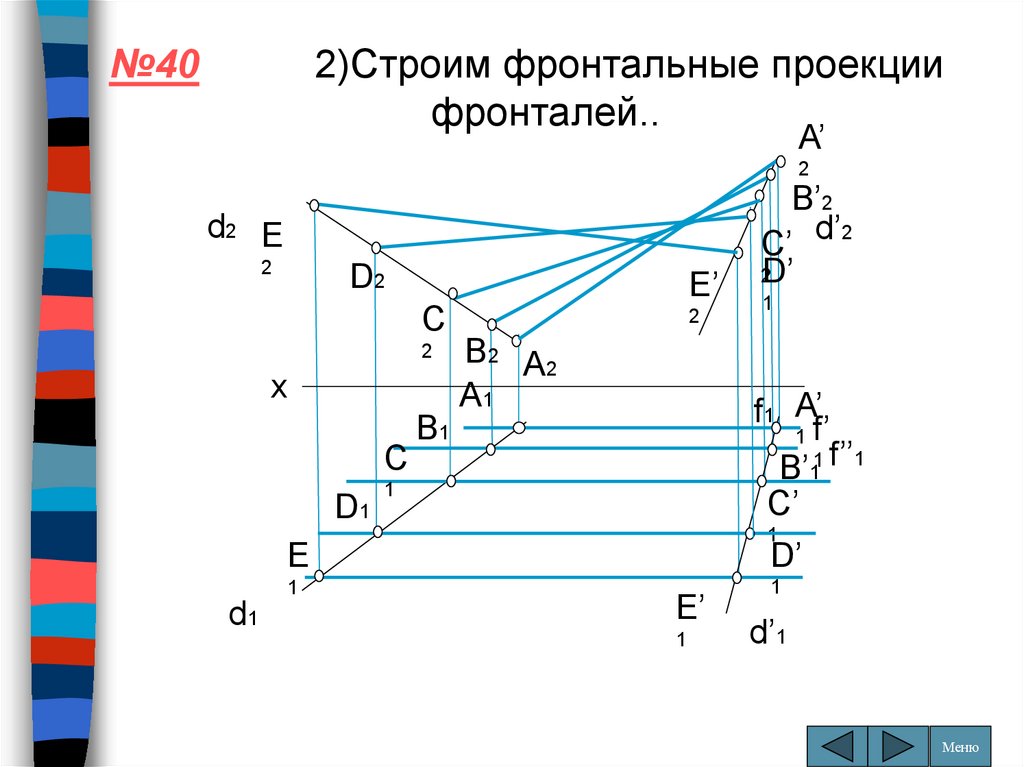
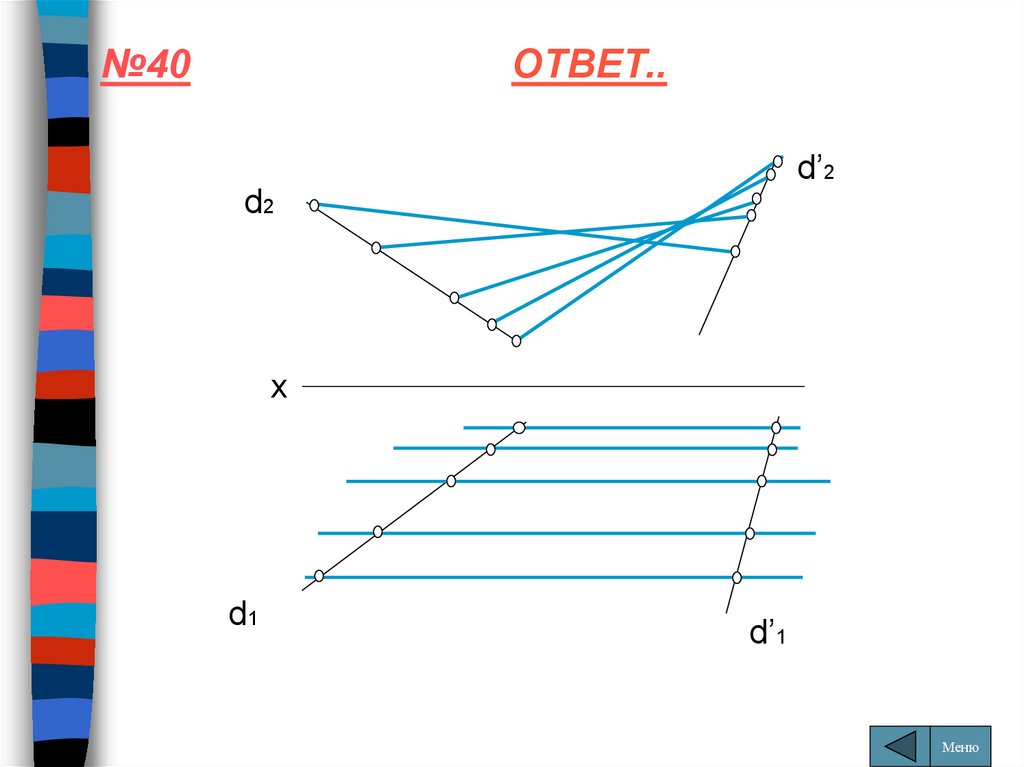


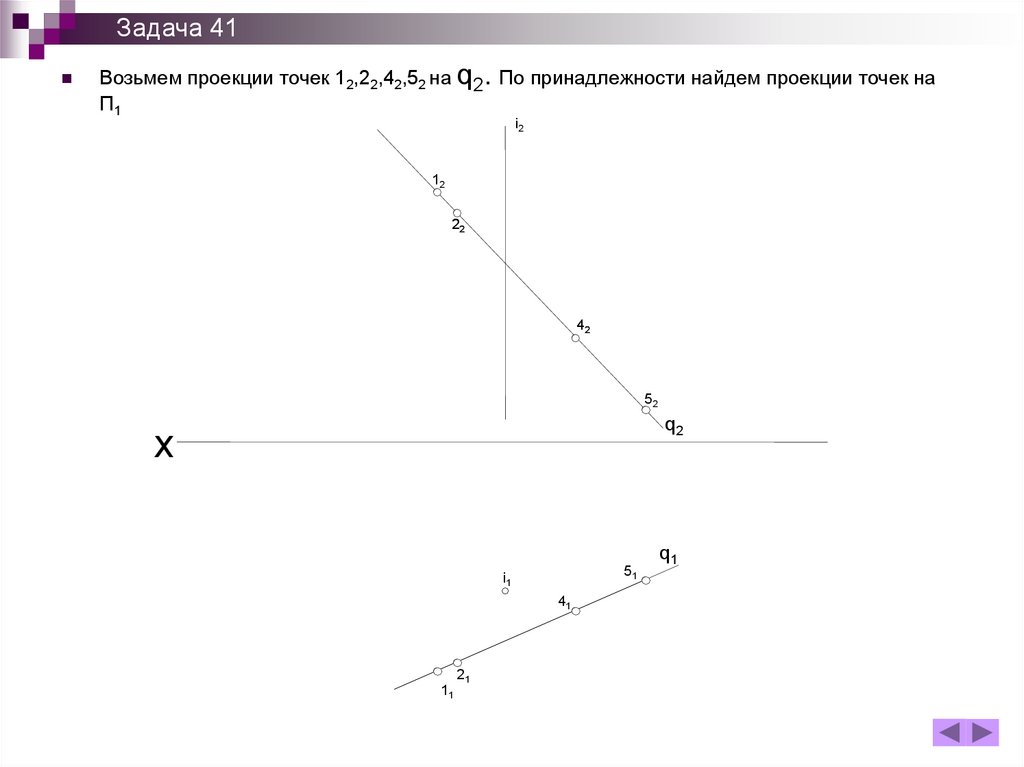
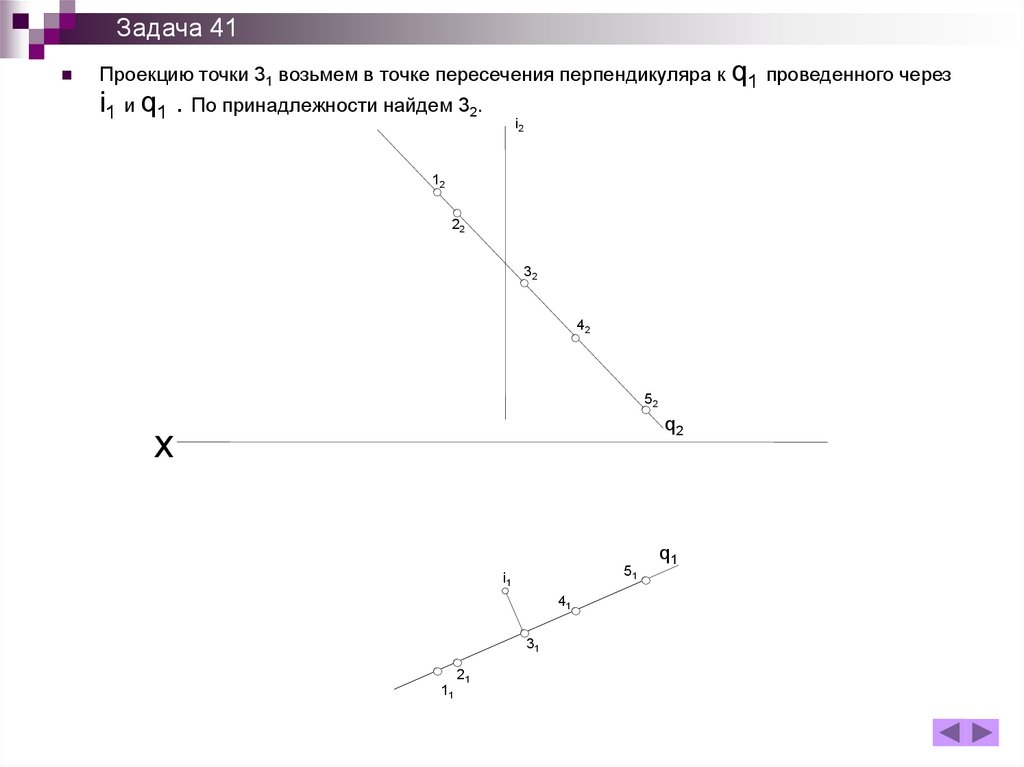
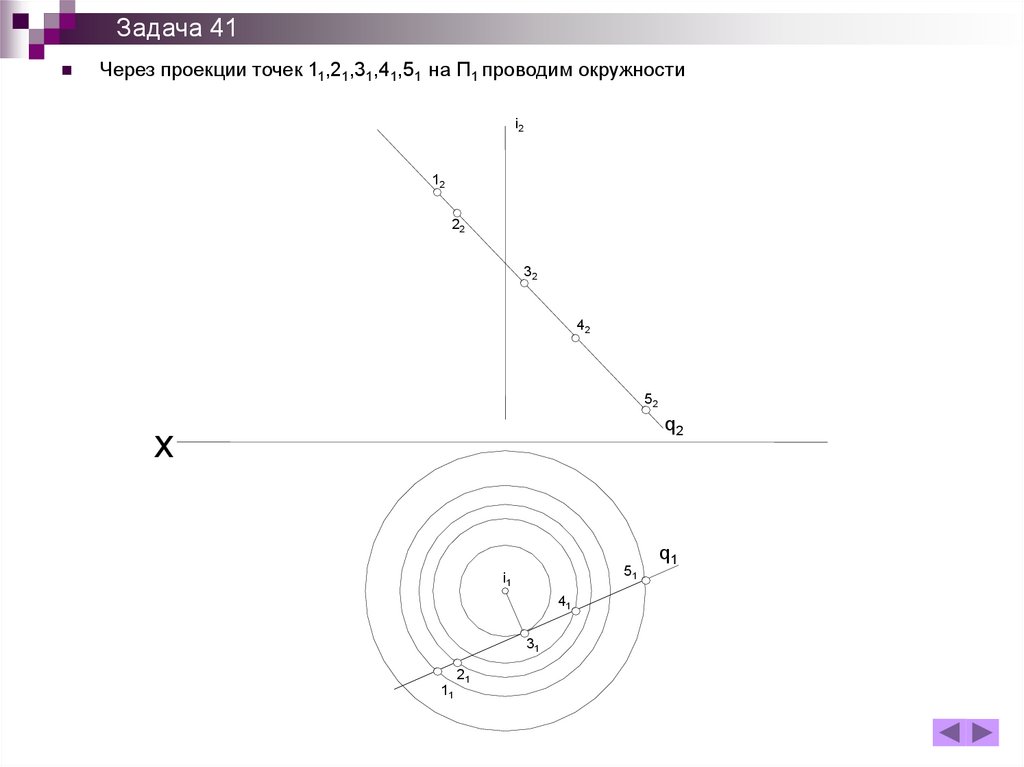
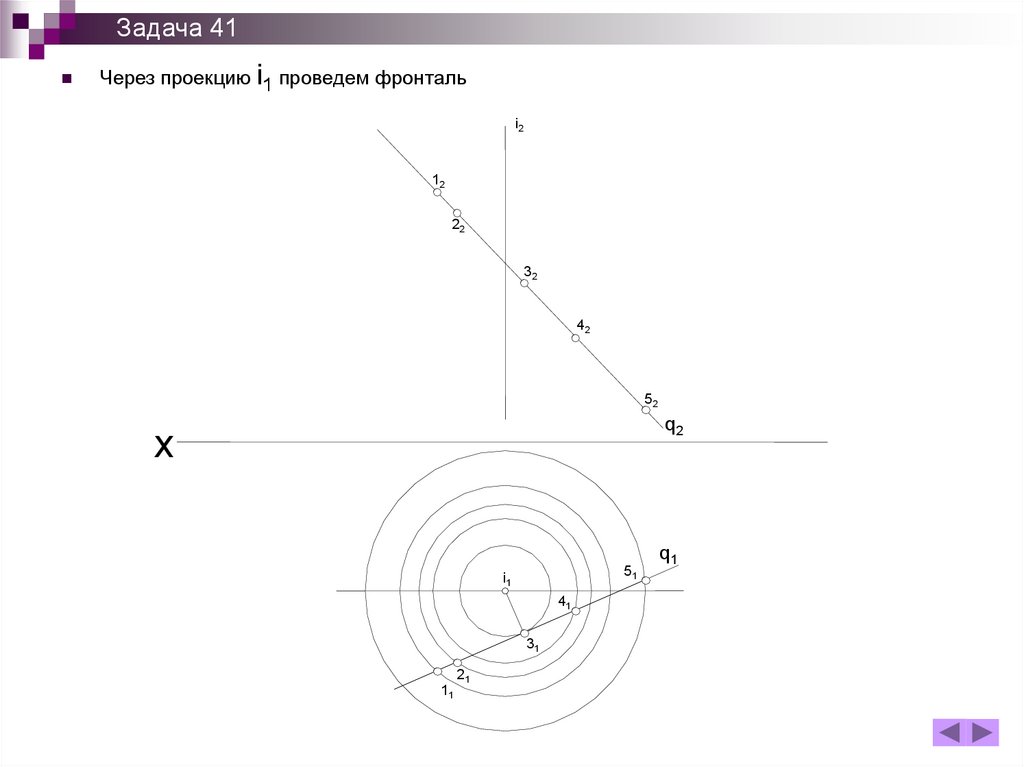
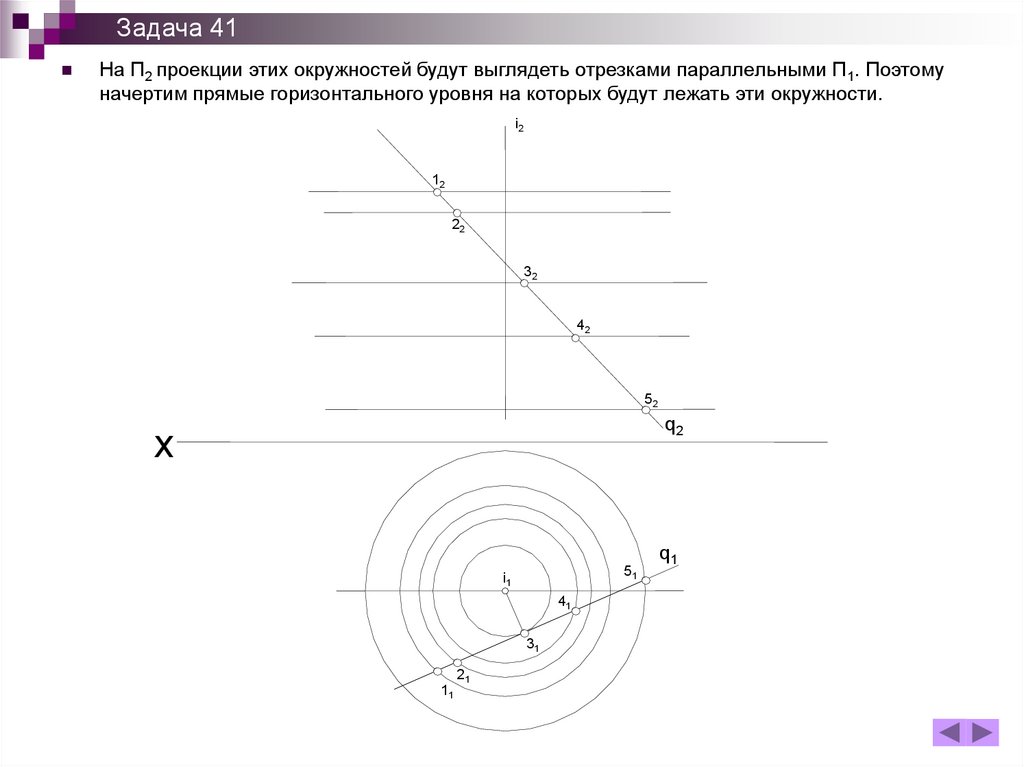
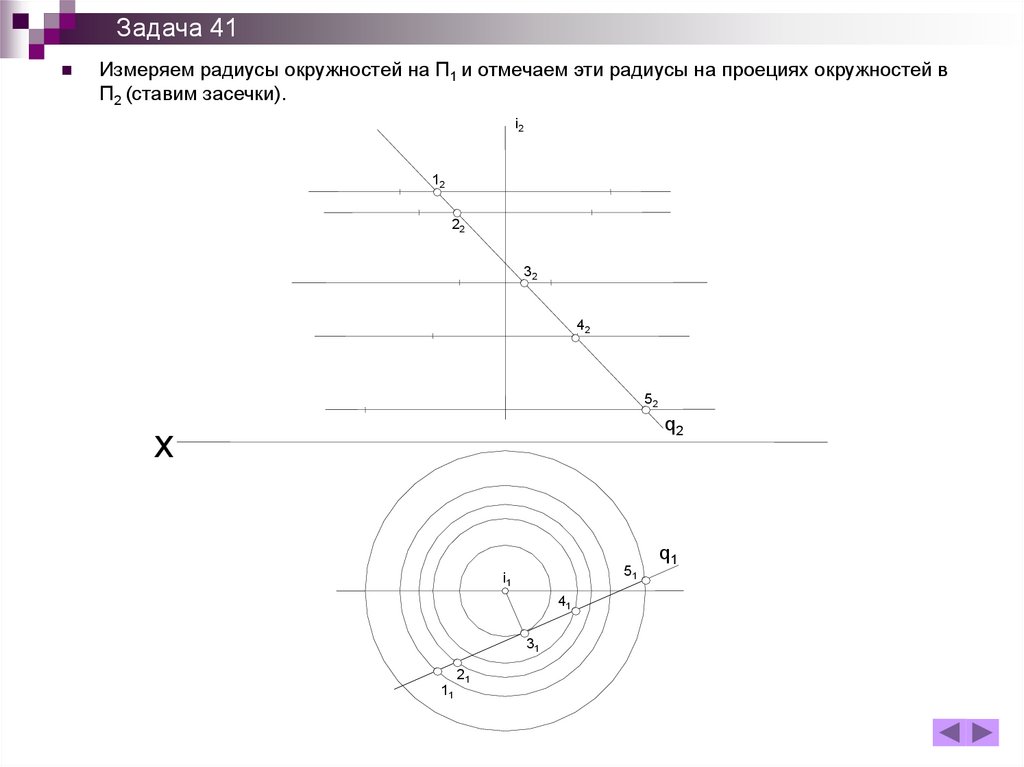
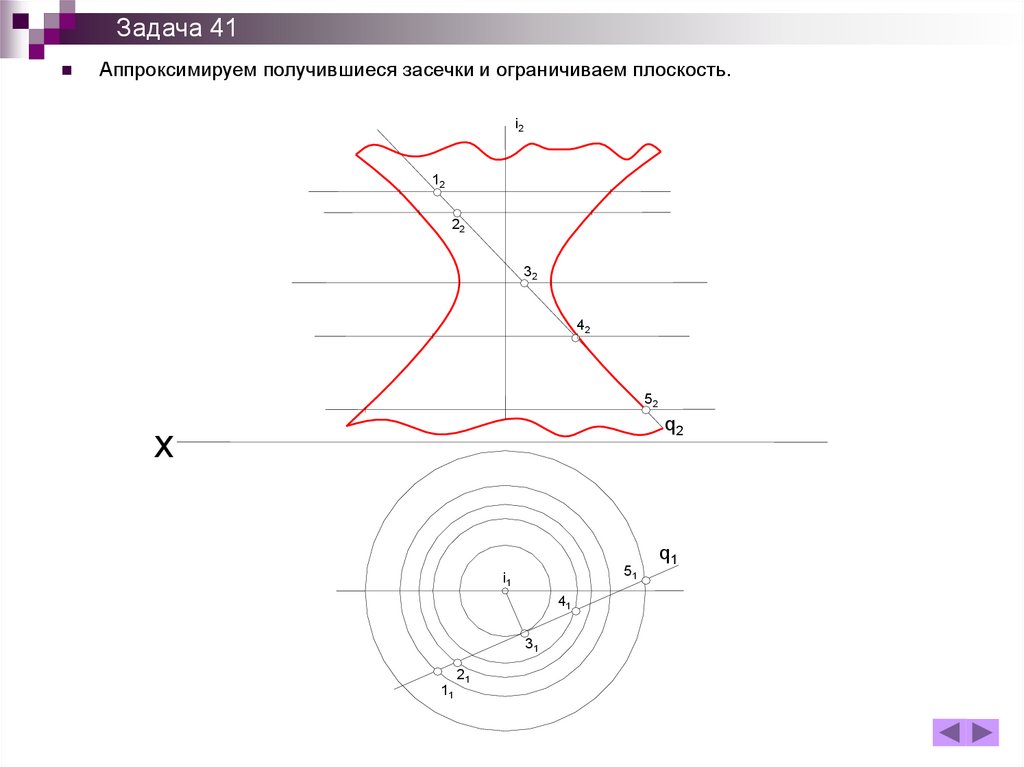
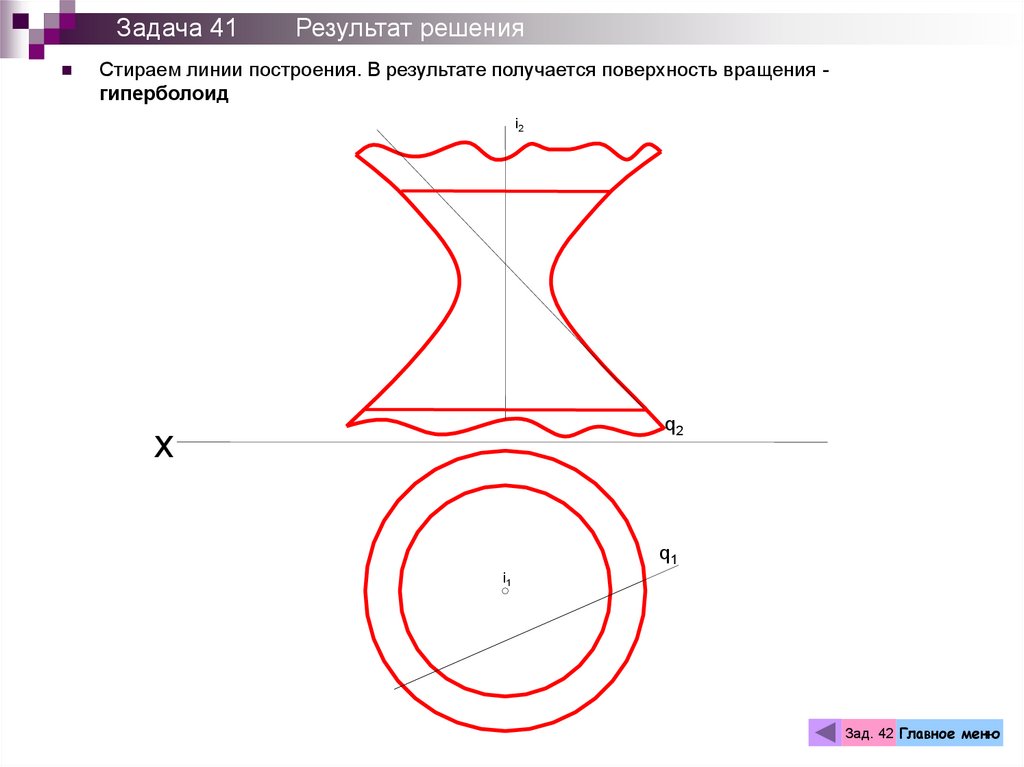

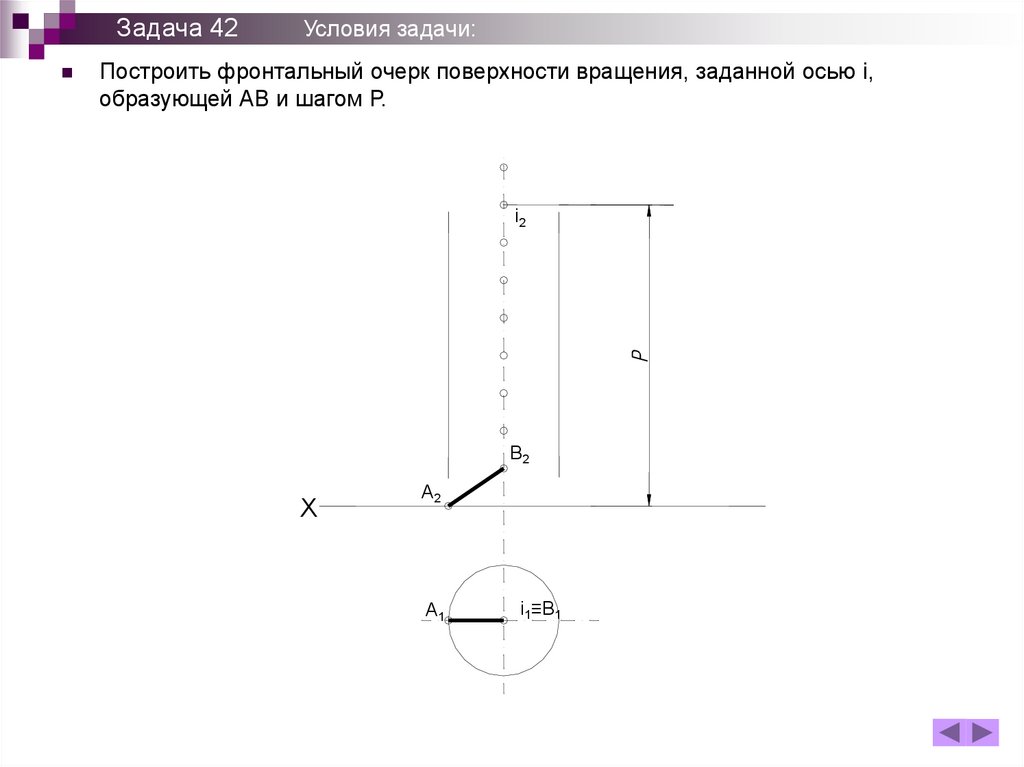
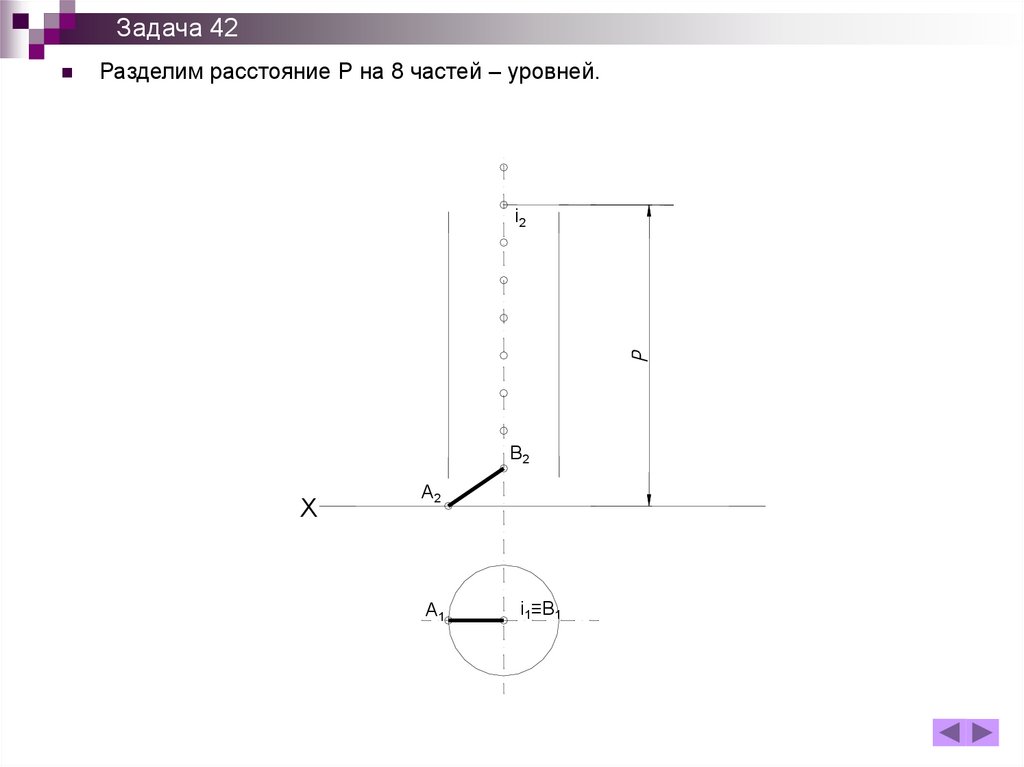
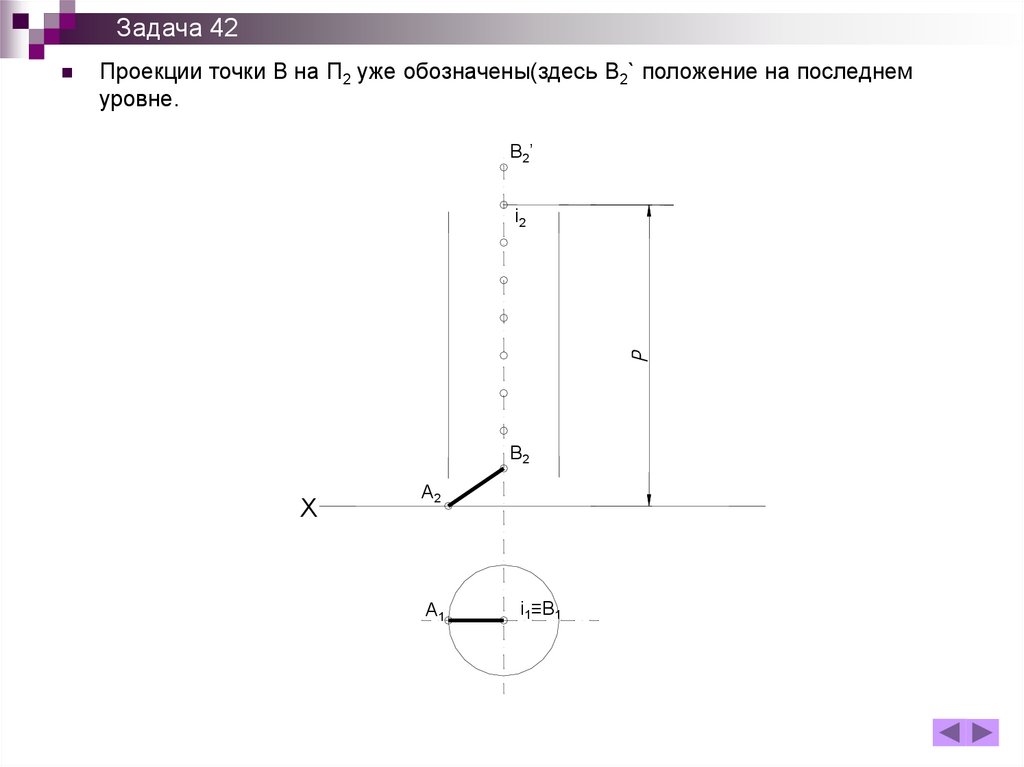
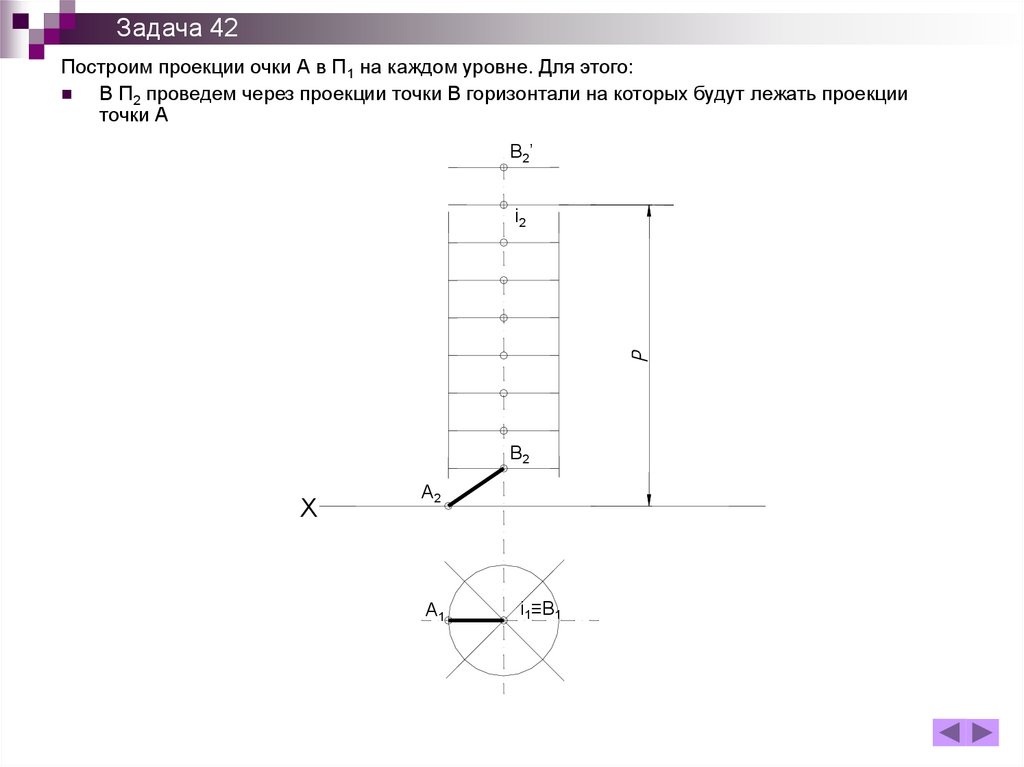
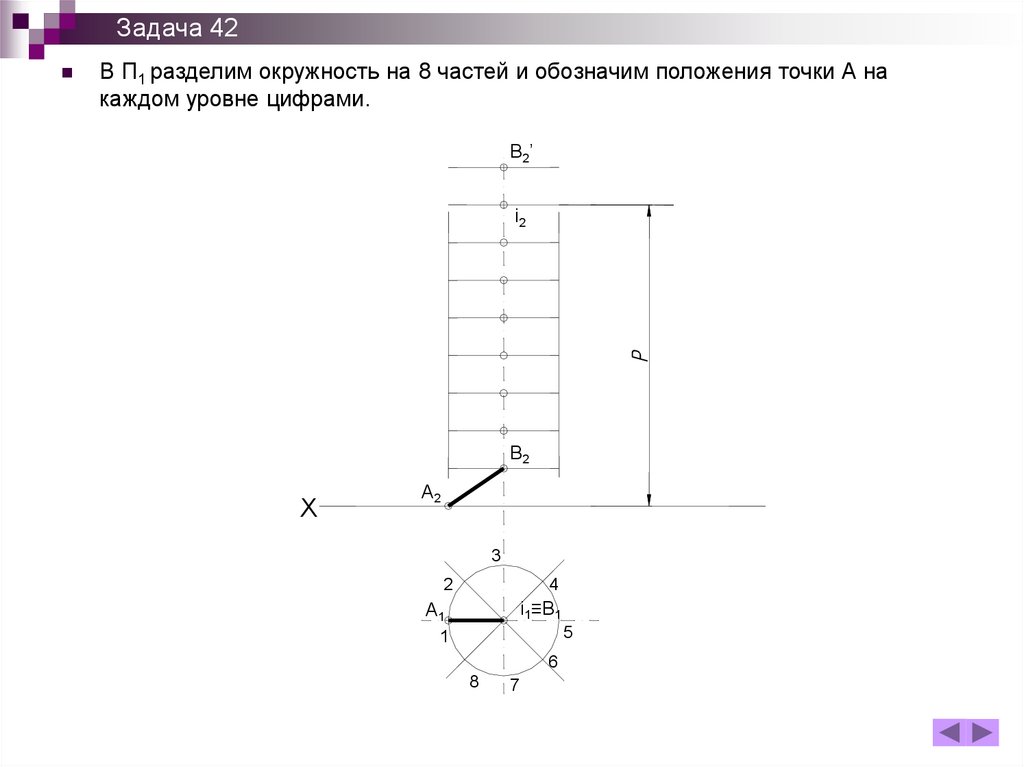
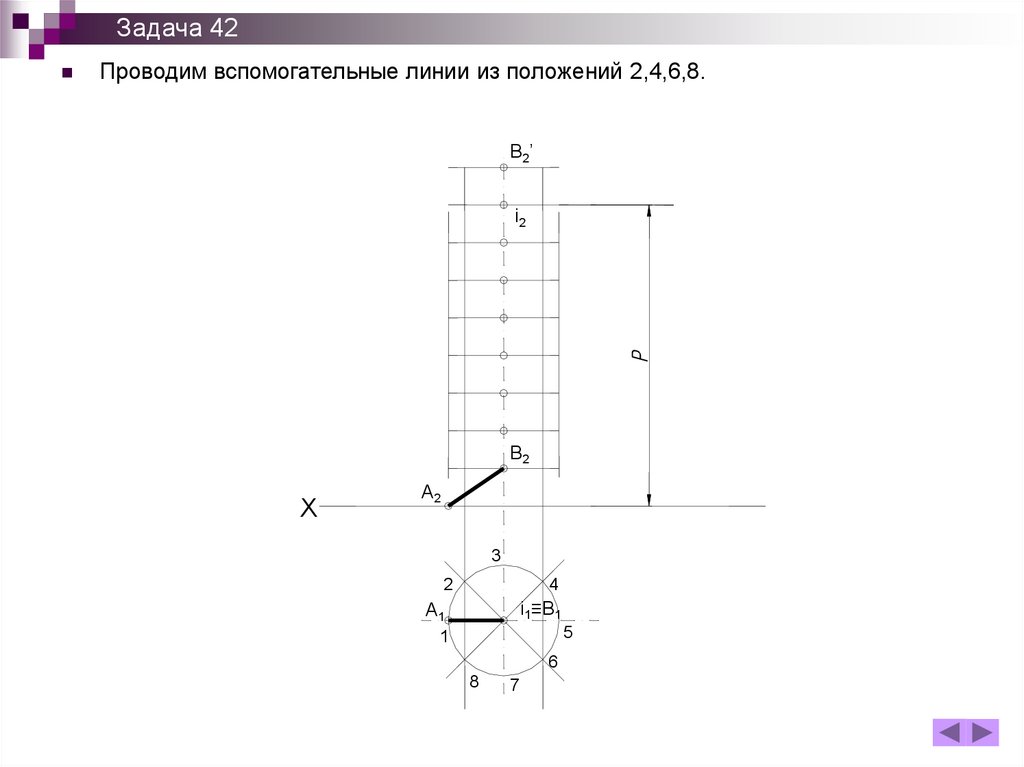
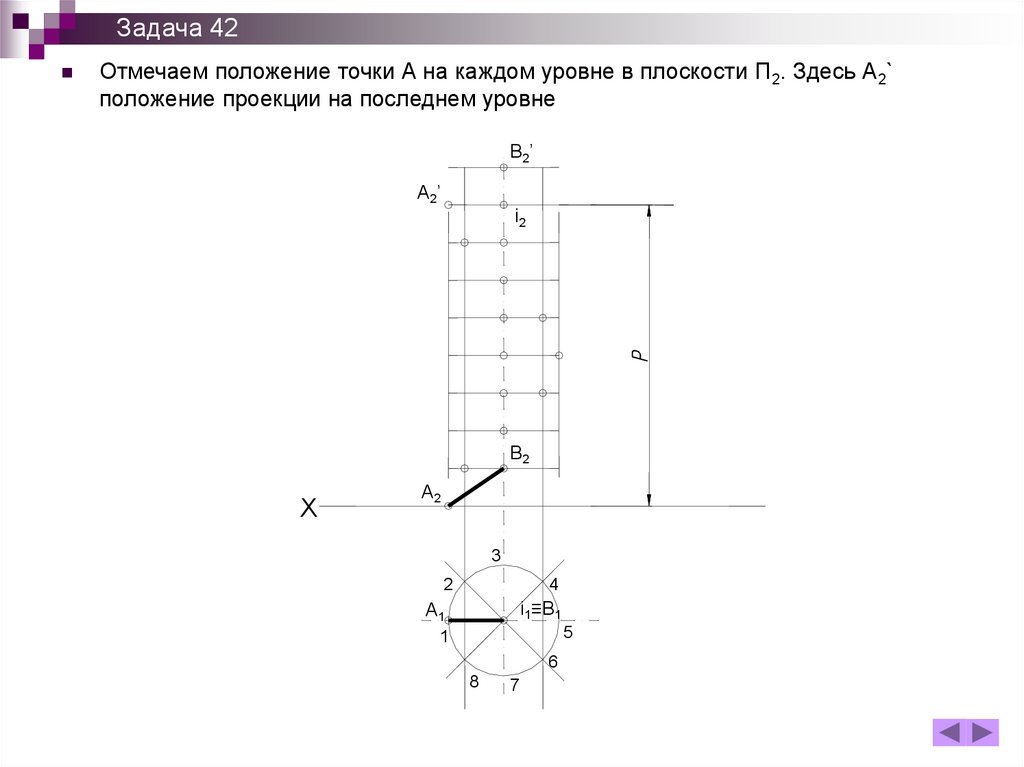
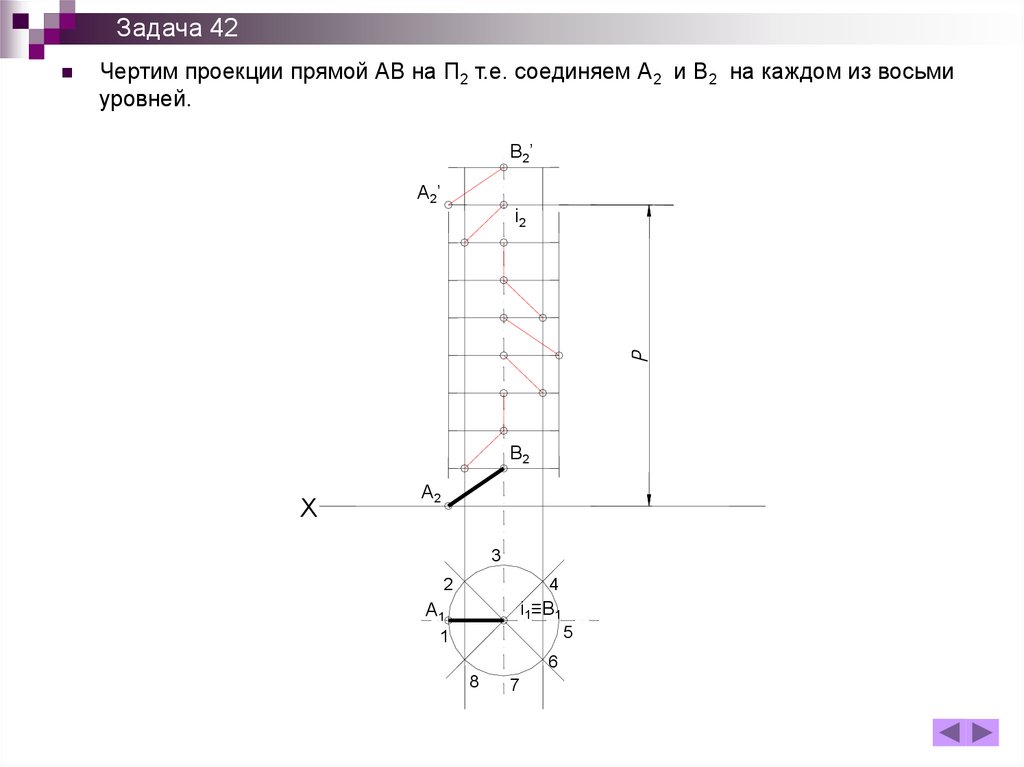
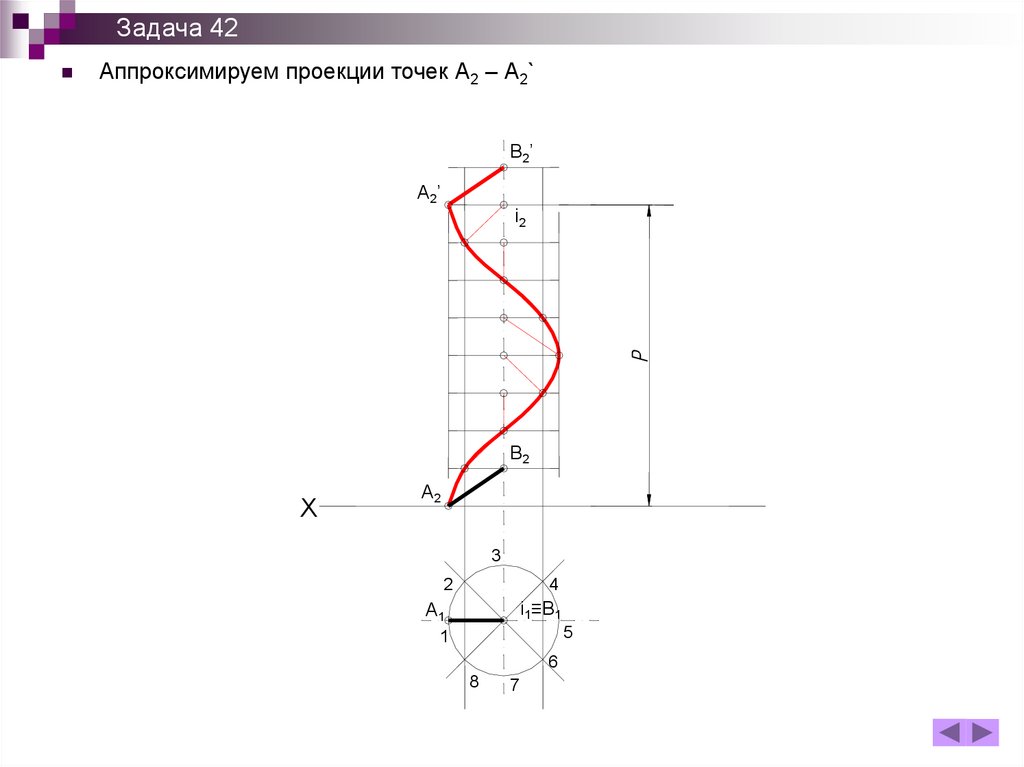
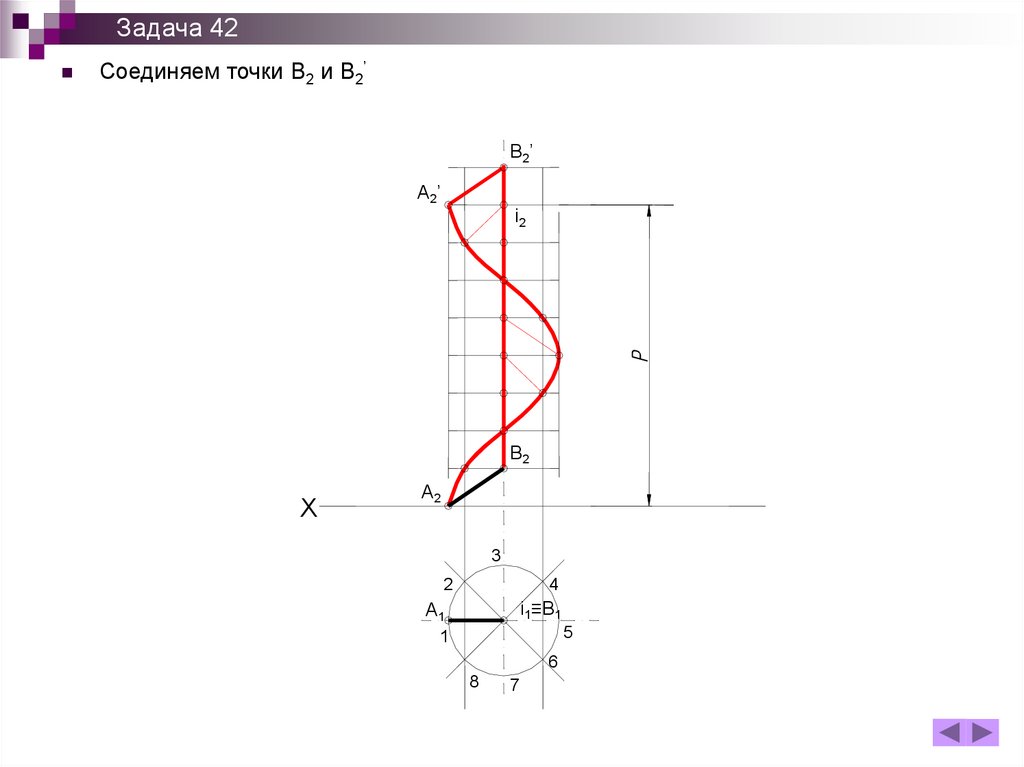
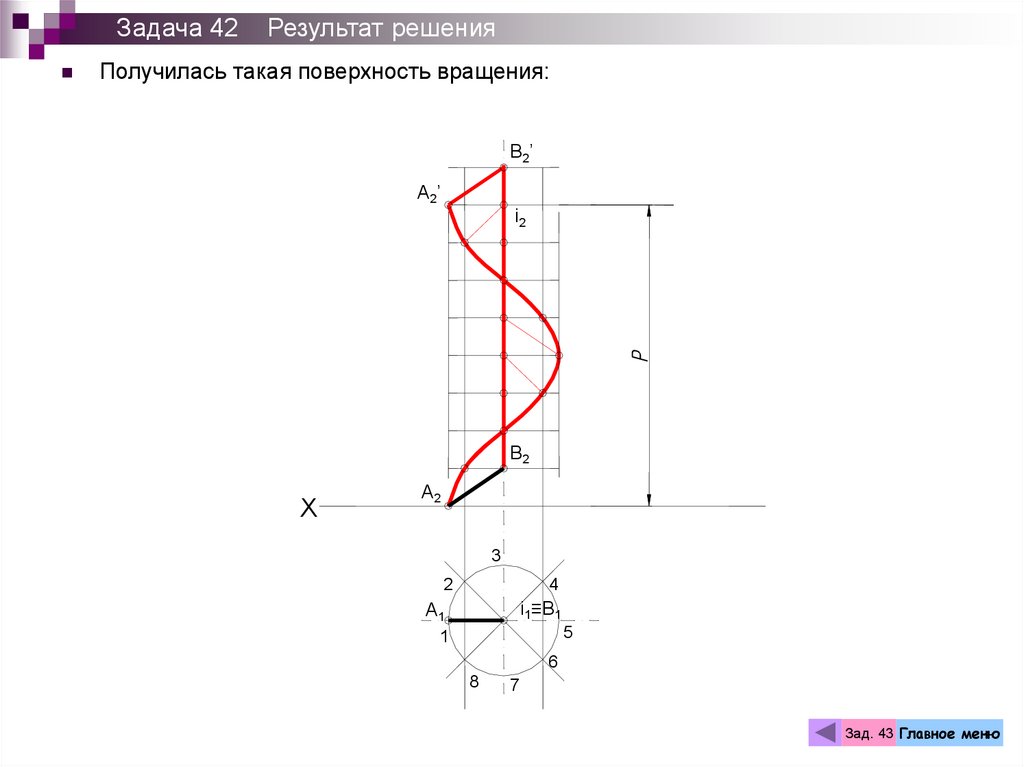

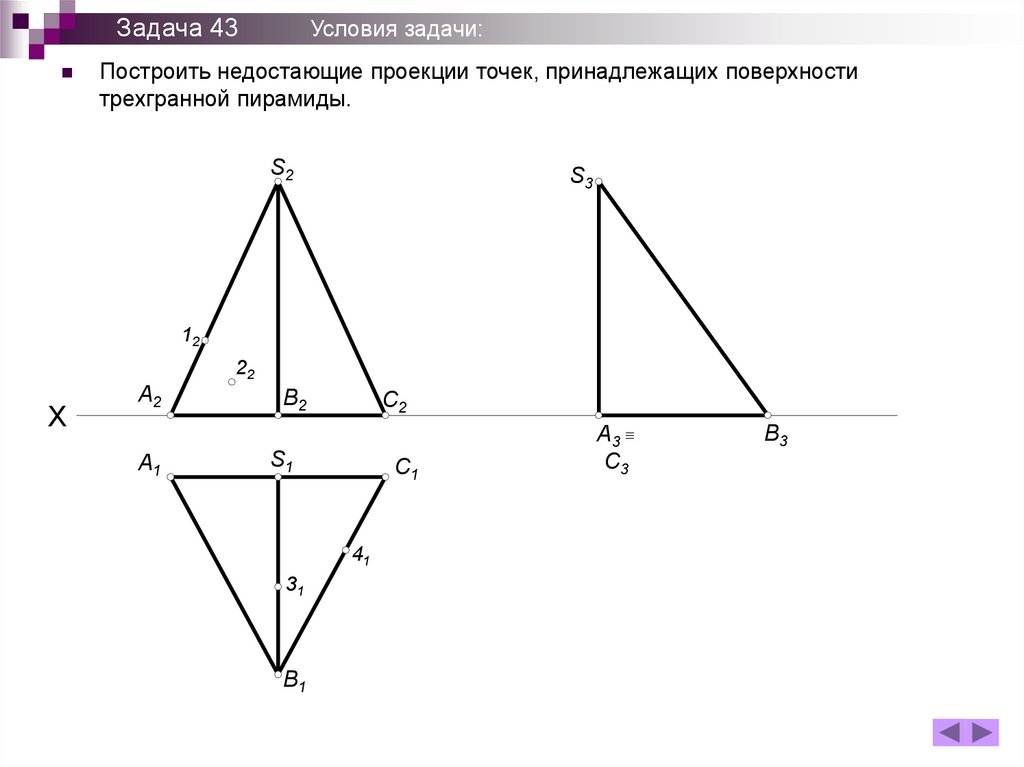
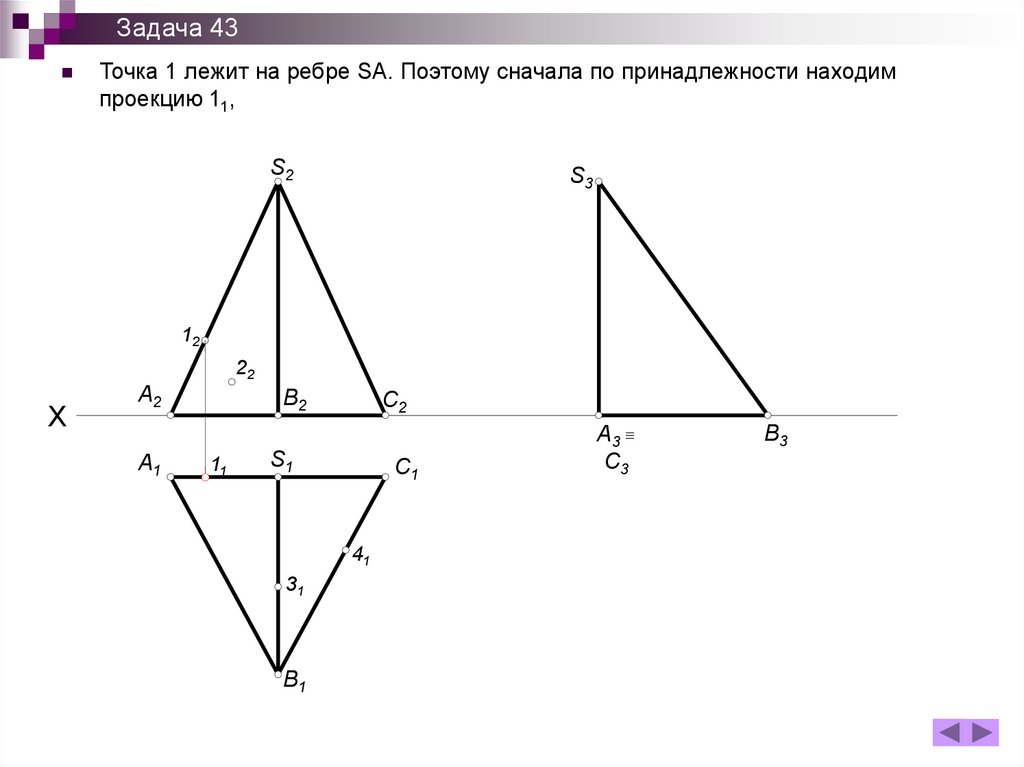
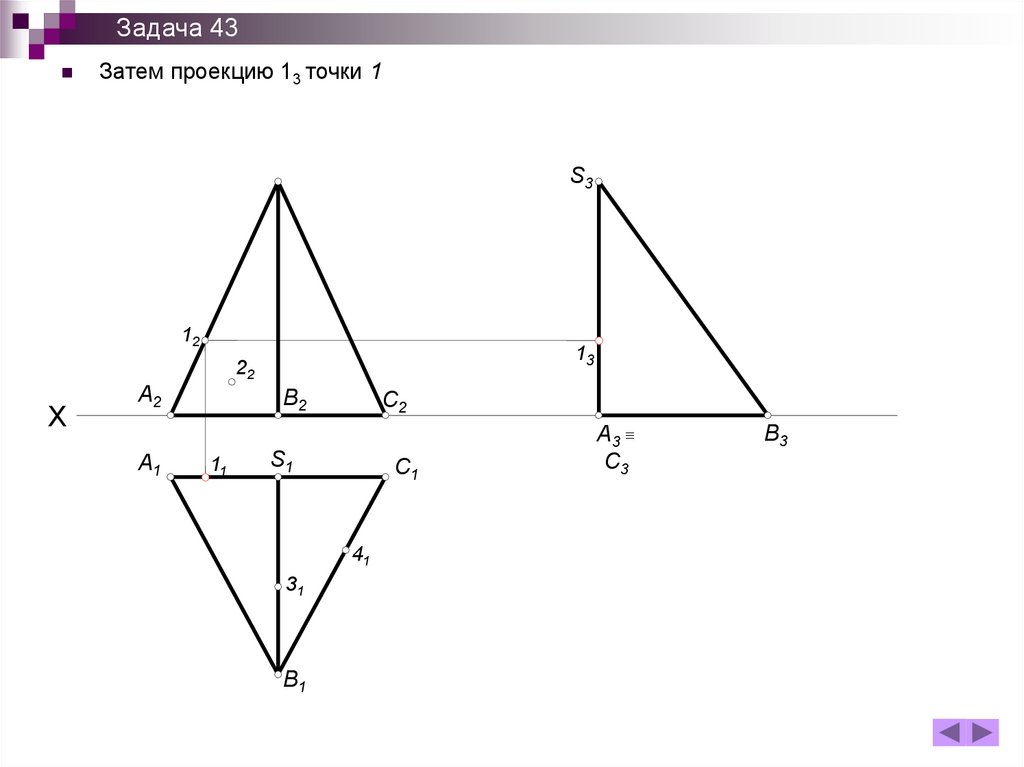
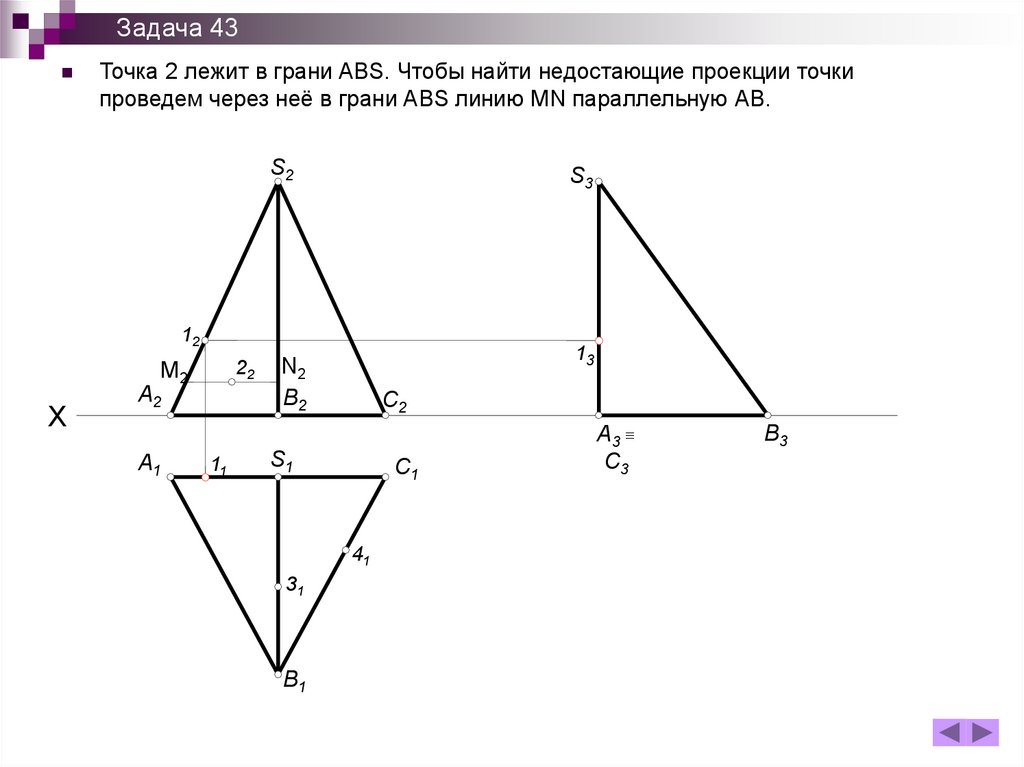
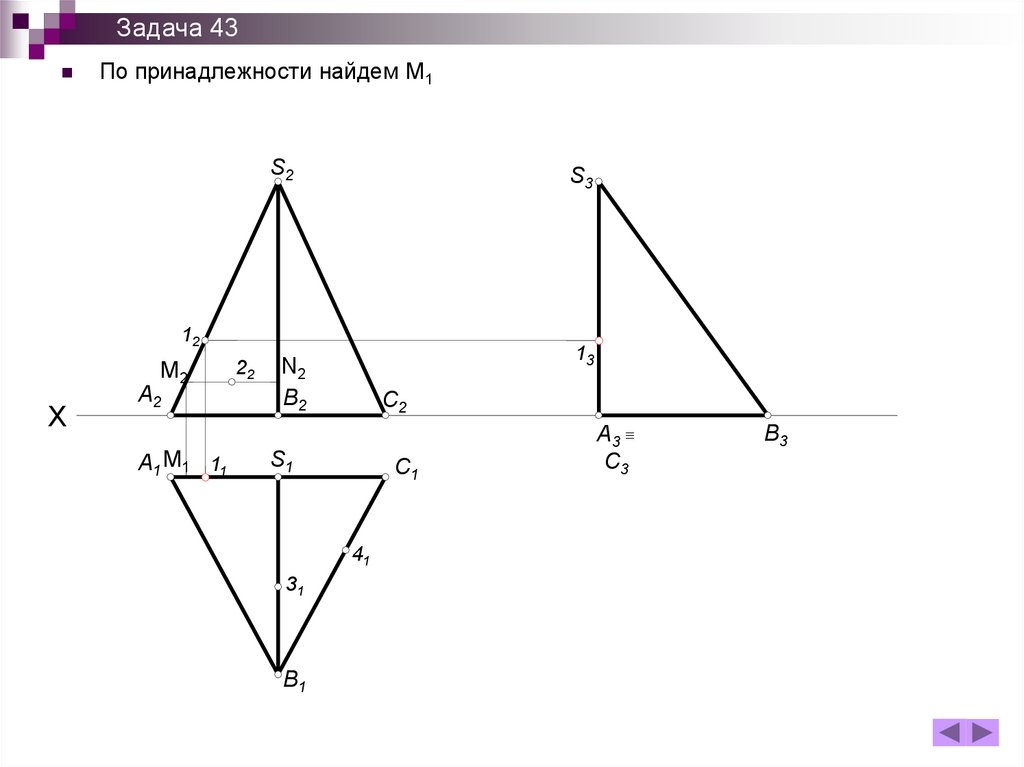
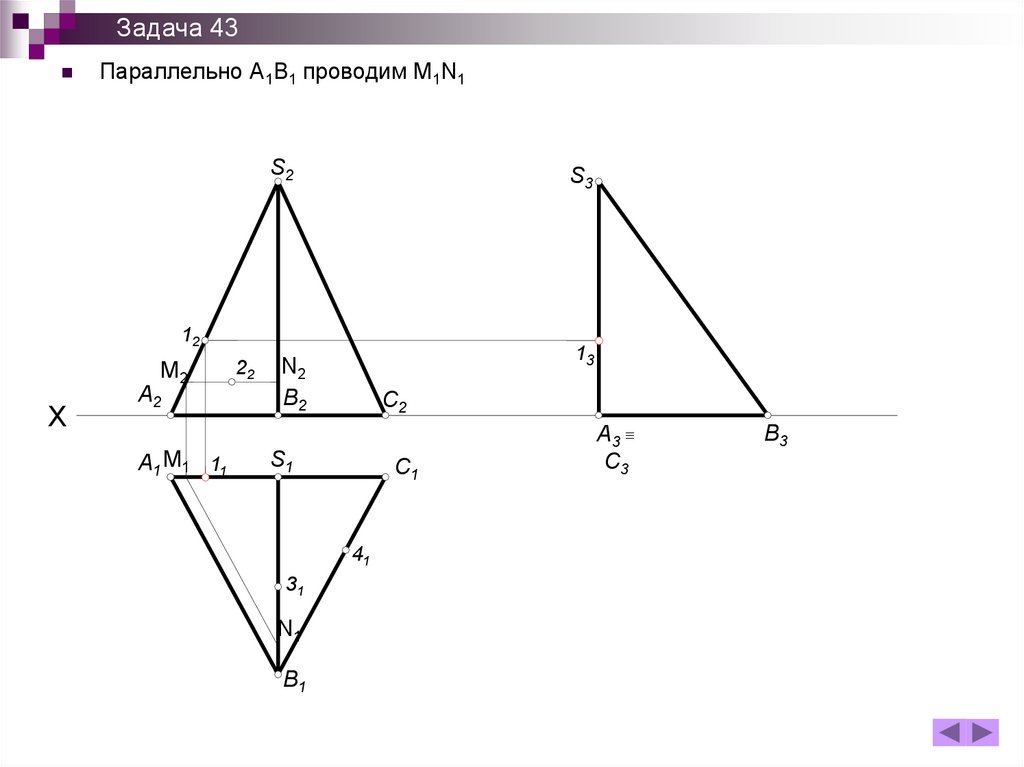
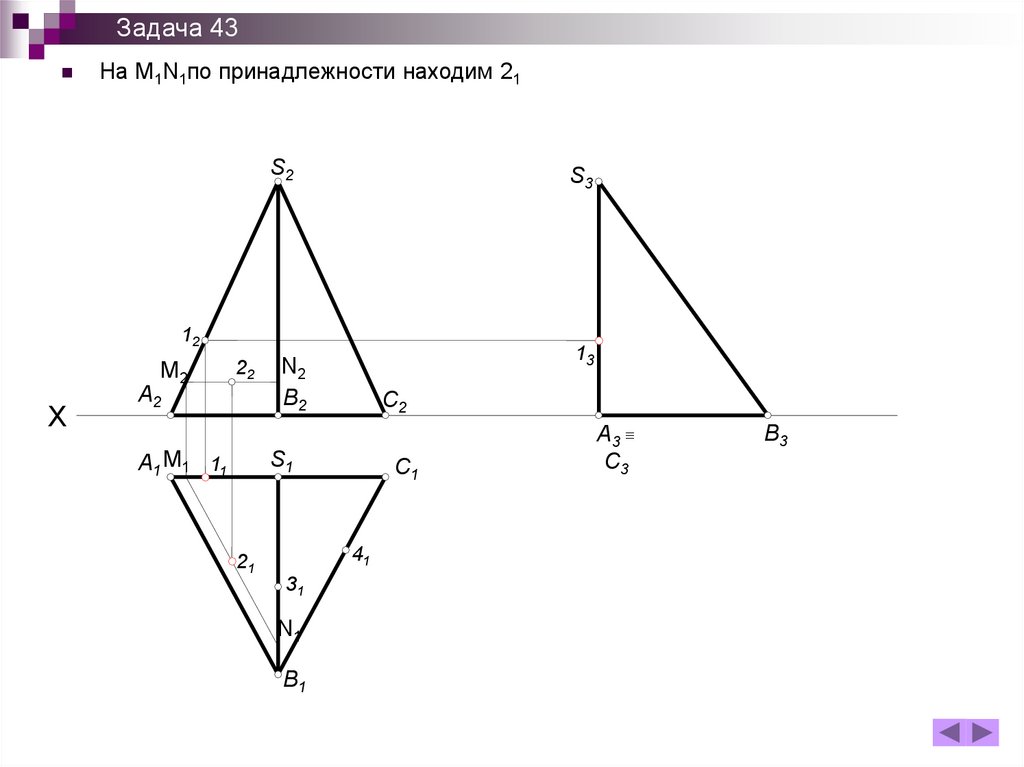
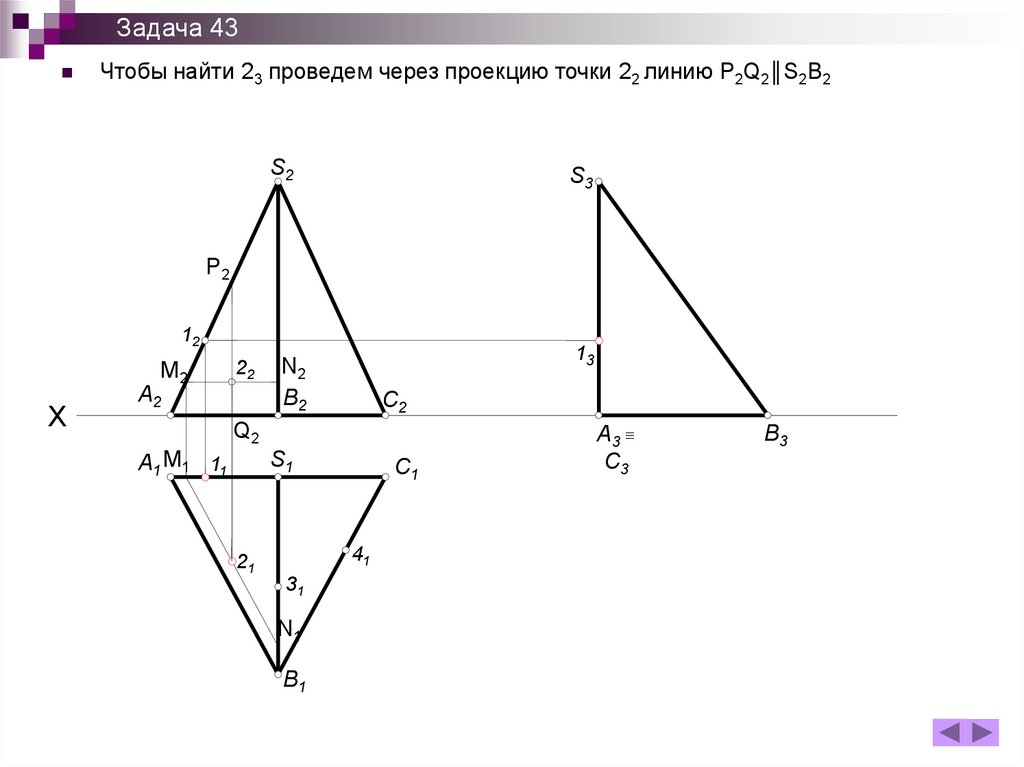
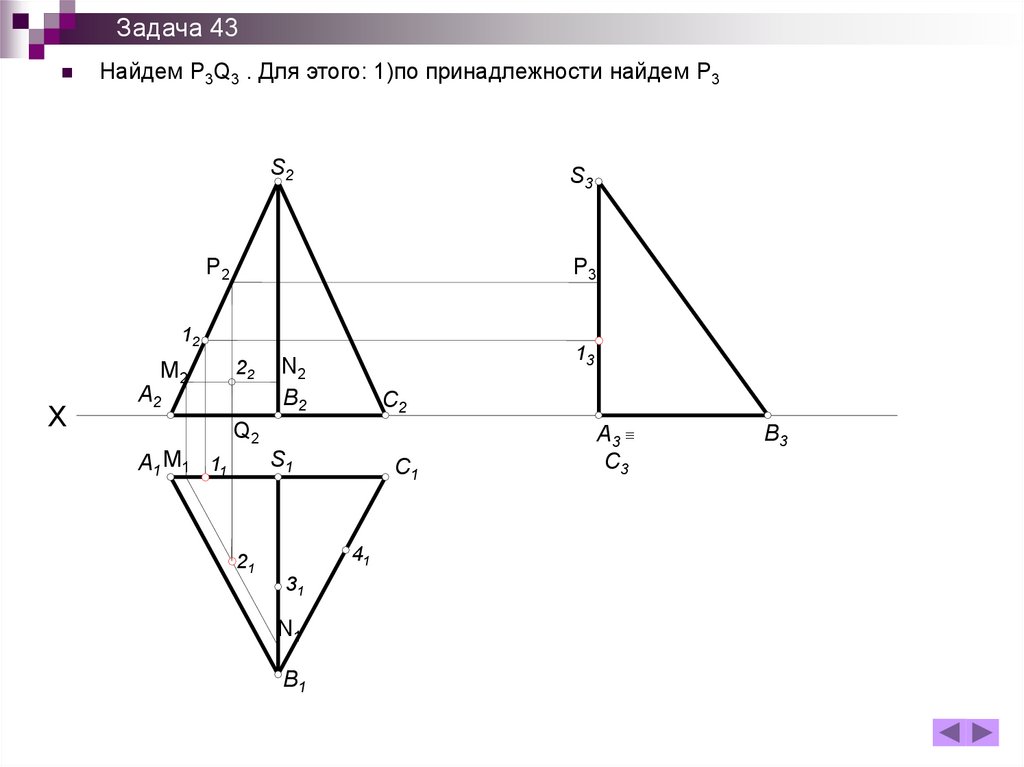
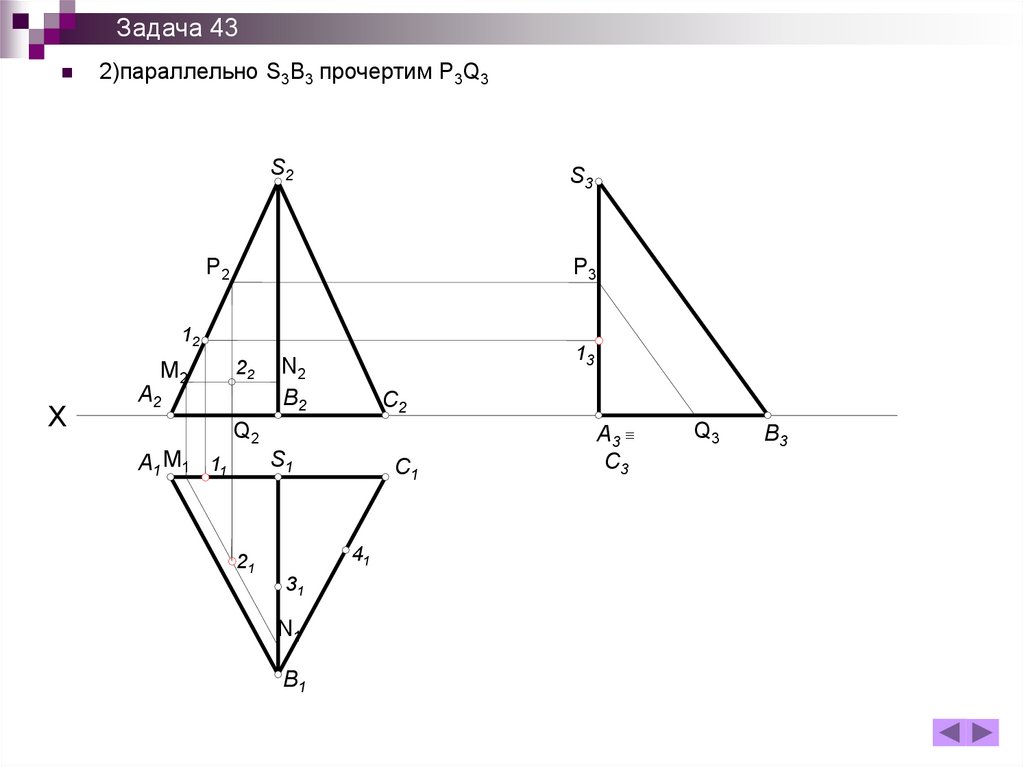
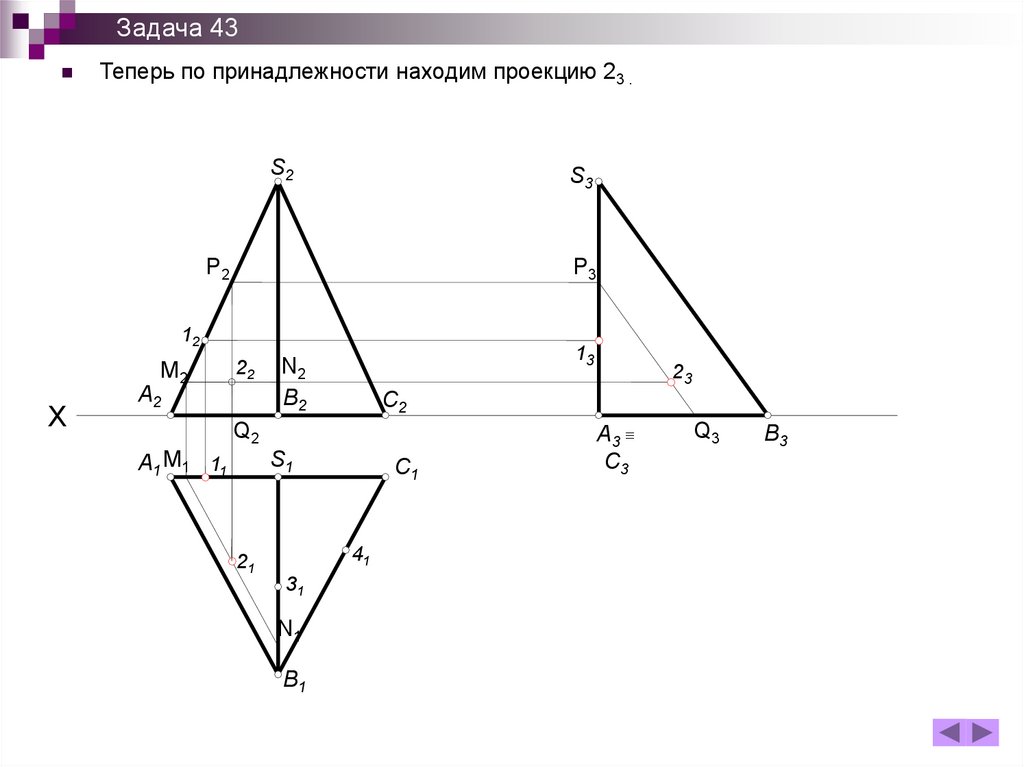
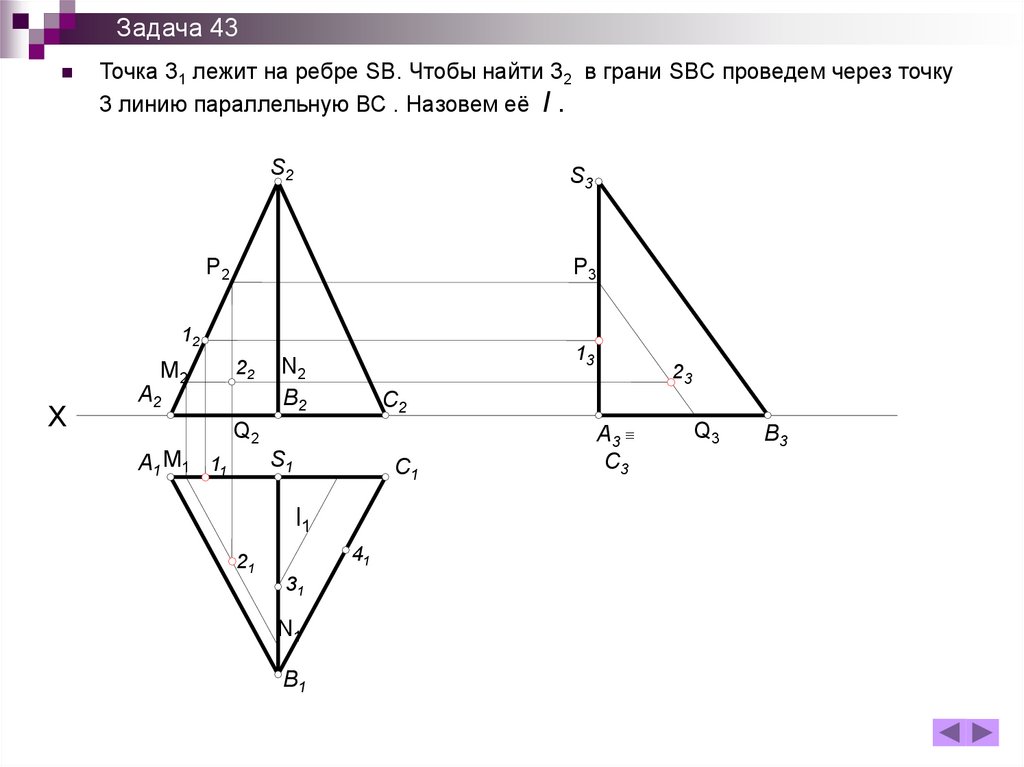
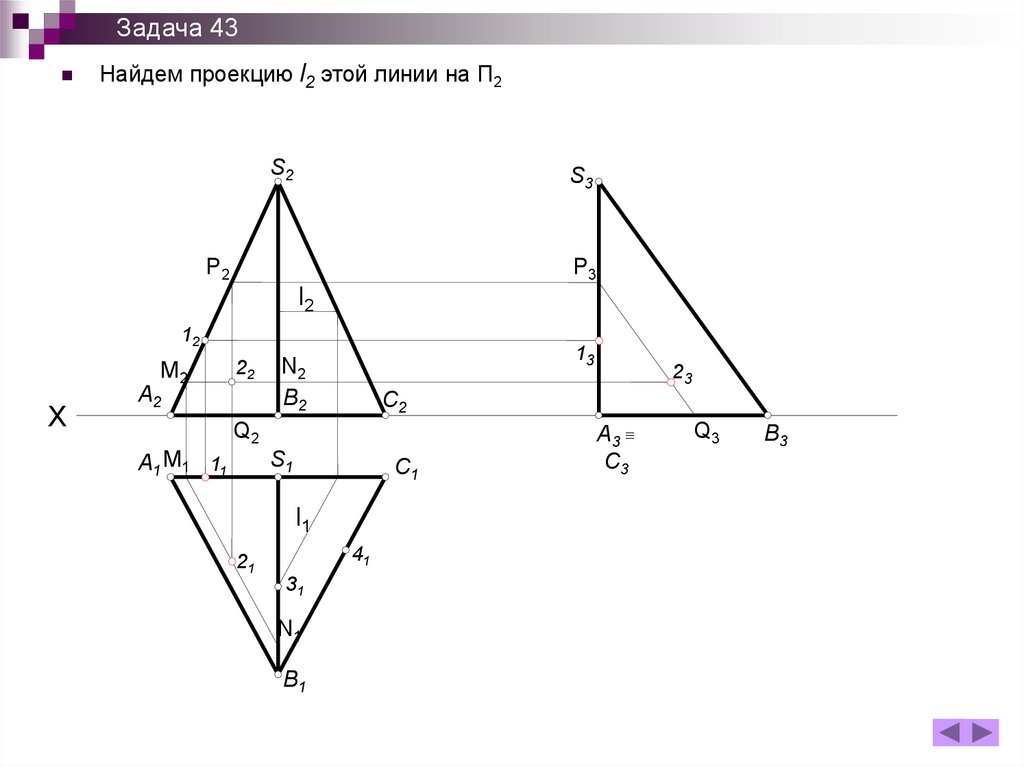
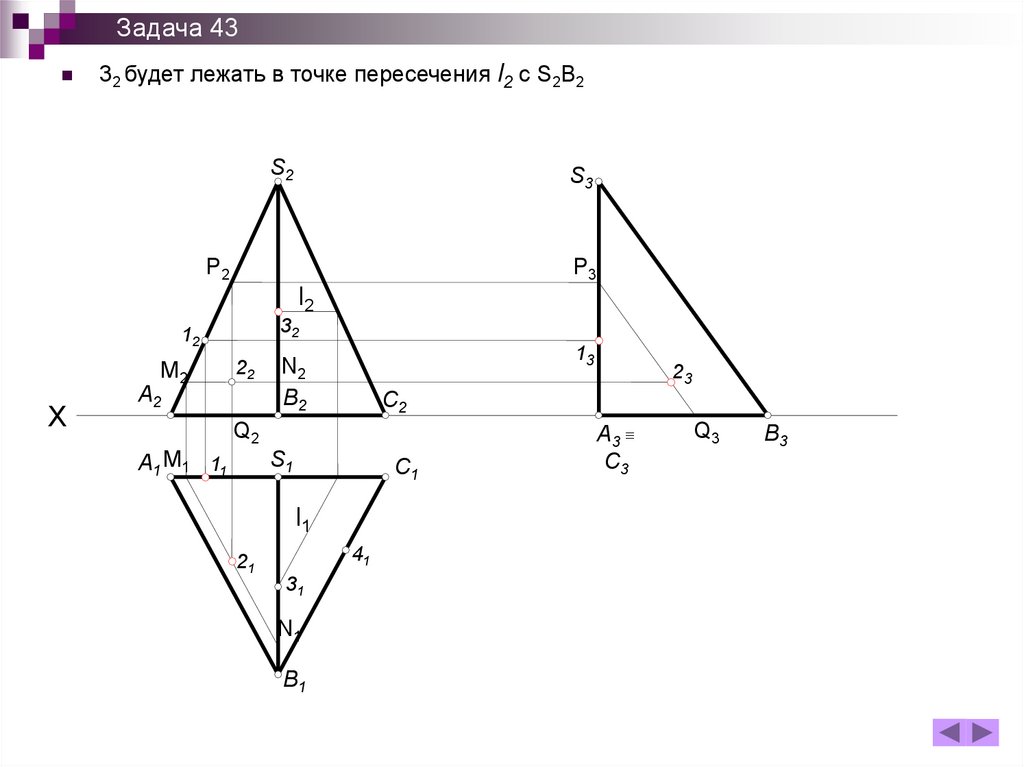
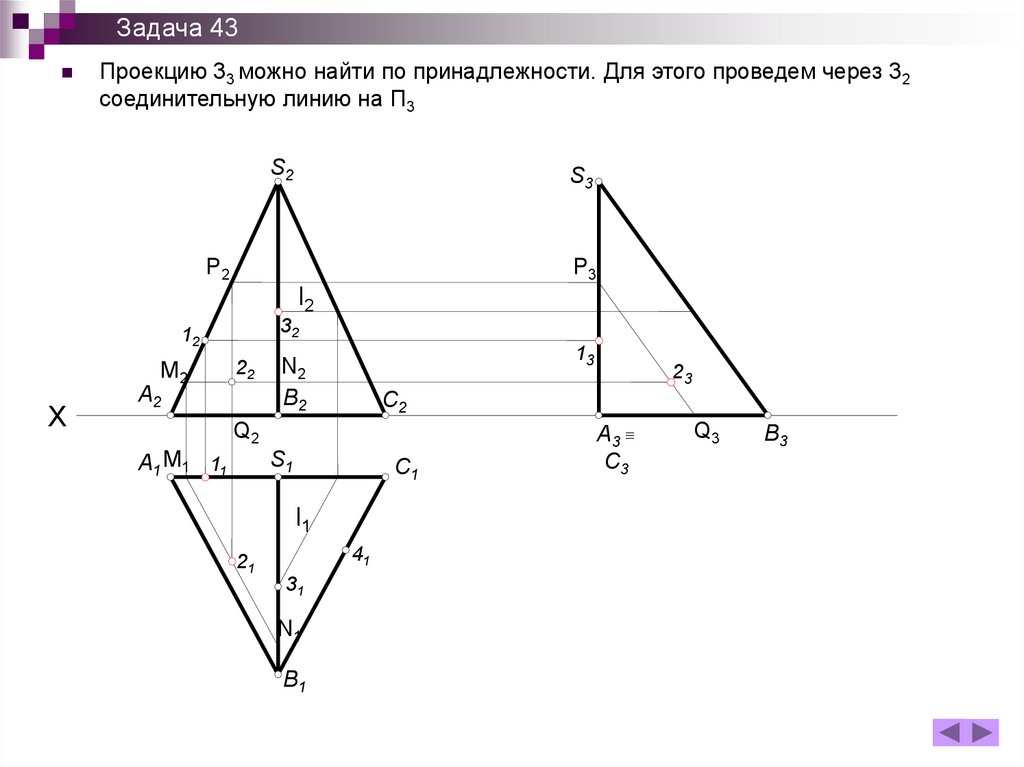
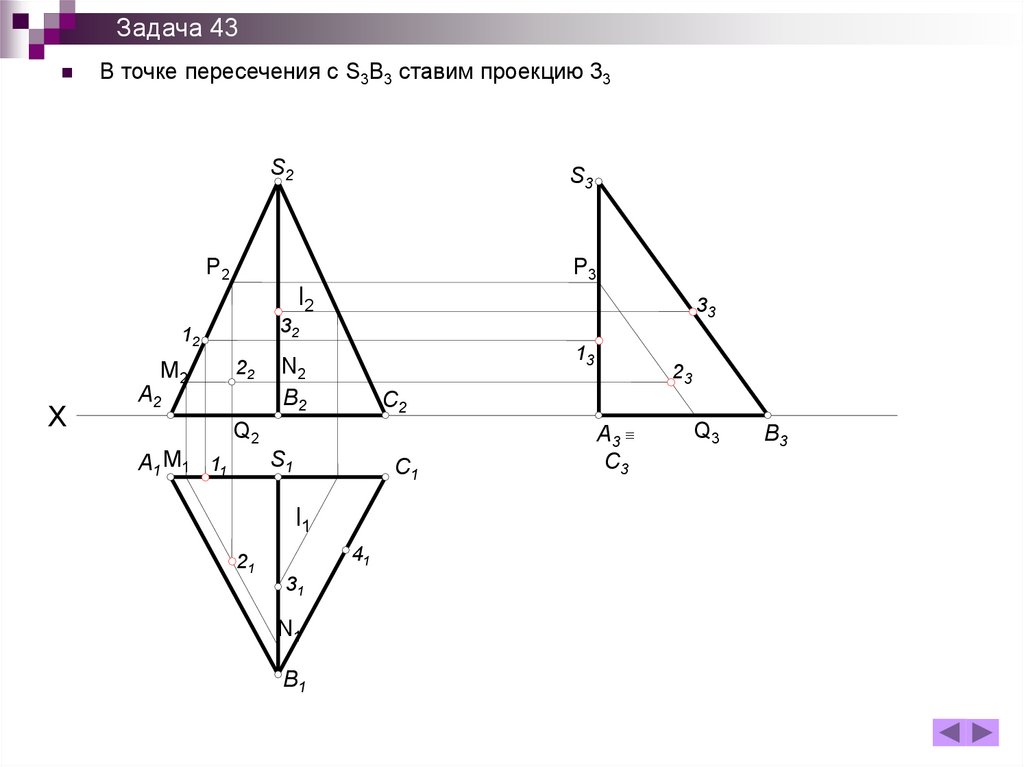
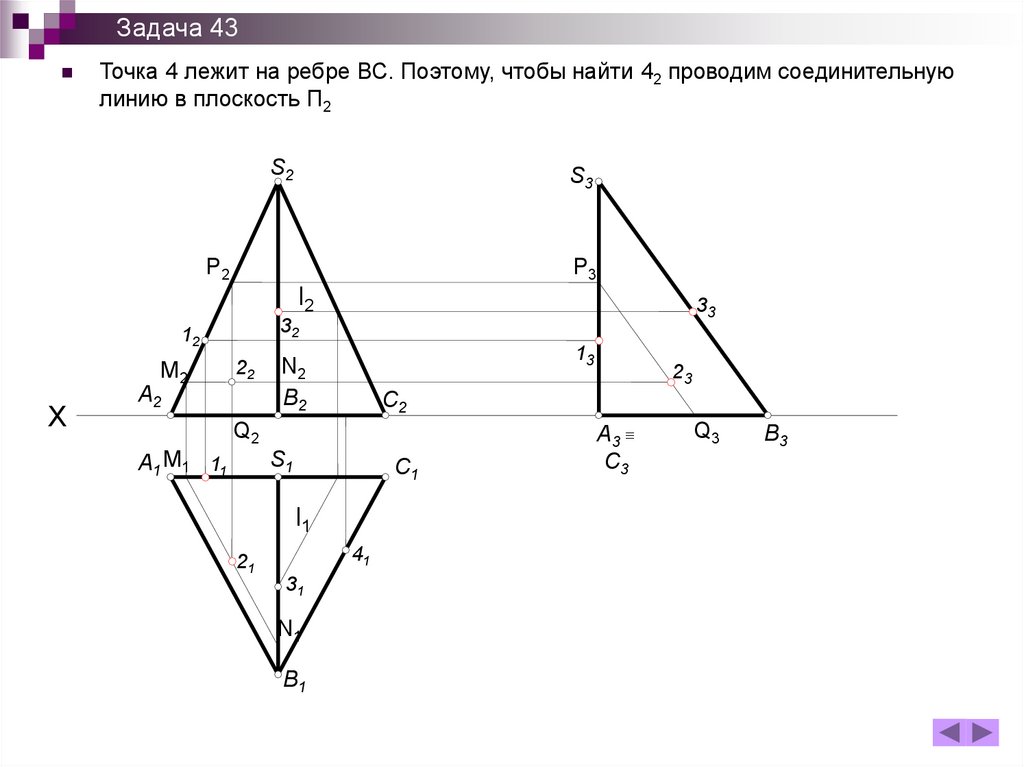
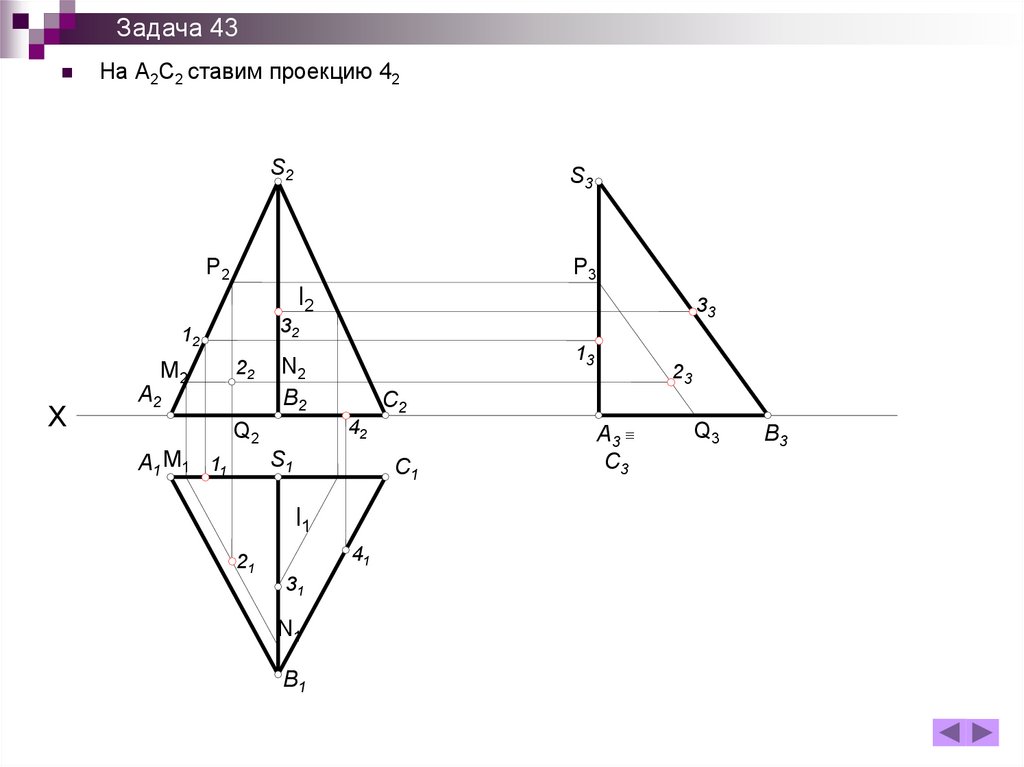
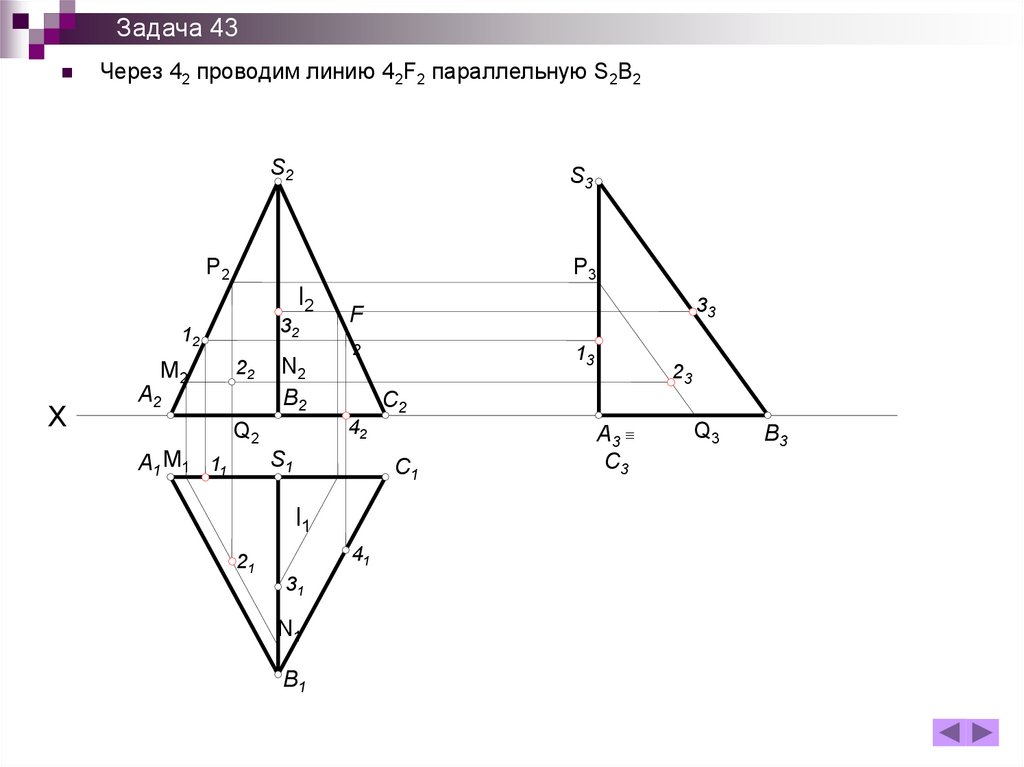
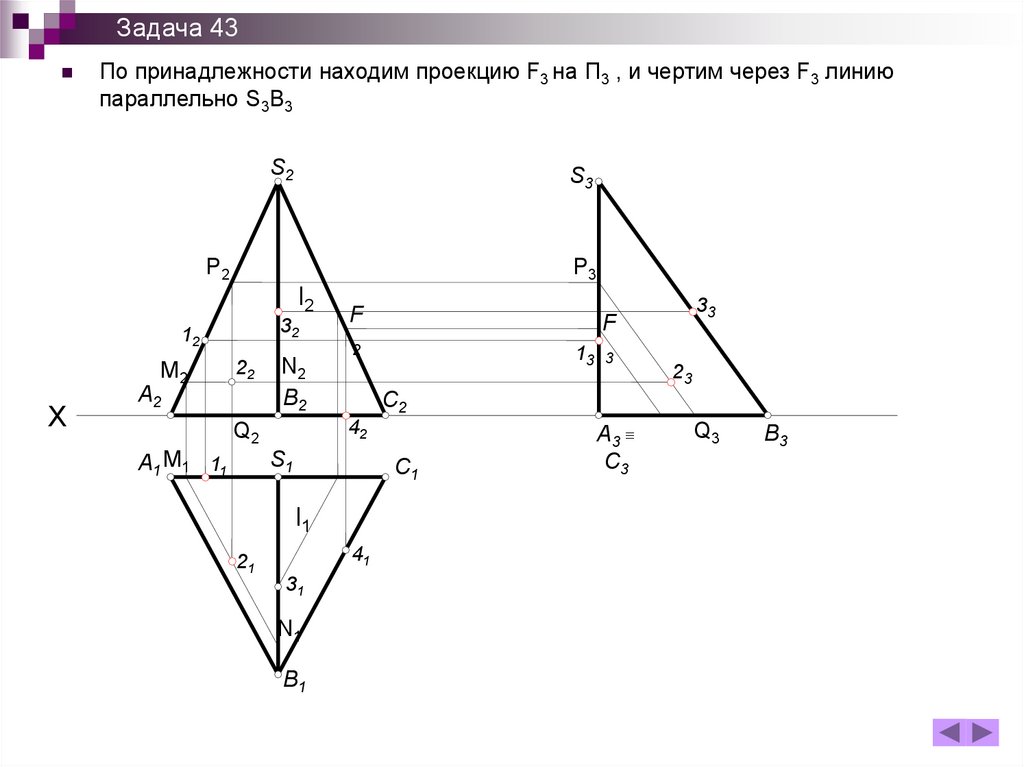
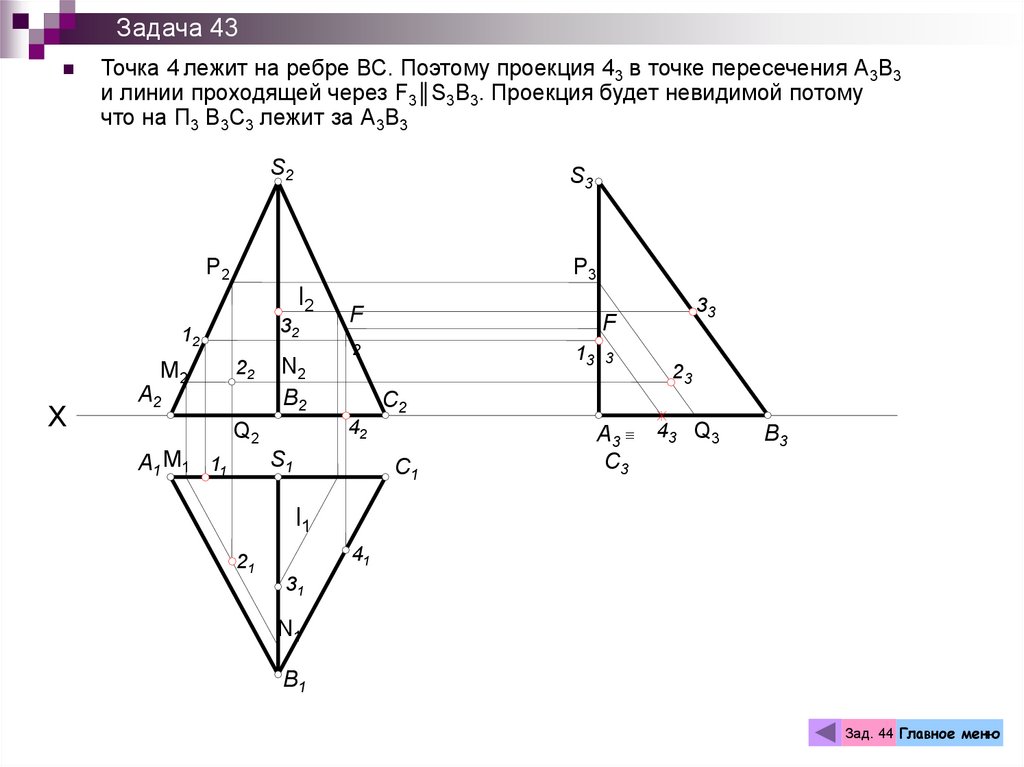

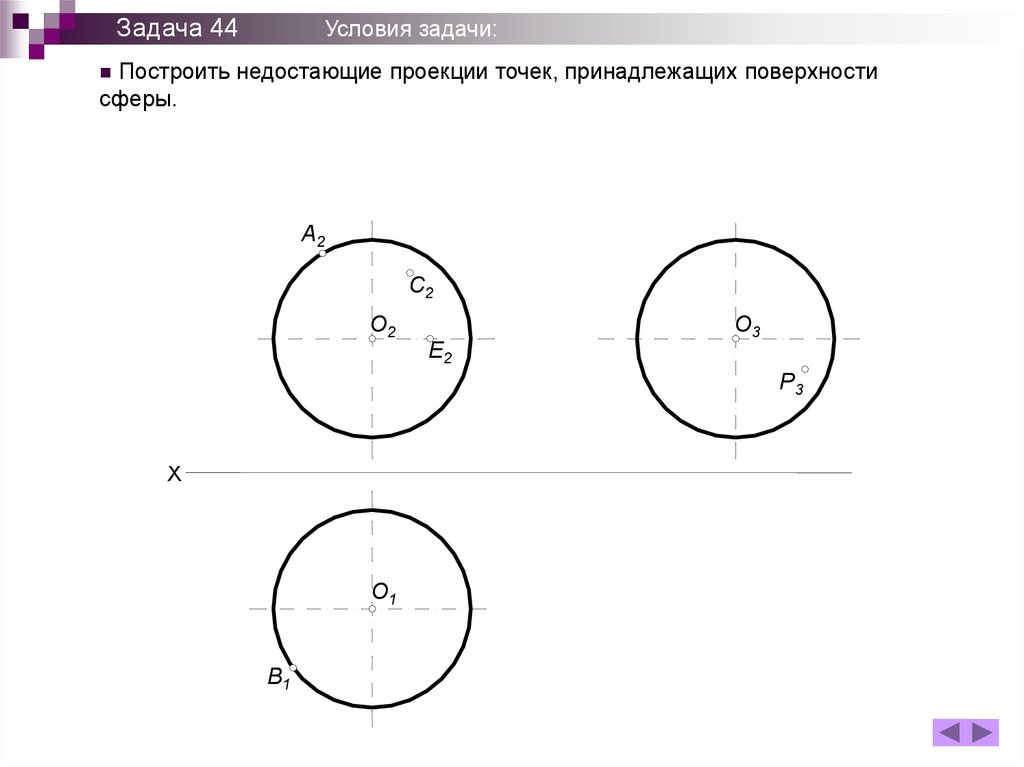
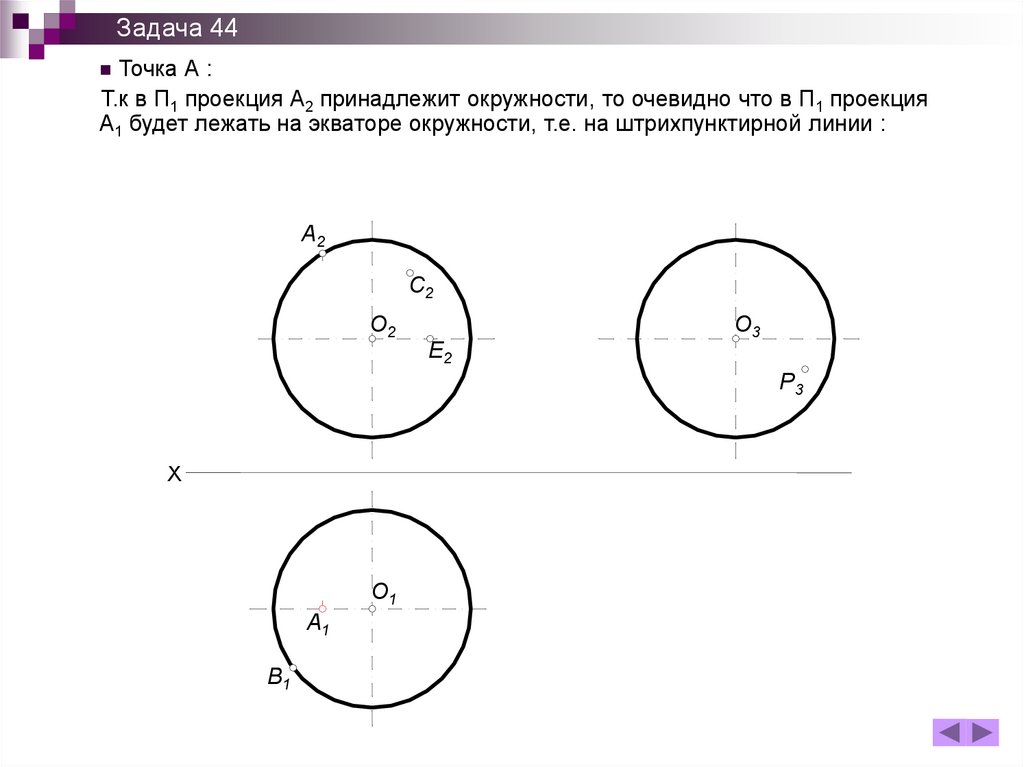
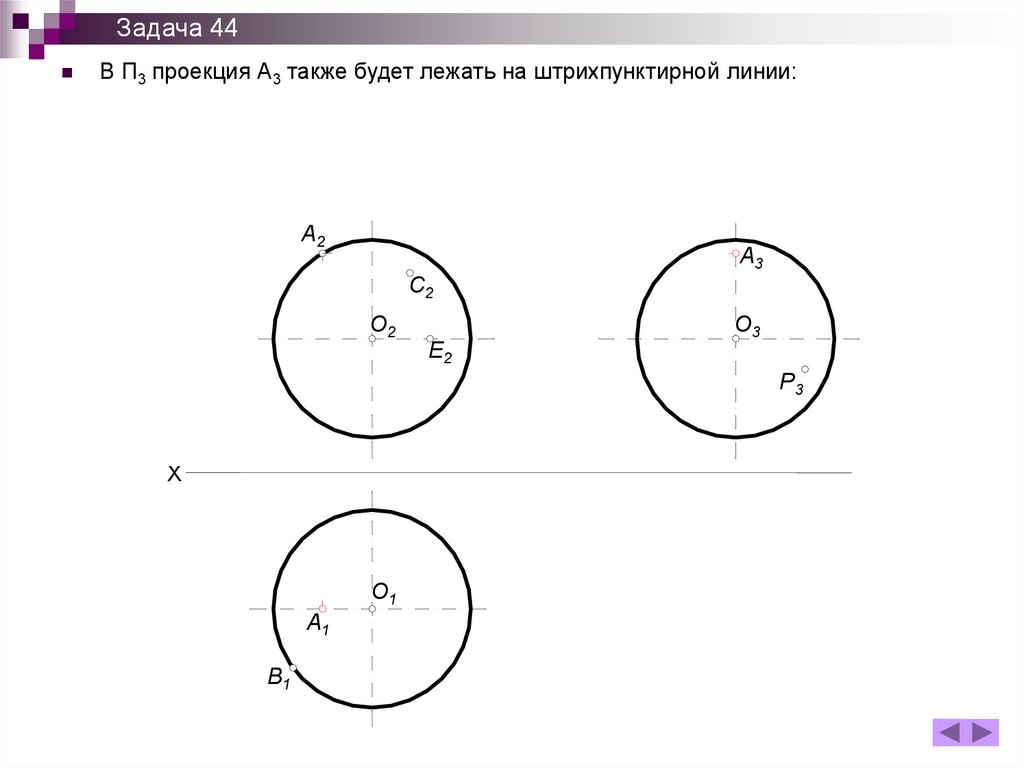
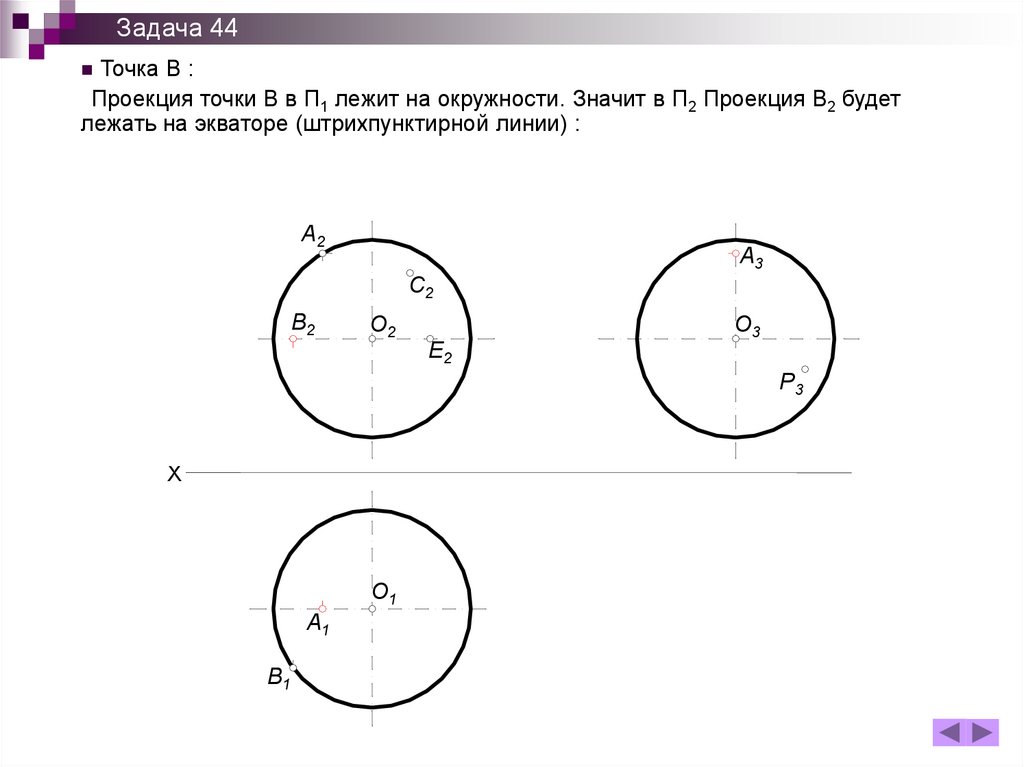
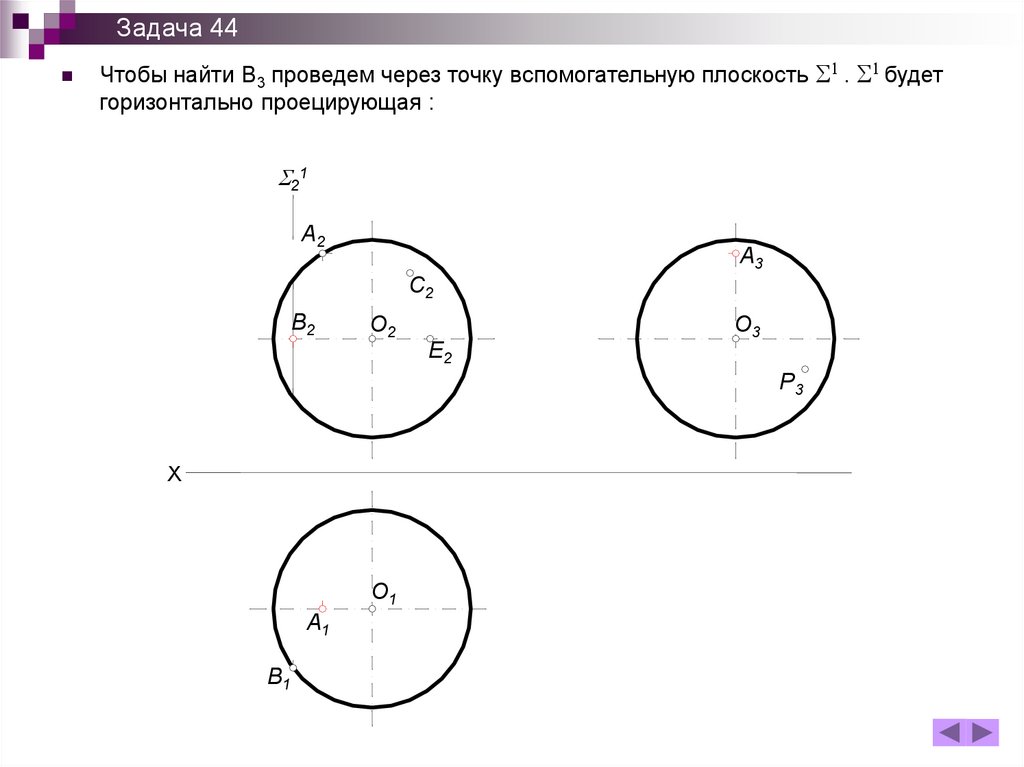
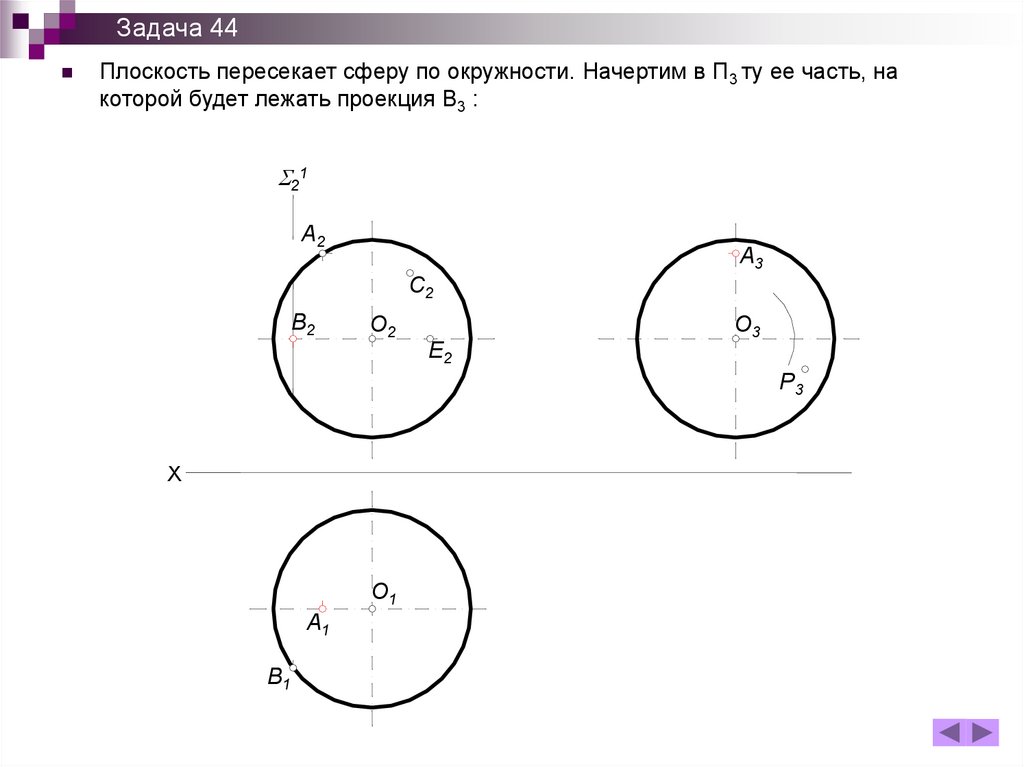
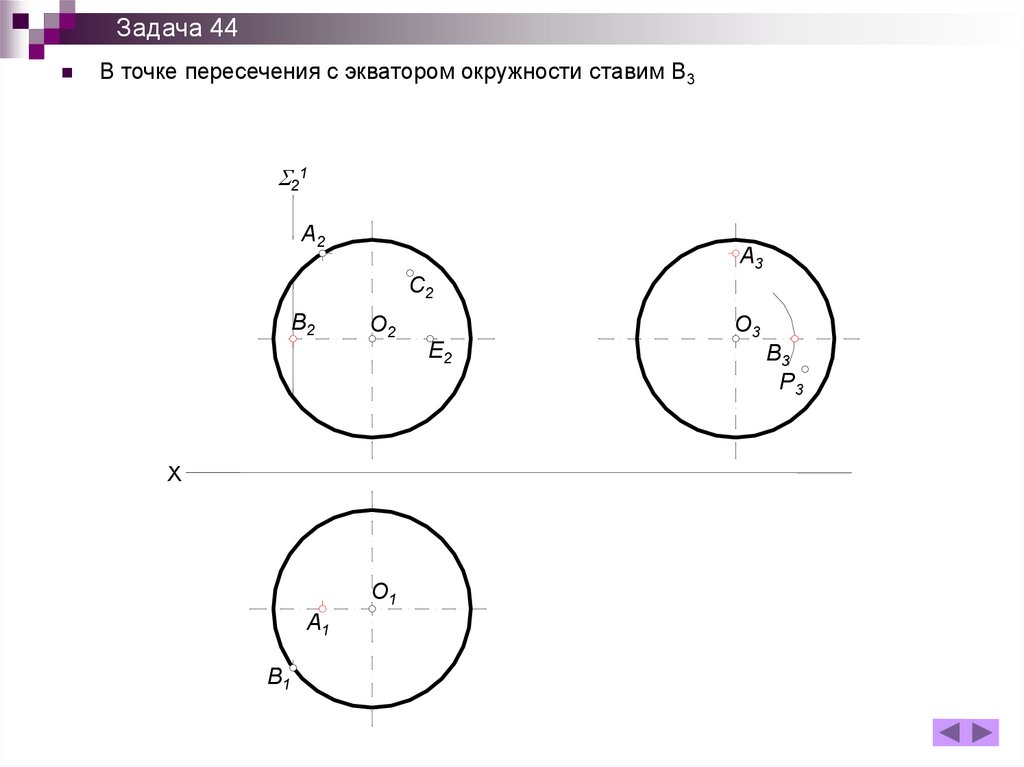
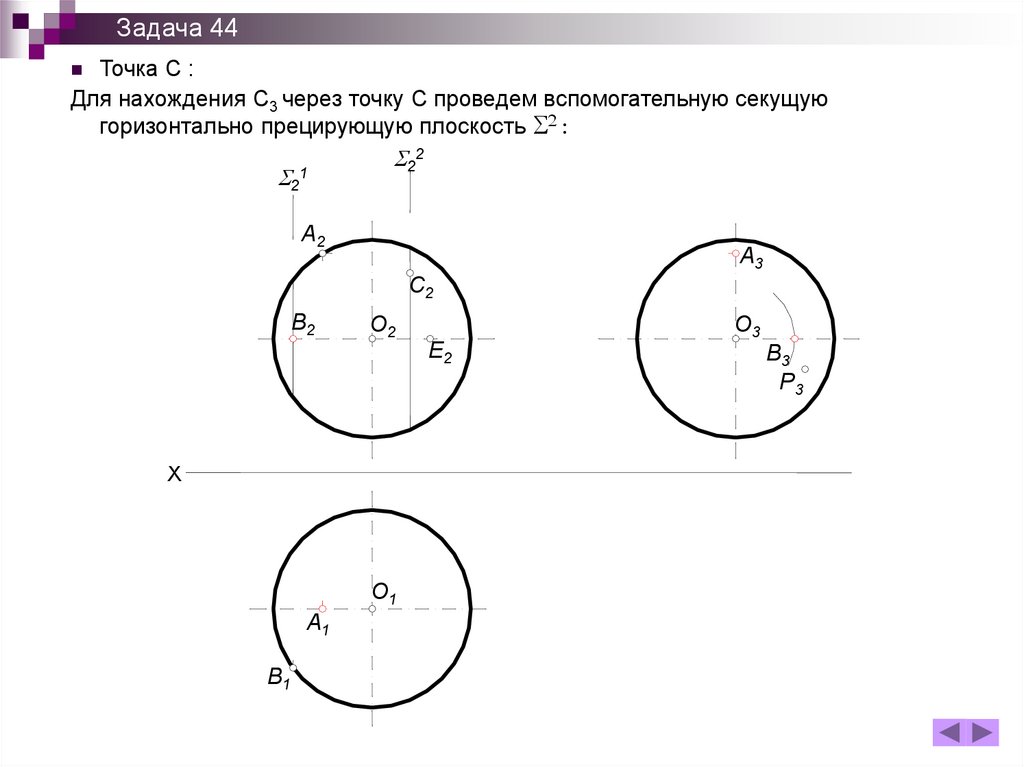
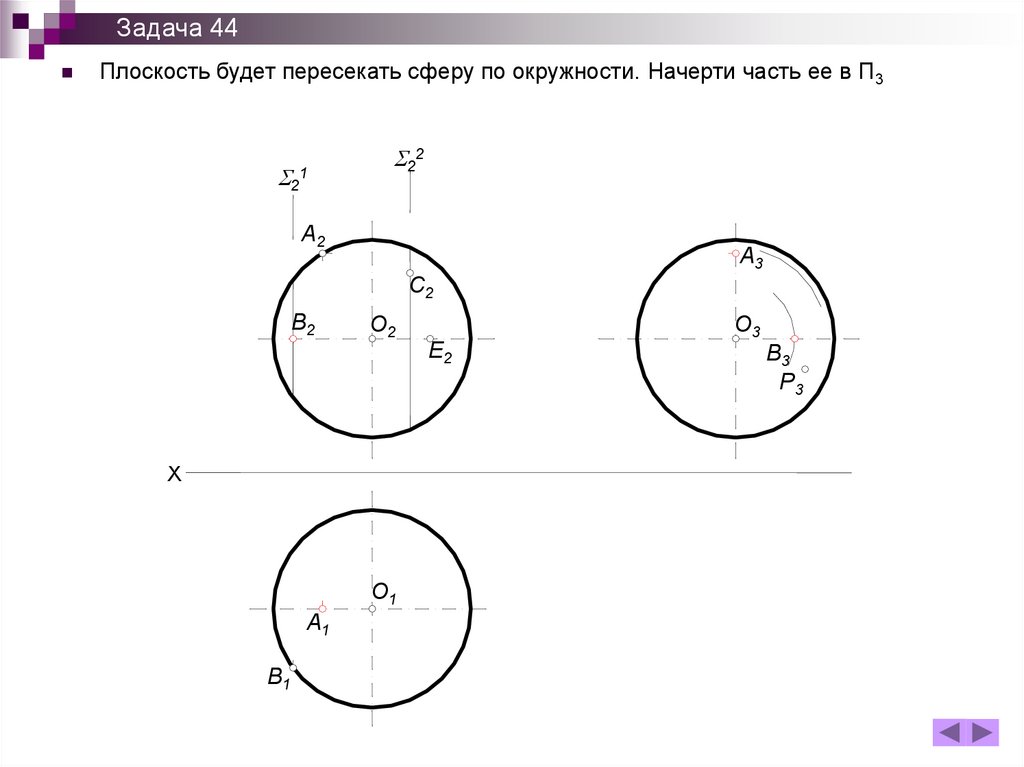
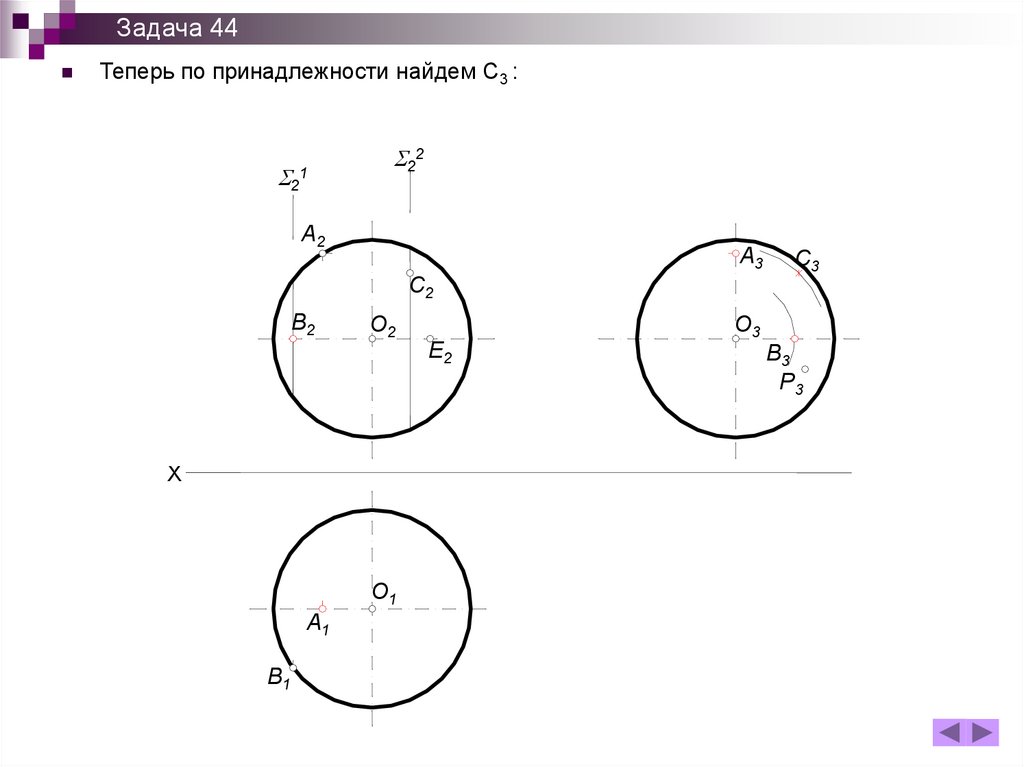
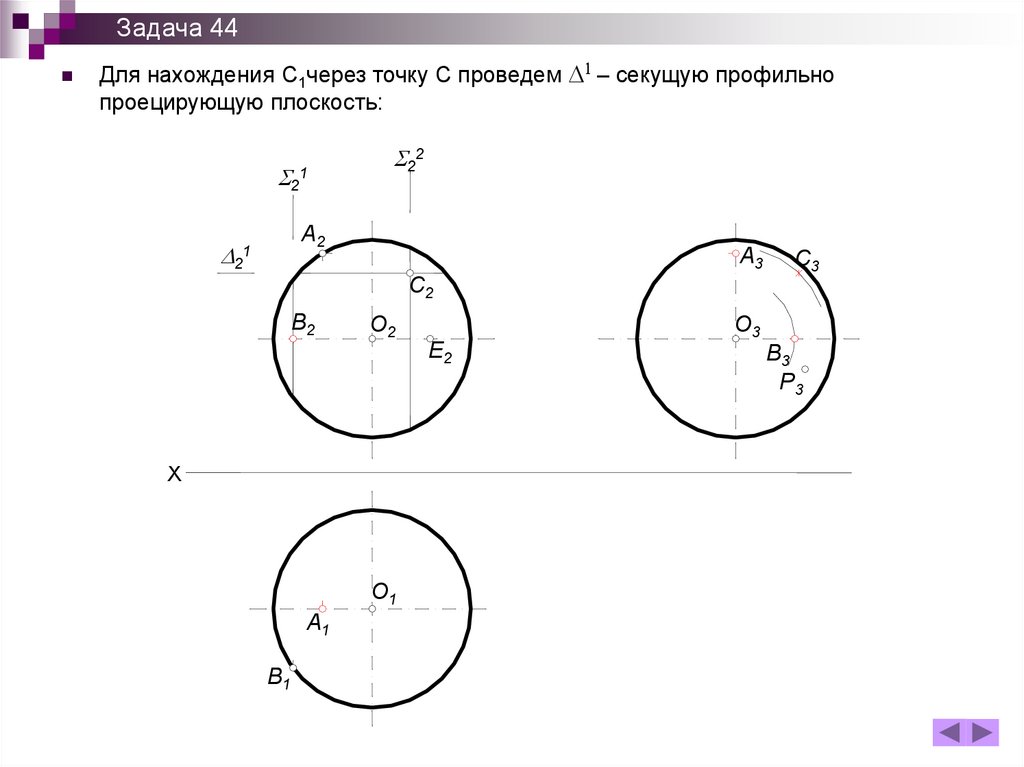
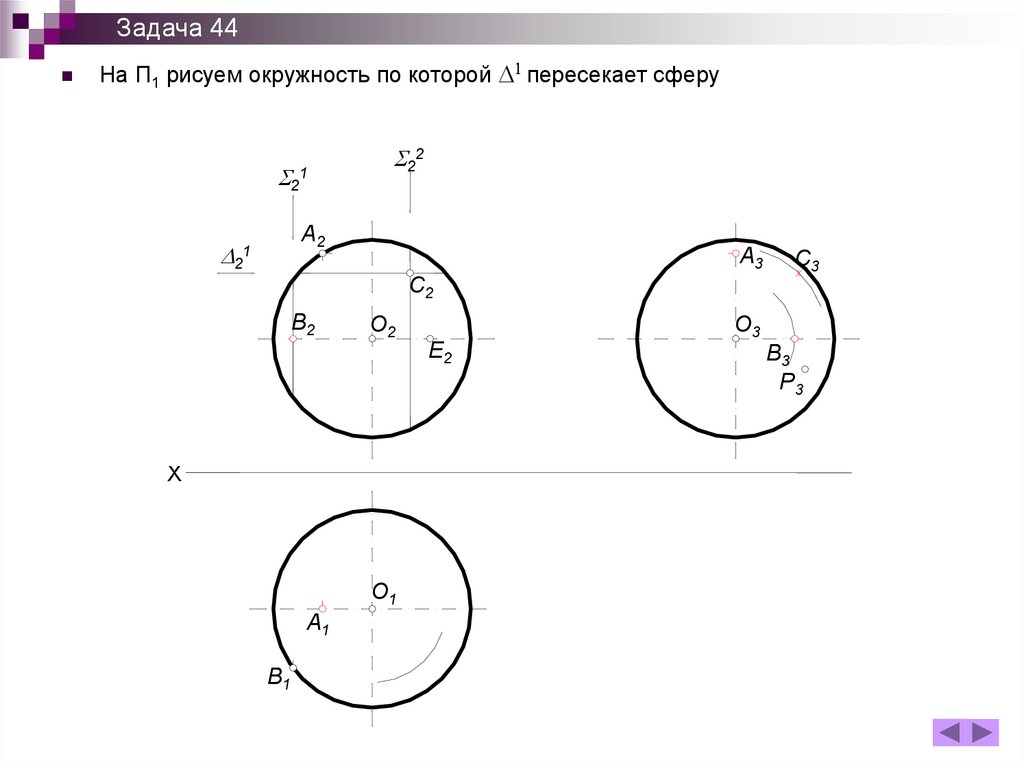
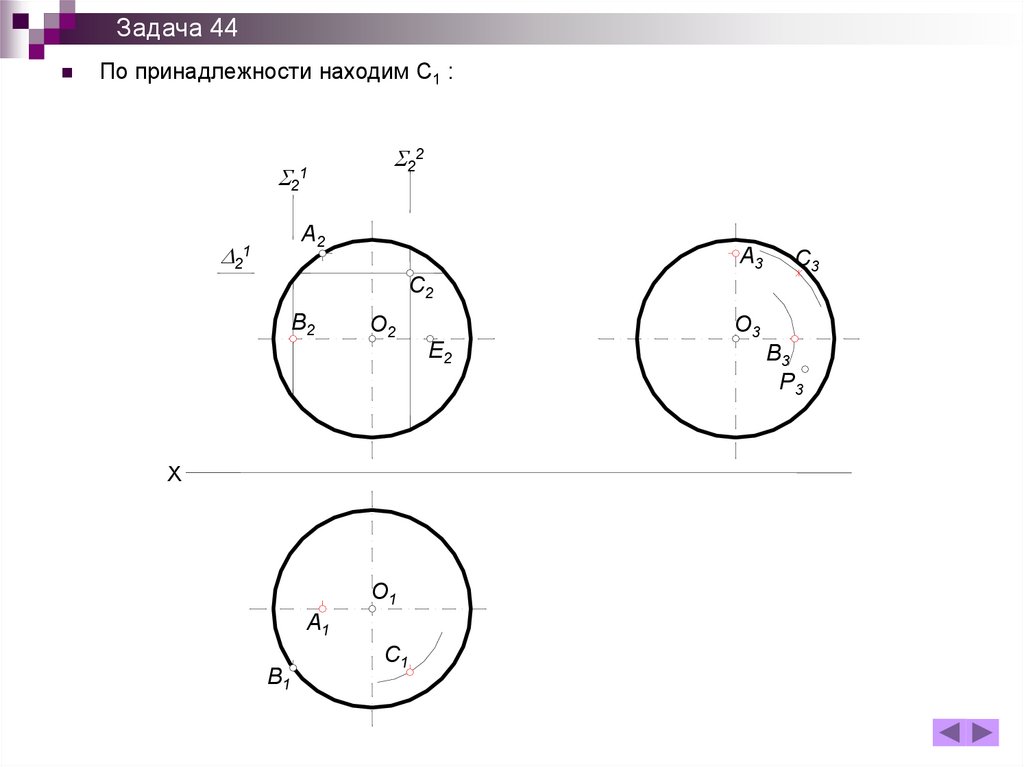
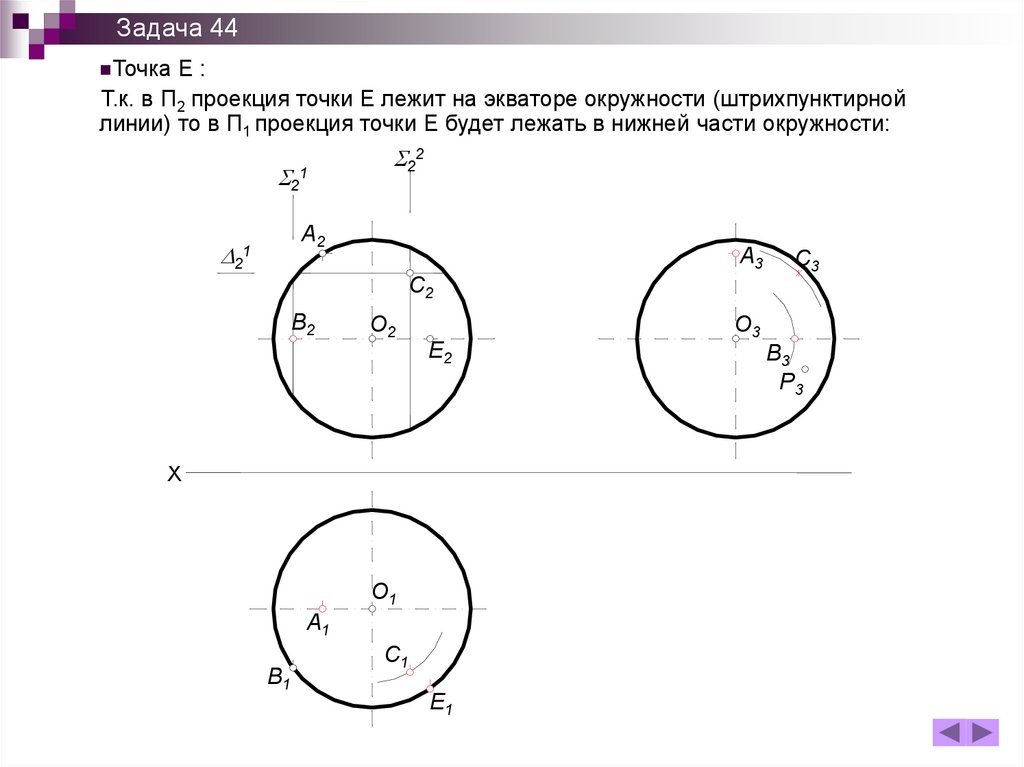
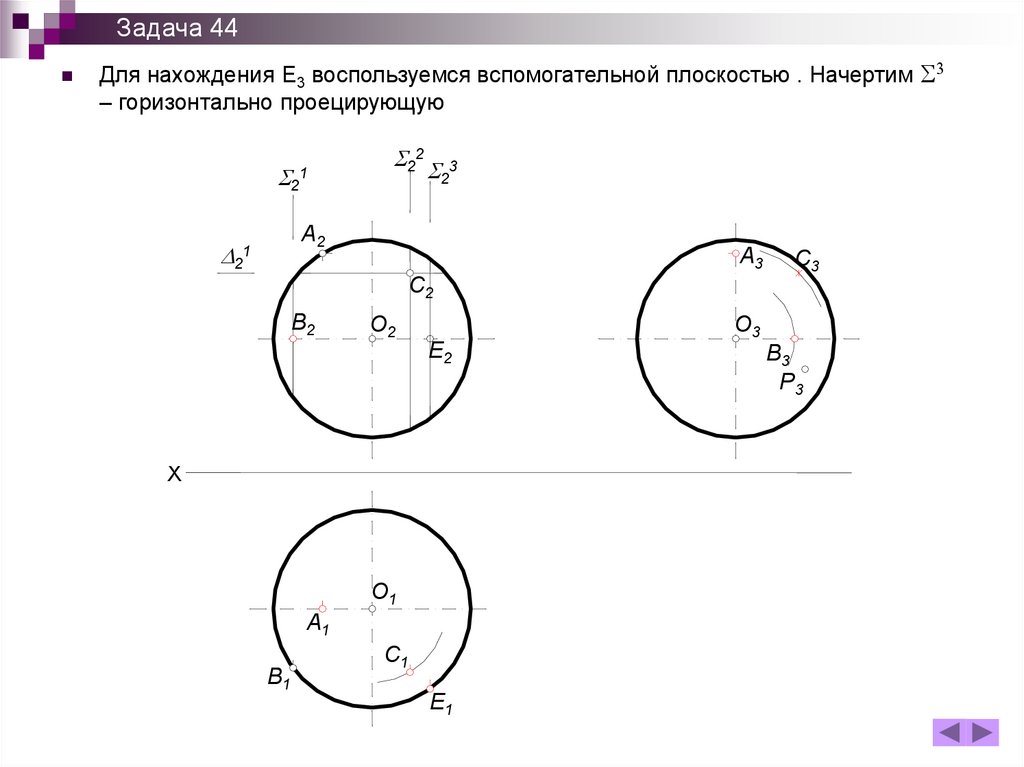
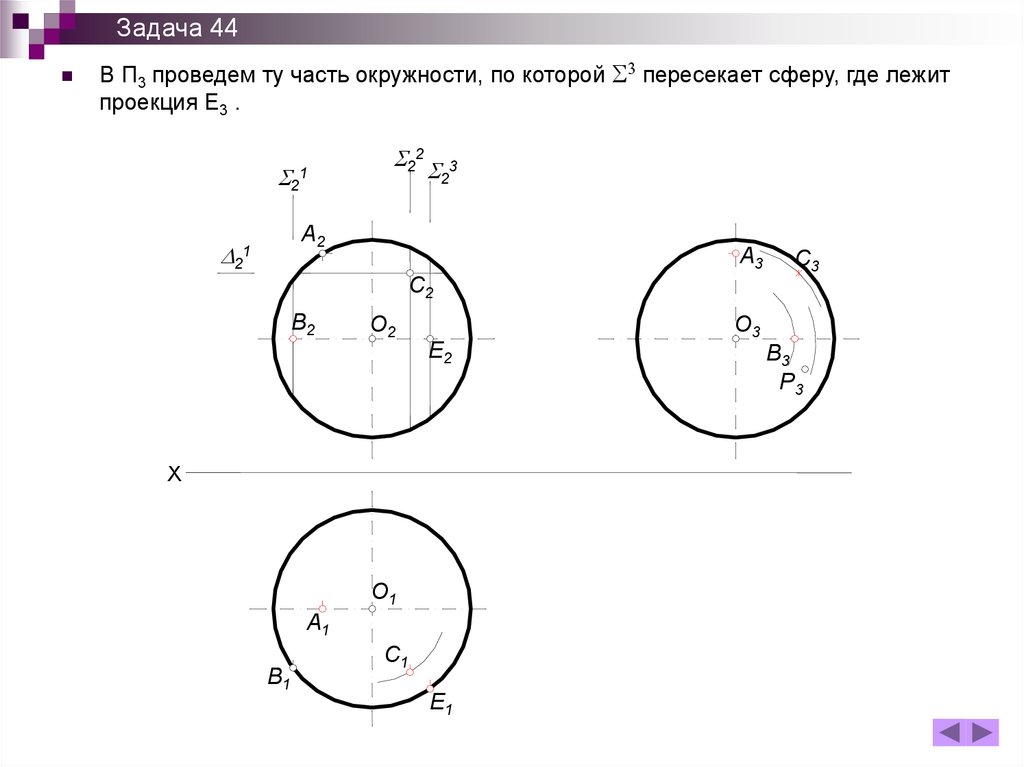
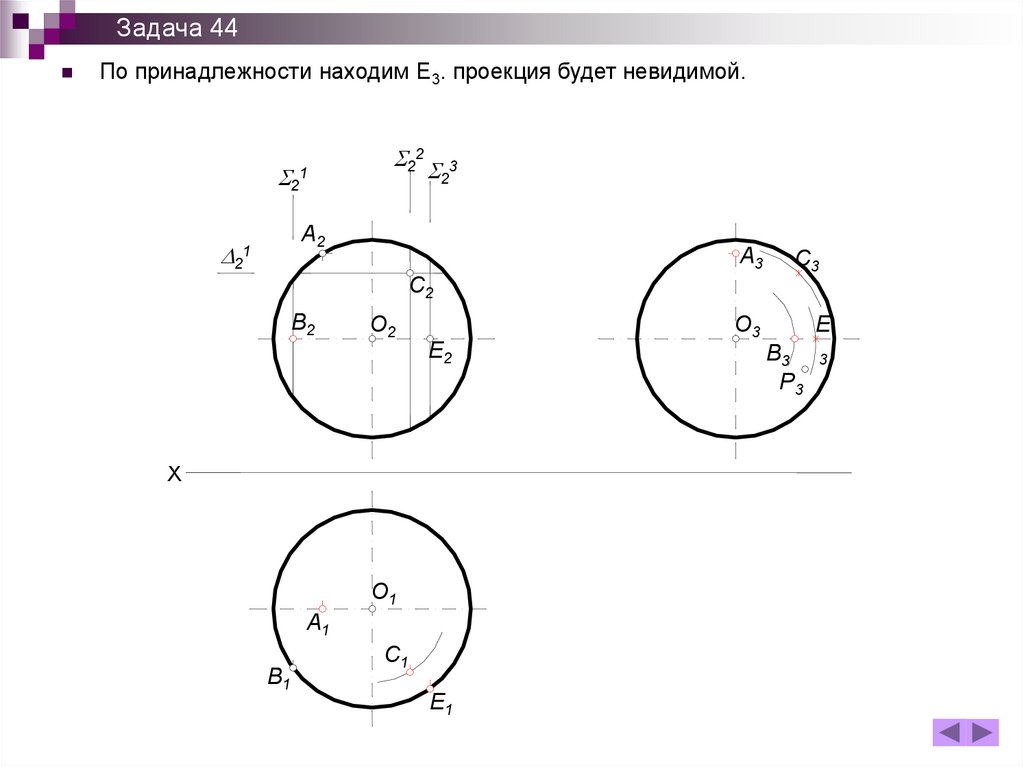
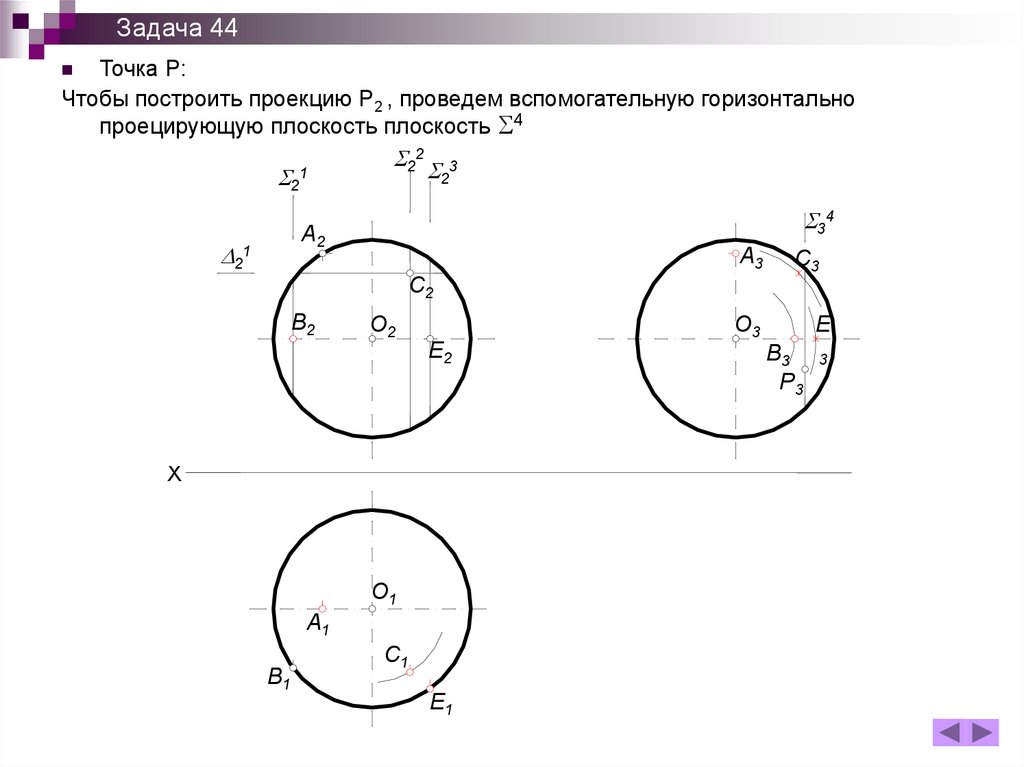
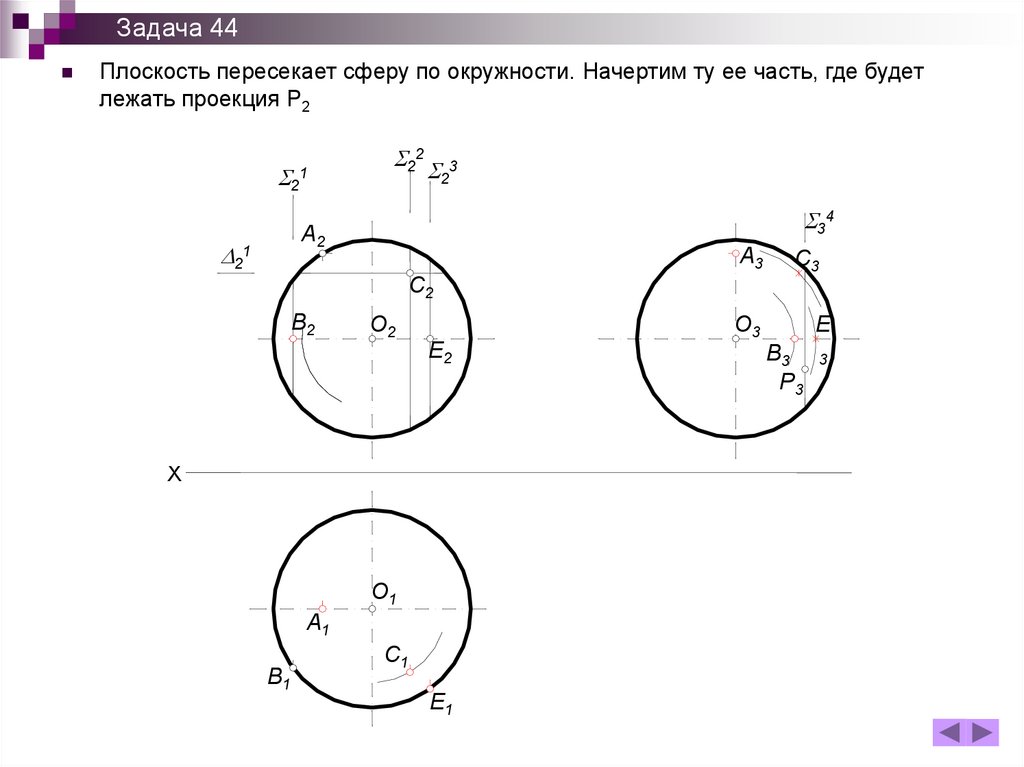
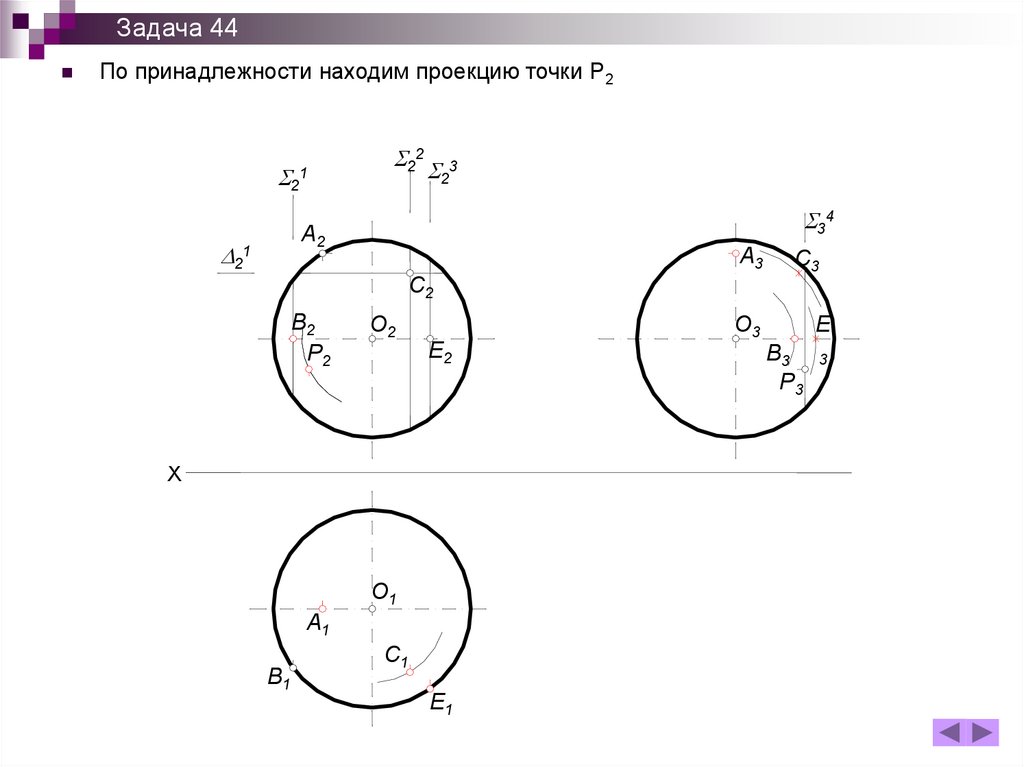
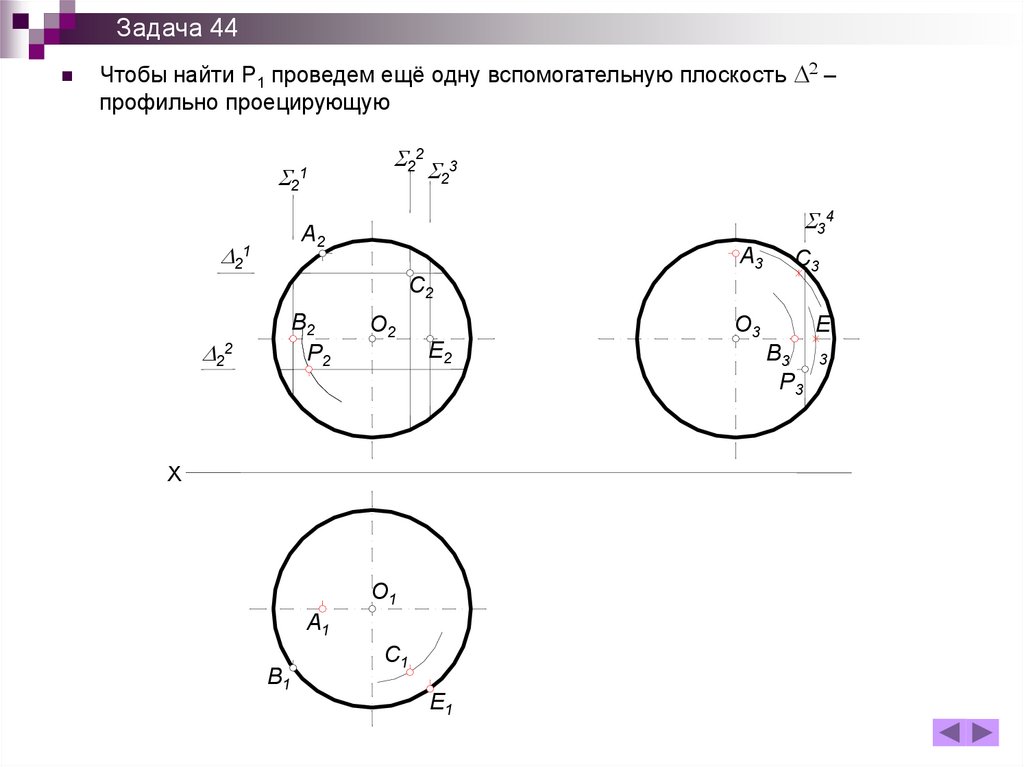
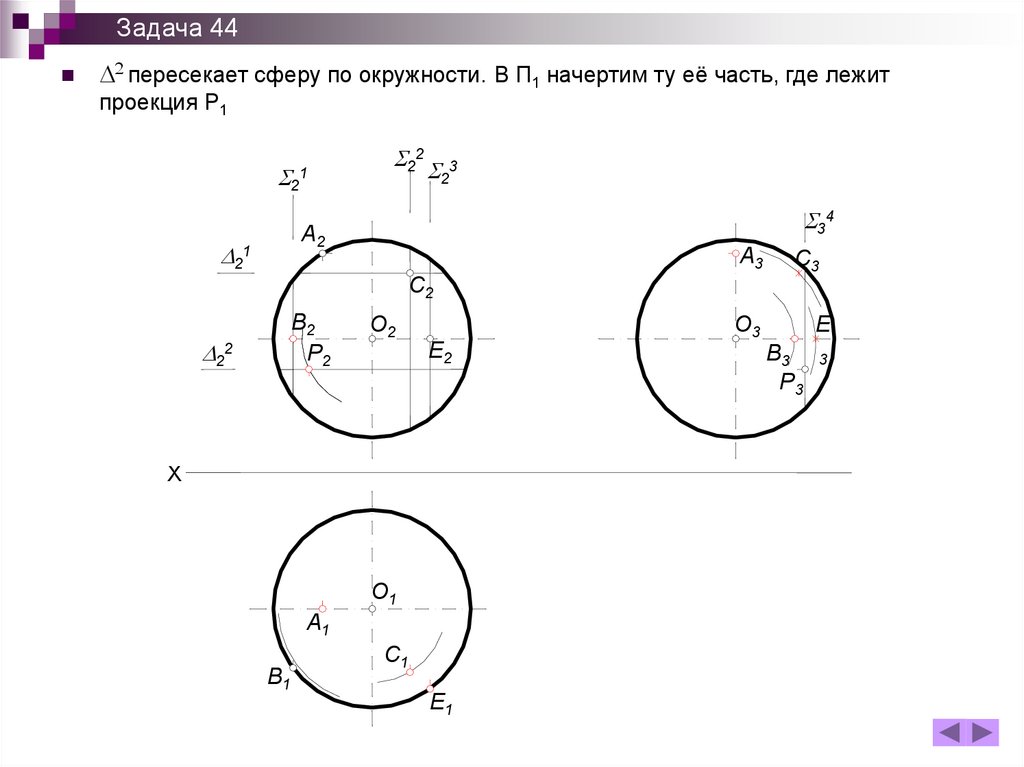
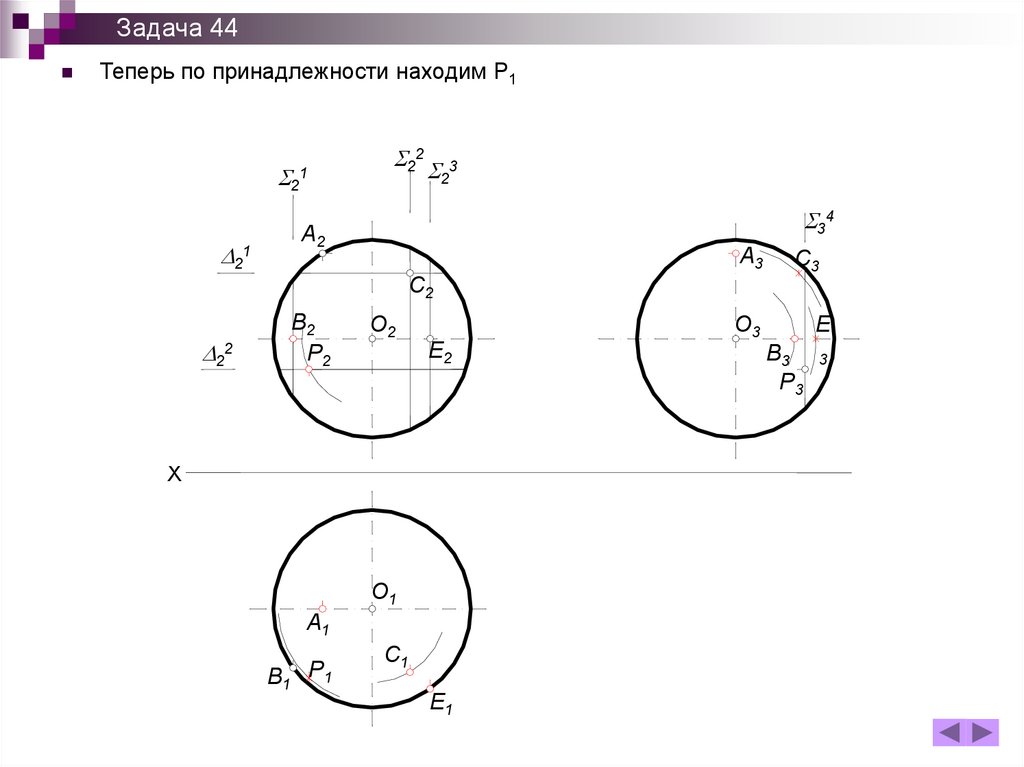
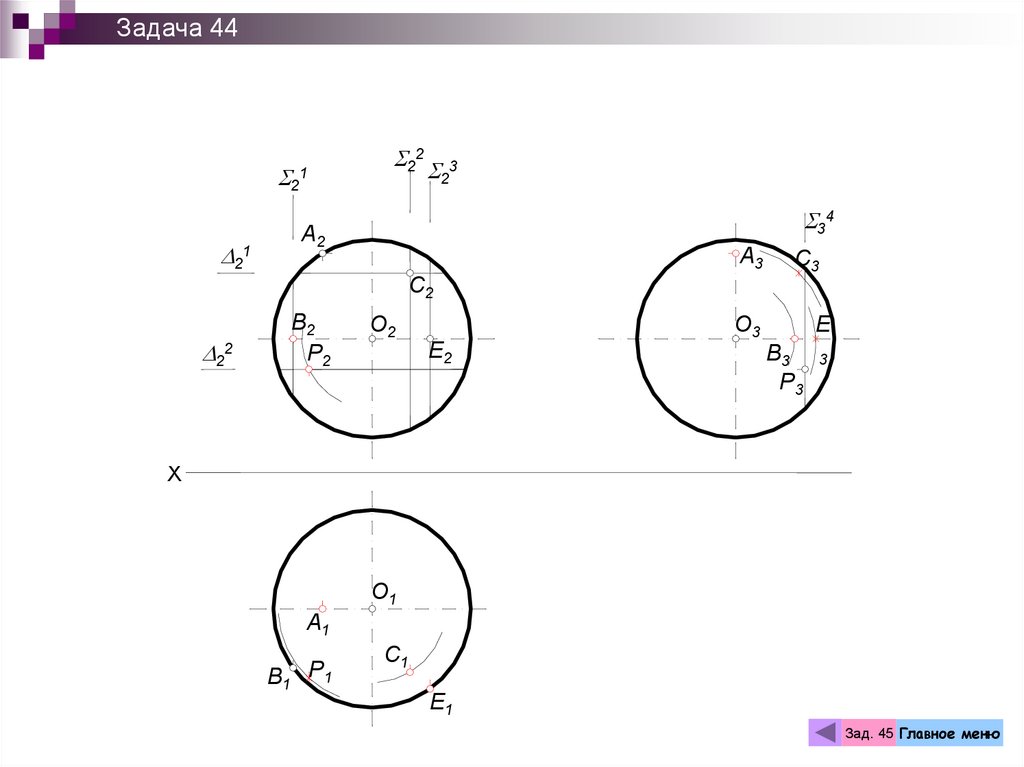

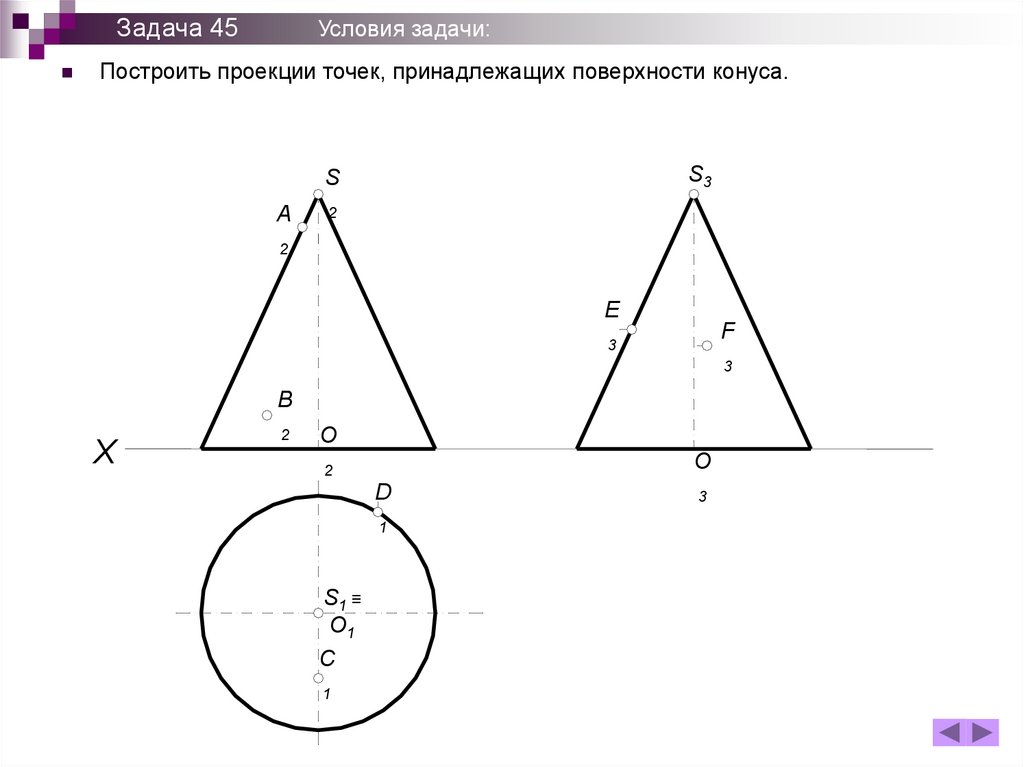
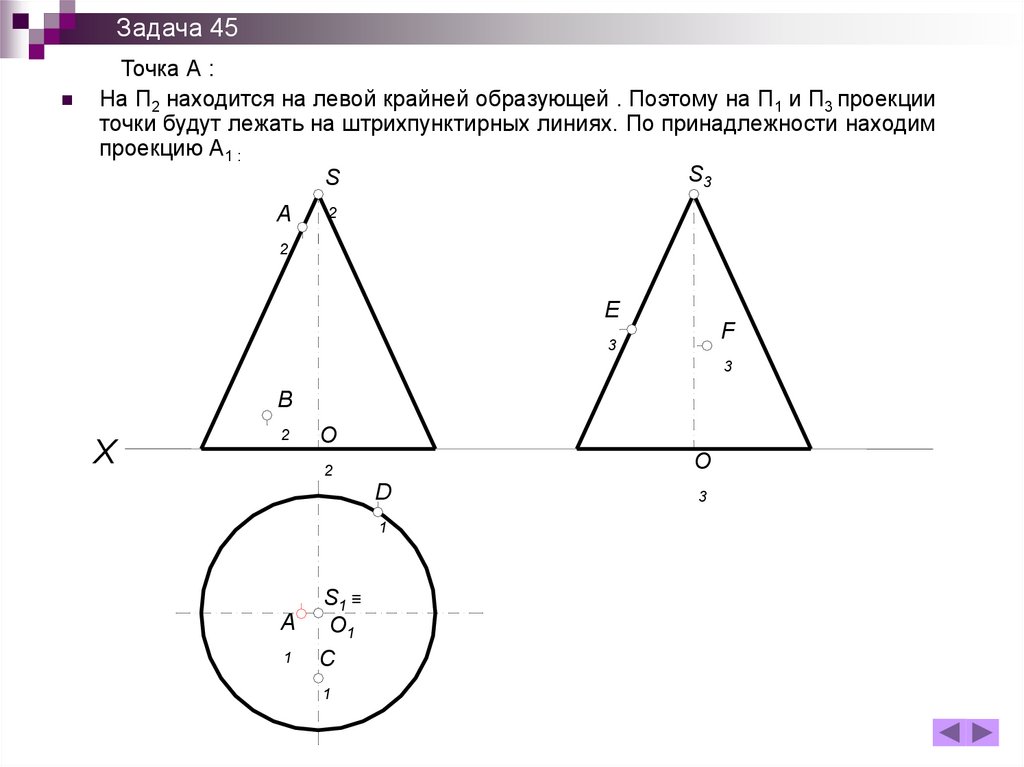
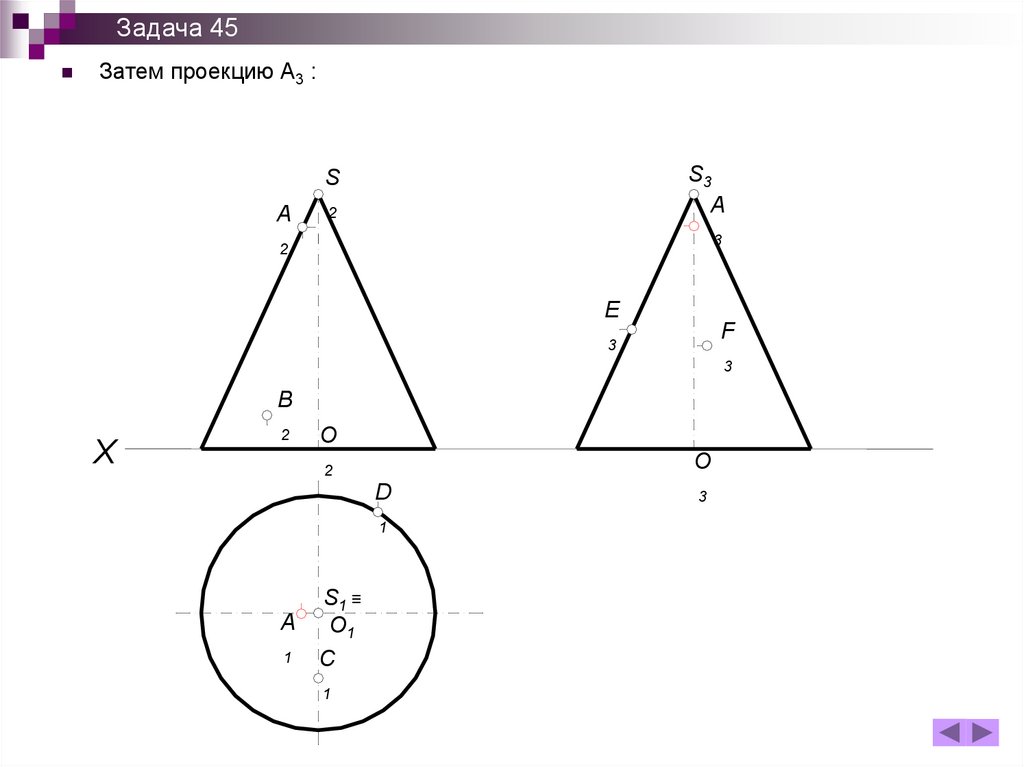
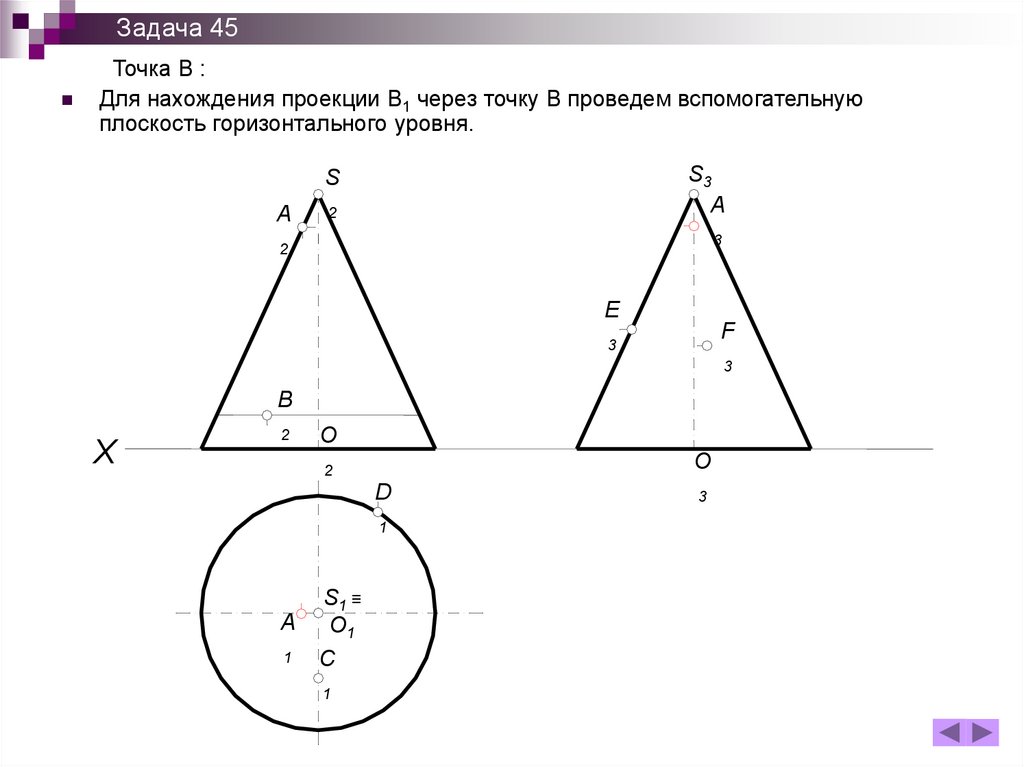
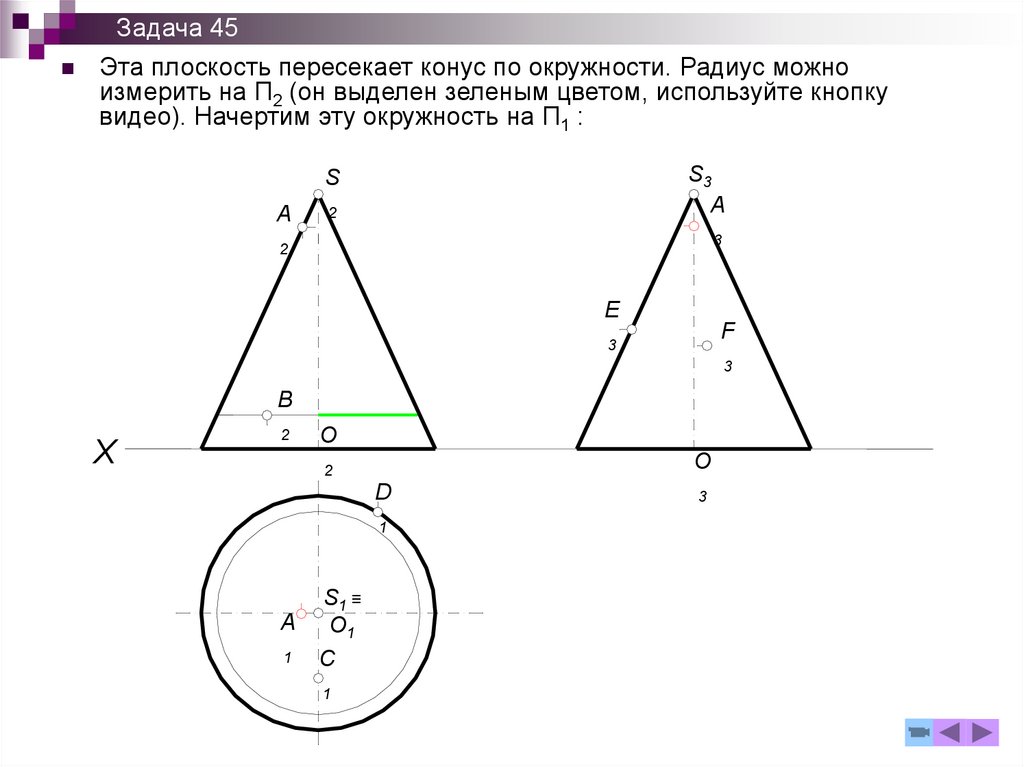
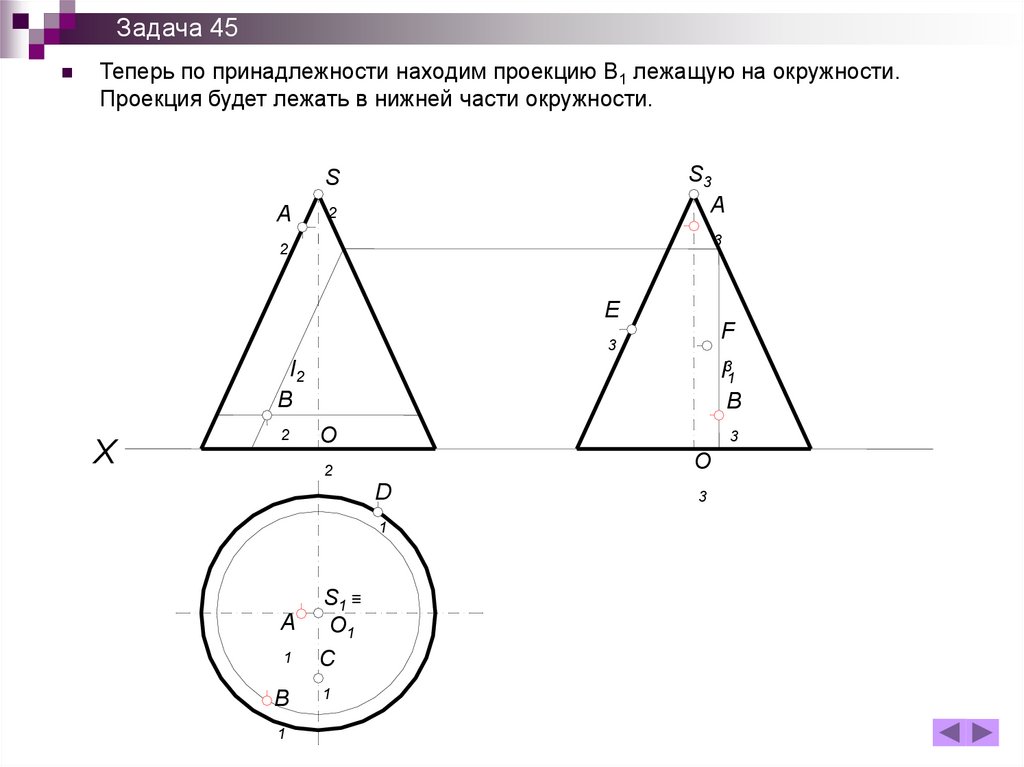
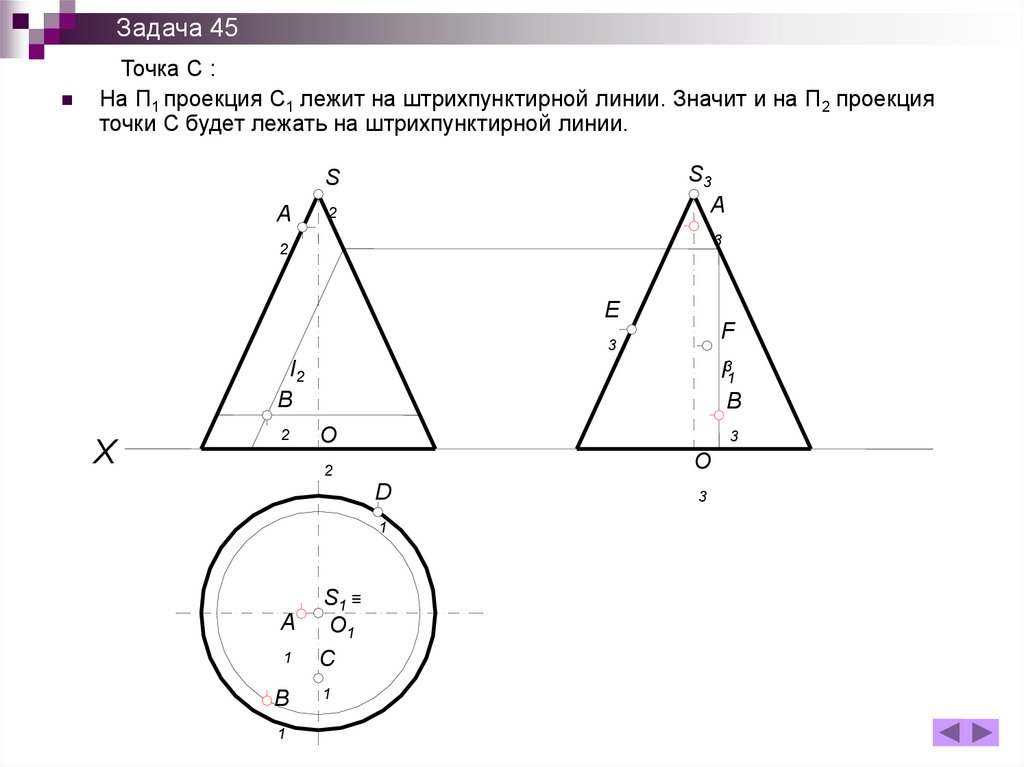
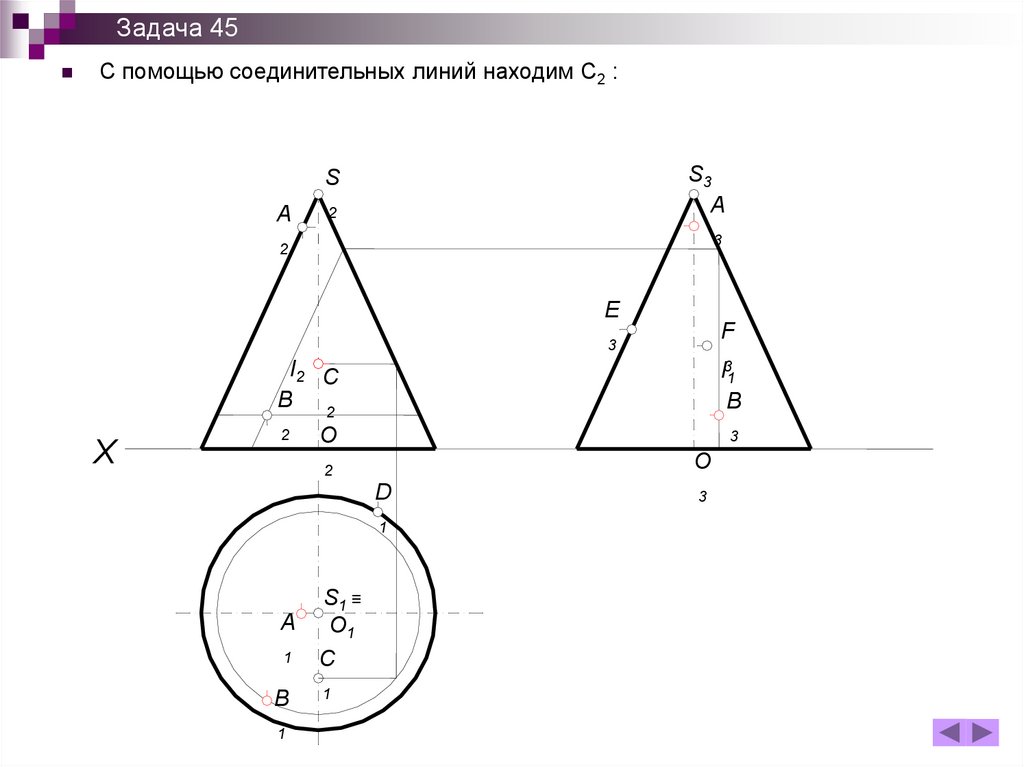
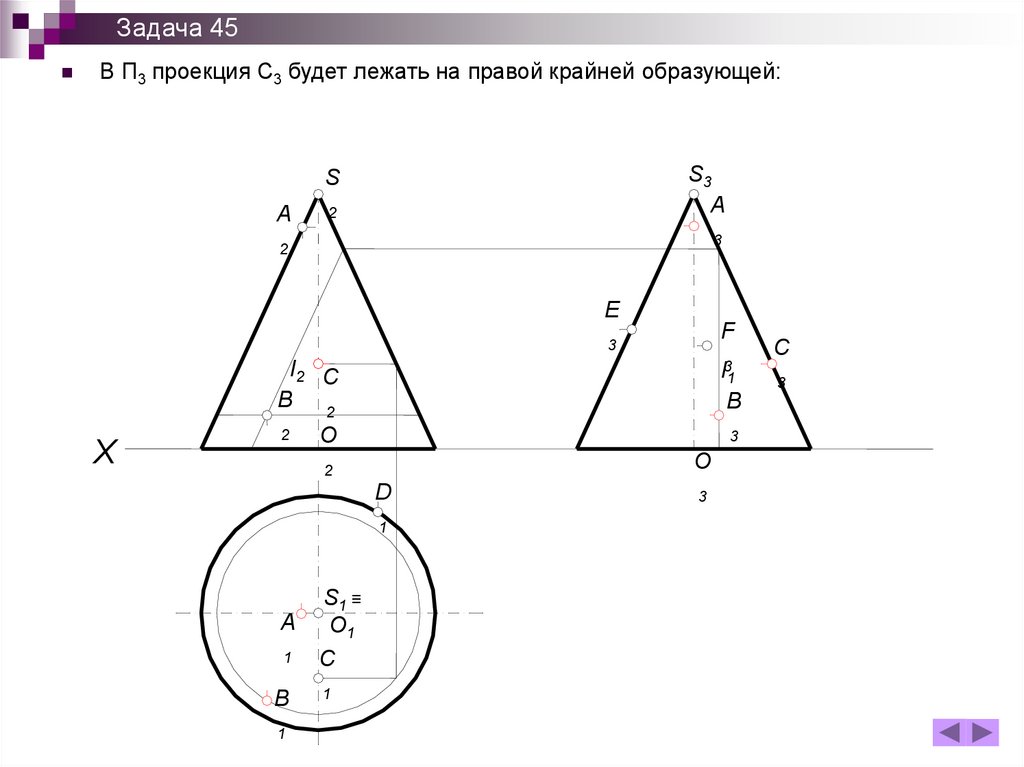
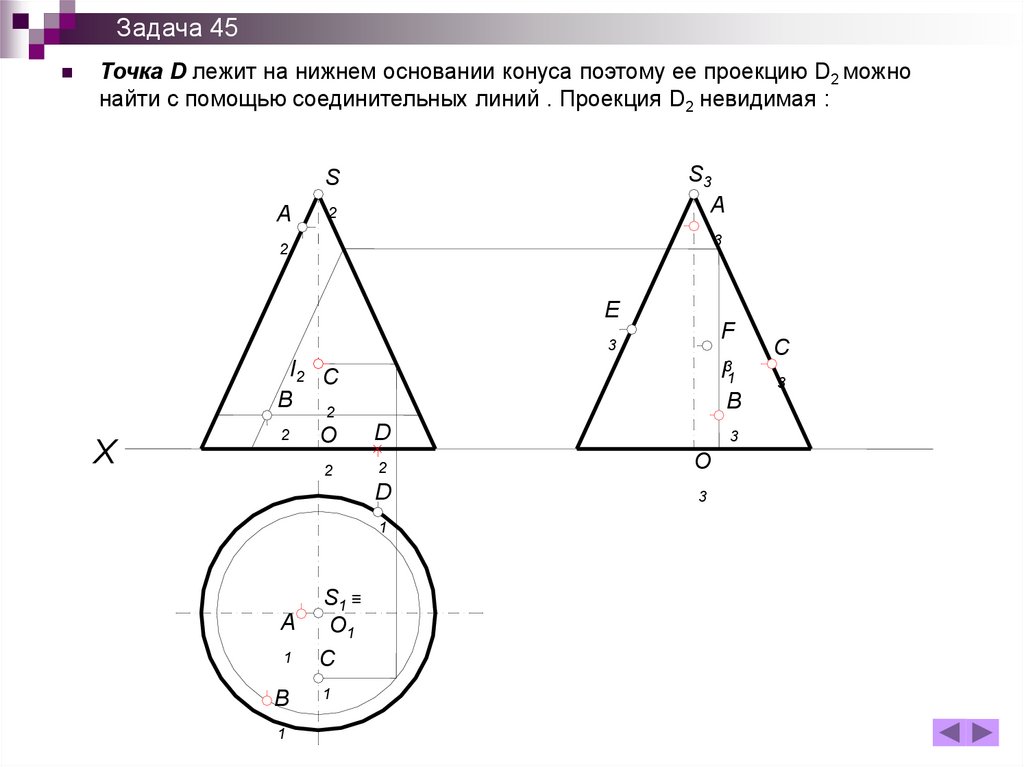
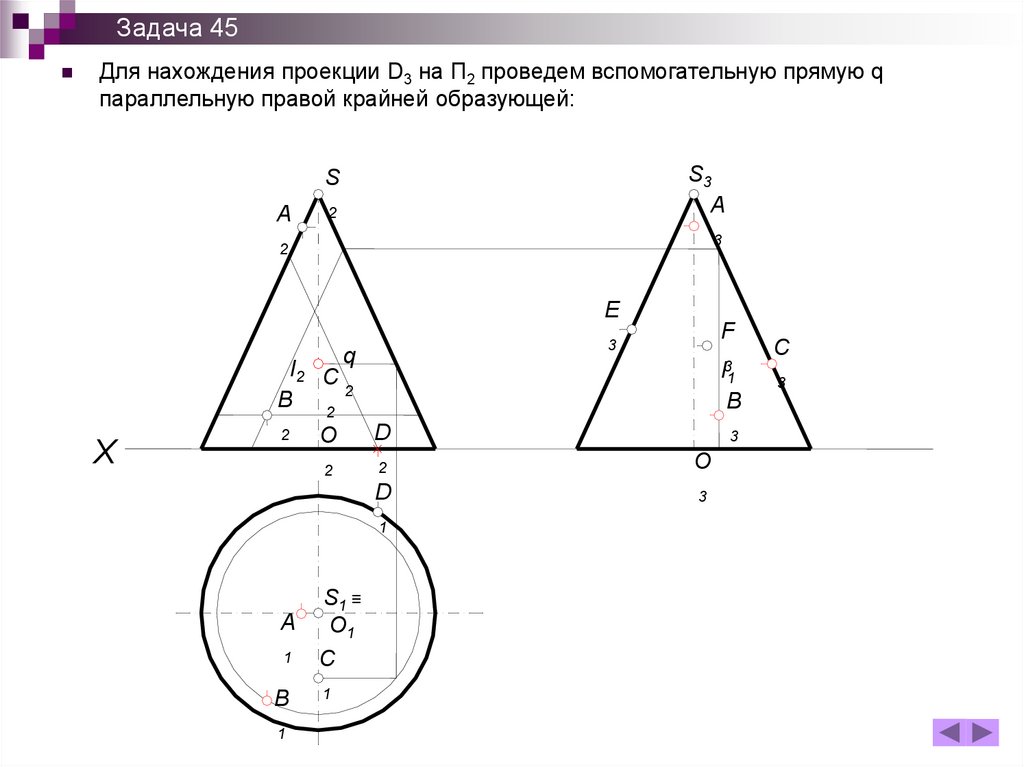
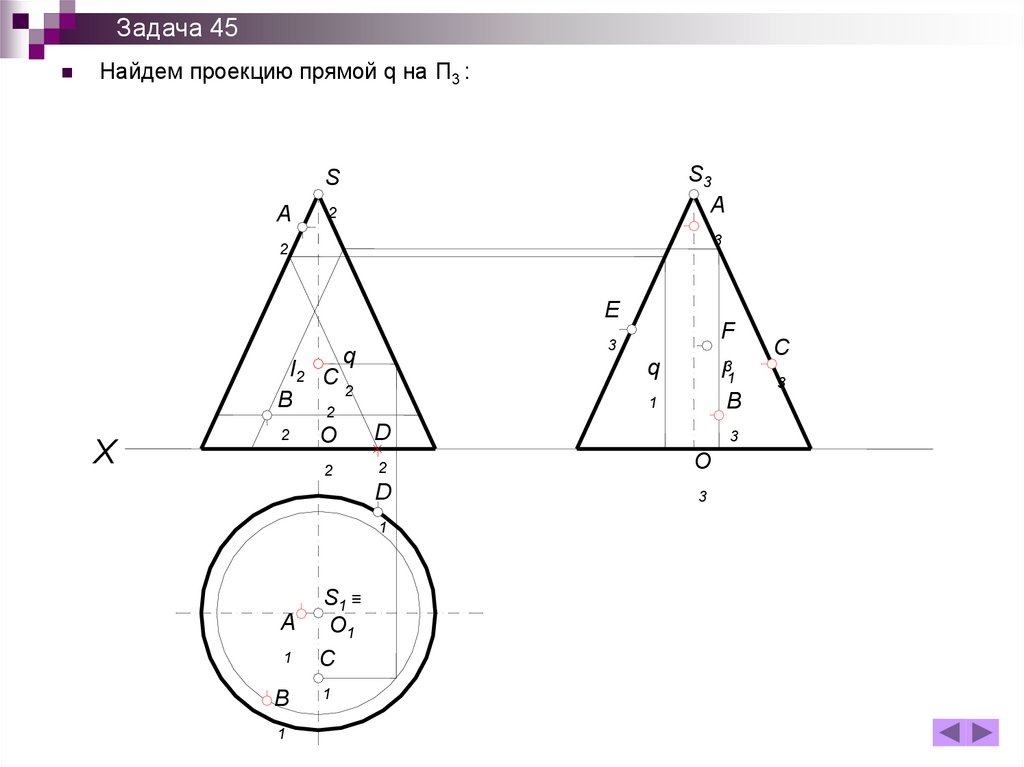
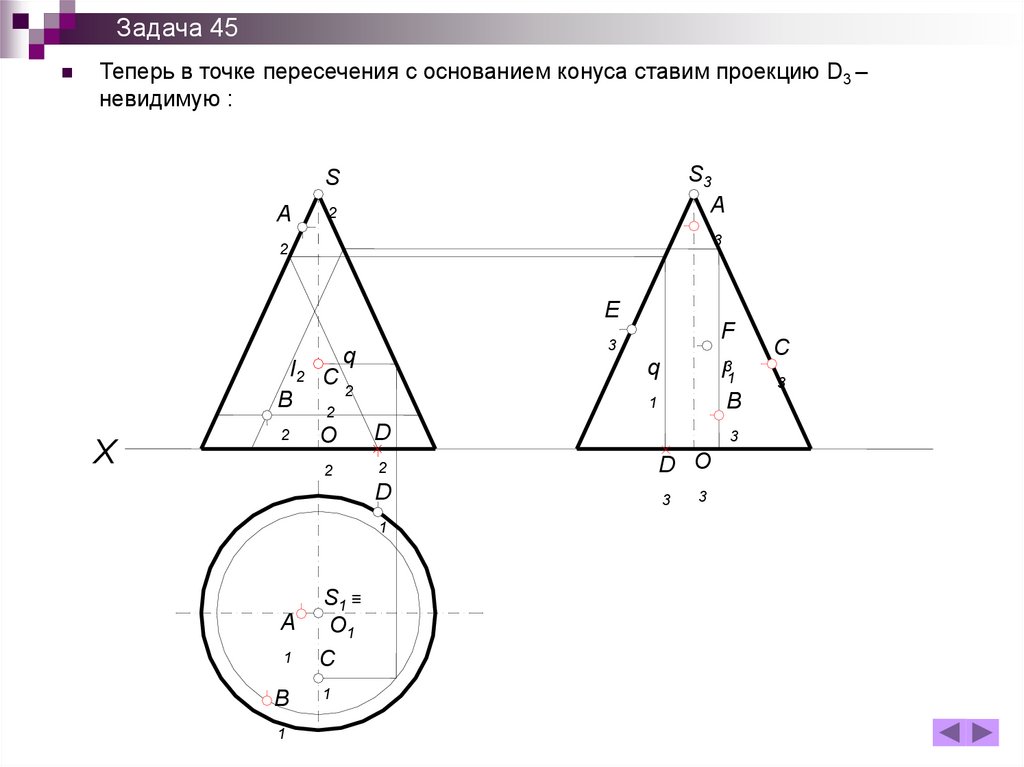
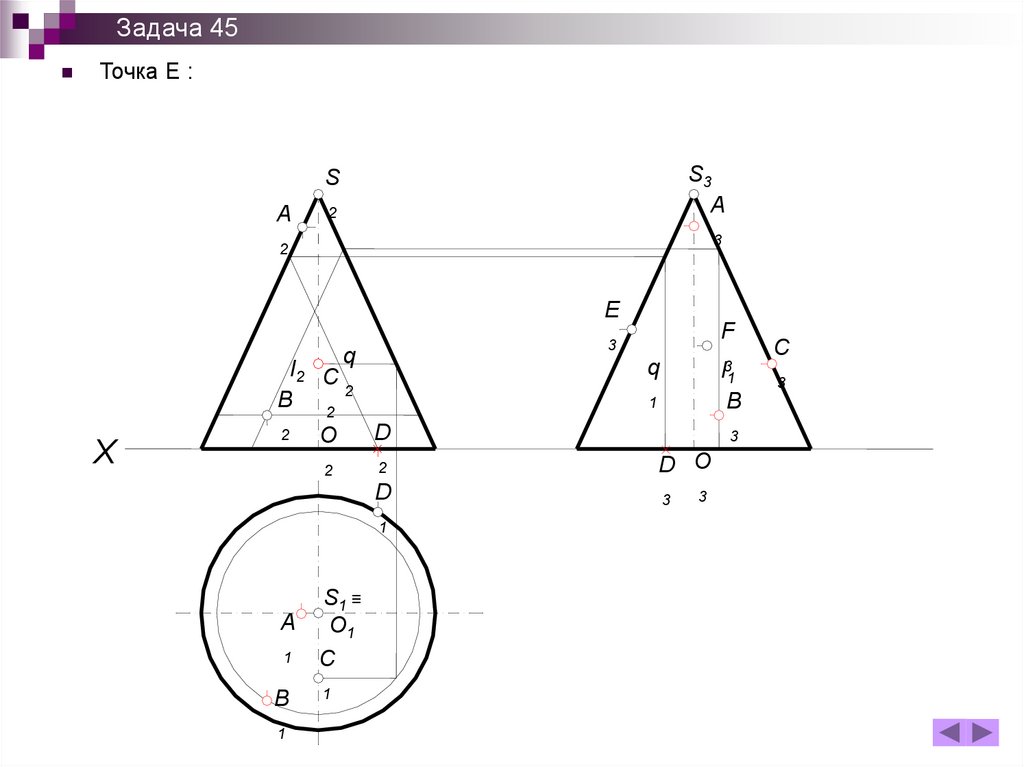
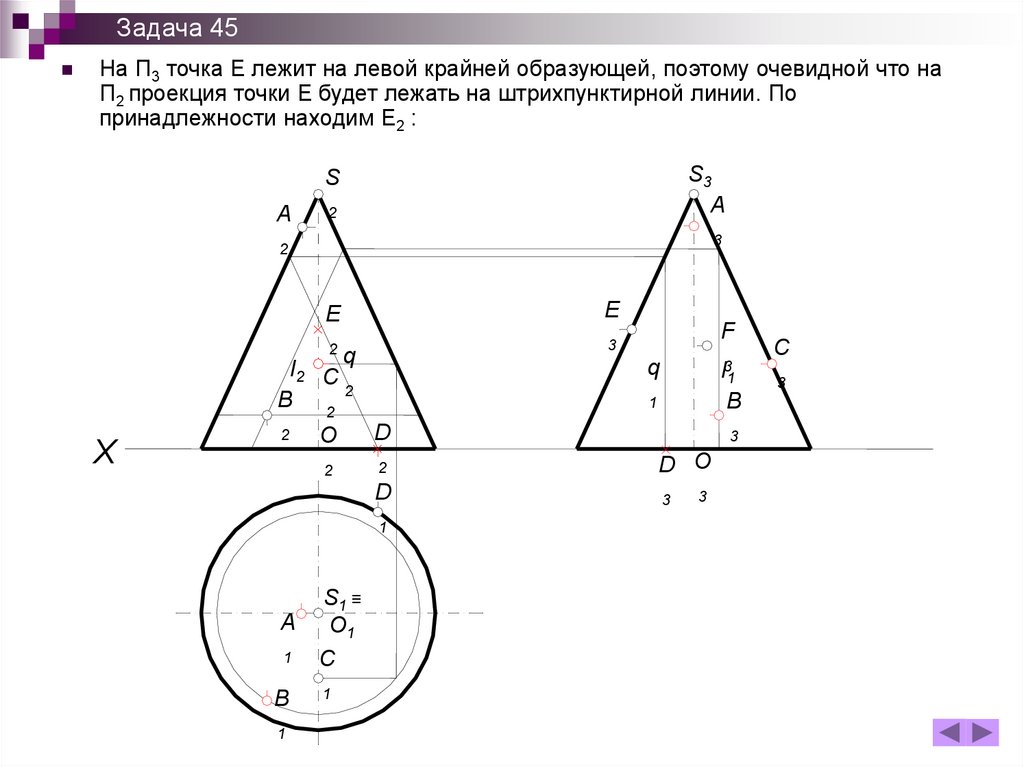
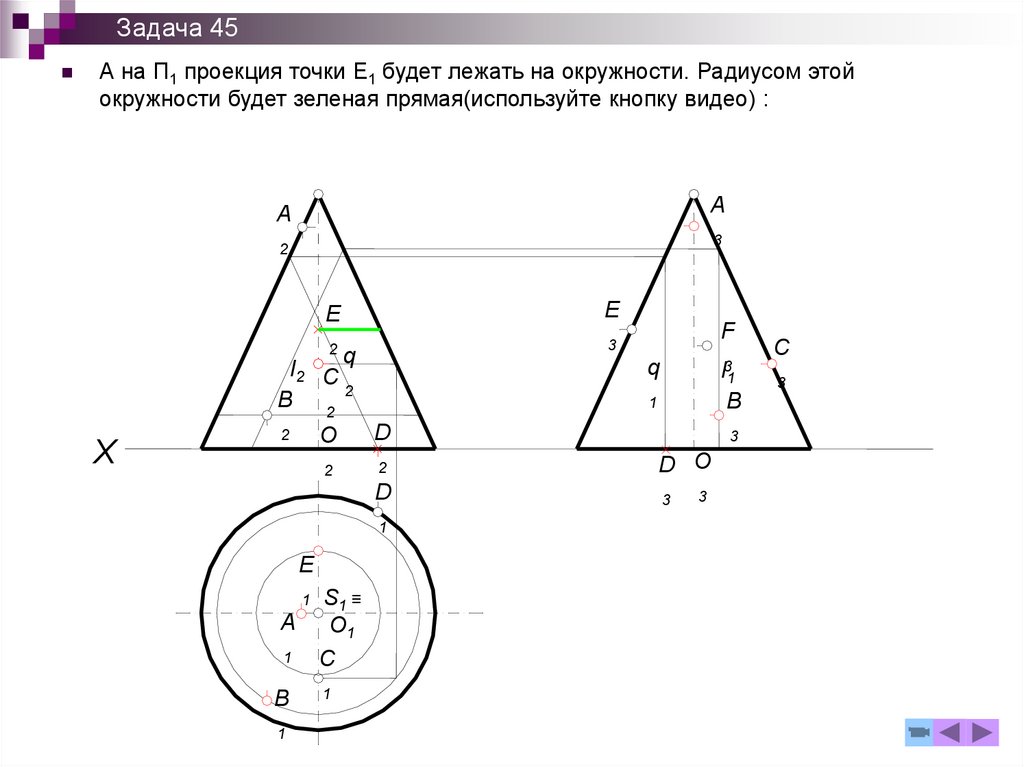
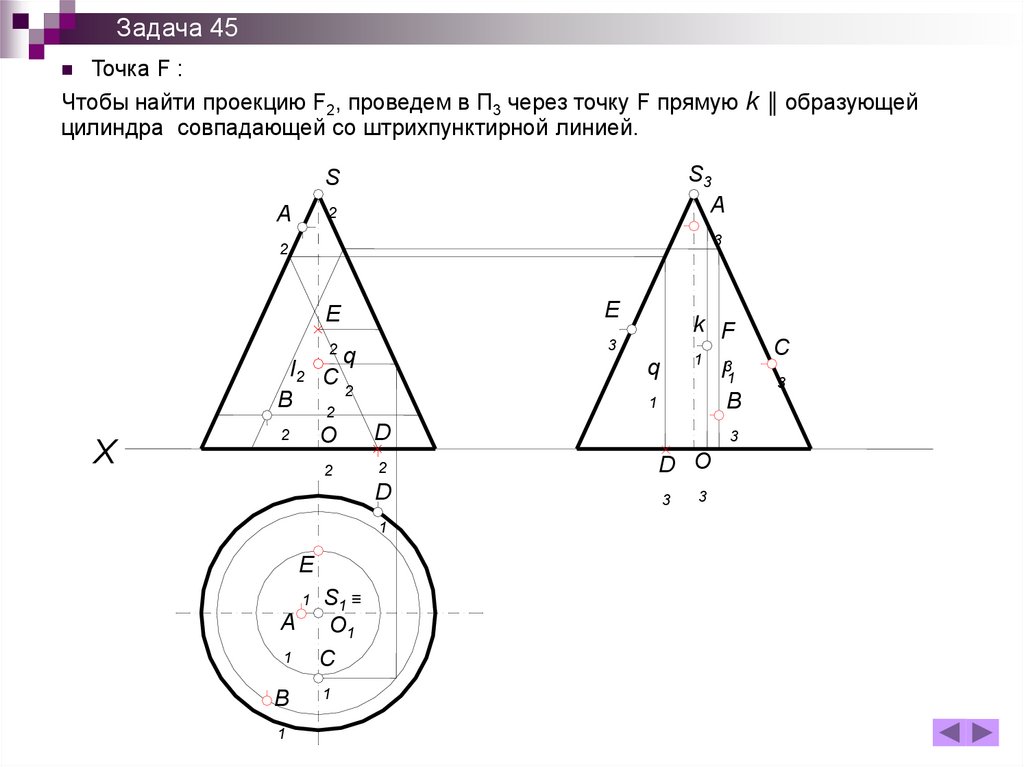
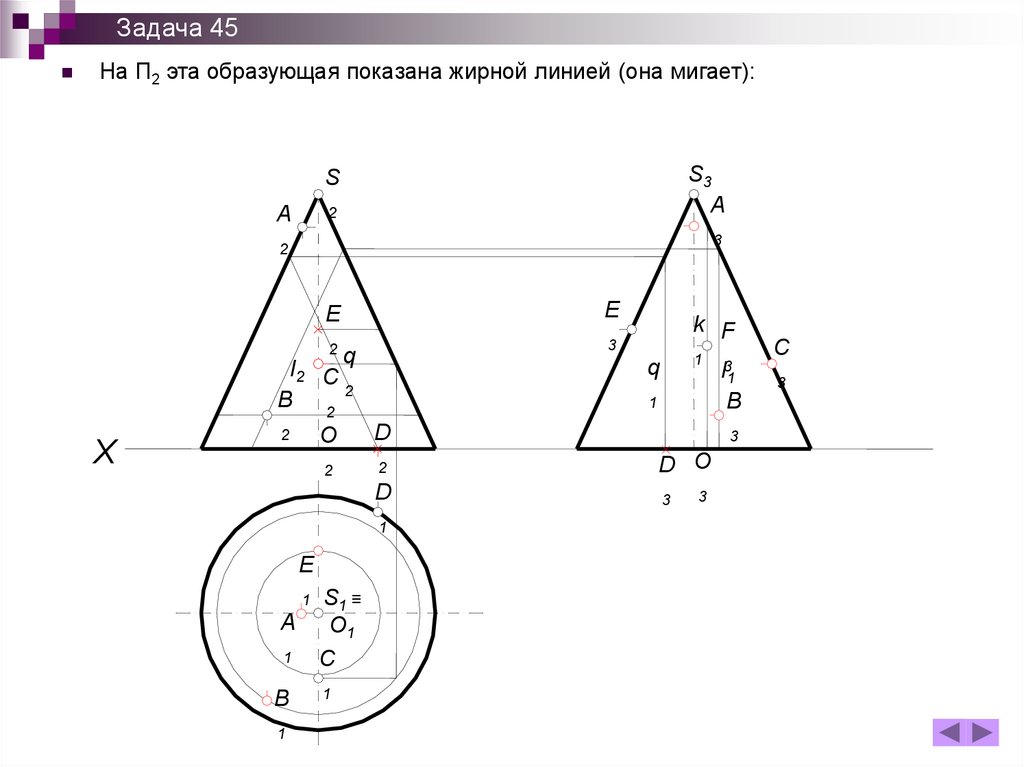
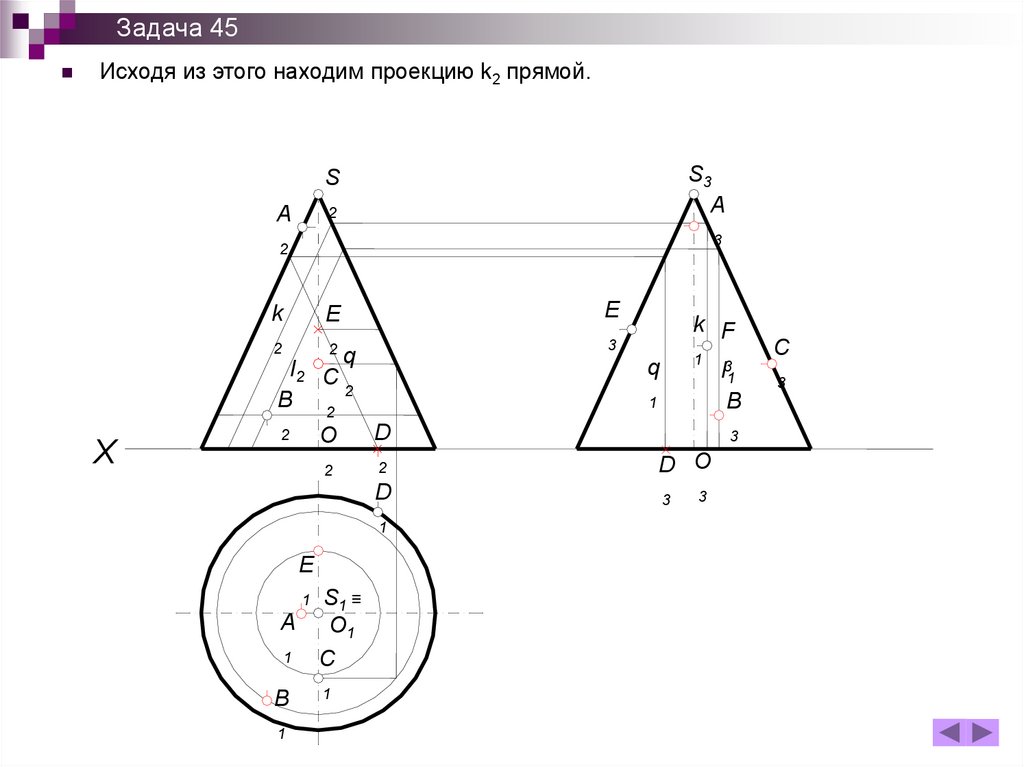
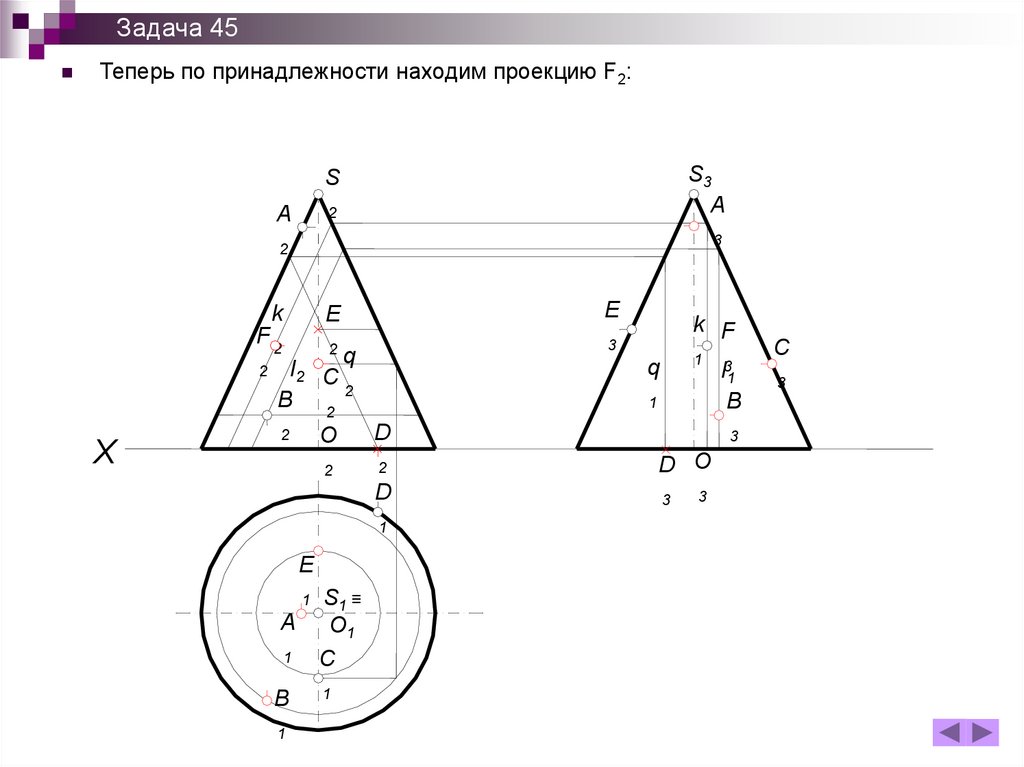
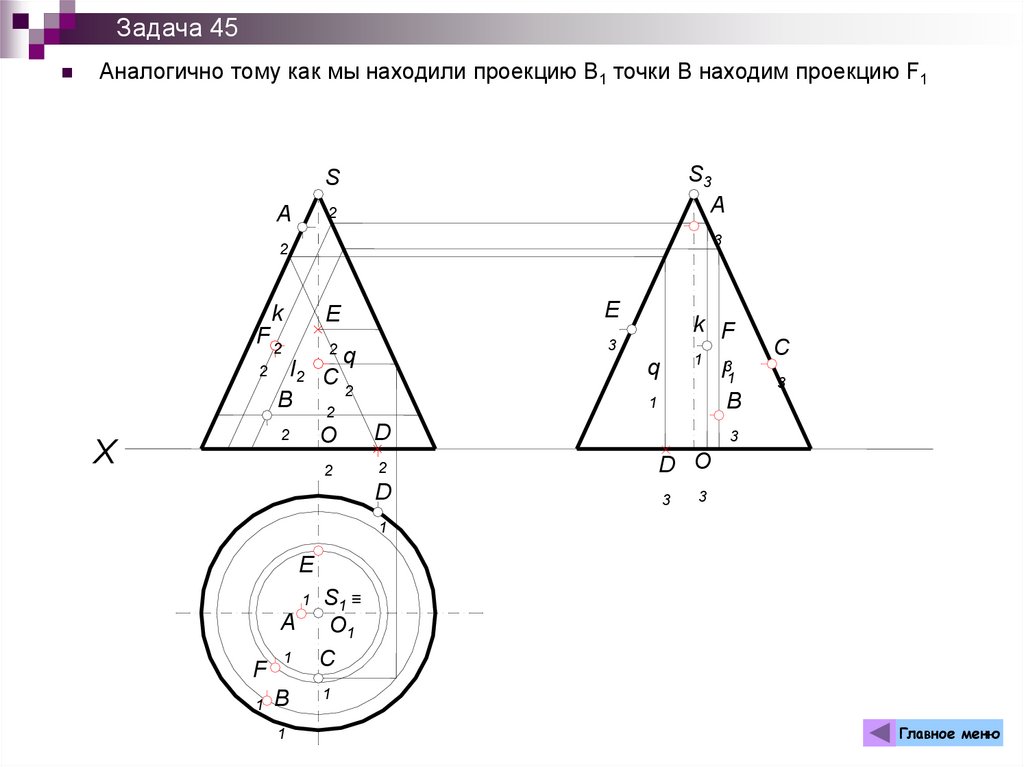
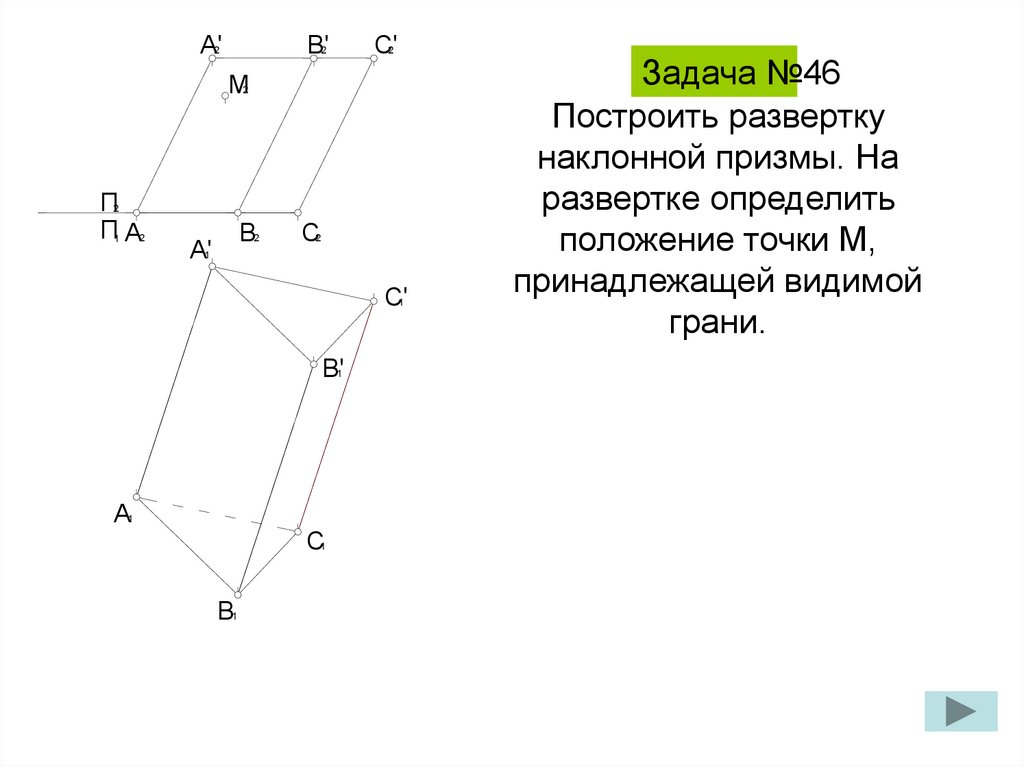
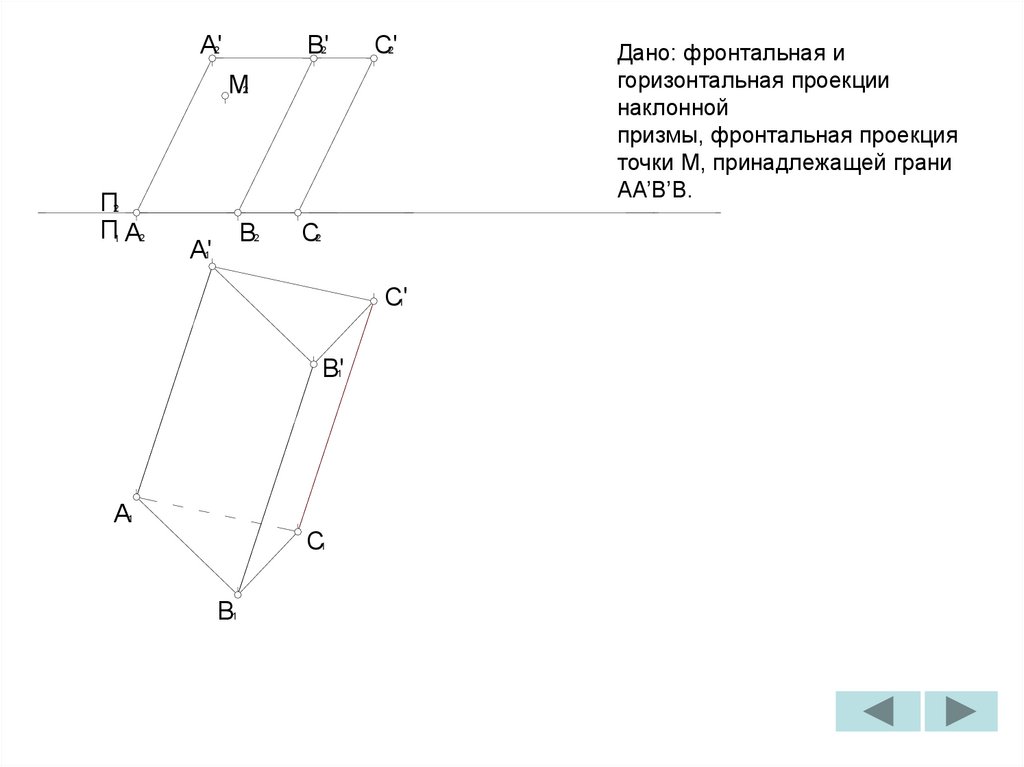
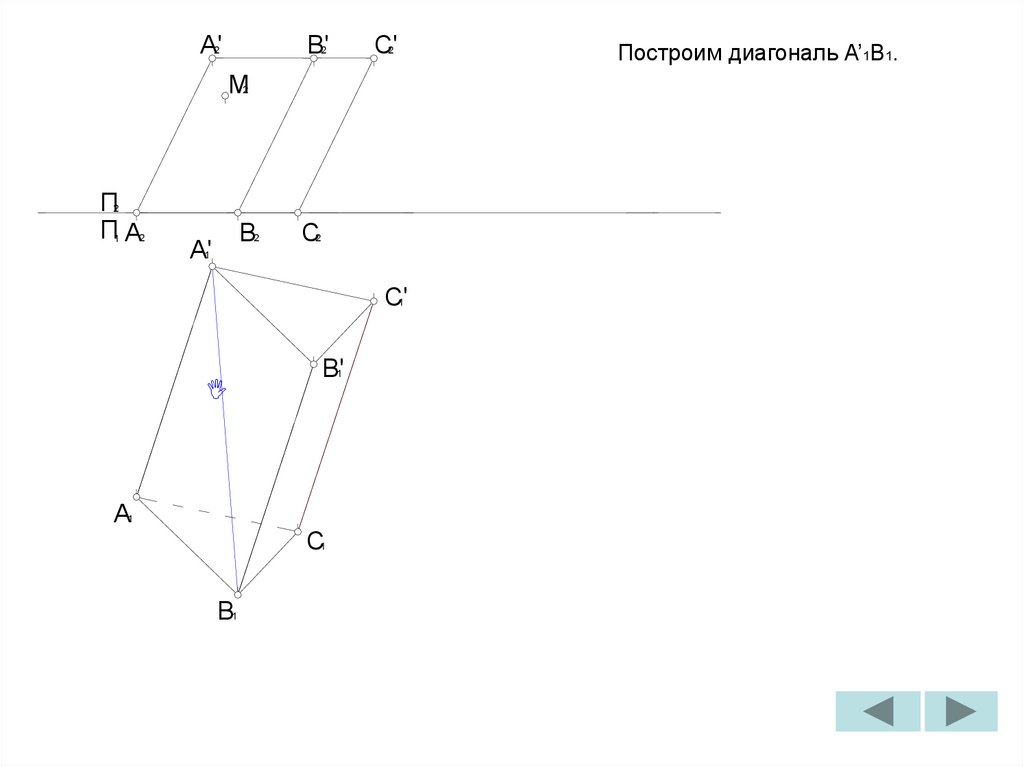
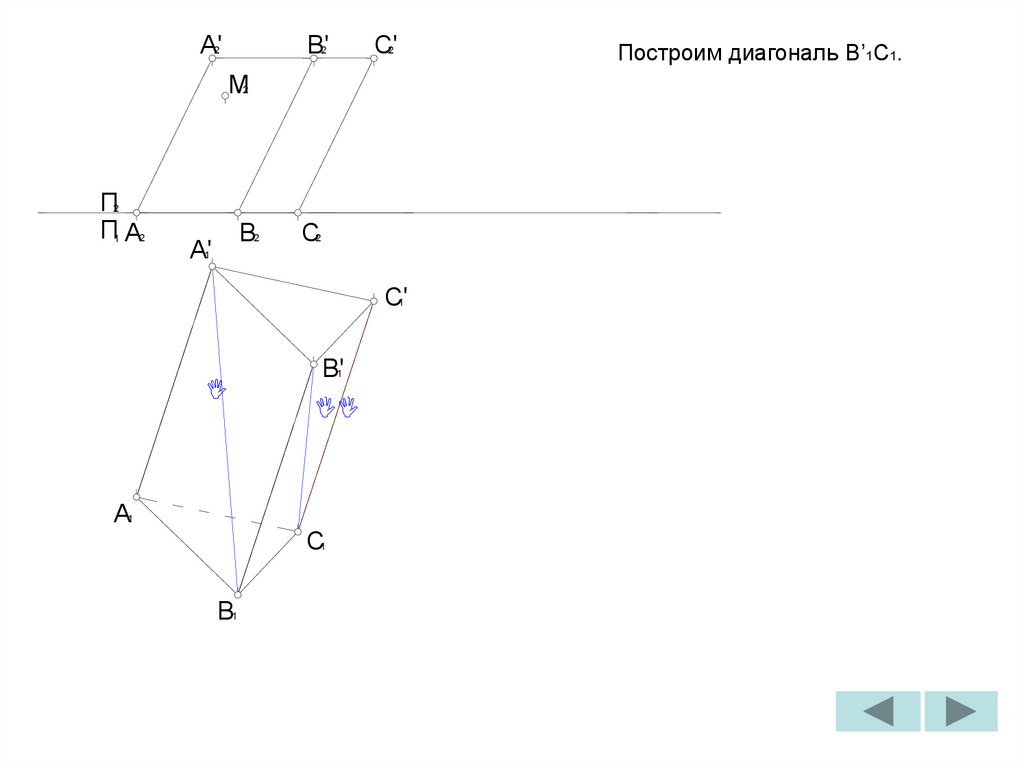
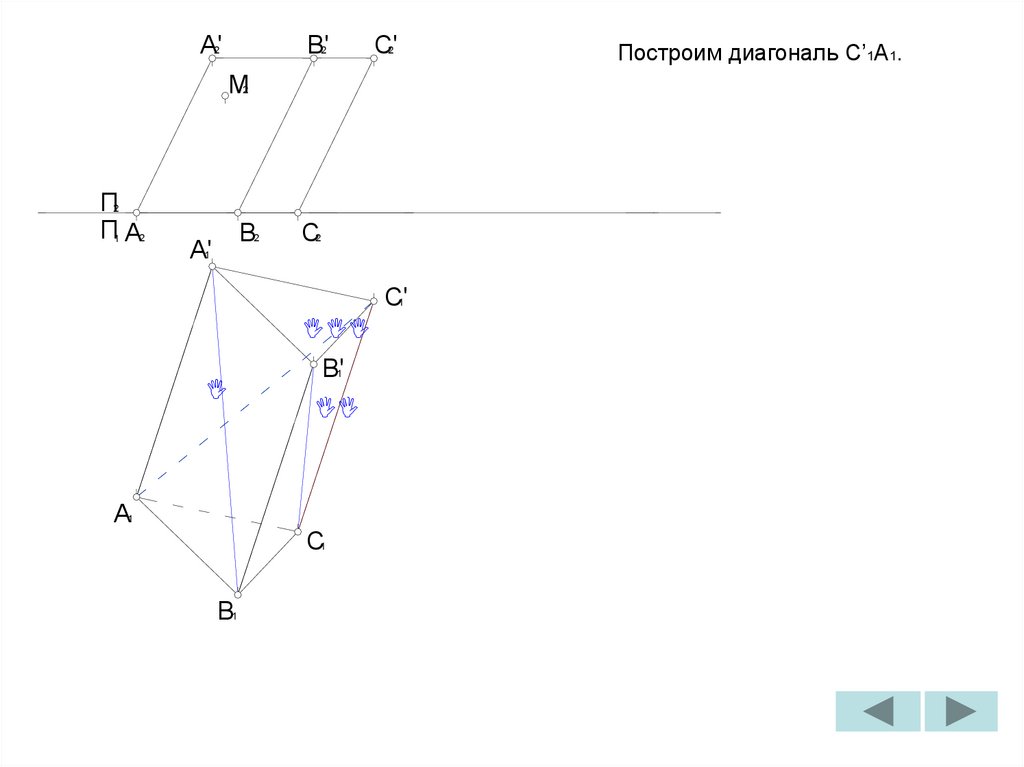
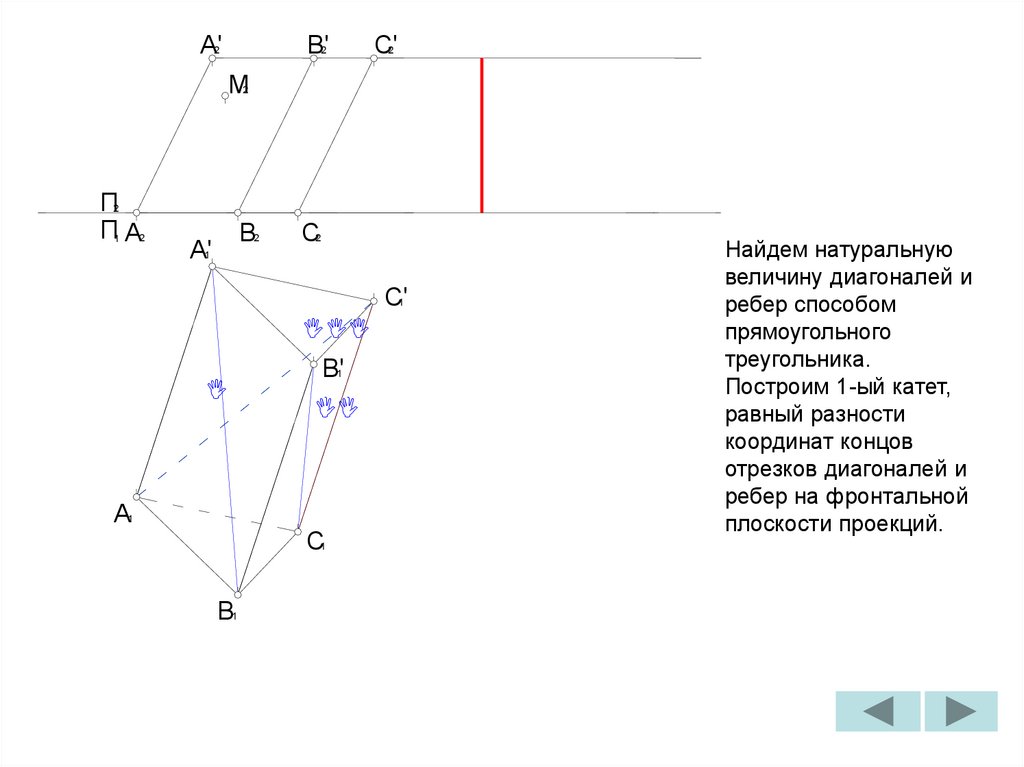
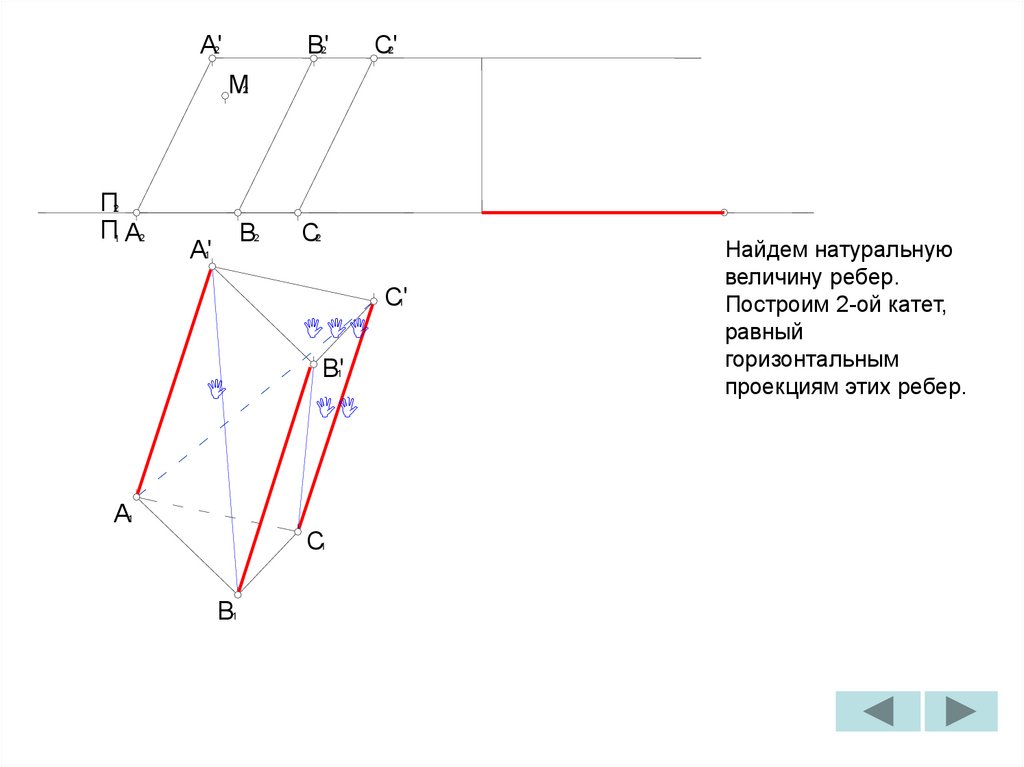
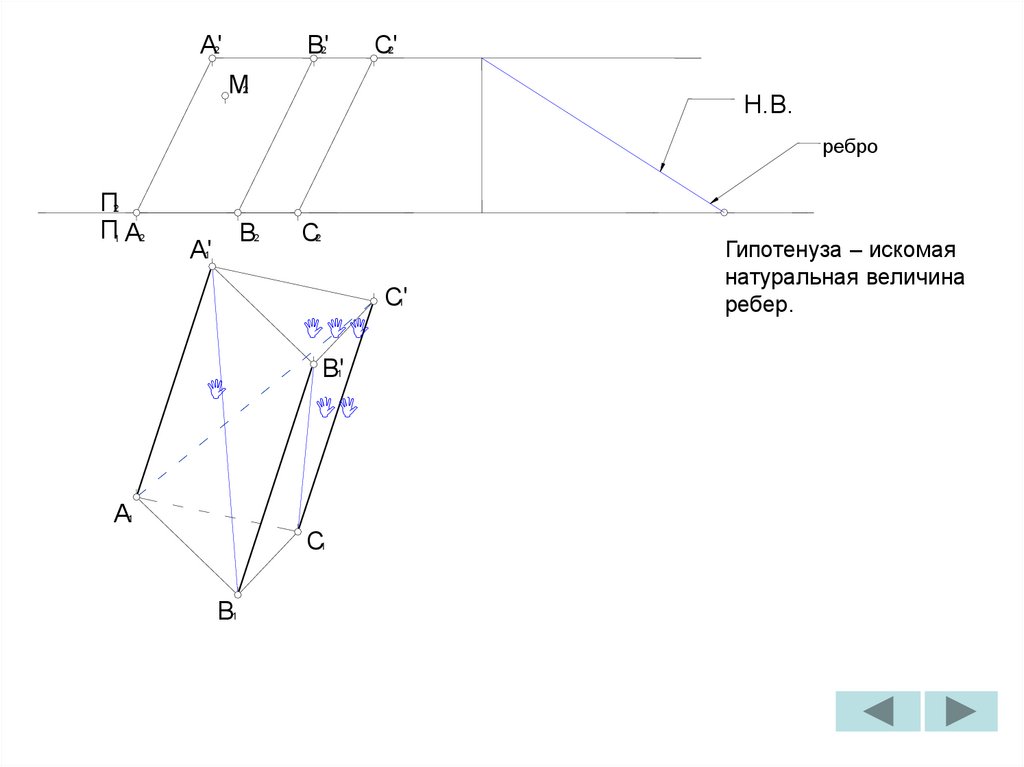
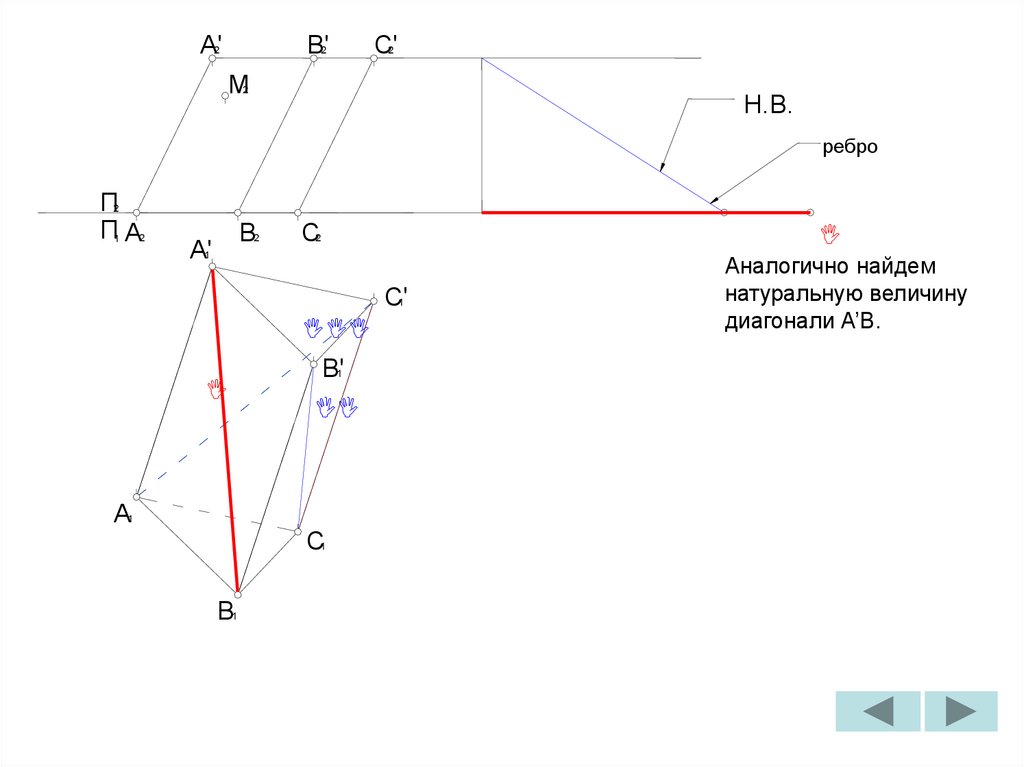
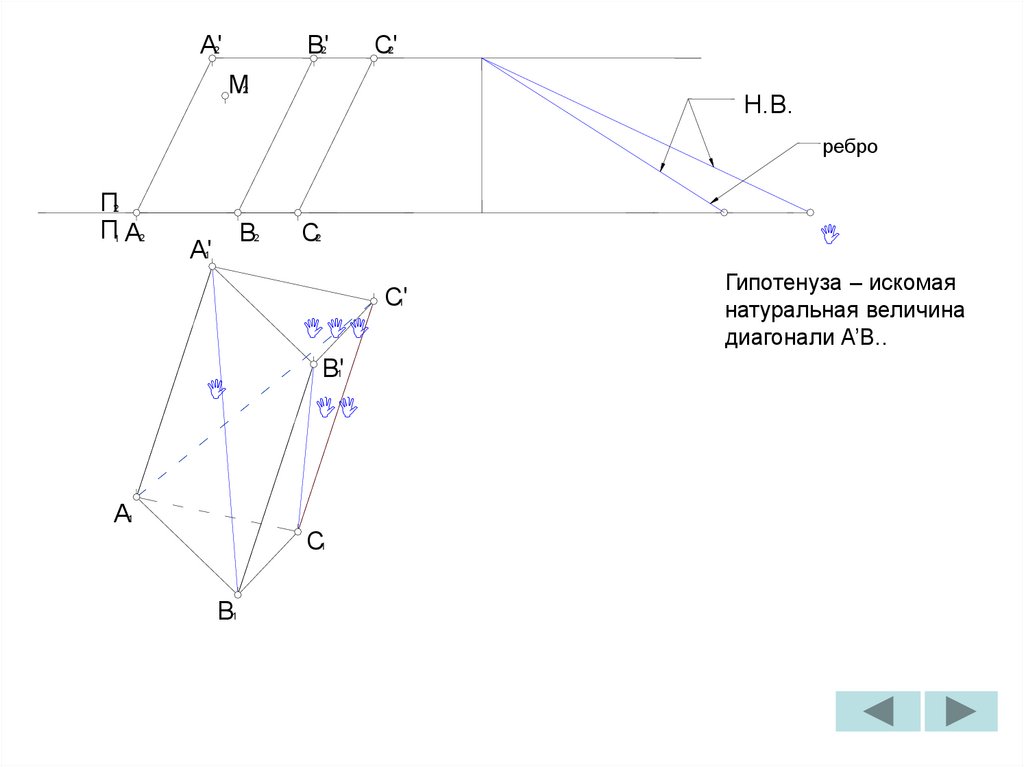
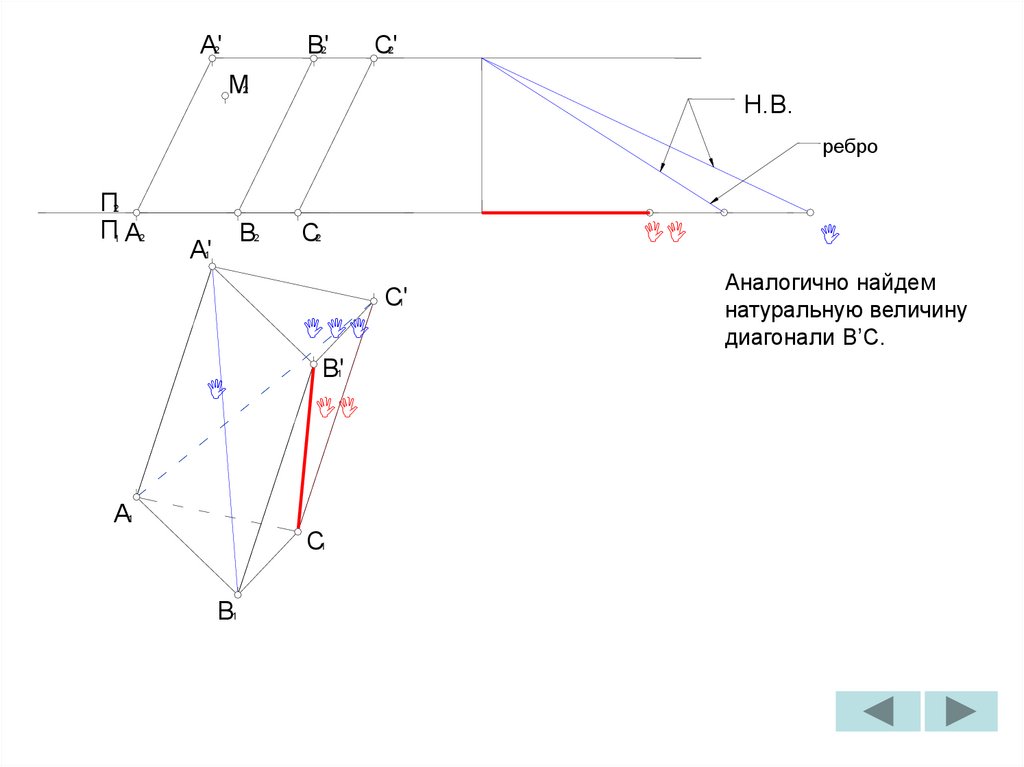
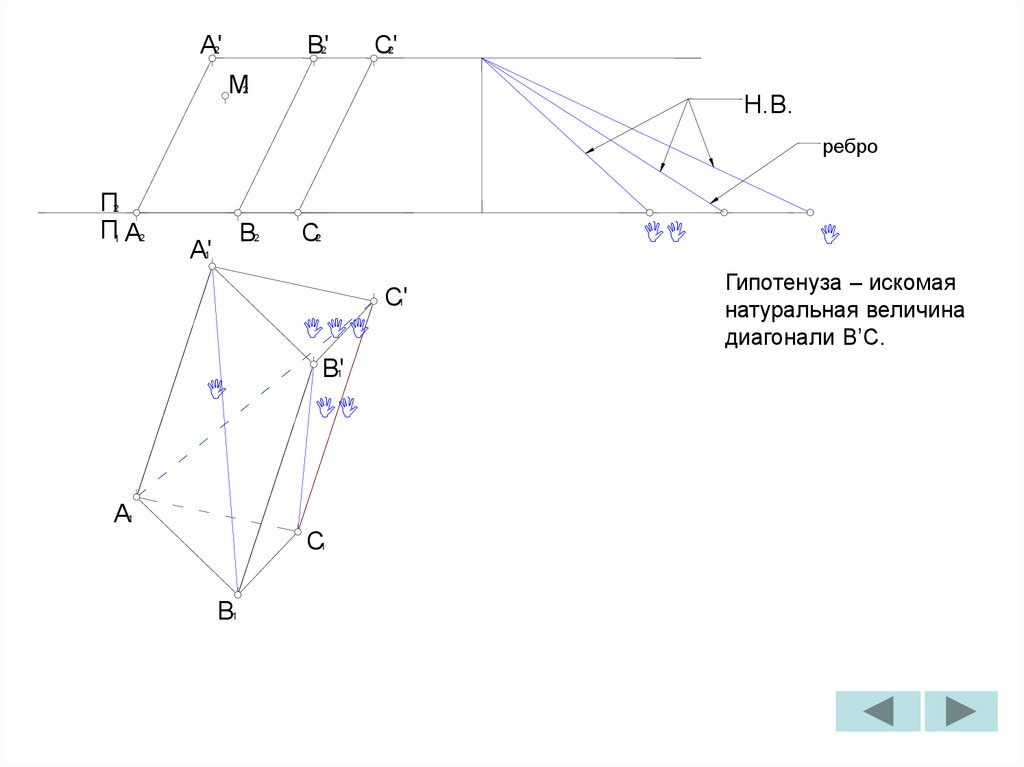
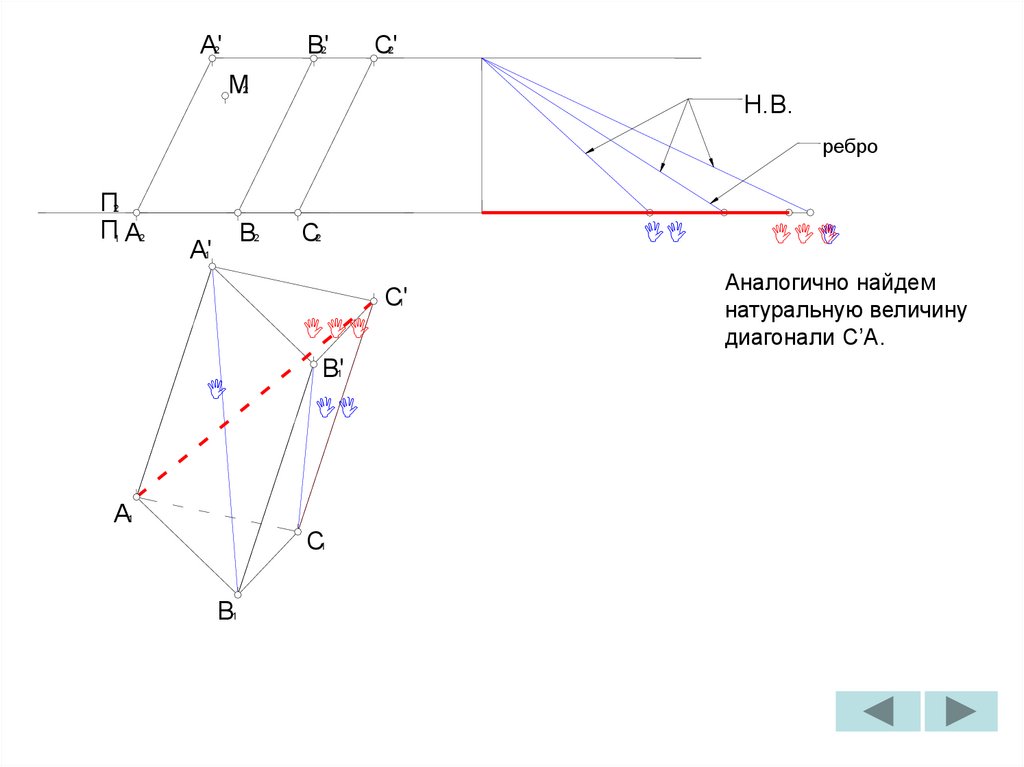
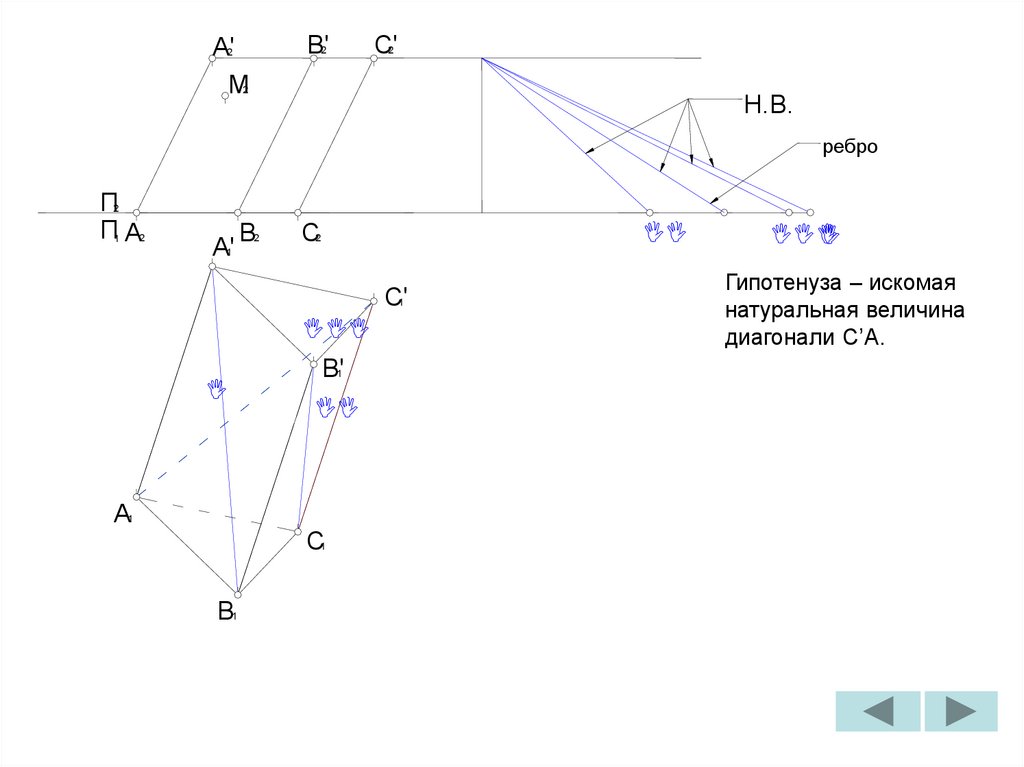
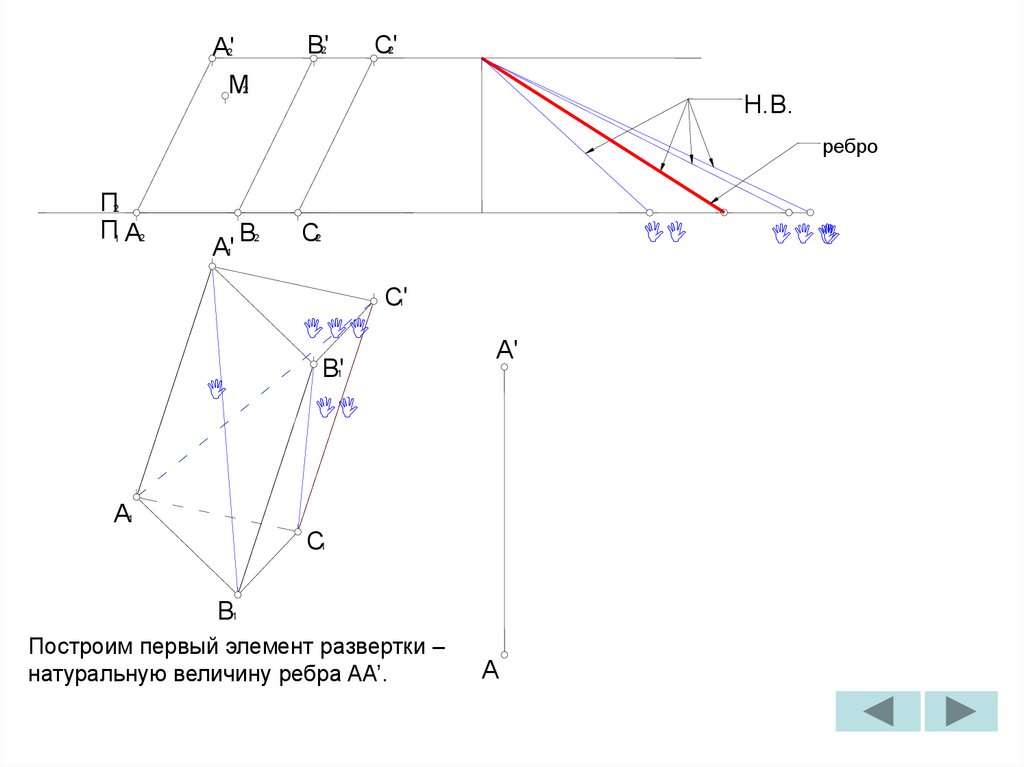
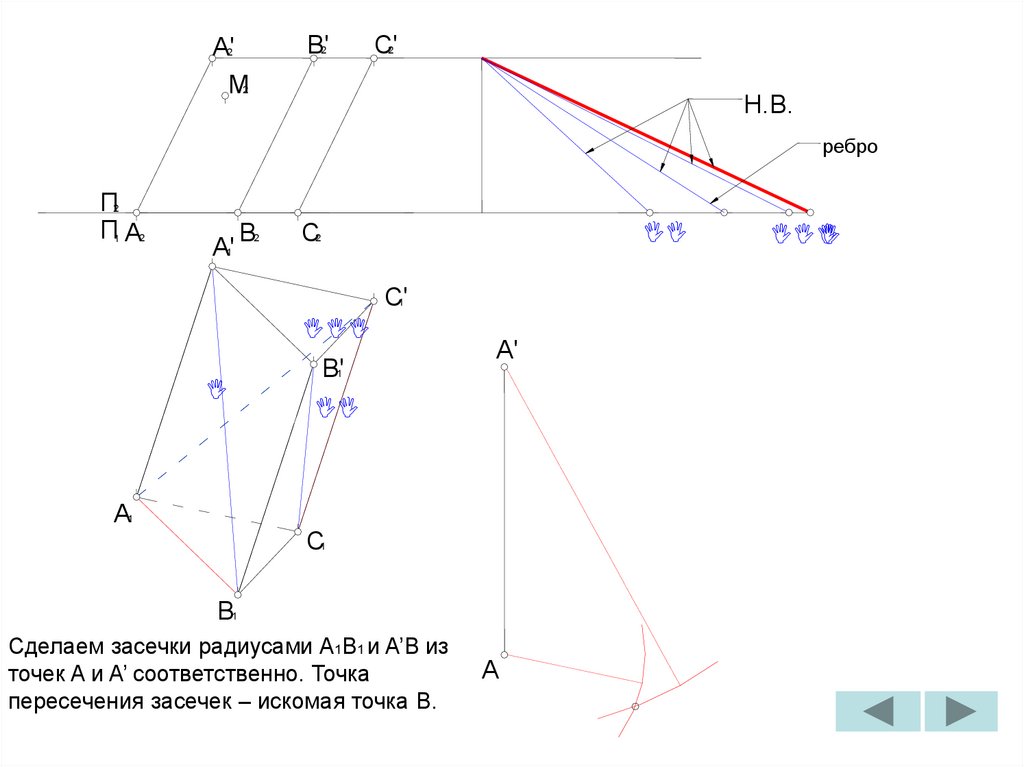
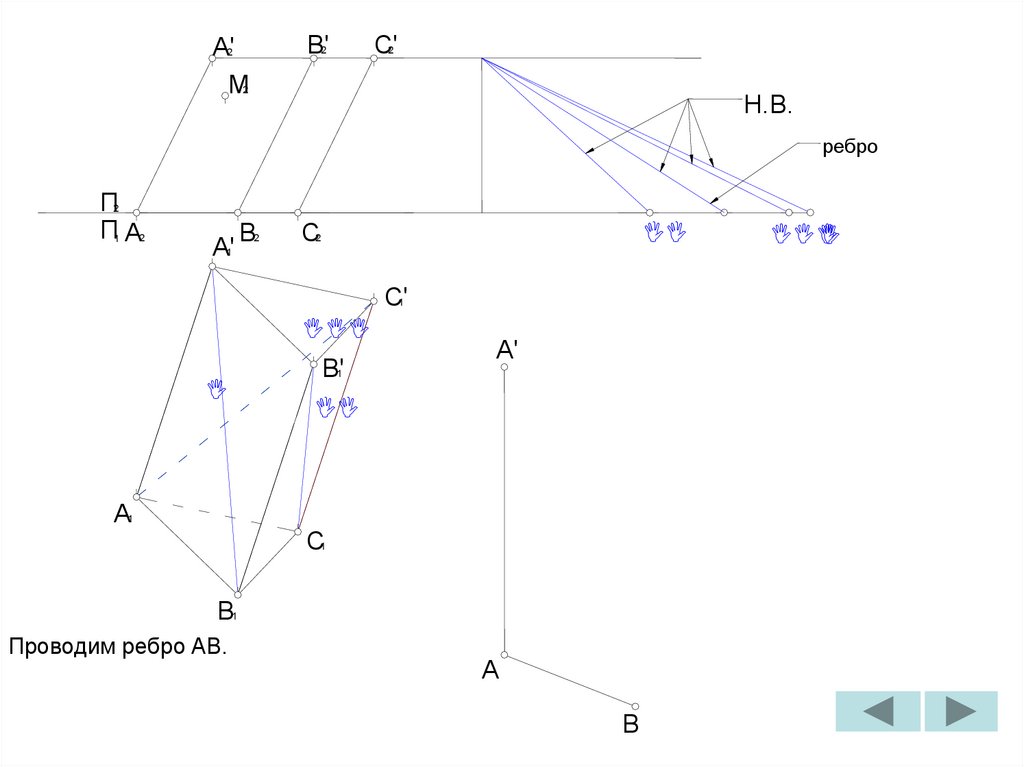
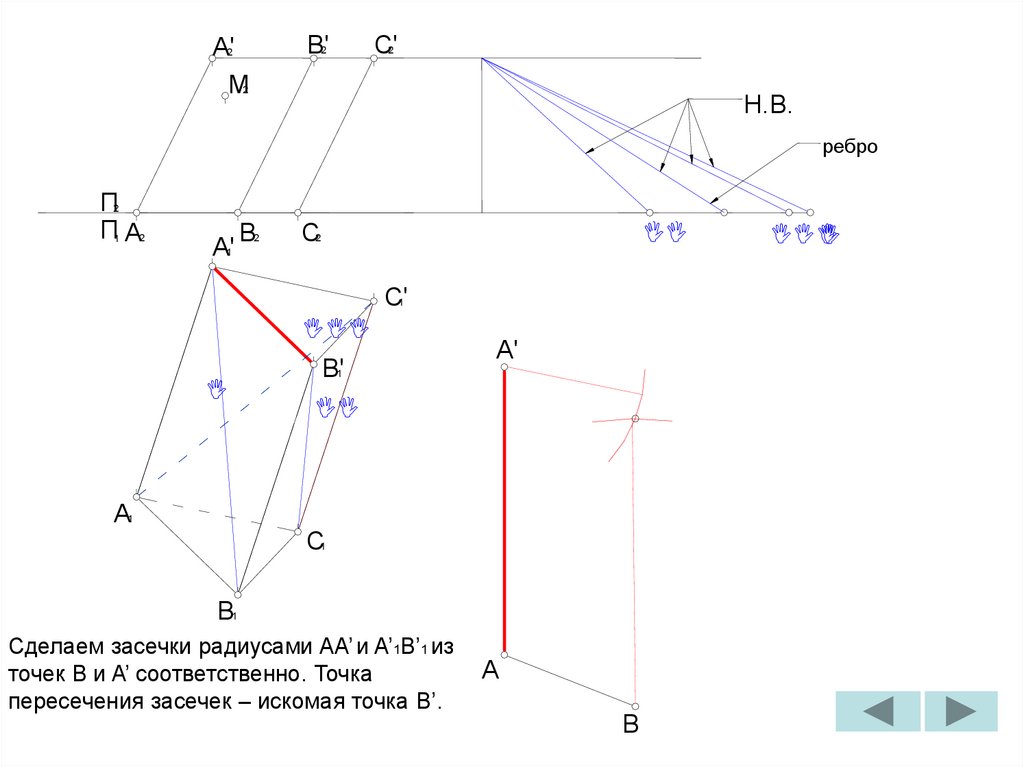
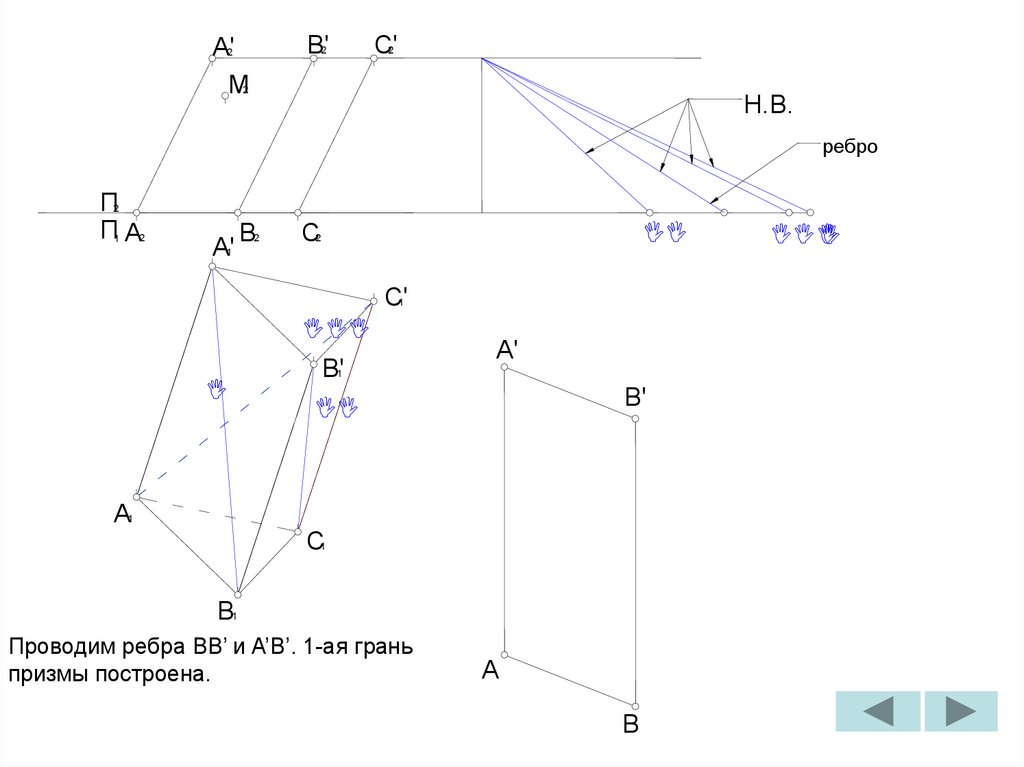
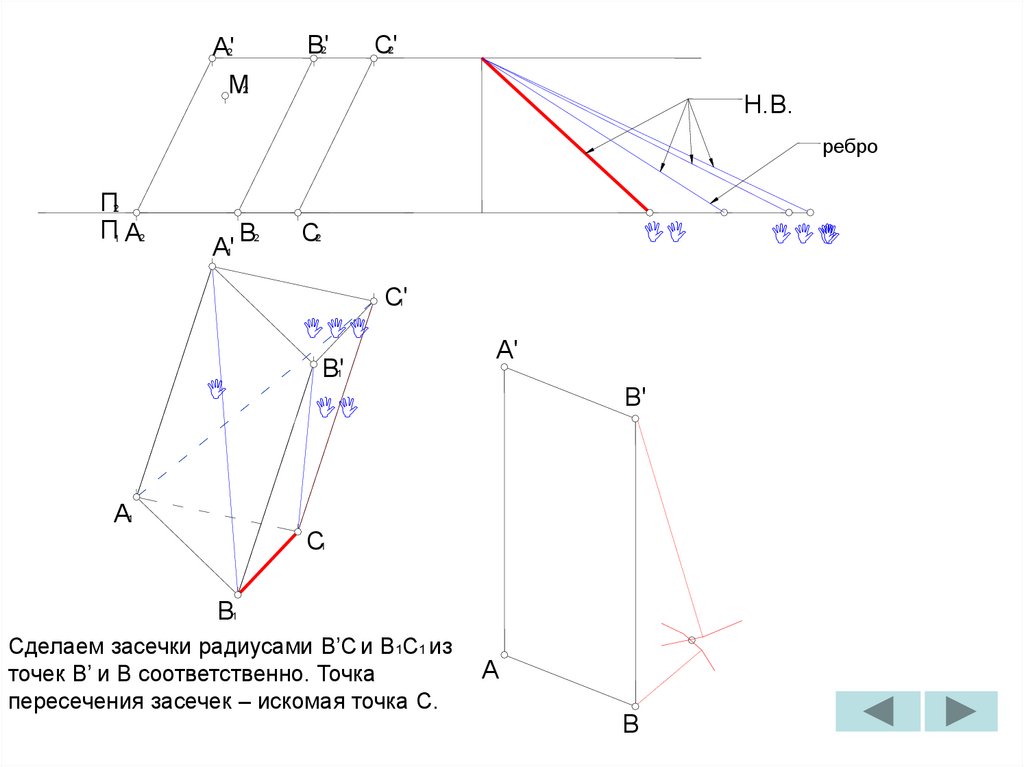
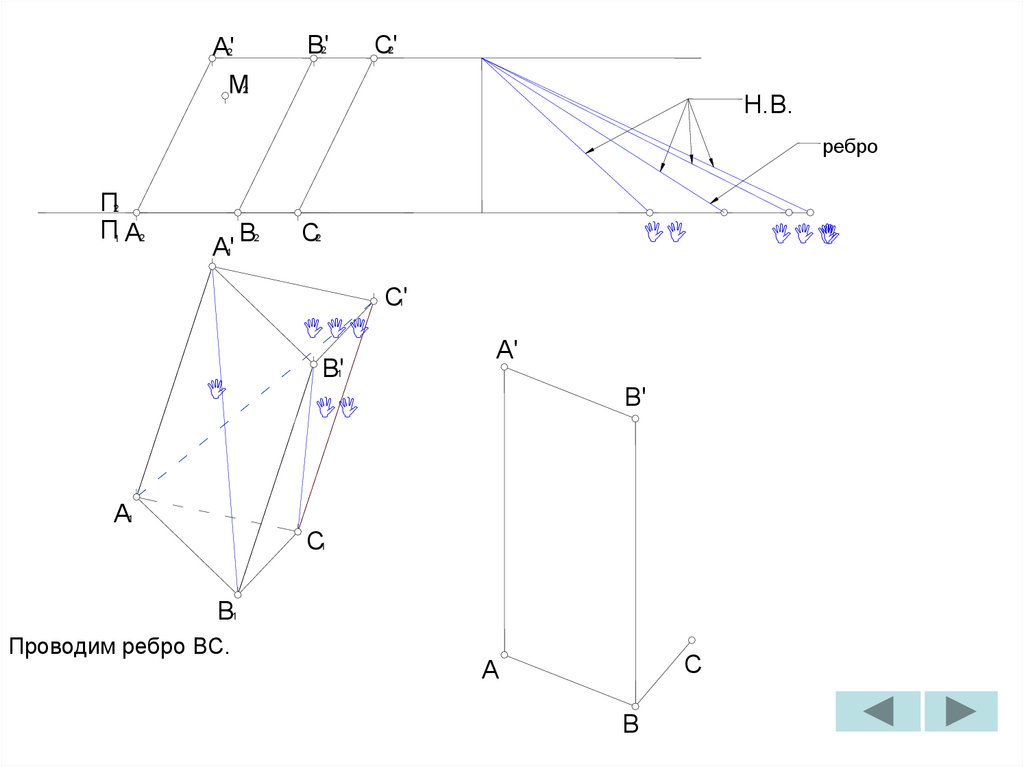
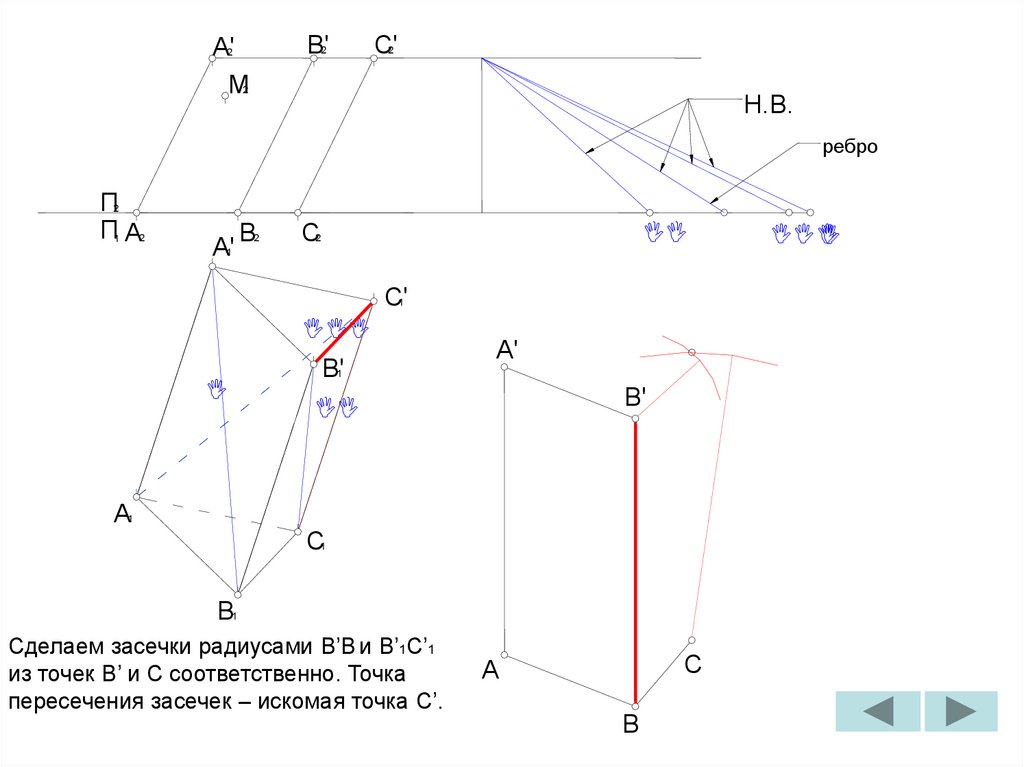
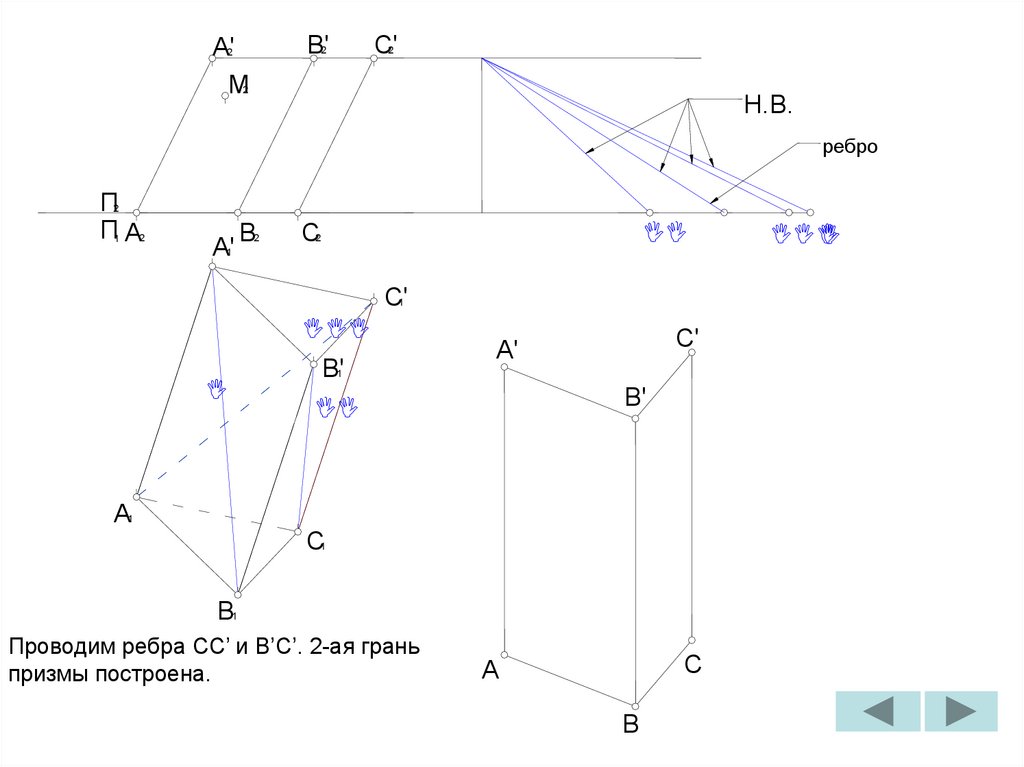
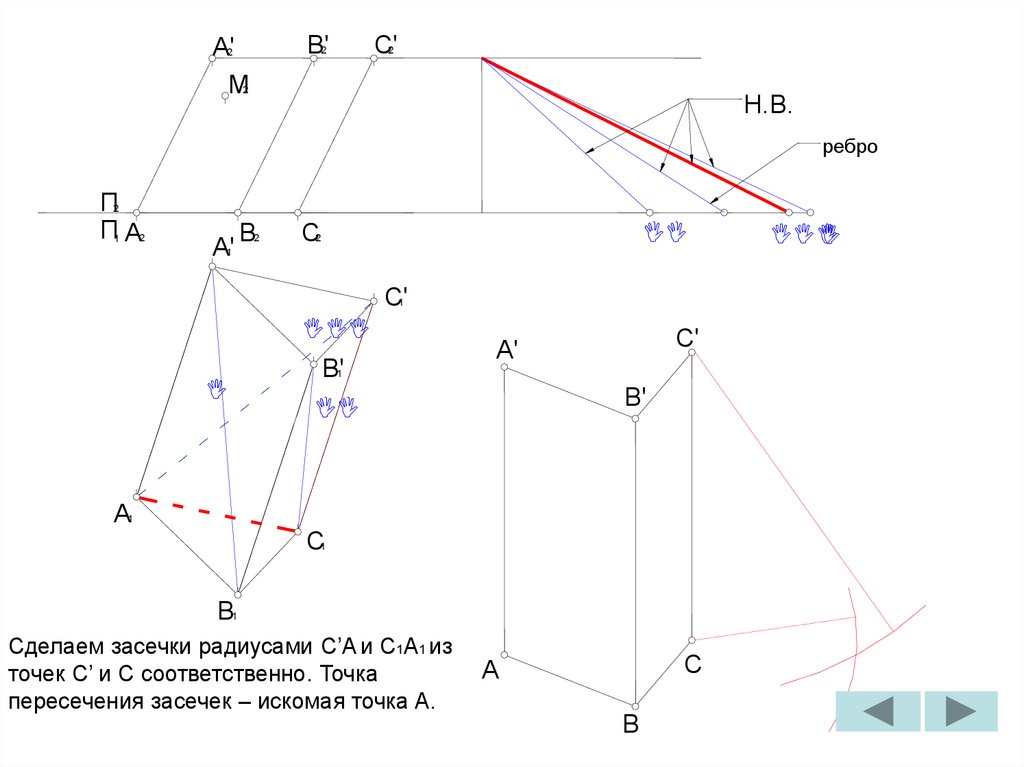
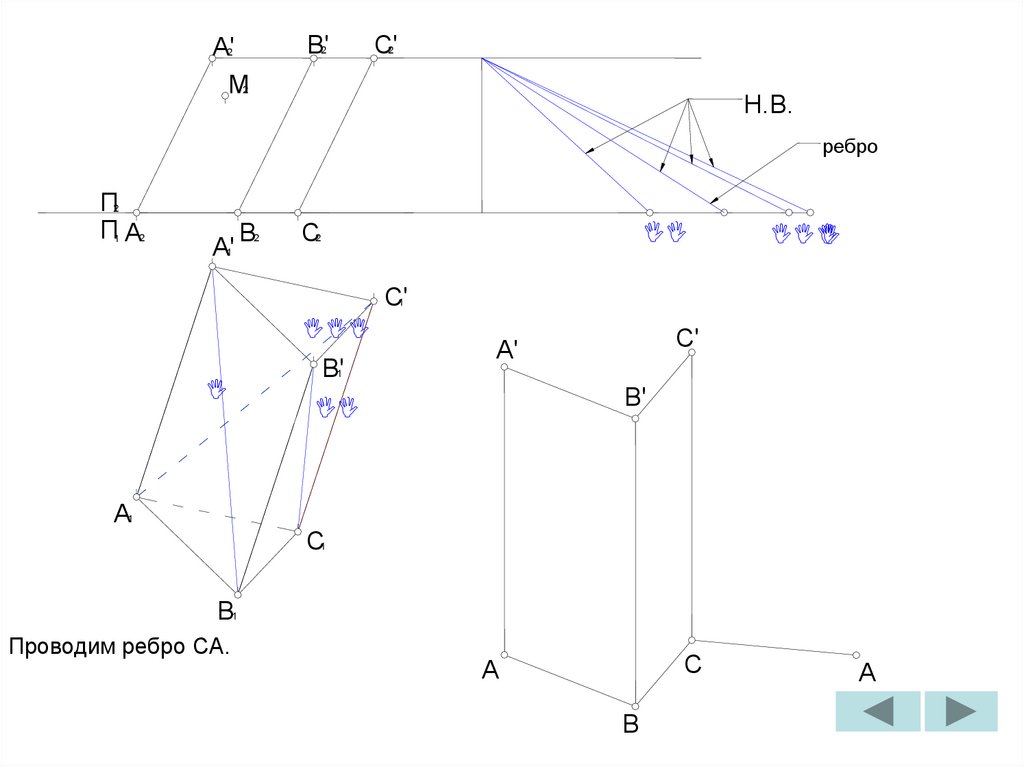
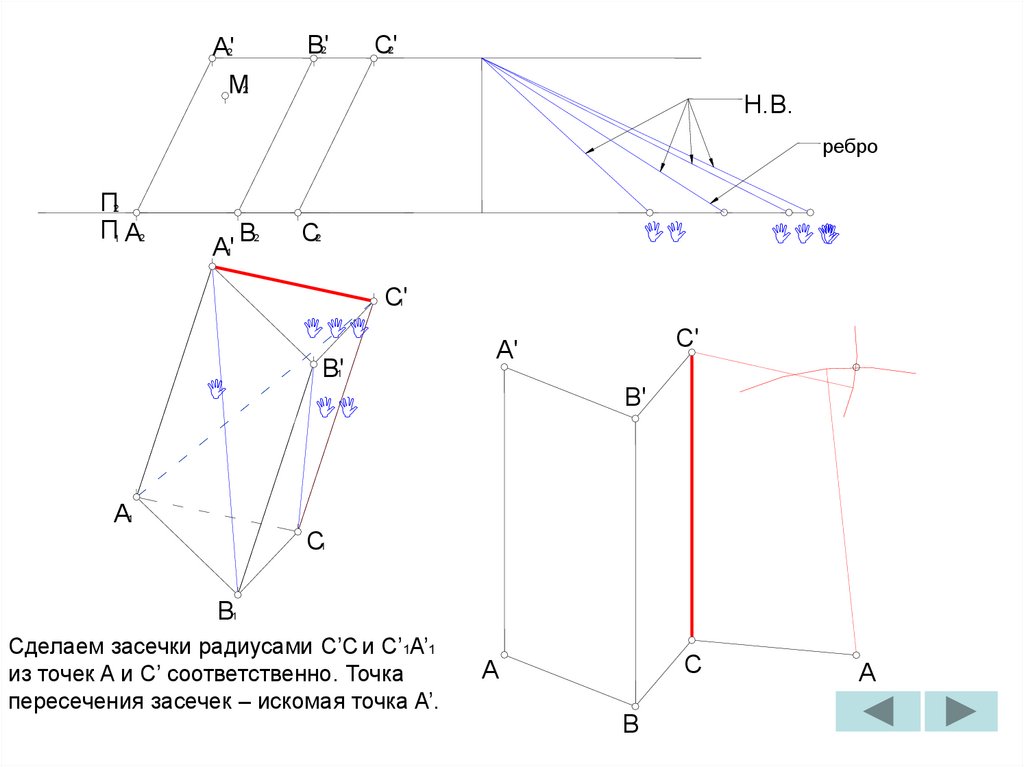
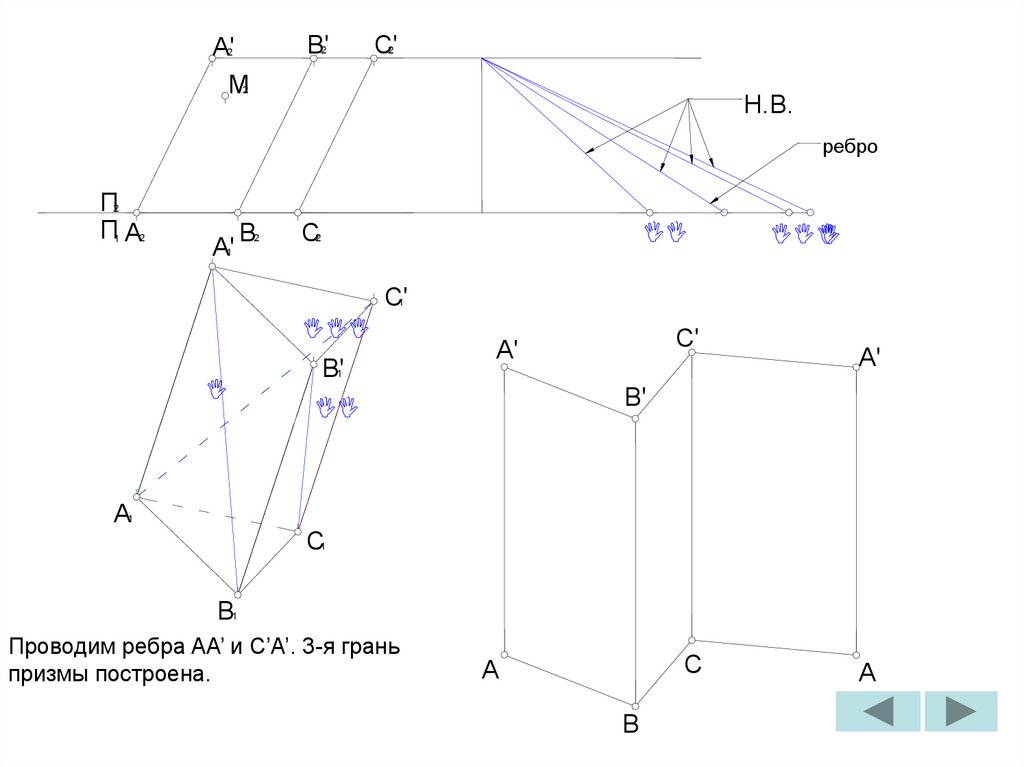
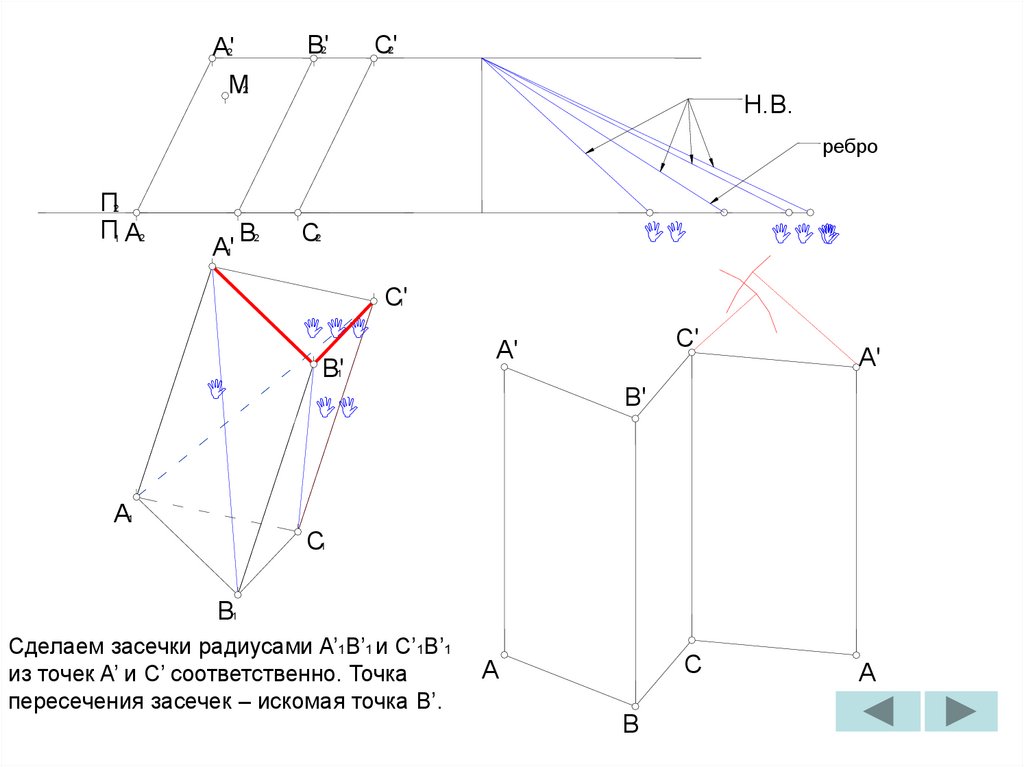
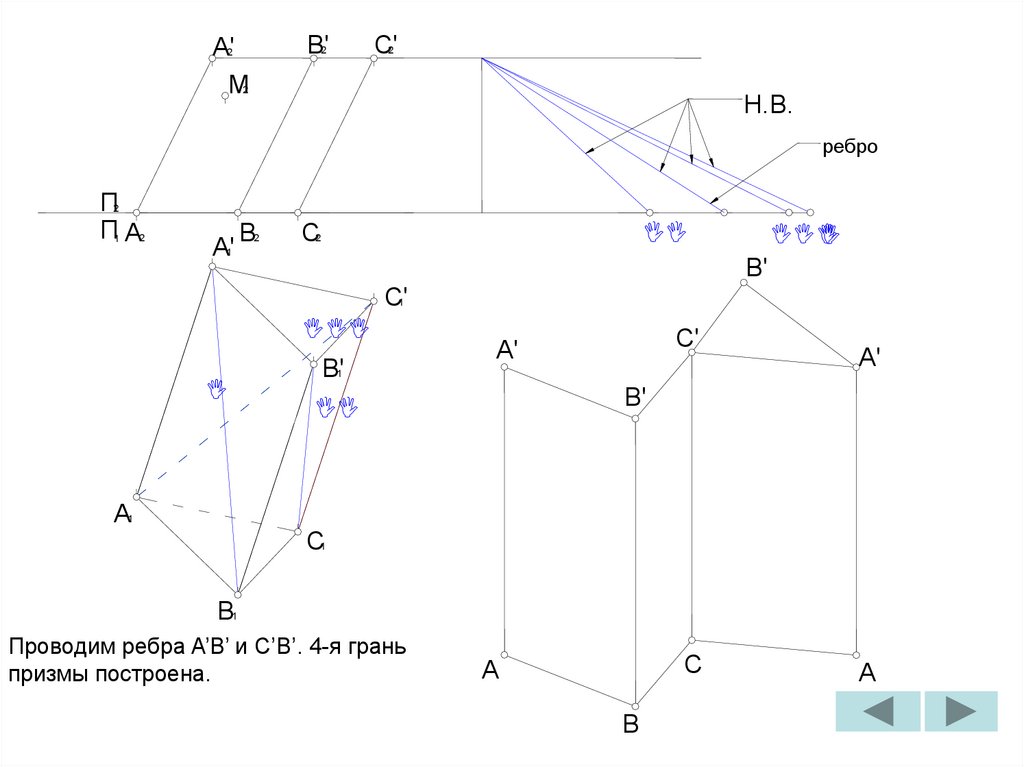
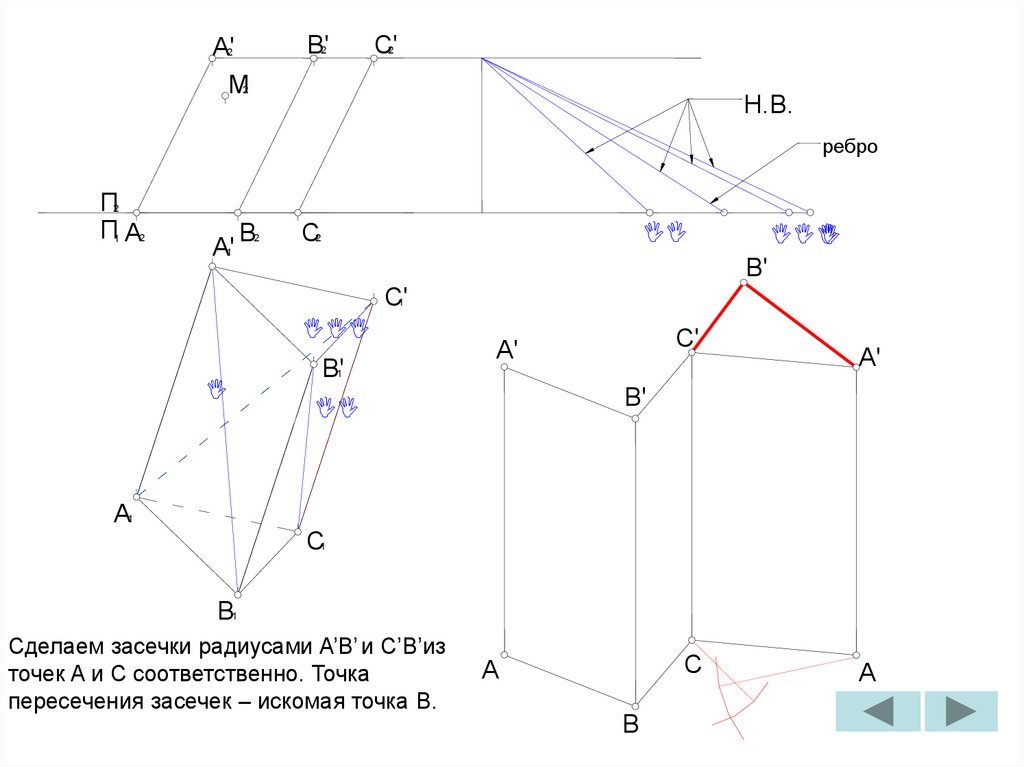
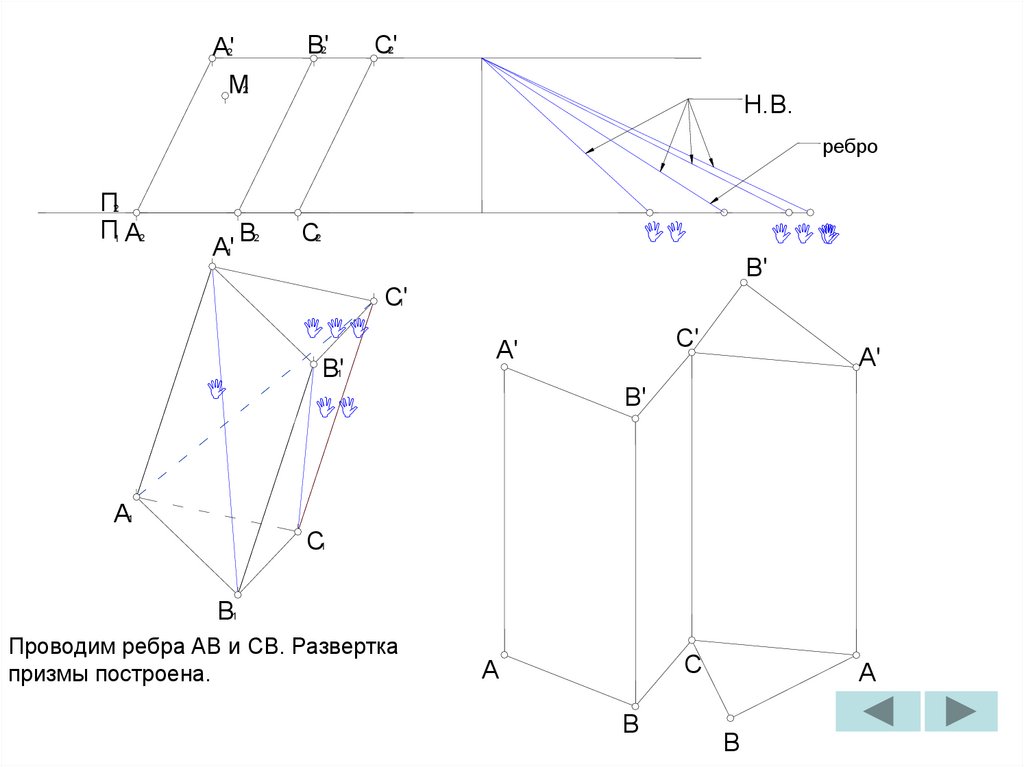
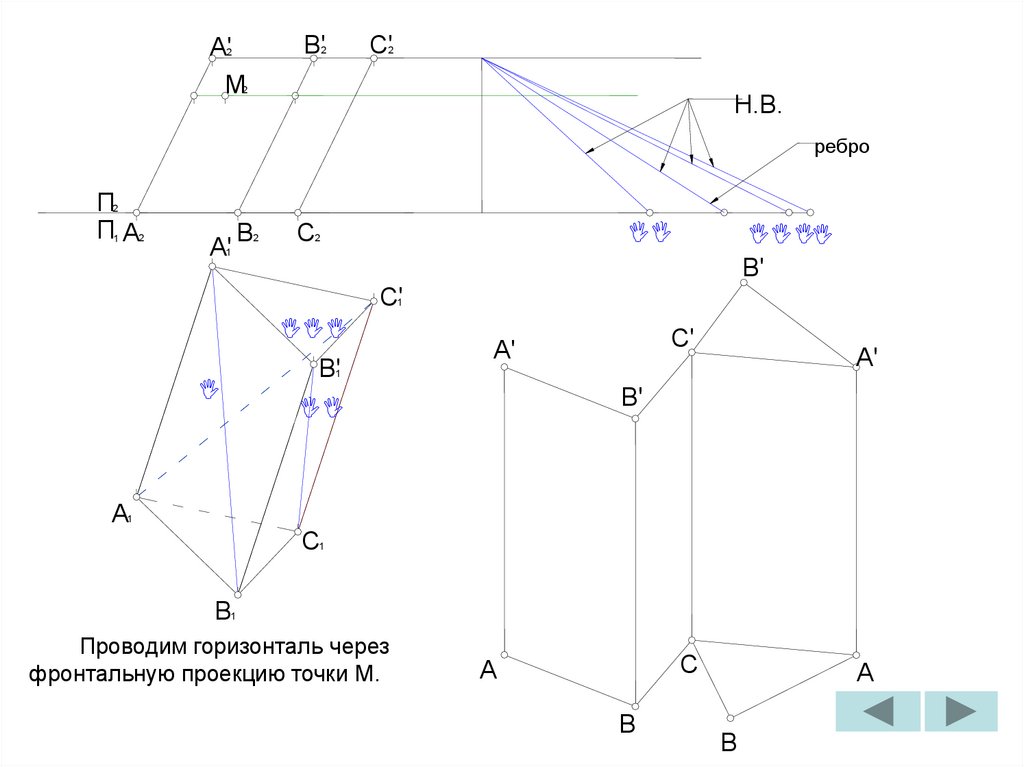
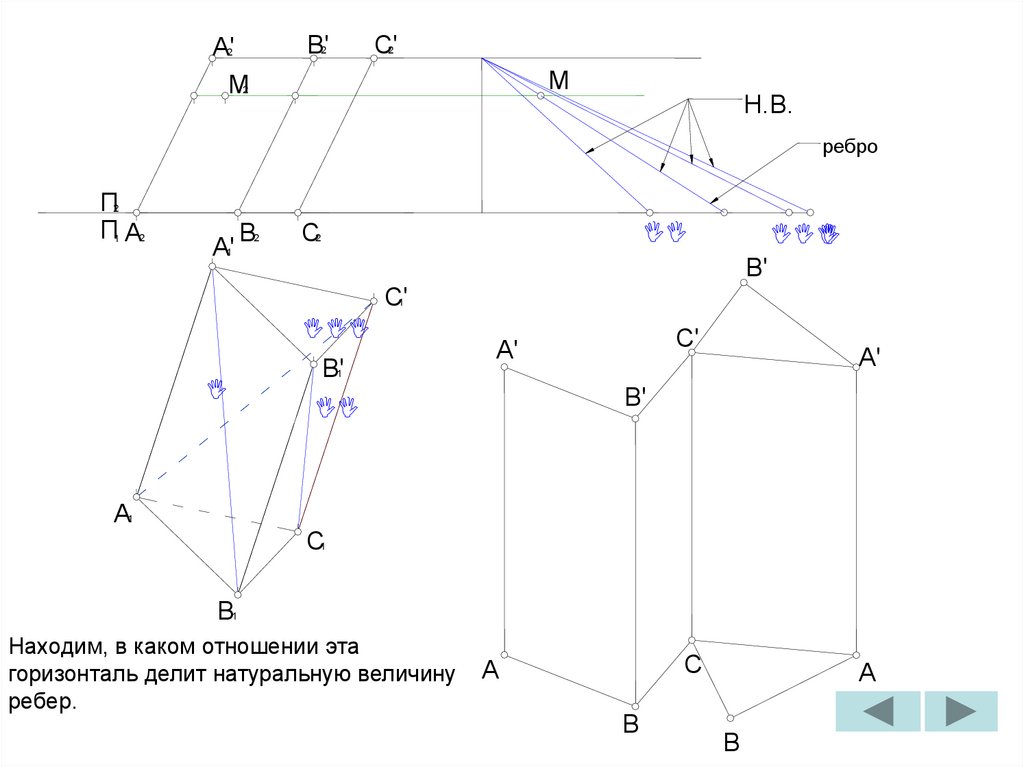
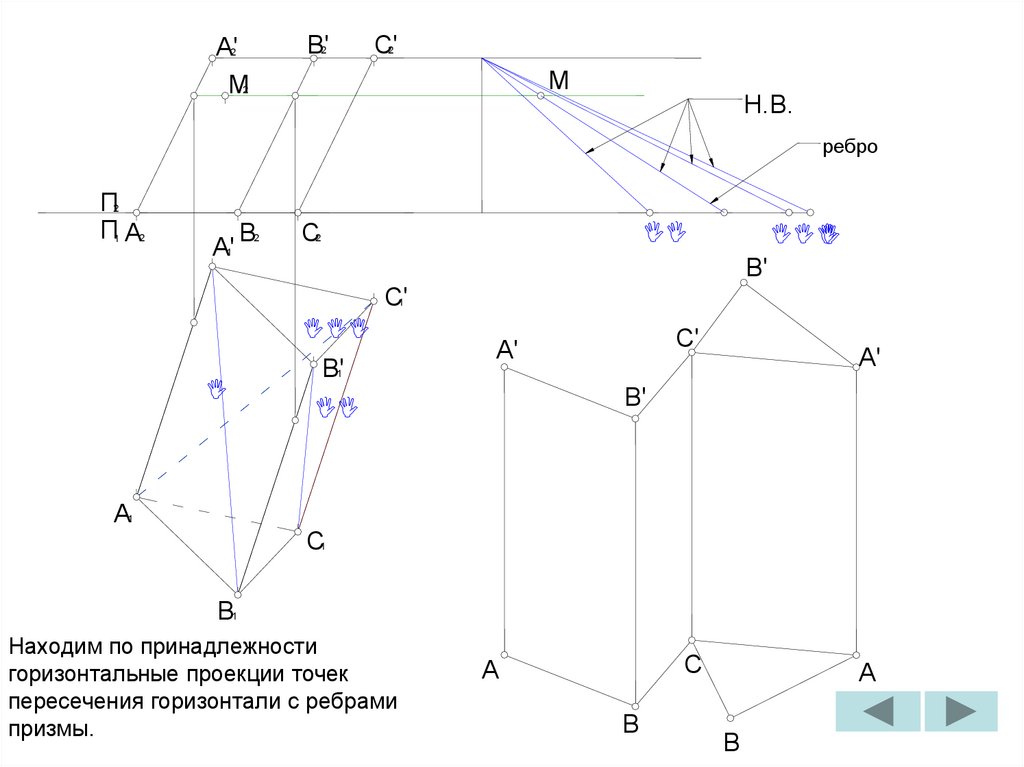
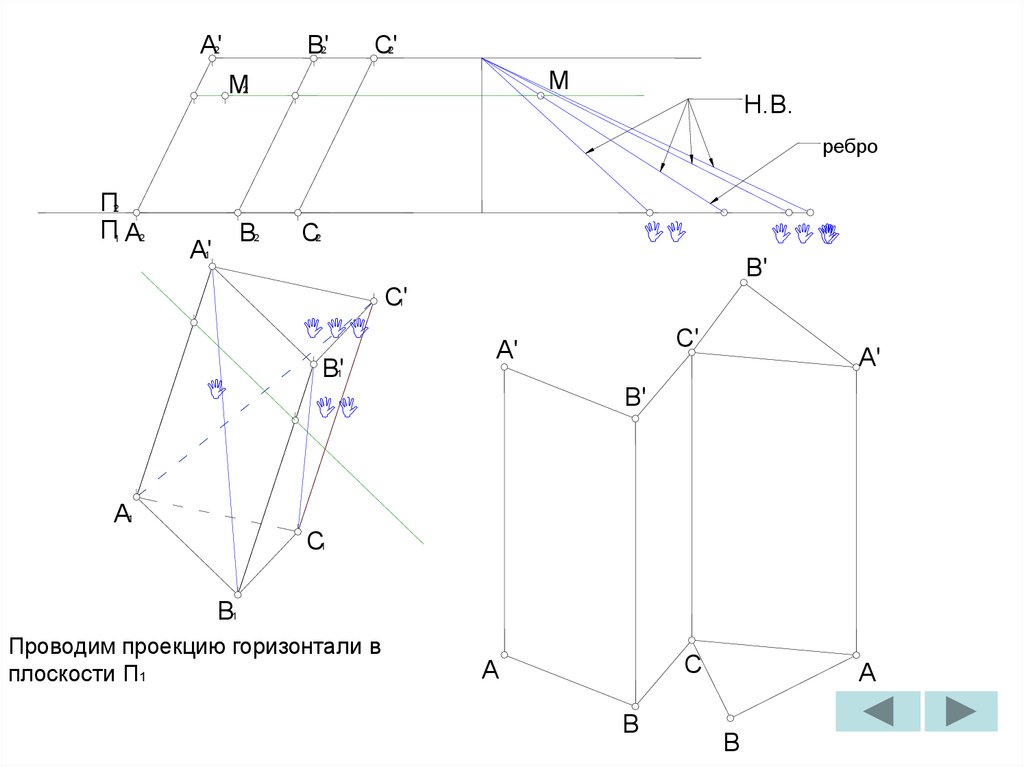
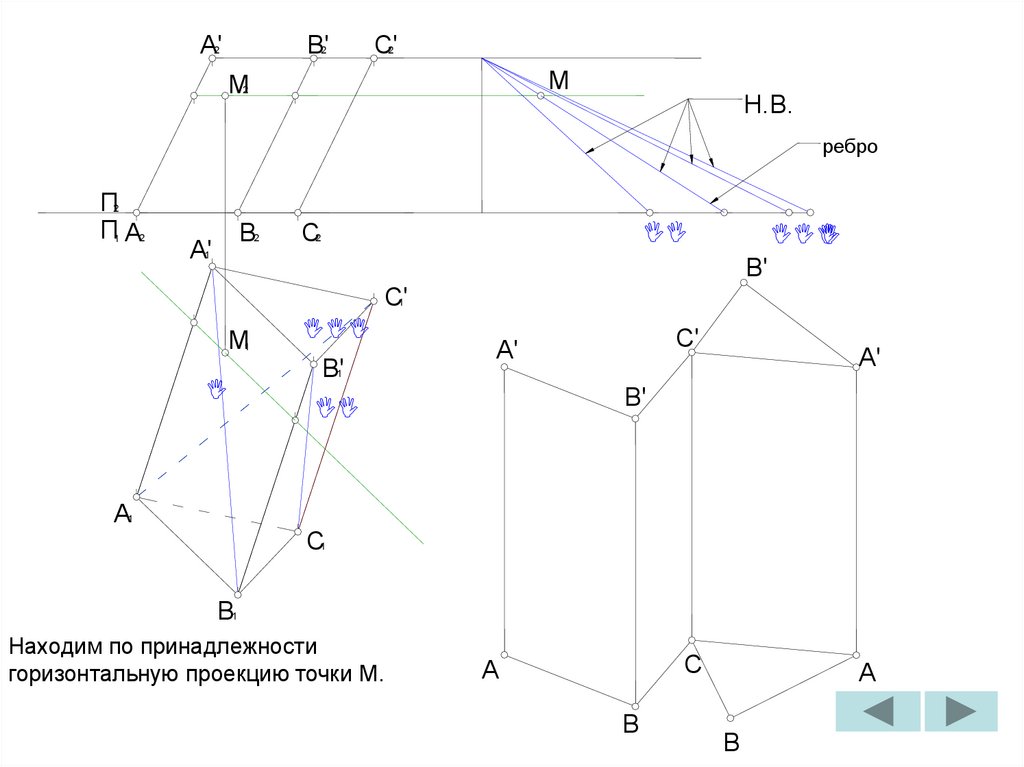
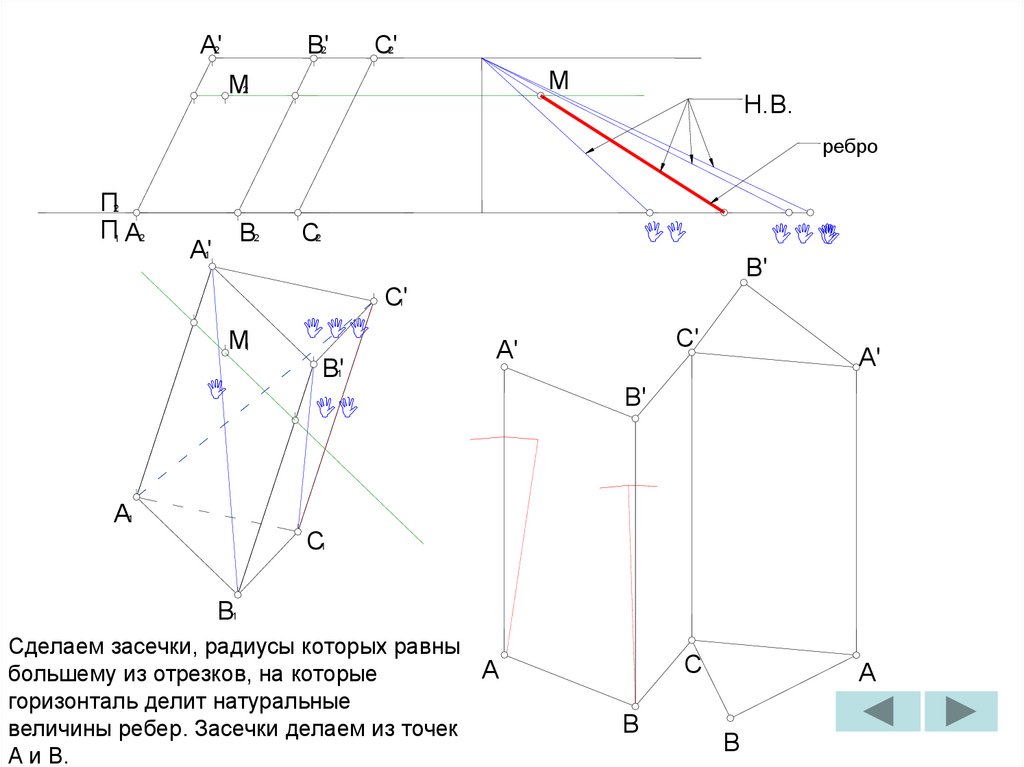
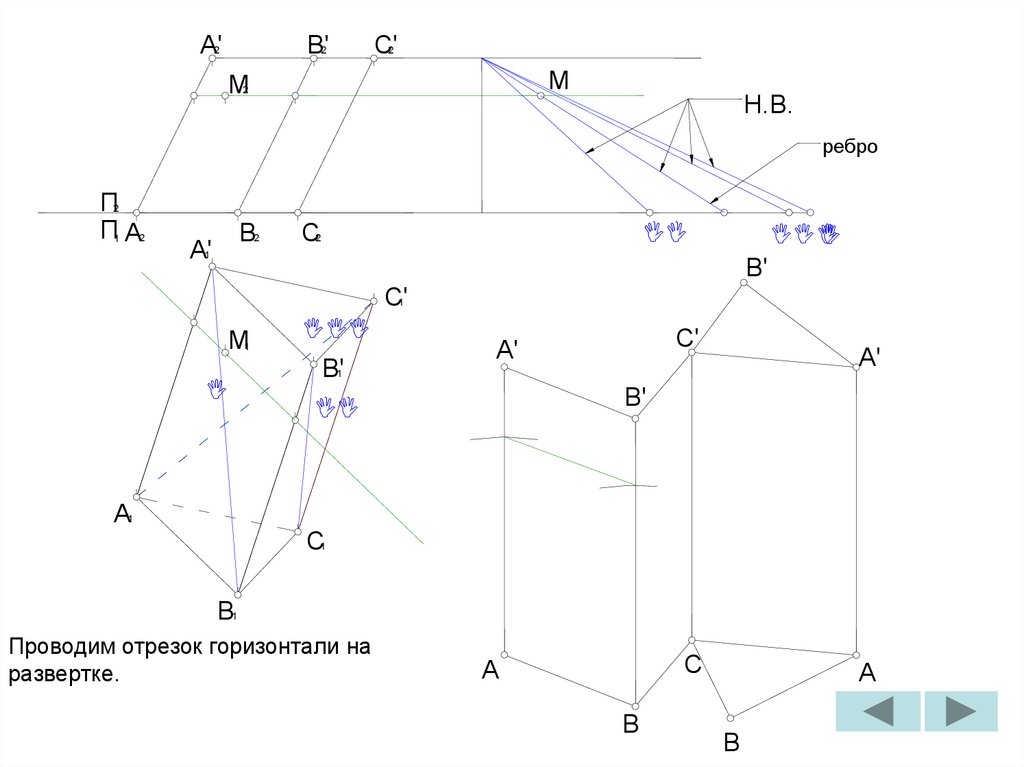
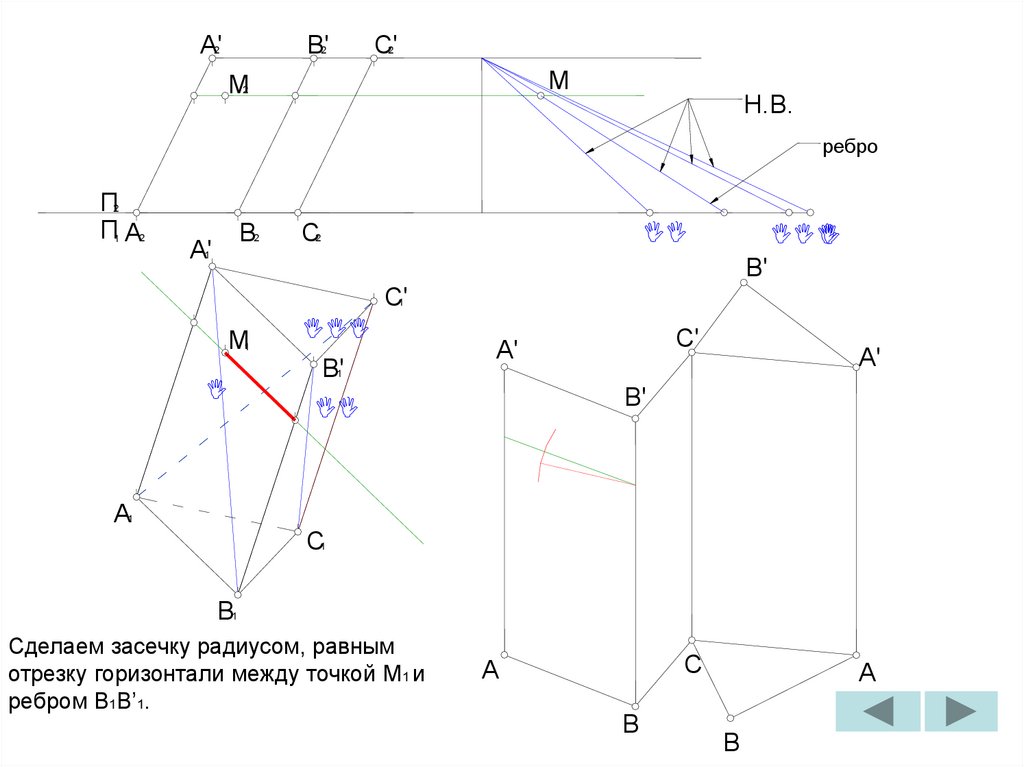
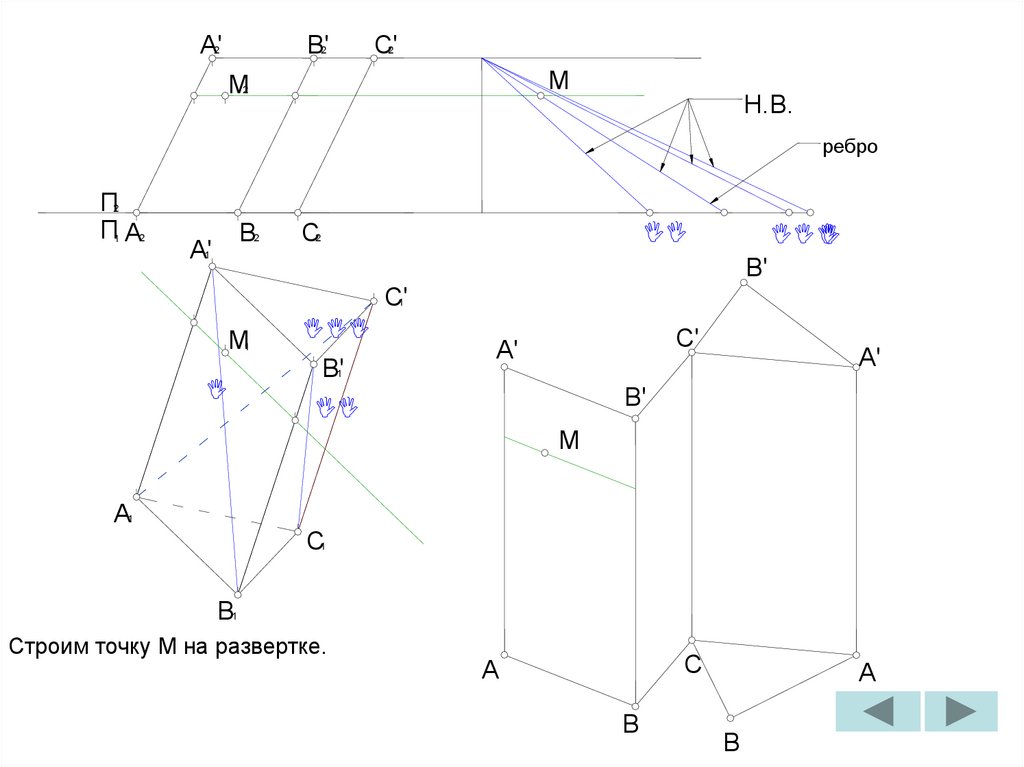
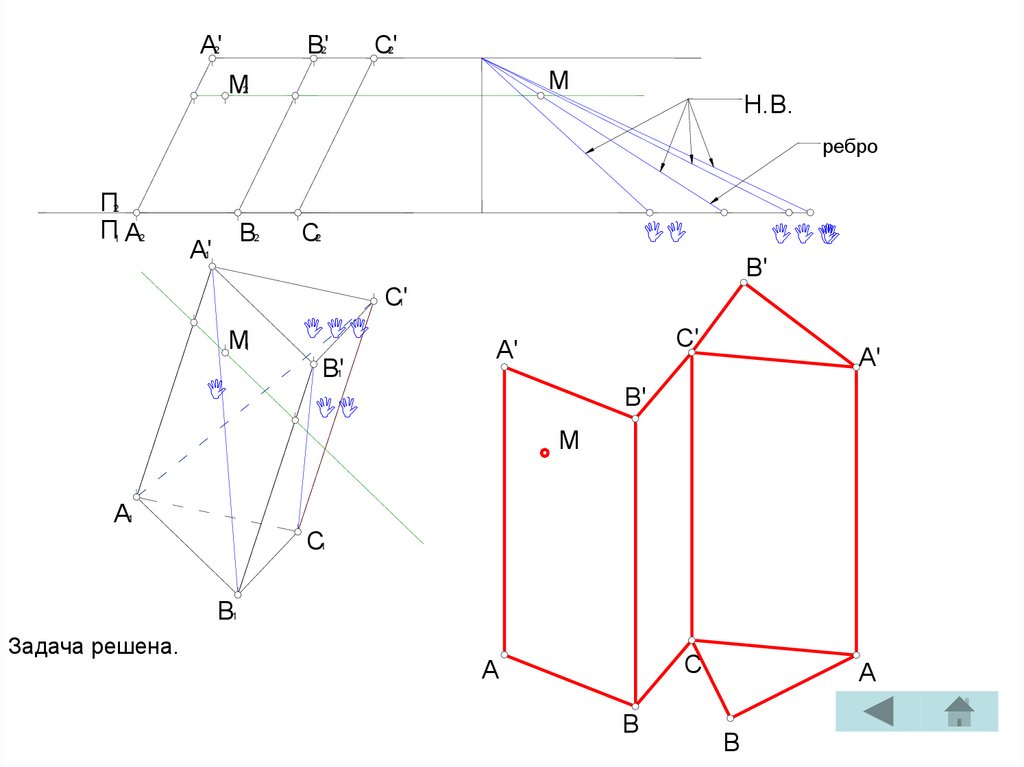
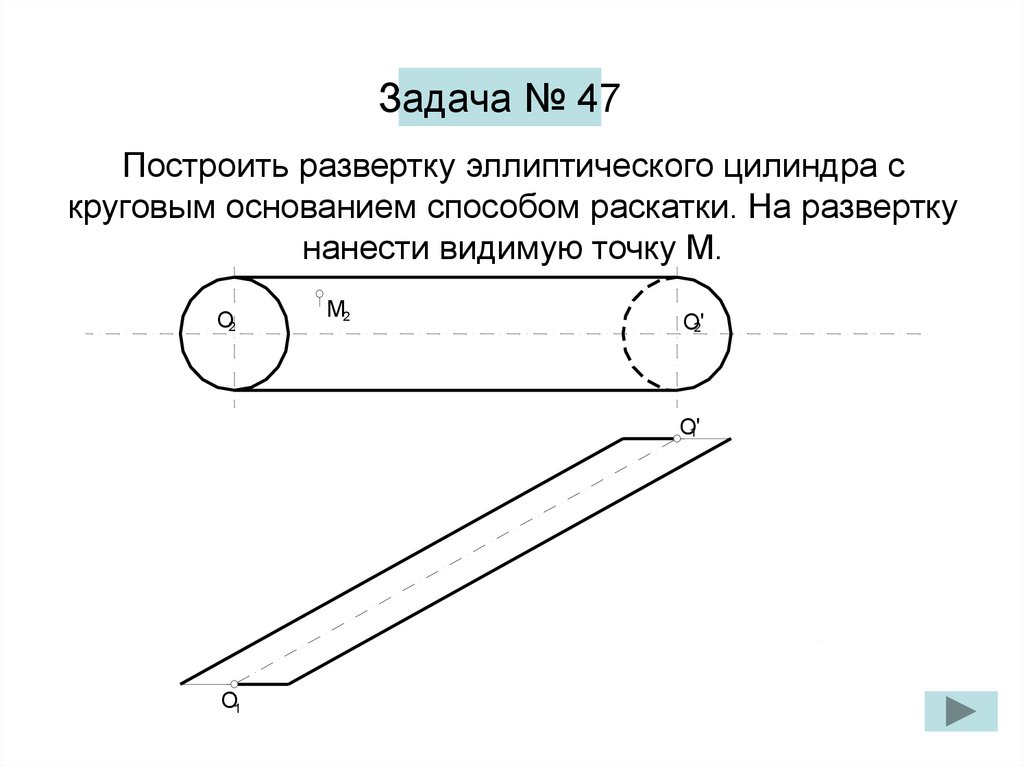
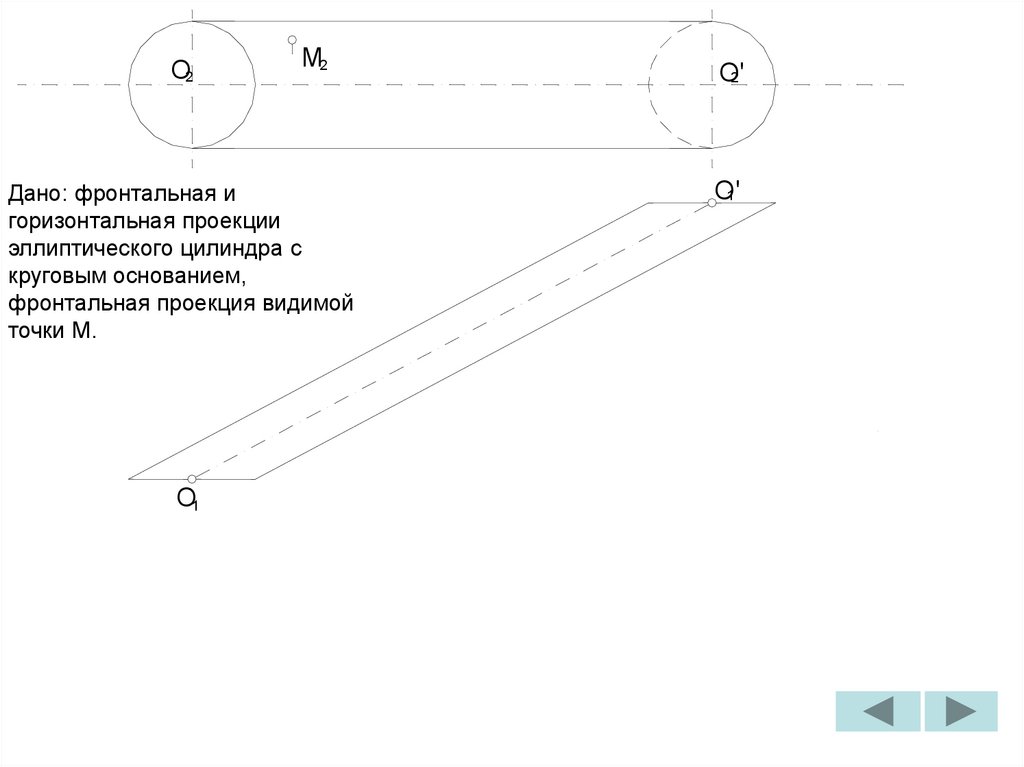
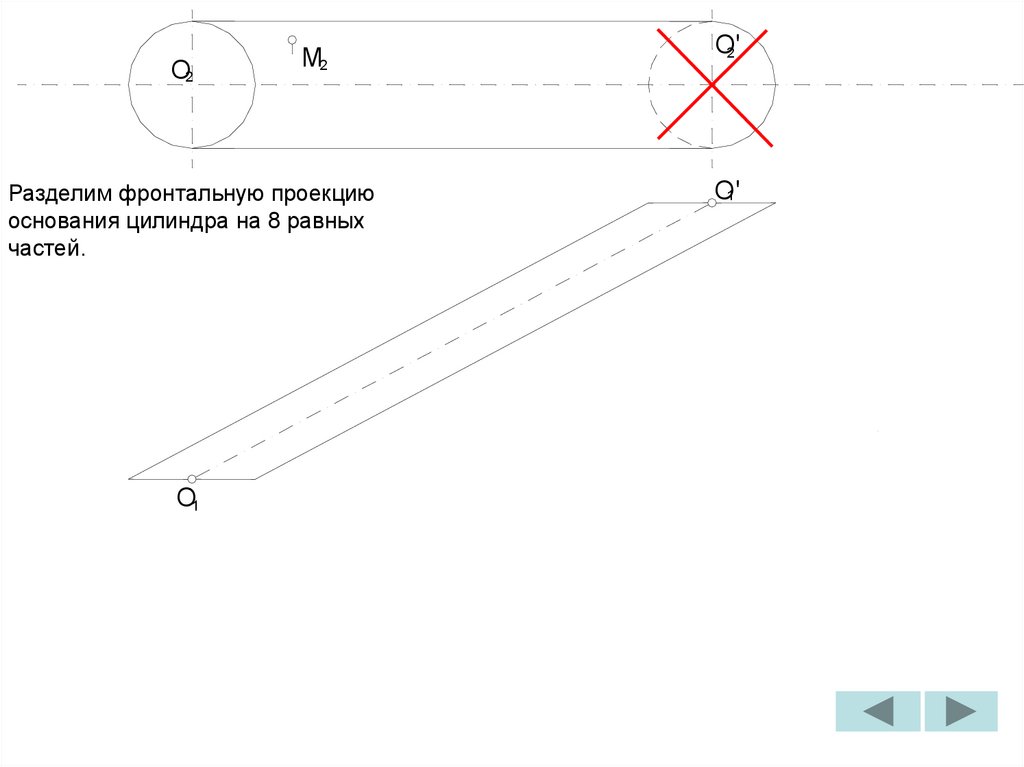
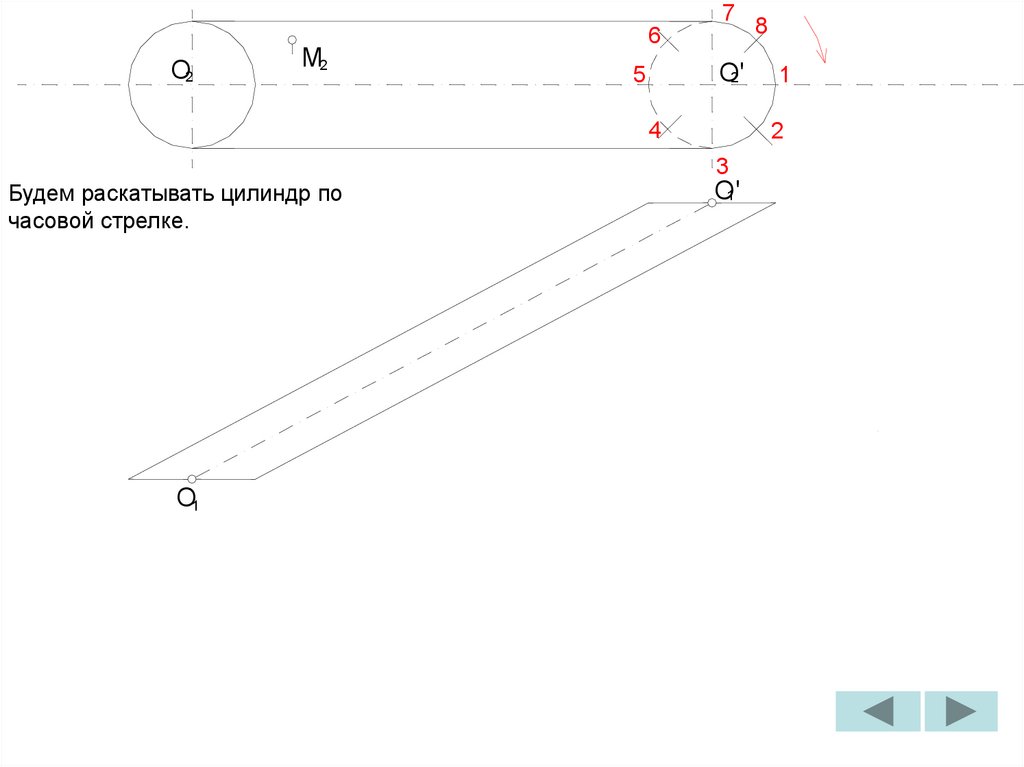
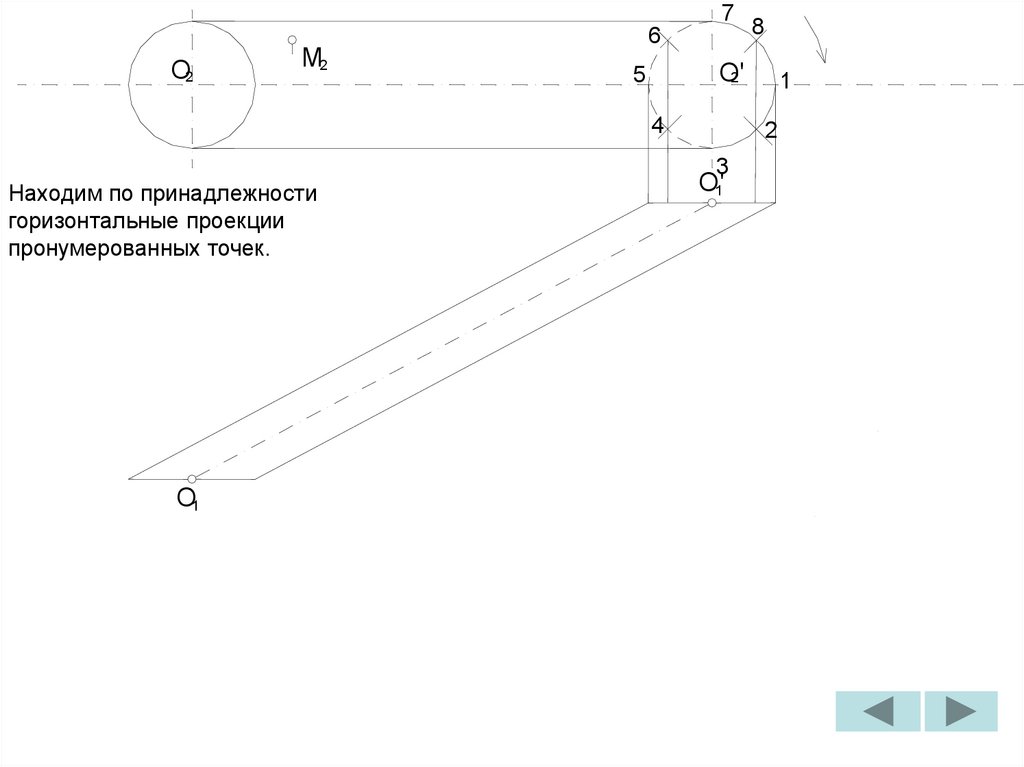
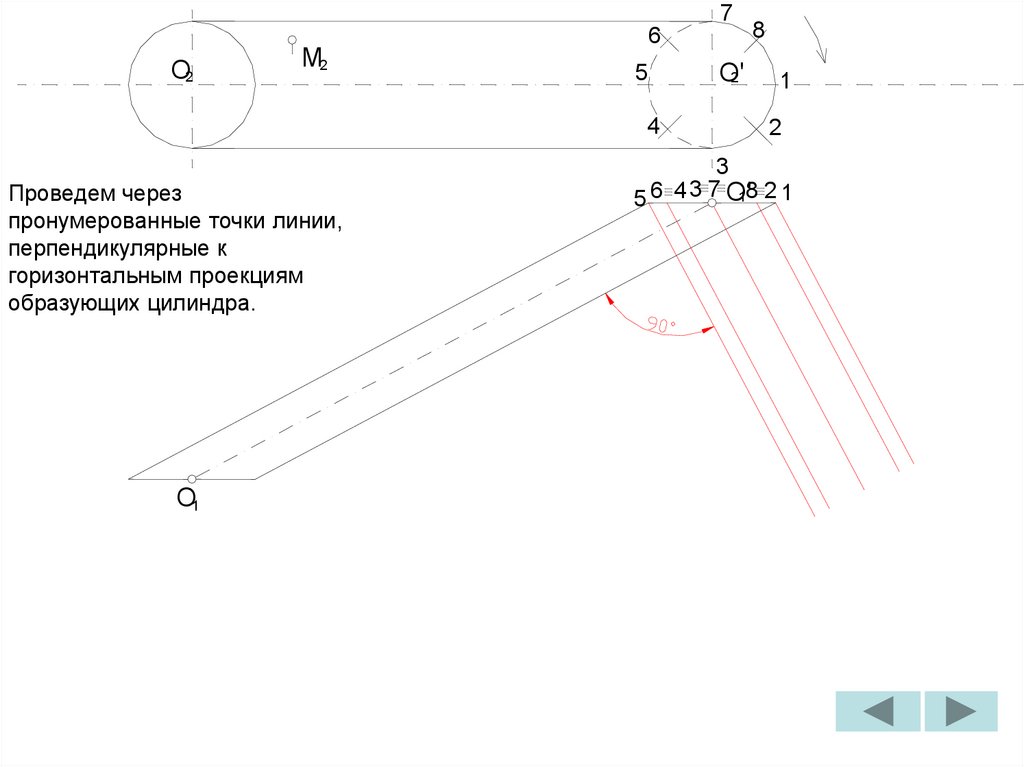
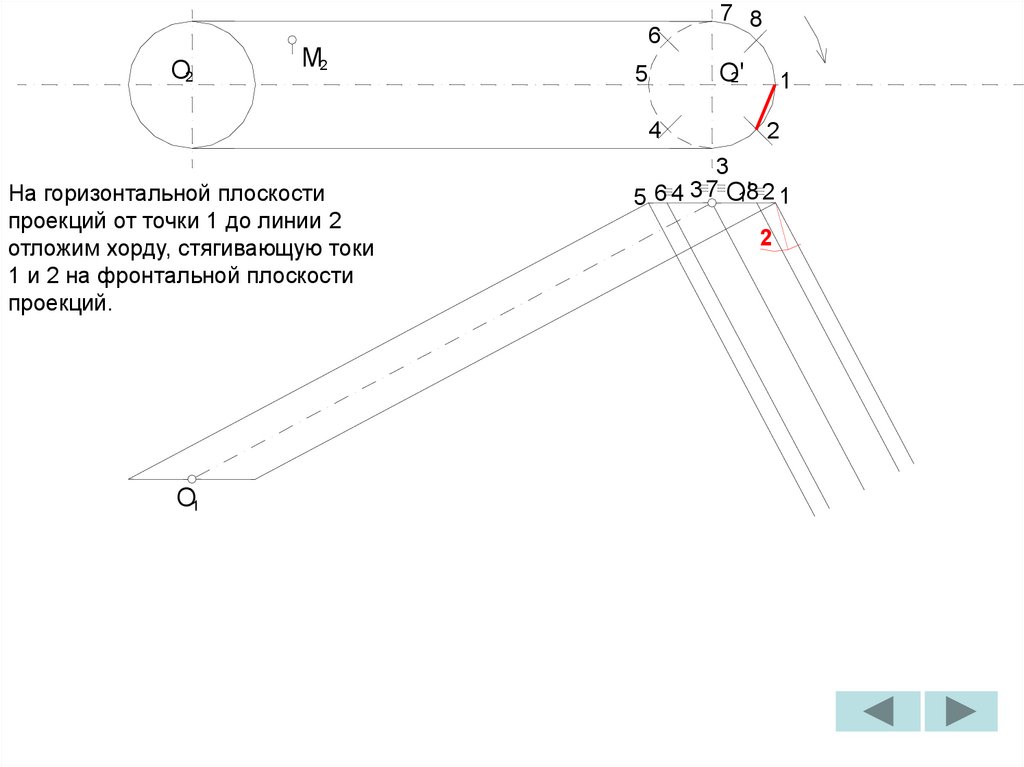
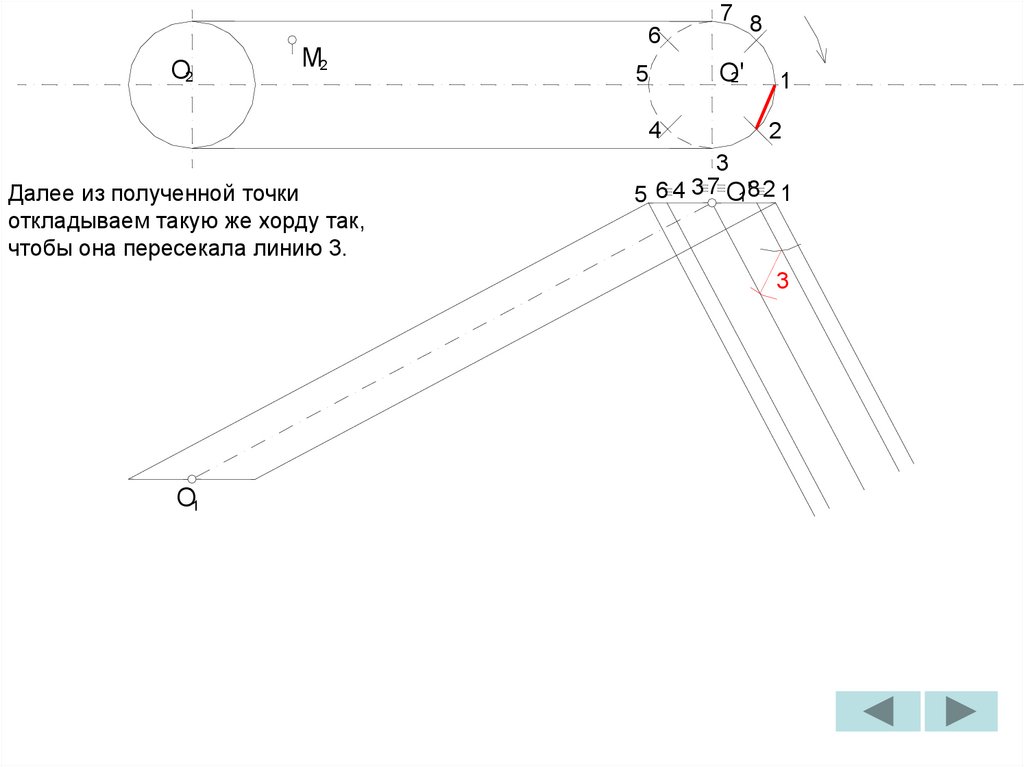
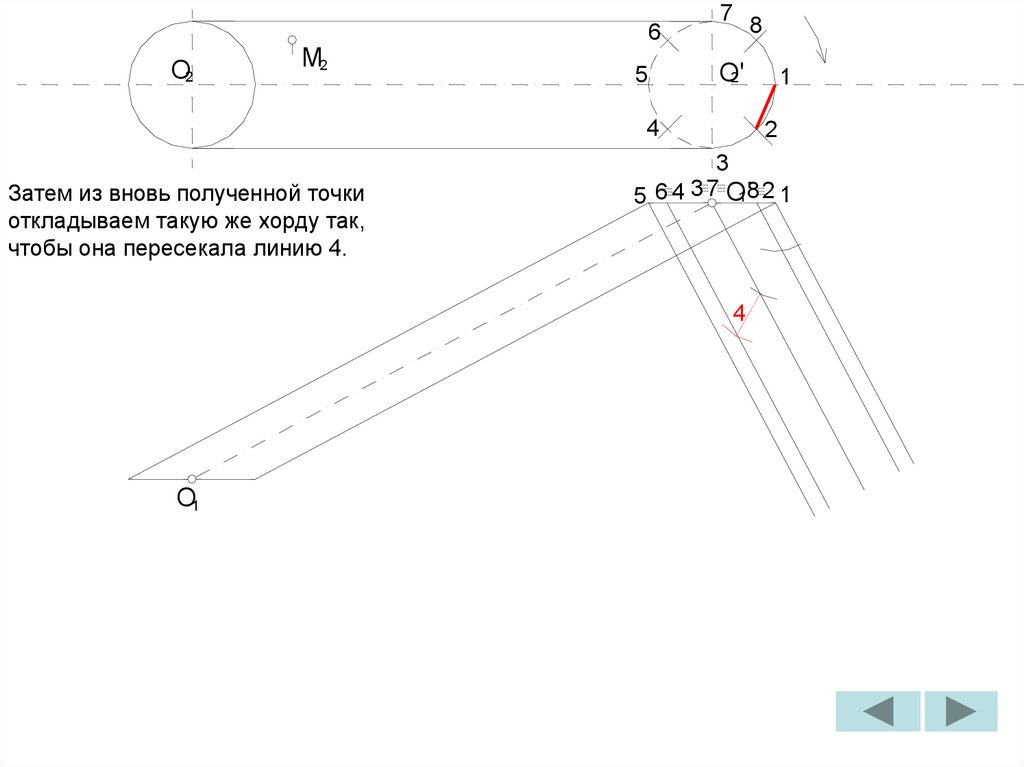
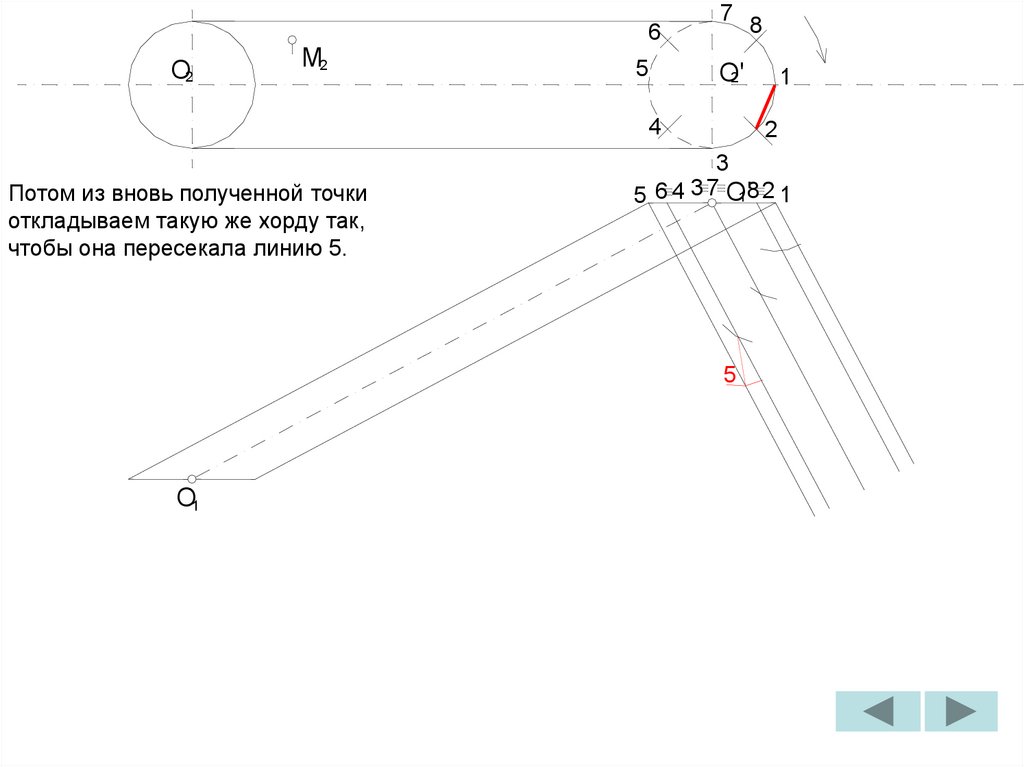
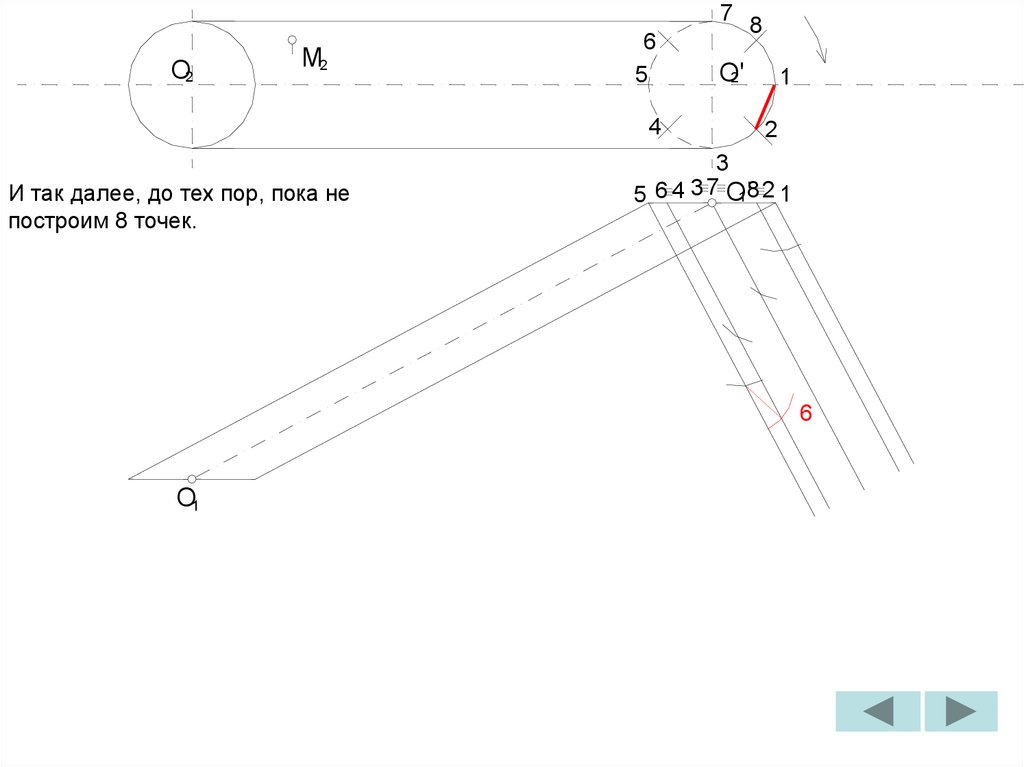
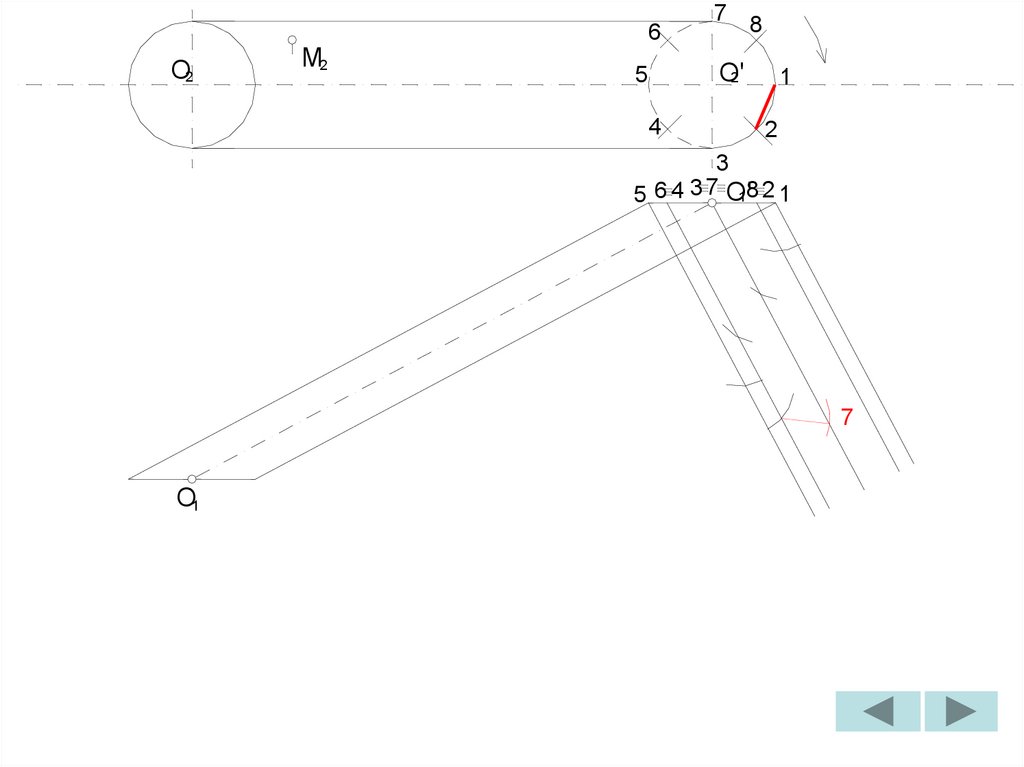
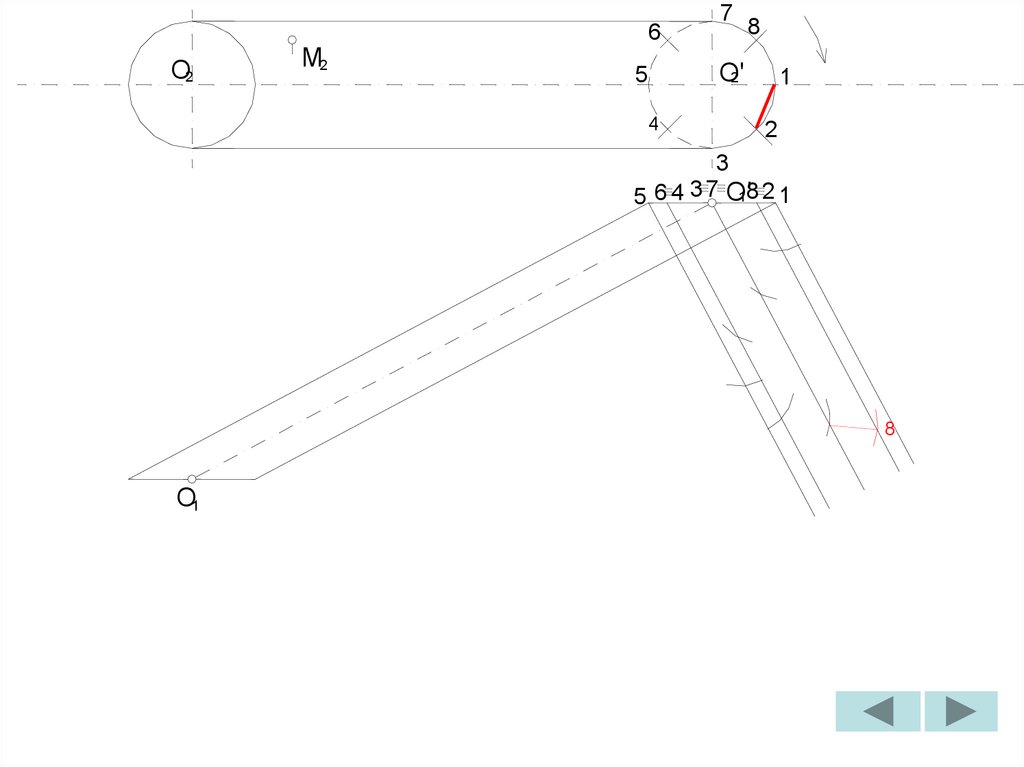
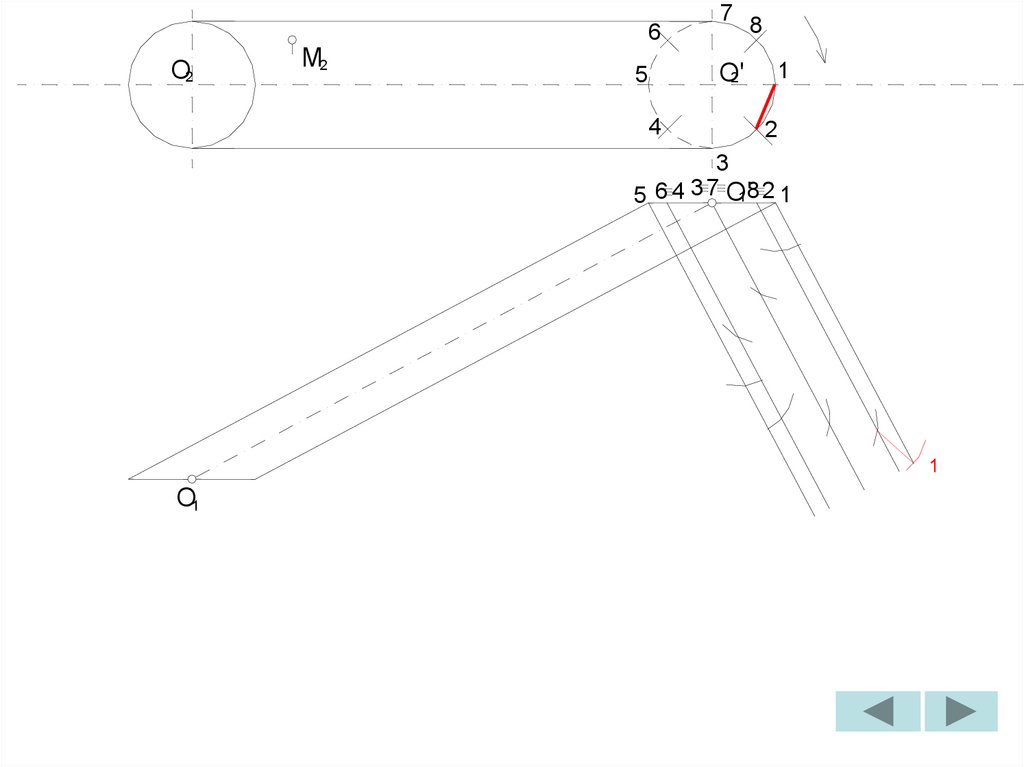
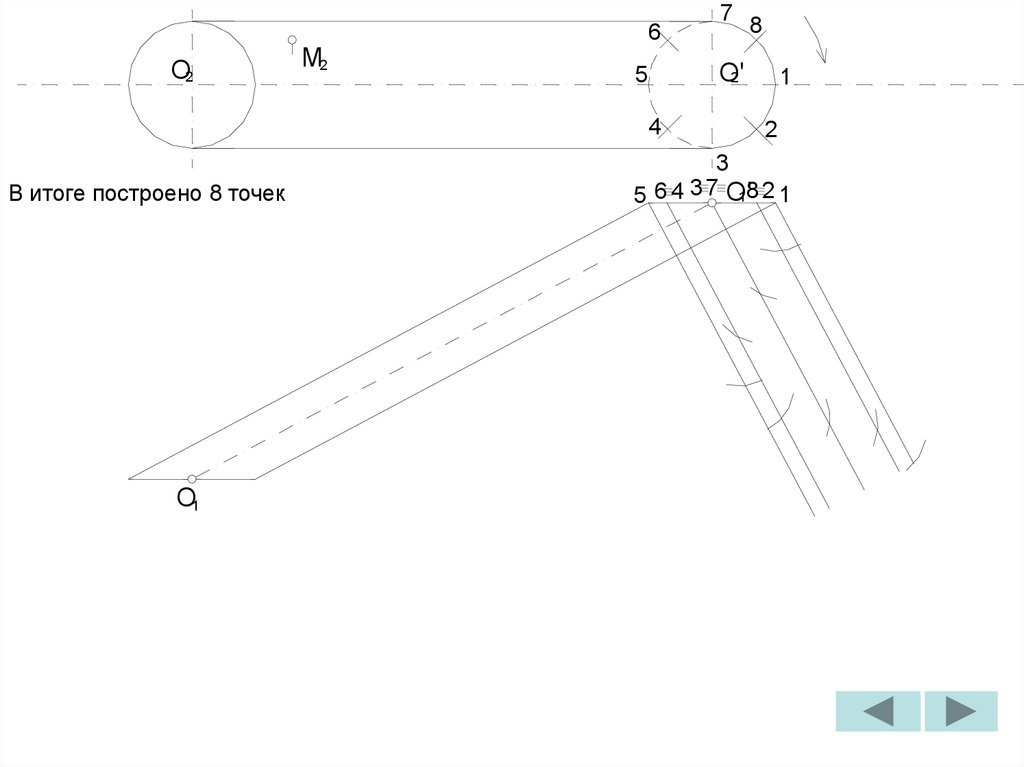
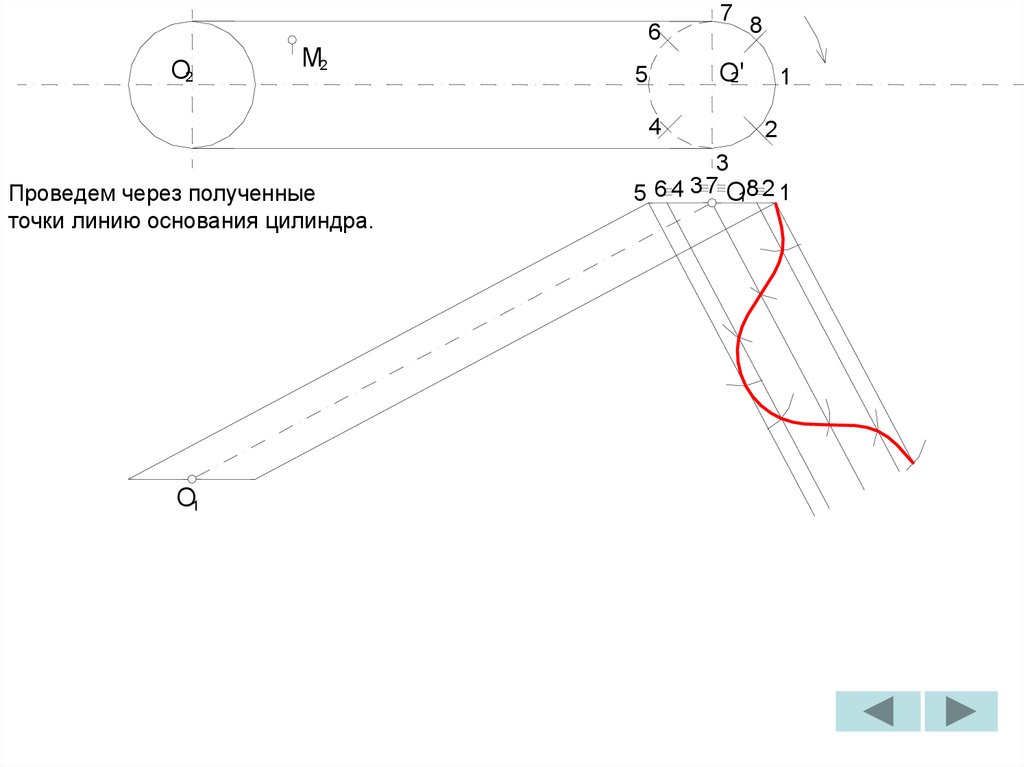
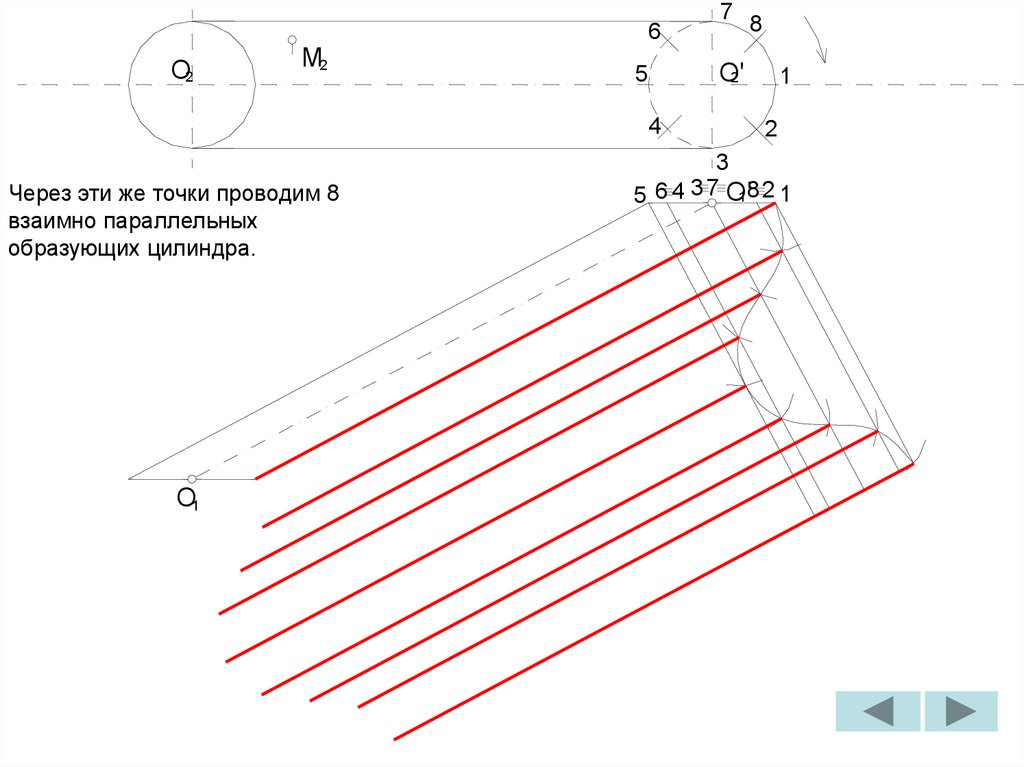
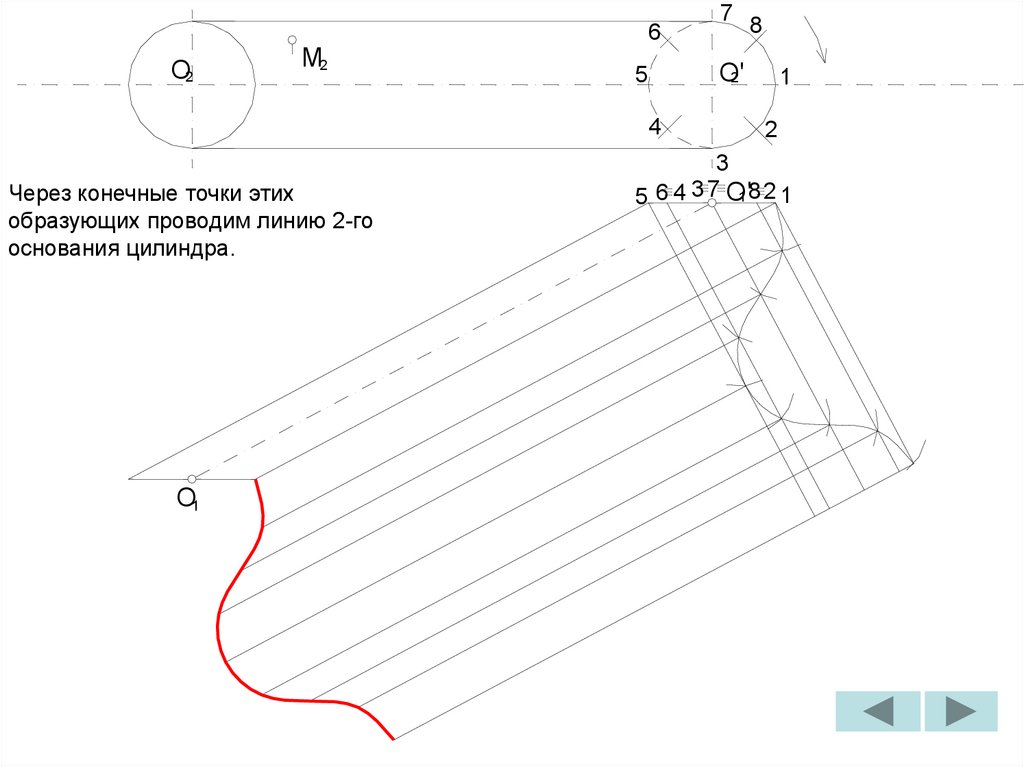
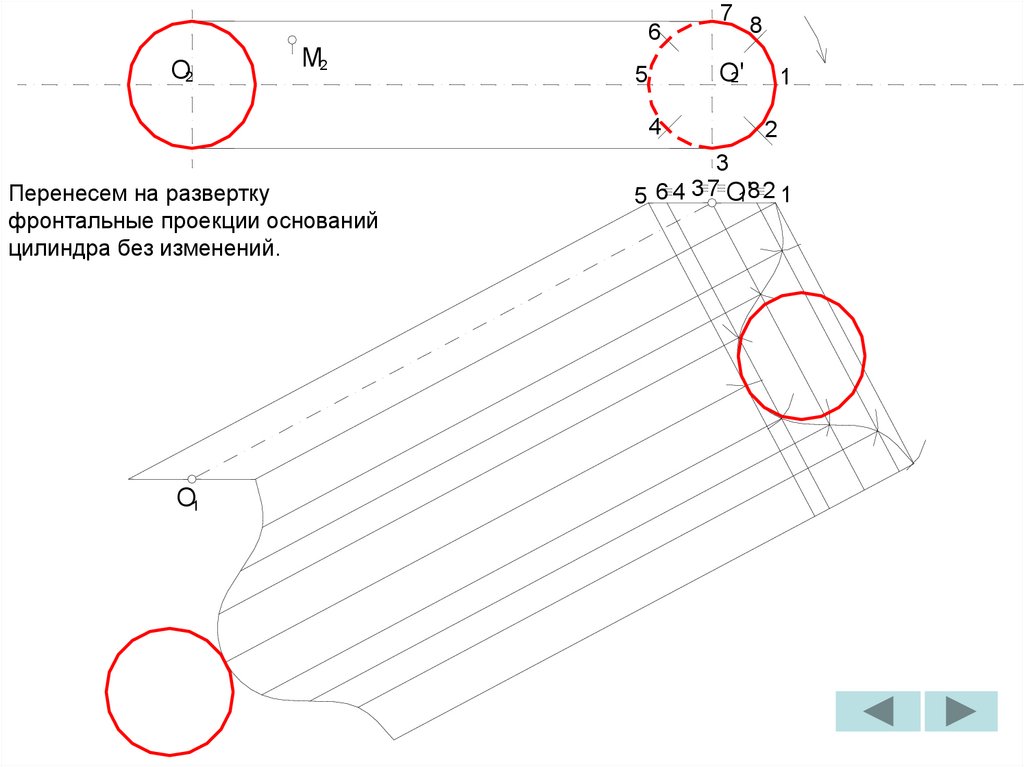
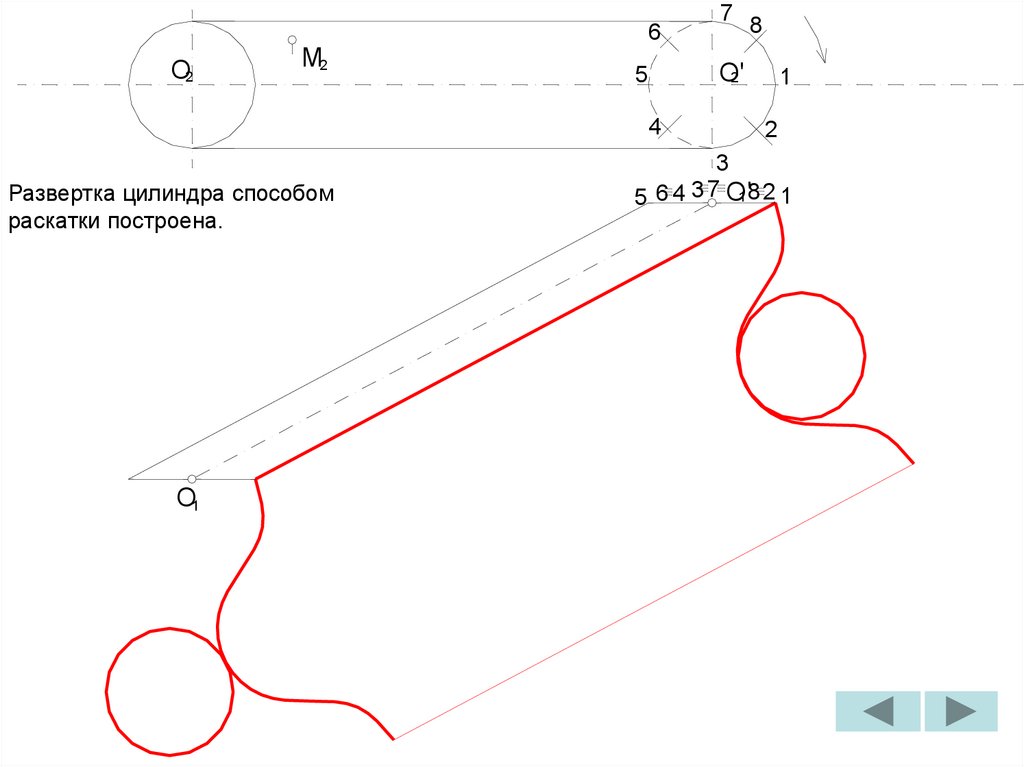
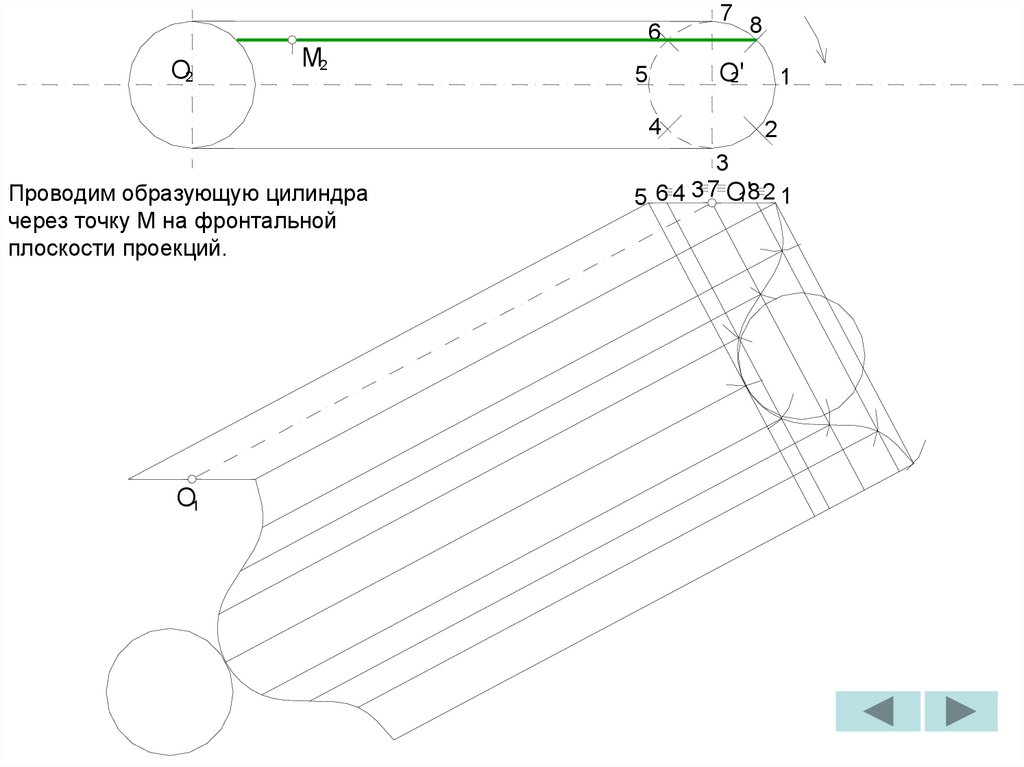
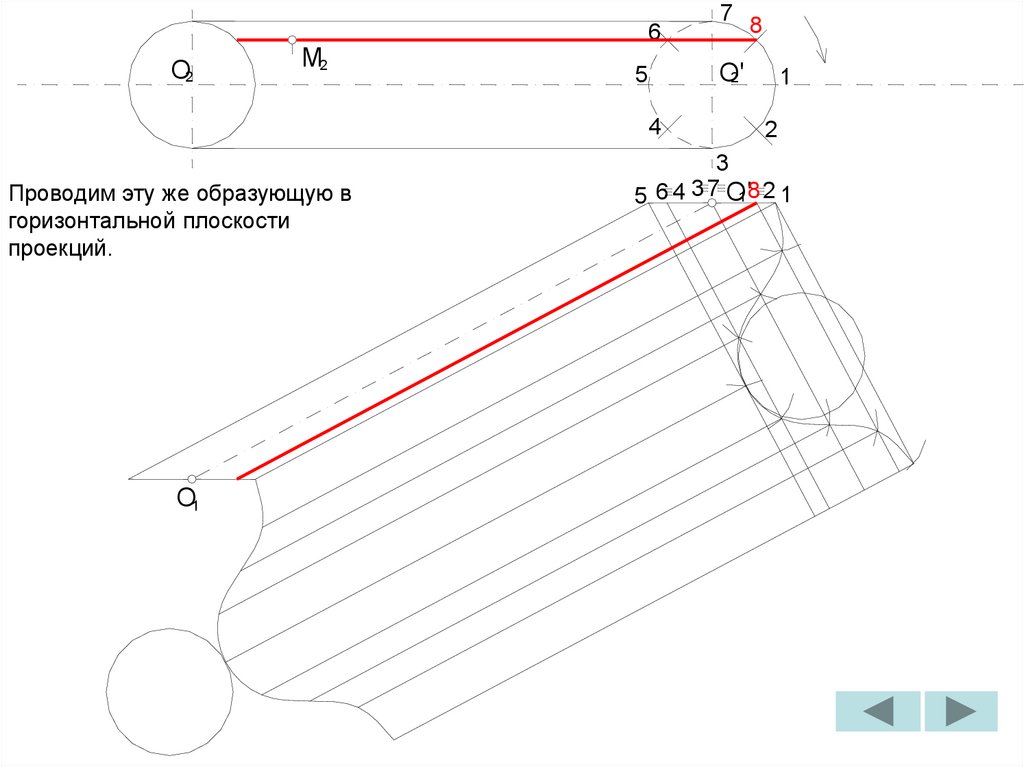
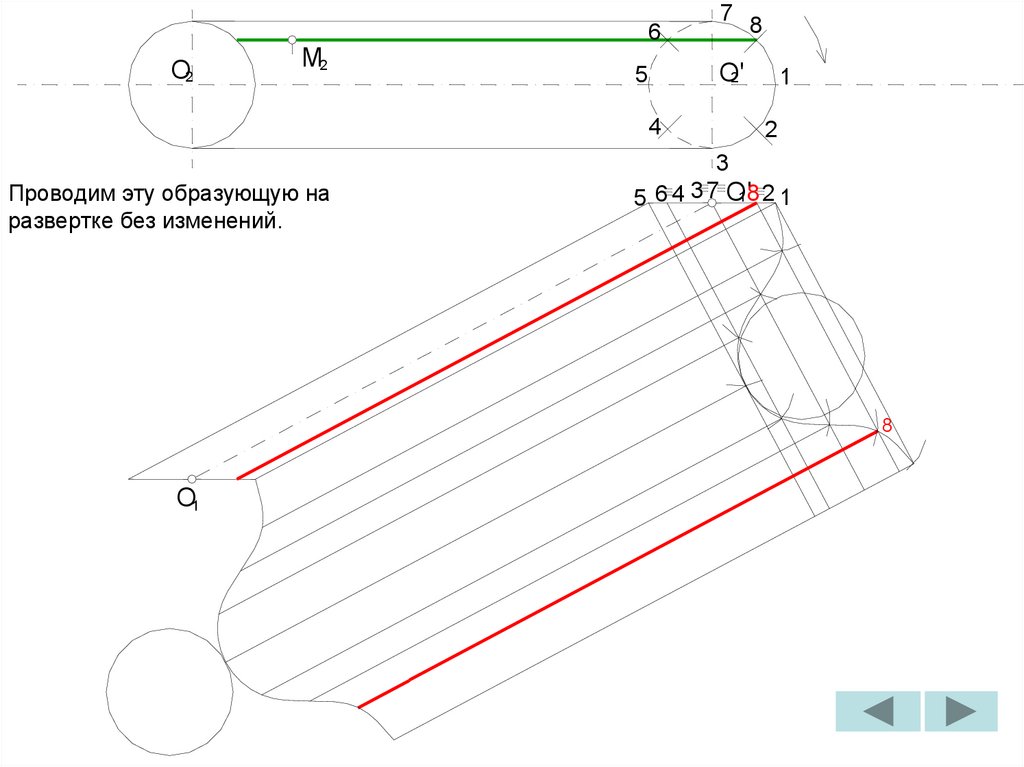
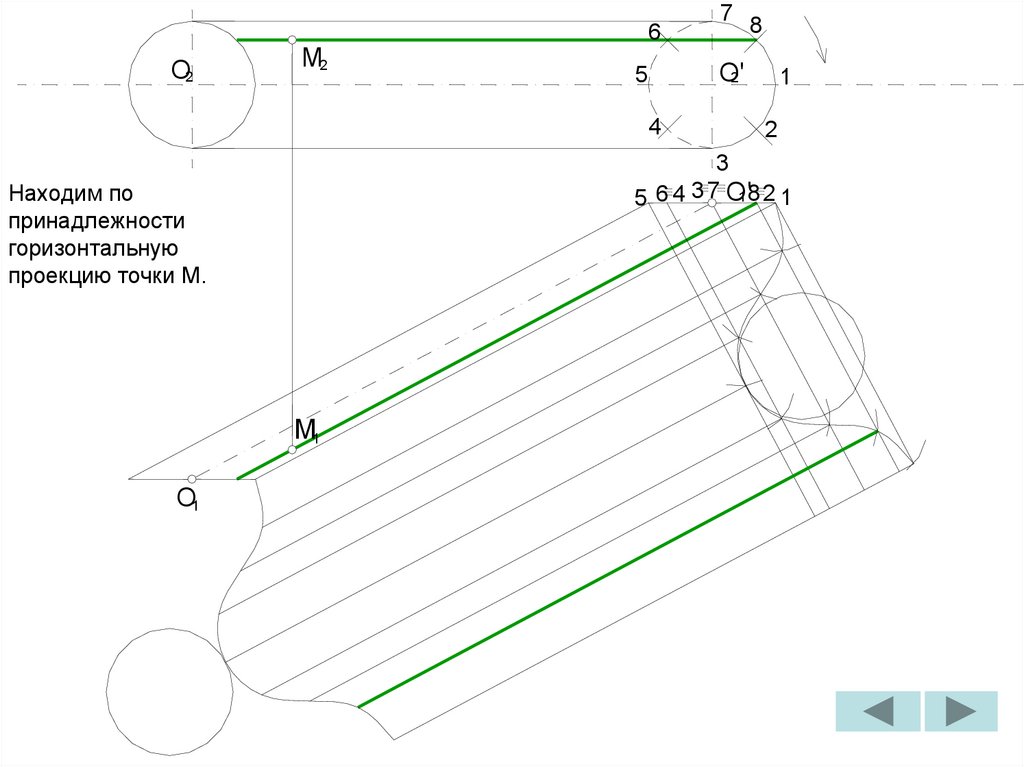
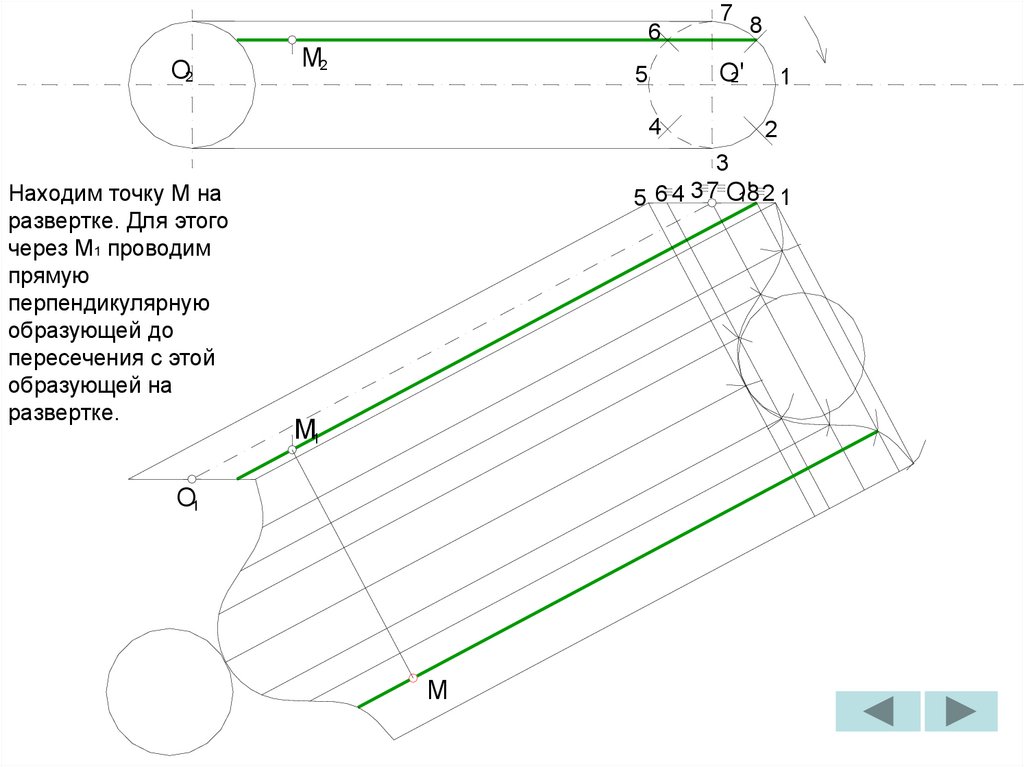
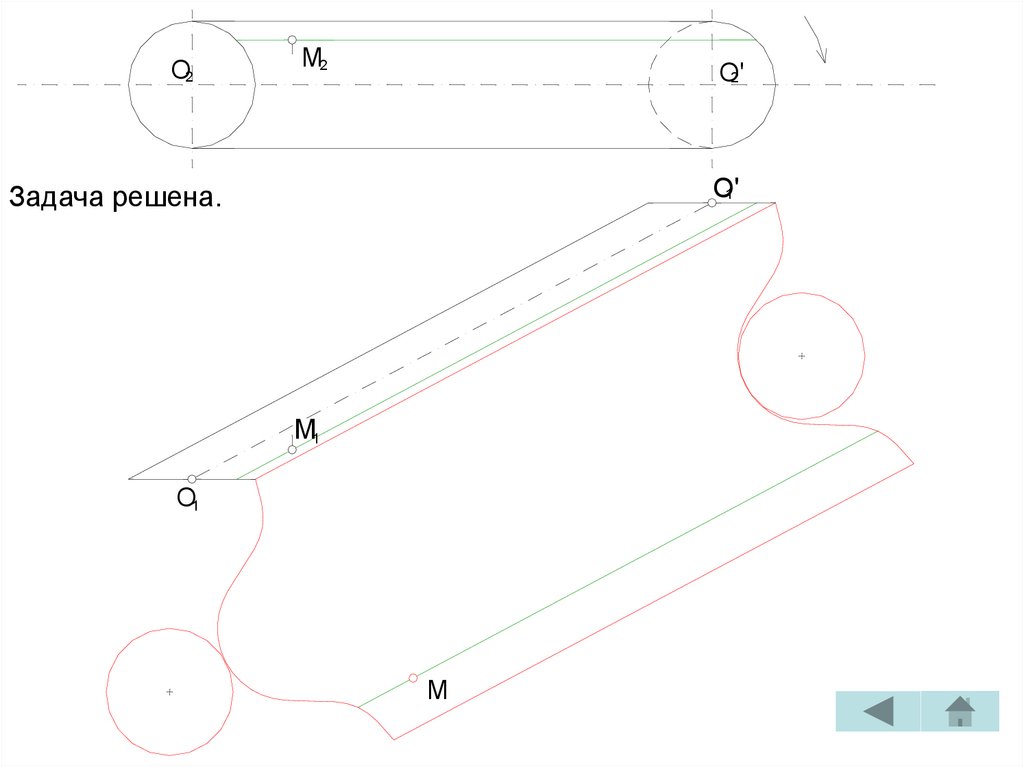

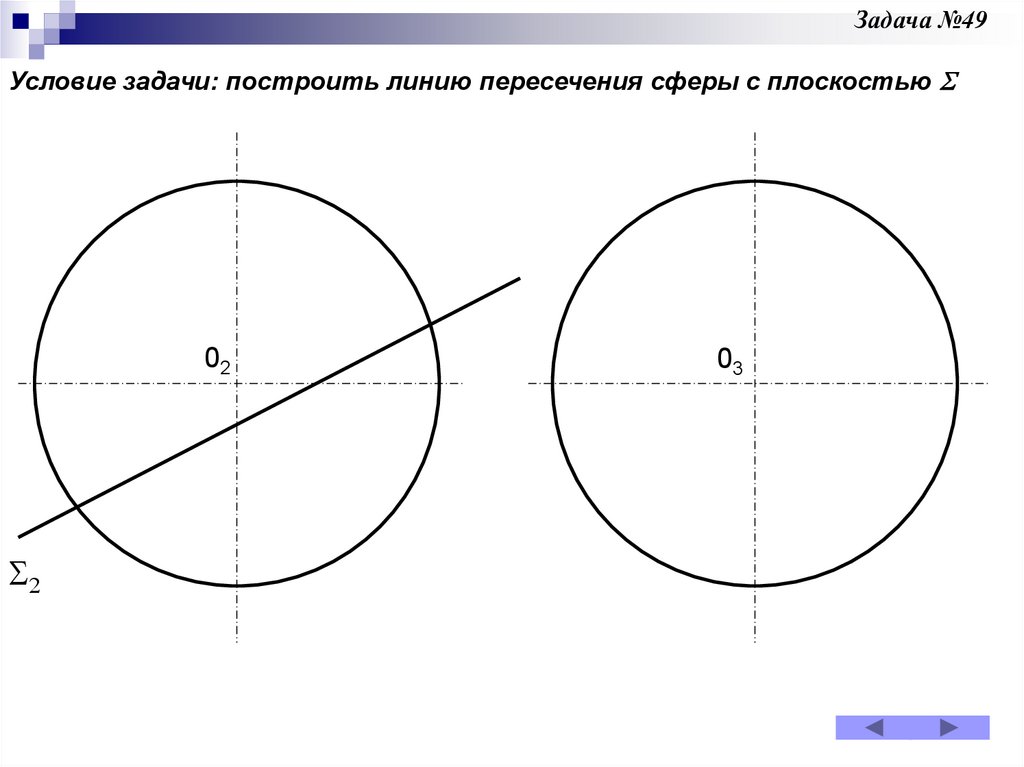
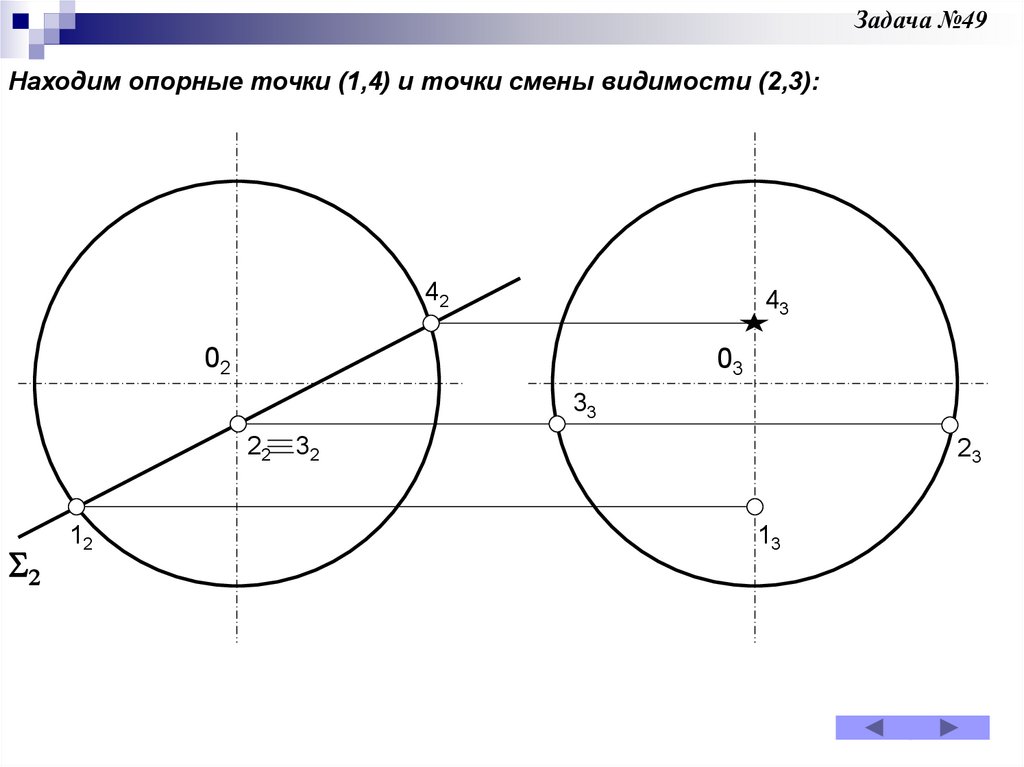
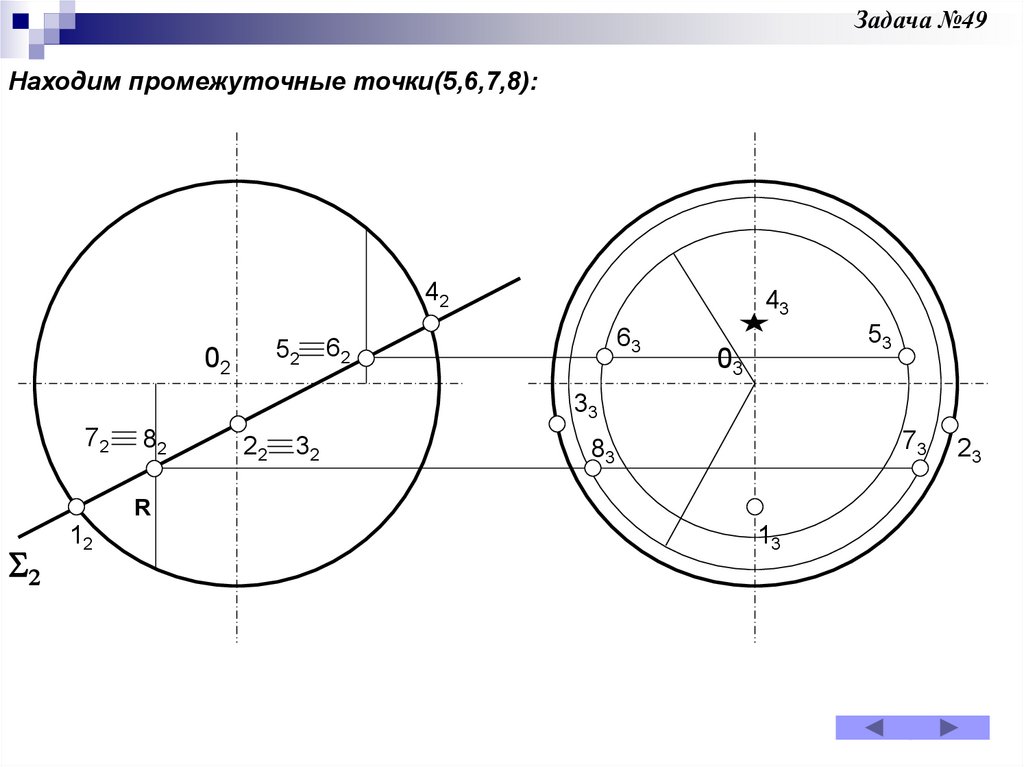
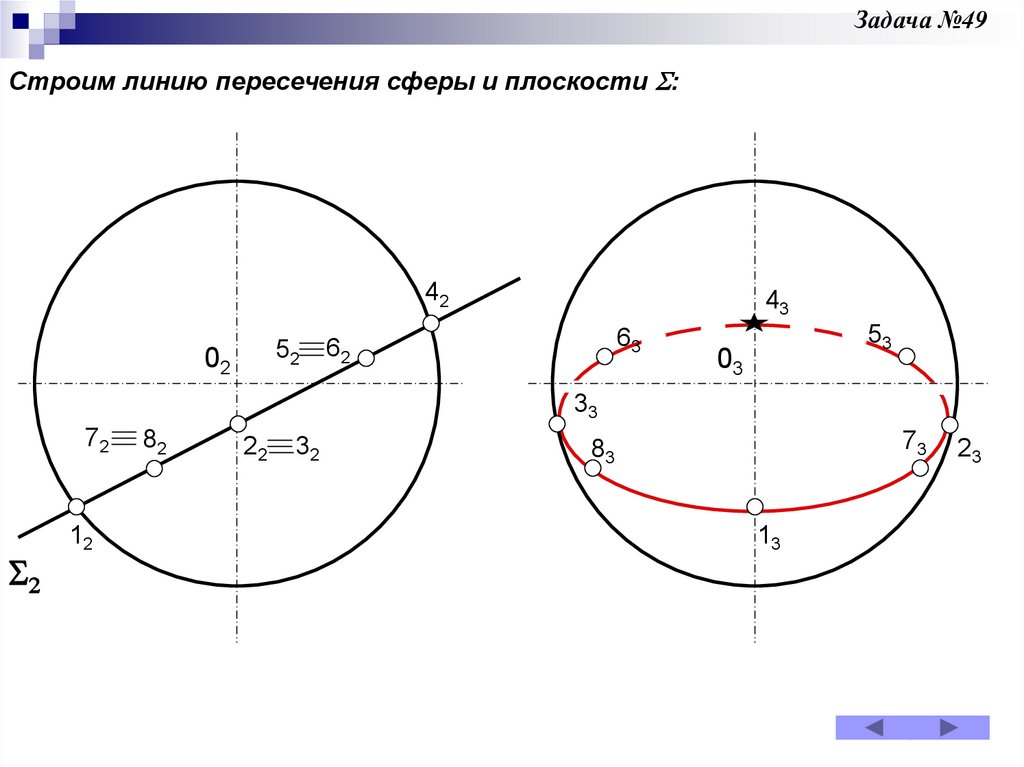
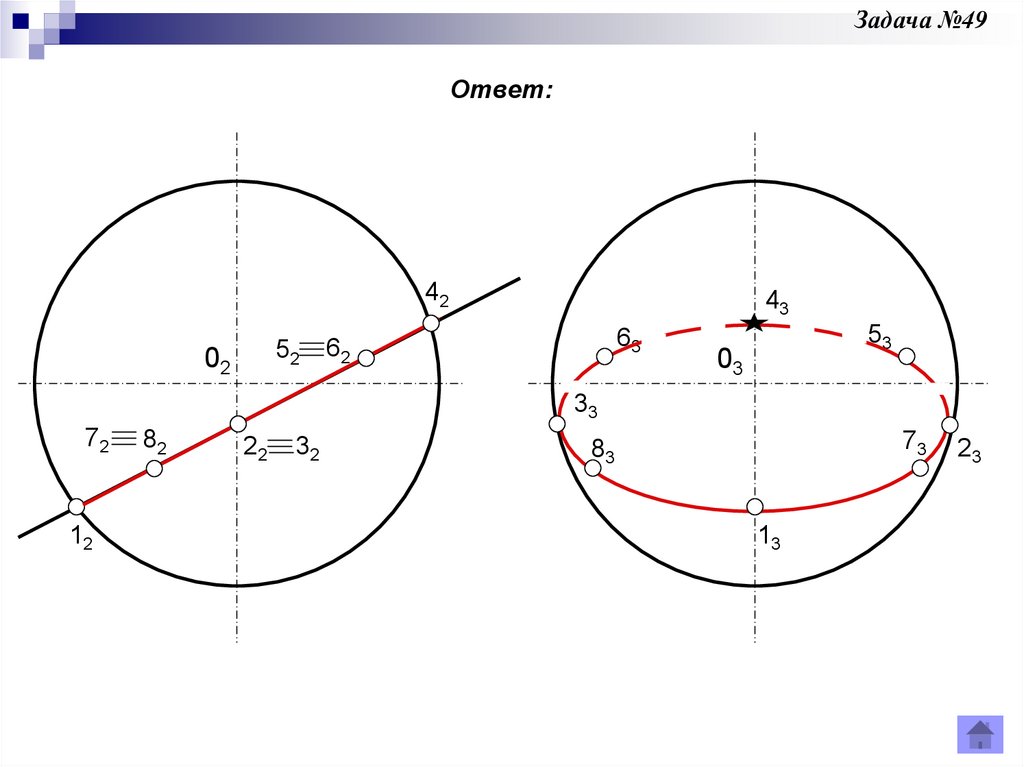

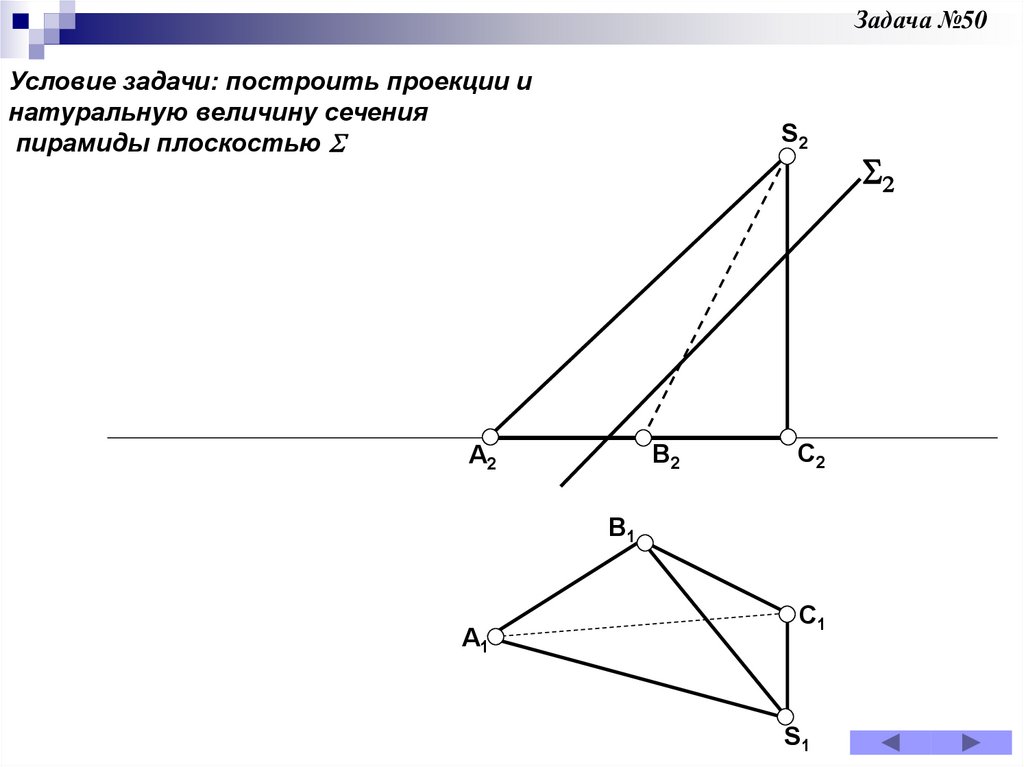
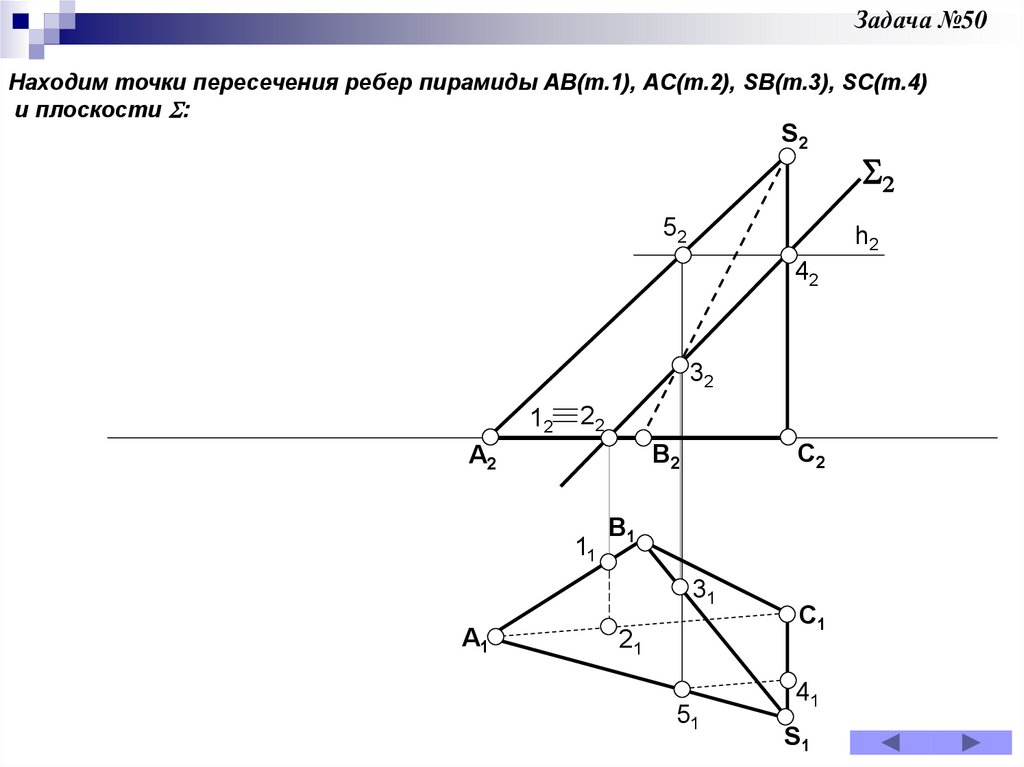
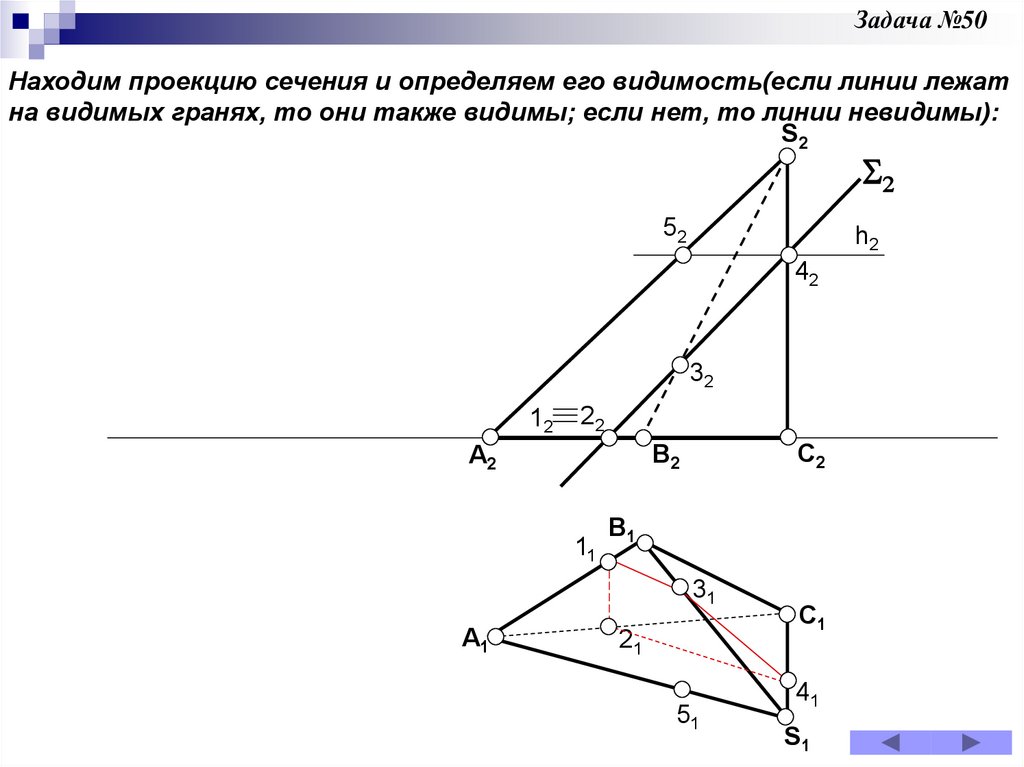
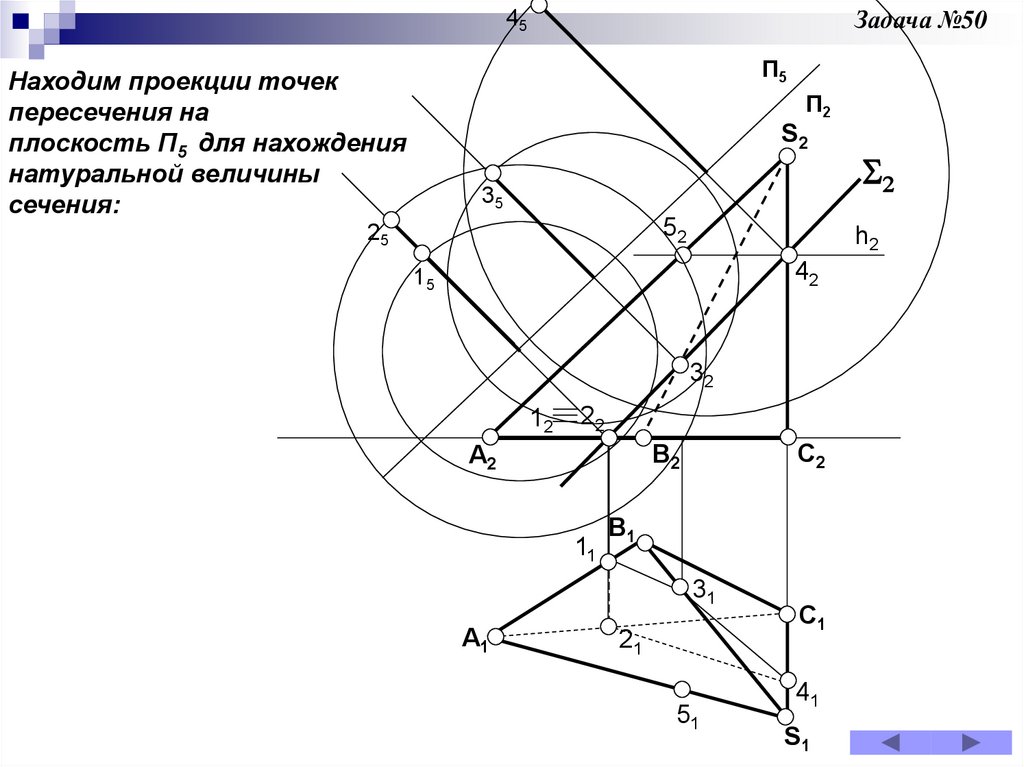
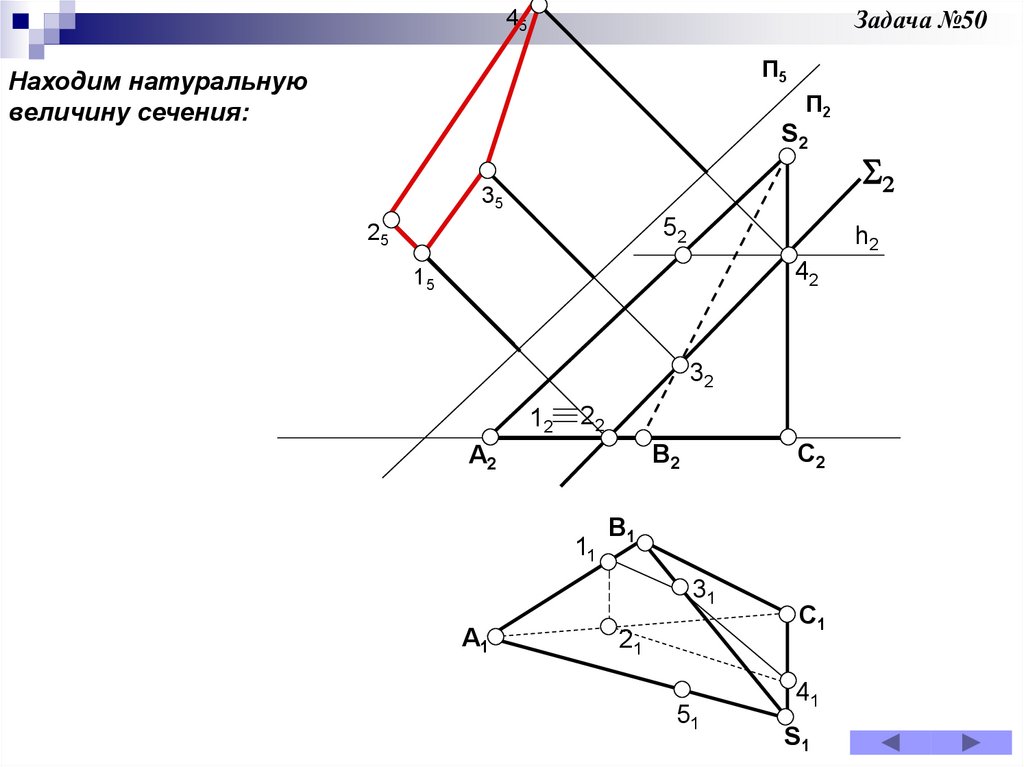
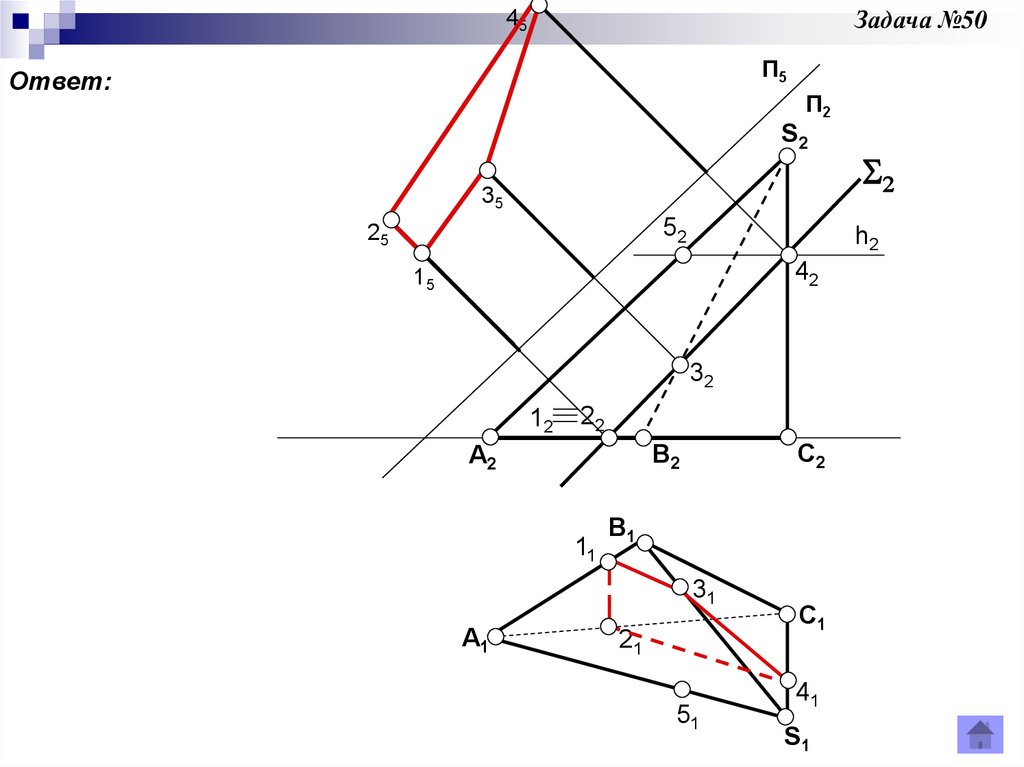

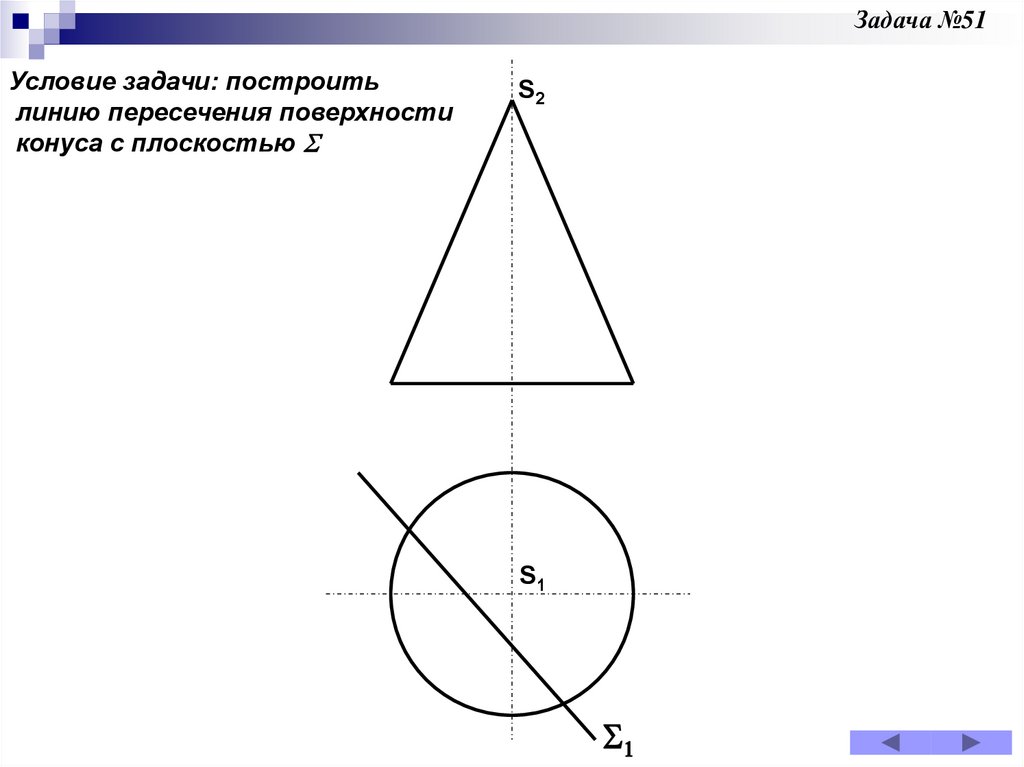
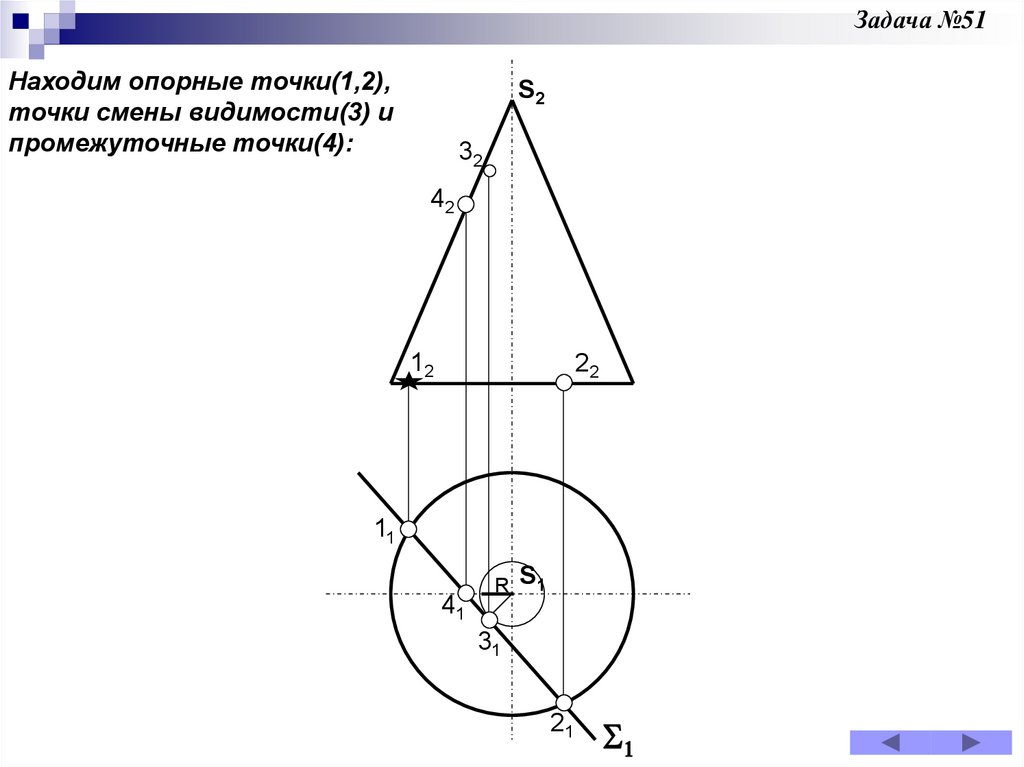
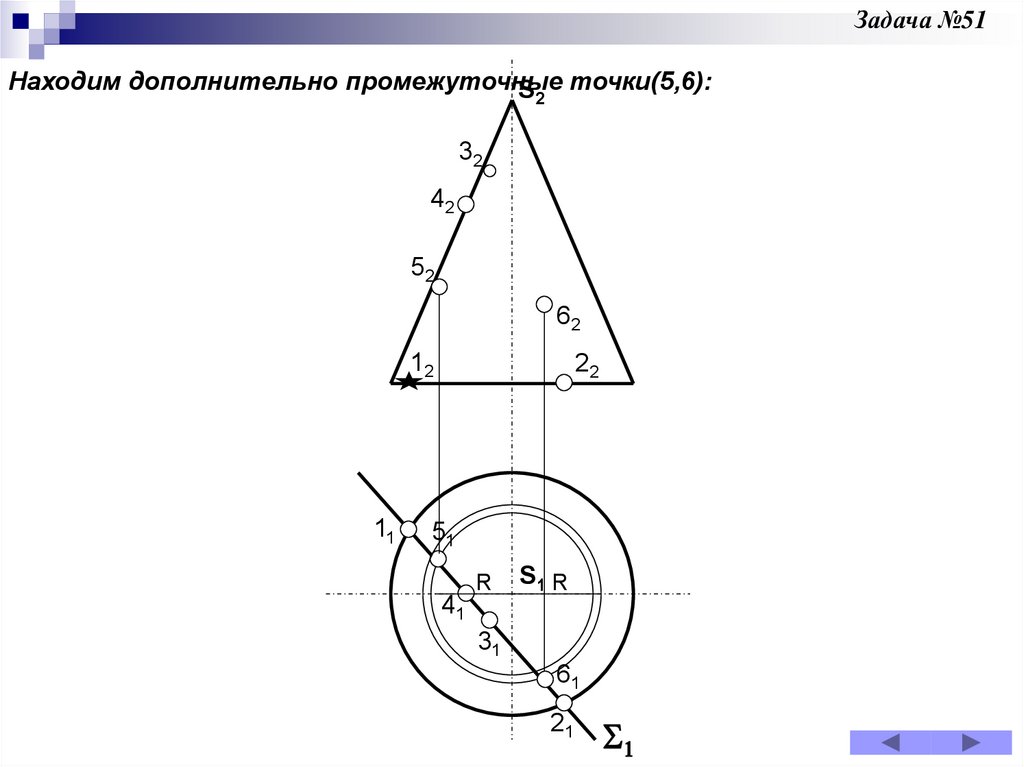
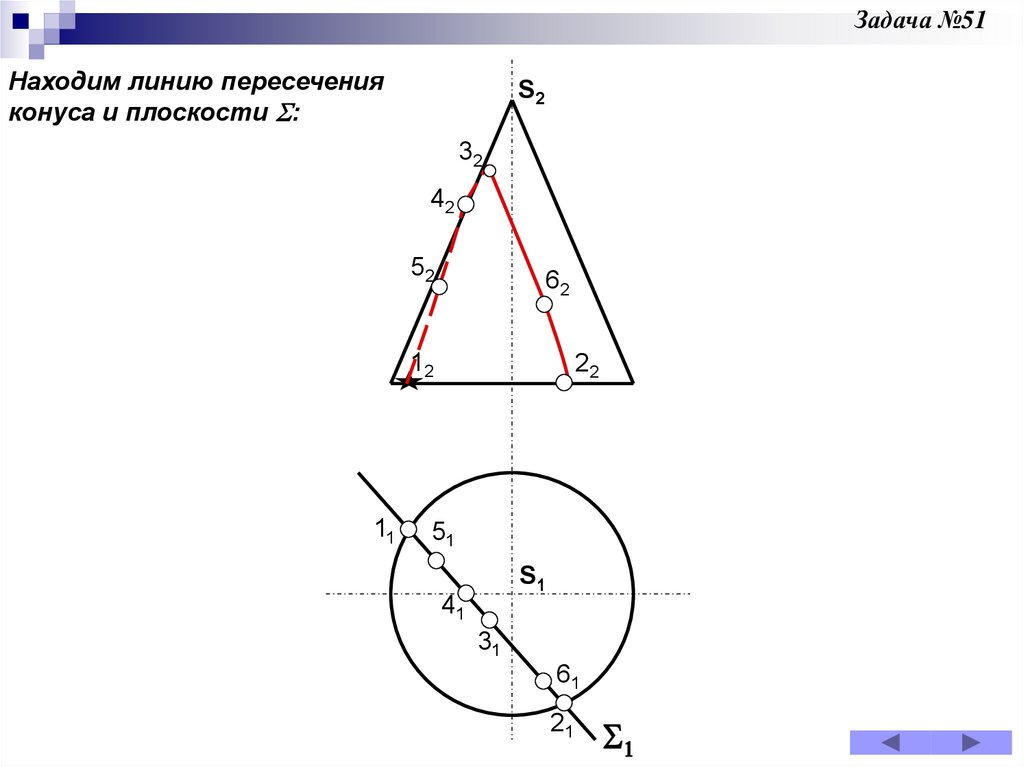
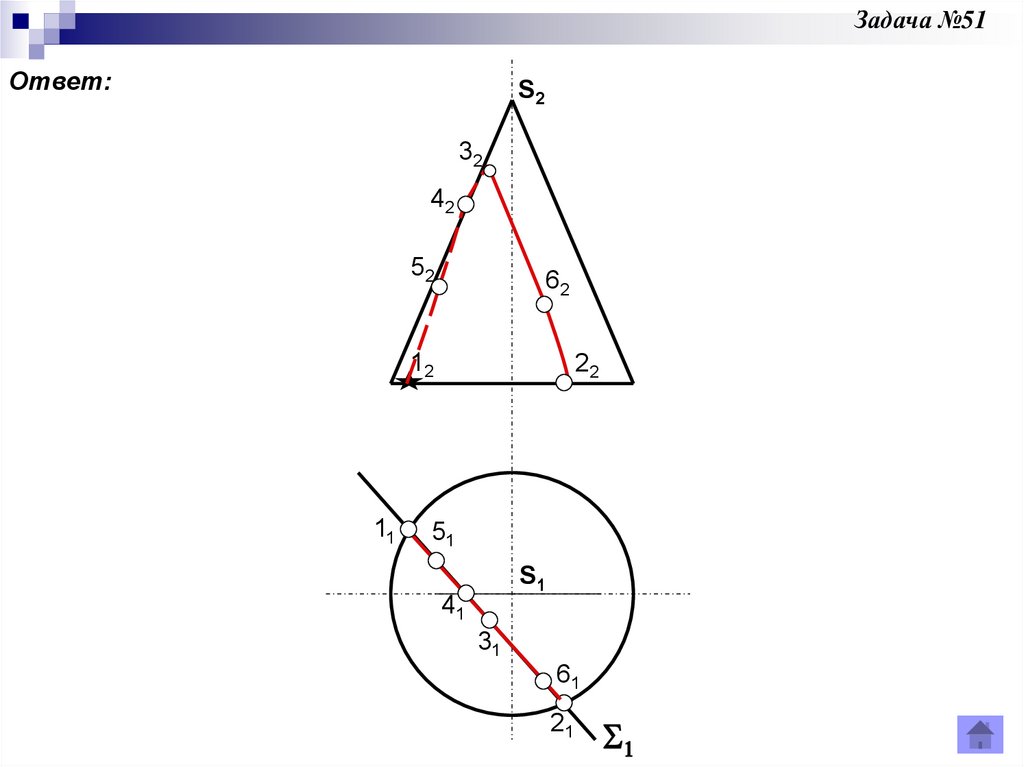

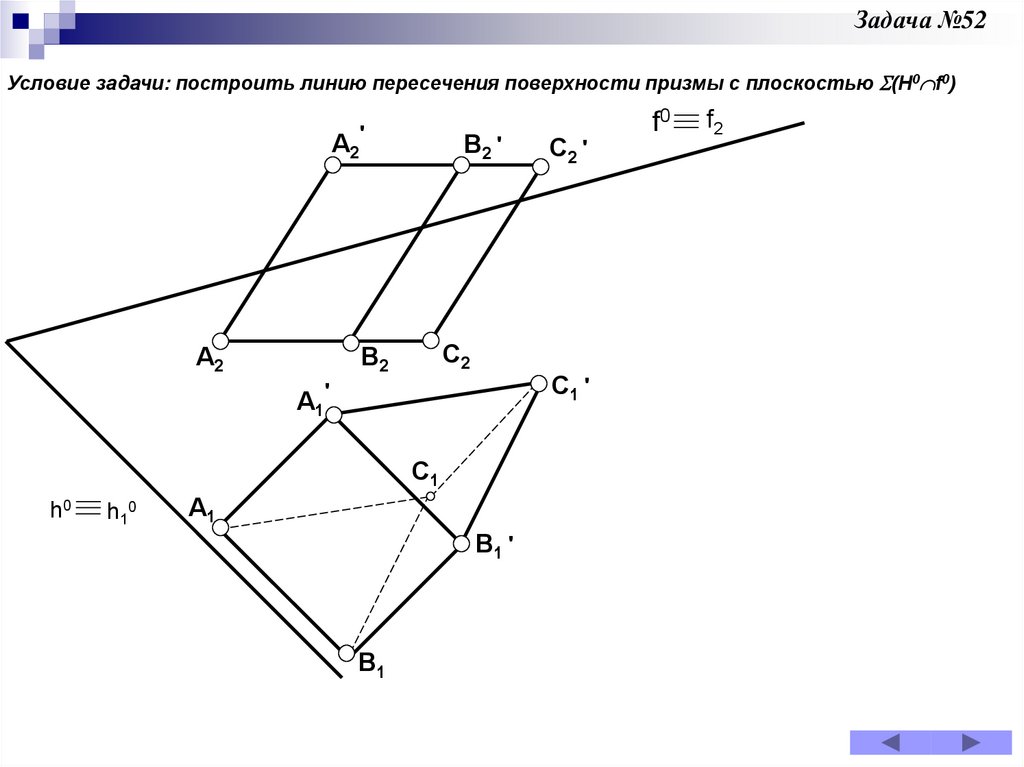
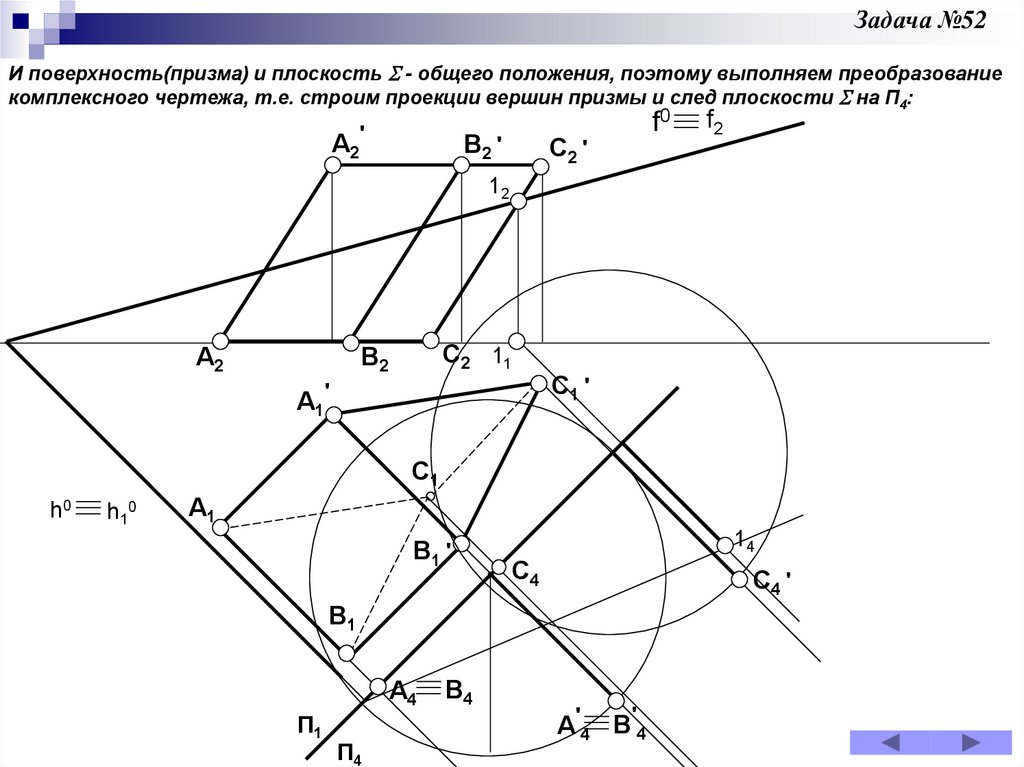
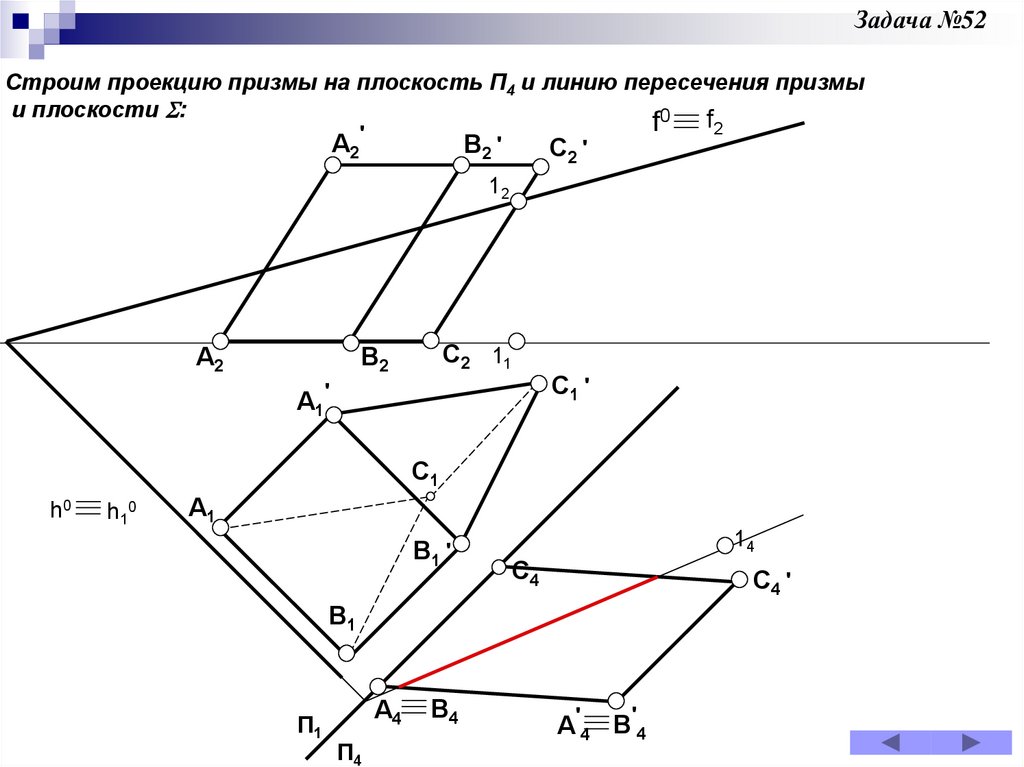
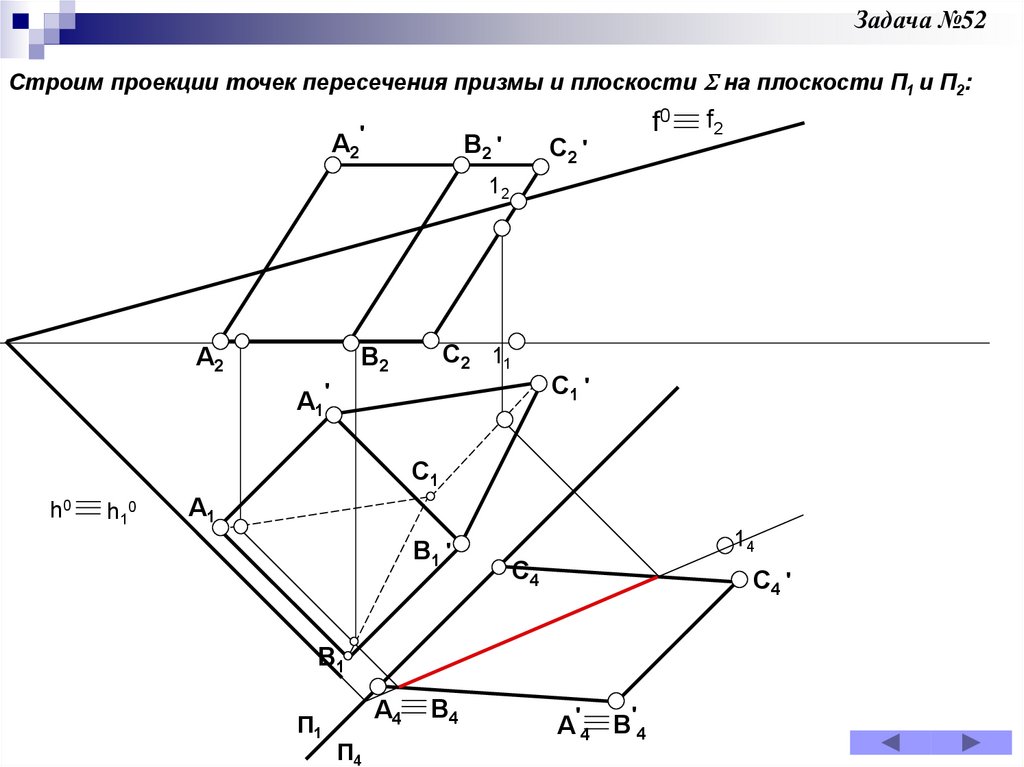
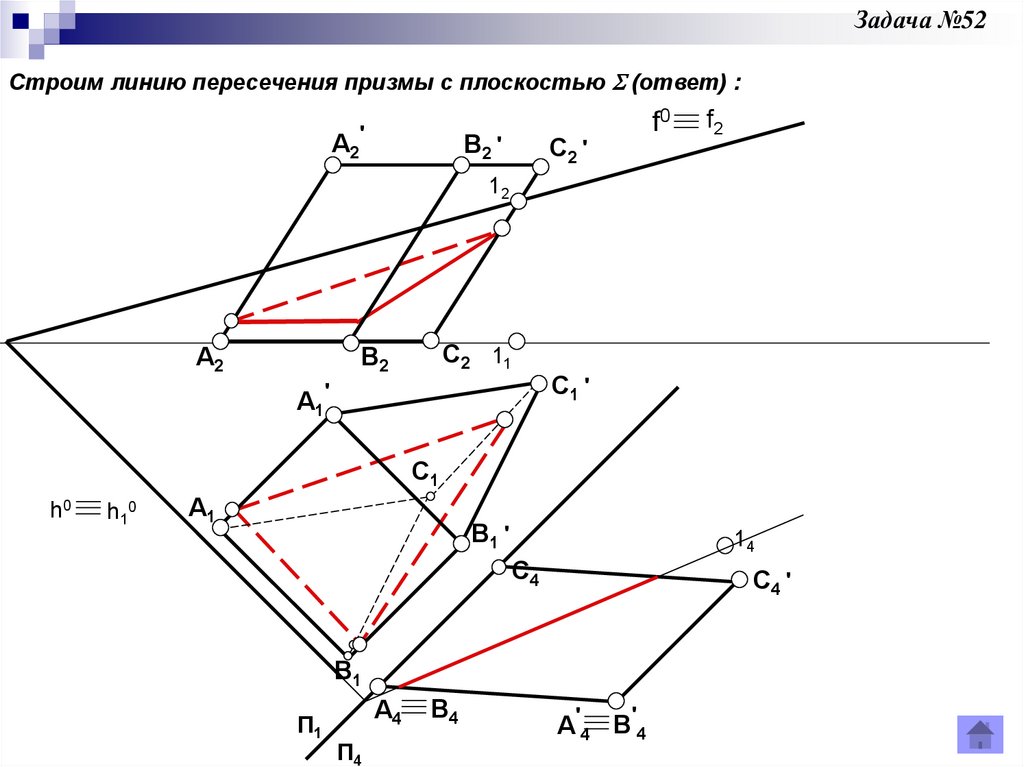
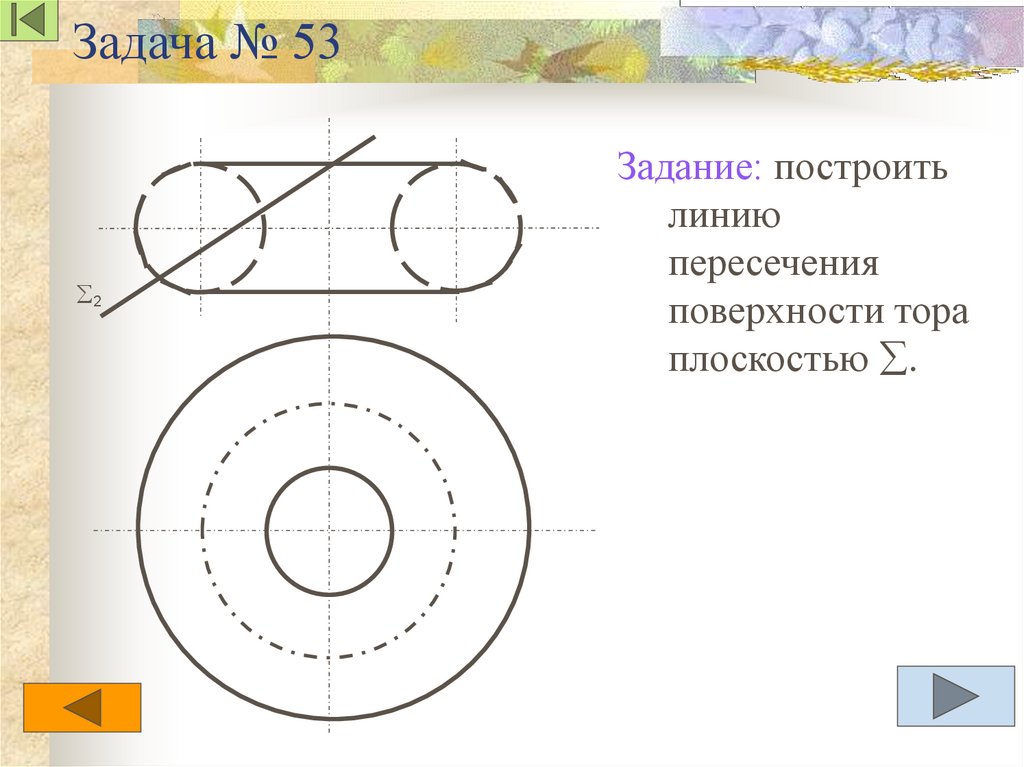

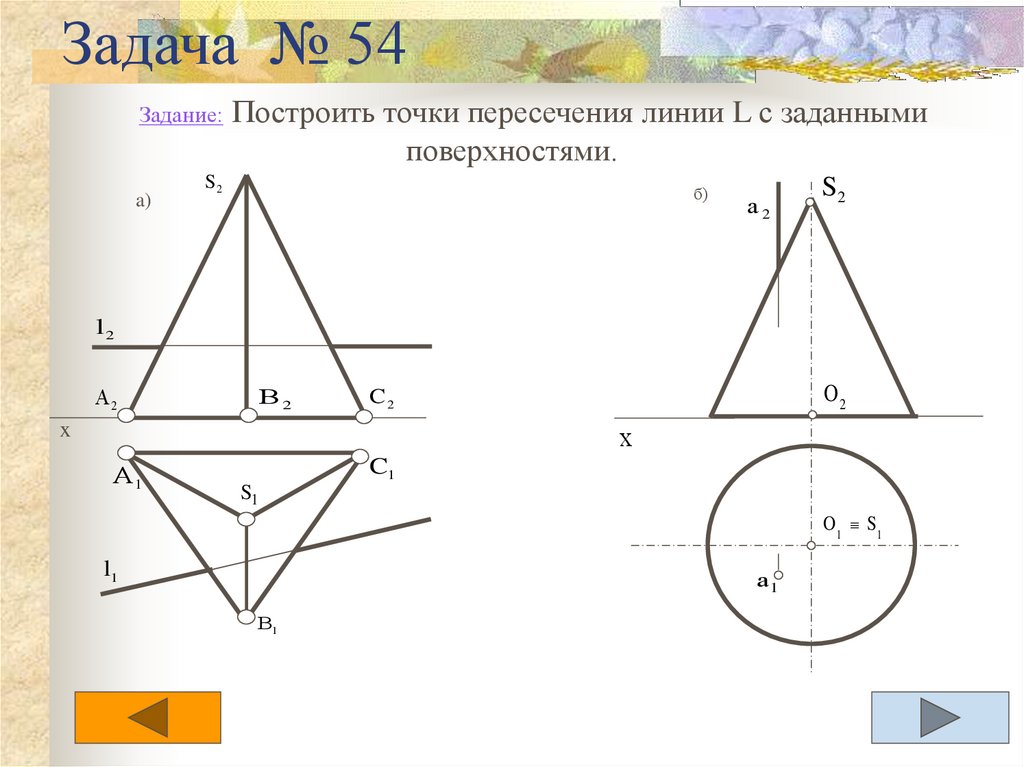
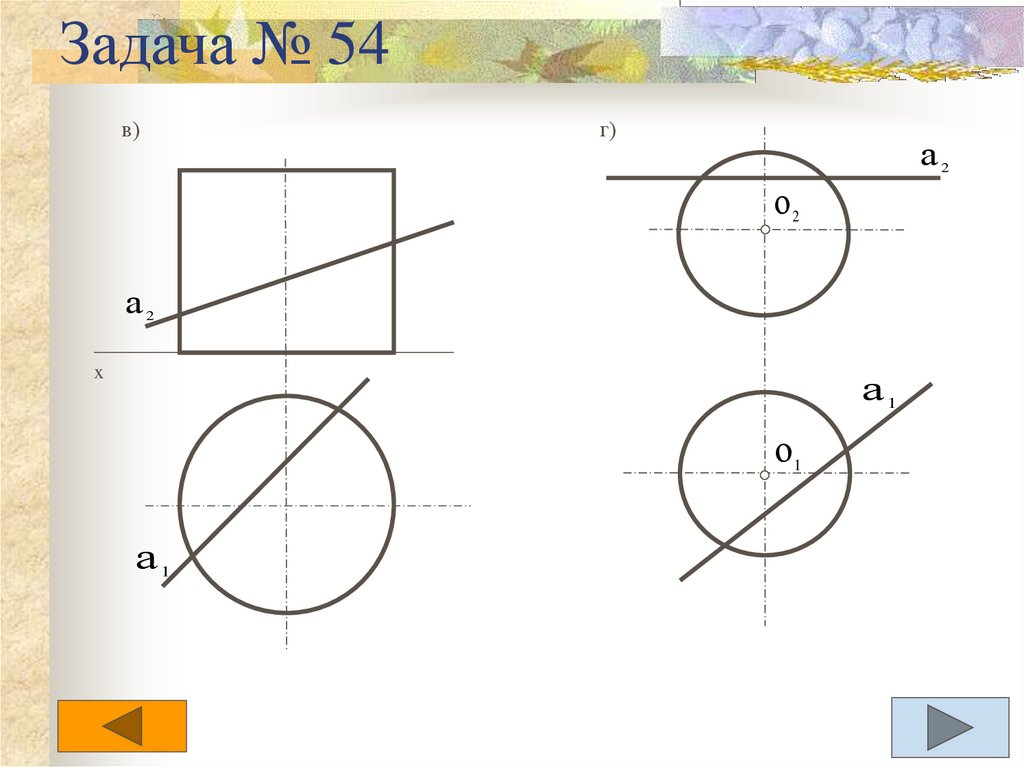
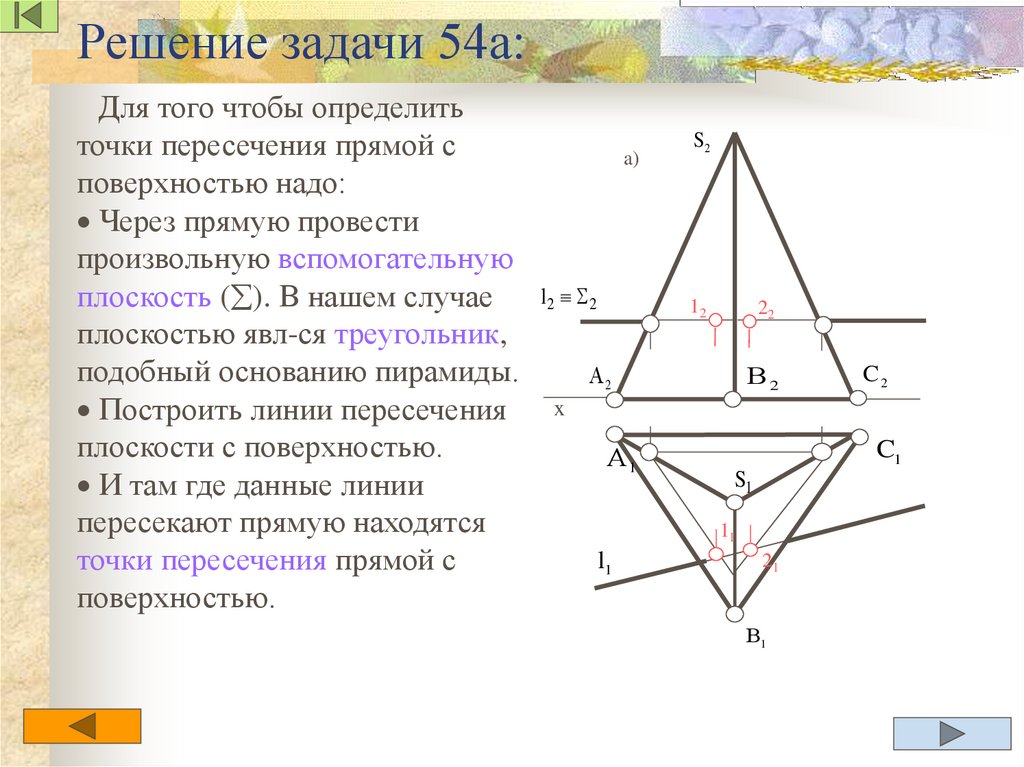




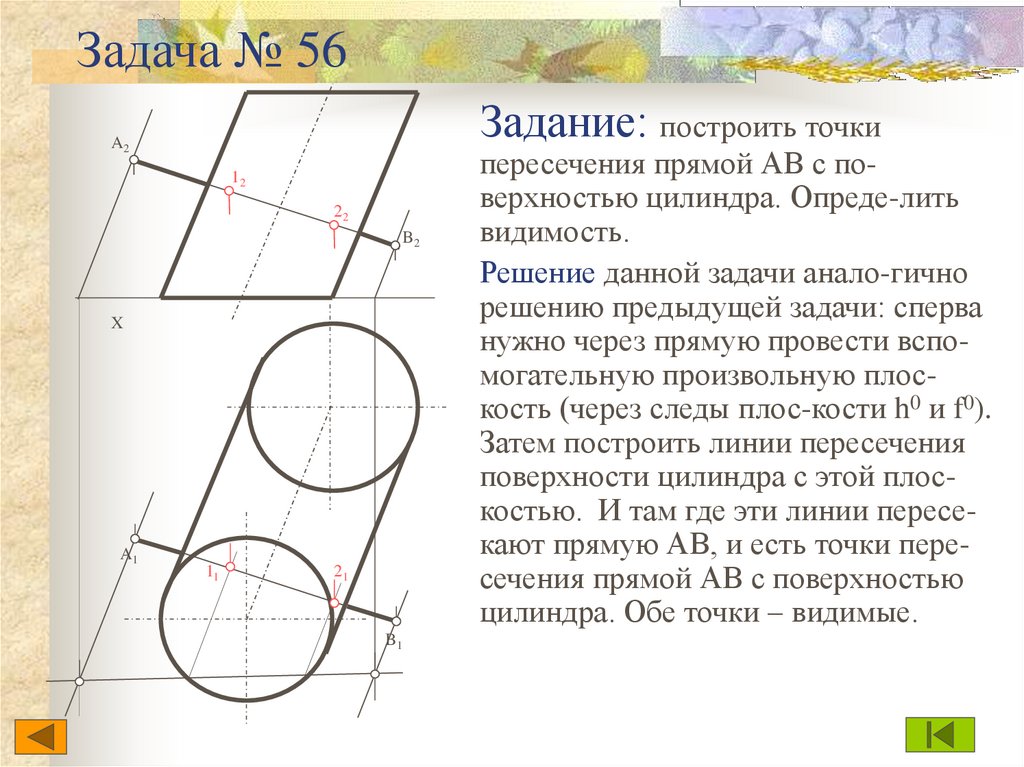
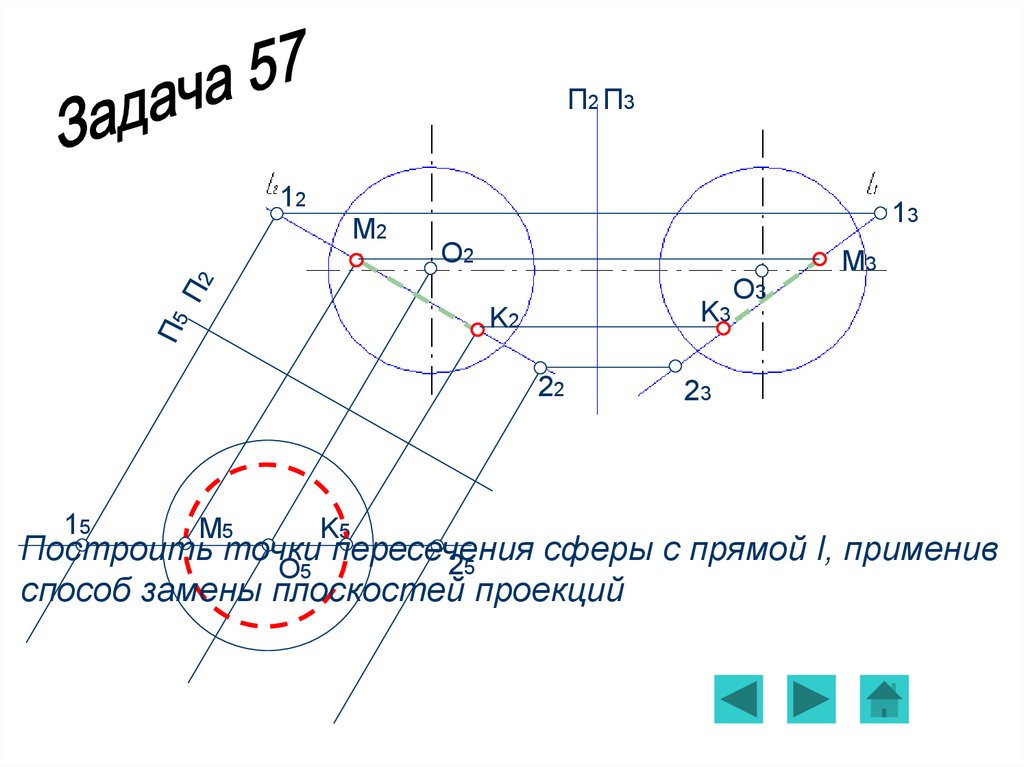
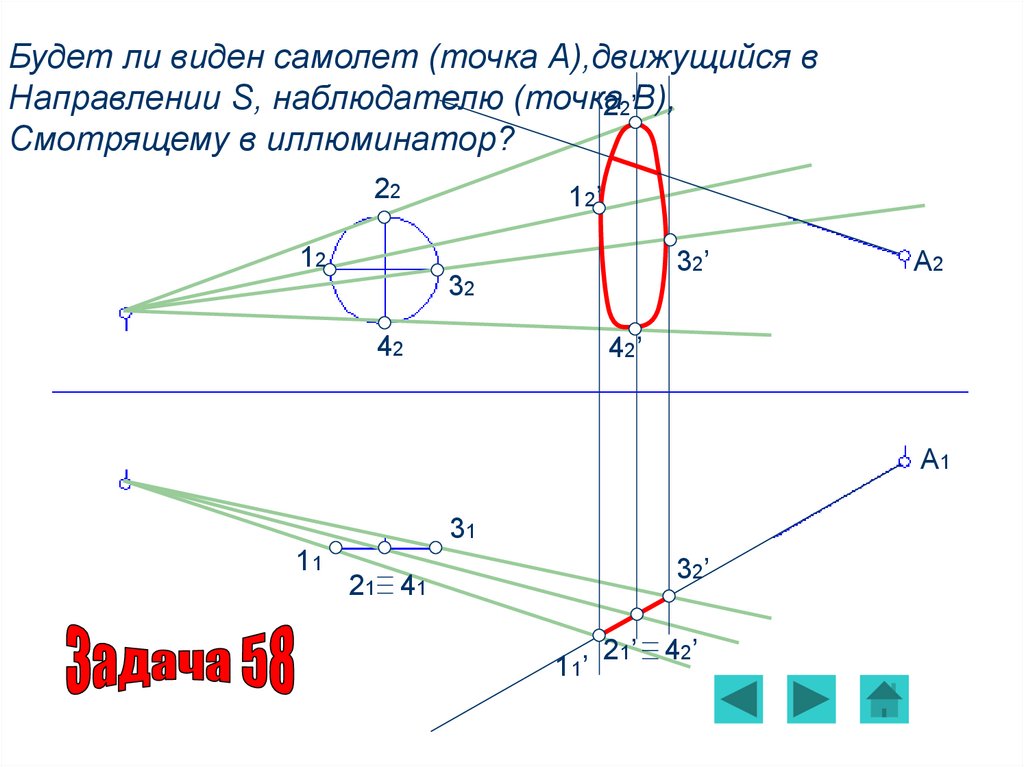
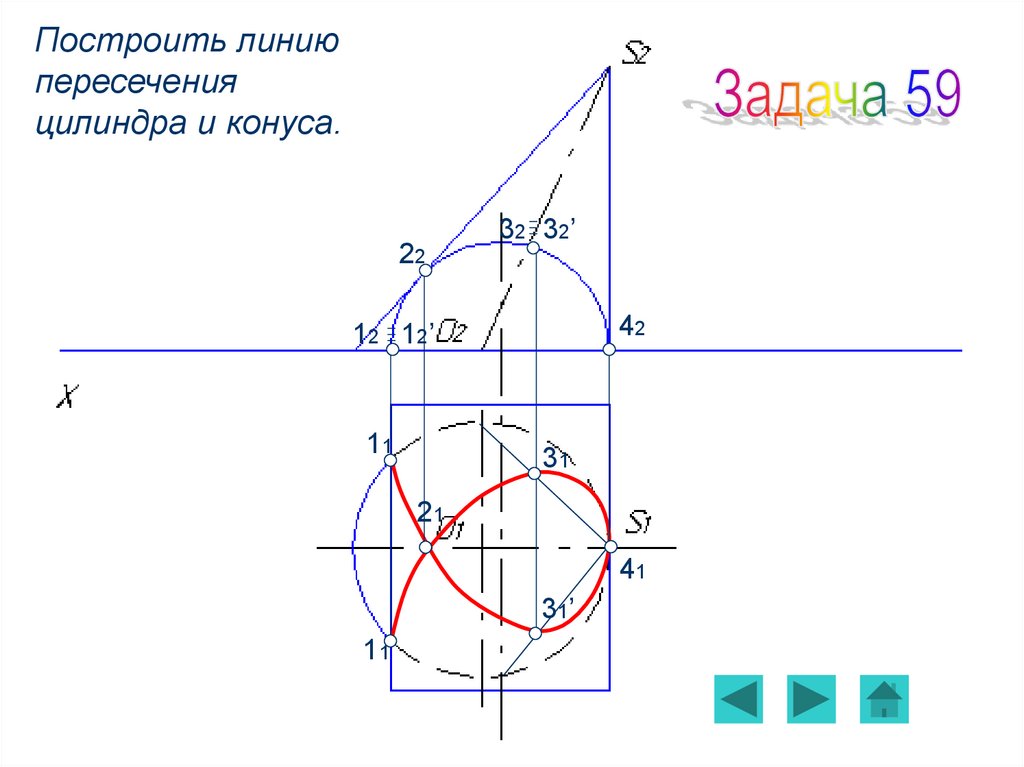
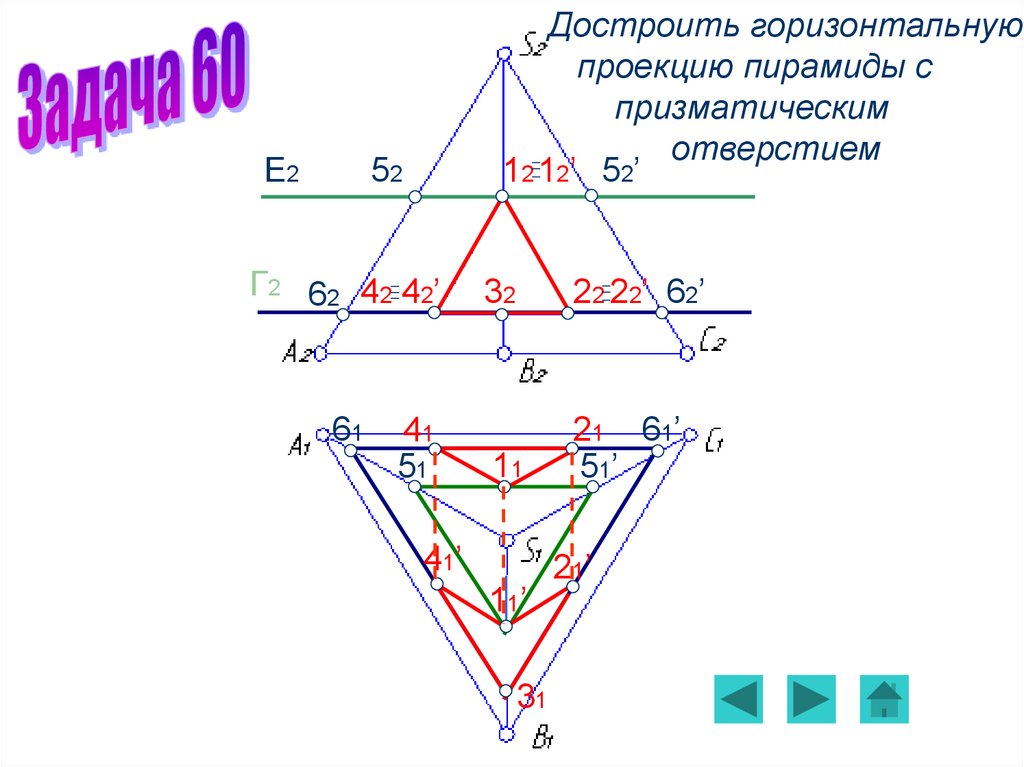
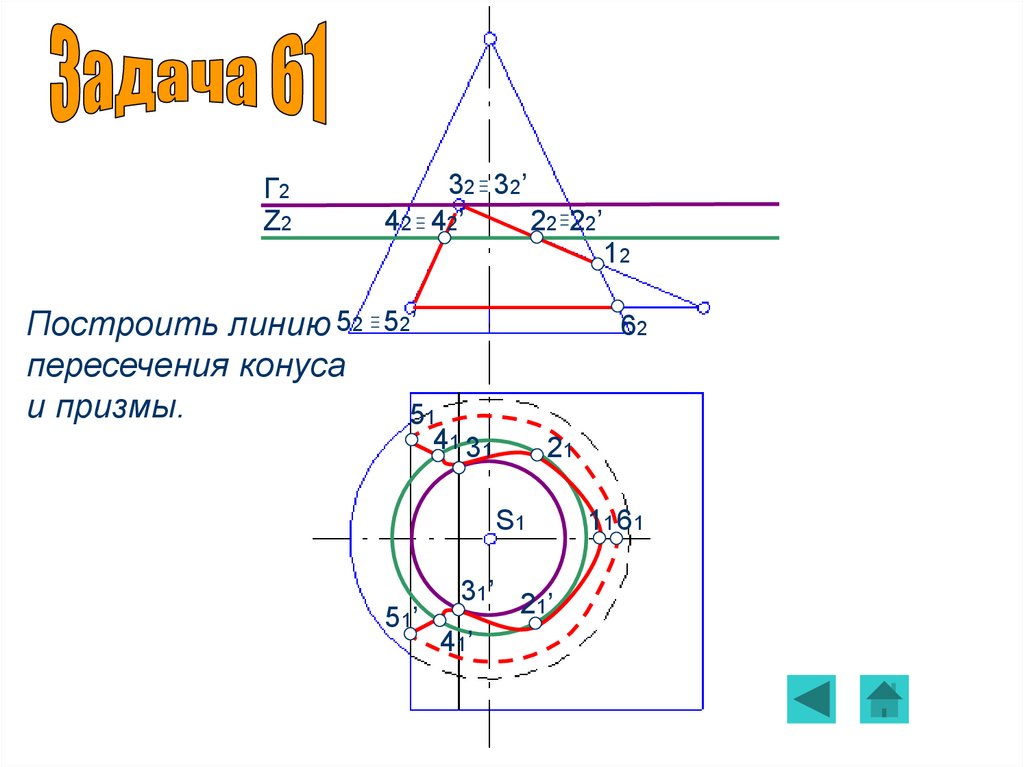

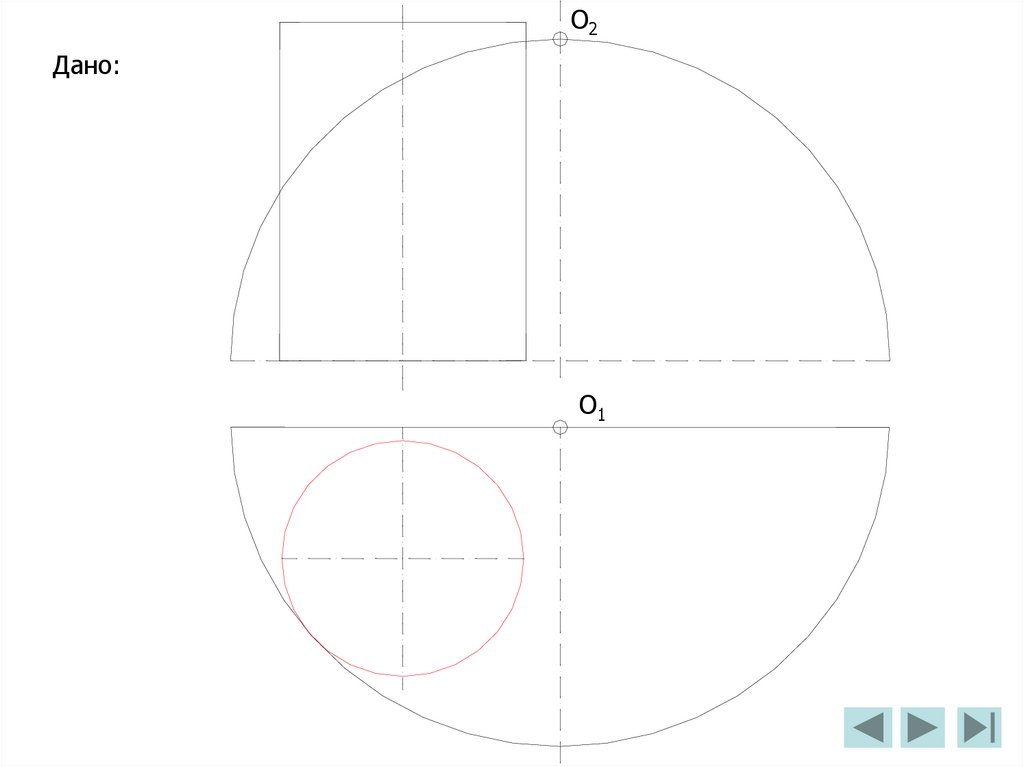
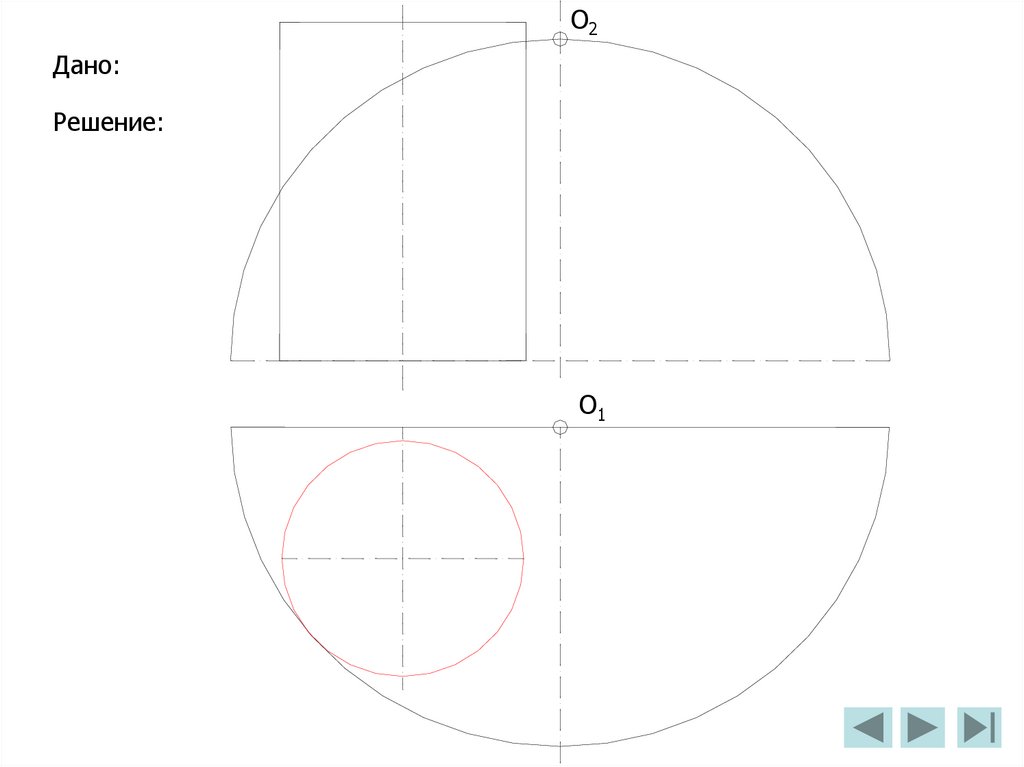
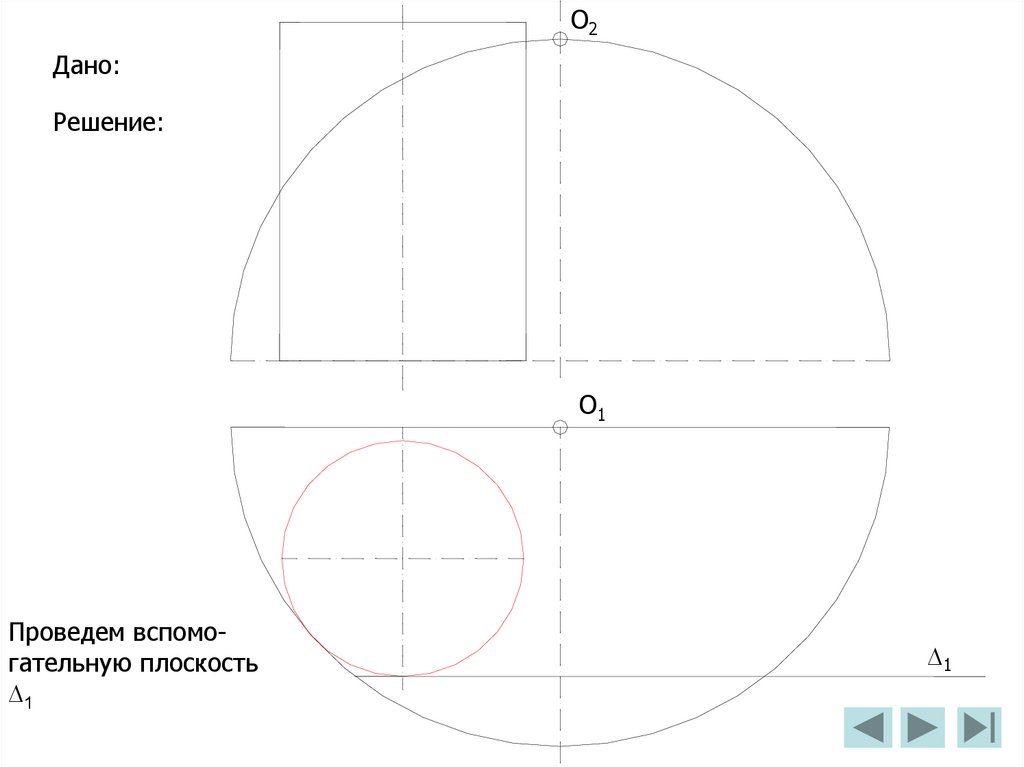
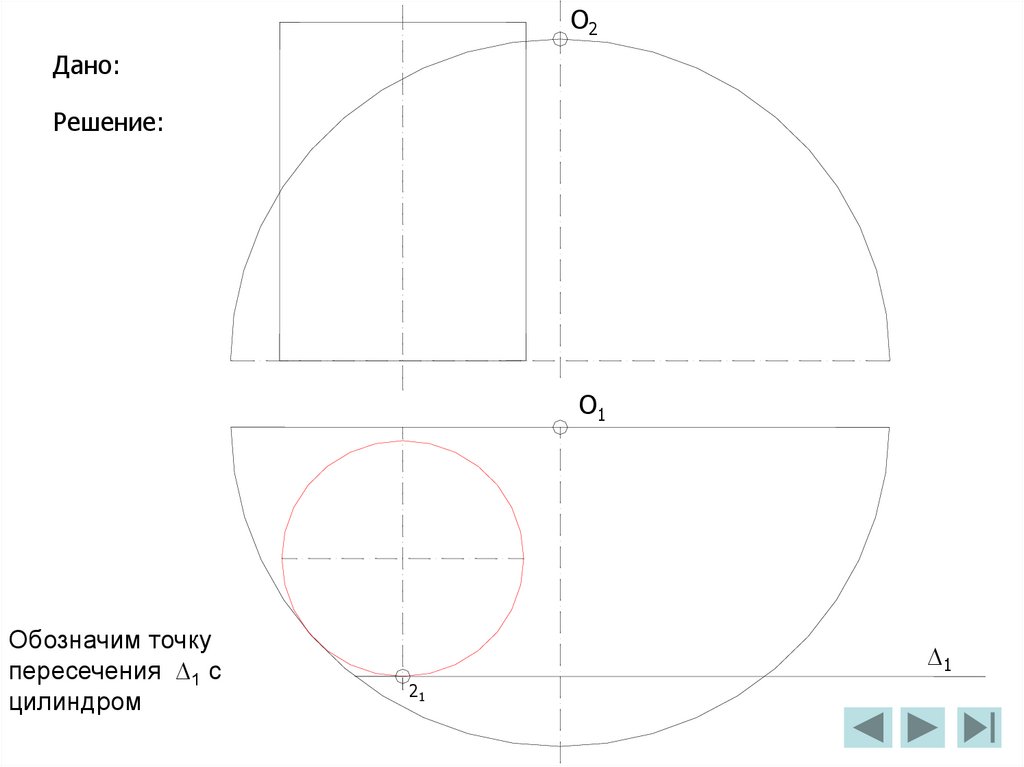
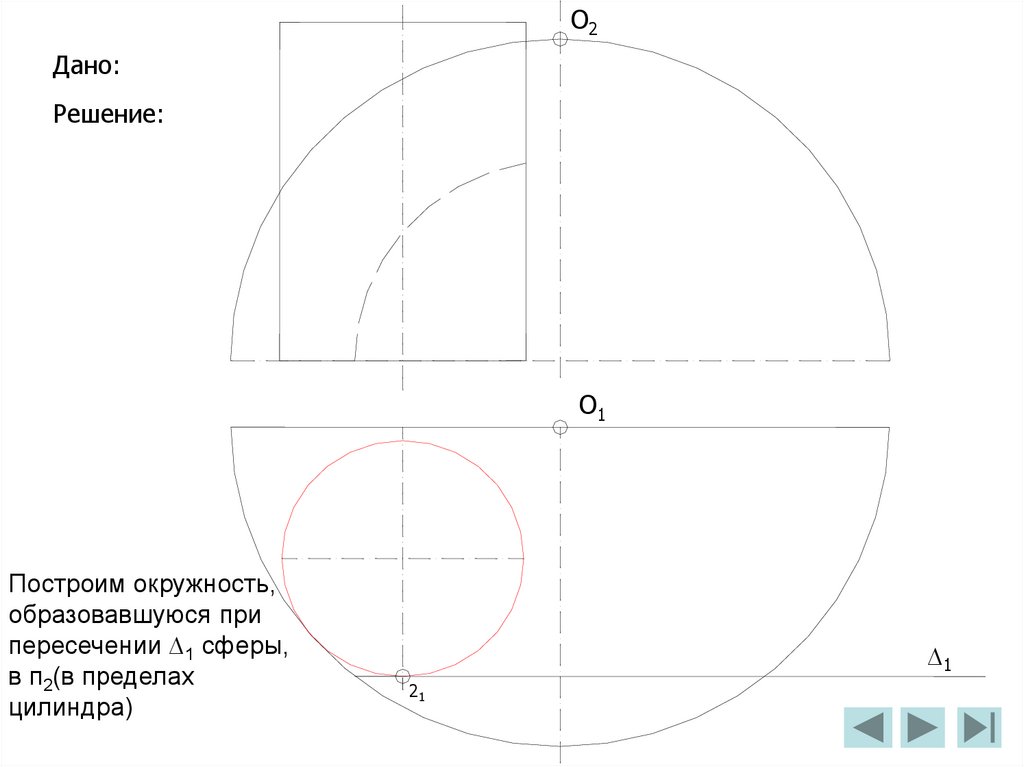
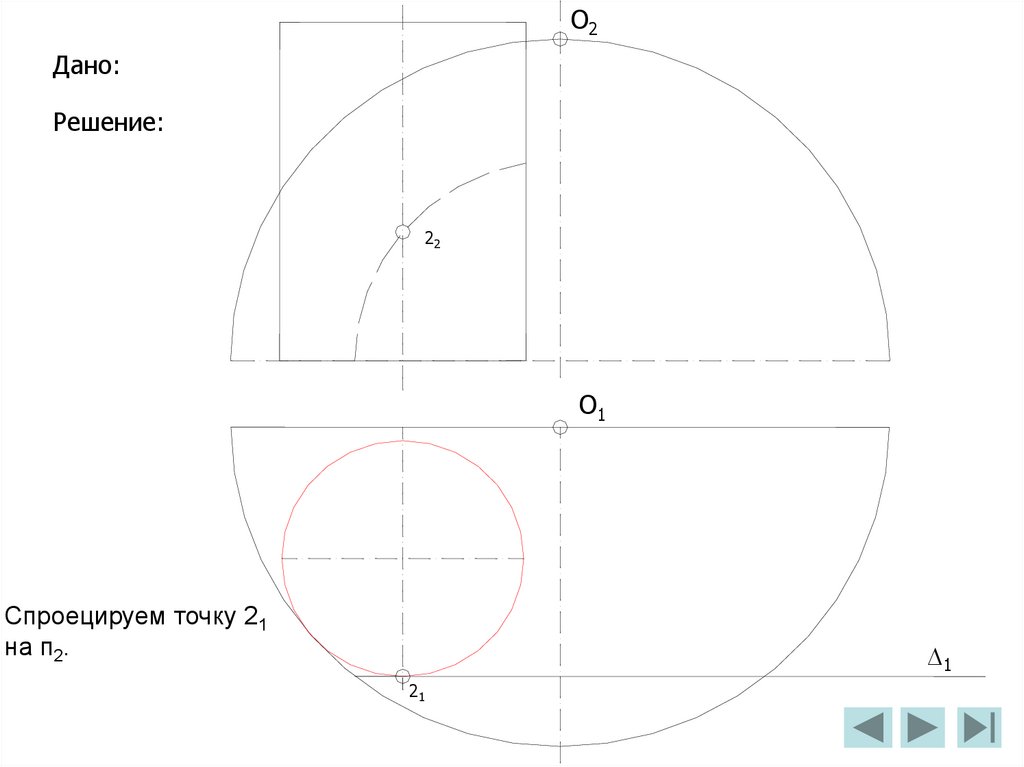
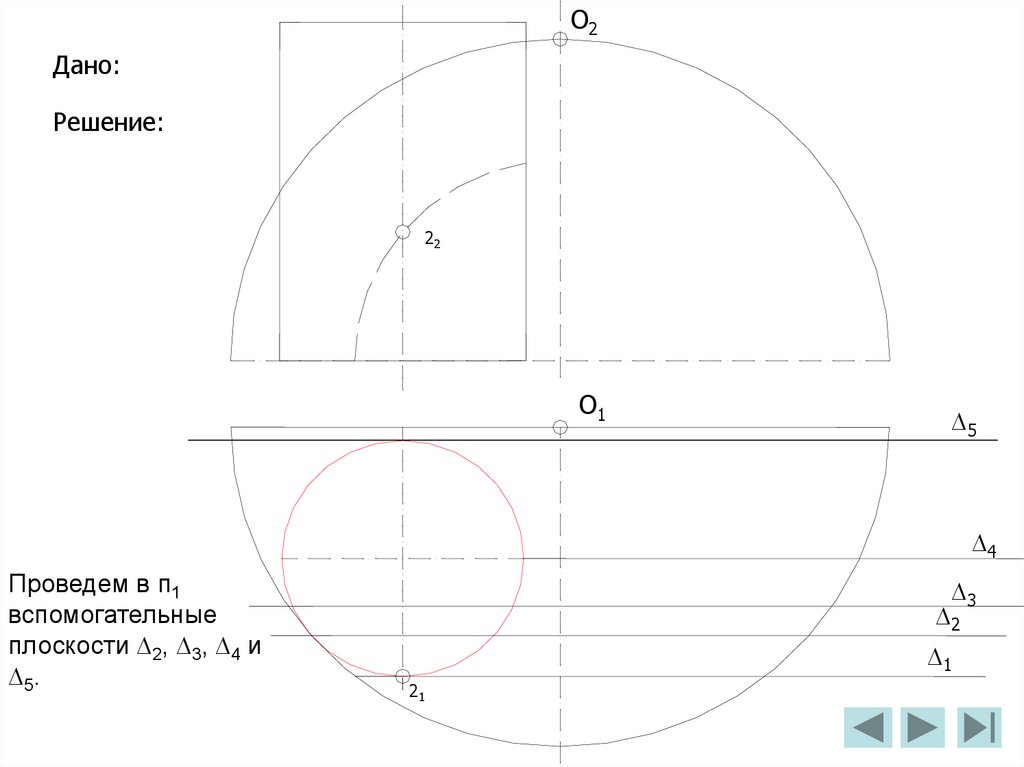
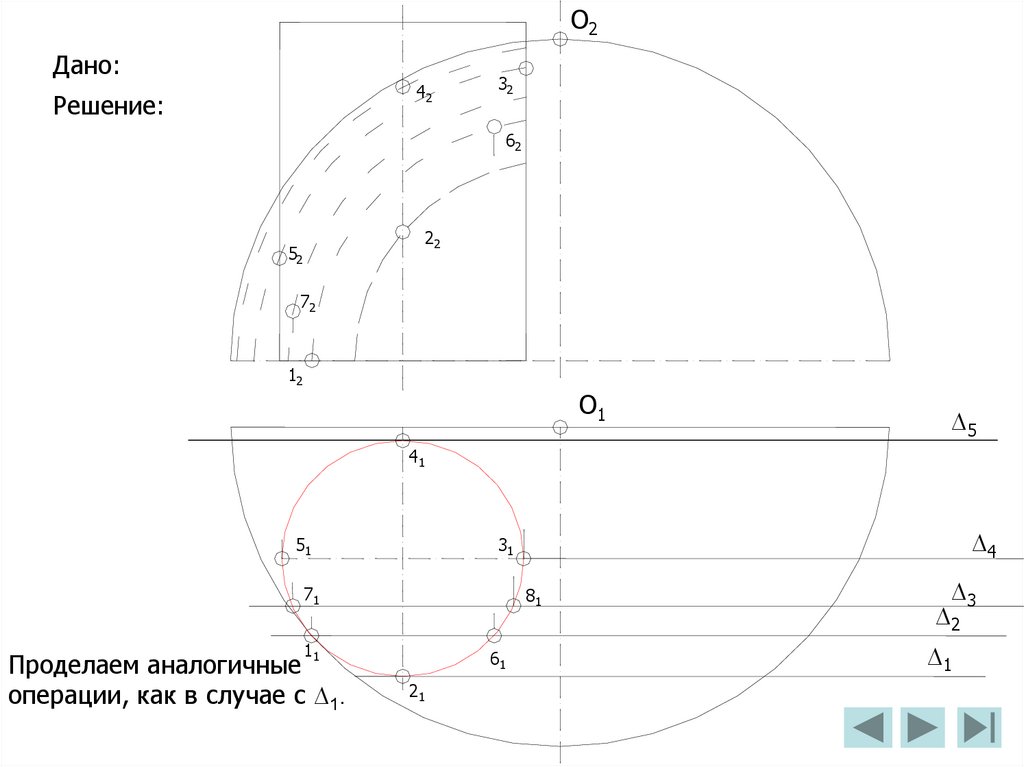
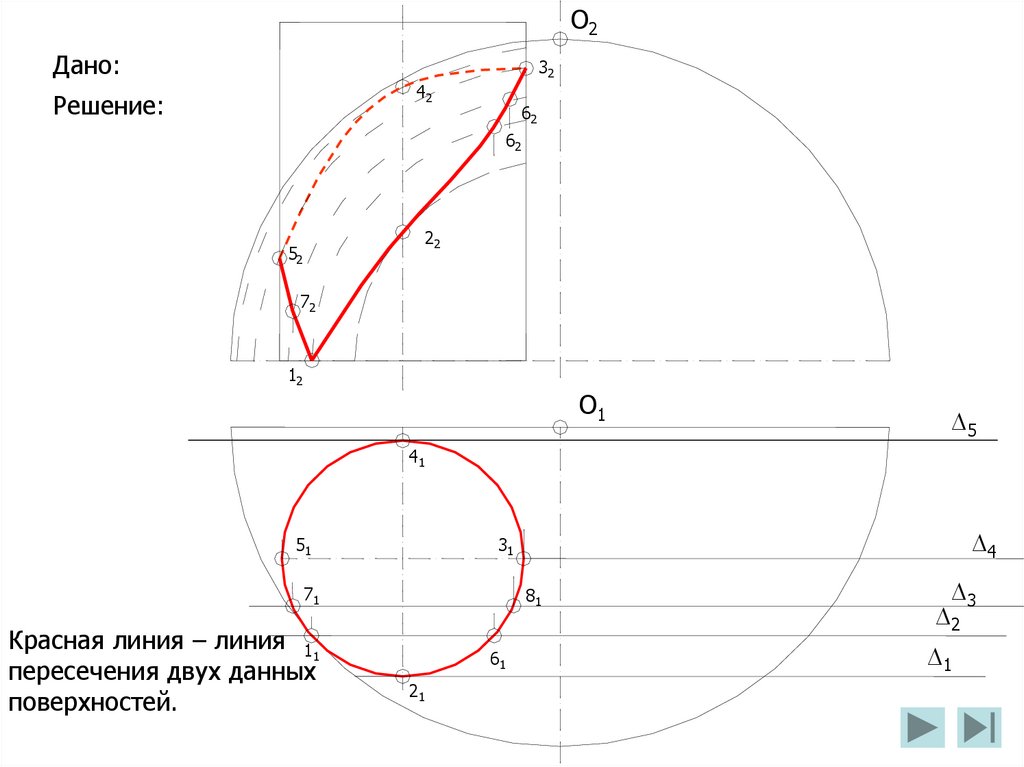
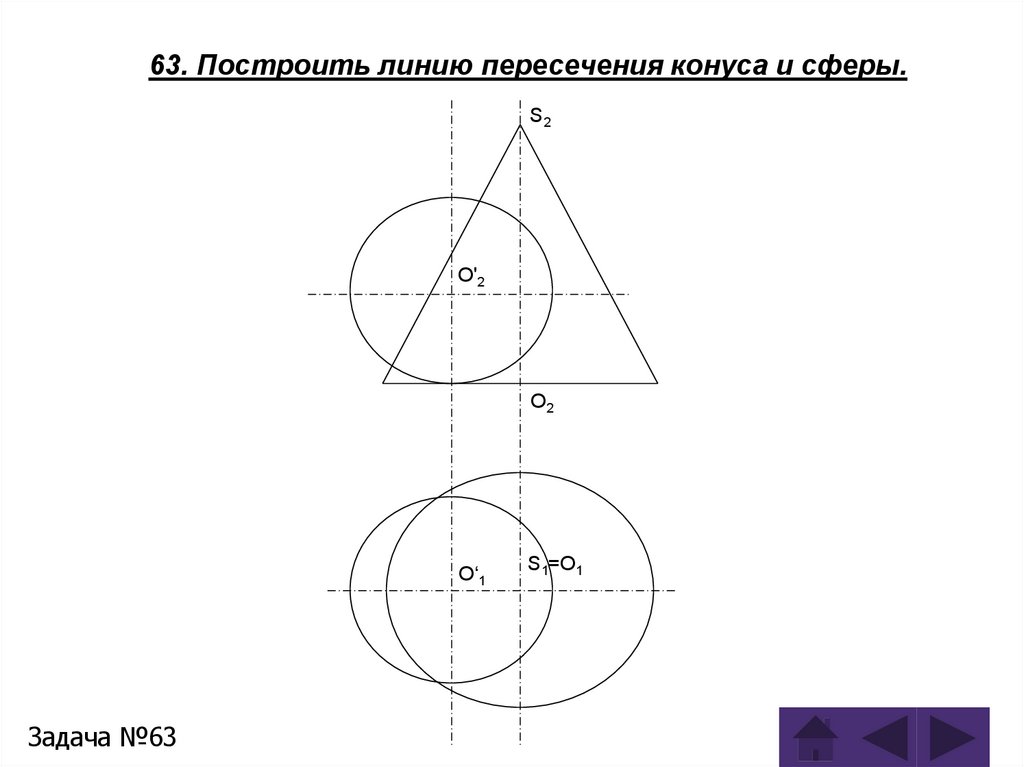
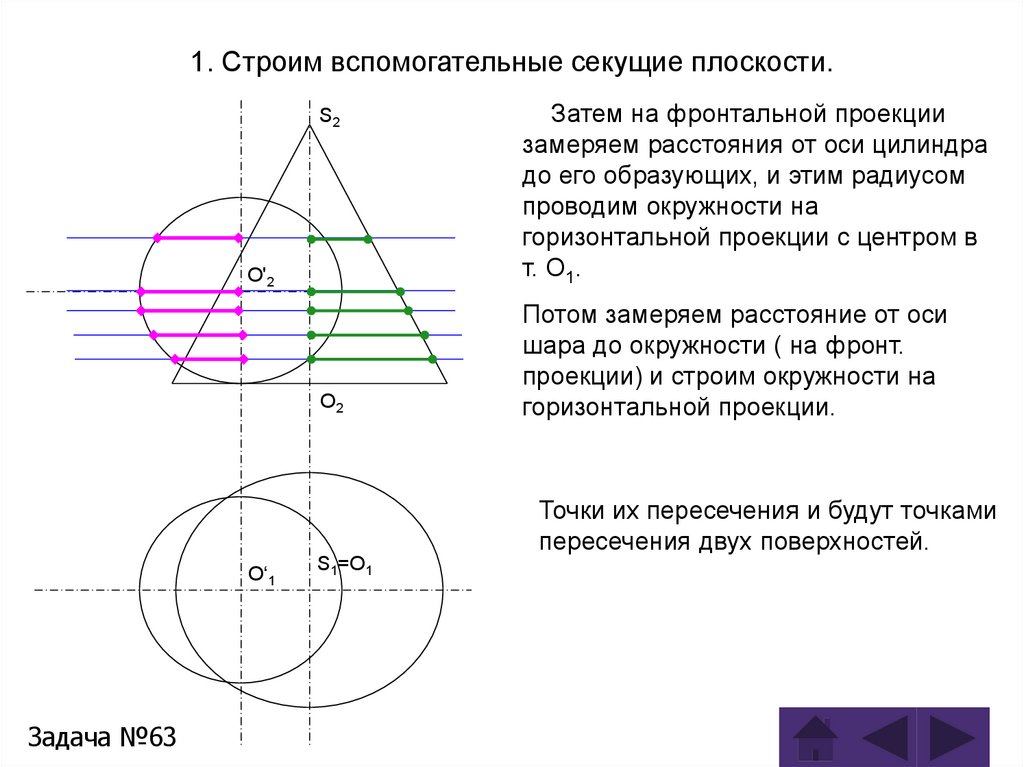
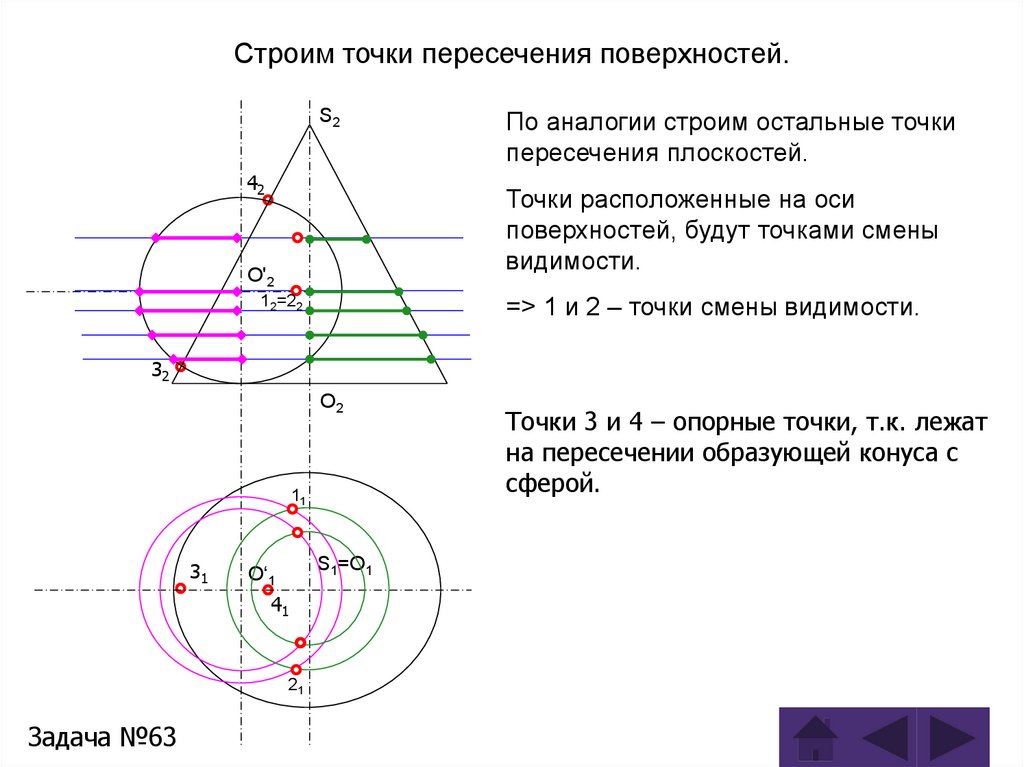
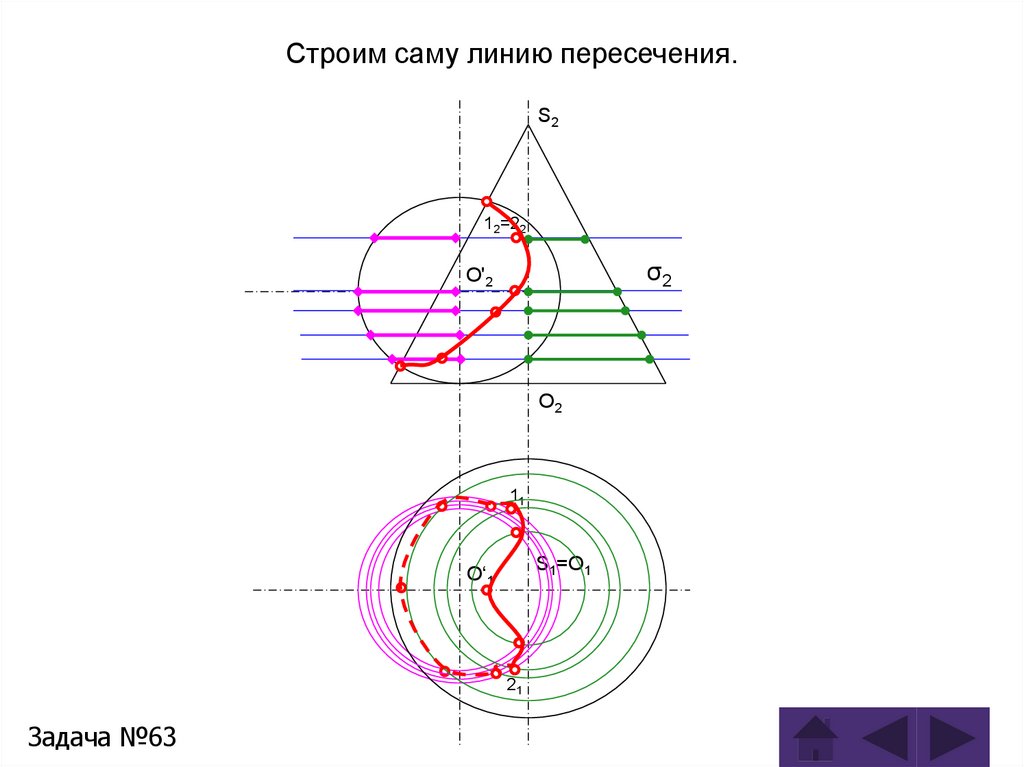
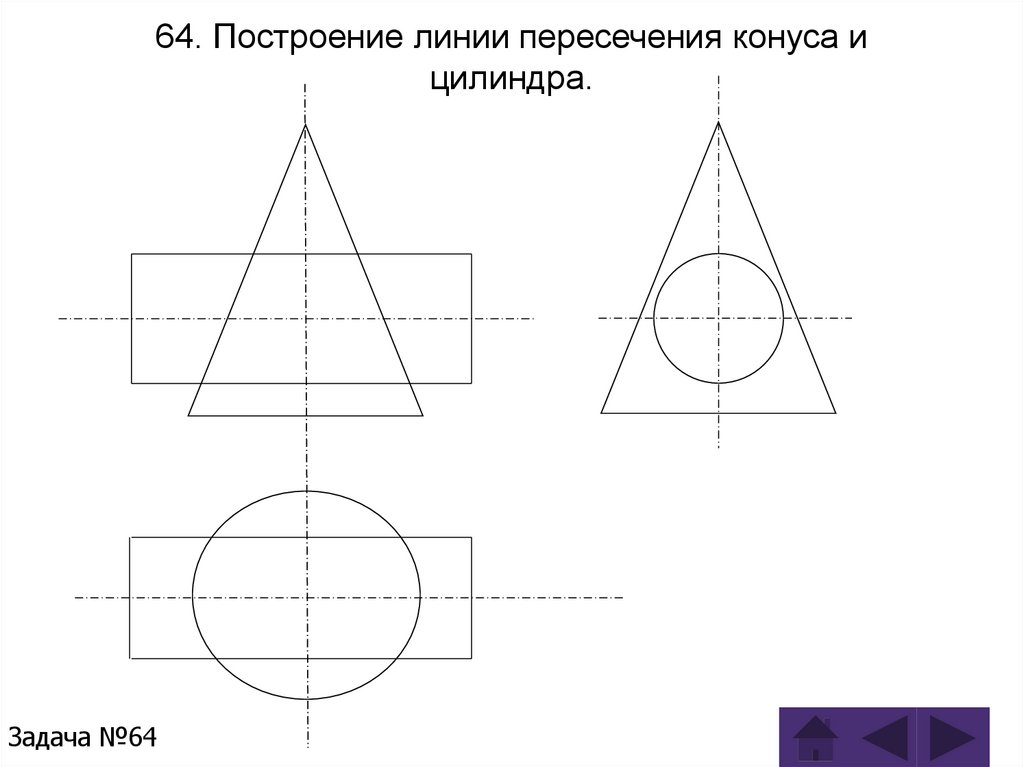
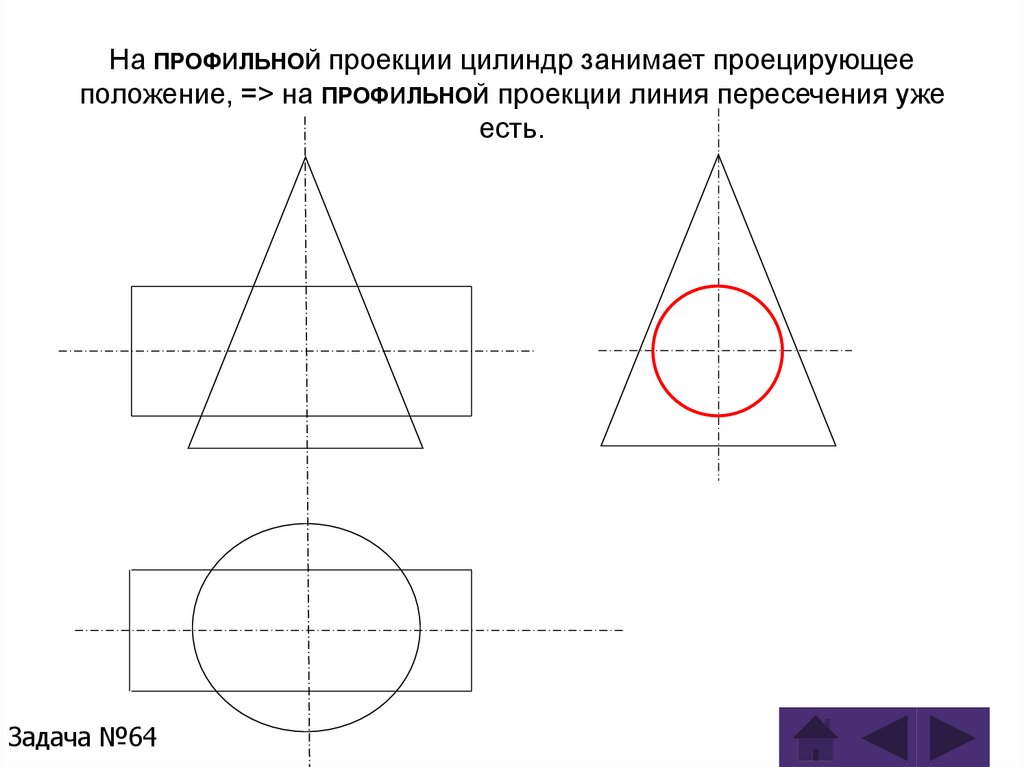
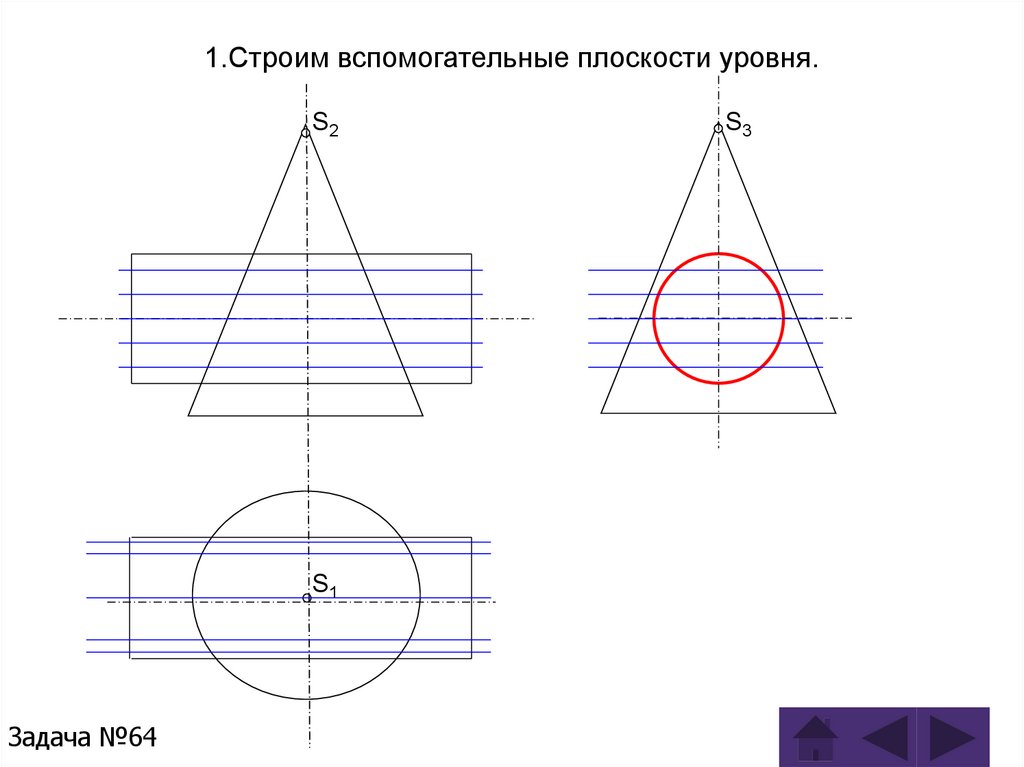
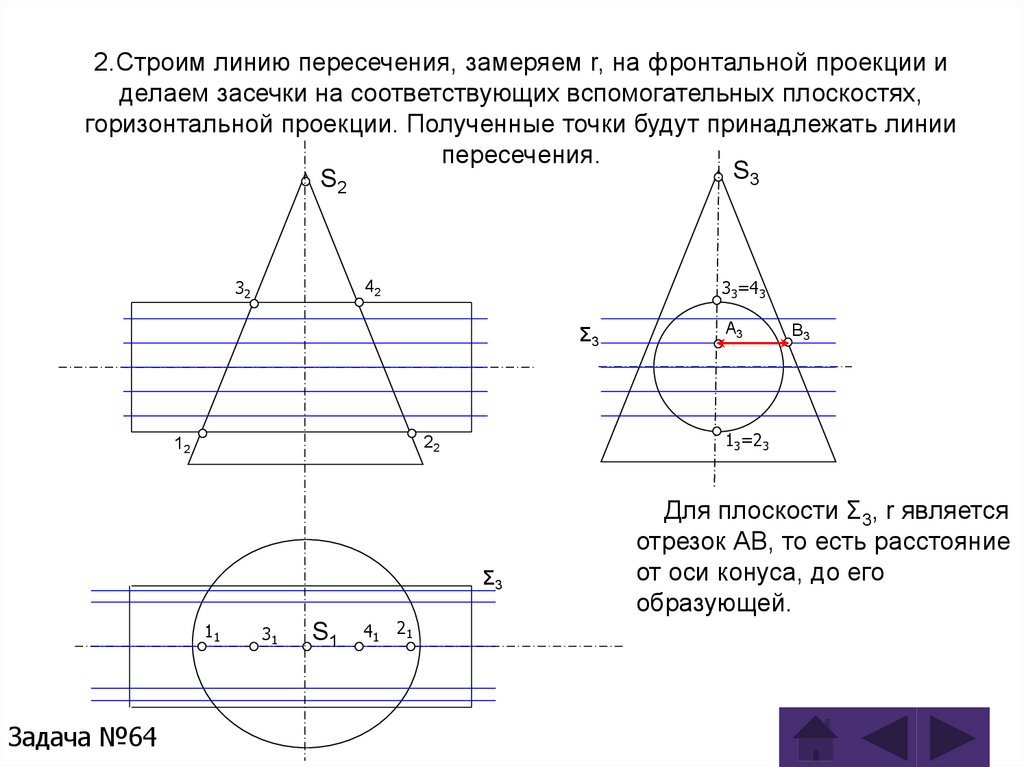
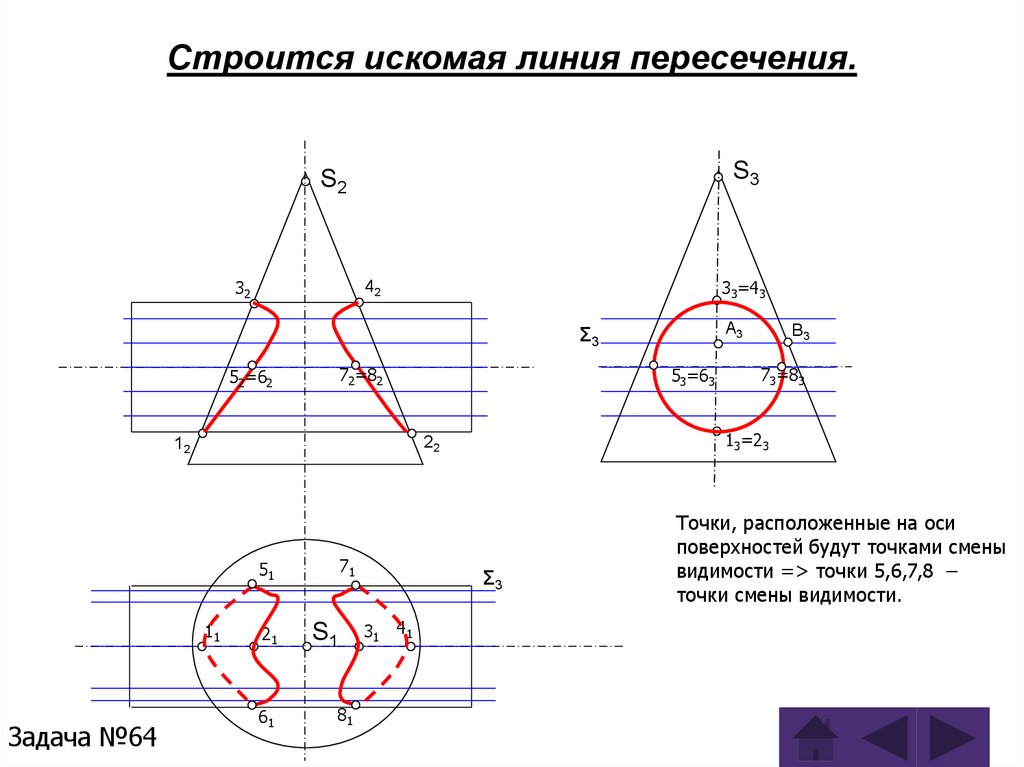
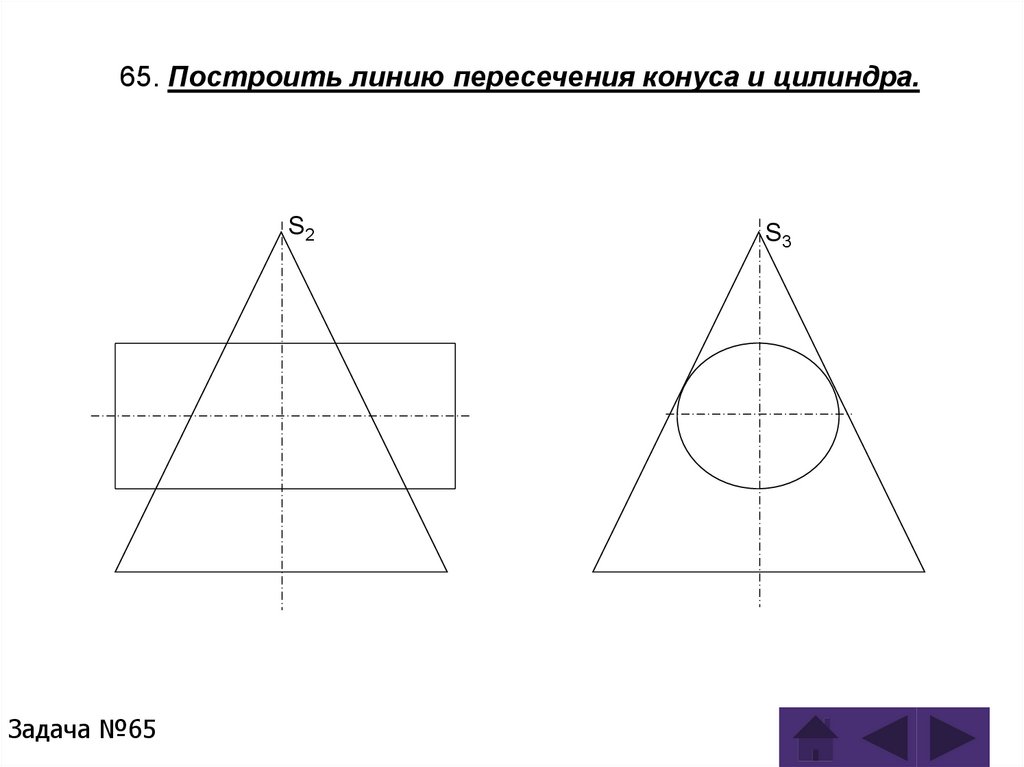
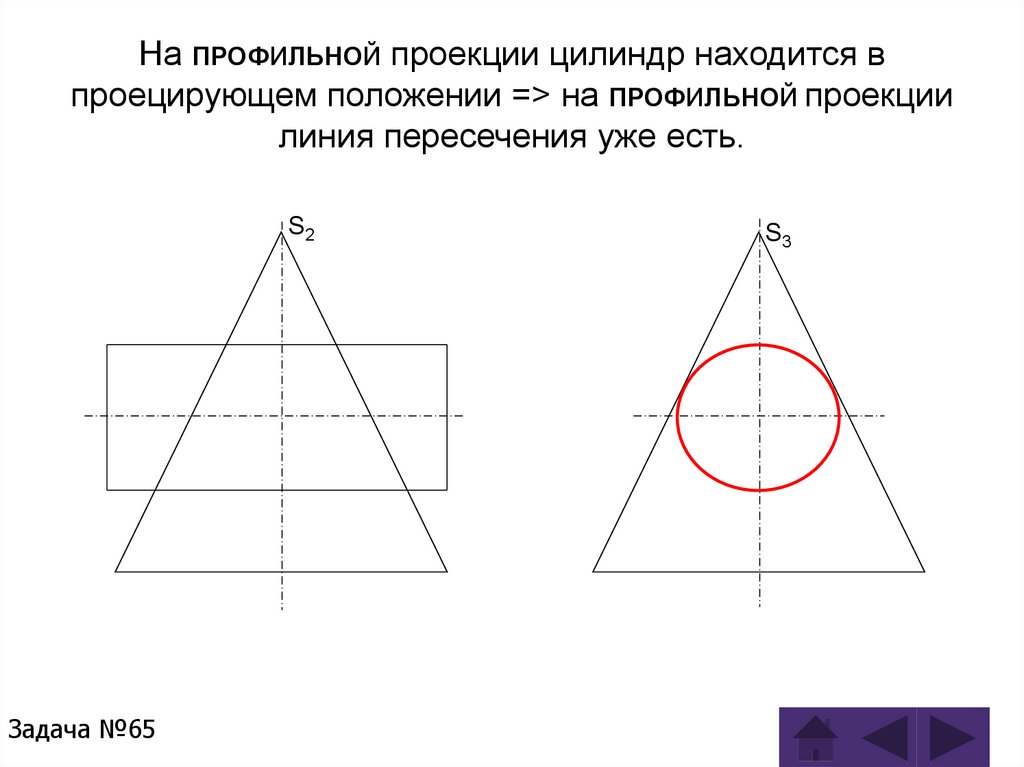
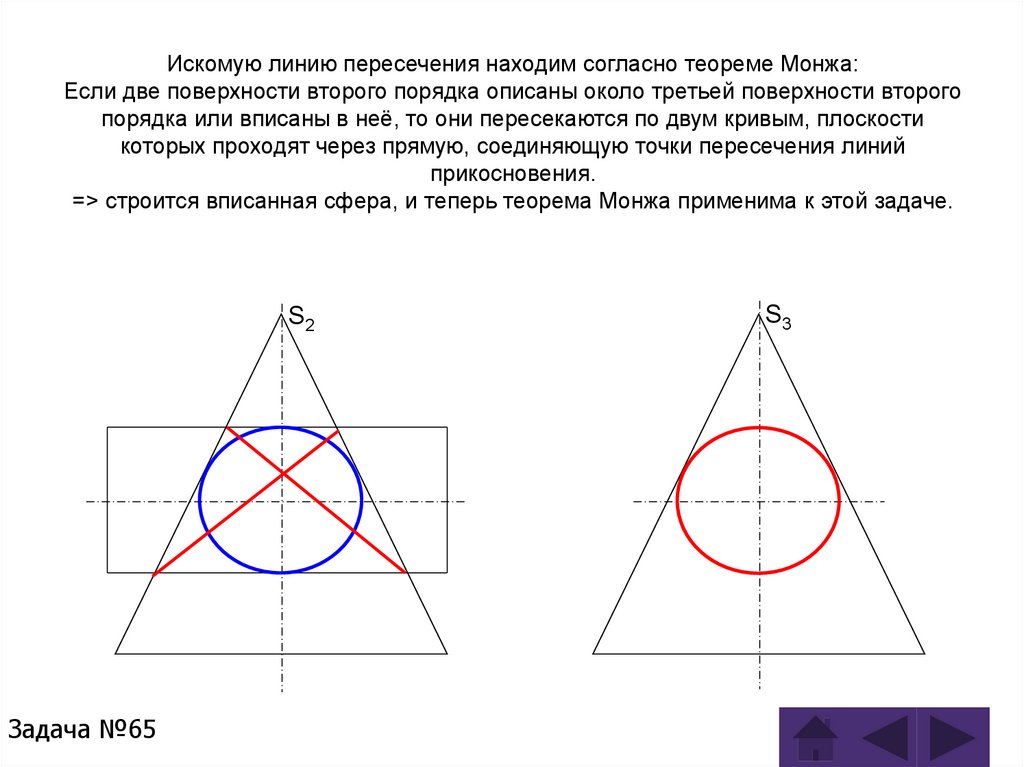
 drafting
drafting








