Similar presentations:
Начертательная геометрия
1. Начертательная геометрия
Лектор:профессор кафедры теоретической и
прикладной механики
Соломонов Константин Николаевич
1
2. Содержание курса лекций
Тема 1. Основы проецирования.Тема 2. Решение метрических задач.
Тема 3. Решение позиционных
задач.
2
3.
Основная литература1. Чекмарёв А.А. Начертательная геометрия и черчение. –
М.: Высшее образование, 2008.
2. Соломонов К.Н., Чиченёва О.Н., Мокрецова Л.О.,
Головкина В.Б. Начертательная геометрия: курс лекций.
– М.: МИСиС, 2007.
3. Соломонов К.Н., Бусыгина Е.Б., Чиченёва О.Н.
Начертательная геометрия: учебник для вузов. – М.:
МИСиС, 2003.
3
4. Тема 1. Основы проецирования
1.2.
3.
4.
5.
Методы проецирования.
Комплексный чертеж – эпюр Монжа.
Проецирование прямой.
Проецирование плоскости.
Образование поверхностей.
4
5.
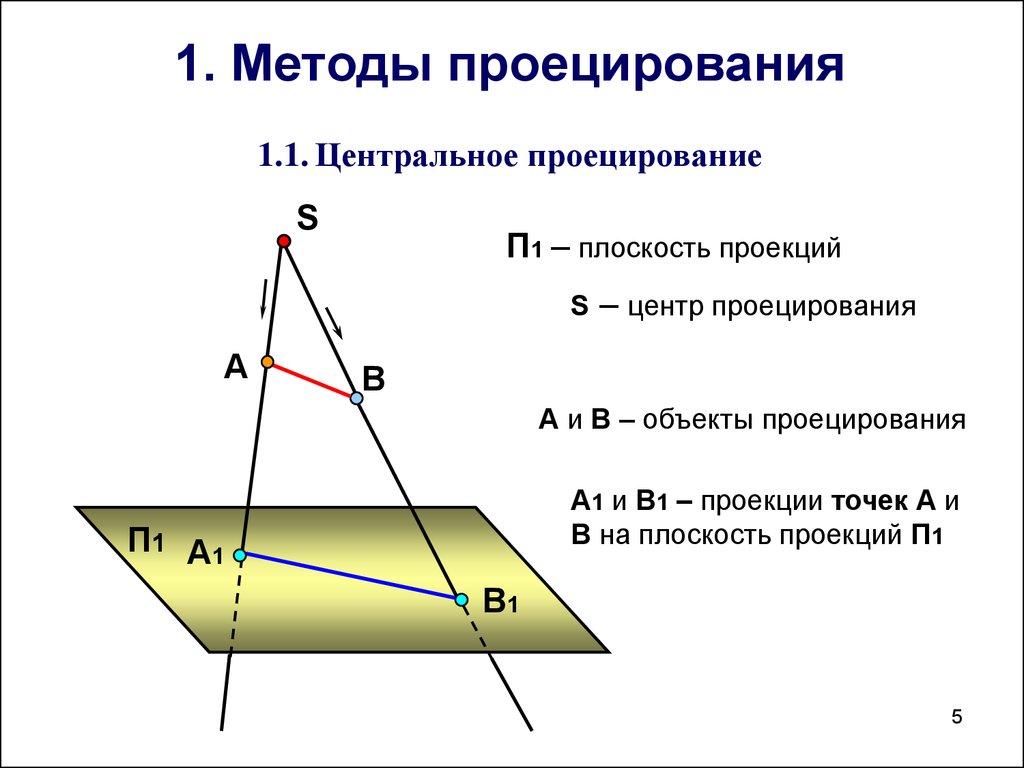
1. Методы проецирования1.1. Центральное проецирование
S
П1 – плоскость проекций
S – центр проецирования
А
В
А и В – объекты проецирования
А1 и В1 – проекции точек А и
В на плоскость проекций П1
П1 A1
В1
5
6.
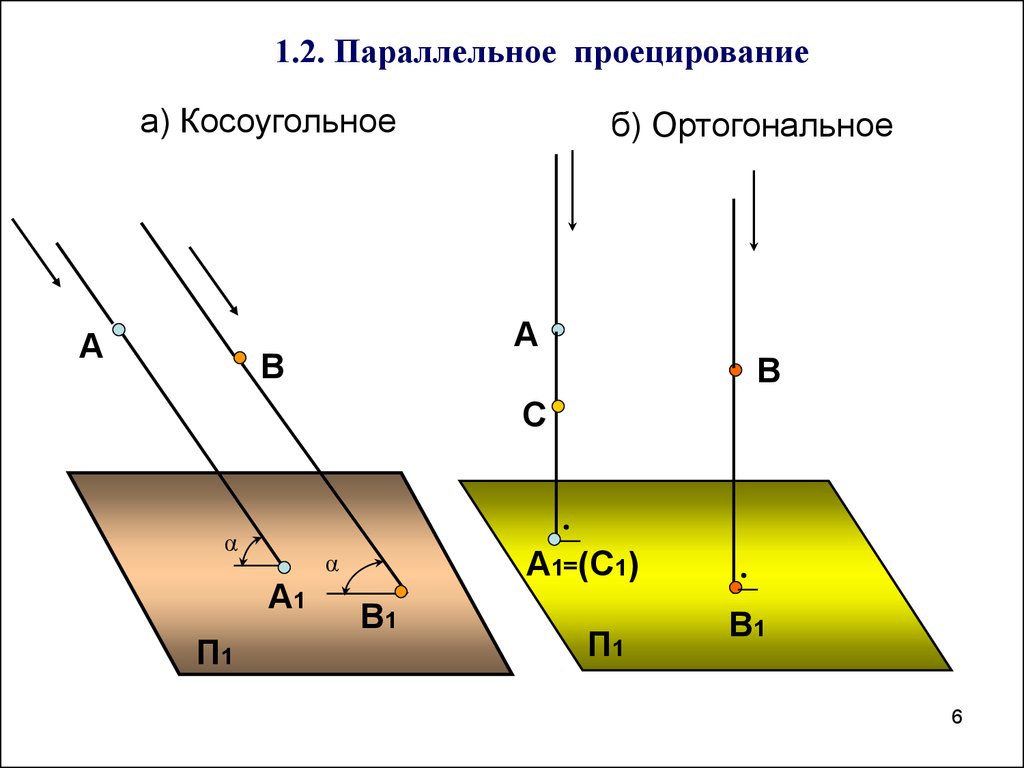
1.2. Параллельное проецированиеа) Косоугольное
А
б) Ортогональное
А
В
В
С
α
А1
П1
А1=(С1)
α
В1
П1
В1
6
7.
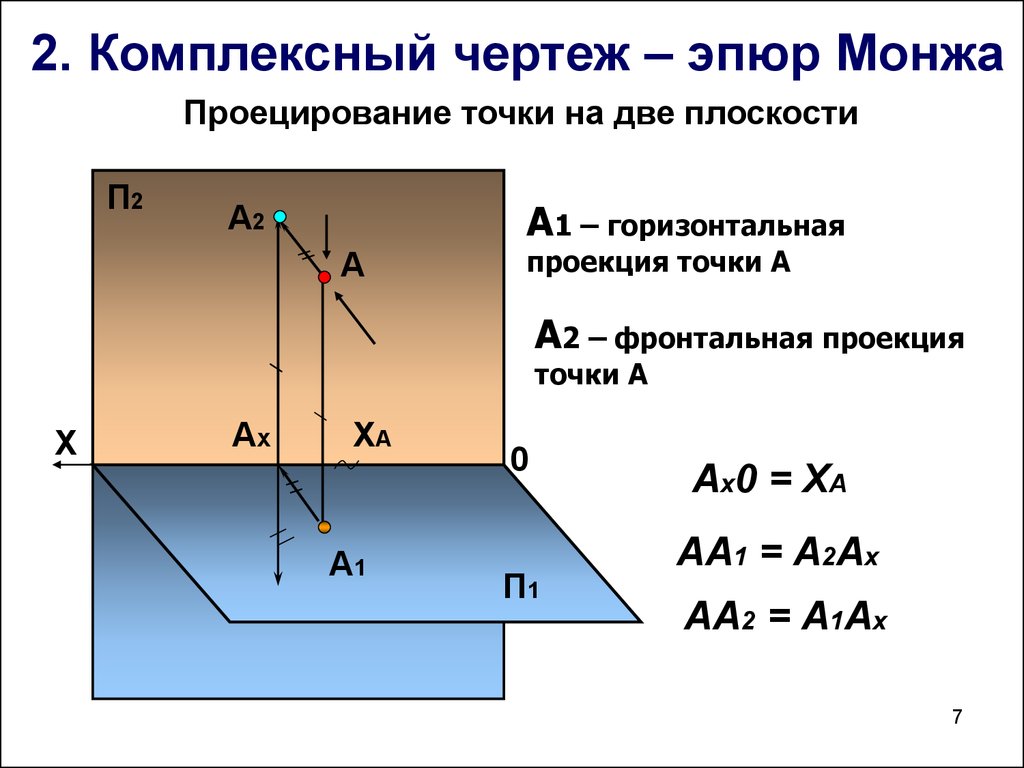
2. Комплексный чертеж – эпюр МонжаПроецирование точки на две плоскости
П2
А1 – горизонтальная
А2
А
проекция точки А
А2 – фронтальная проекция
точки А
Х
Ах
ХА
А1
0
П1
Ах0 = ХА
АА1 = А2Ах
АА2 = А1Ах
7
8. Монж, Гаспар Gaspard Monge
Дата рождения: 10 мая 1746 г.Место рождения: Бон,
Бургундия, Франция
Дата смерти: 28 июля 1818 г.
Место смерти: Париж, Франция
Французский математик-геометр
8
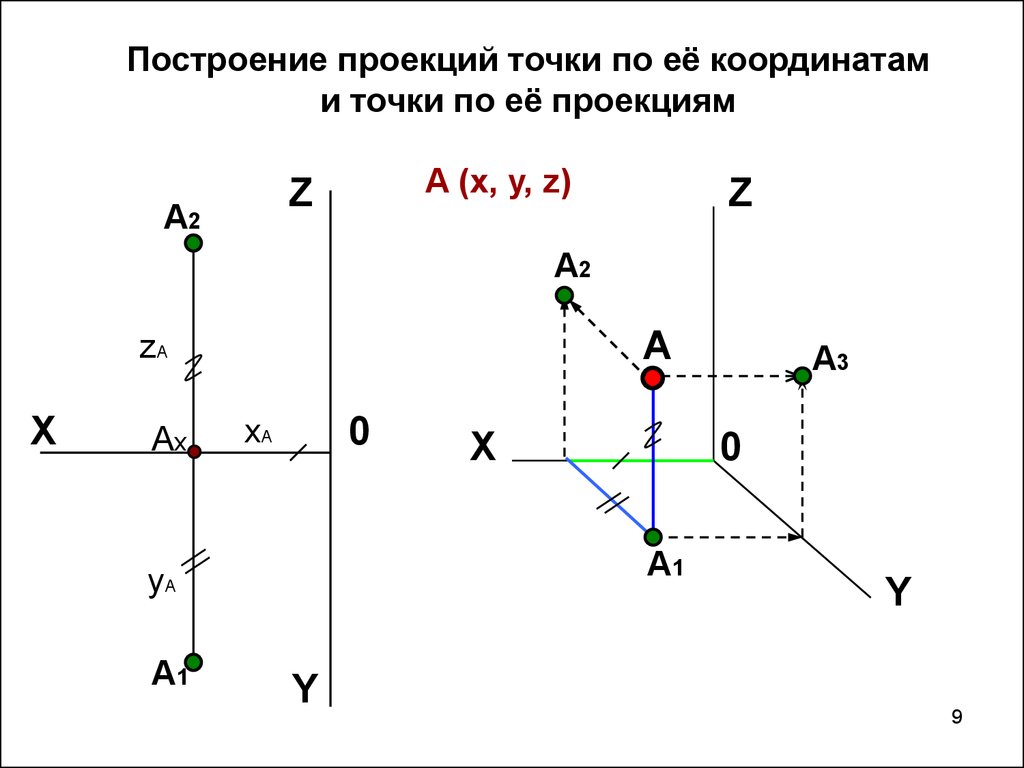
9. Построение проекций точки по её координатам и точки по её проекциям
A (x, y, z)Z
A2
Z
A2
A
zA
X
Ax
0
xA
0
A1
yA
A1
X
Y
A3
Y
9
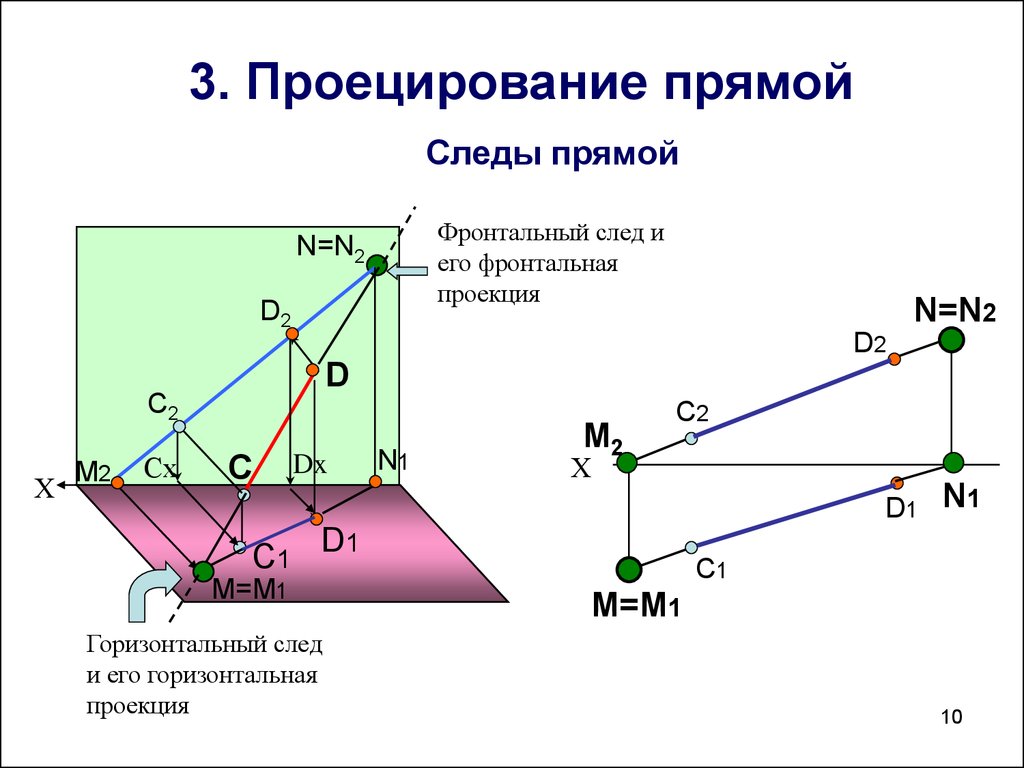
10. 3. Проецирование прямой
Следы прямойФронтальный след и
его фронтальная
проекция
N=N2
D2
N=N2
D2
D
С2
Х
M2
Сх
С
Dx
N1
M2
С2
Х
C1 D1
М=M1
Горизонтальный след
и его горизонтальная
проекция
D1 N1
С1
М=M1
10
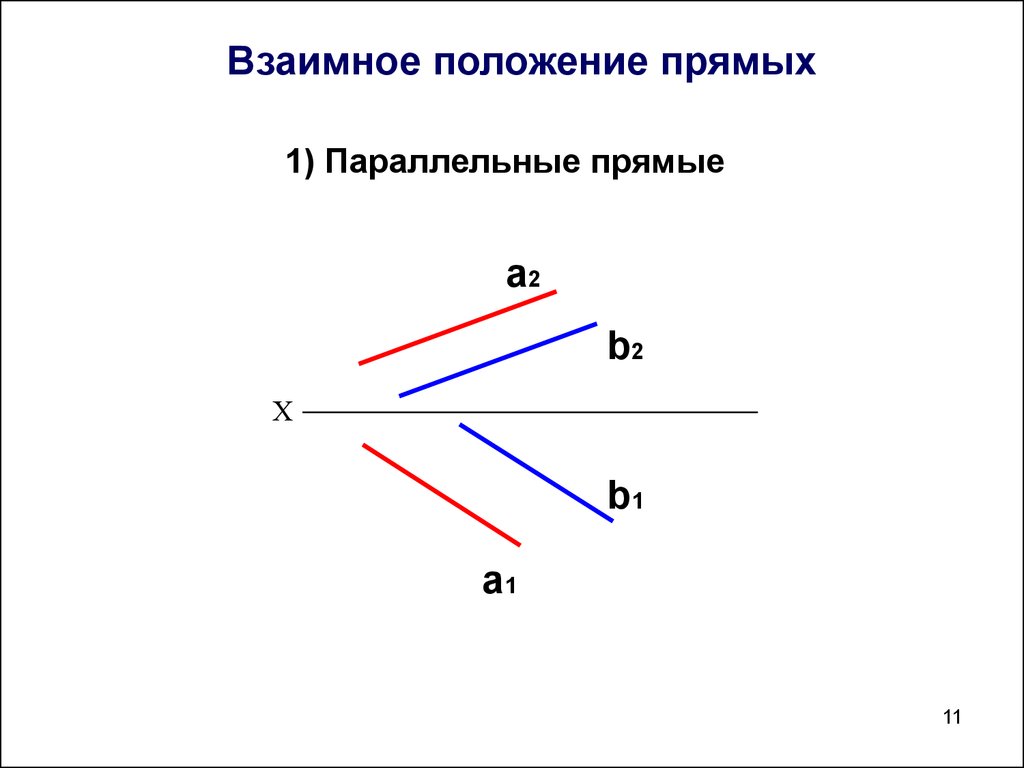
11. Взаимное положение прямых
1) Параллельные прямыеа2
b2
Х
b1
a1
11
12. 2) Пересекающиеся прямые
К2G2
d2
с2
Х
G1
d1
с1
Если с ∩ d = К ,
то
с2 ∩ d2 = К2 ,
а
с1 ∩ d1 = К1,
при этом К2К1 ┴ Х.
К1
12
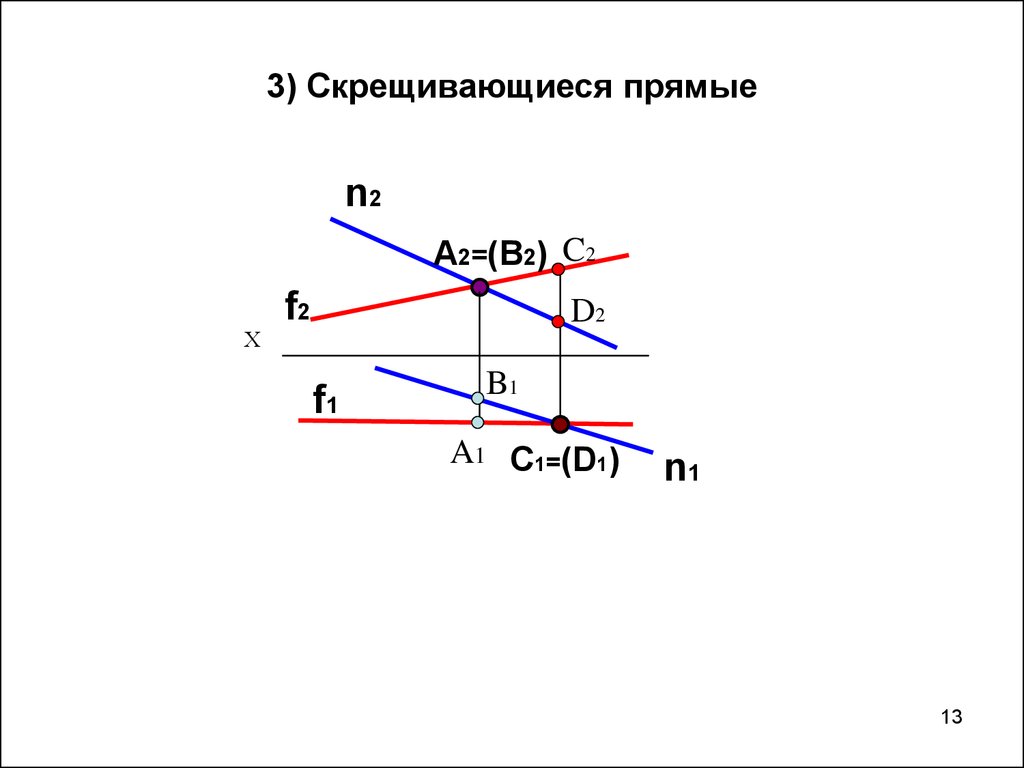
13. 3) Скрещивающиеся прямые
n2A2=(B2) C2
Х
f2
D2
f1
B1
A1 C1=(D1)
n1
13
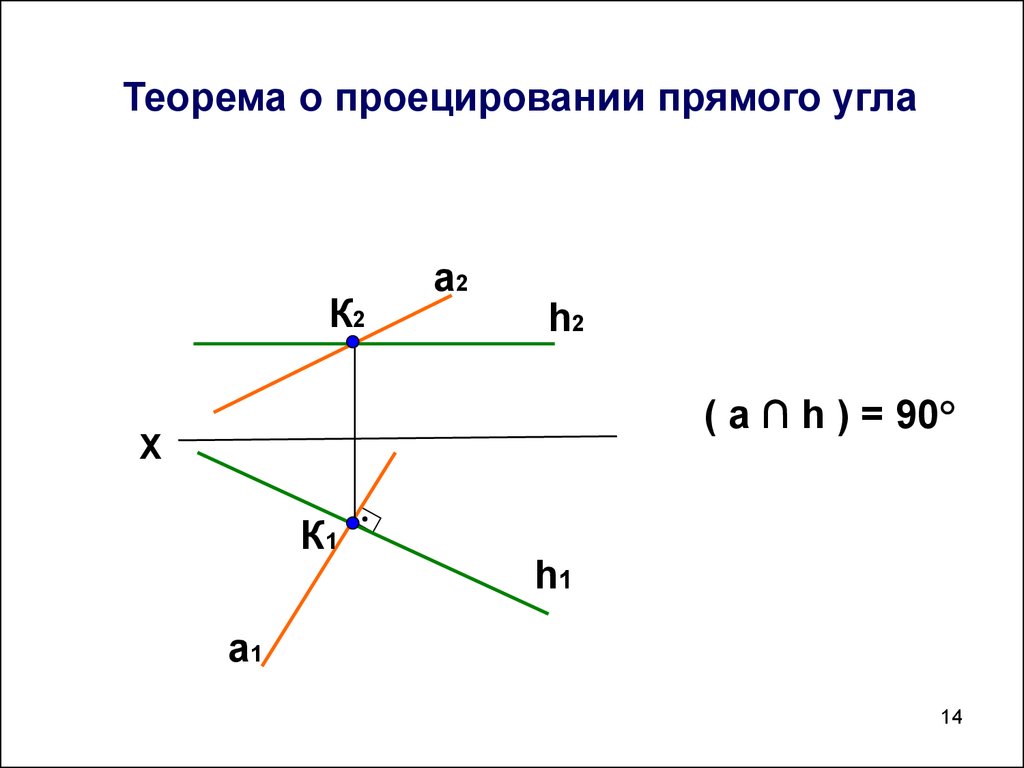
14. Теорема о проецировании прямого угла
К2а2
h2
( a ∩ h ) = 90°
Х
К1
h1
а1
14
15.
4. Проецирование плоскостиСпособы задания плоскости
а) тремя точками, б) точкой и прямой, в) параллельными прямыми,
г) пересекающимися прямыми, д) плоской фигурой
А2
m2
С2
М2
f2
K2
n2
e2
В2
e1
n1
В1
K1
f1
m1
А1
С1
М1
15
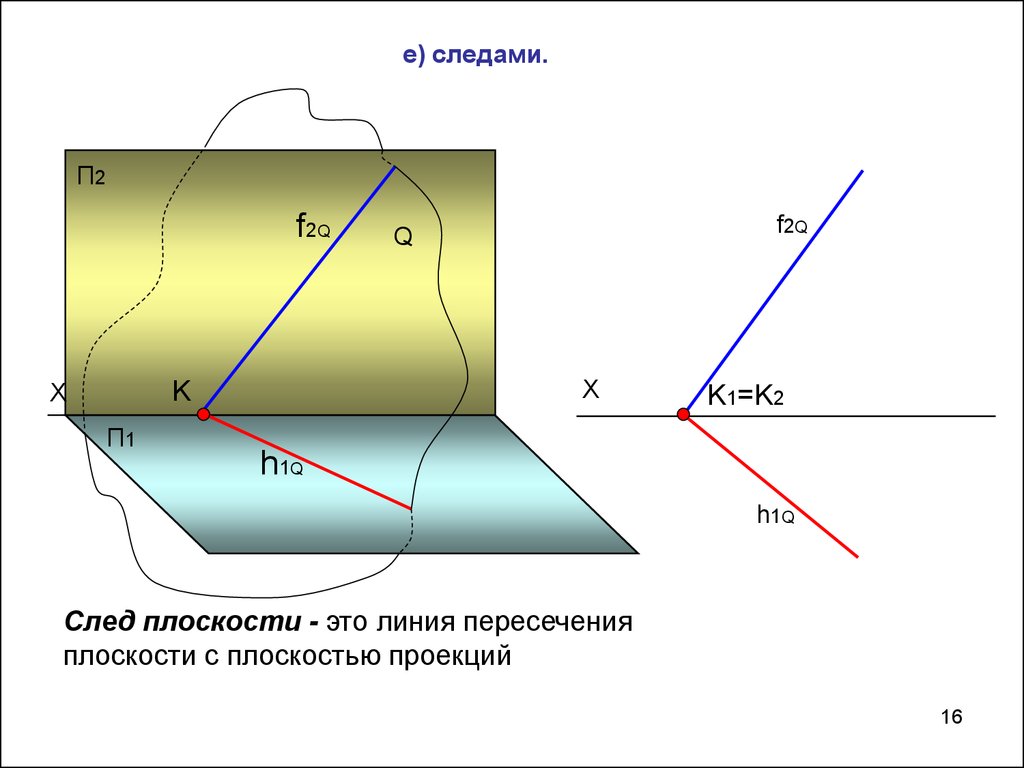
16.
е) следами.П2
f2Q
Х
Х
K
П1
f 2Q
Q
K1=K2
h1Q
h1Q
След плоскости - это линия пересечения
плоскости с плоскостью проекций
16
17.
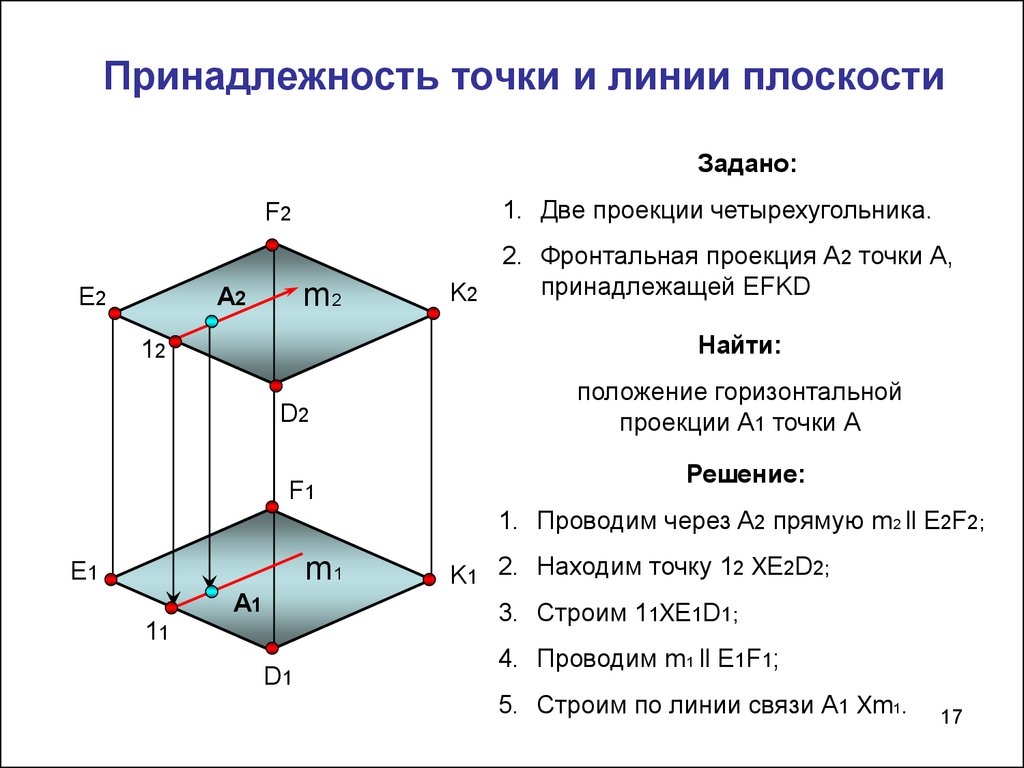
Принадлежность точки и линии плоскостиЗадано:
1. Две проекции четырехугольника.
F2
Е2
m2
А2
K2
2. Фронтальная проекция А2 точки А,
принадлежащей EFKD
Найти:
12
D2
F1
положение горизонтальной
проекции А1 точки А
Решение:
1. Проводим через A2 прямую m2 ll E2F2;
m1
Е1
А1
11
D1
K1 2. Находим точку 12 XE2D2;
3. Строим 11XE1D1;
4. Проводим m1 ll E1F1;
5. Строим по линии связи А1 Xm1.
17
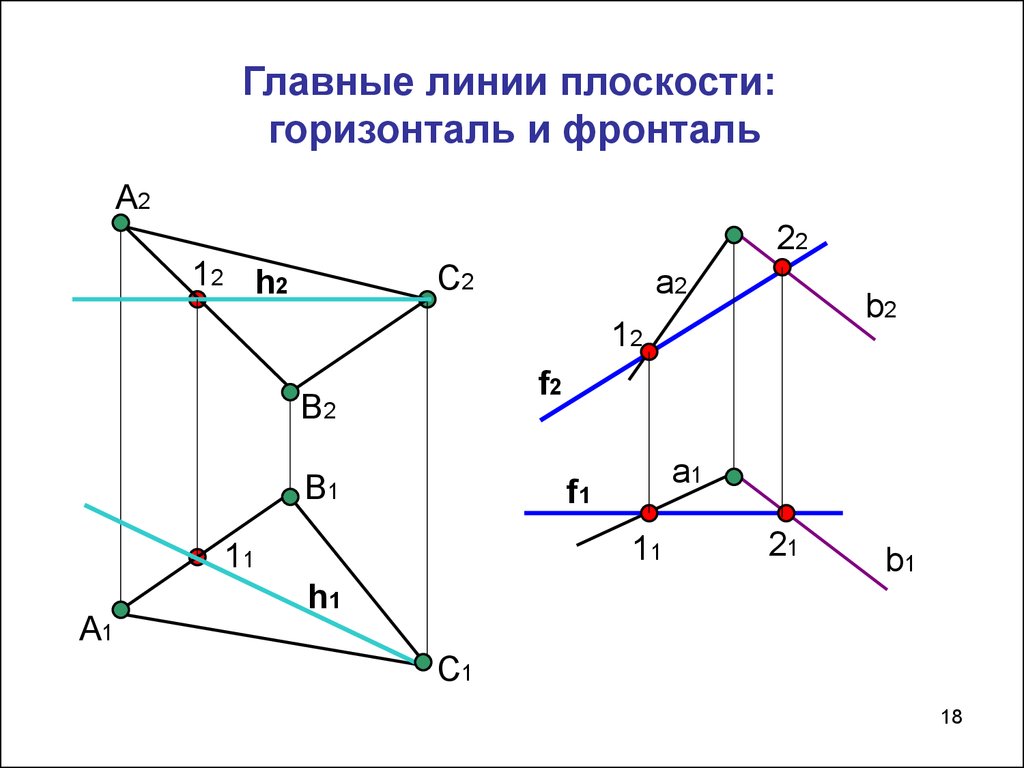
18. Главные линии плоскости: горизонталь и фронталь
A222
12 h2
C2
a2
b2
12
f2
B2
B1
a1
f1
11
11
21
b1
h1
A1
C1
18
19. Взаимное положение плоскостей
Плоскости в пространстве могут бытьпараллельны или пересекаться.
1. Параллельность плоскостей. Для параллельности плоскостей
достаточно, чтобы две пересекающиеся прямые одной плоскости
были параллельны двум пересекающимся прямым другой плоскости.
2. Пересечение плоскостей. Результатом пересечения двух
плоскостей является прямая линия, для построения которой
достаточно найти две точки, общие для пересекающихся плоскостей.
3. Перпендикулярность плоскостей. Две плоскости взаимно
перпендикулярны, если одна из них содержит перпендикуляр к
другой. Прямая, перпендикулярная плоскости, называется нормалью
плоскости и перпендикулярна двум пересекающимся прямым,
лежащим в этой плоскости.
19
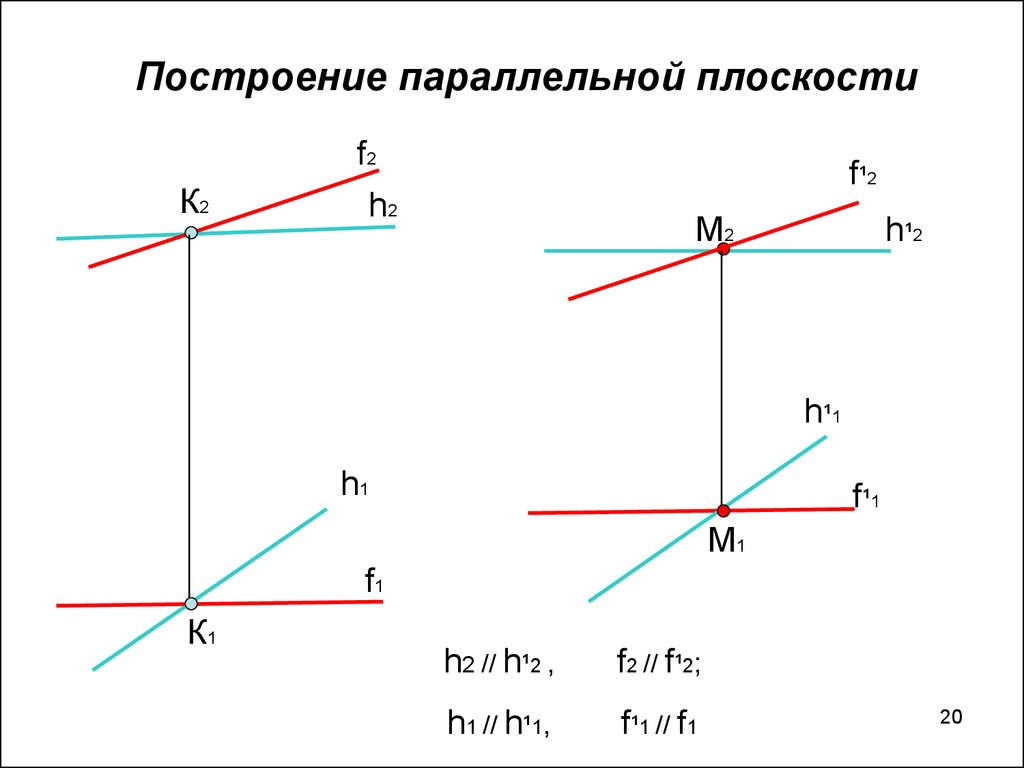
20. Построение параллельной плоскости
f2К2
f ¹2
h2
M2
h¹2
h¹1
h1
f ¹1
M1
f1
К1
h2 // h¹2 ,
f2 // f¹2;
h1 // h¹1,
f¹1 // f1
20
21. Изображение пересекающихся плоскостей
NQ
M
Δ
21
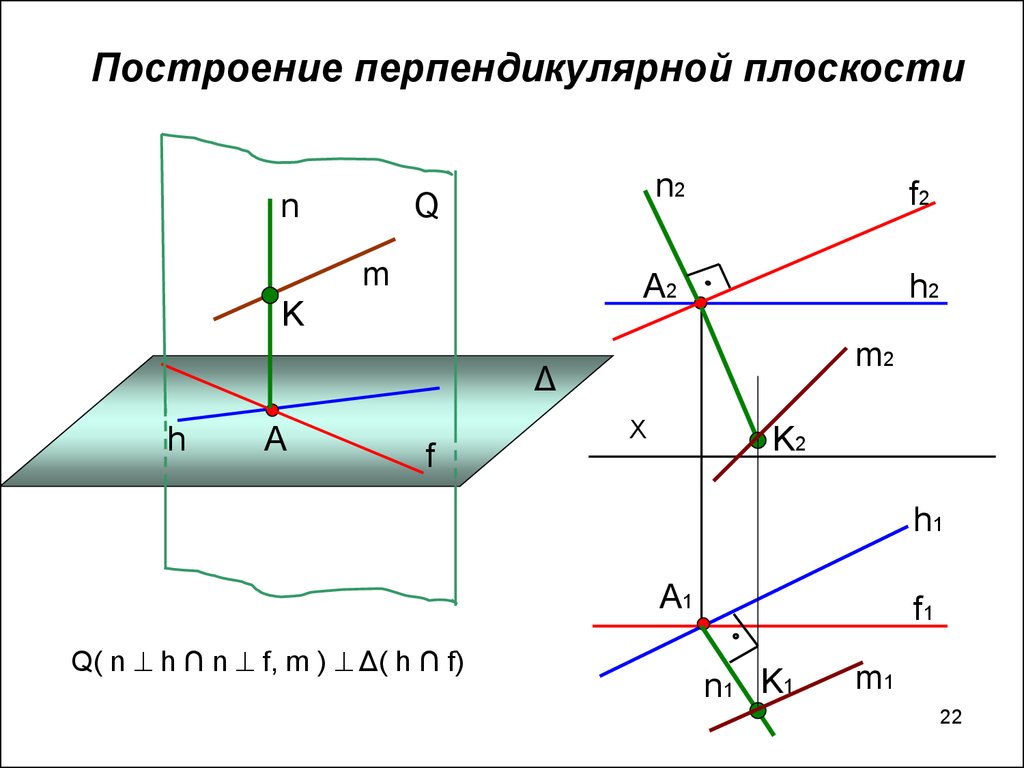
22.
Построение перпендикулярной плоскостиn
n2
f2
A2
h2
Q
m
K
m2
Δ
h
А
f
Х
K2
h1
A1
Q( n h ∩ n f, m ) Δ( h ∩ f)
f1
n1 K1
m1
22
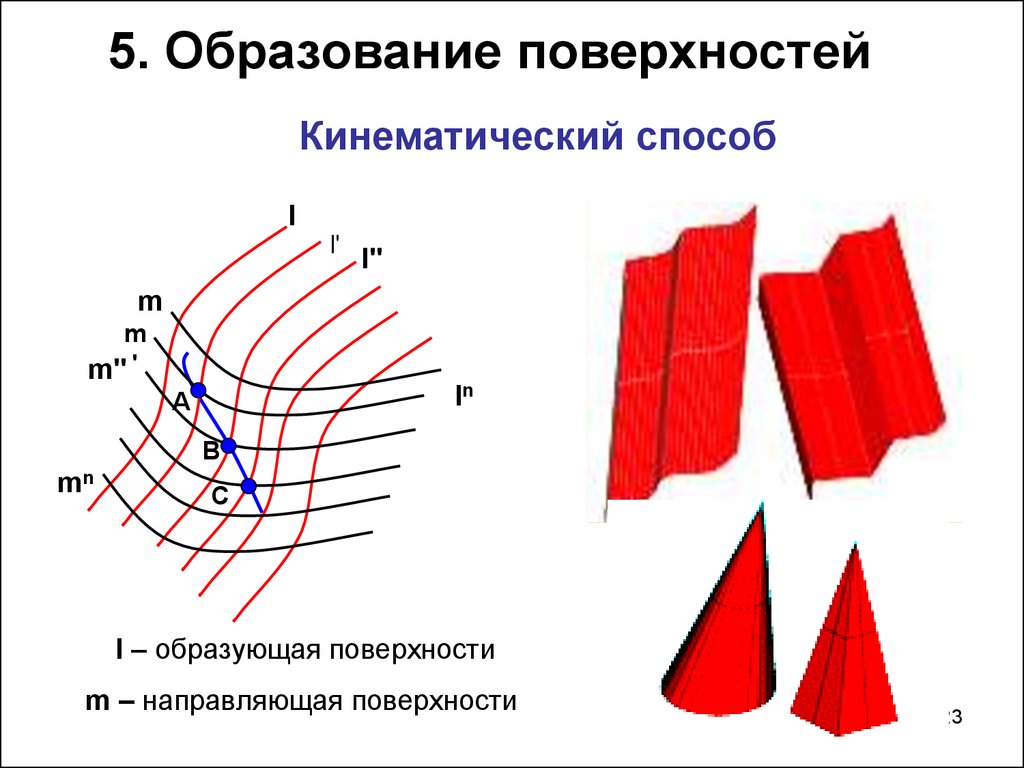
23. 5. Образование поверхностей
Кинематический способl
l'
l"
m
m
m" '
ln
A
B
mn
C
l – образующая поверхности
m – направляющая поверхности
23
24. Статический способ
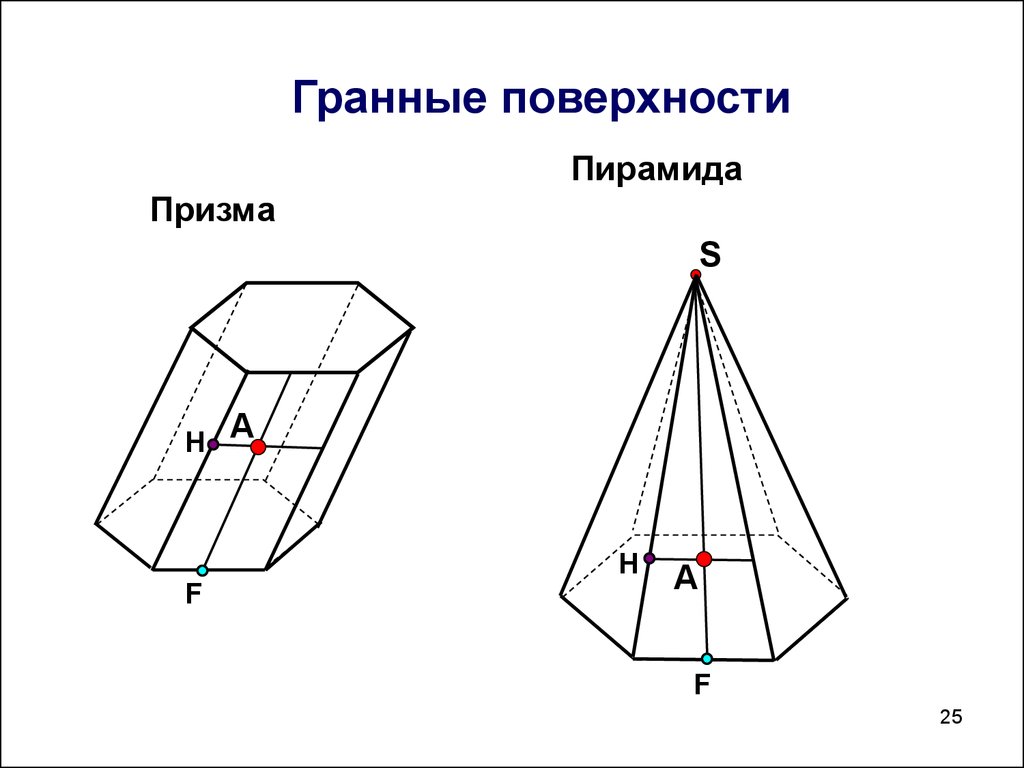
2425. Гранные поверхности
ПирамидаПризма
S
H
А
H
F
A
F
25
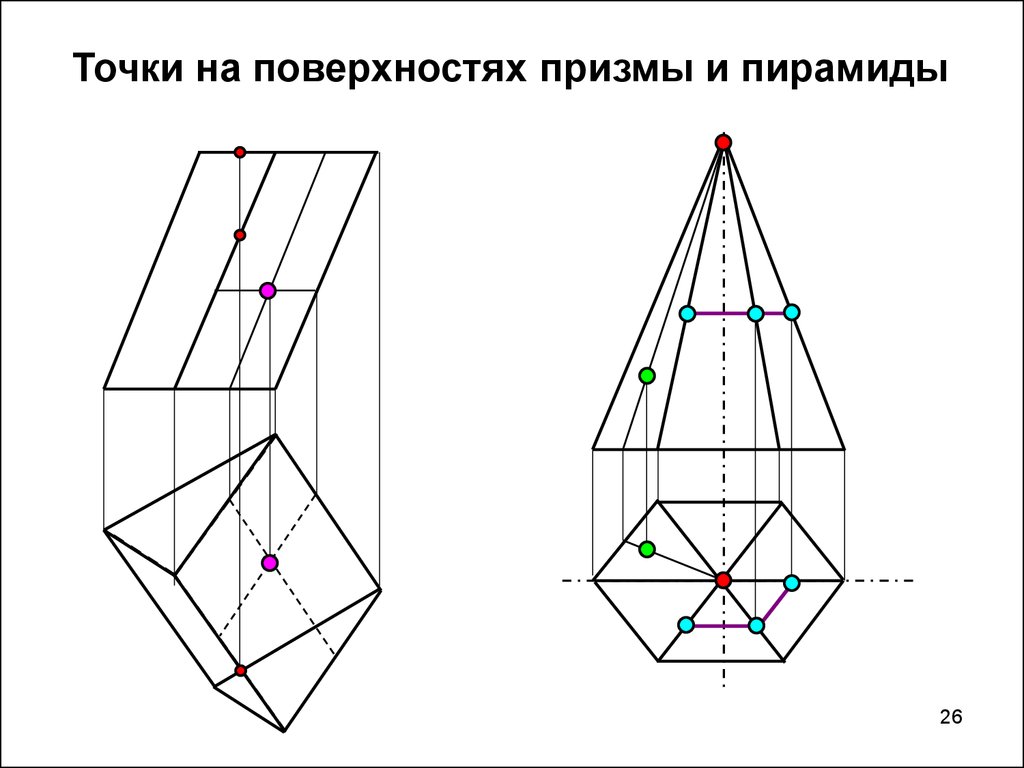
26. Точки на поверхностях призмы и пирамиды
2627.
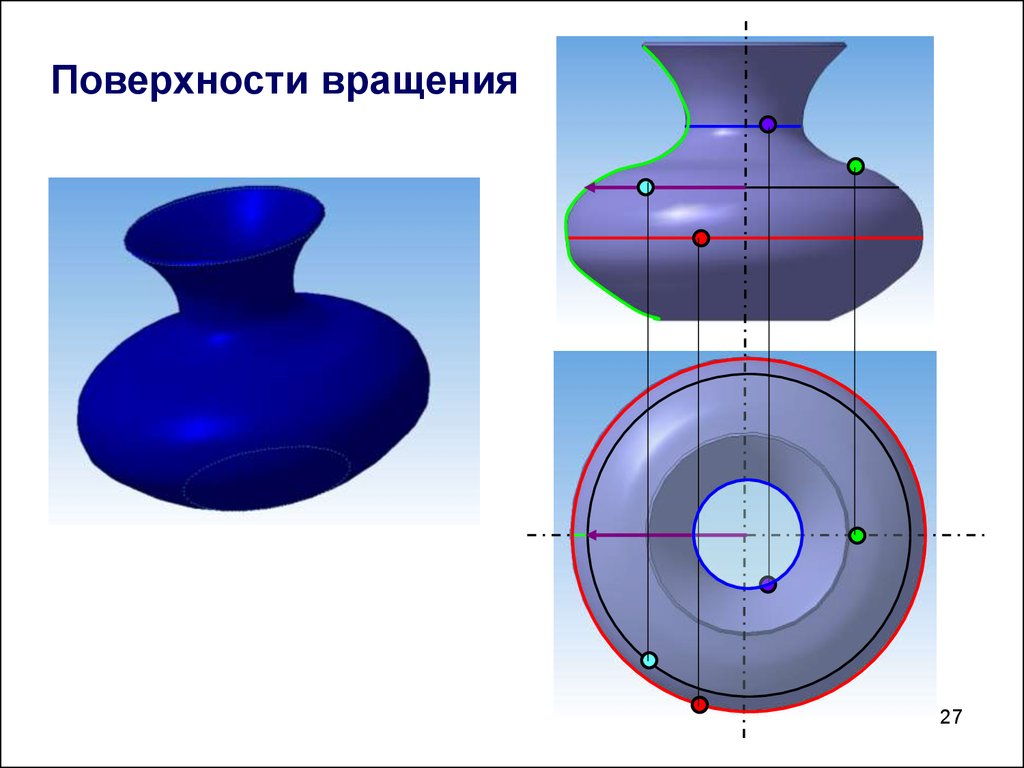
Поверхности вращения27
28. Цилиндр
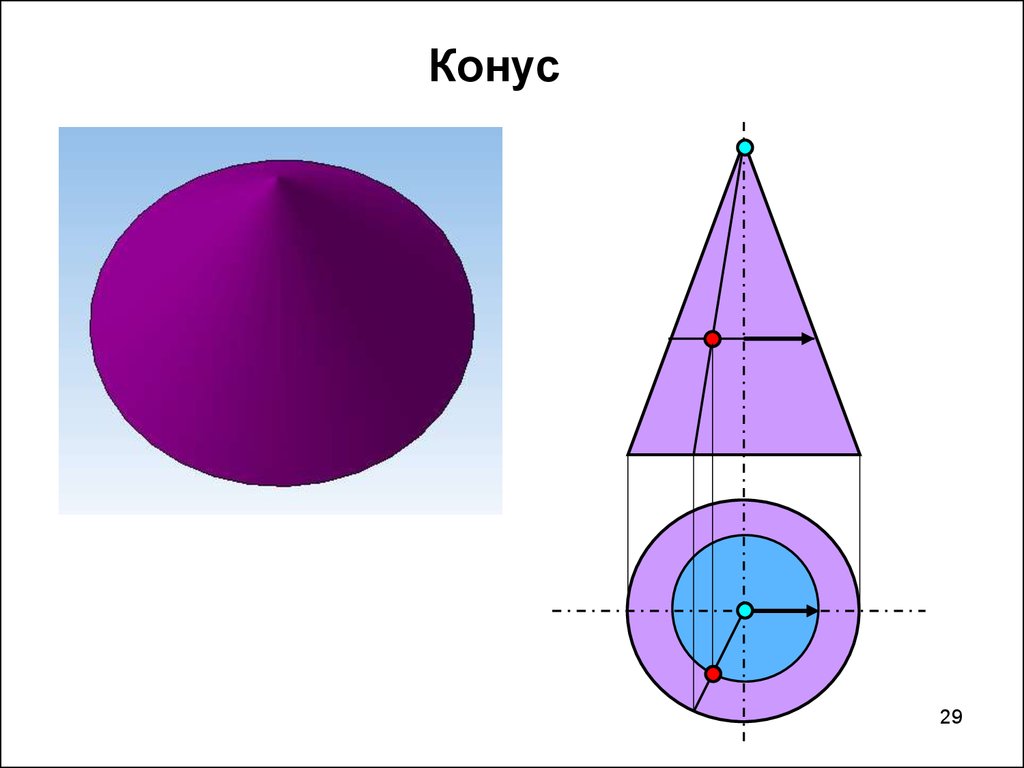
2829. Конус
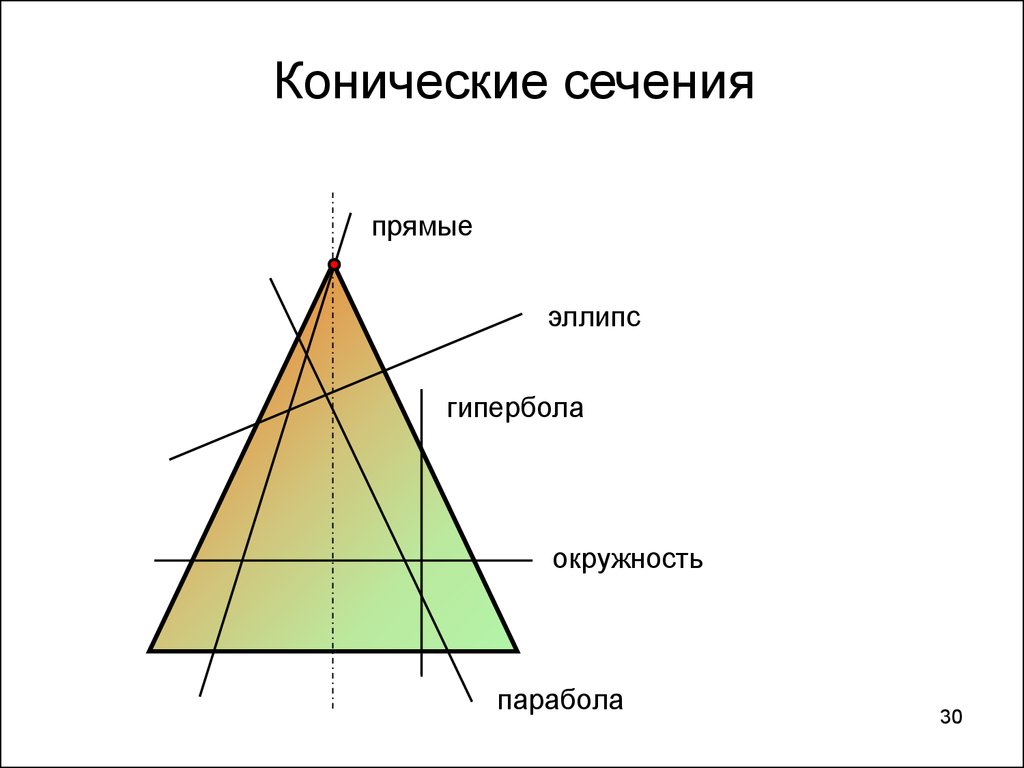
2930. Конические сечения
прямыеэллипс
гипербола
окружность
парабола
30
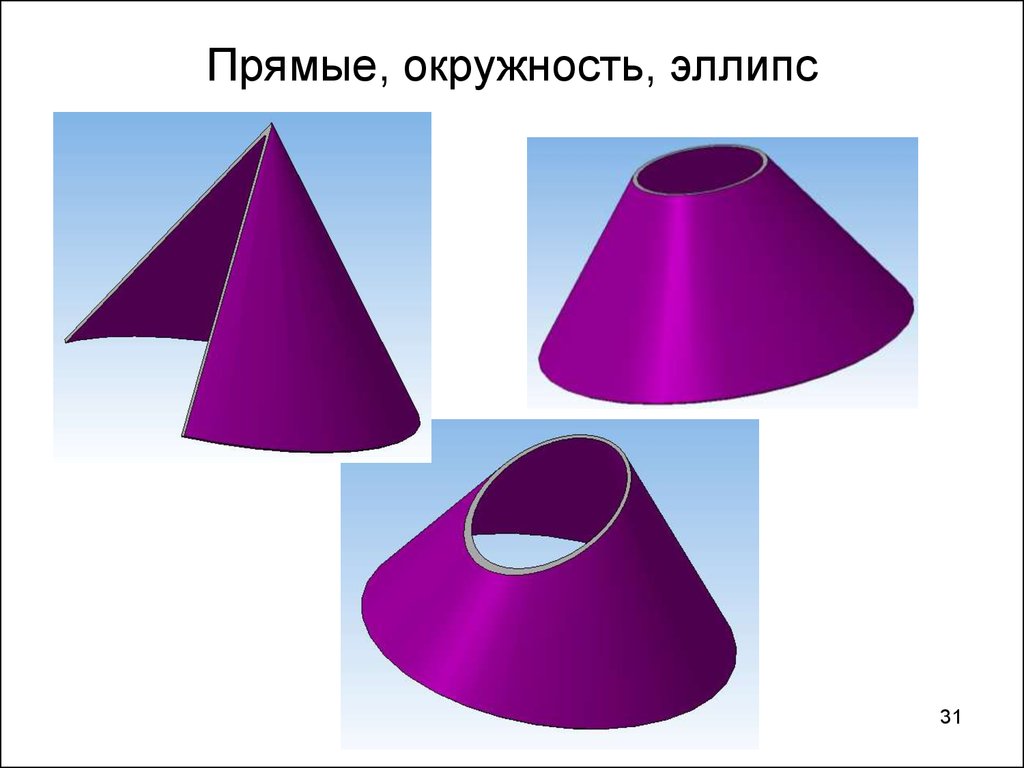
31. Прямые, окружность, эллипс
3132. Парабола
3233. Гипербола
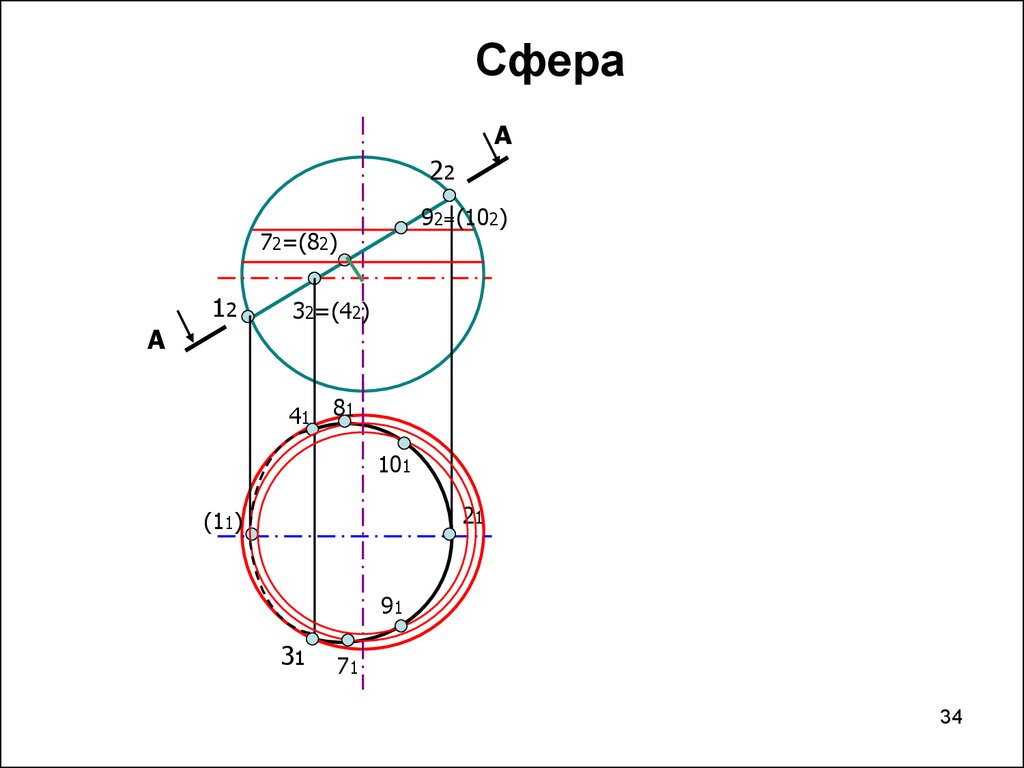
3334. Сфера
А22
92=(102)
72=(82)
12
А
32=(42)
41 81
101
21
(11)
91
31
71
34
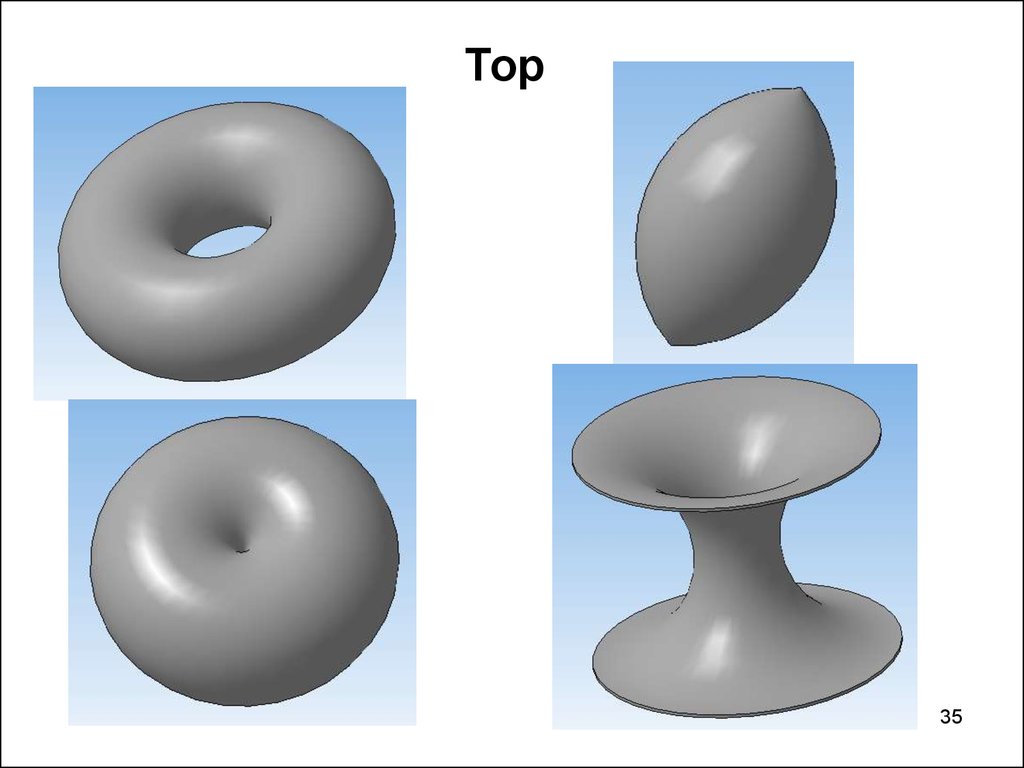
35.
Тор35













 drafting
drafting








